Wurzelfunktionen
Definition
Die Funktion  mit
mit ![\(f(x)=\sqrt[n]{x}\)](https://www.schullv.de/resources/formulas/2aedae08bb55ff63a35c71a2dc3b2d39325b46b77f02f63b6d63324285f3de7b_light.svg) mit
mit 
 und
und 
 heißt Wurzelfunktion.
Beispiele:
Quadratwurzelfunktion:
heißt Wurzelfunktion.
Beispiele:
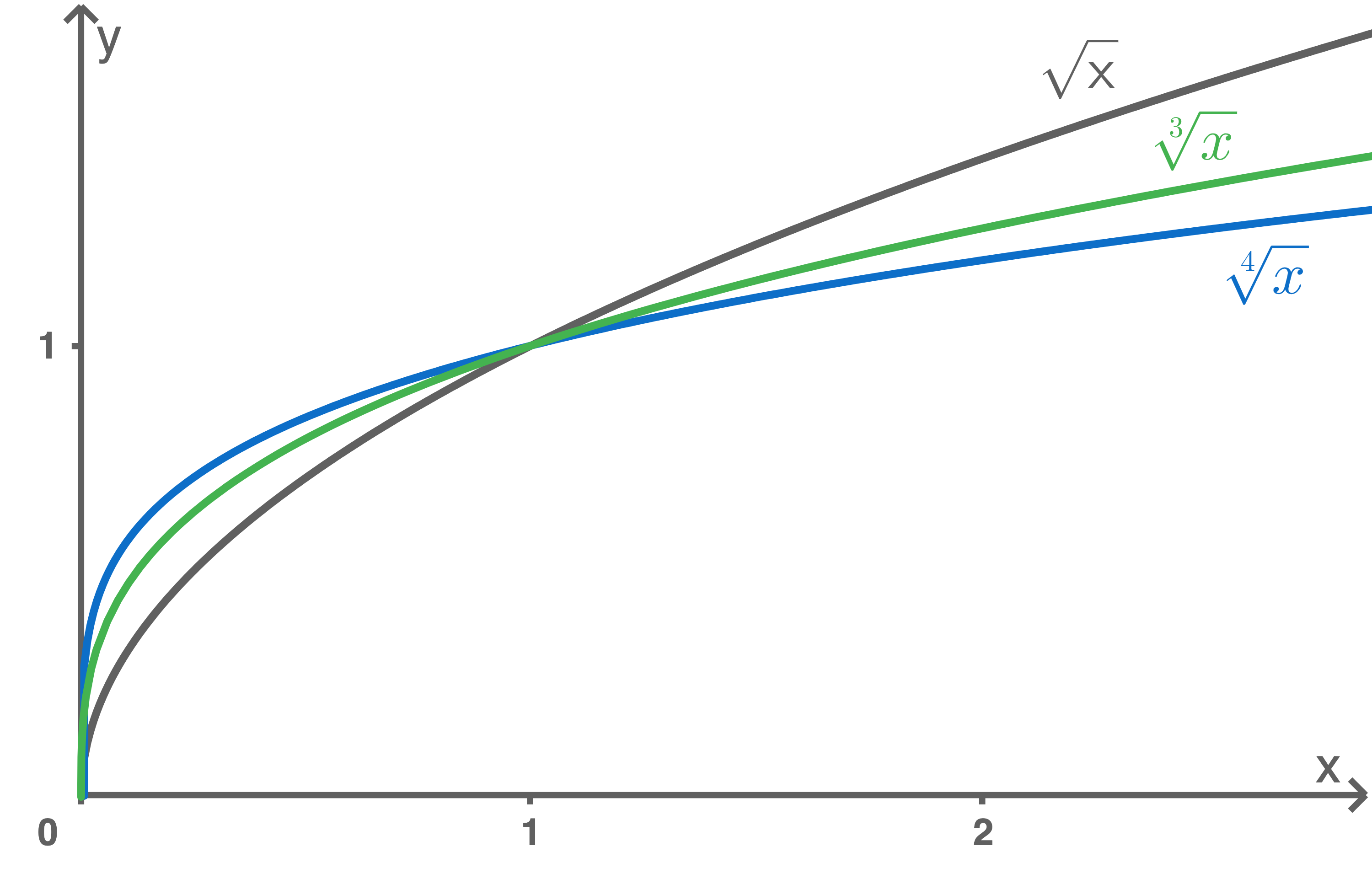
Quadratwurzelfunktion:  Kubikwurzelfunktion:
Kubikwurzelfunktion: ![\(f(x)=\sqrt[3]{x}\)](https://www.schullv.de/resources/formulas/66969a667e5fff593e8420143978eb87156d8c28d2e9a8f24f0bb0f5887e8ca8_light.svg)
Inverse Funktion
Eine Funktion
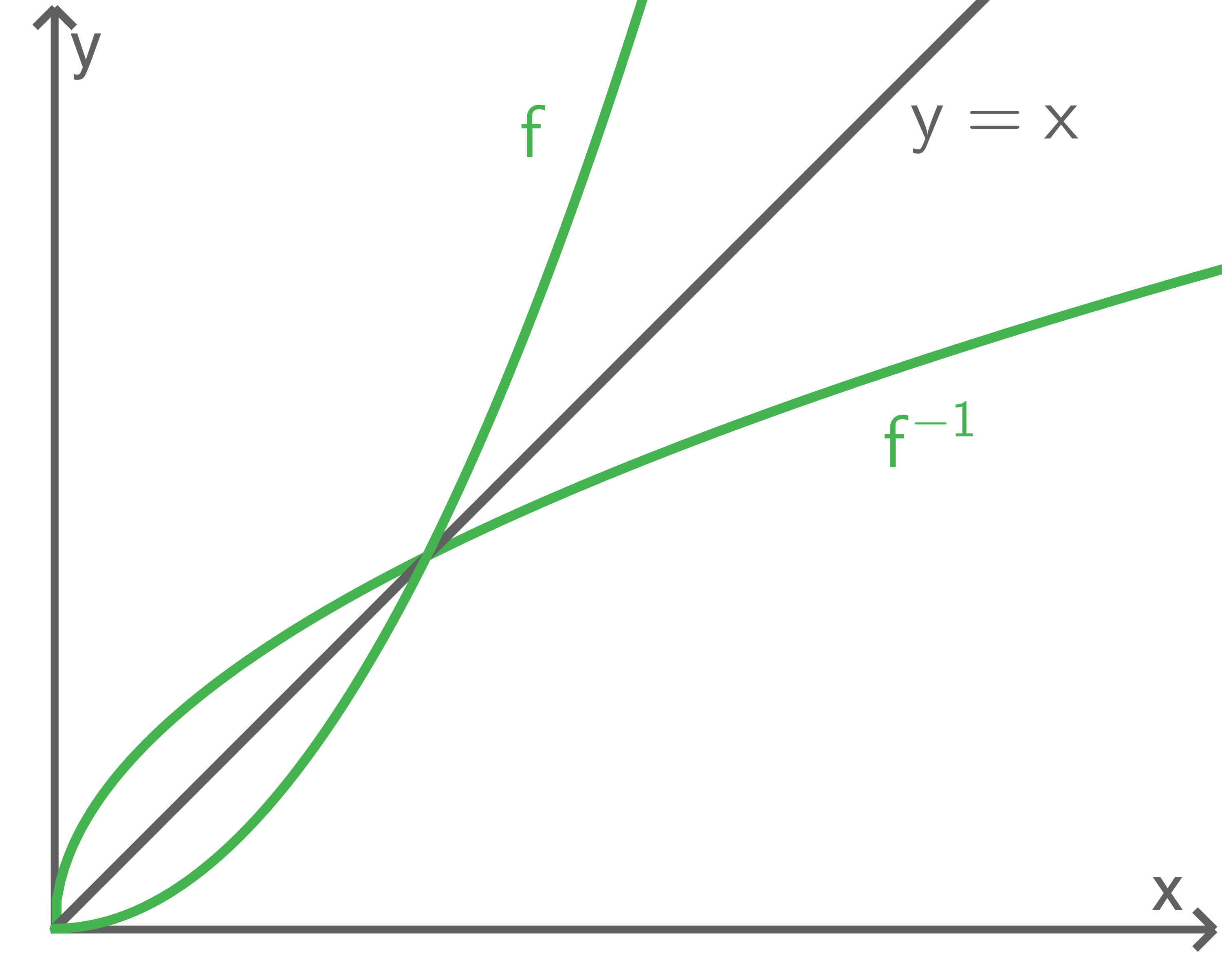
Die inverse Funktion zur Quadratfunktion  mit
mit  ist durch
ist durch  gegeben.
Da beispielsweise dem Wert
gegeben.
Da beispielsweise dem Wert  der Quadratfunktion die
der Quadratfunktion die  -Werte
-Werte  und
und  zugeordnet werden können, ist die Einschränkung
zugeordnet werden können, ist die Einschränkung  notwendig, da sonst keine eindeutige Zuordnung möglich ist.
notwendig, da sonst keine eindeutige Zuordnung möglich ist.
1
Erstelle eine geeignete Wertetabelle und skizziere den Graphen der Wurzelfunktion.






a)
b)
c)
d)
e)
f)
2
Die angegebenen Punkte liegen auf dem Graphen der Funktionsgleichung. Bestimme die fehlenden Koordinaten.




![\(y=\sqrt[3]{x}\quad\)](https://www.schullv.de/resources/formulas/0b96e7f1a5aefc9d72b63195ccd7d129436126adba9a881bbf4419553bc1e189_light.svg)



a)
b)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
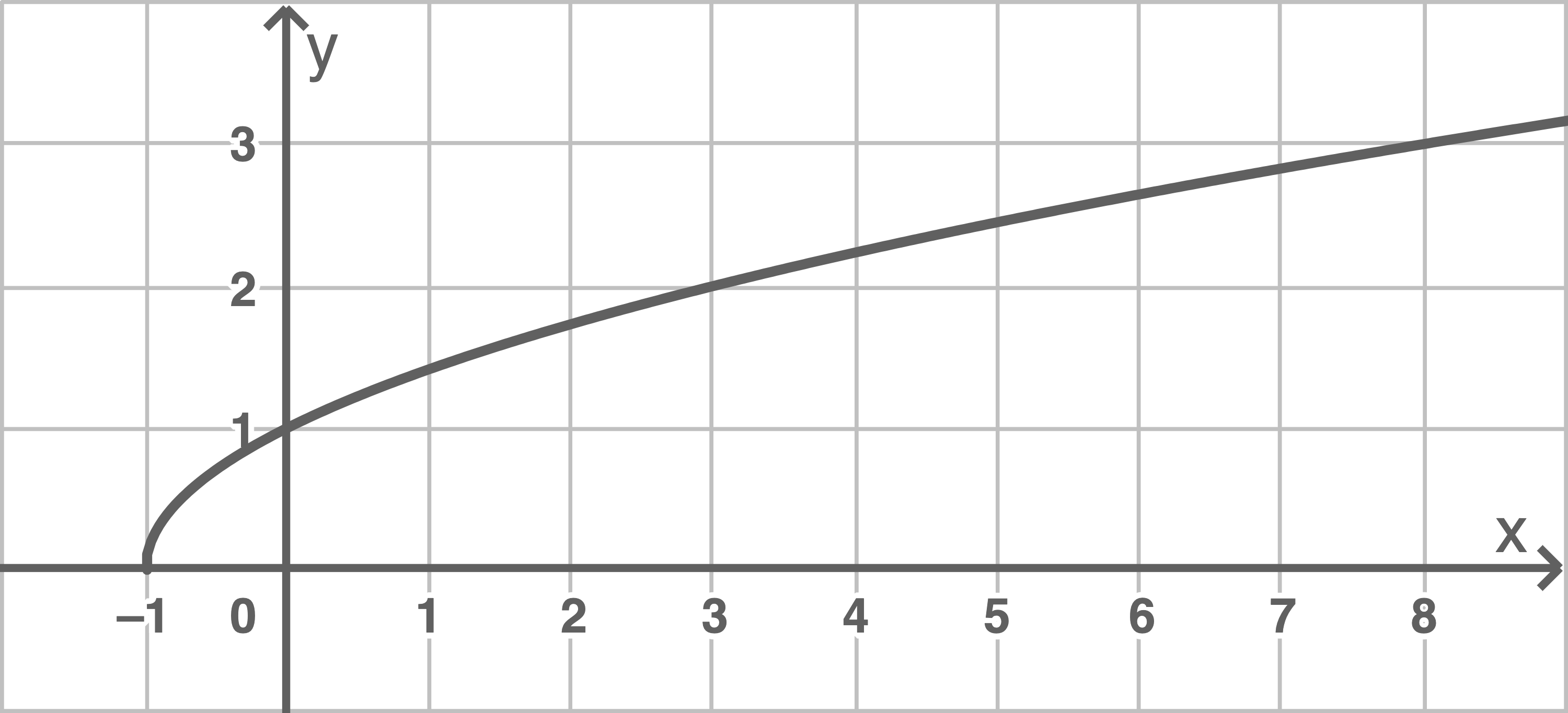
a)
| -1 | 0 | 3 | 8 | |
| 0 | 1 | 2 | 3 |
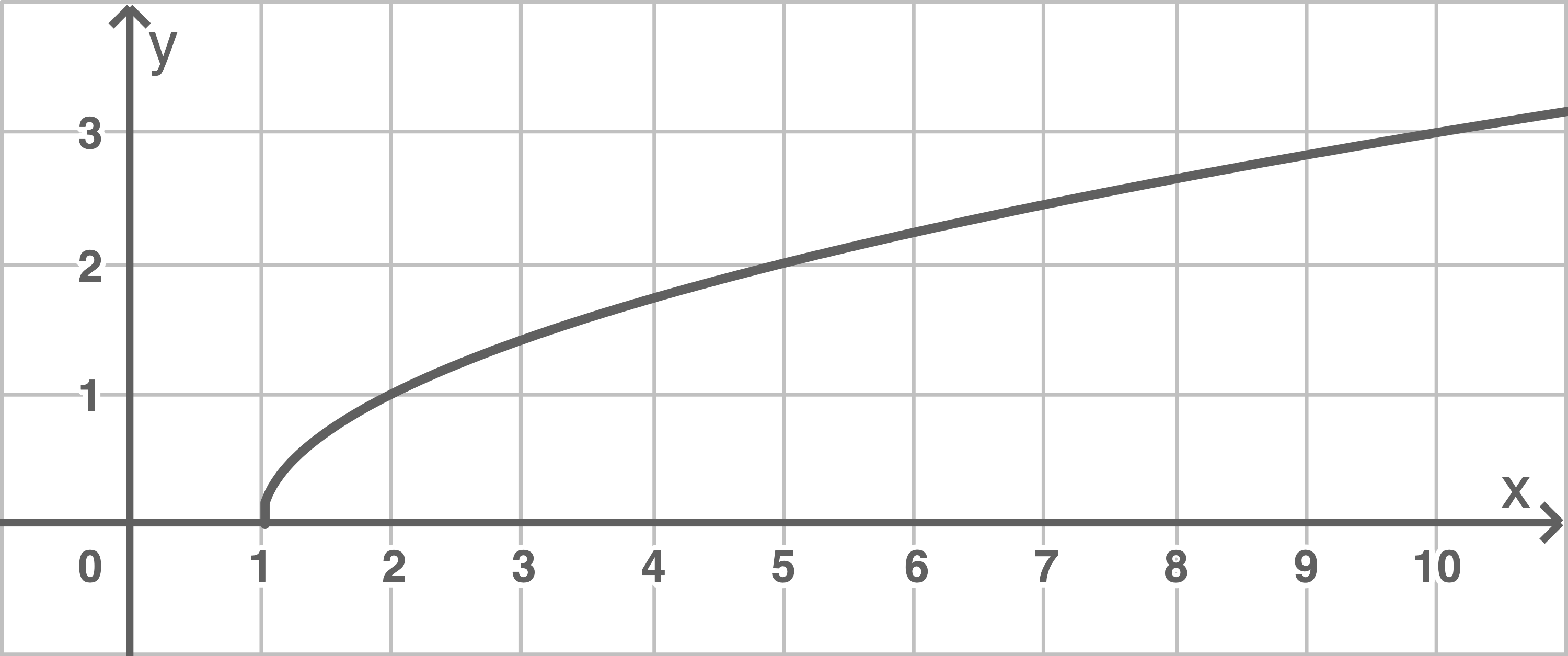
b)
| 1 | 2 | 5 | 10 | |
| 0 | 1 | 2 | 3 |
c)
| 0 | 1 | 4 | 9 | |
| 1 | 2 | 3 | 4 |
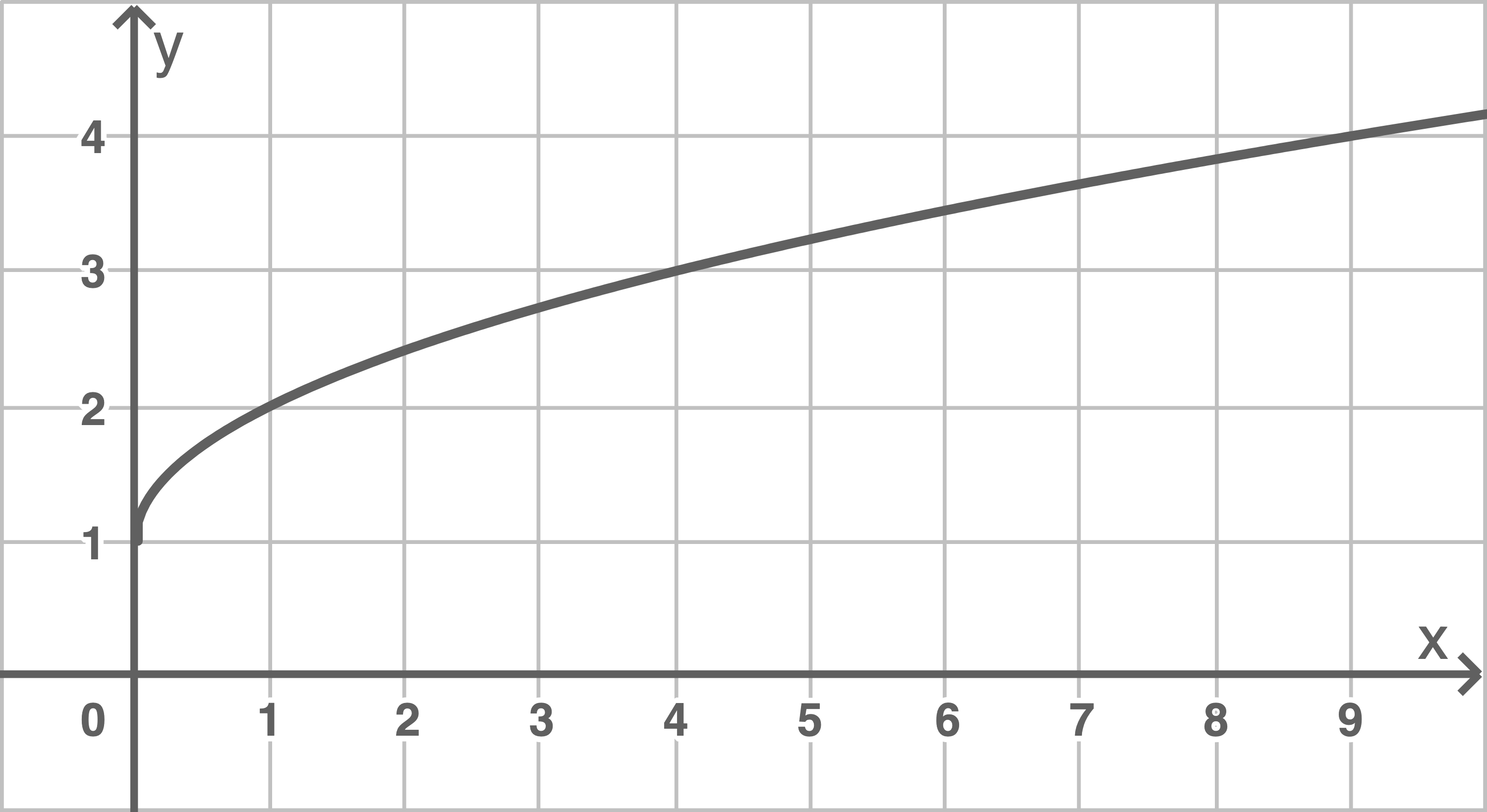
d)
| 0 | 1 | 4 | 9 | |
| -1 | 0 | 1 | 2 |
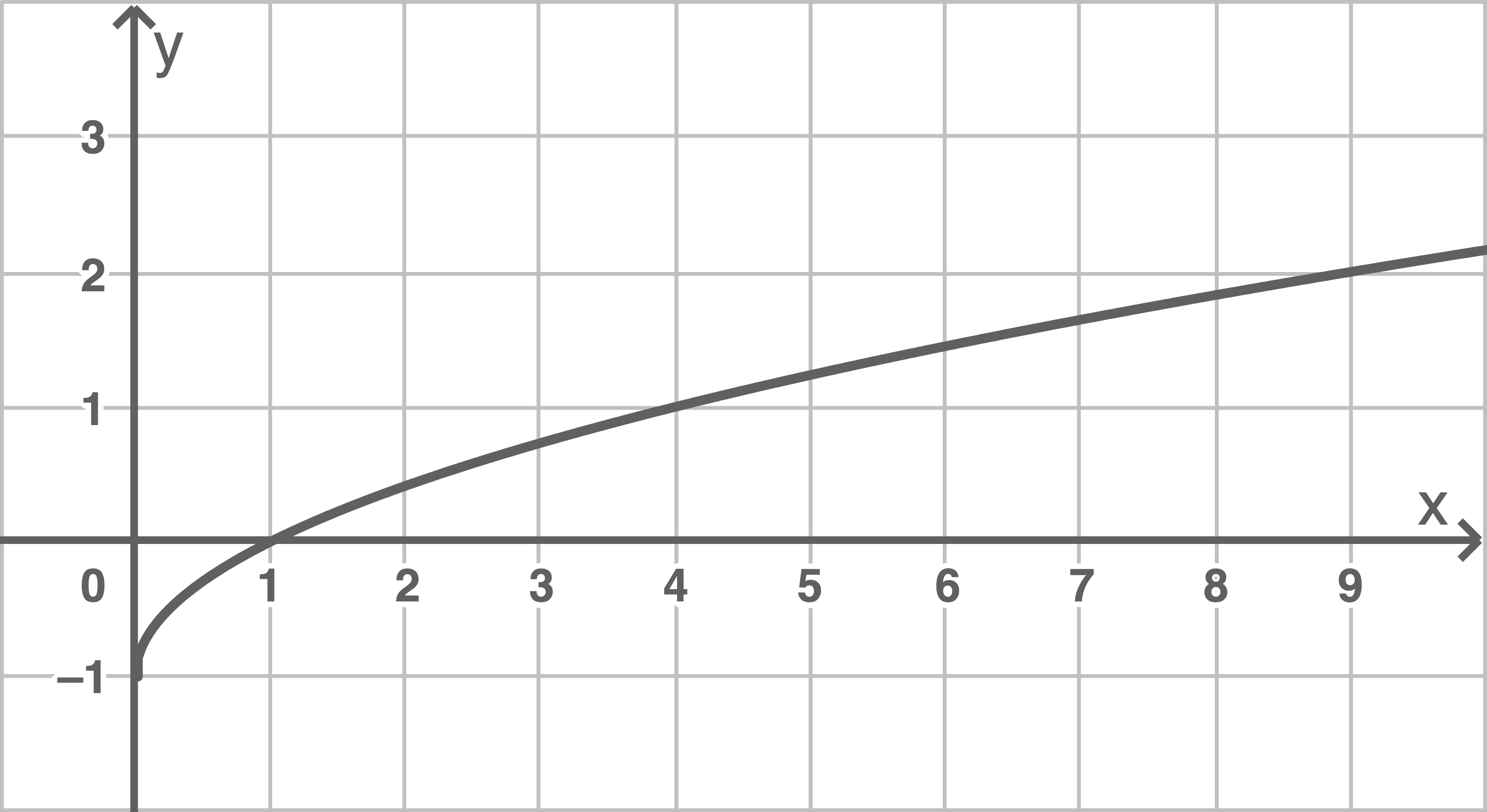
e)
| 0 | 1 | 4 | 9 | |
| 0 | 2 | 4 | 6 |
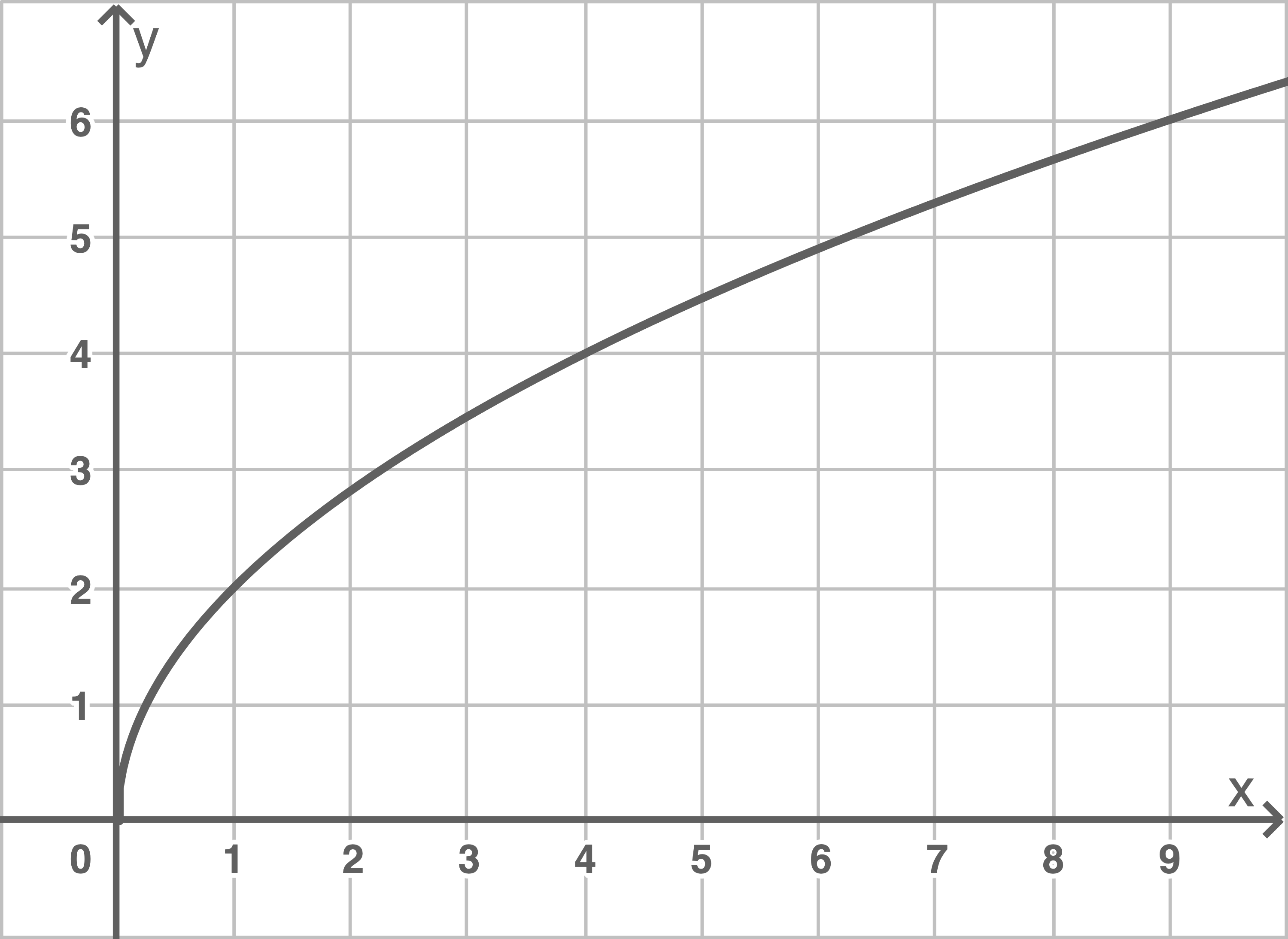
f)
| 0 | 1 | 4 | 9 | |
| 0 | -2 | -4 | -6 |
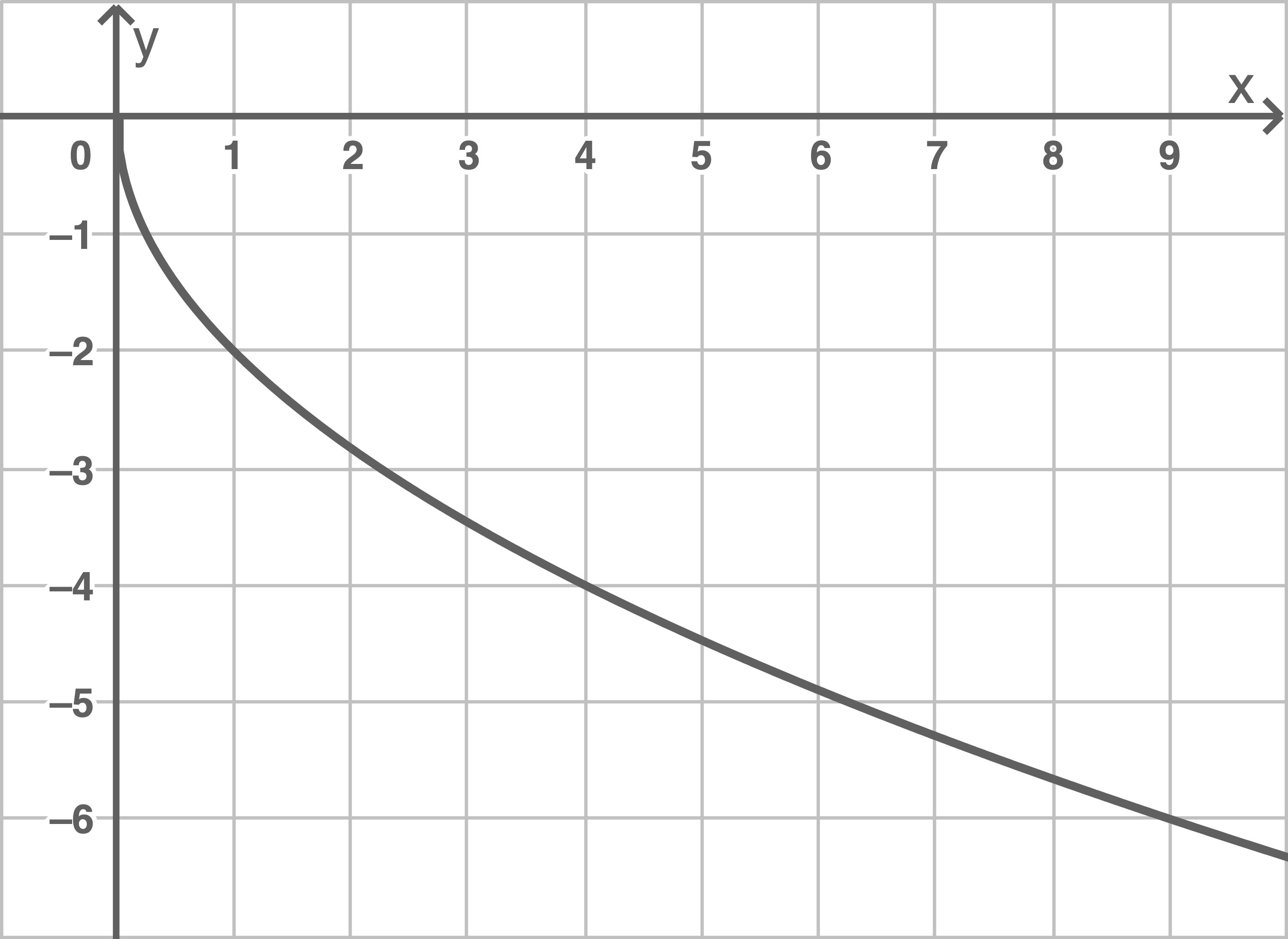
2
a)
b)