Wahlteil B

Aufgabe 1

Im Rechteck $ABCD$ liegt das Drachenviereck $EGCF.$

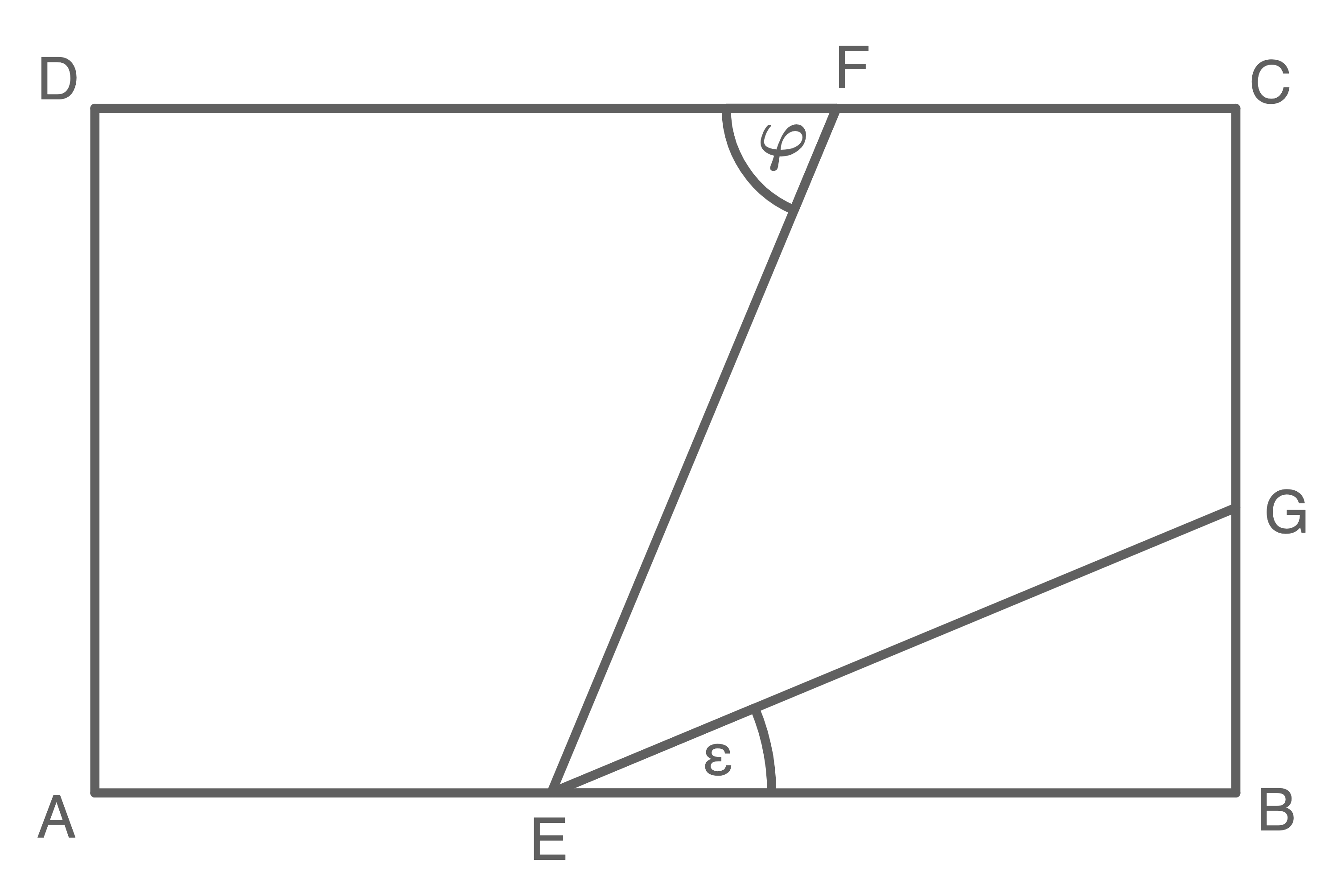
Es gilt:

$\begin{array}[t]{rll} \overline{AB} & =& 9,4 \,\text{cm} \\ \overline{BE} & =& 5,6 \,\text{cm} \\ \varepsilon & =& 20,0^{\circ} \end{array}$

Berechne den Winkel $\varphi.$
Berechne den Umfang des Vierecks $AEFD.$

baden württemberg realschule abschlussprüfung 2024

(5 P)

Die Parabeln $p_1$ und $p_2$ sind zwei nach oben geöffnete verschobene Normalparabeln.
Die Parabel $p_1$ hat den Scheitelpunkt $S_1(1 \mid 1).$
Die Parabel $p_2$ schneidet die $x$ -Achse in den Punkten $N_1(-6 \mid 0)$ und $N_2(-2 \mid 0).$

Bestimme die Funktionsgleichungen von $p_1$ und $p_2$ .

Die Gerade $g$ verläuft durch den Scheitelpunkt $S_1$ und den Punkt $A(2 \mid-1).$

Berechne die Funktionsgleichung von $g.$

Der Punkt $S_2$ ist der Scheitelpunkt der Parabel $p_2.$

Berechne die Entfernung zwischen $S_1$ und $S_2.$

Milo behauptet: „Die Parabeln $p_1$ und $p_2$ sowie die Gerade $g$ schneiden sich in einem gemeinsamen Punkt.“

Überprüfe diese Behauptung. Begründe deine Antwort rechnerisch.

(5 P)

Aufgabe 2

Die Gerade $g$ hat die Funktionsgleichung $y=-x-3.$
Sie schneidet die $x$ -Achse im Punkt $A$ und die $y$ -Achse im Punkt $B.$

Bestimme die Koordinaten der Punkte $A$ und $B$ .

Durch die Punkte $A$ und $B$ verläuft die nach oben geöffnete verschobene Normalparabel $p.$

Berechne die Funktionsgleichung der Parabel $p$ und die Koordinaten ihres Scheitelpunktes $S.$

Die beiden Punkte $P(x_P \mid 12)$ und $Q(x_Q \mid 12)$ liegen auf der Parabel $p.$
Sie bilden zusammen mit dem Scheitelpunkt $S$ das Dreieck $PSQ.$

Berechne den Flächeninhalt des Dreiecks $PSQ.$

(5 P)

Die Abbildung zeigt den Achsenschnitt eines zusammengesetzten Körpers und den Parallelschnitt einer quadratischen Pyramide.
Der zusammengesetzte Körper besteht aus einer Halbkugel und einem Kegel.

Es gilt:

$\begin{array}[t]{rll} s & =& 14,4 \mathrm{~cm} \\ \delta & =& 42,0^{\circ} \\ h_{\text {ges }} & =& h_{\text {Pyr }} \end{array}$

Der Durchmesser $d$ des zusammengesetzten Körpers ist genauso lang wie die Grundkante $a$ der quadratischen Pyramide.

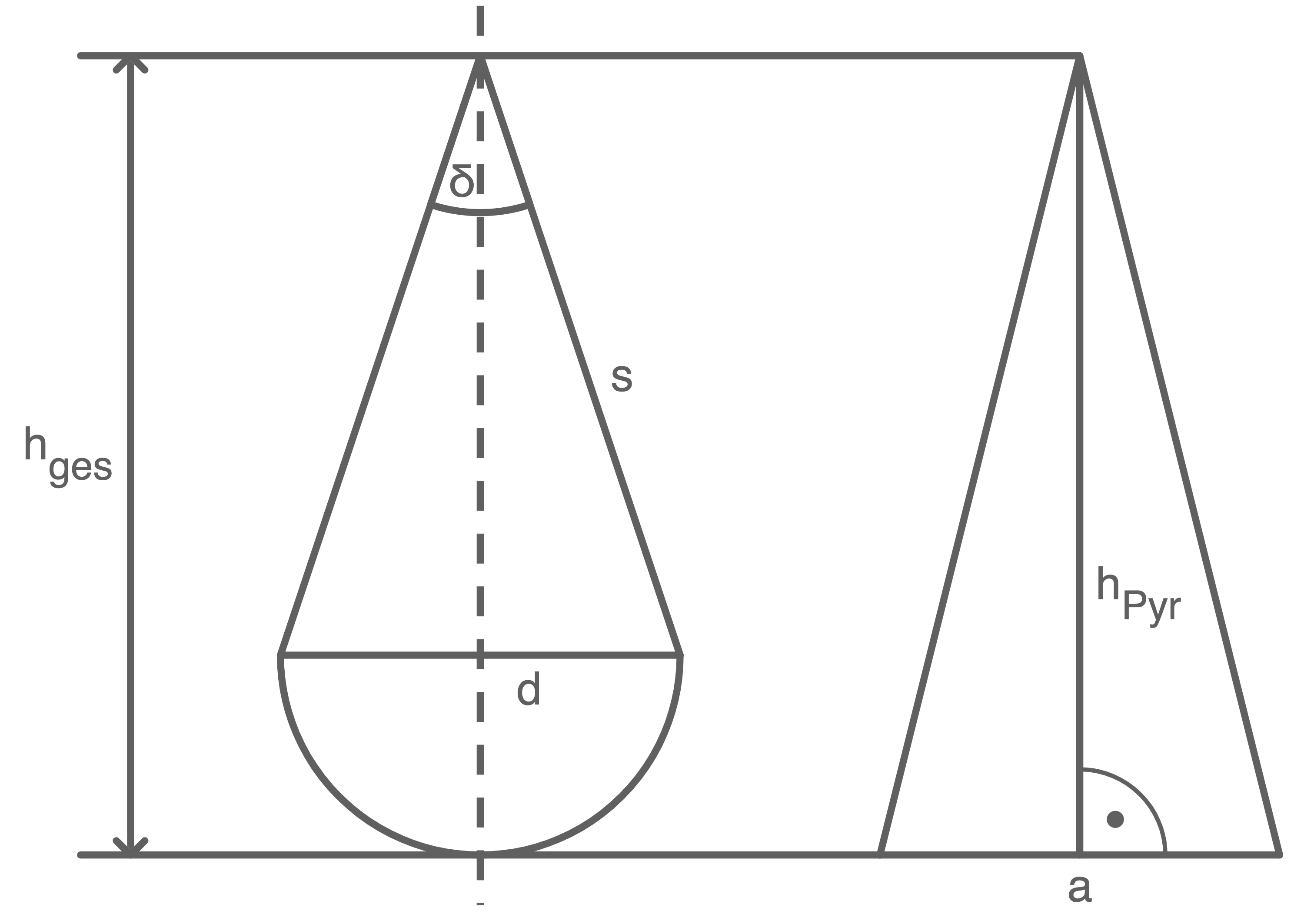
Berechne die Differenz der Oberflächeninhalte der beiden Körper.

(5 P)

Aufgabe 3

Beim Schulfest bietet die Klasse 10a ein Angelspiel an. Dabei dürfen die Spieler zweimal nacheinander einen Gegenstand aus einem Gefäß angeln. Die Gegenstände werden nicht zurückgelegt. In dem Gefäß liegen fünf Fische, drei Seesterne und zwei Muscheln.

Berechne die Wahrscheinlichkeit für das Ereignis „zweimal Muschel“.

Für ein Glückspiel wird der gegebene Gewinnplan eingesetzt.

Ereignis	Gewinn
zweimal Muschel	9,00 €
zweimal Seestern	4,00 €
Muschel und Seestern	2,50 €
Einsatz 1,00 €

Berechne den Erwartungswert.

Der Gewinnplan soll so verändert werden, dass das Spiel fair wird. Dazu soll der Gewinn von „zweimal Muschel“ verändert werden, während alles andere unverändert bleibt.

Wie hoch muss der Gewinn für „zweimal Muschel“ sein?

(5 P)

Die Vorderseite einer Tennishalle hat annähernd die Form einer Parabel.
Sie lässt sich mit der Funktionsgleichung $y=a x^2+c$ beschreiben.

Die maximale Höhe der Halle beträgt $12\,\text{m}.$ Die Halle hat am Boden eine Breite von $40 \,\text{m}.$

Gib eine mögliche Funktionsgleichung an.

In die Vorderseite der Tennishalle soll eine rechteckige Fensterfläche mittig eingebaut werden. Dazu werden zwei Vorschläge geprüft.

Vorschlag 1:
Die Fensterfläche soll eine Höhe von $10 \,\text{m}$ haben.
Die beiden oberen Eckpunkte berühren den Parabelbogen (siehe Abbildung).

Berechne den Flächeninhalt dieser Fensterfläche.

Vorschlag 2:
Die Fensterfläche soll eine Breite von $10\,\text{m}$ haben.

Berechne die größtmögliche Höhe dieser Fensterfläche.
Welche der beiden Fensterflächen ist größer? Berechne.

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

Winkel $\boldsymbol{\varphi}$ berechnen

Aufgrund des Symmetrie des Drachenvierecks hat der Winkel $\varphi$ die gleiche Größe wie der Winkel $\sphericalangle BGE.$ Daher gilt:

$\varphi=\sphericalangle BGE=180,0°-90,0°-20,0°$ $=\underline{\underline{70,0°}}$

Umfang des Vierecks $\boldsymbol{AEFD}$ berechnen

1. Schritt: $\boldsymbol{\overline{AD}}$ bestimmen

Aufgrund der Symmetrie des Drachenvierecks gilt $\overline{AD}=\overline{BE}=\underline{5,6\,\text{cm}}.$

2. Schritt: $\boldsymbol{\overline{AE}}$ berechnen

$\overline{AE}=\overline{AB}-\overline{BE}=9,4\,\text{cm}-5,6\,\text{cm}=$ $\underline{3,8\,\text{cm}}$

3. Schritt: $\boldsymbol{\overline{EF}}$ berechnen

Aufgrund der Symmetrie des Drachenvierecks gilt $\overline{EF}=\overline{EG}.$ Damit folgt:

$\begin{array}[t]{rll} \cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EG}} \\[5pt] \cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EF}} \\[5pt] \cos 20,0°&=& \dfrac{5,6\,\text{cm}}{\overline{EF}} \quad \scriptsize \mid\;\cdot \overline{EF} \\[5pt] \cos 20,0°\cdot \overline{EF}&=& 5,6\,\text{cm} \quad \scriptsize \mid\; :\cos 20,0°\\[5pt] \overline{EF}&=& \dfrac{5,6\,\text{cm}}{\cos 20,0°} \\[5pt] \overline{EF}&=& \underline{5,96\,\text{cm}} \end{array}$

4. Schritt: $\boldsymbol{\overline{DF}}$ berechnen

Zunächst muss die Länge der Strecke $\overline{BG}$ berechnet werden:

Rechenweg anzeigen

$\overline{BG}=2,04\,\text{cm}$

Damit folgt für die Länge der Strecke $\overline{CF}:$

$\begin{array}[t]{rll} \overline{CF}&=& \overline{CG} \\[5pt] &=& \overline{AD}-\overline{BG} \\[5pt] &=& 5,6\,\text{cm}-2,04\,\text{cm} \\[5pt] &=& 3,56\,\text{cm} \end{array}$

Insgesamt gilt dann für die Strecke $\overline{DF}:$

$\begin{array}[t]{rll} \overline{DF}&=& \overline{AB}-\overline{CF} \\[5pt] &=& 9,4\,\text{cm}-3,56\,\text{cm} \\[5pt] &=& \underline{5,84\,\text{cm}} \end{array}$

5. Schritt: Umfang berechnen

Rechenweg anzeigen

$u= \underline{\underline{21,2\,\text{cm}}}$

Funktionsgleichungen von $\boldsymbol{p_1}$ und $\boldsymbol{p_2}$ bestimmen

$p_1:y=(x-1)^2+1=\underline{\underline{x^2-2x+2}}$

$p_2:y=(x+6)(x+2)=\underline{\underline{x^2+8x+12}}$

Funktionsgleichung von $\boldsymbol{g}$ berechnen

Steigung $m$ berechnen:

$m=\dfrac{y_A-y_{S_1}}{x_A-x_{S_1}}=\dfrac{-1-1}{2-1}=-2$

Die allgemeine Geradengleichung hat die Form $y=m\cdot x+c.$ Einsetzen von $m$ und der Koordinaten des Punktes $S_1(1\mid 1)$ liefert:

$\begin{array}[t]{rll} 1&=& -2\cdot 1+c \quad \scriptsize \mid\; +2\\[5pt] 3&=& c \end{array}$

Daraus folgt $\underline{\underline{g:y=-2x+3}}.$

Entfernung zwischen $\boldsymbol{S_1}$ und $\boldsymbol{S_2}$ berechnen

Zunächst müssen die Koordinaten von $S_2$ bestimmt werden. Dazu wird die Funktionsgleichung $p_2$ in Scheitelpunktform gebracht:

$\begin{array}[t]{rll} y&=& x^2+8x+12 \\[5pt] &=& x^2+8x+16-16+12 \\[5pt] &=& (x+4)^2-4 \end{array}$

Es lässt sich direkt der Scheitelpunkt $S_2(-4\mid -4)$ ablesen.

Nun lässt sich der Abstand der beiden Scheitelpunkte berechnen:

$\begin{array}[t]{rll} \overline{S_1S_2}&=& \sqrt{(1-(-4))^2+(1-(-4))^2} \\[5pt] &=& \sqrt{50} \\[5pt] &=& \underline{\underline{7,07\,\text{[LE]}}} \end{array}$

Behauptung überprüfen

Schnittpunkt der Parabeln berechnen:

$\begin{array}[t]{rll} x^2-2x+2&=& x^2+8x+12 \quad \scriptsize \mid\; -x^2 \\[5pt] -2x+2&=& 8x+12 \quad \scriptsize \mid\; +2x \\[5pt] 2&=& 10x+12 \quad \scriptsize \mid\; -12 \\[5pt] -10&=& 10x \quad \scriptsize \mid\; :10 \\[5pt] -1&=& x \end{array}$

Zugehörigen $y$ -Wert berechnen:

$y=(-1)^2-2\cdot (-1)+2=5$

Die beiden Parabeln schneiden sich im Punkt $P(-1\mid 5).$ Mit der Punktprobe kann überprüft werden, ob dieser Punkt auch auf der Geraden $g$ liegt:

$\begin{array}[t]{rll} 5&=& -2\cdot (-1)+3 \\[5pt] 5&=& 5 \end{array}$

Die Aussage ist wahr. Somit schneiden sich die drei Graphen in einem gemeinsamen Punkt, die Behauptung stimmt also.

Lösung 2

Koordinaten bestimmen

Schnittpunkt mit $x$ -Achse bestimmen:

$\begin{array}[t]{rll} 0&=& -x-3 \quad \scriptsize \mid\;+x \\[5pt] x&=& -3 \end{array}$

$\underline{\underline{A(-3 \mid 0)}}$

Schnittpunkt mit $y$ -Achse bestimmen:

$y=-0-3=-3$

$\underline{\underline{B(0\mid -3)}}$

Funktionsgleichung und Scheitelpunkt berechnen

Die verschobene Normalparabel ist von der Form $p:y=x^2+ax+c.$ Einsetzen der Koordinaten des Punktes $B(0\mid -3)$ liefert:

$\begin{array}[t]{rll} -3&=& 0^2+a\cdot 0+c \\[5pt] -3&=& c \end{array}$

Es gilt also $p:y=x^2+ax-3.$ Einsetzen der Koordinaten des Punktes $A(-3\mid 0)$ liefert:

$\begin{array}[t]{rll} 0&=& (-3)^2+a\cdot (-3)-3 \\[5pt] 0&=& 6-3a \quad \scriptsize \mid\; +3a \\[5pt] 3a&=& 6 \quad \scriptsize \mid\; :3 \\[5pt] a&=& 2 \end{array}$

Insgesamt gilt also $\underline{\underline{p:y=x^2+2x-3}}.$

Umformen in die Scheitelpunktform liefert schließlich den Scheitelpunkt:

$\begin{array}[t]{rll} y&=& x^2+2x-3 \\[5pt] &=& x^2+2x+1-1-3 \\[5pt] &=& (x+1)^2-4 \end{array}$

Nun lässt sich der Scheitelpunkt $\underline{\underline{S(-1\mid -4)}}$ ablesen.

Flächeninhalt des Dreiecks berechnen

$\begin{array}[t]{rll} 12&=& x_{P/Q}^2+2x_{P/Q}-3 \quad \scriptsize \mid\; -12 \\[5pt] 0&=& x_{P/Q}^2+2x_{P/Q}-15 \end{array}$

$\begin{array}[t]{rll} x_{P/Q}&=& -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt] &=& -\dfrac{2}{2}\pm\sqrt{\left(\dfrac{2}{2}\right)^2-(-15)} \\[5pt] &=& -1\pm 4 \\[5pt] x_P&=& 3 \\[5pt] x_Q&=& -5 \end{array}$

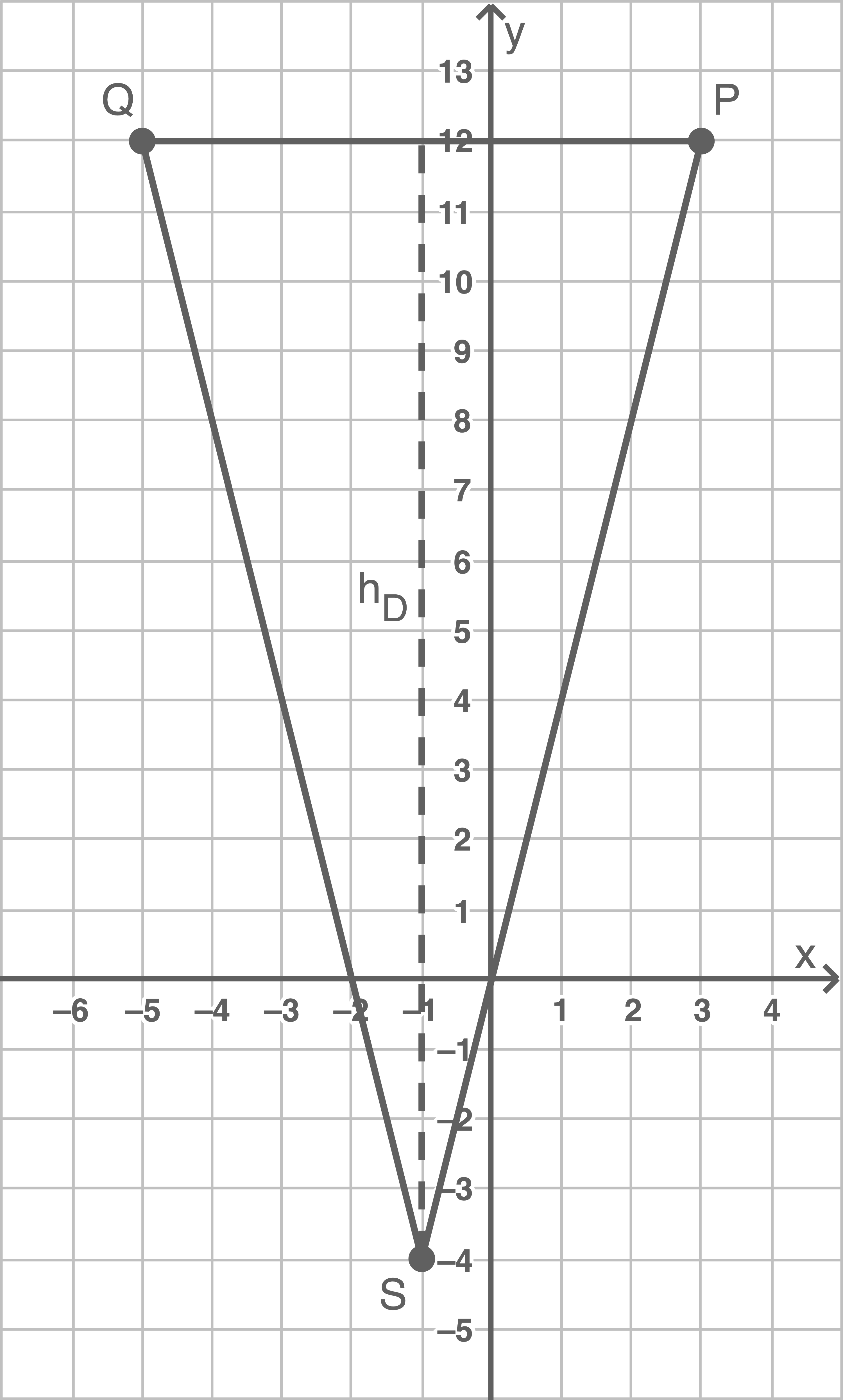Mithilfe der Skizze lässt sich die Länge der Grundseite $g=8$ und die Höhe $h=16$ des Dreiecks ablesen. Damit folgt für den Flächeninhalt des Dreiecks:

$\begin{array}[t]{rll} A&=& \dfrac{1}{2}\cdot 16\cdot 8 \\[5pt] &=& \underline{\underline{64\,\text{[FE]}}} \end{array}$

1. Schritt: Radius $\boldsymbol{r}$ berechnen

Rechenweg anzeigen

$r=\underline{5,16\,\text{cm}}$

2. Schritt: $\boldsymbol{h_{\textbf{Ke}}}$ berechnen

$\begin{array}[t]{rll} \tan \dfrac{\delta}{2}&=& \dfrac{r}{h_\text{Ke}} \\[5pt] \tan 21,0°&=& \dfrac{5,16\,\text{cm}}{h_\text{Ke}} \quad \scriptsize \mid\;\cdot h_\text{Ke} \\[5pt] \tan 21,0°\cdot h_\text{Ke}&=& 5,16\,\text{cm} \quad \scriptsize \mid\; :\tan 21,0° \\[5pt] h_\text{Ke}&=& \dfrac{5,16\,\text{cm}}{\tan 21,0°} \\[5pt] h_\text{Ke}&=& \underline{13,44\,\text{cm}} \end{array}$

3. Schritt: $\boldsymbol{h_{\textbf{Pyr}}}$ berechnen

$\begin{array}[t]{rll} h_{\text{Pyr}}&=& h_{\text{Ke}}+r \\[5pt] &=& 13,44\,\text{cm}+5,16\,\text{cm} \\[5pt] &=& \underline{18,60\,\text{cm}} \end{array}$

4. Schritt: Höhe $\boldsymbol{h_s}$ der Seitenflächen der Pyramide berechnen

$\begin{array}[t]{rll} h_s^2&=& h_\text{Pyr}^2+\left(\dfrac{a}{2}\right)^2 \\[5pt] h_s^2&=& (18,60\,\text{cm})^2+(5,16\,\text{cm})^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt] h_s&=& \sqrt{(18,60\,\text{cm})^2+(5,16\,\text{cm})^2} \\[5pt] h_s&=& \underline{19,30\,\text{cm}} \end{array}$

5. Schritt: Differenz der Oberflächeninhalte berechnen

Rechenweg anzeigen

$O_\text{zgs}=\underline{401\,\text{cm}^2}$

Rechenweg anzeigen

$O_\text{Pyr}=\underline{505\,\text{cm}^2}$

$\begin{array}[t]{rll} O_\text{Diff}&=& 505\,\text{cm}^2-401\,\text{cm}^2 \\[5pt] &=& \underline{\underline{104\,\text{cm}^2}} \end{array}$

Lösung 3

Wahrscheinlichkeit für Ereignis berechnen

Es sind insgesamt $5+3+2$ Gegenstände.

Rechenweg anzeigen

$P(\text{zweimal Muschel})=\underline{\underline{2,2\,\%}}$

Erwartungswert berechnen

$P(\text{zweimal Muschel})=\underline{\dfrac{1}{45}}$

$P(\text{zweimal Seestern})=\dfrac{3}{10}\cdot \dfrac{2}{9}=\dfrac{6}{90}$ $=\underline{\dfrac{1}{15}}$

Rechenweg anzeigen

$P(\text{Muschel und Seestern})=\underline{\dfrac{2}{15}}$

Rechenweg anzeigen

$E=\underline{\underline{-0,20\,\text{€}}}$

Gewinn für „zweimal Muschel“ berechnen

Neuen Preis $x$ für Gewinn für „zweimal Muschel“ bei fairem Spiel berechnen:

Rechenweg anzeigen

$18,00 \,\text{€}= x$

Für ein faires Spiel muss der Gewinn für „zweimal Muschel“ $\underline{\underline{18,00 \,\text{€}}}$ betragen.

Funktionsgleichung angeben

Die Parabel hat den Scheitelpunkt $S(0\mid 12).$ Einsetzen der Koordinaten des Punktes in die allgemeine Funktionsgleichung liefert:

$\begin{array}[t]{rll} 12&=& a\cdot 0^2+c \\[5pt] 12&=& c \end{array}$

Außerdem kommt die Halle im Punkt $P(20\mid 0)$ auf dem Boden auf. Einsetzen der Koordinaten liefert weiter:

$\begin{array}[t]{rll} 0&=& a\cdot 20^2+12 &\quad \scriptsize \mid\; -12 \\[5pt] -12&=& a\cdot 400 &\quad \scriptsize \mid\; :400 \\[5pt] -0,03&=& a \end{array}$

Eine mögliche Funktionsgleichung lautet:

$\underline{\underline{y=-0,03x^2+12}}$

Flächeninhalt der Fensterfläche berechnen

Eckpunkte auf dem Parabelbogen berechnen:

$\begin{array}[t]{rll} -0,03x^2+12&=& 10 \quad \scriptsize \mid\;-12 \\[5pt] -0,03x^2&=& -2 \quad \scriptsize \mid\;:(-0,03) \\[5pt] x^2&=& 66,67 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt] x&=& \pm 8,17 \end{array}$

Die Fensterfläche hat also eine Höhe von $10\,\text{m}$ und eine Breite von $8,17\,\text{m}-(-8,17\,\text{m})=16,34\,\text{m}.$ Für den Flächeninhalt ergibt sich:

$A= 10\,\text{m}\cdot 16,34\,\text{m}=\underline{\underline{163,4\,\text{m}^2}}$

Größtmögliche Höhe berechnen

Da das Fenster symmetrisch zur $y$ -Achse gebaut wird, muss der Funktionswert an der Stelle $x=5$ berechnet werden.

$y=-0,03\cdot 5^2+12=11,25$

Die Fensterfläche könnte höchstens $\underline{\underline{11,25\,\text{m}}}$ hoch sein.

Fensterflächen vergleichen

Fensterfläche bei Vorschlag 2:

$A=11,25\,\text{m}\cdot 10\,\text{m}=112,5\,\text{m}^2\lt 163,4\,\text{m}^2$

Die Fensterfläche von Vorschlag 1 ist größer.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?