Wahlteil B
Aufgabe 1
a)
Gegeben sind das rechtwinklige Dreieck  und das gleichschenklige Dreieck
und das gleichschenklige Dreieck 
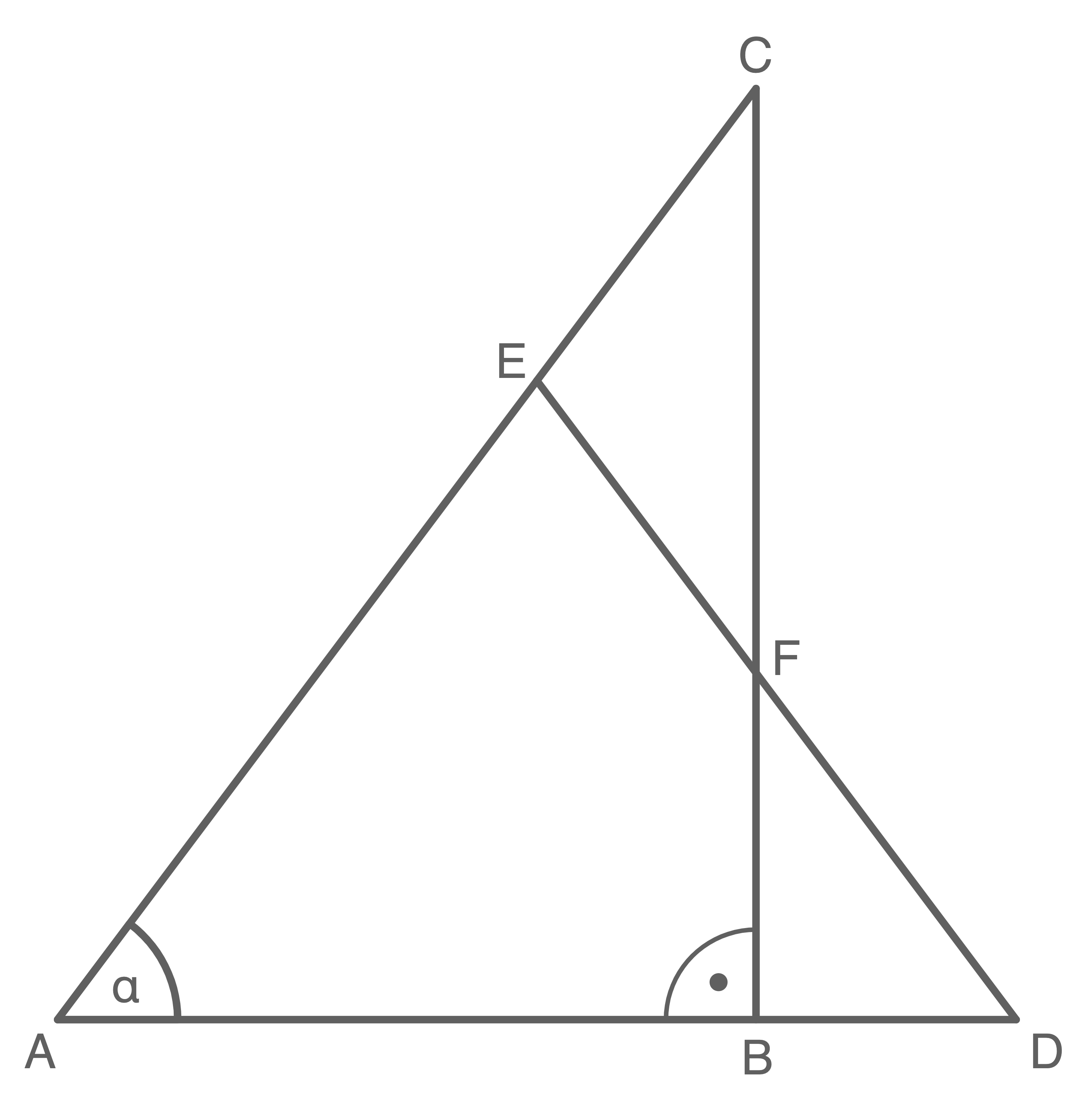 Es gilt:
Es gilt:





- Berechne die Länge von
- Berechne den Umfang des Vierecks
(5 P)
b)
Die Punkte  und
und  liegen auf einer nach oben geöffneten verschobenen Normalparabel
liegen auf einer nach oben geöffneten verschobenen Normalparabel 
 mit der
mit der  -Achse und die Punkte
-Achse und die Punkte  und
und  bilden ein Viereck.
bilden ein Viereck.
 und
und  verlaufen jeweils auf den Diagonalen des Vierecks.
verlaufen jeweils auf den Diagonalen des Vierecks.
Sie schneiden sich im Punkt
- Gib die Funktionsgleichung der Parabel
in der Normalform
an.
- Berechne den Flächeninhalt dieses Vierecks.
Sie schneiden sich im Punkt
- Berechne die Koordinaten des Schnittpunktes
Aufgabe 2
a)
Der Punkt  liegt auf der Parabel
liegt auf der Parabel  mit der Funktionsgleichung
mit der Funktionsgleichung  Die Gerade
Die Gerade  schneidet die Parabel
schneidet die Parabel  im Punkt
im Punkt  und im Scheitelpunkt
und im Scheitelpunkt 
 an der
an der  -Achse entsteht der Punkt
-Achse entsteht der Punkt 
 ist der Scheitelpunkt einer nach oben geöffneten verschobenen Normalparabel
ist der Scheitelpunkt einer nach oben geöffneten verschobenen Normalparabel 
 mit der
mit der  -Achse ist der Scheitelpunkt
-Achse ist der Scheitelpunkt  der Parabel
der Parabel  Die Parabel
Die Parabel  der Form
der Form  geht außerdem durch die Scheitelpunkte
geht außerdem durch die Scheitelpunkte  und
und 
- Berechne die Funktionsgleichungen der Parabel
und der Geraden
- Gib die Funktionsgleichung von
in der Form
an.
- Berechne die Funktionsgleichung der Parabel
(5 P)
b)
In einer quadratischen Pyramide liegt das gleichschenklige Dreieck 
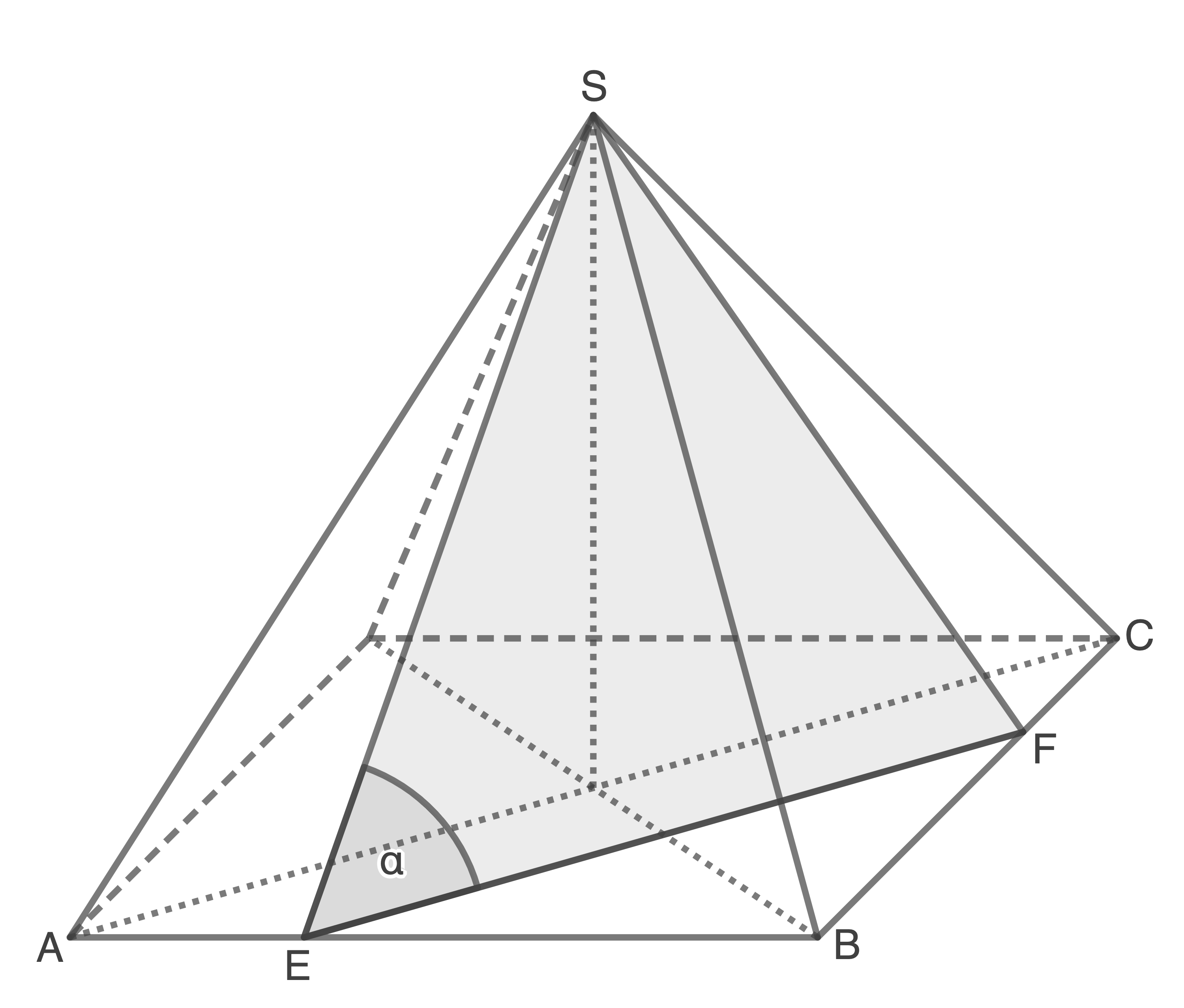 Es gilt:
Es gilt:




- Berechne den Flächeninhalt des Dreiecks
- Berechne das Volumen der quadratischen Pyramide.
Aufgabe 3
a)
Zehn gleich große Karten sind mit vier verschiedenen Symbolen (Handball, Radfahren, Laufen, Fußball) bedruckt.
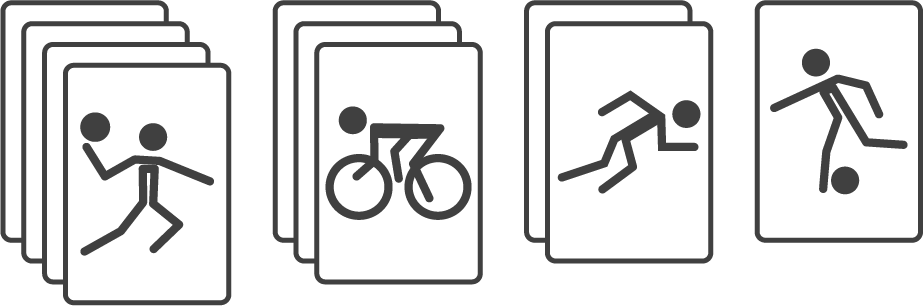 Sie sind nach den vier Symbolen in Stapeln sortiert (siehe Abbildung).
Sie sind nach den vier Symbolen in Stapeln sortiert (siehe Abbildung).
Die Karten werden gemischt und verdeckt auf den Tisch gelegt.
Sie werden für ein Glücksspiel eingesetzt.
Dabei werden zwei Karten gleichzeitig gezogen.
Für das Spiel wird der abgebildete Gewinnplan geprüft.
Berechne den Erwartungswert. Der Veranstalter möchte langfristig pro Spiel einen Erlös von 
 erzielen.
erzielen.

Die Karten werden gemischt und verdeckt auf den Tisch gelegt.
Sie werden für ein Glücksspiel eingesetzt.
Dabei werden zwei Karten gleichzeitig gezogen.
Für das Spiel wird der abgebildete Gewinnplan geprüft.
| Ereignis | Gewinn |
|---|---|
zweimal  |
9,00 € |
 und und  |
6,00 € |
 und und  |
3,00 € |
| andere Ereignisse | kein Gewinn |
| Einsatz pro Spiel: 1,00 € | |
- Wie hoch muss dann der Gewinn für "
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?
(5 P)
b)
Die Flugbahn eines Speers ist nahezu parabelförmig.
 (Skizze nicht maßstabsgetreu)
Der Abwurfpunkt A liegt 1,80 m über der Abwurflinie.
(Skizze nicht maßstabsgetreu)
Der Abwurfpunkt A liegt 1,80 m über der Abwurflinie.
Der Speer erreicht nach 20 m, in horizontaler Richtung von der Abwurflinie gemessen, seine maximale Höhe von 9,80 m. beschrieben werden. Die Wurfweite beträgt 38,15 m.
beschrieben werden. Die Wurfweite beträgt 38,15 m.
 (Skizze nicht maßstabsgetreu)
(Skizze nicht maßstabsgetreu)
Der Speer erreicht nach 20 m, in horizontaler Richtung von der Abwurflinie gemessen, seine maximale Höhe von 9,80 m.
- Berechne eine mögliche Funktionsgleichung der Flugkurve des Speers.
- Wie weit fliegt der Speer?
- Gib die Höhe dieses Abwurfpunktes an.
Aufgabe 4
a)
Die Gerade  und die verschobene Normalparabel
und die verschobene Normalparabel  gehen durch die beiden Punkte
gehen durch die beiden Punkte  und
und 
Der Punkt liegt auf der Parabel
liegt auf der Parabel 
Die Gerade steht senkrecht auf
steht senkrecht auf  und geht durch
und geht durch 
Die Gerade schneidet die beiden Koordinatenachsen in den Punkten
schneidet die beiden Koordinatenachsen in den Punkten  und
und  Berechne die Koordinaten von
Berechne die Koordinaten von  und
und 
Der Punkt
Die Gerade
Die Gerade
(5 P)
b)
Ein DIN-A4-Blatt hat die Eckpunkte  ,
,  ,
,  und
und 
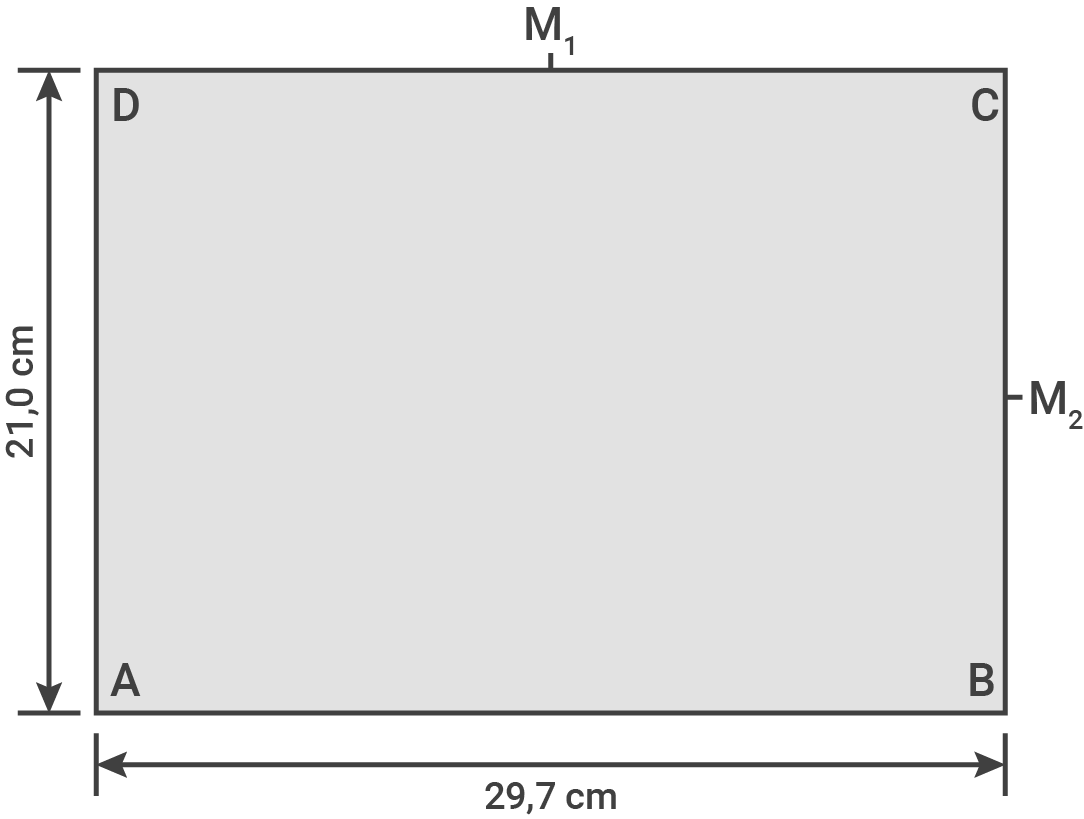
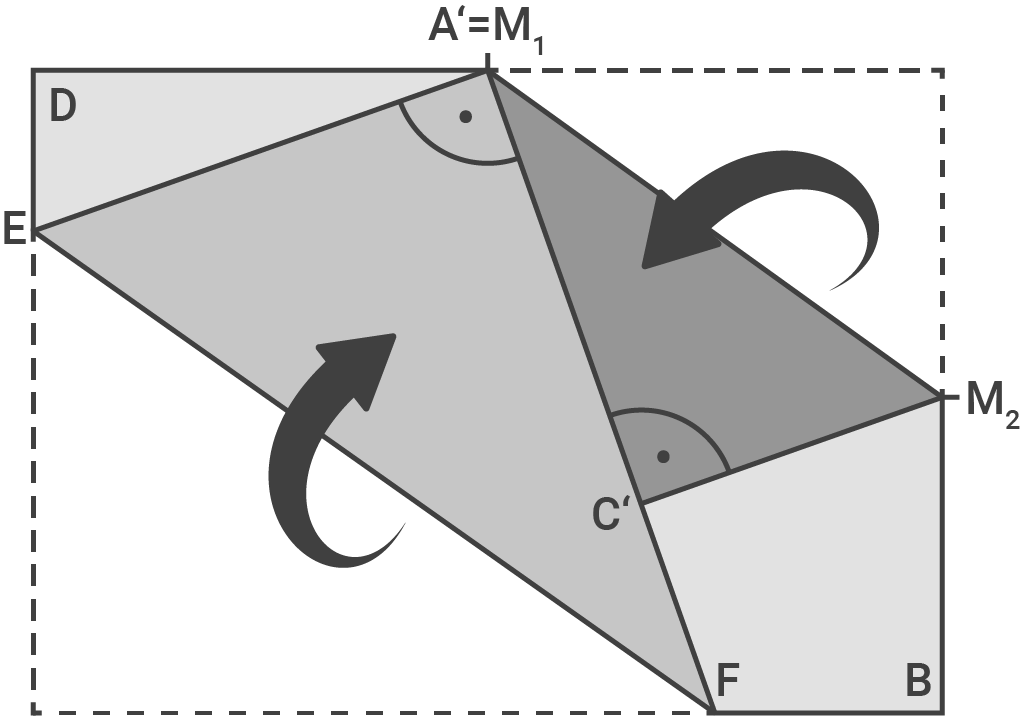 Die Punkte
Die Punkte  und
und  halbieren die Seitenlängen des DIN-A4-Blatts.
halbieren die Seitenlängen des DIN-A4-Blatts.
Das DIN-A4-Blatt wird wie abgebildet gefaltet. Der Punkt wird zu
wird zu  und liegt nach dem Falten auf
und liegt nach dem Falten auf 
Der Punkt wird zum Punkt
wird zum Punkt  Die beiden Papierkanten stoßen entlang von
Die beiden Papierkanten stoßen entlang von  aneinander.
Berechne die Flächeninhalte des Dreiecks
aneinander.
Berechne die Flächeninhalte des Dreiecks  und des Vierecks
und des Vierecks  .
.


Das DIN-A4-Blatt wird wie abgebildet gefaltet. Der Punkt
Der Punkt
Lösung 1
a)
Länge der Strecke  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
Dazu wird zunächst die Länge der Strecke
berechnen
Dazu wird zunächst die Länge der Strecke  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overline{AB}}{\overline{AC}} \quad \scriptsize \mid\;\cdot\overline{AC}\;\\[5pt]
\cos(\alpha)\cdot \overline{AC}&=&\overline{AB} \quad \scriptsize \mid\; :\cos(\alpha) \\[5pt]
\overline{AC}&=&\dfrac{\overline{AB}}{\cos(\alpha)}\\[5pt]
\overline{AC} &=&\dfrac{13,2\,\text{cm}}{\cos(55^\circ)}\\[5pt]
\overline{AC} &=& 23,01\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/c3d5204d2ec558c4dcc216970b07a6a102b170f63aede46b10f96486cd75b543_light.svg) Damit kann nun die Länge der Strecke
Damit kann nun die Länge der Strecke  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AC}-\overline{CE} \\[5pt]
&=& 23,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& \underline{ 15,01\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/23e52ccdfce04b53322bfcdd6d292c12543a8b6a4fbbb6c7cb3f56cf4dc220d3_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Das Dreieck
berechnen
Das Dreieck  ist gleichschenklig.
Begründung:
ist gleichschenklig.
Begründung:
1.

2.
3.
4.
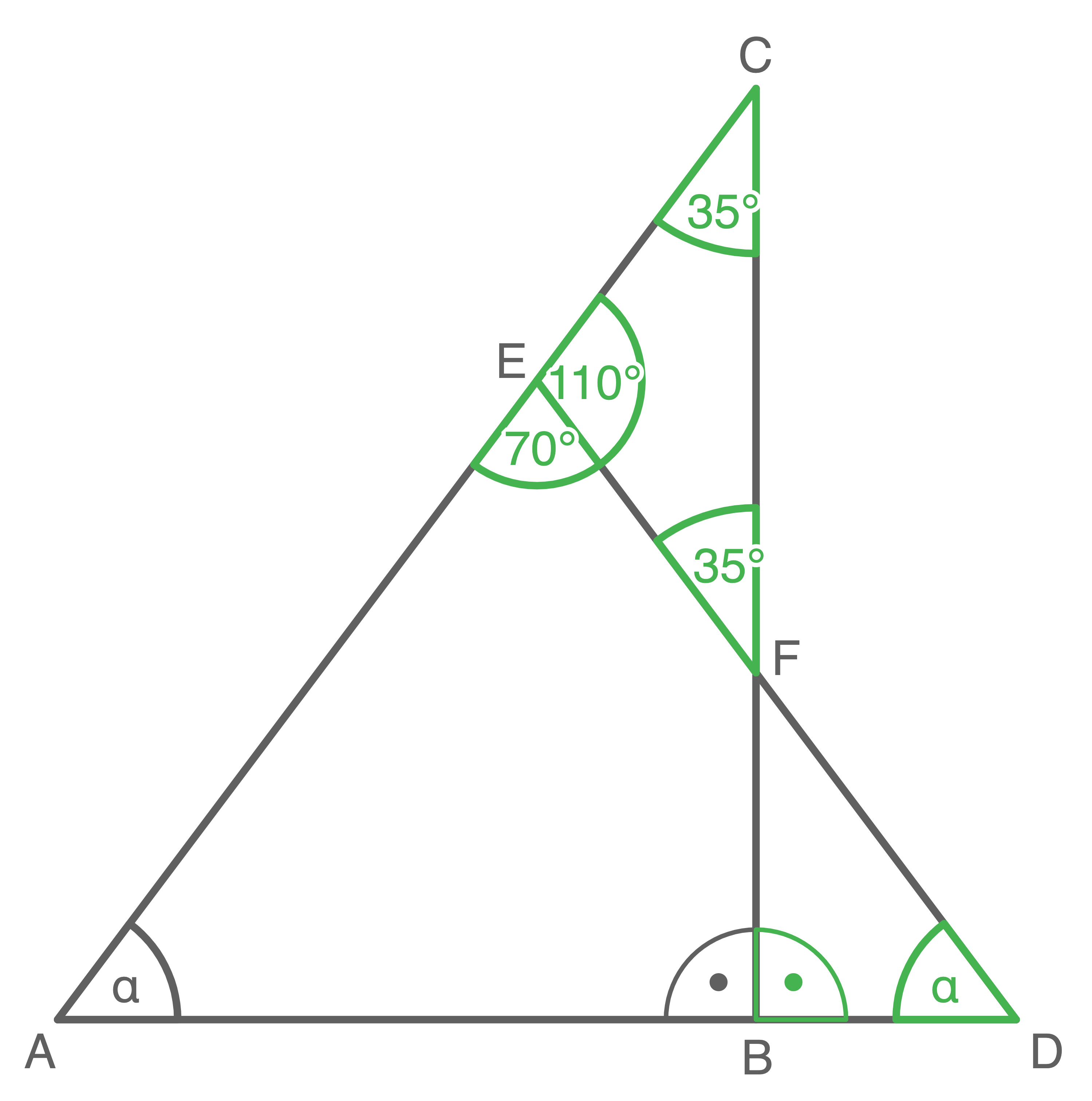 Daraus folgt:
Daraus folgt:  Da das Dreieck
Da das Dreieck  gleichschenklig ist, gilt:
gleichschenklig ist, gilt:  Damit kann nun die Länge der Strecke
Damit kann nun die Länge der Strecke  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\overline{DF}&=& \overline{DE}-\overline{EF} \\[5pt]
&=& \overline{AE}-\overline{EF} \\[5pt]
&=& 15,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& 7,01\,\text{cm}\\[5pt]
&=& \underline{\underline{ 7\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/f442d6c586f7ceed40a2c62e2ed229ff65b9eb637998beee9d8e69756df7832e_light.svg) Umfang des Vierecks
Umfang des Vierecks  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BF}}{\overline{DF}}\quad \scriptsize \mid\;\cdot \overline{DF} \\[5pt]
\sin(\alpha)\cdot\overline{DF} &=& \overline{BF}\\[5pt]
\sin(55^\circ)\cdot 7\,\text{cm} &=& \overline{BF}\\[5pt]
5,73\,\text{cm} &\approx& \overline{BF}\\
\overline{BF} &\approx&\underline{ 5,73\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/e90a5538e6fb7f872f89722bb621d98782b2bb1b49c43cf408512f2fc3dab053_light.svg) 2. Schritt: Umfang berechnen
2. Schritt: Umfang berechnen
1.
2.
3.
4.

b)
Funktionsgleichung der Parabel angeben

 und
und  in
in  eingesetzt, ergibt ein lineares Gleichungssystem:
eingesetzt, ergibt ein lineares Gleichungssystem:
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
8&=& -1-(-4)-c \quad \scriptsize \\[5pt]
8&=& 3-c \quad \scriptsize \mid\; -3\\[5pt]
5&=& -c \quad \scriptsize \mid\; \cdot (-1)\\[5pt]
-5&=& c \quad \scriptsize \\[5pt]
c&=& -5
\end{array}\)](https://www.schullv.de/resources/formulas/7193d5d5d0a7306310bdb98cb253ef39499bba2c22013926e989c68a52b2af9b_light.svg) Die Funktionsgleichung der Parabel lautet
Die Funktionsgleichung der Parabel lautet 
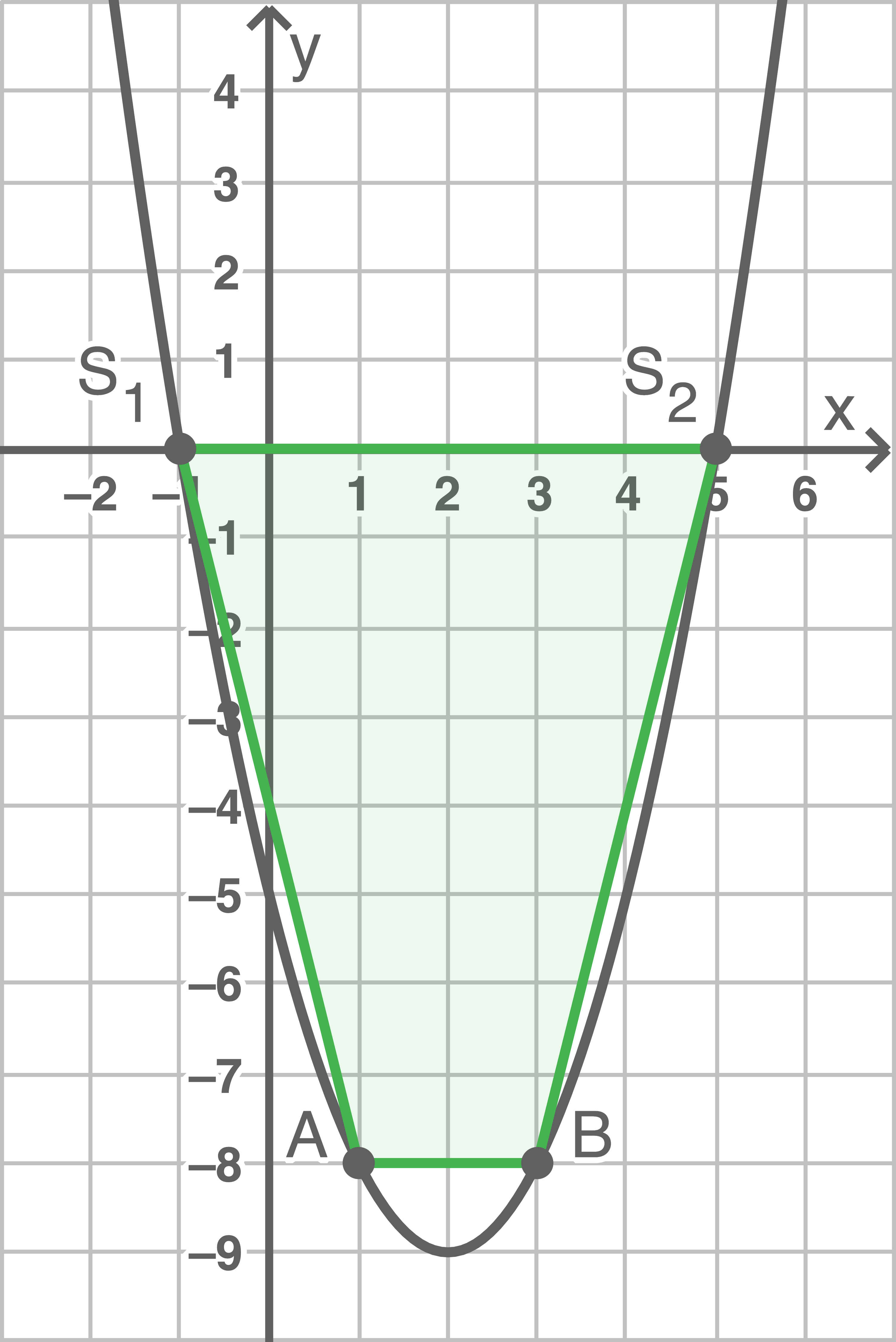 Es handelt sich um ein Trapez mit folgendem Flächeninhalt:
Es handelt sich um ein Trapez mit folgendem Flächeninhalt:
![\(\begin{array}[t]{rll}
A&=& \dfrac{a+c}{2}\cdot h \\[5pt]
&=& \dfrac{6\,\text{LE}+2\,\text{LE}}{2}\cdot 8\,\text{LE} \\[5pt]
&=& \underline{\underline{ 32\,\text{FE}}} \end{array}\)](https://www.schullv.de/resources/formulas/4517b34e2f9b17b0fe33d83f536faec3683faf07a5604f717b621ade10829611_light.svg)
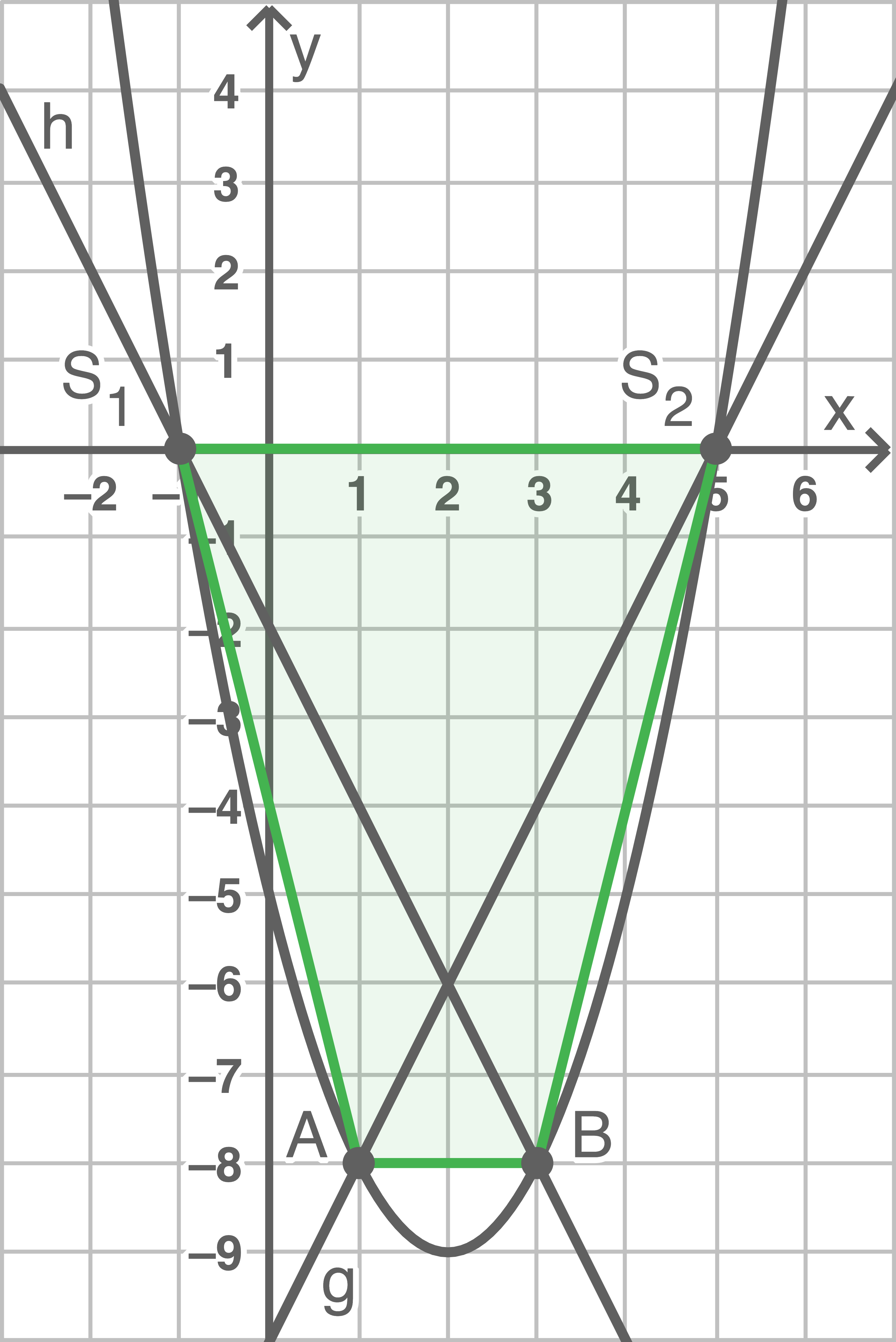 Gerade
Gerade  aufstellen:
Die Steigung von
aufstellen:
Die Steigung von  ist durch die Symmetrie gegeben:
ist durch die Symmetrie gegeben: 
![\(\begin{array}[t]{rll}
h:y&=& -2x+c_h\quad \scriptsize \mid\;S_1(-1|0)\\[5pt]
0&=& -2 \cdot (-1)+c_h \\[5pt]
0&=& 2+c_h \quad \scriptsize \mid\; -2\\[5pt]
-2&=& c_h \\[5pt]
c_h&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/d9f07cfc40e6dd02c212795d8f11df151e2c3c93ddb992fa41959f0496bf0425_light.svg) Daraus folgt:
Daraus folgt: 
 und
und  gleichsetzen:
gleichsetzen:
![\(\begin{array}[t]{rll}
2x-10&=&-2x-2 \quad \scriptsize\mid +10 \\[5pt]
2x&=&-2x+8 \quad \scriptsize \mid\;+2x \\[5pt]
4x&=&8\quad\scriptsize\mid :4\\[5pt]
x&=&2
\end{array}\)](https://www.schullv.de/resources/formulas/5f0f7aa7838637b887ca8c362164f902e74c049baa99c9e212bc925f854fa47e_light.svg)
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& 2 \cdot 2 -10 &\quad \scriptsize \\[5pt]
&=& -6
\end{array}\)](https://www.schullv.de/resources/formulas/ca3516207c26b8bd4fe04c42003d979e4c6706edbe543e77db04695e2e4e3464_light.svg) Daraus folgt:
Daraus folgt: 

Koordinaten des Schnittpunkts  berechnen
Gerade
berechnen
Gerade  aufstellen:
aufstellen:

 und
und  in
in  eingesetzt, ergibt ein lineares Gleichungssystem:
eingesetzt, ergibt ein lineares Gleichungssystem:

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-8&=& 2+c_g \quad \scriptsize \mid\; -2 \\[5pt]
-10 &=& c_g\\
c_g&=& -10
\end{array}\)](https://www.schullv.de/resources/formulas/786b204e51ddf5e228f05f0aed756119187a375bc34b0ebc901d8cf3480940f1_light.svg) Daraus folgt:
Daraus folgt: 

Lösung 2
a)
Funktionsgleichungen berechnen
Funktionsgleichung von  aufstellen:
aufstellen:
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& x^2+ bx+7 \quad \mid\scriptsize A(-4\mid -1) \\[5pt]
-1&=& (-4)^2+b\cdot (-4)+7\quad \\[5pt]
-1&=& 23-4b\scriptsize \quad \mid\;-23 \\[5pt]
-24 &=& -4b \quad \scriptsize \mid\;:(-4) \\[5pt]
6&=&b \\
b&=&6
\end{array}\)](https://www.schullv.de/resources/formulas/72d7f70337ea288f653d42229f6805600ca247d4b72c96f1163b89a383548068_light.svg) Daraus folgt:
Daraus folgt:  Funktionsgleichung von
Funktionsgleichung von  aufstellen
Scheitelpunkt
aufstellen
Scheitelpunkt  durch quadratische Ergänzung bestimmen:
durch quadratische Ergänzung bestimmen:
![\(\begin{array}[t]{rll}
y&=& x^2+6x+7 \\[5pt]
&=& x^2+2\cdot 3\cdot x+7 \\[5pt]
&=& x^2+2\cdot 3\cdot x+3^2-3^2+7 \\[5pt]
&=& (x+3)^2-9+7 &\quad \scriptsize \\[5pt]
&=& (x+3)^2-2
\end{array}\)](https://www.schullv.de/resources/formulas/3ec020167f29ef419033a1734f126ce5590d1cc42a871c59212d3e76b8af83a1_light.svg) Somit gilt:
Somit gilt: 
 und
und  in die allgemeine Geradengleichung
in die allgemeine Geradengleichung  eingesetzt, ergibt ein lineares Gleichungssystem:
eingesetzt, ergibt ein lineares Gleichungssystem:

 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
-1&=& -1\cdot (-4)+c &\quad \scriptsize \\[5pt]
-1&=& 4+c \quad \scriptsize \mid\; -4\\[5pt]
-5 &=& c\\
c &=& -5
\end{array}\)](https://www.schullv.de/resources/formulas/4f84f4fb6a562c654ba703c3146d5875b261fb8789d6a6ff42118812e080b4d8_light.svg) Daraus folgt:
Daraus folgt:  Funktionsgleichung von
Funktionsgleichung von  angeben
Durch Spiegelung von
angeben
Durch Spiegelung von  an der
an der  -Achse gilt:
-Achse gilt:  Mit Hilfe der Scheitelpunktform lässt sich
Mit Hilfe der Scheitelpunktform lässt sich  aufstellen:
aufstellen:
![\(\begin{array}[t]{rll}
y&=& (x-3)^2-2 &\quad \scriptsize \\[5pt]
&=& x^2-6x+9-2 \\[5pt]
&=& x^2-6x+7
\end{array}\)](https://www.schullv.de/resources/formulas/ec981cb60e7b5bd88ae7bd7b379a9b6de77e023b2c7168d72fd30c7bc0cdfddd_light.svg) Es gilt also
Es gilt also  Funktionsgleichung von
Funktionsgleichung von  berechnen
Schnittpunkt der Geraden
berechnen
Schnittpunkt der Geraden  mit der
mit der  -Achse berechnen:
-Achse berechnen:
![\(\begin{array}[t]{rll}
y&=& -x-5 \quad \scriptsize \mid\;x=0 \\[5pt]
y&=& 0-5 &\quad \scriptsize \\[5pt]
y&=& -5
\end{array}\)](https://www.schullv.de/resources/formulas/474dfd3340fa6d4e6e9ae277e26f45fb9c194411a5731d0e8f36cd9ee73127dd_light.svg) Daraus folgt:
Daraus folgt:  und
und 
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& ax^2+c \quad \scriptsize \mid\; S_2(3\mid -2) \\[5pt]
-2&=& a\cdot 3^2-5 \quad \scriptsize \mid\; +5\\[5pt]
3&=& a\cdot 9 \quad \scriptsize \mid\; :9\\[5pt]
\dfrac{3}{9}&=& a \\[5pt]
\dfrac{1}{3}&=& a \\[5pt]
a&=& \dfrac{1}{3}
\end{array}\)](https://www.schullv.de/resources/formulas/5296cb32390407c0751958817e5e00895b960c5618fd3c0554694addd9b1d4df_light.svg) Daraus folgt:
Daraus folgt: 
b)
Flächeninhalt des Dreiecks  berechnen
berechnen
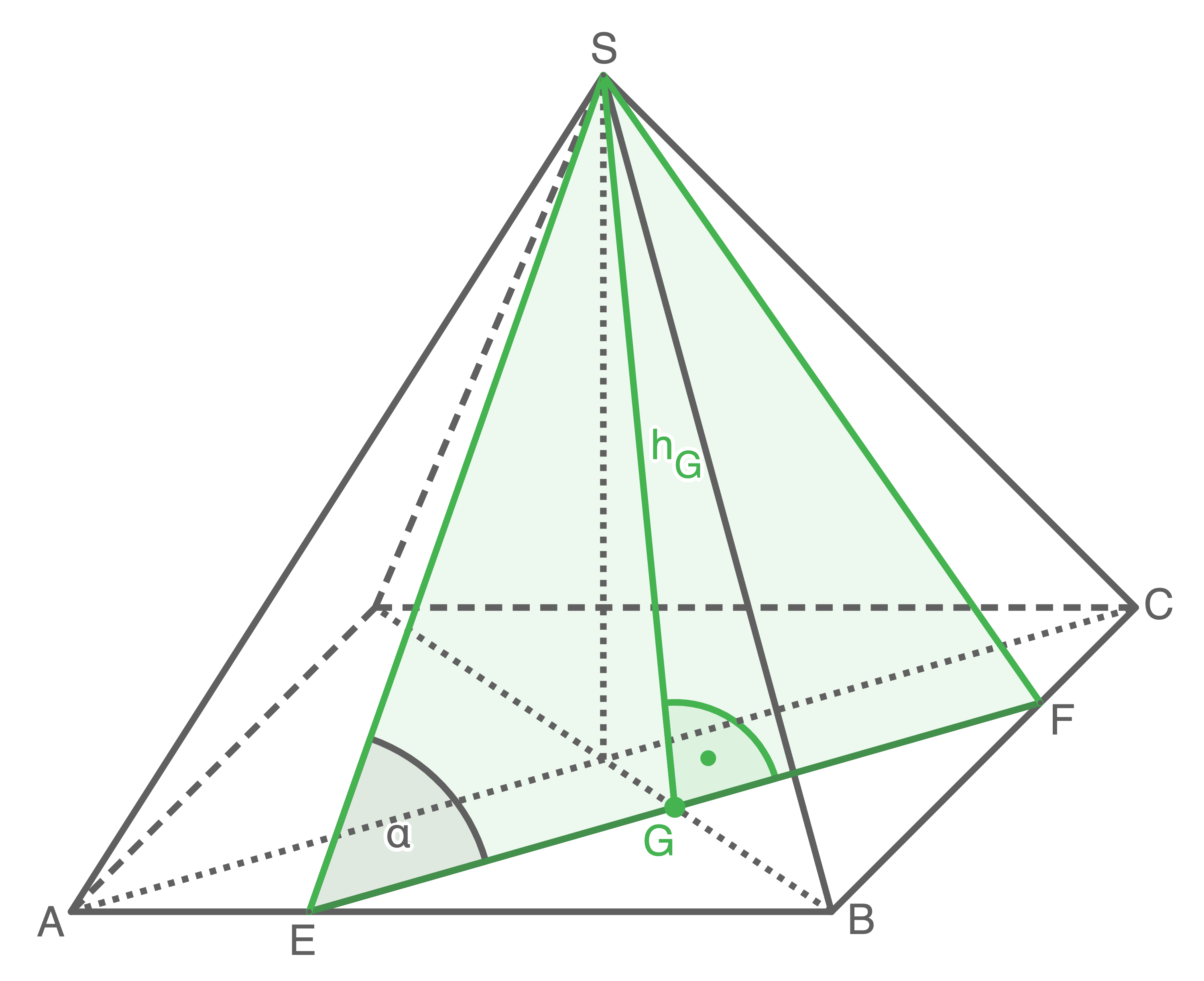 Formel zur Berechnung des Flächeninhalts:
Formel zur Berechnung des Flächeninhalts:  1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{EG}&=&\dfrac{1}{2}\cdot \overline{EF}\\[5pt]
&=& \dfrac{1}{2}\cdot 12,6\,\text{cm} \\[5pt]
&=& \underline{ 6,3\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a5aff0b1a2368974bf83d0d58824de5e666d1c2920ee4e5cf1e93f3f05448bf9_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
3. Schritt: Flächeninhalt berechnen
berechnen
3. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{EFS}&=& \dfrac{1}{2}\cdot 12,6\,\text{cm}\cdot 19,39\,\text{cm}&\quad \scriptsize \\[5pt]
& =& 122,16\,\text{cm}^2
\\[5pt]
& =& \underline{\underline{ 122,2\,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/658f45eff5938b71ca33ff7bdcc542bc846cf4a25f54688116e8b03f22564462_light.svg) Volumen der quadratischen Pyramide berechnen
Volumen der quadratischen Pyramide berechnen
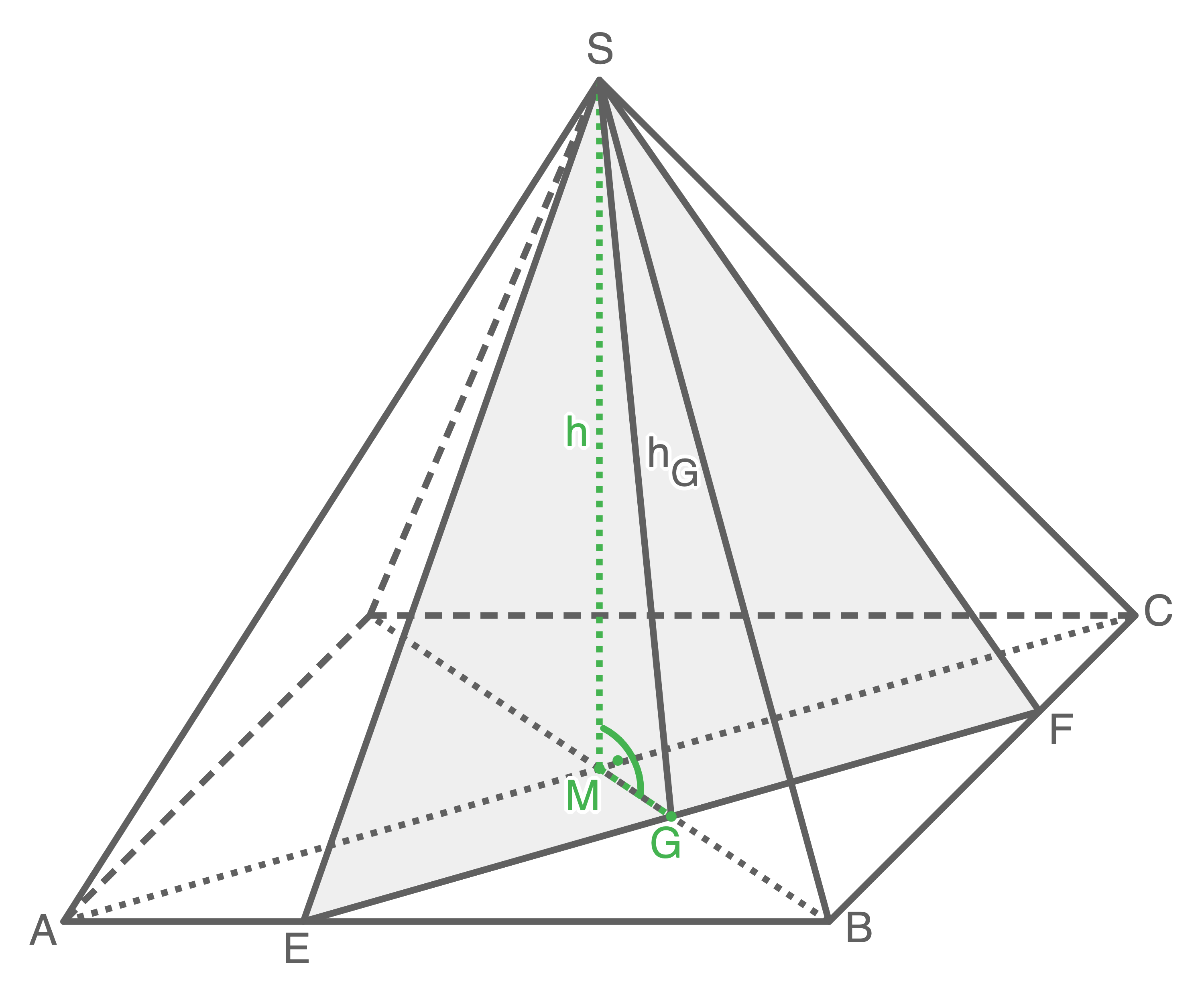 Formel zur Berechnung des Volumens:
Formel zur Berechnung des Volumens:  1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2&=& \overline{AB}^2+\overline{BC}^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\overline{AC} &=& \sqrt{\overline{AB}^2+\overline{BC}^2} \\[5pt]
\overline{AC} &=& \sqrt{(12,6\,\text{cm})^2+(12,6\,\text{cm})^2} \\[5pt]
\overline{AC}&=& \underline{ 17,82\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/0957378fa0c3a2ee81eb32f6f8b13cea0e20addb49ded35a61c8edf8bb8131f7_light.svg) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{MB}=\overline{AM}&=& \dfrac{1}{2}\cdot \overline{AC}&\\[5pt]
&=&\dfrac{1}{2}\cdot 17,82 \,\text{cm} \\[5pt]
&=&\underline{ 8,91 \,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a0c12bede9132bbf831462d78cb77732133aee2551d207d551faa1ed6557a9f0_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  mit dem Zweiten Strahlensatz berechnen
4. Schritt: Länge der Strecke
mit dem Zweiten Strahlensatz berechnen
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{MG}&=& \overline{MB}-\overline{GB} \\[5pt]
&=& 8,91\,\text{cm}-6,3\,\text{cm} \\[5pt]
&=& \underline{ 2,61\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/f97038fbbc195d314942b33767942561de32148db25fdac1201f82f255fcd7f8_light.svg) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
6. Schritt: Volumen berechnen
berechnen
6. Schritt: Volumen berechnen
![\(\begin{array}[t]{rll}
V &=& \dfrac{1}{3}\cdot \overline{AB}^2\cdot h \\[5pt]
&=& \dfrac{1}{3}\cdot (12,6\,\text{cm})^2\cdot 19,21\,\text{cm} \\[5pt]
&=& 1016,59\,\text{cm}^3
\\[5pt]
V &=& \underline{\underline{ 1016,6\,\text{cm}^3}}
\end{array}\)](https://www.schullv.de/resources/formulas/af1276eda5c255348c01df36fee826382384f4e3ce9c2317a1a17f03c9c405f4_light.svg)


Lösung 3
a)
Erwartungswert berechnen
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?

 und
und 
 und
und 
 und
und  " sein, wenn alles andere unverändert bleibt?
" sein, wenn alles andere unverändert bleibt?
b)
Funktionsgleichung berechnen
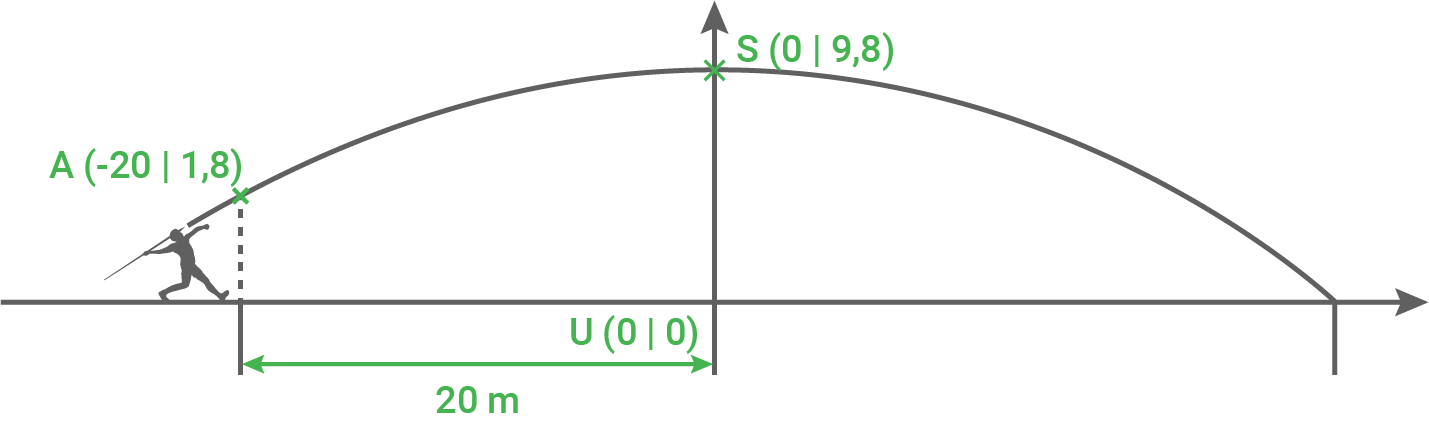 Parabelform:
Parabelform: 
 daher gilt:
daher gilt:  Punkt
Punkt  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
1,8&=& a \cdot (-20)^2+9,8 \quad \scriptsize \mid\; -9,8\\[5pt]
-8&=& a \cdot 400 \quad \scriptsize \mid\; :400\\[5pt]
-0,02&=& a\\
a&=& -0,02
\end{array}\)](https://www.schullv.de/resources/formulas/1ce6a7e369415d231547867770a5561de2f6e07b2dfd662de4bcb04f69830958_light.svg) Eine mögliche Funktionsgleichung lautet also:
Eine mögliche Funktionsgleichung lautet also:  Wie weit fliegt der Speer?
Nullstellen der Parabel berechnen:
Wie weit fliegt der Speer?
Nullstellen der Parabel berechnen:
![\(\begin{array}[t]{rll}
-0,02x^2+9,8&=& 0 \quad \scriptsize \mid\; -9,8 \\[5pt]
-0,02x^2&=& -9,8 \quad \scriptsize \mid\; :(-0,02)\\[5pt]
x^2&=& 490 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&=& -22,14 \\[5pt]
x_2&=& +22,14
\end{array}\)](https://www.schullv.de/resources/formulas/dabf98f1e1d50182303e60bc6181549b8495c52d3a618ba591af6766e5c0311d_light.svg) Der Speer stößt also am Punkt
Der Speer stößt also am Punkt  auf dem Boden auf.
Wurfweite
auf dem Boden auf.
Wurfweite  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
w&=& x_N -x_A &\quad \scriptsize \\[5pt]
&=& 22,14 - (-20) &\quad \scriptsize \\[5pt]
&=& 42,14\\[5pt]
w&=& \underline{\underline{ 42,1}}
\end{array}\)](https://www.schullv.de/resources/formulas/cb1f93cf491c002303bd53544e72b79e93e88e021a8d28facad3efe6311945d6_light.svg) Der Speer fliegt also
Der Speer fliegt also  weit.
Höhe des Abwurfpunktes angeben
Nullstellen der Parabel berechnen:
weit.
Höhe des Abwurfpunktes angeben
Nullstellen der Parabel berechnen:
![\(\begin{array}[t]{rll}
-\dfrac{1}{30}\cdot x^2+13&=&0 \quad \scriptsize \mid\; -13 \\[5pt]
-\dfrac{1}{30}\cdot x^2&=&-13 \quad \scriptsize \mid\; :\left(-\dfrac{1}{30}\right)\\[5pt]
x^2&=& 390\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&=& -19,75\\[5pt]
x_2&=& +19,75
\end{array}\)](https://www.schullv.de/resources/formulas/bb0d9cf718e5b85da77f32b1f42c944298c5bfe91857524d533a6ceebcd99534_light.svg)
 -Koordinate des Abwurfspunkts berechnen:
-Koordinate des Abwurfspunkts berechnen:
![\(\begin{array}[t]{rll}
x_{A2}&=& x_2- \,\text{Wurfweite} &\quad \scriptsize \\[5pt]
&=& 19,75- 38,15 &\quad \scriptsize \\[5pt]
&=& -18,4
\end{array}\)](https://www.schullv.de/resources/formulas/1c902a7dcaa57466628967dfa5f8cad11b3b86c36a284b5be66e6588e3716f81_light.svg)
 -Koordinate des Abwurfspunkts berechnen:
-Koordinate des Abwurfspunkts berechnen:
![\(\begin{array}[t]{rll}
y&=&-\dfrac{1}{30}x^2+13 \quad \scriptsize \mid\; x_{A2}=-18,4\\[5pt]
y&=&-\dfrac{1}{30}\cdot (-18,4)^2+13 &\quad \scriptsize \\[5pt]
&=& 1,71
\\[5pt]
y&=& \underline{\underline{ 1,7}}
\end{array}\)](https://www.schullv.de/resources/formulas/8b66a255e77e81cfb31065138b46d687715512badeb6559f8fb208d2d269a27a_light.svg) Der Abwurfpunkt befindet sich auf einer Höhe von ungefähr
Der Abwurfpunkt befindet sich auf einer Höhe von ungefähr 

Lösung 4
a)
Parabelgleichung  ermitteln
ermitteln
 und
und  in die allgemeine Parabelform
in die allgemeine Parabelform  eingesetzt ergibt ein lineares Gleichungssystem:
eingesetzt ergibt ein lineares Gleichungssystem:
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
3&=& 4+2\cdot (-6)+c \quad \scriptsize \\[5pt]
3&=& -8+c \quad \scriptsize \mid\;+8\\[5pt]
11&=& c \\[5pt]
c&=& 11
\end{array}\)](https://www.schullv.de/resources/formulas/d7706474527407a039a3040f2661aac495d9c34dcf212b7ae22bbaa986251ef2_light.svg) Somit gilt:
Somit gilt: 
 -Koordinate von Punkt
-Koordinate von Punkt  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
y&=&x^2-6x+11 \quad \scriptsize \mid\;C(4\mid y_c) \\[5pt]
y_c &=&4^2-6\cdot 4+11 &\quad \scriptsize \\[5pt]
y_c &=& 16-24+11 &\quad \scriptsize \\[5pt]
y_c&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/b4eb3154c096ad2359fd462b685af1b73ccd9895e47b9da77841d804e7a271c9_light.svg) Somit gilt:
Somit gilt:  Geradengleichung
Geradengleichung  ermitteln
1. Schritt: Steigungsfaktor
ermitteln
1. Schritt: Steigungsfaktor  berechnen
berechnen
![\(\begin{array}[t]{rll}
m_g&=& \dfrac{y_A-y_B}{x_A-x_B}&\quad \scriptsize \\[5pt]
m_g&=& \dfrac{3-11}{2-6}&\quad \scriptsize \\[5pt]
m_g&=& \dfrac{-8}{-4}&\quad \scriptsize \\[5pt]
m_g&=& \underline{ 2}
\end{array}\)](https://www.schullv.de/resources/formulas/ffd402133f9d42a6acefabbe3d21e09c0c0a15d354f2e48d10da82b4441fe023_light.svg) 2. Schritt: Steigungsfaktor
2. Schritt: Steigungsfaktor  berechnen
Da
berechnen
Da  senkrecht zu
senkrecht zu  liegt, gilt:
liegt, gilt:
![\(\begin{array}[t]{rll}
m_h\cdot m_g&=& -1 \quad \scriptsize \mid\; :m_g \\[5pt]
m_h&=&\dfrac{-1}{m_g} \quad \scriptsize \mid\; m_g=2 \\[5pt]
m_h &=& \underline{ -\dfrac{1}{2}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/25c54a968857dad4a6cd4190c6cf7255e0b9408f5aa7eb6d142a89c704294e14_light.svg) 3. Schritt:
3. Schritt:  -Achsenabschnitt
-Achsenabschnitt  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=& m_h\cdot x+c_h \quad \scriptsize \mid\; m_h=-\dfrac{1}{2}\\[5pt]
y&=& -\dfrac{1}{2}\cdot x+c_h \quad \scriptsize \mid \, C (4\mid 3)\\[5pt]
3&=& -\dfrac{1}{2}\cdot 4+c_h \\[5pt]
3&=& -2+c_h \quad \scriptsize \mid\; +2\\[5pt]
5&=& c_h\\
c_h&=&\underline{ 5}
\end{array}\)](https://www.schullv.de/resources/formulas/0f52d86898c18d7052c0962bdcff99dc3ef4a2ebdf4e33b0701018a65c22dbca_light.svg) Somit gilt:
Somit gilt:  Skizze
Skizze
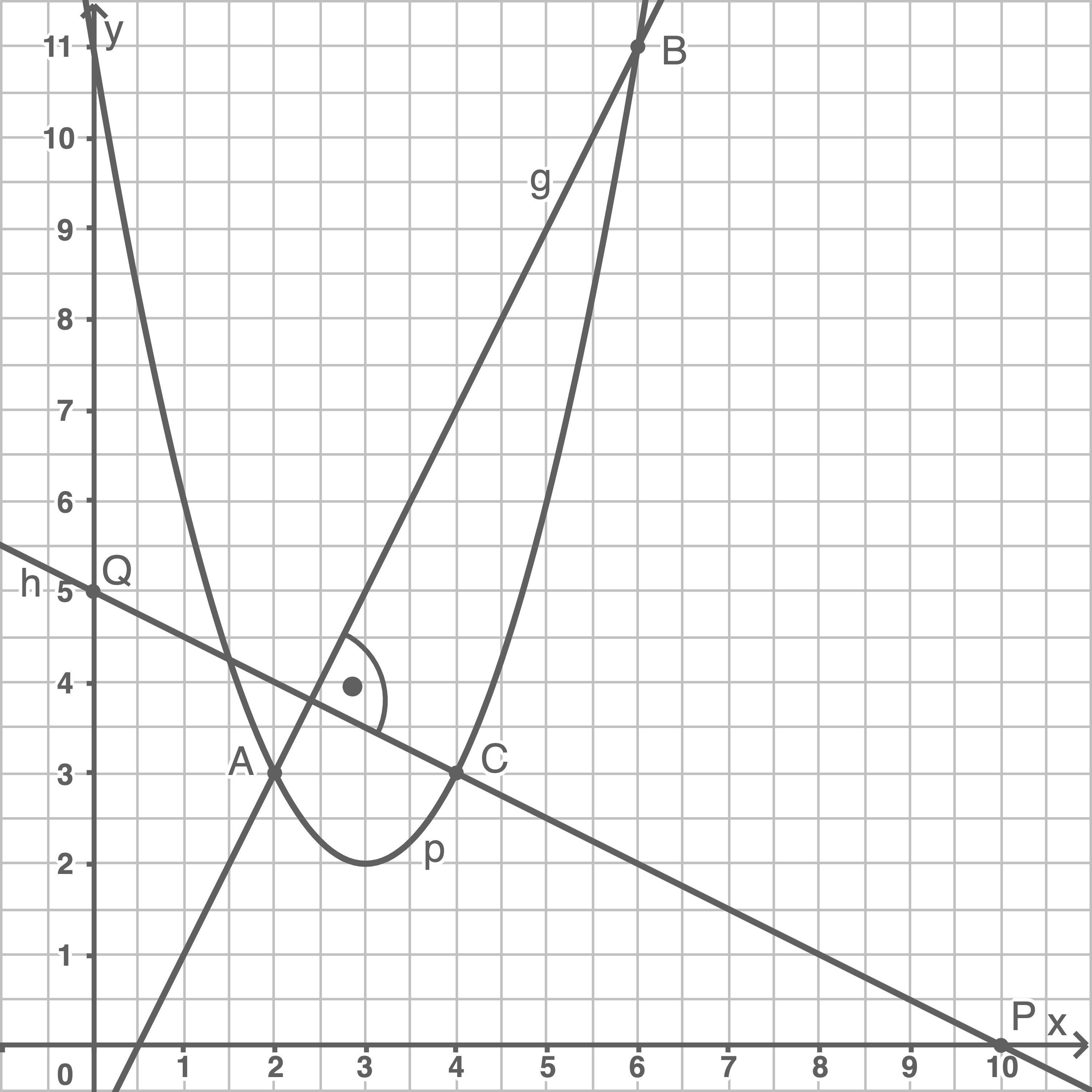 Koordinaten von Punkt
Koordinaten von Punkt  berechnen
Da
berechnen
Da  auf der
auf der  -Achse liegt, gilt
-Achse liegt, gilt 
![\(\begin{array}[t]{rll}
y&=& -\dfrac{1}{2}x+5 \quad \scriptsize \mid\; y=0 \\[5pt]
0&=& -\dfrac{1}{2}x+5 \quad \scriptsize \mid\; +\dfrac{1}{2}x\\[5pt]
\dfrac{1}{2}x&=& 5 \quad \scriptsize \mid\; \cdot 2\\[5pt]
x&=& 10
\end{array}\)](https://www.schullv.de/resources/formulas/321f3e19e454ea84d2d4e2f98c4153ce7f1c73b13fc4f3862cfe719e04f4b2bf_light.svg) Somit gilt:
Somit gilt:  Koordinaten von Punkt
Koordinaten von Punkt  berechnen
Da
berechnen
Da  auf der
auf der  -Achse liegt, gilt
-Achse liegt, gilt 
![\(\begin{array}[t]{rll}
y&=& -\dfrac{1}{2}x+5 \quad \scriptsize \mid\; x=0\\[5pt]
y &=&-\dfrac{1}{2}\cdot 0+5 &\quad \scriptsize \\[5pt]
y&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/6d885cbe440421d70558cd664918a4ba49c28e19f75c854bdf7159c6446d3e6c_light.svg) Somit gilt:
Somit gilt: 

b)
Flächeninhalt des Dreicks  berechnen
berechnen
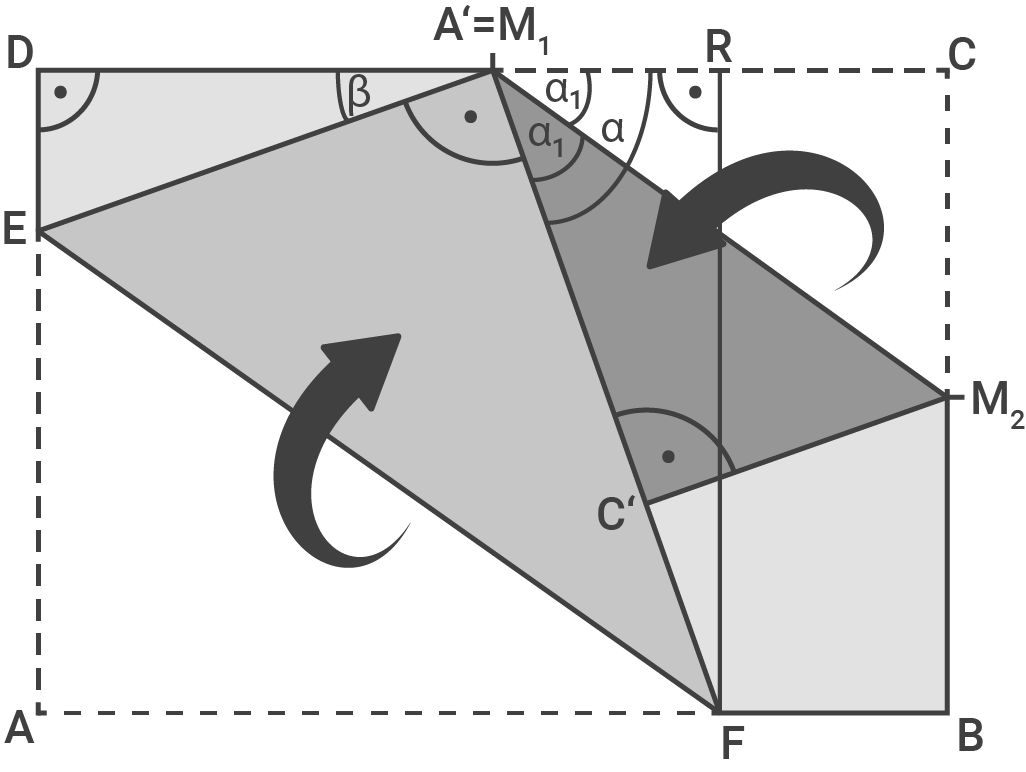 Formel zur Berechnung des Flächeninhalts:
Formel zur Berechnung des Flächeninhalts:  1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{M_1D}&=&\dfrac{1}{2}\cdot \overline{CD} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 29,7\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 14,85\,\text{cm} }
\end{array}\)](https://www.schullv.de/resources/formulas/3d9fbaffe4dbb5b97f45c2daec732203949a4b902e974d3d8131497ec77dc096_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\overline{M_2C}&=&\dfrac{1}{2}\cdot \overline{BC} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 21\,\text{cm} \\[5pt]
&=& 10,5\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/ac8b25910fe10b53ddf7e0d4c8e1639bf43217eb9189cc4701fc5c7062c62571_light.svg) Länge der Strecke
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\overline{CM_1}&=& \overline{M_1D}\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/01a42a981c85c5be87fca248b698c30909994a08653cc2d082494b1f7a82b9de_light.svg) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& \dfrac{\overline{M_2C}}{\overline{CM_1}} \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{\overline{M_2C}}{\overline{CM_1}}\right)&\quad \scriptsize \\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{10,5}{14,85}\right) &\quad \scriptsize \\[5pt]
\alpha_1&=& 35,26^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/e57eca650d4171d3cf121b42ce2dcf7a812409af71ef5370c51e960524f7d07c_light.svg) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\alpha&=& 2\cdot \alpha_1 &\quad \scriptsize \\[5pt]
&=& 2\cdot 35,26^{\circ} &\quad \scriptsize \\[5pt]
&=& 70,52^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/a27c941edeb256924ba0eb0c3d447d3029732e24be5909fafce5b4be9ac8e694_light.svg) Größe des Winkels
Größe des Winkels  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-90^{\circ}-\alpha &\quad \scriptsize \\[5pt]
&=& 180^{\circ}-90^{\circ}- 70,52^{\circ} &\quad \scriptsize \\[5pt]
&=& 19,48^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/caad616af3534117695b0c1340653bbb808f338c9f3c635d7f32814198792058_light.svg) Länge der Strecke
Länge der Strecke  berechnen:
3. Schritt: Flächeninhalt berechnen
berechnen:
3. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{EM_1D}&=&\dfrac{1}{2}\cdot \overline{M_1D}\cdot \overline{DE} \\[5pt]
&=&\dfrac{1}{2}\cdot 14,85\,\text{cm} \cdot 5,25\,\text{cm} \\[5pt]
&=& 38,98\,\text{cm} ^2
\\[5pt]
&=& \underline{\underline{ 39\,\text{cm} ^2 }}
\end{array}\)](https://www.schullv.de/resources/formulas/57fafd6519face23afbb394874d57ca47e348f8853ab5a8cf5081636993452a2_light.svg) Flächeninhalt des Vierecks
Flächeninhalt des Vierecks  berechnen
Formel zur Berechnung des Flächeninhalts:
berechnen
Formel zur Berechnung des Flächeninhalts:  1. Schritt: Flächeninhalt des Dreiecks
1. Schritt: Flächeninhalt des Dreiecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{M_1M_2C}&=&\dfrac{1}{2}\cdot \overline{M_2C}\cdot \overline{CM_1} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 10,5\,\text{cm} \cdot 14,85\,\text{cm} &\quad \scriptsize \\[5pt]
&= & \underline{ 77,96 \,\text{cm}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/acd4772e511e0755038f93e30e6e0b6b7999c7d448c17c8a5695bcb7721e1fce_light.svg) 2. Schritt: Flächeninhalt des Trapezes
2. Schritt: Flächeninhalt des Trapezes  berechnen
Formel zur Berechnung des Flächeninhalts:
berechnen
Formel zur Berechnung des Flächeninhalts:  Länge der Strecke
Länge der Strecke  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha) &=&\dfrac{\overline{FR}}{\overline{RM_1}} \quad \scriptsize \mid\; \cdot \overline{RM_1} \\[5pt]
\tan(\alpha)\cdot \overline{RM_1} &=& \overline{FR} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{RM_1} &=& \dfrac{\overline{FR} }{\tan(\alpha)} \quad \scriptsize \\[5pt]
\overline{RM_1} &=& \dfrac{21\,\text{cm} }{\tan(70,52^{\circ} )} \quad \scriptsize \\[5pt]
\overline{RM_1}&=& 7,43\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/e4166b73dfb87e198a4a7a2b7f52f6a983305bfb53b9edaaa6aa31663d150b69_light.svg)
![\(\begin{array}[t]{rll}
\overline{CR}&=&\overline{CM_1}-\overline{RM_1} &\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm} - 7,43\,\text{cm} &\quad \scriptsize \\[5pt]
&=& 7,42\,\text{cm} = \overline{BF}
\end{array}\)](https://www.schullv.de/resources/formulas/a21da804fbc58efb640cbefb4de390df5765309fc4615c1172da3d4ea463cd3d_light.svg) Es gilt also:
Es gilt also:
3. Schritt: Flächeninhalt des Vierecks berechnen
berechnen

3. Schritt: Flächeninhalt des Vierecks