Pflichtteil A2

Aufgabe 1

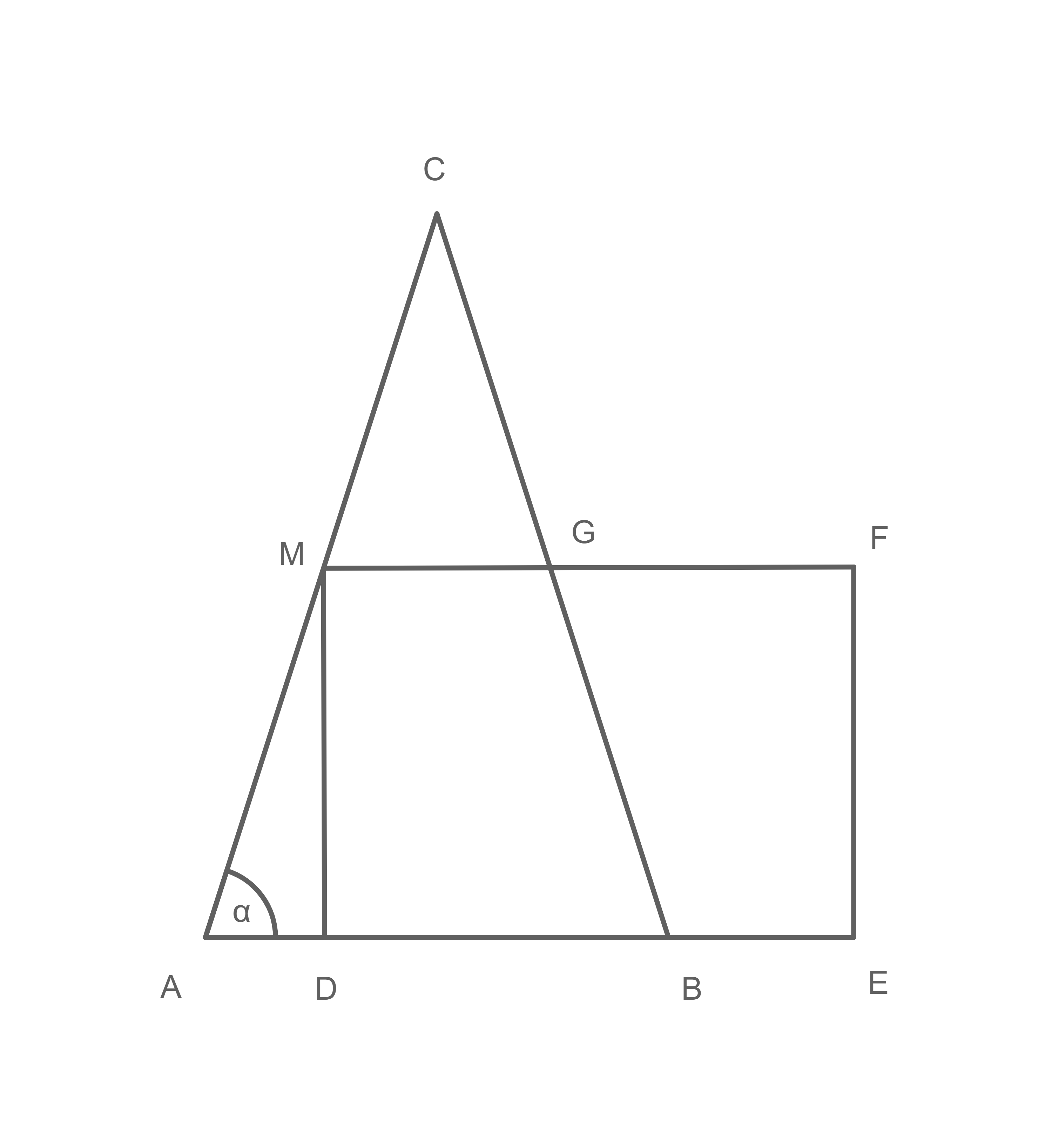
Das Dreieck $ABC$ und das Rechteck $DEFM$ haben die Punkte $D, B, G$ und $M$ gemeinsam.

Es gilt:

$\alpha = 70,0^\circ$

$\overline{AC}=14,8\;\text{cm}$

$\overline{AE}=13,6\;\text{cm}$

$\overline{AC}=\overline{BC}.$

$M$ halbiert die Strecke $\overline{AC}.$

Berechne den Flächeninhalt des Vierecks $BEFG.$

Geometrische Darstellung eines Dreiecks und eines Rechtecks mit beschrifteten Punkten und einem Winkel.

(4 P)

Aufgabe 2

Das abgebildete Zirkuszelt ist ein zusammengesetzter Körper.
Dieser besteht annähernd aus einem Zylinder mit aufgesetztem Kegel.

Der Hersteller gibt folgende Maße an:

$V_{ges}=500 \,\text{m}^{3}$

$s=7,45\,\text{m}$

$\epsilon=20.0^\circ$

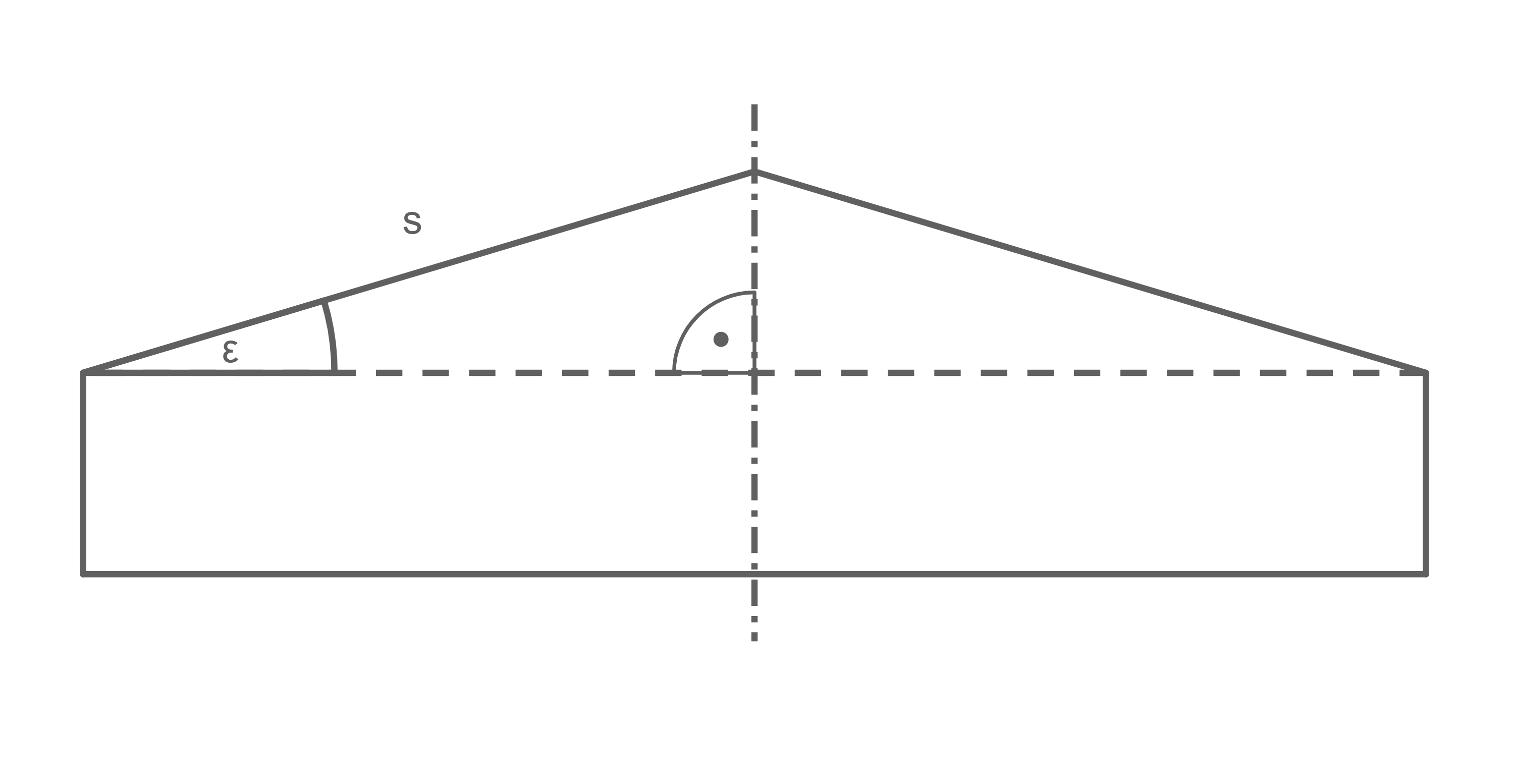
Diagramm eines geometrischen Problems mit Winkeln und Linien.

Bunt gestreiftes Zelt mit rotem und gelbem Design auf einem Sandplatz, umgeben von blauem Himmel.

Das Dach und die Seitenwand des Zirkuszeltes bestehen aus einer Kunststoffplane.

Wie viele $\text{m}^{2}$ Kunststoffplane werden benötigt? Berechne.

(3,5 P)

Aufgabe 3

Die Diagramme enthalten Informationen zum Müllaufkommen in Deutschland im Jahr 2023.

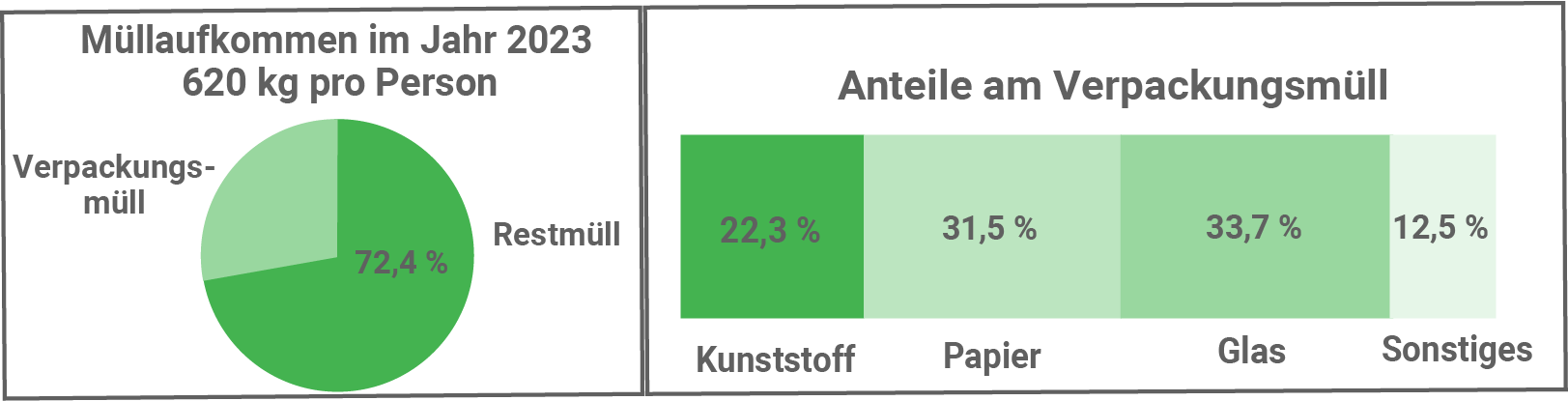
Diagramm zum Müllaufkommen 2023: Verteilung von Verpackungsmüll nach Materialien.

Berechne die Menge des Restmülls pro Person im Jahr 2023 in Kilogramm.
Wie viele Kilogramm Glas wurden im Jahr 2023 pro Person entsorgt? Berechne.

Laut einer Prognose sinkt das Müllaufkommen in den sieben Jahren von 2023 bis 2030 pro Person jährlich jeweils um $1,5\,\%$ bezogen auf das Vorjahr.

Berechne das Müllaufkommen pro Person im Jahr 2030 in Kilogramm.

(3 P)

Aufgabe 4

Familie Bauer veranstaltet anlässlich eines Kindergeburtstages ein Entenrennen.
Dabei werden zwölf gleich große Plastikenten zeitgleich in einen Bach gesetzt.
Es sind sieben rote, zwei blaue und drei gelbe Enten.

Berechne die Wahrscheinlichkeit für folgende Ereignisse:

Die ersten beiden Enten, die durchs Ziel schwimmen, sind blau.
Die ersten beiden Enten, die durchs Ziel schwimmen, sind gelb und rot.

Am Start werden von den zwölf Enten zwei rote Enten weggenommen.

Thiara behauptet: „Jetzt liegt die Wahrscheinlichkeit, dass zwei rote Enten Platz 1 und 2 belegen, bei genau $25 \,\%.$ "

Gelbe Gummi-Ente mit rotem Schnabel und Augen, auf weißem Hintergrund.

SparkFun Electronics, 24079-Debugging-Duck-Side2, CC BY 2.0

Überprüfe Thiaras Behauptung durch Rechnung oder Argumentation.

(3 P)

Aufgabe 5

In einer Fußgängerzone wurden zwei Umfragen durchgeführt.
Dabei wurde nach den durchschnittlichen Ausgaben für den Wocheneinkauf gefragt.
Am Dienstag wurden 21 Personen und am Freitag 25 Personen befragt.
Die Ergebnisse dieser beiden Umfragen sind im Diagramm und in der Strichliste dargestellt.

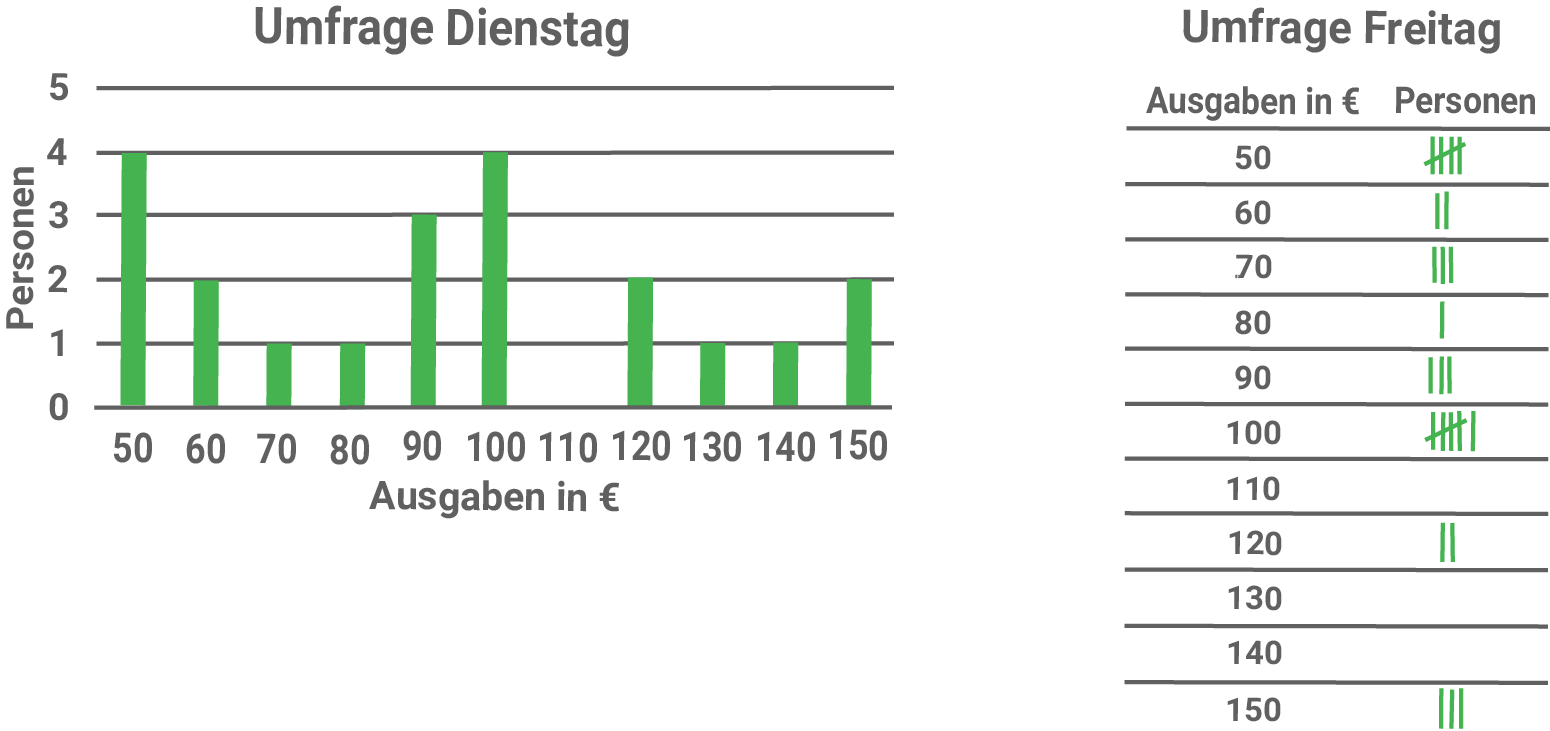
Balkendiagramm zur Umfrage über Ausgaben am Dienstag und Freitag, dargestellt in Personen und Euro.

Welche Umfrage gehört zu dem abgebildeten Boxplot?
Begründe mit Hilfe der Kennwerte.

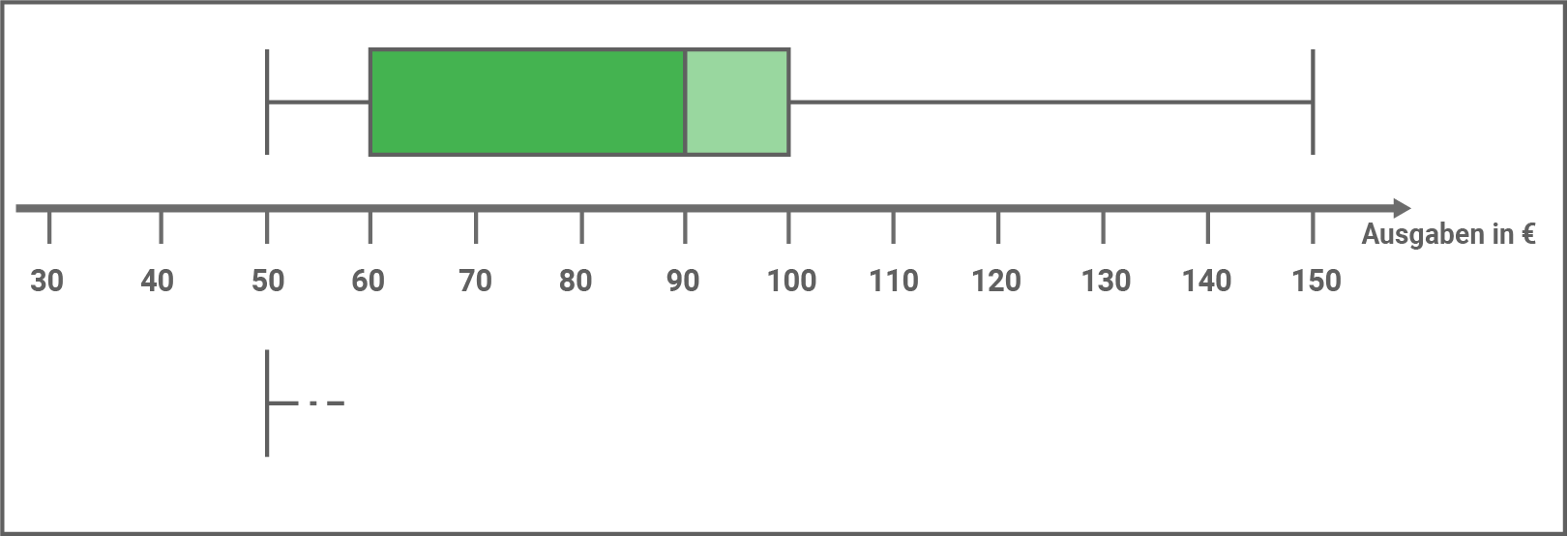
Boxplot-Diagramm zur Darstellung von Ausgaben in Euro, mit Werten von 30 bis 150 Euro.

Ergänze den Boxplot für die andere Umfrage.

Bei der Umfrage vom Freitag kommen nachträglich die vier Werte $50\,\text{€}$ , $60\,\text{€}$ , $70\,\text{€}$ und $80\,\text{€}$ hinzu.

Ändert sich aufgrund dieser vier Werte der zugehörige Boxplot? Begründe.

(3,5 P)

Aufgabe 6

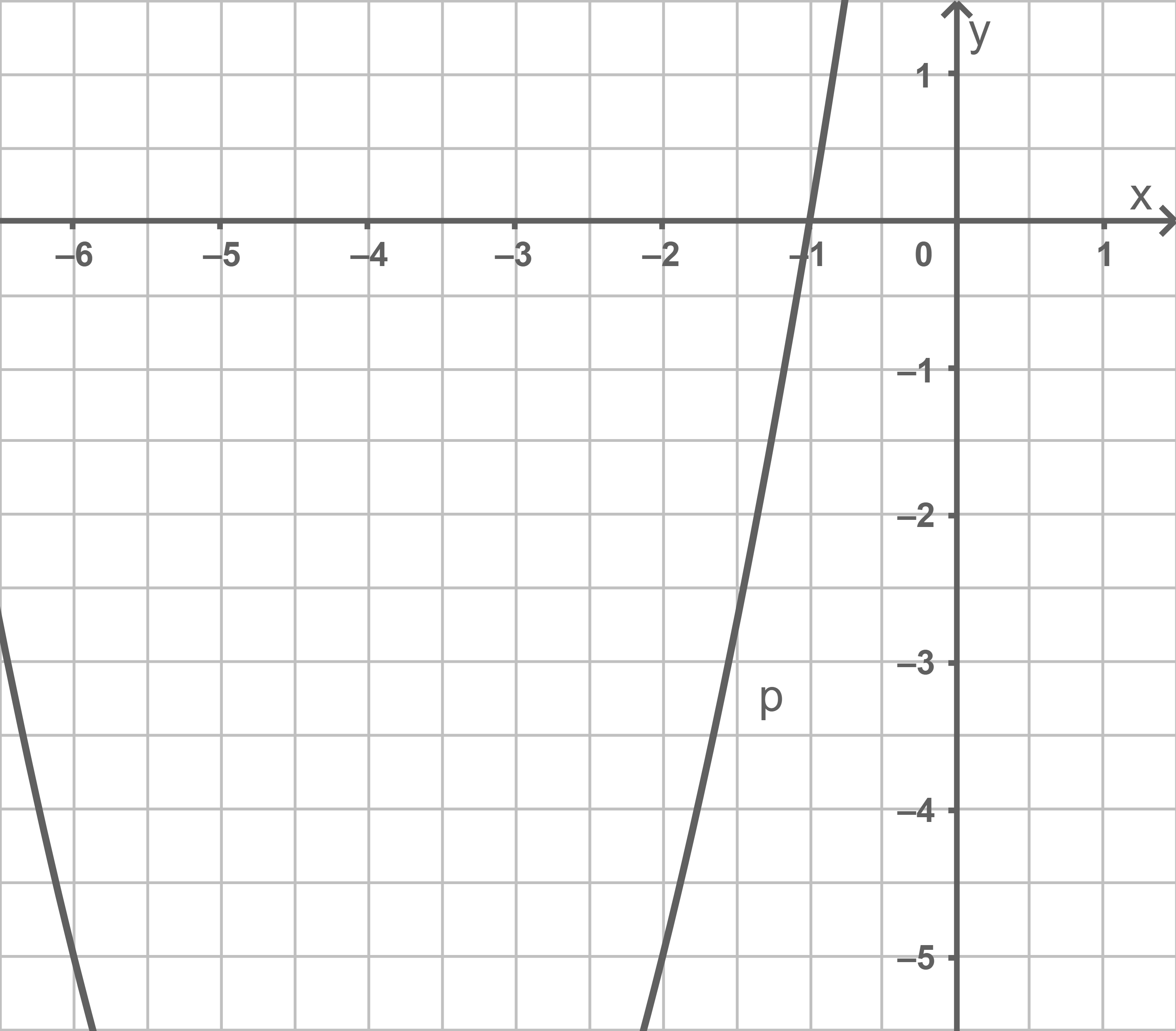
Das Schaubild zeigt den Ausschnitt der nach oben geöffneten verschobenen Normalparabel $p.$
Die Punkte $A(-2\mid-5)$ und $B(-6\mid-5)$ liegen auf $p.$

Bestimme die Funktionsgleichung der Parabel $p.$

Die Parabel $p$ besitzt mit der $x$ -Achse die beiden Schnittpunkte $N_1(-1\mid0)$ und $N_2.$

Eine Gerade $g$ geht durch den Scheitelpunkt $S$ der Parabel $p$ und durch $N_2.$

Berechne die Funktionsgleichung der Geraden $g.$

Graph eines mathematischen Funktionsverlaufs mit Koordinatensystem und Achsenbeschriftung.

(3 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\overline{AM}=\frac{1}{2}\cdot \overline{AC}=\frac{1}{2}\cdot 14,8\;\text{cm}=7,4\;\text{cm}$

$\cos(\alpha)=\frac{Ankathete}{Hypotenuse}=\frac{\overline{AD}}{\overline{AM}}$

$\begin{array}[t]{rlll} \cos(70^\circ)&=&\dfrac{\overline{AD}}{7,4\;\text{cm}} &\mid\;\cdot 7,4\;\text{cm} \\[5pt] \overline{AD}&=&2,53\;\text{cm} \end{array}$

Für $\overline{DM}$ kann gleich vorgegangen werden:

$\sin(\alpha)=\frac{Gegenkathete}{Hypotenuse}=\frac{\overline{DM}}{\overline{AM}}$

$\begin{array}[t]{rlll} \sin(70^\circ)&=&\dfrac{\overline{DM}}{7,4\;\text{cm}} &\mid\;\cdot 7,4\;\text{cm} \\[5pt] \overline{DM}&=&6,95\;\text{cm} \end{array}$

Da $ABC$ ein gleichschenkliges Dreieck ist, folgt:

$\overline{AB}=2\cdot \overline{AC}\cdot \cos(\alpha)$

$\overline{AC}$ einsetzen ergibt:

$\overline{AB}=2\cdot 14,8\;\text{cm}\cdot \cos(70^\circ)=10,12\;\text{cm}$

Weitere benötigte Strecken:

$\overline{BE}=\overline{AE}-\overline{AB}=3,48\;\text{cm}$

$\overline{MG}=\frac{\overline{AB}}{2}=5,06\;\text{cm}$

Rechenweg anzeigen

$\overline{DB}=7,59\;\text{cm} \quad \overline{DE}=11,07\;\text{cm}$

Flächeninhalt Rechteck:

Rechenweg anzeigen

$A_{DEFM}=76,97\;\text{cm}^{2}$

Flächeninhalt Trapez:

Rechenweg anzeigen

$A_{DBGM}=44,0\;\text{cm}^{2}$

Gesuchte Fläche des Vierecks $BEFG:$

Rechenweg anzeigen

$A_{BEFG}=33,0\;\text{cm}^{2}$

Lösung 2

Da der Kegel im Querschnitt ein rechtwinkliges Dreieck mit der Hypotenuse $s$ bildet und der Winkel $\epsilon$ gegeben ist, können der Radius und die Höhe des Kegels wie folgt berechnet werden:

$\begin{array}[t]{rlll} r&=&s\cdot \cos(\epsilon) \\[5pt] &=& 7,45\cdot \cos(20^\circ)\\[5pt] &=& 7,0\;\text{m} \end{array}$

$\begin{array}[t]{rlll} h_K&=&s\cdot \sin(\epsilon) \\[5pt] &=& 7,45\cdot \sin(20^\circ)\\[5pt] &=& 2,55\;\text{m} \end{array}$

Zylinderhöhe $h_Z$ durch das gegebene Gesamtvolumen berechnen:

Rechenweg anzeigen

$h_z=2,40\;\text{m}$

Planenfläche berechnen:

Mantel Zylinder:

$\begin{array}[t]{rlll} A_Z&=& 2\pi\cdot r\cdot h_Z \\[5pt] &=& 2\pi\cdot 7,0\;\text{m}\cdot 2,40\;\text{m} \\[5pt] &=&105,6\;\text{m}^2 \end{array}$

Mantel Kegel:

$\begin{array}[t]{rlll} A_K&=& \pi\cdot r \cdot s \\[5pt] &=&\pi\cdot 7,0\;\text{m}\cdot 7,45\;\text{m} \\[5pt] &=&163,8\;\text{m}^2 \end{array}$

Rechenweg anzeigen

$A_{ges}=269,4\;\text{m}^{2}$

Es werden etwa $269,4\;\text{m}^2$ Kunststoffplane für Seitenwand und Dach benötigt.

Lösung 3

Restmüll pro Person 2023:

$620\;\text{kg}\cdot 0,724=448,9\;\text{kg}$

Anteil Verpackungsmüll berechnen:

$100-72,4=27,6$

$620\;\text{kg}\cdot 0,276=171,1\;\text{kg}\;$ [Anteil Verpackungsmüll pro Person 2023]

$171,1\;\text{kg}\cdot 0,337=57,7\;\text{kg}\;$

Im Jahr 2023 wurden pro Person $57,7\;\text{Kilogramm}$ Glas entsorgt.

$7$ jähriger Rückgang um $1,5\,\text{%}:$

$1-0,015=0,985$

$620\;\text{kg}\cdot 0,985^7=557,76\;\text{kg}\;$

Laut Prognose beträgt das Müllaufkommen pro Person im Jahr 2030 $557,76\;\text{Kilogramm}.$

Lösung 4

Wahrscheinlichkeiten:

$\text{P(rot)}= \frac{7}{12}$ , $\text{P(blau)}= \frac{2}{12}$ , $\text{P(gelb)}= \frac{3}{12}$

Wahrscheinlichkeit, dass zuerst zwei blaue Enten durchs Ziel schwimmen:

$\text{P(zwei blaue)}=\frac{2}{12}\cdot \frac{1}{11}=\frac{1}{66}\; \text{ bzw. } 1,5\,\text{%}$

Für das Ereignis "Die ersten beiden Enten, die durchs Ziel schwimmen, sind gelb und rot" gibt es zwei Möglichkeiten:

$\text{P(gelb dann rot)}=\frac{3}{12}\cdot \frac{7}{11}=\frac{7}{44}$

$\text{P(rot dann gelb)}=\frac{7}{12}\cdot \frac{3}{11}=\frac{7}{44}$

Daraus folgt:

Rechenweg anzeigen

$\text{P(eine gelbe und eine rote)}=\frac{7}{22}$

Thiaras Behauptung stimmt nicht, denn:

Rechnerische Begründung:

$\text{P(zwei rote)}=\frac{5}{10}\cdot \frac{4}{9}=\frac{2}{9} \,\text{ bzw. } 22,2\,\text{%}$ [Wahrscheinlichkeit nach Abzug der beiden roten Enten]

Argumentative Begründung:

Es handelt sich um einen Zufallsversuch ohne Zurücklegen.
Die Wahrscheinlichkeit für die erste rote Ente beträgt nun $\frac{1}{2}$ und für die zweite rote Ente weniger als $\frac{1}{2}.$ Somit ist das Produkt kleiner als $\frac{1}{4}.$

Lösung 5

Der Boxplot gehört zu der Umfrage Freitag.

Eine mögliche Begründung:
Die beiden Umfragen unterscheiden sich nur im oberen Quartil.
In der Umfrage Freitag beträgt das obere Quartil $q_0=100\,\text{€}.$

min $q_u$ $z$ $q_0$ max

Umfrage Dienstag $50$ $60$ $90$ $120$ $150$

Umfrage Freitag $50$ $60$ $90$ $100$ $150$

Der Boxplot ändert sich. Mögliche Begründung:
Der Zentralwert liegt nun bei $80\,\text{€}.$

Lösung 6

Punkte in die Standardform einer verschobenen Normalparabel $(y=x^{2}+bx+c)$ einsetzen:

Punkt $A(-2\mid -5)$ einsetzen:

$\begin{array}[t]{rlll} -5&=&(-2)^{2}-2b+c \\[5pt] -5&=&4-2b+c &\mid\;-4+2b \\[5pt] c&=&-9+2b \\[5pt] \end{array}$

Punkt $B(-6\mid -5)$ einsetzen:

Rechenweg anzeigen

$b=8$

$b$ einsetzen:

$\begin{array}[t]{rlll} c&=&-9+2\cdot 8 \\[5pt] c&=&-9+16 \\[5pt] c&=&7 \end{array}$

$b$ und $c$ in die Standardform einsetzen:

$y=x^2+8x+7$ $\;\text{(Scheitelpunktform} p: y=(x+4)^2-9)$

Parabelgleichung gleich null setzen und mit Hilfe der Mitternachtsformel die $x$ -Koordinate des Nullpunktes berechnen:

Rechenweg anzeigen

$x_1=-1 \quad x_2=-7$

$x_2$ einsetzen um die $y$ -Koordinate zu erhalten:

$y=(-7)^{2}+8\cdot (-7)+7=0$

So erhält man folgenden Punkt:

$N_2=(-7\mid0)$

$S$ und $N_2$ in die Gleichung $m=\frac{y_2-y_1}{x_2-x_1}$ einsetzen, um die Steigung $m$ zu erhalten:

$\begin{array}[t]{rlll} m&=&\dfrac{0-(-9)}{(-7)-(-4)} \\[5pt] &=& \dfrac{9}{-3}\\[5pt] &=& -3 \end{array}$

$S$ und $m$ in die Geradengleichung $y=mx+b$ einsetzen und nach $b$ auflösen:

$\begin{array}[t]{rlll} y&=&mx+b \\[5pt] -9&=&(-3)\cdot (-4)+b \\[5pt] -9&=&12+b \\[5pt] b&=&-21 \end{array}$

So ergibt sich folgende Gleichung für die Gerade $g$ :

$g:y=-3x-21$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

	min	$q_u$	$z$	$q_0$	max
Umfrage Dienstag	$50$	$60$	$90$	$120$	$150$
Umfrage Freitag	$50$	$60$	$90$	$100$	$150$