Wahlteil B

Aufgabe 1

Im rechtwinkligen Trapez $ABCD$ liegt das rechtwinklige Dreieck $AEC.$

Es gilt:

$\overline{AD}=3,8\;\text{cm}$

$\overline{AB}=12,9\;\text{cm}$

$\alpha_1=65,0^\circ$

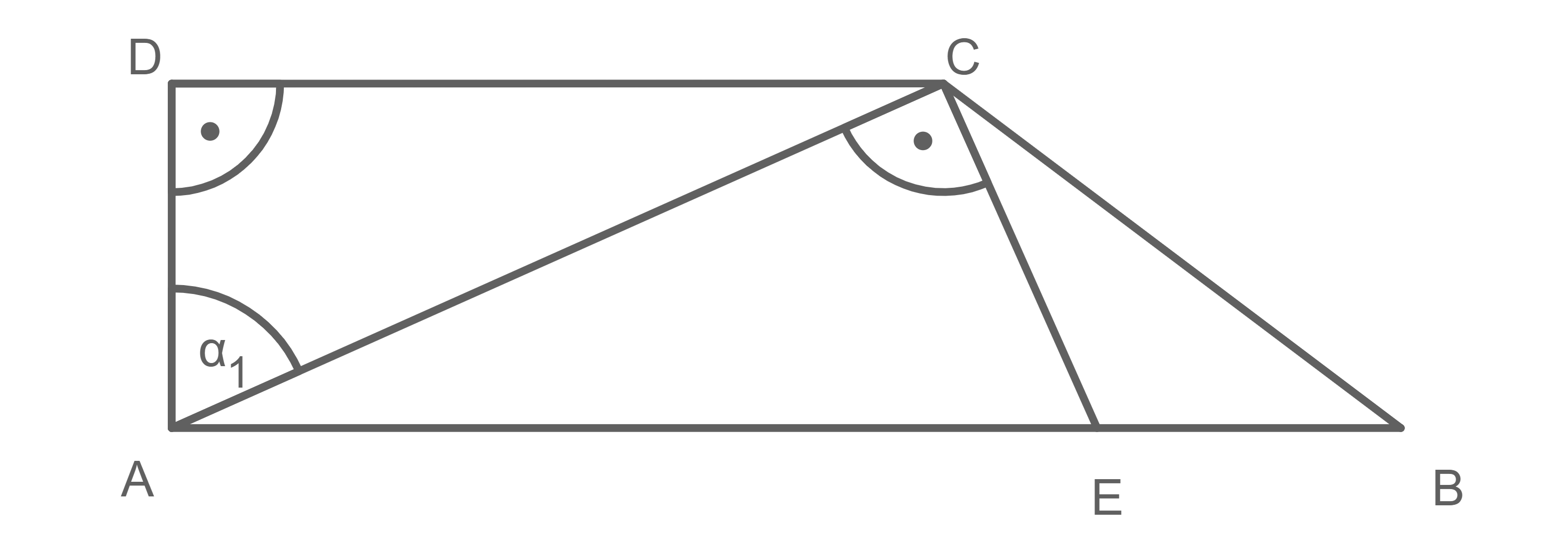
Geometrische Darstellung mit Figuren und Winkeln in einem Rechteck und Dreieck.

Berechne den Umfang des Dreiecks $EBC.$

(5 P)

Die Parabel $p_1$ mit der Funktionsgleichung $y = 0,25x^2 + c$ geht durch den Punkt $C(2\mid7).$

Berechne die Funktionsgleichung von $p_1.$

Die Parabel $p_2$ ist eine verschobene, nach oben geöffnete Normalparabel mit den beiden Punkten $A(0\mid-1)$ und $B(-1\mid2).$ Sie hat den Scheitelpunkt $S_2.$

Berechne die Funktionsgleichung von $p_2.$

Die Parabel $p_3$ mit dem Scheitelpunkt $S_3$ hat die Funktionsgleichung $y =(x - 5)^2 -2.$

Die Punkte $S_2$ , $S_3$ und $C$ bilden das Dreieck $S_2S_3C.$

Berechne den Flächeninhalt des Dreiecks $S_2S_3C.$

Der Punkt $C$ bewegt sich auf der Parabel $p_1.$
Dadurch entsteht der Punkt $C_1$ und somit das Dreieck $S_2S_3C_1.$

Für welchen Punkt $C_1$ hat das Dreieck $S_2S_3C_1$ den kleinsten Flächeninhalt?
Gib die Koordinaten von $C_1$ an. Begründe.

(5 P)

Aufgabe 2

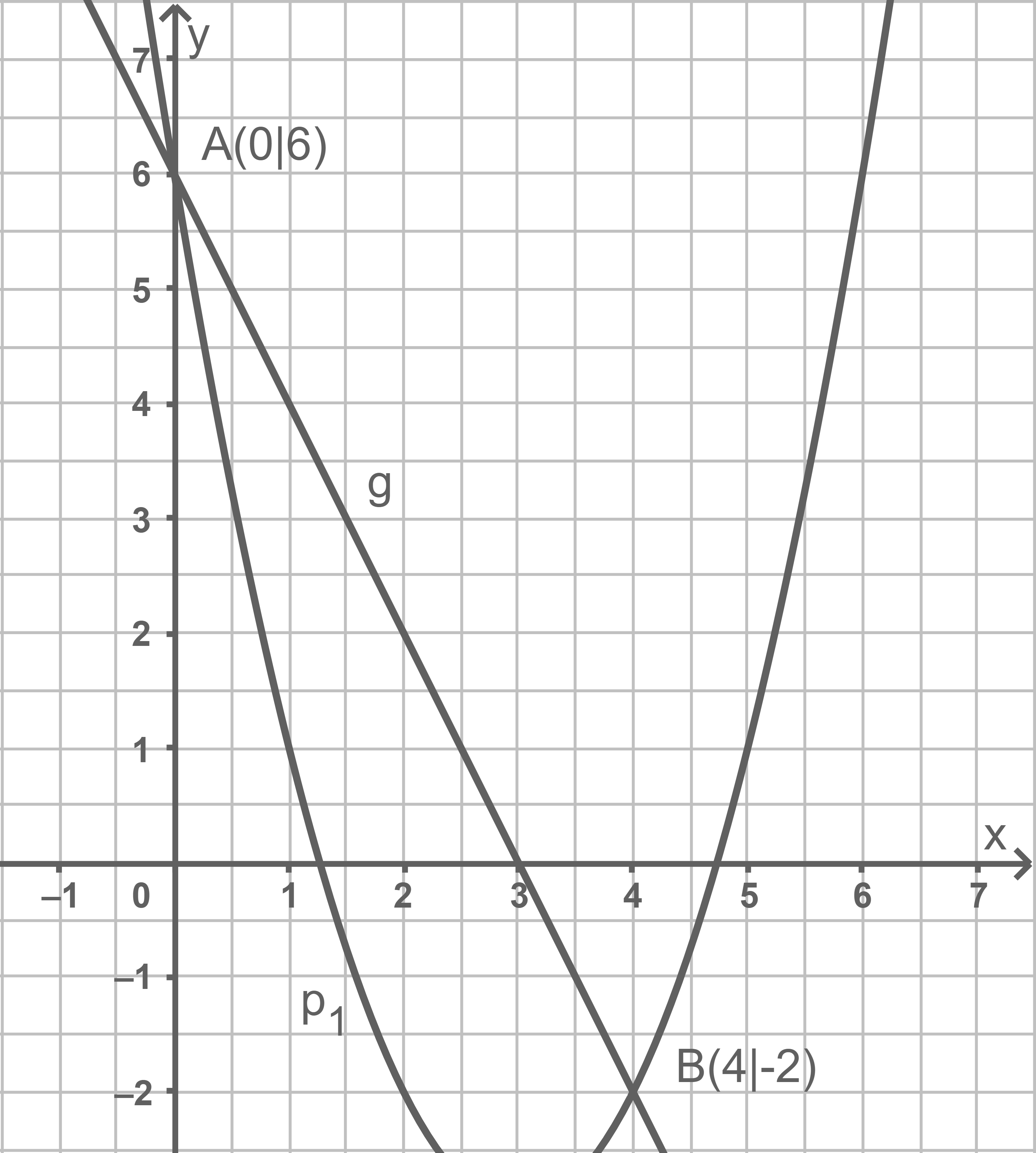
Die Abbildung zeigt die verschobene Normalparabel $p_1$ und die Gerade $g.$
Die Gerade $g$ schneidet die Parabel $p_1$ in den Punkten $A$ und $B.$

Bestimme die Funktionsgleichungen von $p_1$ und $g.$ Entnimm geeignete Werte aus dem Schaubild.

Die Parabel $p_2$ hat die Funktionsgleichung $y = x^2 + bx + 37,5$ und geht durch den Punkt $C(5\mid2,5).$

Berechne die Koordinaten des Scheitelpunkts $S_2$ von $p_2.$

Die Gerade $h$ ist senkrecht zu $g$ und geht durch den Scheitelpunkt $S_2$ von $p_2.$

Berechne die Funktionsgleichung der Geraden $h.$

Die Gerade $h$ schneidet die Gerade $g$ im Punkt $D.$

Berechne die Entfernung von $S_2$ zu $D.$

Graph mit zwei Funktionen und Koordinatenpunkten A und B auf einem Koordinatensystem.

(5 P)

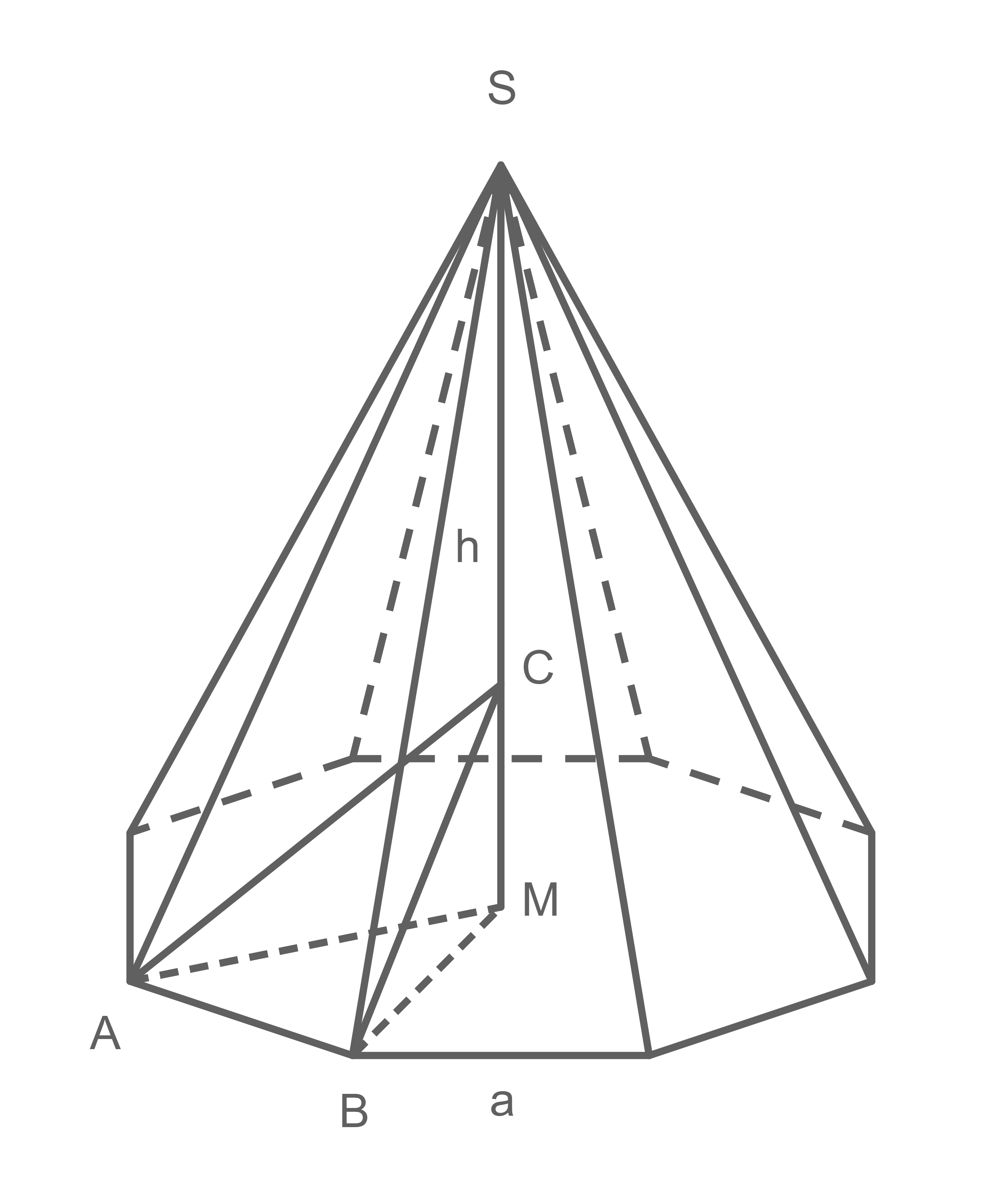
Von einer regelmäßigen achtseitigen Pyramide sind bekannt:

$a = 6,2\;\text{cm}$ (Grundkante)

$h = 14,4\;\text{cm}$ (Höhe der Pyramide)

Berechne den Flächeninhalt des Manteldreiecks $ABS.$

Der Punkt $C$ liegt auf der Höhe $h.$ Der Flächeninhalt des Dreiecks $ABC$ beträgt $27,9\,\text{cm}^{2}.$

Berechne die Länge der Strecke $\overline{SC}.$

Diagramm eines geometrischen Körpers mit Punkten S, A, B, C und M. Linien und Höhen sind eingezeichnet.

(5 P)

Aufgabe 3

Die Klasse 9c sammelt 2-Euro-Münzen für ein Glücksspiel. In einem Behälter liegen drei französische, sieben spanische und zehn deutsche Münzen. Es werden zwei Münzen gleichzeitig gezogen.

Berechne die Wahrscheinlichkeit, zwei Münzen aus verschiedenen Ländern zu ziehen.

Für das Glücksspiel wird der abgebildete Gewinnplan verwendet.

Berechne den Erwartungswert. Macht die Klasse 9c auf lange Sicht Gewinn?

Die Klasse 9c plant bei dem Glücksspiel langfristig $20\,\text{Cent}$ pro Spiel zu gewinnen.

Wie hoch müsste dann der Gewinn für "zwei französische Münzen" sein, wenn alles andere unverändert bleibt? Berechne.

(5 P)

2-Euro-Münze aus Deutschland mit dem Jahr 2009 und dem Motiv des Saarlandes.

Ereignis	Gewinn
zwei französische Münzen	$20,00\,\text{€}$
zwei spanische Münzen	$5,00\,\text{€}$
zwei deutsche Münzen	$2,00\,\text{€}$
Einsatz pro Spiel:	$1,50\,\text{€}$

Bild einer Münze mit dem Porträt eines Mannes und Blattmotiven, geprägt im Jahr 2002.

Unknown authorUnknown author, 2 Euro, Italy, CC BY 4.0

Das Foto zeigt das Viaduc de Garabit in Frankreich.

Die beiden Bögen der Brücke sind annähernd parabelförmig.

Sie haben auf der Höhe der beiden Betonsockel eine Spannweite von $165\;\text{m}.$

Die beiden Bögen enden auf den beiden Betonsockeln in einer Höhe von $47\;\text{m}$ über der Wasseroberfläche.

Der obere Bogen hat über der Wasseroberfläche eine maximale Höhe von $122\;\text{m}.$

Rote Stahlbogenbrücke über ruhigem Fluss zwischen bewaldeten Hängen unter leicht bewölktem Himmel

Pymouss, Anglards-de-Saint-Flour - Viaduc de Garabit 20200813-02, CC BY-SA 4.0

Berechne eine mögliche Funktionsgleichung für den oberen Brückenbogen.

Der untere Bogen kann mit einer Funktionsgleichung der Form $y = ax² + c$ beschrieben werden. Für den Faktor $a$ des unteren Brückenbogens gilt: $a = -\frac{1}{100}.$

Wie groß ist der Abstand zwischen den höchsten Punkten der beiden Brückenbögen? Berechne.

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

Beim Punkt $A,$ bilden die Winkel $\sphericalangle DAC$ und $\sphericalangle CAE$ zusammen einen rechten Winkeln. Da $\sphericalangle DAC$ bekannt ist:

$\begin{array}[t]{rlll} 90^\circ-\sphericalangle \text{DAC}&=& \sphericalangle \text{CAE} \\[5pt] 90^\circ-65^\circ&=&25^\circ \end{array}$

Nun kann die Länge $\overline{AC}$ durch Längenbeziehungen innerhalb eines rechtwinkligen Dreiecks errechnet werden:

Rechenweg anzeigen

$\overline{AC}=8,99\;\text{cm}$

Das Gleiche Verfahren kann nun für die Strecken $\overline{DC}, \overline{CE}$ und $\overline{AE}$ verwendet werden.

$\overline{DC}:$

$\begin{array}[t]{rlll} \tan(\alpha_1)&=&\dfrac{Gegenkathete}{Ankathete} \\[5pt] \tan(65^\circ)&=&\dfrac{\overline{DC}}{\overline{AD}} \\[5pt] \tan(65^\circ)&=&\dfrac{\overline{DC}}{3,8\;\text{cm}} &\mid\; \cdot 3,8\;\text{cm} \\[5pt] \overline{DC}&=&\tan(65^\circ)\cdot 3,8\;\text{cm} \\[5pt] \overline{DC}&=&8,15\;\text{cm} \end{array}$

$\overline{CE}:$

Rechenweg anzeigen

$\overline{CE}=4,19\;\text{cm}$

$\overline{AE}:$

Rechenweg anzeigen

$\overline{AE}=9,92\;\text{cm}$

Daraus folgt dann:

Rechenweg anzeigen

$\overline{EB}=2,98\;\text{cm}$

Um den Umfang des Dreiecks $EBC$ bestimmen zu können, muss die Strecke $CB$ ermittelt werden.

Senkrechte durch $C$ errichten:

Durch Punkt $C$ verläuft die Senkrechte $\overline{CF} \perp \overline{AB}.$ Sie ist ebenso lang wie die Höhe $\overline{AD}.$

Hilfsstrecke bestimmen:

$\overline{BF}=\overline{AB}-\overline{DC}=4,75\;\text{cm}$

Rechtwinkliges Dreieck $BCF$ betrachten:

Mit Hilfe des Satz des Pythagoras $\overline{BC}$ bestimmen:

$\overline{BC}^{2}=\overline{BF}^{2}+\overline{CF}^{2}$

Zahlenwerte einsetzen:

$\begin{array}[t]{rlll} \overline{BC}^{2}&=&4,75^{2}+3,8^{2} &\mid\; \sqrt{\;} \\[5pt] \overline{BC}&=&\sqrt{4,75^{2}+3,8^{2}} \\[5pt] \overline{BC}&=&6,08\;\text{cm} \end{array}$

Der Umfang $\overline{EBC}$ ergibt sich aus:

Rechenweg anzeigen

$\overline{EBC}=13,3\;\text{cm}$

Der Umfang des Dreiecks $EBC$ beträgt $13,3\;\text{cm}.$

Punkt $C(2\mid 7)$ in $p_1$ einsetzen und nach $c$ auflösen:

$\begin{array}[t]{rlll} 7&=&0,25\cdot 2^2+c \\[5pt] 7&=&1+c \\[5pt] c&=&6 \end{array}$

Somit lautet die Funktionsgleichung der Parabel $p_1:y=0,25x^2+6.$

Zur Berechnung von $p_2$ wird die Scheitelpunktform $y=(x-p)^2+q$ benötigt. Dabei ist $(p\mid q)$ der Scheitelpunkt.

$A(0\mid -1)$ und $B(-1\mid 2)$ einsetzen.

Punkt $A(0\mid -1)$ einsetzen:

$\begin{array}[t]{rlll} -1&=&(0-p)^2+q \\[5pt] -1&=&p^2+q \\[5pt] q&=&-1-p^2 \end{array}$

Gleichung $(1)$ : $q=-1-p^{2}$

Punkt $B(-1\mid 2)$ einsetzen:

$\begin{array}[t]{rlll} 2&=&(-1-p)^2+q \\[5pt] 2&=&(1+p)^2+q \end{array}$

Gleichung $(2).$

Gleichung $(1)$ in $(2)$ einsetzen:

$2=(p+1)^2+(-1-p^2)$

Vereinfachen mit Binomischer Formel :

$\begin{array}[t]{rlll} 2&=&(p^2+2p+1)-1-p^2 \\[5pt] 2&=&2p \\[5pt] p&=&1 \end{array}$

$p$ in Gleichung $(1)$ einsetzen um $q$ zu erhalten:

$\begin{array}[t]{rlll} q&=&-1-(1)^2 \\[5pt] q&=&-1-1 \\[5pt] q&=&-2 \end{array}$

Damit lautet die Parabel $p_2:y=(x-1)^2-2$ bzw. $y=x^2-2x-1$ mit dem Scheitelpunkt $S_2(1\mid-2).$

Aus $p_3:y=(x-5)^2-2$ ergibt sich der Scheitelpunkt $S_3=(5\mid -2).$

Damit liegen $S_2(1\mid-2)$ , $S_3(5\mid-2)$ und $C(2\mid7)$ vor.

Die Strecke $S_2S_3$ liegt waagerecht, da beide $y$ -Koordinaten gleich sind.

Länge der Strecke:

$\left| S_2S_3\right|=5-1=4.$

Diese Strecke nehmen wir als Grundseite an.

Die Höhe ergibt sich als senkrechter Abstand des Punktes $C$ zur Grundseite.

Da unsere Grundseite bei $y=-2$ liegt und der Punkt $C$ den Wert $y=7$ hat, lässt sich die Höhe wie folgt bestimmen:

$h=7-(-2)=9$

Flächeninhalt eines Dreiecks:

$A=\frac{1}{2}\cdot \text{Grundseite}\cdot \text{Höhe}.$

Grundseite und Höhe einsetzen:

$A=\frac{1}{2}\cdot 4\cdot 9= 18$

$A_{S_2S_3C}=18FE$

Die Grundseite $S_2S_3$ bleibt gleich. Die dazugehörige Höhe nimmt für $C_1 = S_1$ den kleinsten Wert an.

Mögliche Begründung:

Nur der Punkt $C_1$ liegt auf $p_1:y=0,25x^2+6.$

Die Grundseite $\overline{S_2S_3}$ bleibt dieselbe, waagerecht auf $y=-2$ mit der Länge $4$ .

Da $p_1:y=0,25x^2+6$ nach oben geöffnet und über der Grundseite liegt, tritt das Minimum im Scheitelpunkt auf.

Also muss der Scheitelpunkt bestimmt werden, indem die Funktionsgleichung in Scheitelpunktform gebracht wird:

$p_1:y=0,25x^2+6=0,25(x-0)^{2}+6$

Hieraus folgt:

$S_1(0\mid 6)$

Somit ist der Flächeninhalt von $A_{S_{2}S_{3}C}$ am kleinsten wenn $C_{1}$ der Scheitelpunkt von $p_{1}$ ist.

Lösung 2

Eine veschobene Normalparabel hat die Form $y=(x-p)^{2}+q.$

Punkt $A(0\mid6)$ einsetzen:

$\begin{array}[t]{rlll} 6&=&(0-p)^2+q \\[5pt] 6&=&p^2+q \\[5pt] q&=&6-p^2 \end{array}$

Punkt $B(4\mid -2)$ einsetzen:

$\begin{array}[t]{rlll} -2&=&(4-p)^2+q \\[5pt] \end{array}$

$q$ einsetzen:

Rechenweg anzeigen

$p=3$

$p$ einsetzen, um $q$ zu erhalten:

$\begin{array}[t]{rlll} q&=&6-p^2 \\[5pt] q&=&6-3^2 \\[5pt] q&=&-3 \end{array}$

$p_1:y=(x-3)^2-3$ bzw. $y=x^2-6x+6.$

Gerade $g$ durch $A$ und $B$ aufstellen.

Steigung $m$ berechnen:

$m=\frac{-2-6}{4-0}=\frac{-8}{4}=-2$

$A$ oder $B$ in Punktsteigungsformel einsetzen. (Hier wurde der Punkt $A$ gewählt.)

$y=m(x-x_A)+y_A$

$y=-2(x-0)+6$

Somit ergibt sich folgende Funktionsgleichung für $g:$

$g:y=-2x+6$

Koordinaten des Scheitelpunkts von $p_2:y=x^2+bx+37,5$ berechnen.

Punkt $C$ einsetzen:

$\begin{array}[t]{rlll} 2,5&=&5^2+5b +37,5 \\[5pt] 2,5&=&5b+ 62,5\\[5pt] 5b&=&-60 \\[5pt] b&=&-12 \end{array}$

$p_2:y=x^2-12x+37,5$

Die Funktionsgleichung liegt in quadtratischer Form ( $y=x^2+b\cdot x+q$ ) vor, dementsprechend können die Koordinaten des Scheitelpunkts wie folgt errechnet werden:

$S_2(-\frac{p}{2}\mid-(\frac{p}{2})^2+q)$

$p$ und $q$ einsetzen:

$S_2(-(\frac{-12}{2})\mid-(\frac{-12}{2})^2+37,5)=(6\mid1,5)$

Als nächstes soll die Funktionsgleichung einer Gerade $h$ gefunden werden, die senkrecht zu $g$ verläuft und durch $S_2$ geht.

Für senkrechte Geraden gilt: $m_g\cdot m_h=-1.$

$\begin{array}[t]{rlll} (-2)\cdot m_h&=&-1 \\[5pt] m_h&=&\dfrac{1}{2} \\[5pt] \end{array}$

$m=\frac{1}{2}$ und $S_2$ in die Punktsteigungsform $y-y_0=m(x-x_0)$ mit $(x_0\mid y_0)=(6\mid 1,5)$ einsetzen:

$\begin{array}[t]{rlll} y-1,5&=&\dfrac{1}{2}(x-6) \\[5pt] y-1,5&=&\dfrac{1}{2}x-3 &\mid\; +1,5\\[5pt] y&=&\dfrac{1}{2}x-1,5 \\[5pt] \end{array}$

Daraus folgt:

$h:y=\frac{1}{2}x-1,5$

Entfernung zwischen den Punkten $S_2$ und $D$ bestimmen. Da $D$ der Schnittpunkt von $h$ und $g$ ist, wird er durch Gleichsetzen der beiden Geradengleichungen berechnet.

$\begin{array}[t]{rlll} \dfrac{1}{2}x-1,5&=&-2x+6 \\[5pt] 2,5x&=&7,5 \\[5pt] x&=&3 \\[5pt] \end{array}$

$x$ -Koordinate in $h$ oder $g$ einsetzen um die $y$ -Koordinate zu erhalten.

$g:y=(-2)\cdot 3+6=0$

Daraus folgt:

$D(3\mid0)$

Abstand zwischen zwei Punkten:

$d=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^2}$

Zahlenwerte einsetzen:

$\begin{array}[t]{rlll} d &=&\sqrt{(6-3)^2+(1,5-0)^2} \\[5pt] &=& \sqrt{3^2+1,5^2} \\[5pt] &=& \sqrt{11,25}\\[5pt] &=& \dfrac{3}{2}\sqrt{5} \\[5pt] &\approx&3,35 \end{array}$

Die Entfernung zwischen dem Punkt $S_2$ und $D$ beträgt ca. $3,35\;\text{LE}.$

Für den Flächeninhalt des Dreiecks $ABS$ , wird dessen Höhe benötigt.

Diese lässt sich über das Apothem bestimmen. Dies ist der senkrechte Abstand vom Mittelpunkt $M$ der Grundfläche zur Mitte der Seite $AB.$

Das regelmäßige Achteck hat einen Mittelpunktswinkel von $45^\circ.$ Für die halbe Grundseite gilt:

$\frac{45^\circ}{2}=22,5^\circ.$

Einsetzen in die Tangens-Formel:

$\tan(22,5^\circ) = \dfrac{\frac{a}{2}}{r}.$

Daraus folgt:

Rechenweg anzeigen

$r\approx 7,5\;\text{cm},$

Schräghöhe $l$ berechnen:.

Hierfür das rechtwinkliges Dreieck mit $h = 14,4\;\text{cm}$ und $r = 7,5\;\text{cm}$ betrachten.

Nach dem Satz des Pythagoras gilt:

Rechenweg anzeigen

$l\approx 16,2\;\text{cm}$

Flächeninhalt des Dreiecks $ABS$ bestimmen:

Rechenweg anzeigen

$A_{ABS}\approx 50,3\;\text{cm}^{2}$

Als letztes ist die Strecke $\overline{SC}$ gesucht.

Flächenformel des Dreiecks $ABC$ mit Basis $AB: A_{ABC}=\frac{1}{2}\cdot AB \cdot p$

Umstellen, um Abstand $p$ zu bestimmen:

$p=\frac{2\cdot A_{ABC}}{a}=\frac{2\cdot 27,9}{6,2}=9,0\;\text{cm}.$

$C$ liegt auf $\overline{SM}.$ Der senkrechte Abstand $p$ setzt sich rechtwinklig aus Apothem $r$ und der Höhe $CM$ zusammen.

Daher gilt im rechtwinkligen Dreieck: $p^2=r^2+CM^2.$

Nach $CM$ umformen und Zahlenwerte einsetzen:

Rechenweg anzeigen

$CM\approx 5,0\;\text{cm}$

Die gesamte Pyramidenhöhe beträgt $h=14,4\;\text{cm}.$ Strecke von der Spitze $S$ bis zu $C$ :

Rechenweg anzeigen

$SC=9,4\;\text{cm}$

Die Länge der gesuchten Strecke $SC$ beträgt $9,4\;\text{cm}.$

Lösung 3

Ausgangswahrscheinlichkeiten:

Rechenweg anzeigen

$P(\text{F-Münze})=\frac{3}{20}$

Wahrscheinlichkeit für zwei Münzen aus verschiedenen Ländern zu ziehen:

Rechenweg anzeigen

$P(\text{verschiedene Länder})=\frac{121}{190}$

Rechenweg anzeigen

$P(2F)=\frac{3}{190}$

Erwartungswert berechnen:

Rechenweg anzeigen

$E=-0,16\,\text{€}$

Der Spieler verliert im Mittel $16\;\text{Cent}.$ Folglich macht die Klasse auf lange Zeit Gewinn.

Für einen geplanten Gewinn von $0,20\,\text{€}$ wird $E=-0,20\,\text{€}$ gesetzt und die Auszahlung von $P(2F)$ mit $x$ bezeichnet. Daraus ergibt sich die Gleichung:

Rechenweg anzeigen

Nach $x$ aufgelöst ergibt sich eine neue Auszahlung von $17,33\,\text{€}$ für $P(2F)$ , damit langfristig ein Gewinn von $0,20\,\text{€}$ erreicht wird.

Die $y$ -Achse verläuft durch den höchsten Punkt des Brückenbogens $S(0\mid 122).$ Für diesen Lösungsansatz wurde Die $x$ -Achse liegt auf der Wasseroberfläche.