Pflichtteil A1

Aufgabe 1

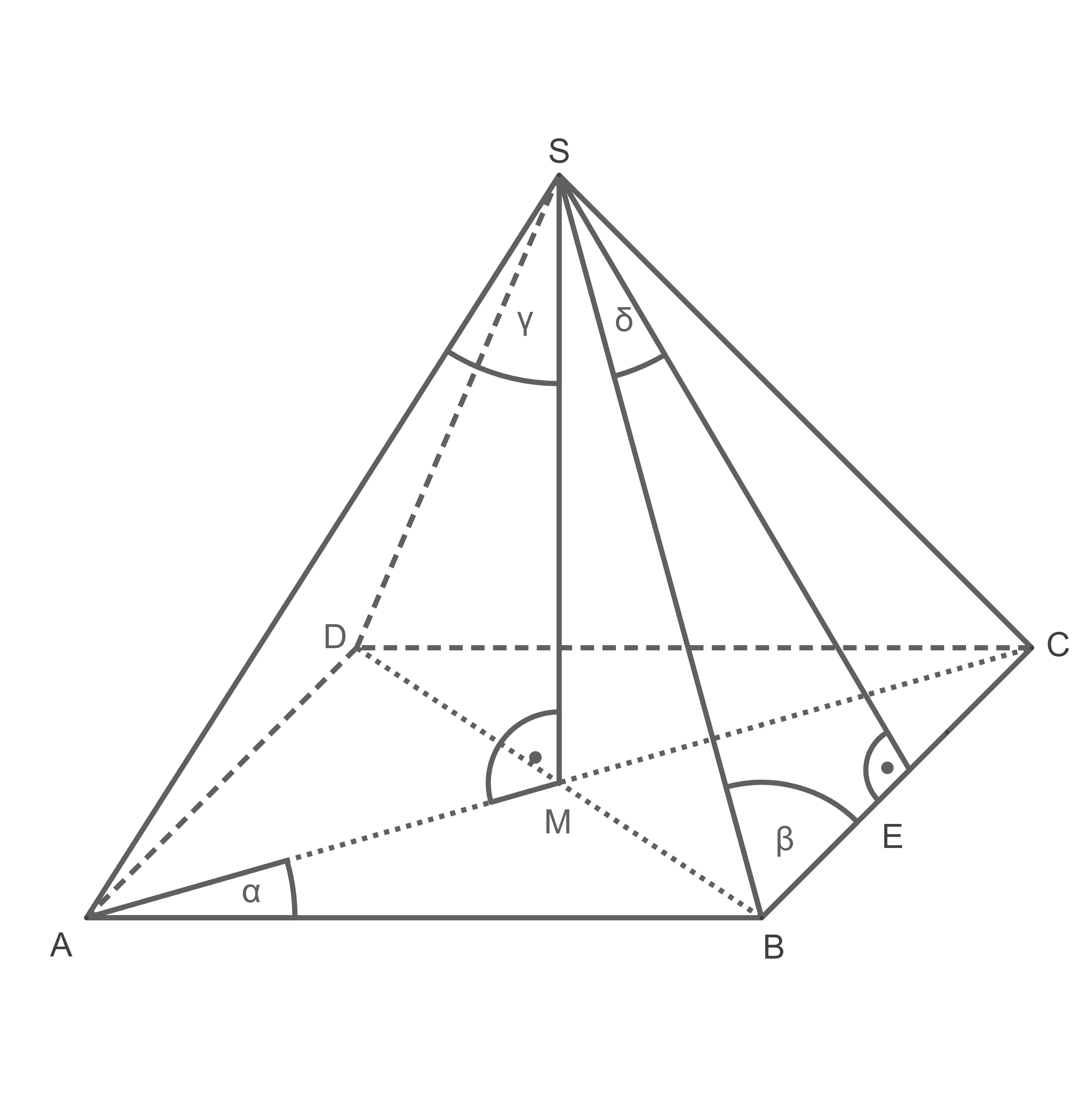
Gegeben ist die abgebildete quadratische Pyramide.

Vervollständige die Gleichungen.

$\sin \gamma=\quad$
	$\overline{AS}$

$\quad = \dfrac{\overline{SE}}{\overline{BE}}$

$\cos\alpha=\quad$	$\overline{AB}$

Diagramm eines geometrischen Problems mit einem Dreieck und verschiedenen Linien und Winkeln.

(1,5 P)

Aufgabe 2

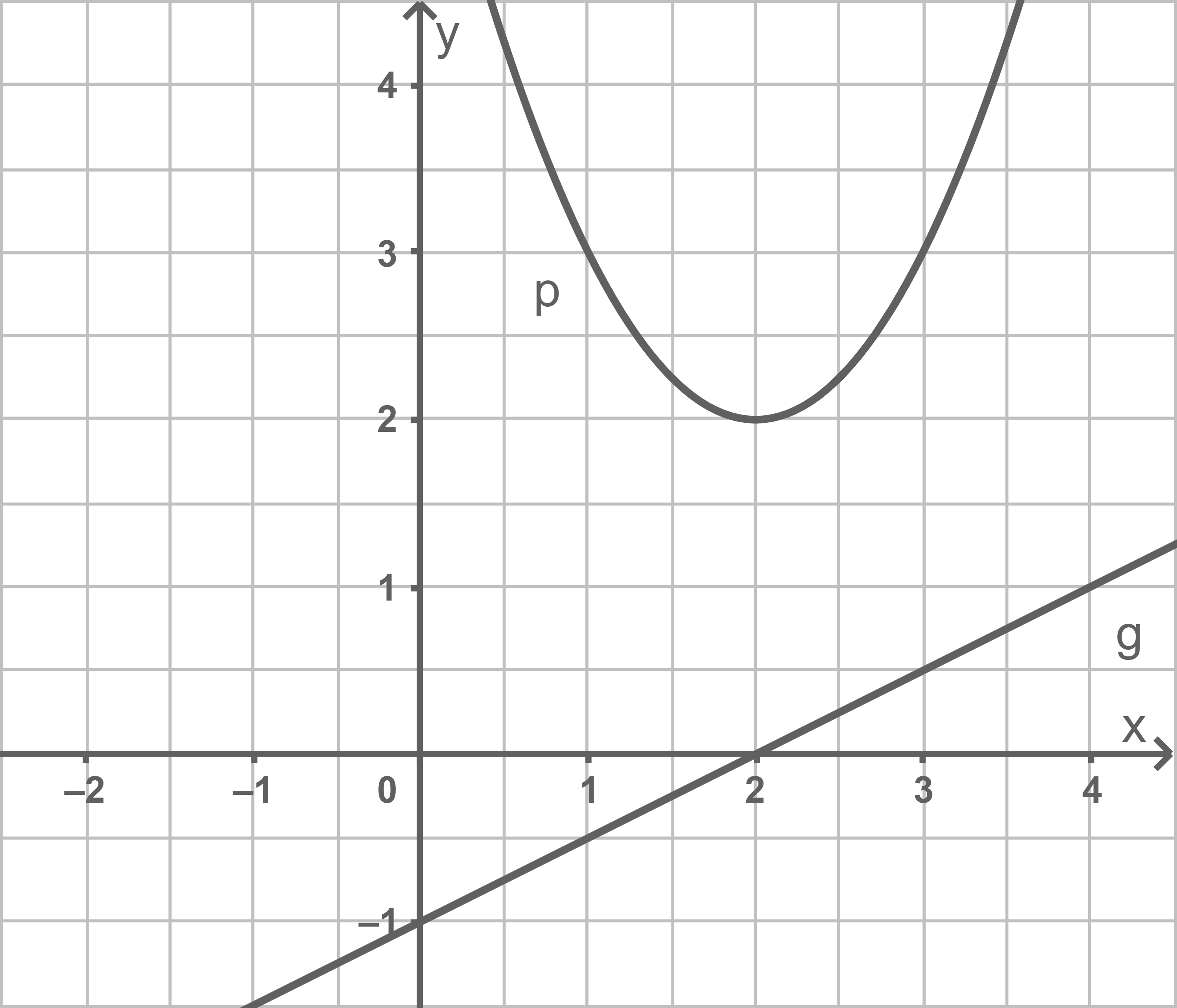
Benjamin hat die verschobene Normalparabel $p$ mit der Funktionsgleichung $y=x^{2}+4x+6$ und die Gerade $g$ mit der Funktionsgleichung $y=2x-1$ falsch gezeichnet.

Welche Fehler hat Benjamin gemacht? Beschreibe die Fehler.

Graph einer Parabel und einer linearen Funktion in einem Koordinatensystem.

(1,5 P)

Aufgabe 3

Löse die Gleichung.

$3x(x+1)-10=5+x+2x^{2}$

(2 P)

Aufgabe 4

Setze das richtige Zeichen $(\lt;=;\gt)$ ein.

$\sin\,10^\circ$  $\sin\, 110^\circ$

$\sin \,50^\circ$  $\sin \, 150^\circ$

(1 P)

Aufgabe 5

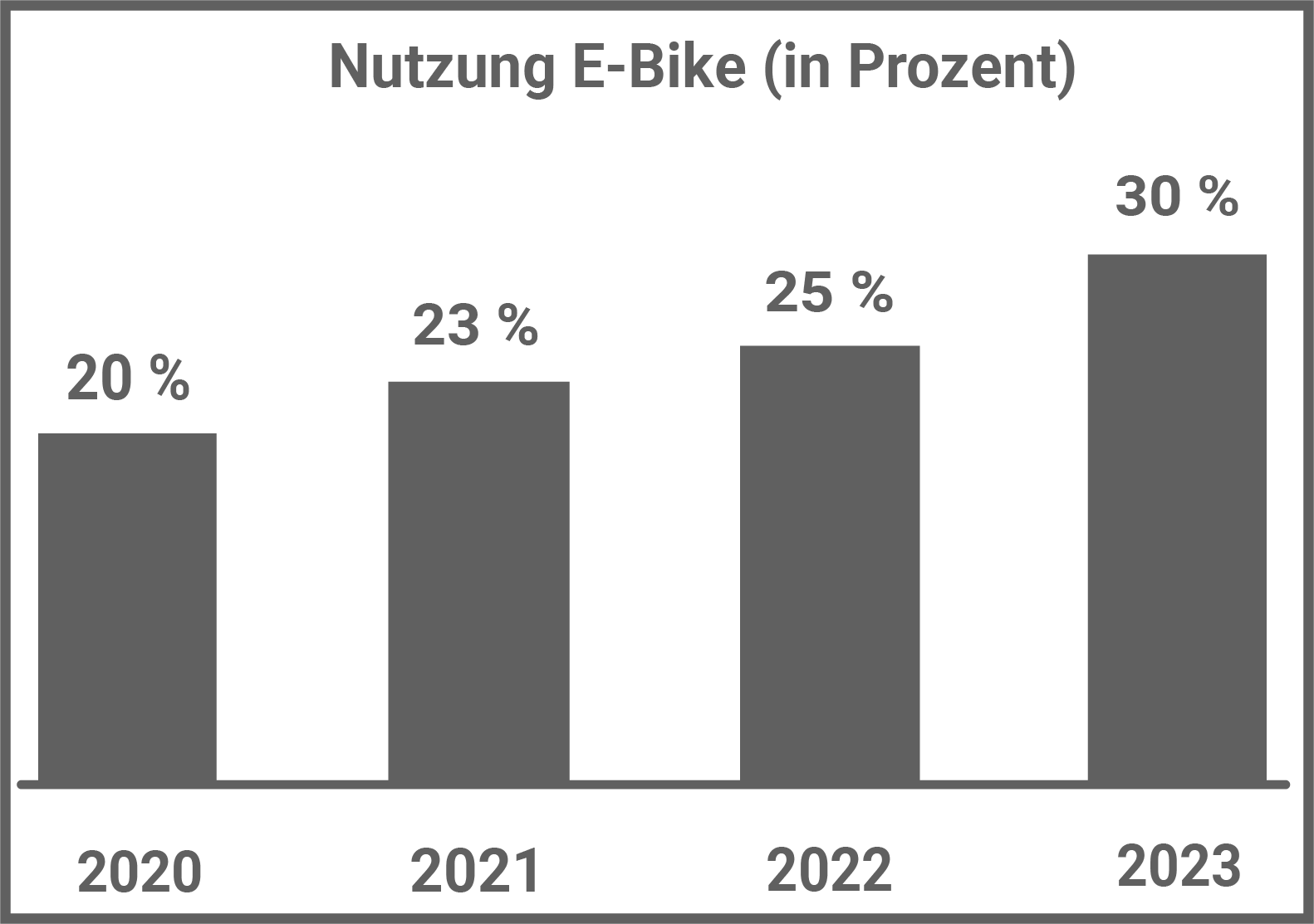
Das Diagramm zeigt die Nutzung von E-Bikes in den Jahren von 2020 bis 2023. Jedes Jahr wurden jeweils 6000 Personen befragt.
Im Diagramm sind die Ergebnisse dieser jährlichen Umfrage in Prozent dargestellt.

Wie viele der befragten Personen nutzten im Jahr 2023 ein E-Bike?
Berechne.

Von den Personen, die im Jahr 2022 ein E-Bike nutzten, waren $40\,\%$ älter als 60 Jahre.

Wie viele Personen waren das?
Berechne.

Balkendiagramm zur Nutzung von E-Bikes in Prozent von 2020 bis 2023.

(1,5 P)

Aufgabe 6

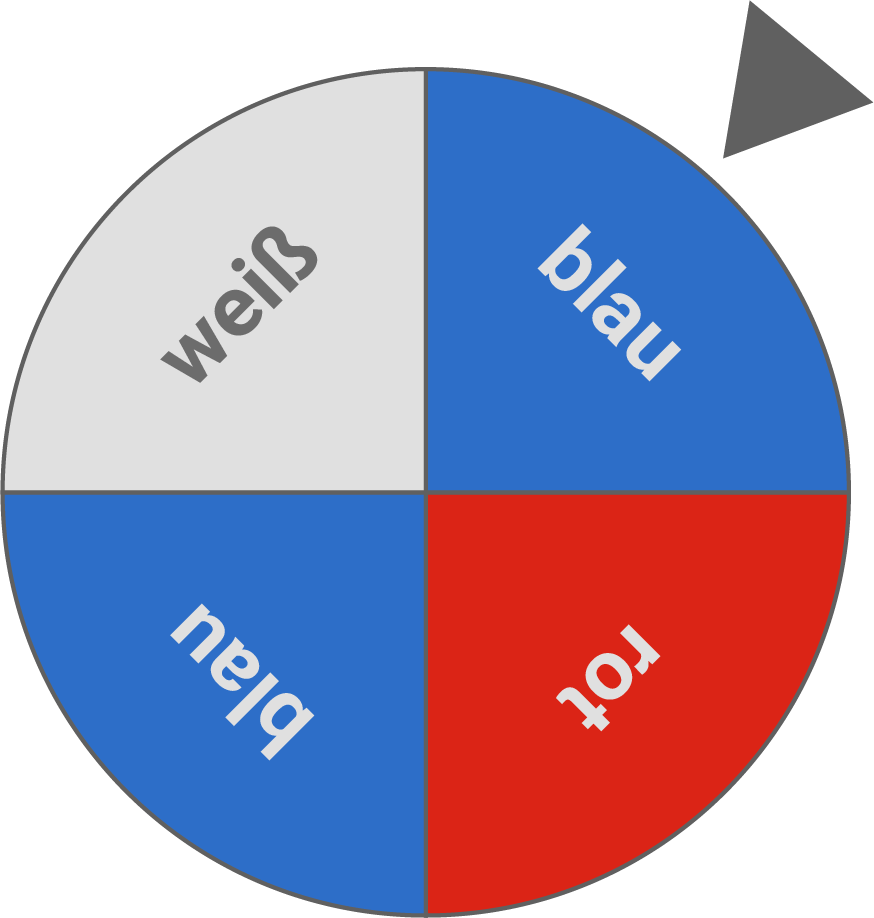
Das abgebildete Glücksrad wird zweimal gedreht.

Berechne die Wahrscheinlichkeit des Ereignisses.

$P(\text{zweimal blau})$

$P(\text{höchstens einmal weiß})$

Farbenspiel mit einem Rad, unterteilt in vier Abschnitte: blau, rot, weiß und blau.

(1 P)

Aufgabe 7

Eva hat drei Muster aus Holzstäbchen gelegt.
Dabei liegt keines der Holzstäbchen über einem anderen.

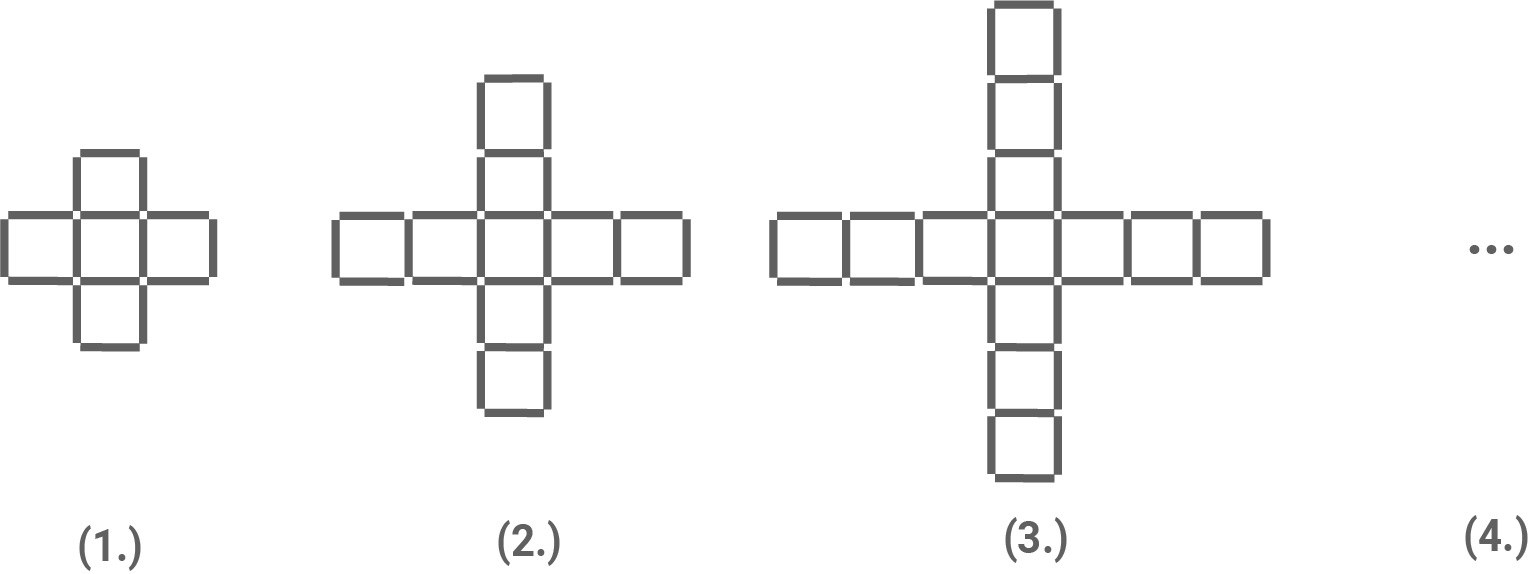
Grafische Darstellung von Mustern mit Kästchen in verschiedenen Anordnungen.

Eva möchte die Anzahl der Holzstäbchen bei jedem Muster berechnen.
Sie überlegt:
„Das erste Muster besteht aus vier Holzstäbchen in der Mitte und zwölf Holzstäbchen außen herum. Beim zweiten Muster kommen zwölf Holzstäbchen dazu."

Welche der beiden Formeln

$s=12n+4$ oder $s=4n+12$

kann nicht für die Berechnung der Anzahl der
Holzstäbchen verwendet werden?
Begründe deine Entscheidung.

$\rightarrow$ $n$ gibt die Stelle des jeweiligen Musters an
$\rightarrow$ $s$ ist die Anzahl der Holzstäbchen eines Musters

(1,5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\sin \gamma=\quad$	$\overline{AM}$
	$\overline{AS}$

$\tan\beta$

$\quad = \dfrac{\overline{SE}}{\overline{BE}}$

$\cos\alpha=\quad$	$\overline{AB}$
	$\overline{AC}$

Lösung 2

Ergebnis anzeigen

Lösung 3

Rechenweg anzeigen

$x_1=3 \quad x_2=-5$

Lösung 4

$\sin(10^\circ)\lt\sin(110^\circ)$

$\sin(50^\circ)\gt\sin(150^\circ)$

Lösung 5

$\begin{array}[t]{rlll} 30\,\% \text{ von }6000&=&\frac{30}{100}\cdot 6000\\[5pt] &=&1800 \end{array}$

Im Jahr 2023 gaben von $6000$ Befragten $1800$ Personen an, ein E-Bike zu nutzen.

1. Anzahl der E-Bike-Nutzer berechnen

$\begin{array}[t]{rlll} 25\,\% \text{ von } 6000&=&\frac{25}{100}\cdot 6000 \\[5pt] &=&1500 \end{array}$

2. Davon sind $40\,\%$ älter als 60 Jahre

$\begin{array}[t]{rlll} 40\,\% \text{ von } 1500&=& \frac{40}{100}\cdot1500\\[5pt] &=& 600 \end{array}$

$600$ Personen sind E-Bike-Nutzer und älter als $60$ Jahre.

Lösung 6

$\text{P(blau)}=\dfrac{2}{4}=\dfrac{1}{2}, \text{P(weiß)}=\dfrac{1}{4}$

$\text{P(zweimal blau)} = \text{P(blau)} \cdot \text{P(blau)} = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4}$ bzw. $25,\text{%}$

Fall 1: keinmal weiß

$\begin{array}[t]{rlll} \text{P(keinmal weiß)}&=&\dfrac{3}{4}\cdot\dfrac{3}{4} \\[5pt] &=&\dfrac{9}{16} \end{array}$

Fall 2: einmal weiß

Zwei Möglichkeiten: (weiß, nicht-weiß) oder (nicht-weiß, weiß)

$\begin{array}[t]{rlll} \text{P(einmal weiß)}&=&\dfrac{1}{4}\cdot\dfrac{3}{4}+\dfrac{3}{4}\cdot\dfrac{1}{4} \\[5pt] &=&\dfrac{6}{16} \end{array}$

Zusammenrechnen:

$\begin{array}[t]{rlll} \text{P(höchstens einmal weiß)}&=& \dfrac{9}{16}+\dfrac{6}{16}\\[5pt] &=&\dfrac{15}{16} \end{array}$

Lösung 7

Die Formel $s=4n+12$ kann nicht verwendet werden.

Rechnerische Begründung (Für das 2. Muster):

$\begin{array}[t]{rlll} s &=& 4n+12 \\[5pt] s(2) &=& 4\cdot 2+12 &=& 20 \\[5pt] 20 &\neq& 28 \end{array}$

Argumentative Begründung:

Bei dieser Formel kämen immer nur $4$ anstatt $12$ Stäbchen hinzu.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?