Pflichtbereich
Aufgabe P1
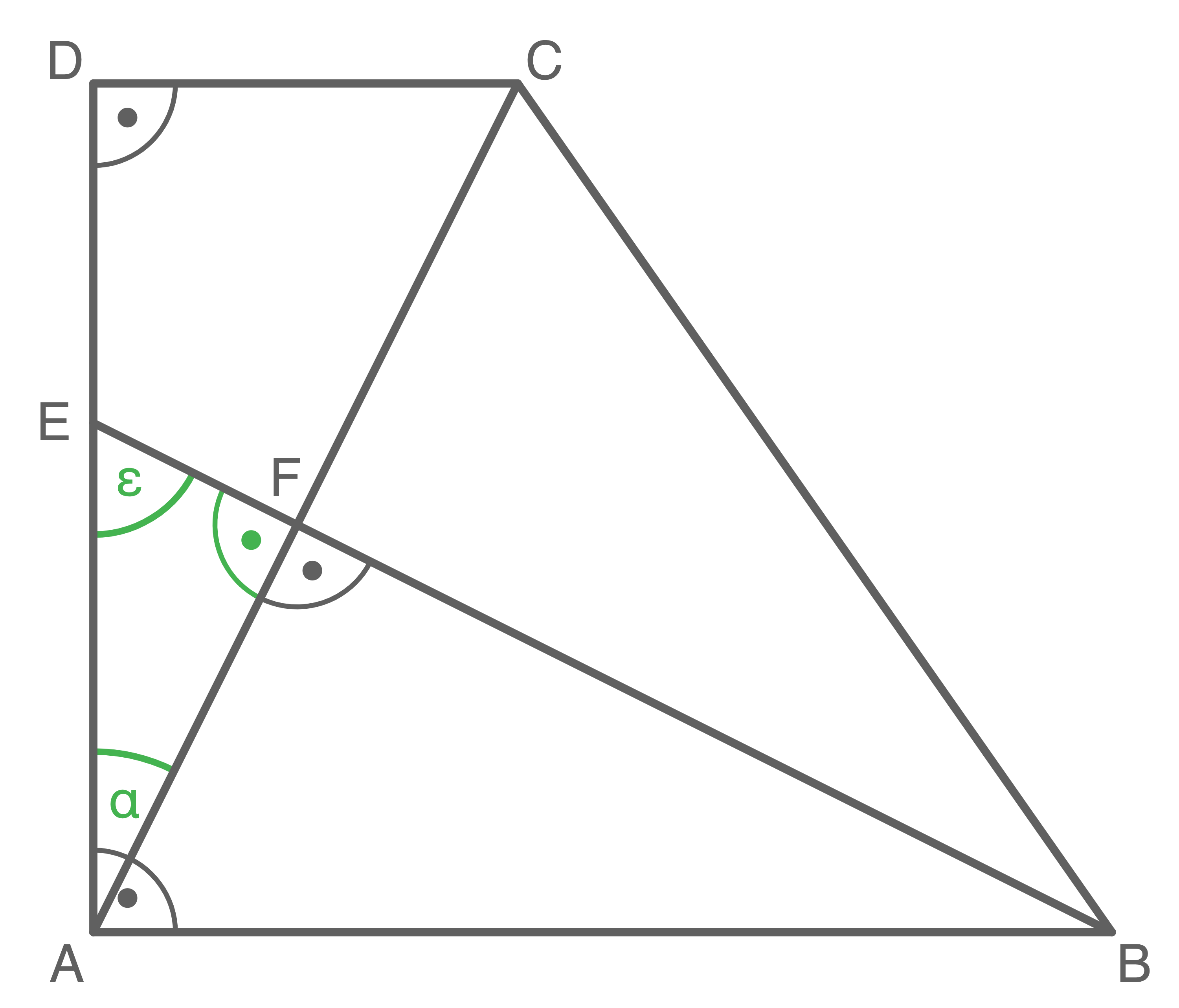
Gegeben ist das Dreieck  .
.
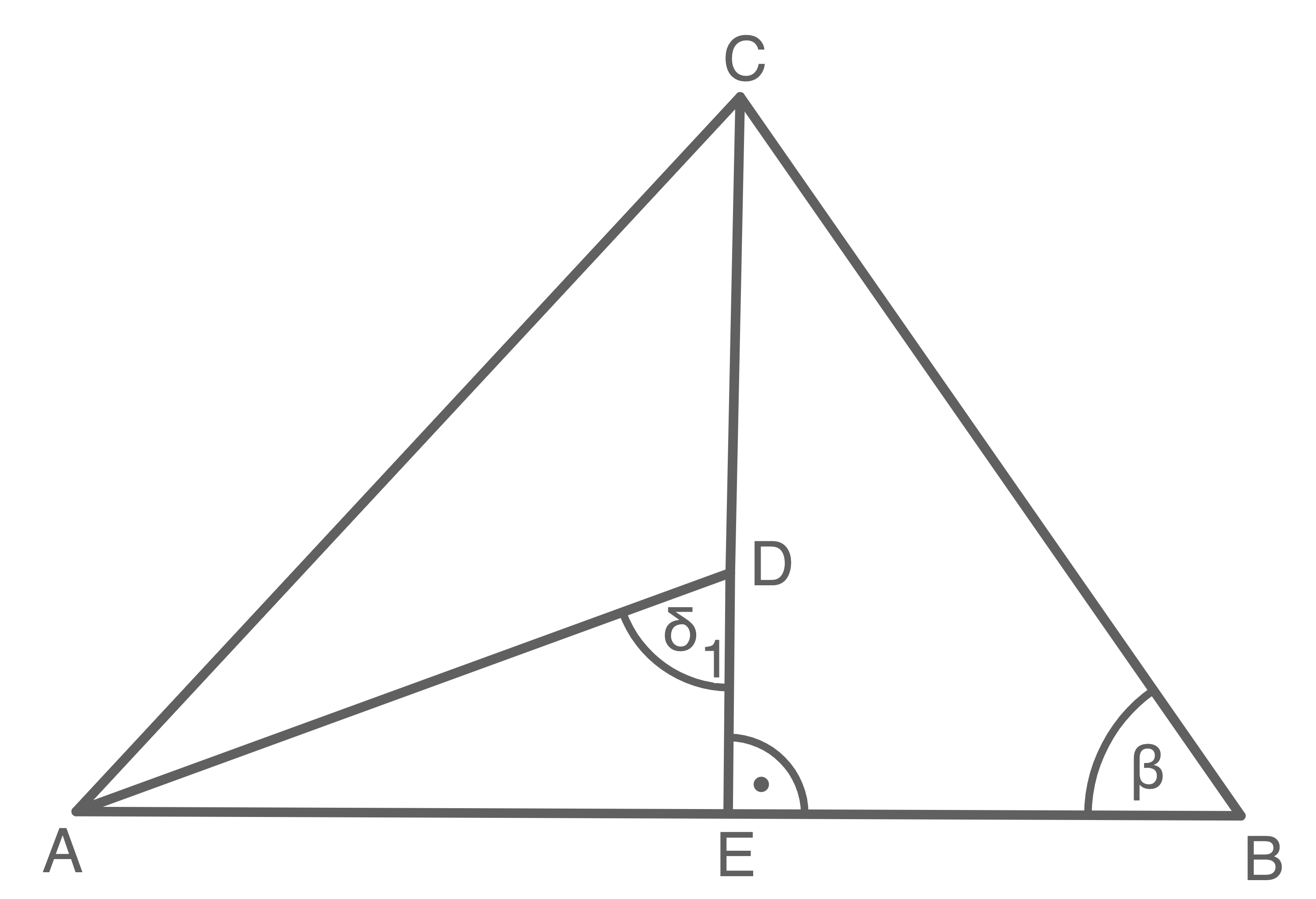 Es gilt:
Es gilt:
![\( \begin{array}[t]{rll}
\overline{BC}&=& 9,0\,\text{cm} \\[5pt]
\overline{AD}&=& 7,3\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/1c547b198142f63ded2730a3f2cde9adb74e4aee8b68a05ef0f3e8708508c607_light.svg)
![\( \begin{array}[t]{rll}
\beta\hspace{.385cm}&=& 55,0^\circ \\[5pt]
\delta_1\hspace{.385cm}&=& 69,4^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/3483a240d077ff877b27eb3f30cb85e103846b60e81ec105280d788fc5000574_light.svg) Berechne die Länge von
Berechne die Länge von  und den Flächeninhalt des Dreiecks
und den Flächeninhalt des Dreiecks  .
.

4 P
Aufgabe P2
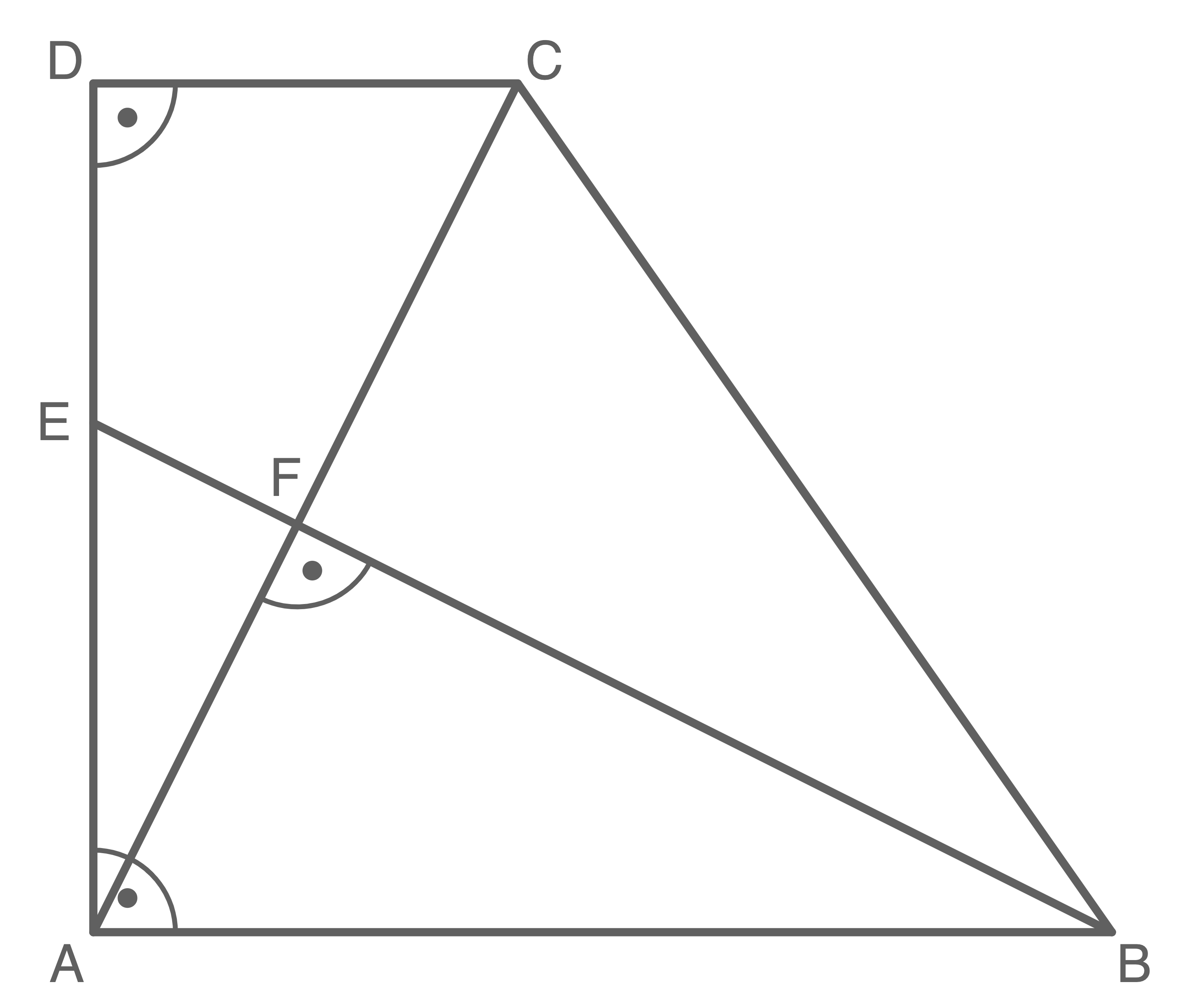
4,5 P
Aufgabe P3
Ein Zylinder und ein Kegel haben gleich große Mantelflächen. Die Durchmesser der beiden Grundflächen sind ebenfalls gleich.
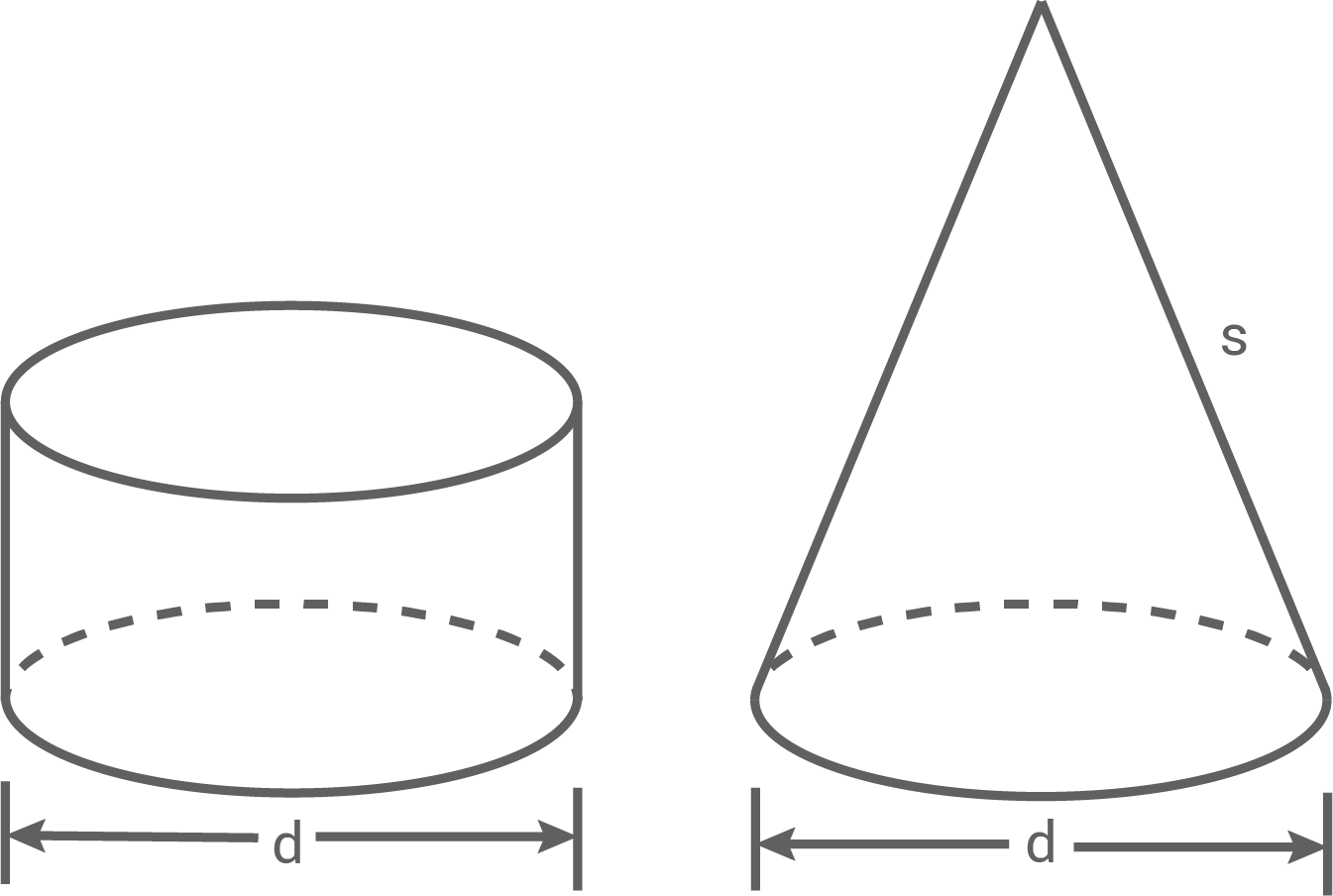 Es gilt:
Es gilt:

4 P
Aufgabe P4
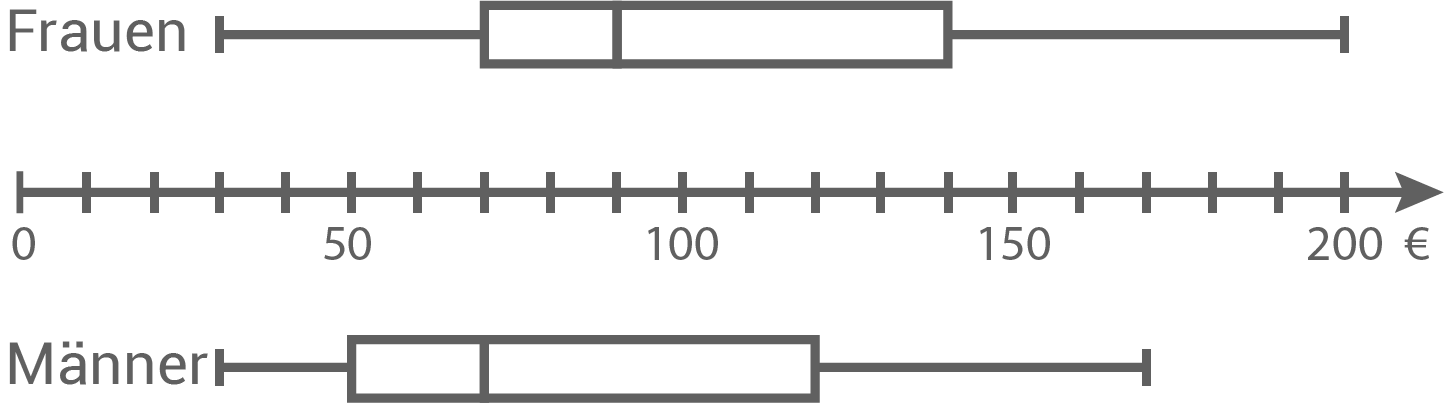
Bei einer Umfrage wurden Frauen und Männer getrennt befragt.
„Wie viele Euro haben Sie für Ihr zuletzt gekauftes Paar Schuhe bezahlt?“ Preise der Frauenschuhe in Euro (gerundet):
Vervollständige den zugehörigen Boxplot.
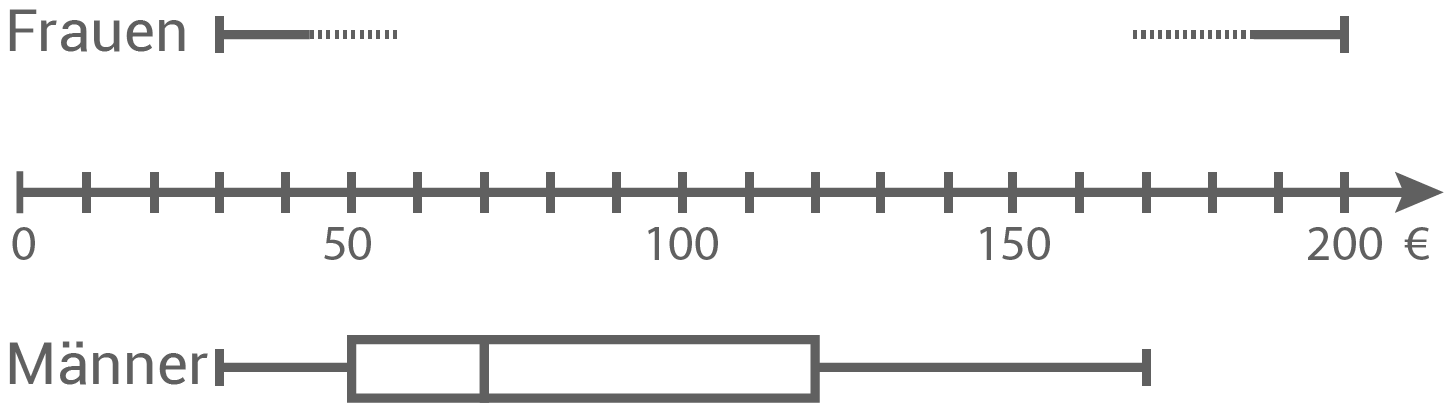 Zum Boxplot der Preise der Männerschuhe gehört die unvollständig ausgefüllte Rangliste. Ergänze passende Werte.
Preise der Männerschuhe in Euro (gerundet):
Zum Boxplot der Preise der Männerschuhe gehört die unvollständig ausgefüllte Rangliste. Ergänze passende Werte.
Preise der Männerschuhe in Euro (gerundet):
„Wie viele Euro haben Sie für Ihr zuletzt gekauftes Paar Schuhe bezahlt?“ Preise der Frauenschuhe in Euro (gerundet):
| 30 |
| 30 |
| 50 |
| 60 |
| 70 |
| 80 |
| 90 |
| 90 |
| 100 |
| 120 |
| 140 |
| 150 |
| 160 |
| 180 |
| 200 |

| Rang | Preis (€) |
|---|---|
| 1 | |
| 2 | 30 |
| 3 | |
| 4 | |
| 5 | 50 |
| 6 | 50 |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | 120 |
| 12 | 140 |
| 13 |
4 P
Aufgabe P5
Gib die Definitionsmenge und die Lösungsmenge der Gleichung an:


3,5 P
Aufgabe P6
Die Parabel  hat die Gleichung
hat die Gleichung 
Eine Gerade mit der Steigung
mit der Steigung  geht durch den Scheitelpunkt der Parabel
geht durch den Scheitelpunkt der Parabel  .
Berechne die Koordianten des zweiten Schnittpunkts
.
Berechne die Koordianten des zweiten Schnittpunkts  der Parabel
der Parabel  und der Geraden
und der Geraden  .
.
Eine Gerade
3,5 P
Aufgabe P7
Hannah legt Buchstabenkärtchen.
Auf dem Tisch liegen bereits folgende vier Buchstabenkärtchen.

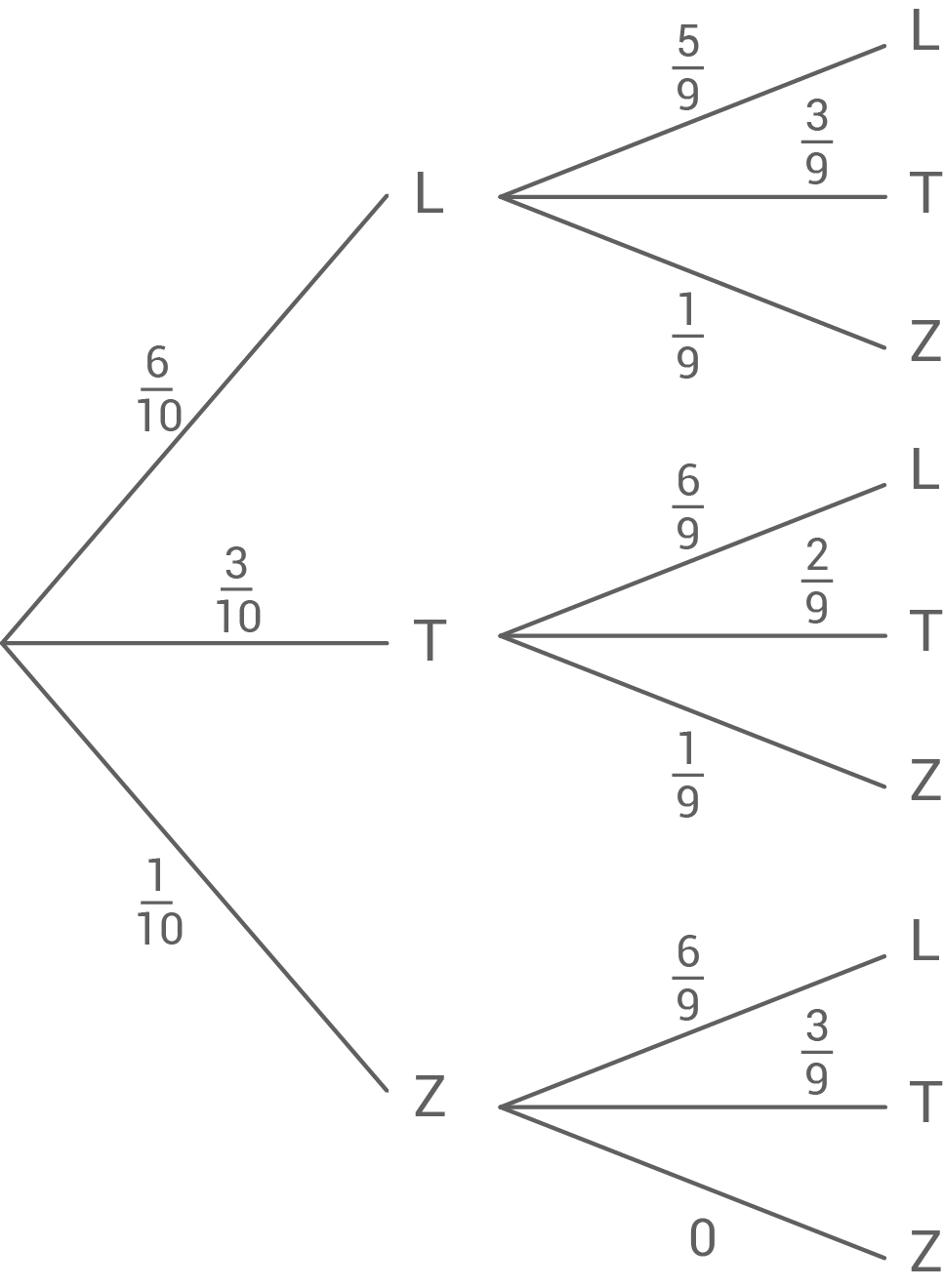
 Wie groß ist die Wahrscheinlichkeit, mit den beiden gezogenen Buchstaben
Wie groß ist die Wahrscheinlichkeit, mit den beiden gezogenen Buchstaben


In einem Beutel befinden sich die abgebildeten zehn Buchstabenkärtchen.
Daraus zieht Hannah zwei Buchstabenkärtchen gleichzeitig.


3,5 P
Aufgabe P8
In der abgebildeten Weltkarte sind die Bevölkerungszahlen der Kontinente für das Jahr 2014 und die voraussichtlichen Werte für das Jahr 2050 dargestellt.
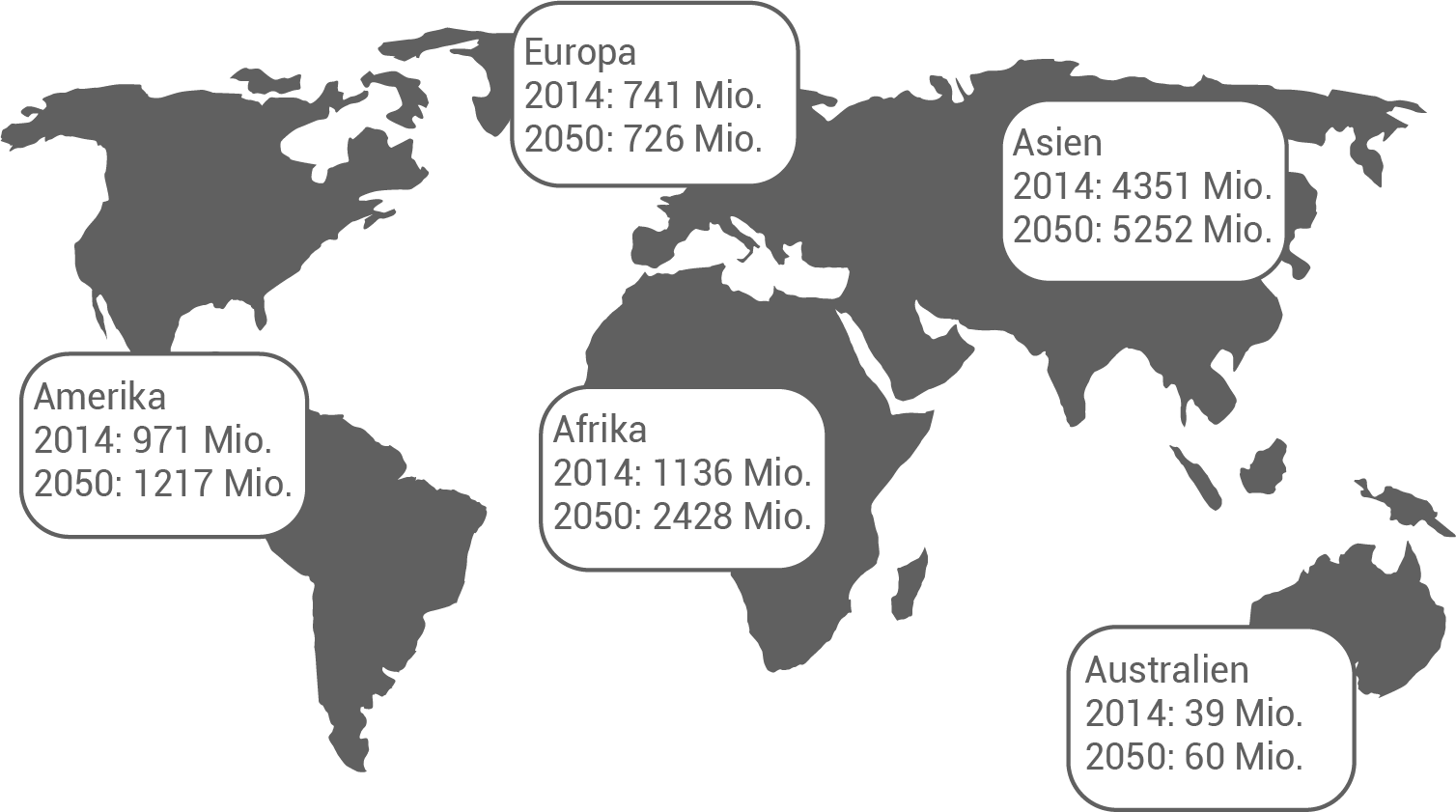 Um wie viel Prozent wird die Bevölkerungszahl von Europa im Zeitraum von 2014 bis 2050 voraussichtlich sinken?
In Afrika steigt die Bevölkerungszahl.
Um wie viel Prozent wird die Bevölkerungszahl von Europa im Zeitraum von 2014 bis 2050 voraussichtlich sinken?
In Afrika steigt die Bevölkerungszahl.
In den drei Jahren von 2014 bis 2017 nimmt sie jährlich durchschnittlich um 2,5 % zu.
Wie hoch ist die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017? Eine Zeitungsmeldung lautet: „Im Jahr 2050 ist etwa jeder vierte Mensch ein Afrikaner.“ Stimmt die Aussage? Begründe deine Antwort.

In den drei Jahren von 2014 bis 2017 nimmt sie jährlich durchschnittlich um 2,5 % zu.
Wie hoch ist die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017? Eine Zeitungsmeldung lautet: „Im Jahr 2050 ist etwa jeder vierte Mensch ein Afrikaner.“ Stimmt die Aussage? Begründe deine Antwort.
3 P
Lösung P1
Länge der Strecke  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\delta_1)&=&\dfrac{\overline{DE}}{\overline{AD}} \quad \scriptsize \mid\;\cdot \, \overline{AD} \\[5pt]
\overline{DE}&=&\cos(\delta_1)\cdot \overline{AD} \\[5pt]
\overline{DE}&=&\cos(69,4^{\circ})\cdot 7,3\,\text{cm} \\[5pt]
\overline{DE}&=&\underline{ 2,57\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/778454b600770f22355316af379008c723fa1749cd4994270d87ca8e3a60f810_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{\overline{CE}}{\overline{BC}} \quad \scriptsize \mid\;\cdot \, \overline{BC} \\[5pt]
\overline{CE}&=&\sin(\beta)\cdot \overline{BC} \\[5pt]
\overline{CE}&=&\sin(55^{\circ})\cdot 9,0\,\text{cm} \\[5pt]
\overline{CE}&=&\underline{ 7,37\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/ff2203f0d67ec5ed63484039260e3a4abe72305ffe20251bb92ef7af601702a4_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}&=&\overline{CE}-\overline{DE} & \\[5pt]
&=&7,37\,\text{cm}-2,57\,\text{cm} \\[5pt]
\overline{CD}&=&\underline{\underline{ 4,8\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/c645d13c22da7bcef2ff6a87102d544afc4fd5bd195cef535e0c64059f94be2d_light.svg) Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}^2+\overline{DE}^2&=&\overline{AD}^2 \quad \scriptsize \mid\;-\,\overline{DE}^2 \\[5pt]
\overline{AE}^2&=&\overline{AD}^2-\overline{DE}^2 \quad \scriptsize \mid\;\,\sqrt{\,\,\,} \\[5pt]
\overline{AE}&=&\sqrt{\overline{AD}^2-\overline{DE}^2} \\[5pt]
\overline{AE}&=&\sqrt{(7,3\,\text{cm})^2-(2,57\,\text{cm})^2} \\[5pt]
\overline{AE}&=&\underline{ 6,83\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/7674a82e7f1990e5bcfeeb81d679e40915532ee62f1fc05e34165dda4c1601a6_light.svg) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot \overline{CD}\cdot \overline{AE} & \\[5pt]
&=&\dfrac{1}{2}\cdot 4,8\,\text{cm}\cdot 6,83\,\text{cm} \\[5pt]
&=&16,39\,\text{cm}^2 \\[5pt]
A&=& \underline{\underline{ 16,4\,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/2822afa3e1e29be4e83aa9a1332fc9c75bbc6893ef335c7d9855304d61a1b708_light.svg)
Lösung P2
Lösung P3
LS_1.png)
Lösung P4
Boxplot vervollständigen
1. Schritt: Rangliste der Preise der Frauenschuhe erstellen
2. Schritt: Kennwerte ermitteln
3. Schritt: Boxplot vervollständigen
 Passende Werte ergänzen
1. Schritt: Kennwerte mithilfe des Boxplots der Männer ermitteln
3. Schritt: Kennwerte in die Rangliste eintragen
Passende Werte ergänzen
1. Schritt: Kennwerte mithilfe des Boxplots der Männer ermitteln
3. Schritt: Kennwerte in die Rangliste eintragen
4. Schritt: Rangliste vollständig ergänzen
| Rang | Preis (€) |
|---|---|
| 1 | 30 |
| 2 | 30 |
| 3 | 50 |
| 4 | 60 |
| 5 | 70 |
| 6 | 70 |
| 7 | 80 |
| 8 | 90 |
| 9 | 90 |
| 10 | 100 |
| 11 | 120 |
| 12 | 140 |
| 13 | 140 |
| 14 | 150 |
| 15 | 160 |
| 16 | 180 |
| 17 | 200 |

| Rang | Preis (€) |
|---|---|
| 1 | 30 |
| 2 | 30 |
| 3 | |
| 4 | 50 |
| 5 | 50 |
| 6 | 50 |
| 7 | 70 |
| 8 | |
| 9 | |
| 10 | 120 |
| 11 | 120 |
| 12 | 140 |
| 13 | 170 |
- Für
gilt:
- Für
und
gilt:
| Rang | Preis (€) |
|---|---|
| 1 | 30 |
| 2 | 30 |
| 3 | 40 |
| 4 | 50 |
| 5 | 50 |
| 6 | 50 |
| 7 | 70 |
| 8 | 80 |
| 9 | 100 |
| 10 | 120 |
| 11 | 120 |
| 12 | 140 |
| 13 | 170 |
Lösung P5
1. Hauptnenner bestimmen
 2. Schritt: Definitionsmenge angeben
2. Schritt: Definitionsmenge angeben

 3. Schritt: Lösungsmenge angeben
Weiter mit der
3. Schritt: Lösungsmenge angeben
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\left(\dfrac{3}{2}\right)^2-(-18)} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{9}{4}+18} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{81}{4}} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm \dfrac{9}{2} \\[5pt]
x_1&=&-\dfrac{3}{2}+ \dfrac{9}{2}= \dfrac{6}{2}=3\\[5pt]
x_2&=&-\dfrac{3}{2}- \dfrac{9}{2}= -\dfrac{12}{2}=-6 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9310cedb7065897ccd9fbc9df86b1c85961787ca077f2feb543c0a8572894c39_light.svg)

 zählt nicht in die Lösungsmenge, da dies in der Definitionsmenge ausgeschlossen wurde.
zählt nicht in die Lösungsmenge, da dies in der Definitionsmenge ausgeschlossen wurde.
Lösung P6
1. Schritt: Koordinaten des Scheitelpunkts der Parabel  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10,5 \\[5pt]
y&=& x^2-2\cdot 3x+10,5 &\quad \scriptsize \\[5pt]
y&=& x^2-2\cdot 3x+3^2-3^2+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2-9+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2+1,5
\end{array}\)](https://www.schullv.de/resources/formulas/2e783a0b5e7a3ca8b32b9afb2fa58884235fe2c199eb4ba81c4d21a36b90a24f_light.svg) Daraus folgt:
Daraus folgt:  2. Schritt: Geradengleichung von
2. Schritt: Geradengleichung von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
y&=&mx+c \quad \scriptsize \mid\;-mx \\[5pt]
c&=& y-mx \quad \scriptsize \mid\;S(3\mid 1,5), m=2 \\[5pt]
c&=&1,5-2\cdot 3& \\[5pt]
c&=&-4,5
\end{array}\)](https://www.schullv.de/resources/formulas/2842eb35d776606606329e8af2fca32eb5e85a205f73723442c49216d58cfc3c_light.svg) Es gilt also
Es gilt also  3. Schritt: Koordinaten des Schnittpunkts
3. Schritt: Koordinaten des Schnittpunkts  berechnen
berechnen
![\(\begin{array}[t]{rll}
p&=&g \\[5pt]
x^2-6x+10,5&=& 2x-4,5 \quad \scriptsize \mid\;-\, 2x\, +4,5 \\[5pt]
x^2-8x+15&=& 0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/03bb6b582551cdf3f1ad7a97bc8c3a721b87d6df1f8d5f69f0ce0594cac4c252_light.svg) Weiter mit der
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{(-8)}{2}\pm \sqrt{\left(\dfrac{-8}{2}\right)^2-15} \\[5pt]
x_{1/2} &=&4\pm \sqrt{16-15} \\[5pt]
x_{1/2} &=&4\pm 1 \\[5pt]
x_1&=&5 \\[5pt]
x_2&=&3
\end{array}\)](https://www.schullv.de/resources/formulas/b33372fad3e8bcb2590d694a2c8741ff3919b0cca098f5f2b5130cdad820ede5_light.svg)
 ist die
ist die  -Koordinate des bekannten Schnittpunkts
-Koordinate des bekannten Schnittpunkts  Deswegen wird
Deswegen wird  in
in  eingesetzt:
eingesetzt:
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=& 2\cdot 5 - 4,5 \\[5pt]
y&=& 10-4,5 \\[5pt]
y&=& 5,5 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2a80286a5ee0281db1e9554124fd82cf44efaa9dfea08550311f1f6d1434a2e3_light.svg) Somit gilt:
Somit gilt: 
Lösung P7
Lösung P8
Um wie viel Prozent wird die Bevölkerungszahl von Europa im Zeitraum von 2014 bis 2050 voraussichtlich sinken?
Voraussichtlichen Bevölkerungsrückgang als absolute Zahl berechnen
![\(\begin{array}[t]{rll}
W&=& 741 \text{ Mio.} - 726 \text{ Mio.}& \\[5pt]
W&=& \underline{ 15\text{ Mio.}}
\end{array}\)](https://www.schullv.de/resources/formulas/683026f3025c08328dc8f1449aee2f92d2c019945150048534b75bbd5fcb7dc7_light.svg) Prozentwert berechnen
Prozentwert berechnen
![\(\begin{array}[t]{rll}
W&=&G\cdot p\,\% &\quad \scriptsize \mid\;:G \\[5pt]
p\,\%&=&\dfrac{W}{G} & \\[5pt]
p\,\%&=&\dfrac{15\text{ Mio.}}{741\text{ Mio.}} & \\[5pt]
p\,\%&=&\underline{\underline{ 2,0\,\%}} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/144f5007f6a9e7adc24c29624e84cd3faf0e26aaff98d29c865c07d1767785fd_light.svg) Die Bevölkerungszahl von Europa wird von 2014 bis zum Jahr 2050 um ungefähr
Die Bevölkerungszahl von Europa wird von 2014 bis zum Jahr 2050 um ungefähr  sinken.
Wie hoch ist die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017?
Formel:
sinken.
Wie hoch ist die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017?
Formel: 
 berechnen
berechnen
![\(\begin{array}[t]{rll}
q_A&=& 1+\dfrac{p}{100} \\[5pt]
&=& 1+\dfrac{2,5}{100} \\[5pt]
q_A&=& \underline{ 1,025 } \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/58cd364874915261a3d45822af8b8fcd951b990471ccbf9057ebfaea8ed4e88f_light.svg) In die Formel einsetzen
In die Formel einsetzen
![\(\begin{array}[t]{rll}
A_{2017}&=& A_{2014}\cdot {q_A}^3 \\[5pt]
&=& 1136\text{ Mio.}\cdot 1,025^3 \\[5pt]
&=& 1\,223,35\text{ Mio.}\\[5pt]
A_{2017}&=& \underline{\underline{ 1\,223,4\text{ Mio.}}}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/73d9c19b00b8d5a26d94a665c86a3367afcdfd4445dbd5c2e5f642bf8da91cae_light.svg) Die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017 liegt bei
Die zu erwartende Bevölkerungszahl in Afrika im Jahr 2017 liegt bei  Stimmt die Aussage?
Alle Bevölkerungszahlen für das Jahr 2050 addieren
Stimmt die Aussage?
Alle Bevölkerungszahlen für das Jahr 2050 addieren
 Anteil berechnen
Anteil berechnen
![\(\begin{array}[t]{rll}
x&=& \dfrac{2428\,\text{Mio.}}{9683\,\text{Mio.}}&\\[5pt]
&=& 0,251 &\\[5pt]
x&=& \underline{\underline{ 25,1\,\%}} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7676345b8a6cf810206cb5bd5487531da52dfa5565cb6b48e775d44bfbb71b77_light.svg) Ja, die Aussage stimmt. Im Jahr 2050 werden ungefähr
Ja, die Aussage stimmt. Im Jahr 2050 werden ungefähr  der Weltbevölkerung afrikanisch sein.
der Weltbevölkerung afrikanisch sein.