Wahlbereich
Aufgabe W1
a)
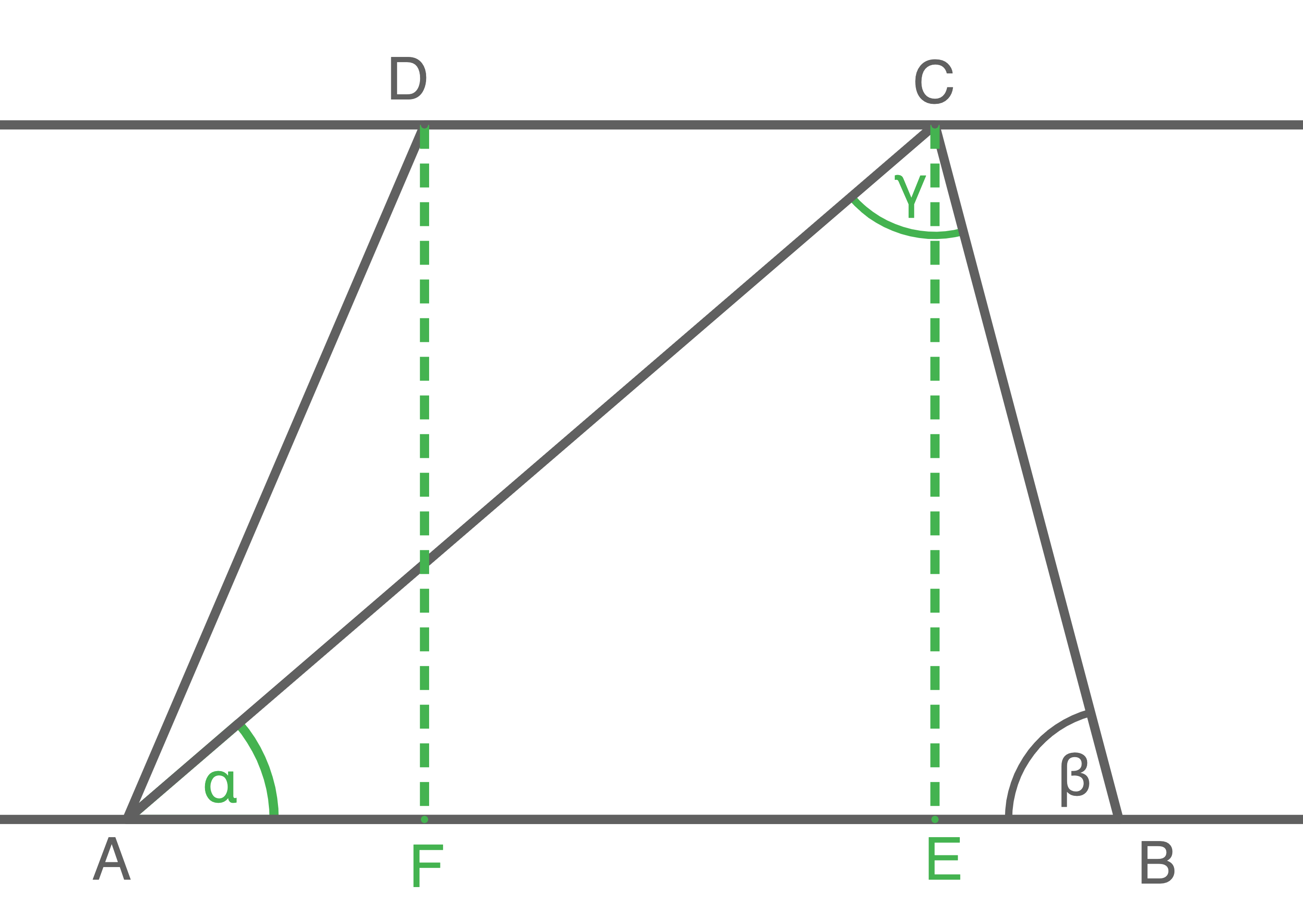
Die Eckpunkte des Vierecks  liegen auf den Parallelen
liegen auf den Parallelen  und
und  .
.
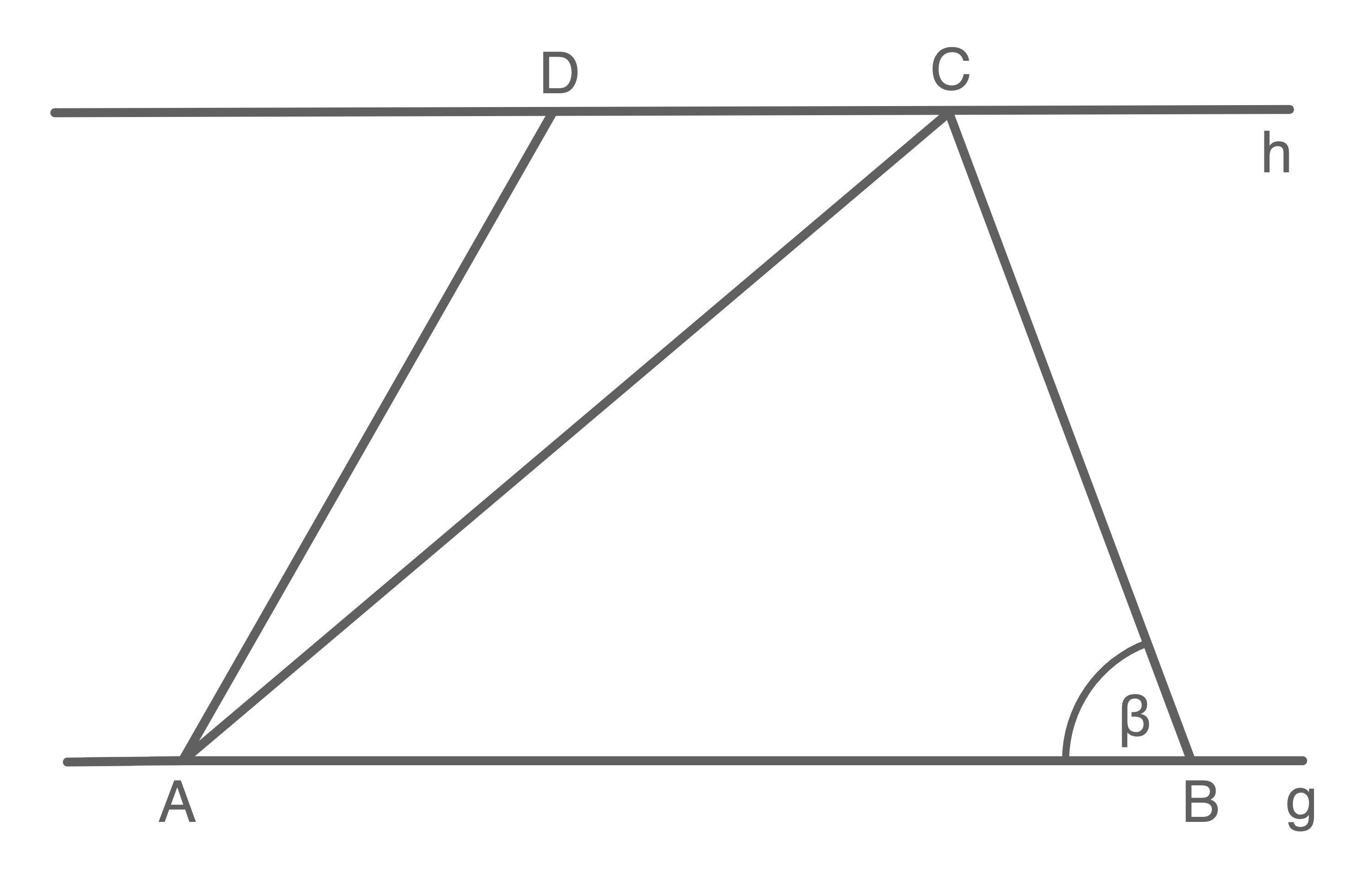 Die Parallelen haben einen Abstand von
Die Parallelen haben einen Abstand von  .
Es gilt:
.
Es gilt:
![\(\begin{array}[t]{rll}
\overline{AD}&=& 10,4\,\text{cm} &\\[5pt]
\beta&=& 70,0^{\circ}&\\[5pt]
\overline{AB}&=&\overline{AC} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fbbc62357e70049f6187b49cfcb1b6d2ec2d5f0bbc6316661cd5a46197ccf789_light.svg) Berechne den Umfang des Vierecks
Berechne den Umfang des Vierecks 

5,5 P
b)
4,5 P
Aufgabe W2
a)
Aus einer Kreisfläche wird die Mantelfläche einer regelmäßigen fünfseitigen Pyramide ausgeschnitten.
 Der Kreis hat einen Radius von
Der Kreis hat einen Radius von  .
Berechne das Volumen der Pyramide.
.
Berechne das Volumen der Pyramide.

5,5 P
b)
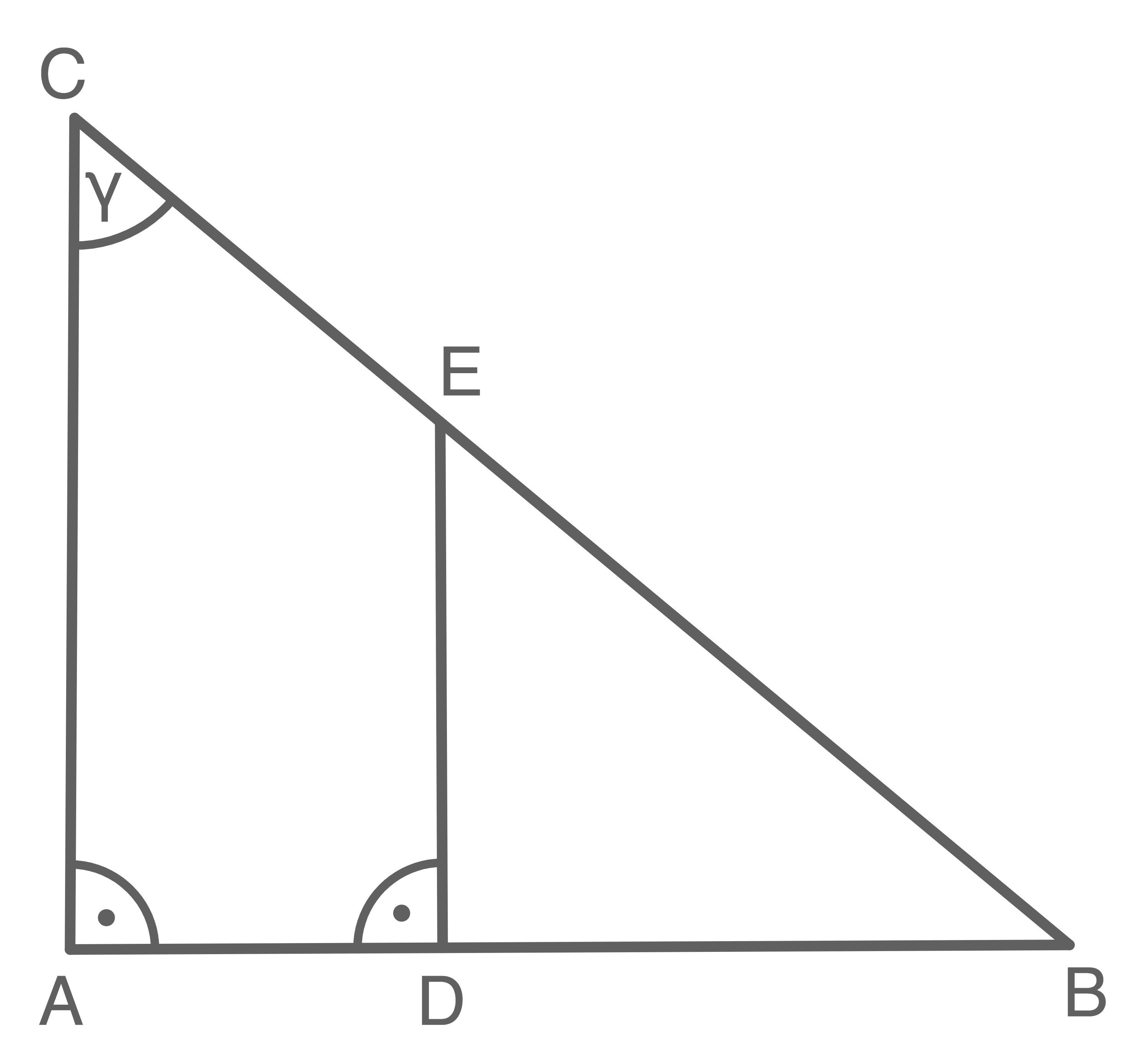
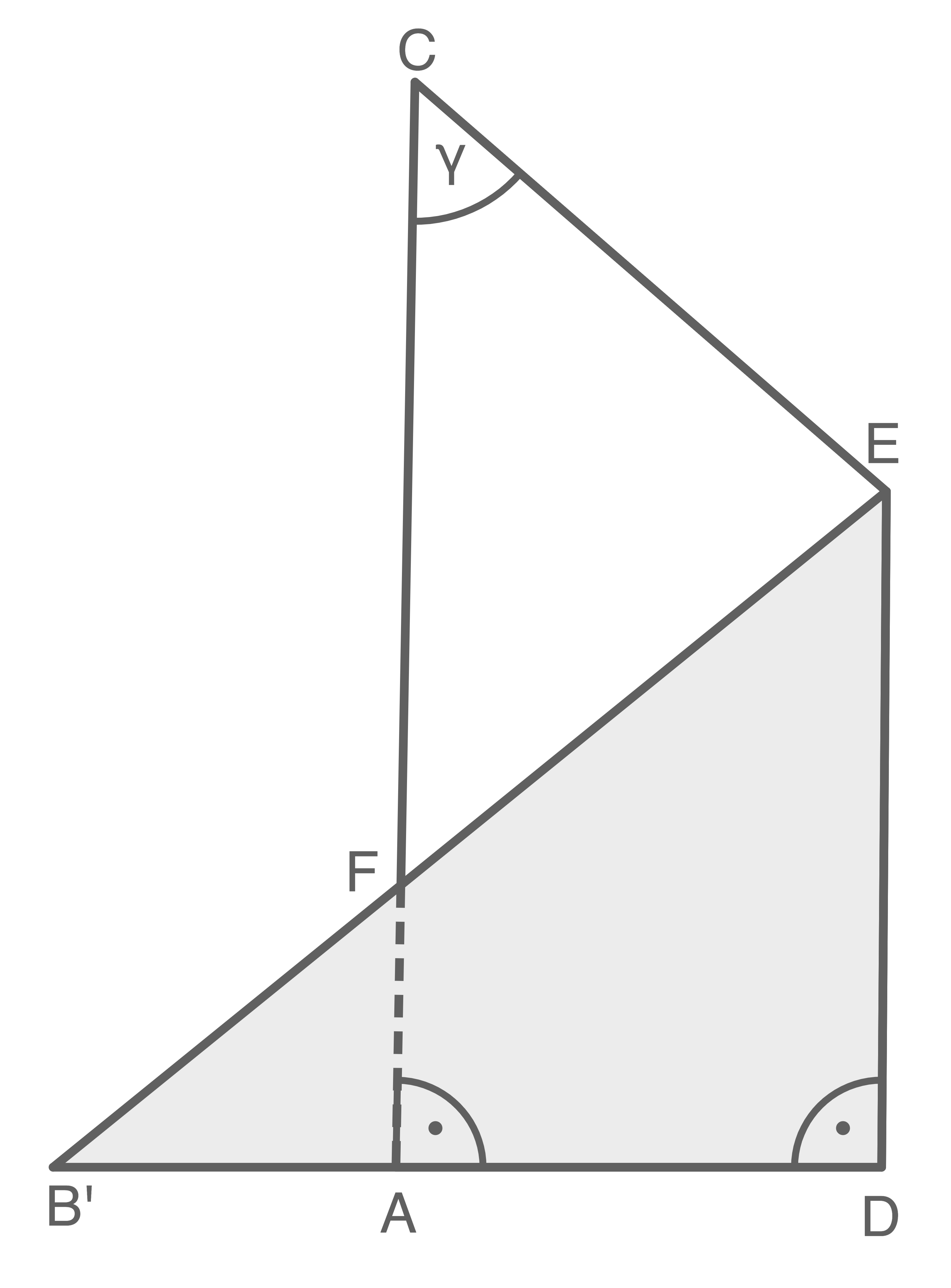
Eine quadratische Pyramide ist zweimal abgebildet.
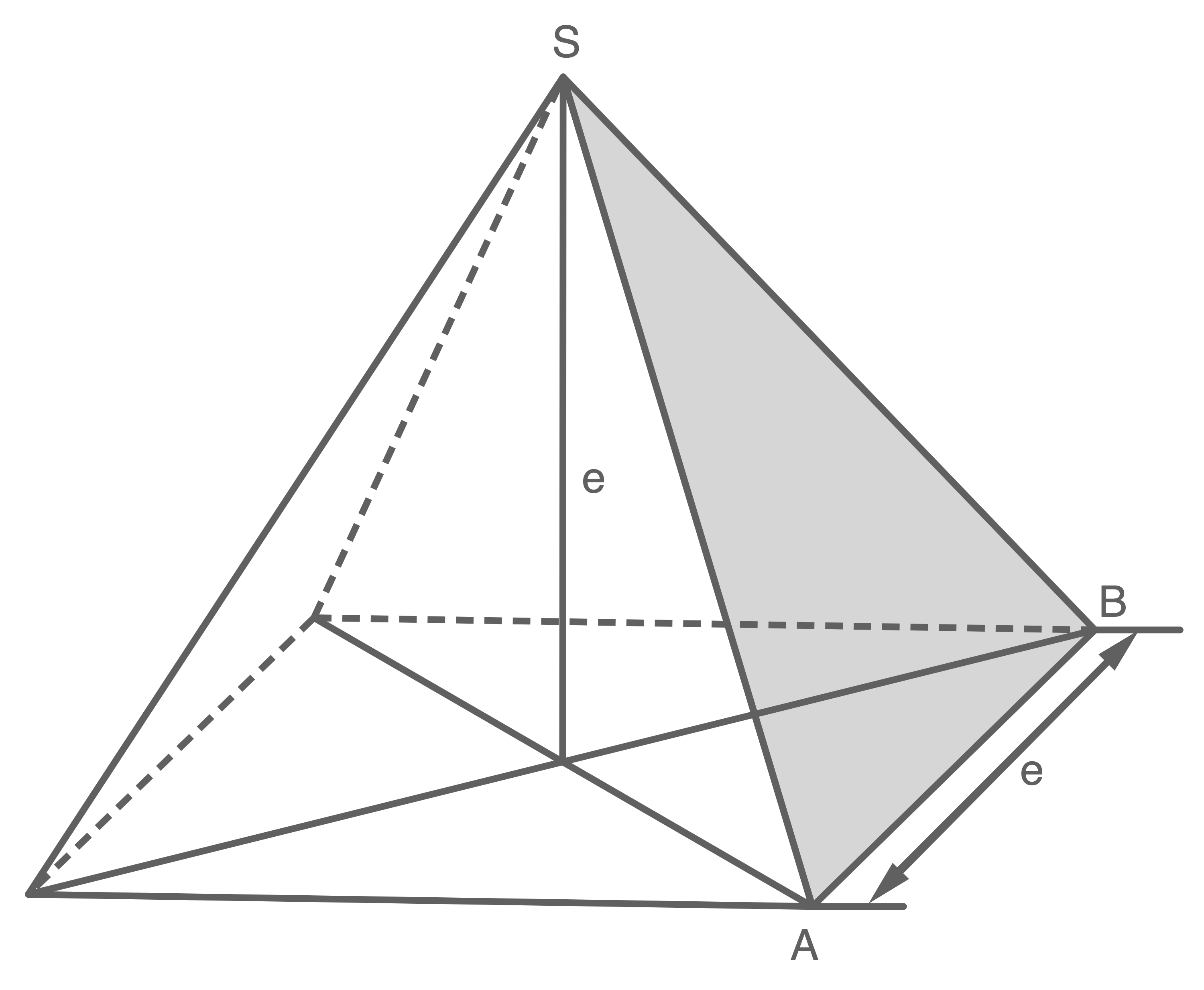
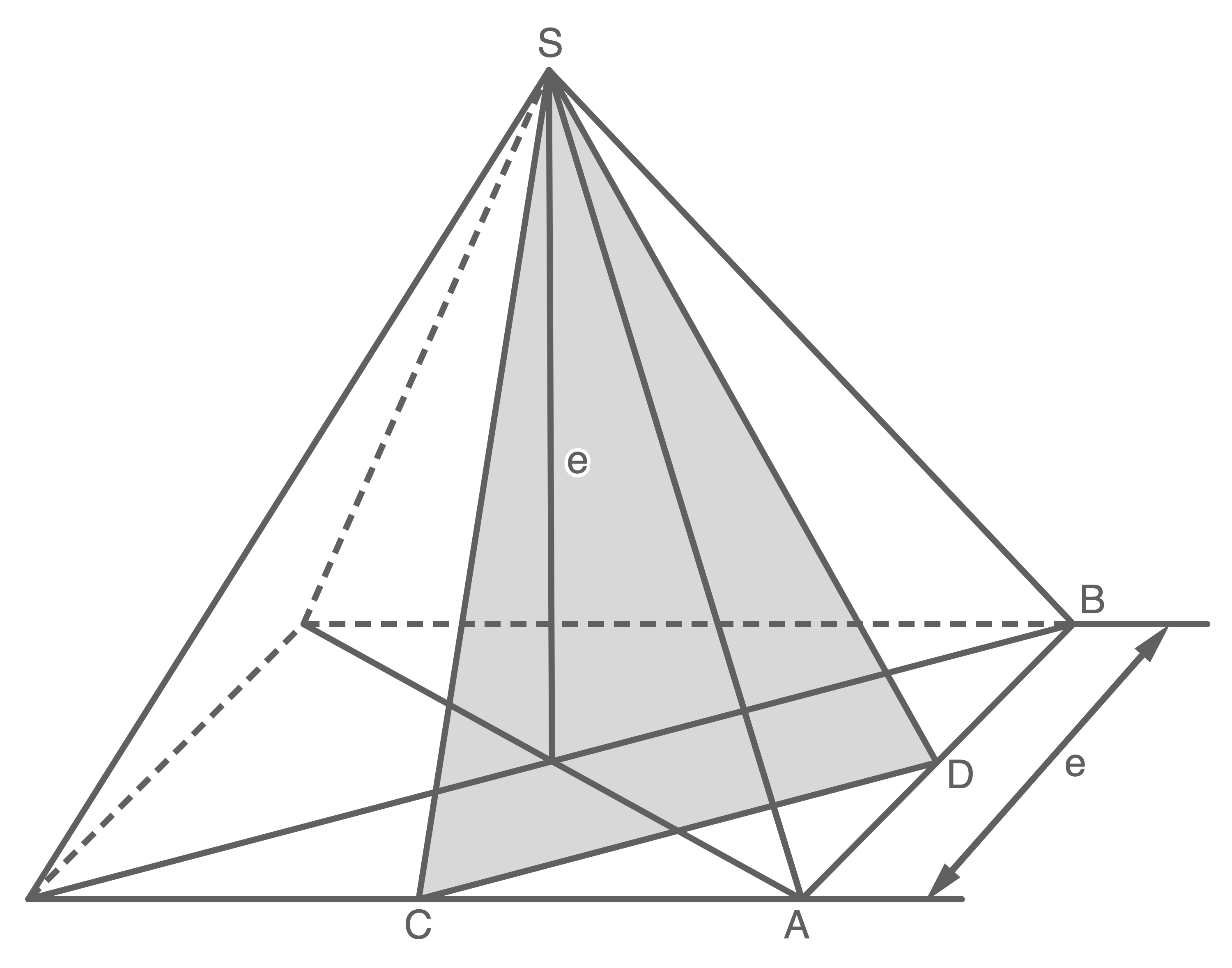 In der linken Abbildung ist das Dreieck
In der linken Abbildung ist das Dreieck  markiert und in der rechten das Dreieck
markiert und in der rechten das Dreieck  .
.
Die Punkte und
und  halbieren jeweils die Grundkante.
Welche der folgenden Formeln gehört zur Dreiecksfläche
halbieren jeweils die Grundkante.
Welche der folgenden Formeln gehört zur Dreiecksfläche  und welche zur Dreiecksfläche
und welche zur Dreiecksfläche  ? Begründe deine Entscheidung ohne Verwendung gerundeter Werte.
(1)
? Begründe deine Entscheidung ohne Verwendung gerundeter Werte.
(1) 
![\(\begin{array}[t]{rll}
A&=& \dfrac{3e^2}{8} &\quad \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5f48ee989f04a418fe86ce37a008a17061dd5c4da246e3ebae0814e3aeb4cc4a_light.svg) (2)
(2) 
![\(\begin{array}[t]{rll}
A&=& \dfrac{e^2}{4}\sqrt{6} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8bd0d4ee068ccdbc0079a9468613005ce1aa52418733a59d84a74e188f55e9c2_light.svg) (3)
(3) 
![\(\begin{array}[t]{rll}
A&=& \dfrac{e^2}{4}\sqrt{5} &\quad \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6e1df4168764250fba0b2725d9885f2358d4fa19f452befe7ad026a7f80decb0_light.svg)


Die Punkte
4,5 P
Aufgabe W3
a)
Das Schaubild zeigt einen Ausschnitt der verschobenen Normalparabel  .
.
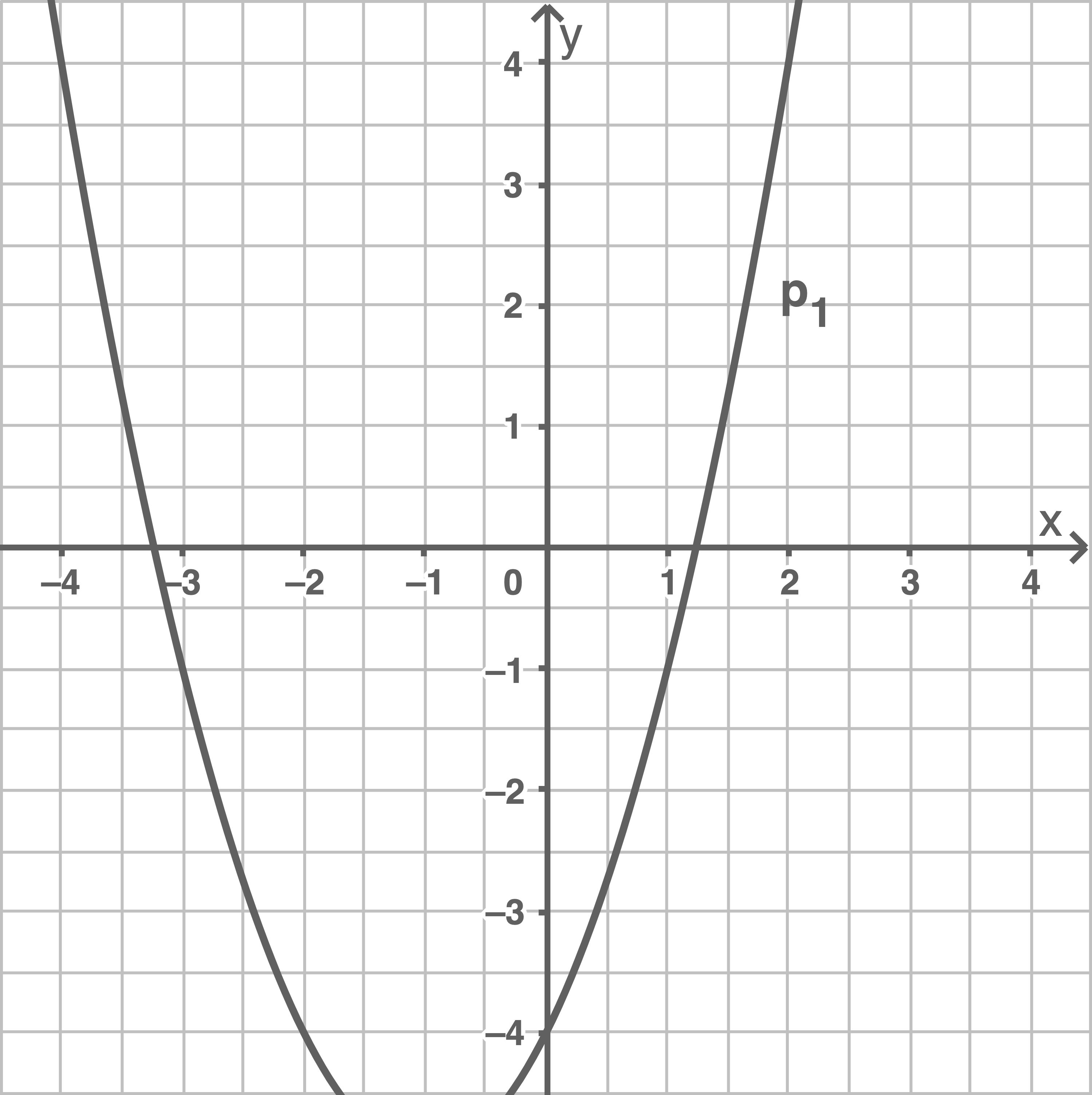 Die Punkte
Die Punkte  und
und  liegen auf
liegen auf  .
.
Bestimme die Gleichung der Parabel .
Die nach unten geöffnete Normalparabel
.
Die nach unten geöffnete Normalparabel  hat den Scheitelpunkt
hat den Scheitelpunkt  .
Durch die beiden Scheitelpunkte verläuft eine Gerade
.
Durch die beiden Scheitelpunkte verläuft eine Gerade  .
Berechne die Gleichung der Geraden
.
Berechne die Gleichung der Geraden  .
Eine Gerade
.
Eine Gerade  verläuft parallel zu
verläuft parallel zu  und geht durch einen der beiden Schnittpunkte von
und geht durch einen der beiden Schnittpunkte von  und
und  .
Berechne eine mögliche Gleichung der Geraden
.
Berechne eine mögliche Gleichung der Geraden 

Bestimme die Gleichung der Parabel
5,5 P
b)
Eine Parabel  hat die Gleichung
hat die Gleichung  und geht durch den Punkt
und geht durch den Punkt  .
Eine nach unten geöffnete Normalparabel
.
Eine nach unten geöffnete Normalparabel  hat die Gleichung
hat die Gleichung  .
Berechne die Koordinaten der Schnittpunkte
.
Berechne die Koordinaten der Schnittpunkte  und
und  von
von  und
und  .
Die Scheitelpunkte
.
Die Scheitelpunkte  und
und  sowie die Schnittpunkte
sowie die Schnittpunkte  und
und  der beiden Parabeln bilden das Viereck
der beiden Parabeln bilden das Viereck  .
Mia behauptet: „Das Viereck
.
Mia behauptet: „Das Viereck  hat zwei rechte Winkel.“
Hat Mia recht? Begründe deine Antwort durch Rechnung.
hat zwei rechte Winkel.“
Hat Mia recht? Begründe deine Antwort durch Rechnung.
4,5 P
Aufgabe W4
a)
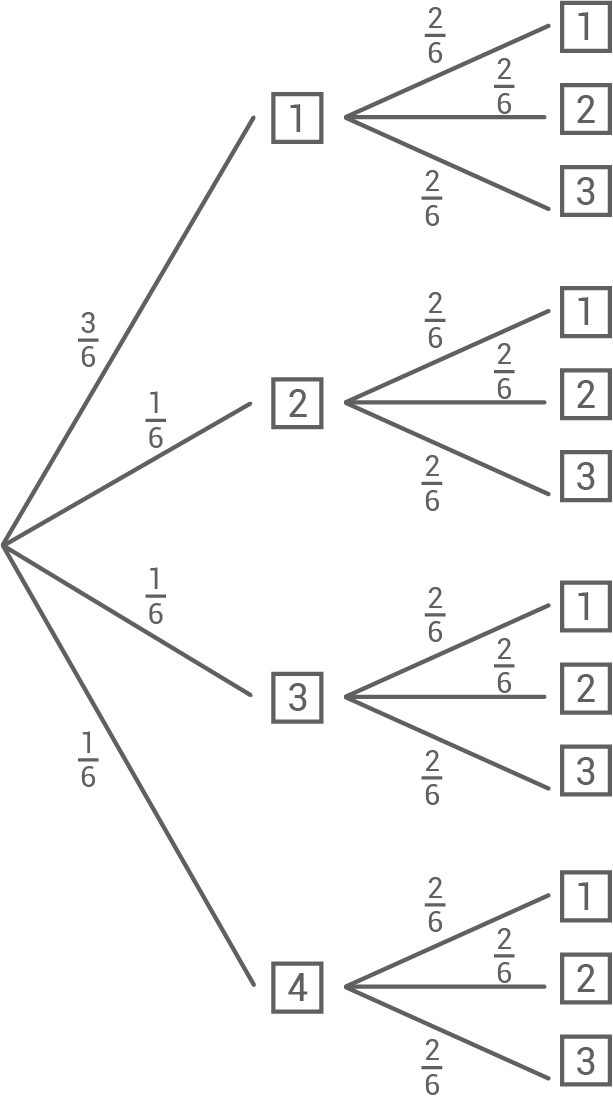
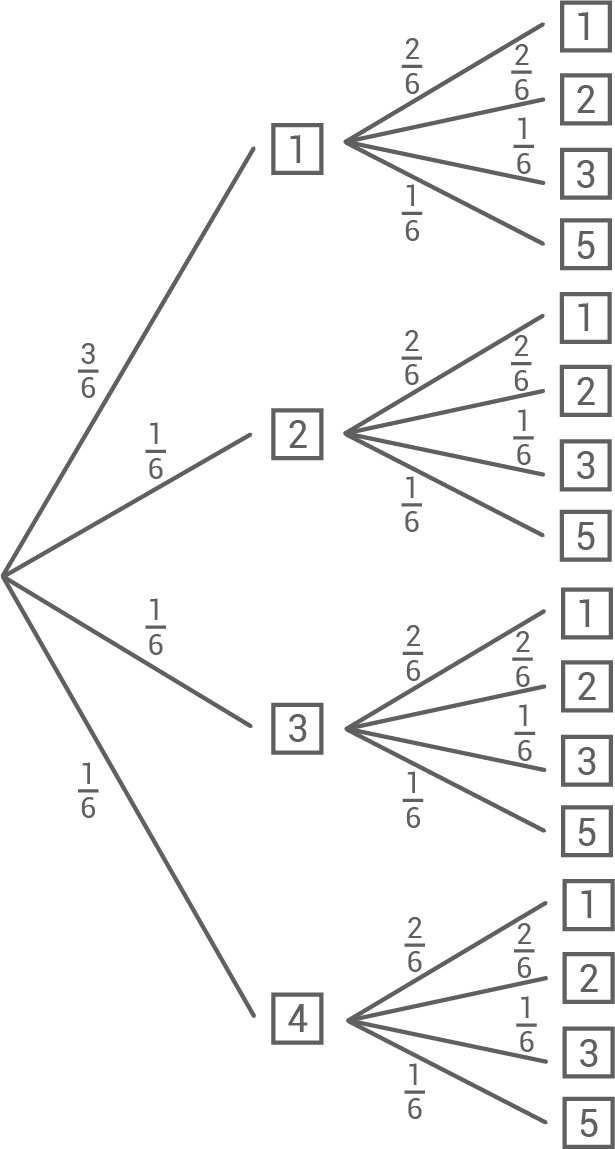
Bei einer Wohltätigkeitsveranstaltung werden zwei Glücksräder eingesetzt.
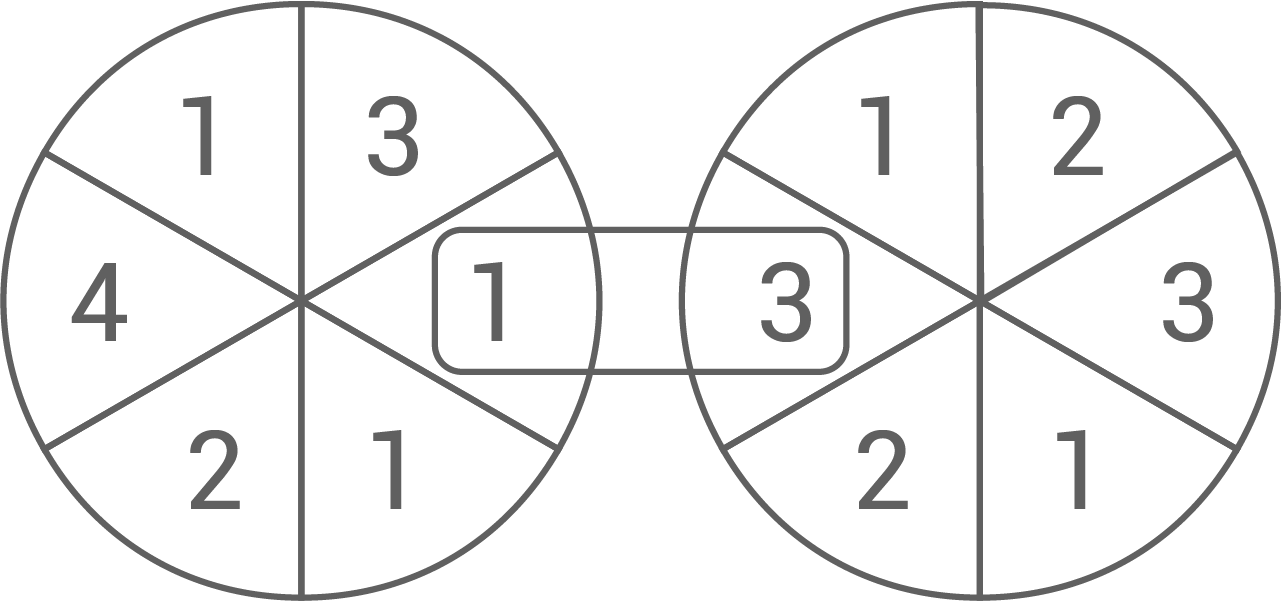 Beide Glücksräder werden gedreht.
Beide Glücksräder werden gedreht.
Wenn sie stehen bleiben, erkennt man im Sichtfenster eine zweistellige Zahl.
Die Abbildung zeigt die Zahl .
Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine Zahl mit zwei gleichen Ziffern zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
.
Mit welcher Wahrscheinlichkeit ist im Sichtfenster eine Zahl mit zwei gleichen Ziffern zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
Berechne den Erwartungswert.
Bei der Wohltätigkeitsveranstaltung soll ein höherer Erlös erzielt werden. Dazu soll beim rechten Glücksrad eine der beiden Dreien durch eine Fünf ersetzt werden.
Der Gewinnplan bleibt gleich. Wäre dies vorteilhaft? Begründe durch Rechnung oder Argumentation.

Wenn sie stehen bleiben, erkennt man im Sichtfenster eine zweistellige Zahl.
Die Abbildung zeigt die Zahl
| Gewinnplan | |
|---|---|
| Ergebnisse | Gewinn |
| zwei gleiche Ziffern | 3,00 € |
| Zahl größer als 40 | 5,00€ |
| restliche Möglichkeiten | kein Gewinn |
| Einsatz 2,00 € | |
Der Gewinnplan bleibt gleich. Wäre dies vorteilhaft? Begründe durch Rechnung oder Argumentation.
5,5 P
b)
Theo wirft im Basketballtraining auf den Korb (siehe Skizze).
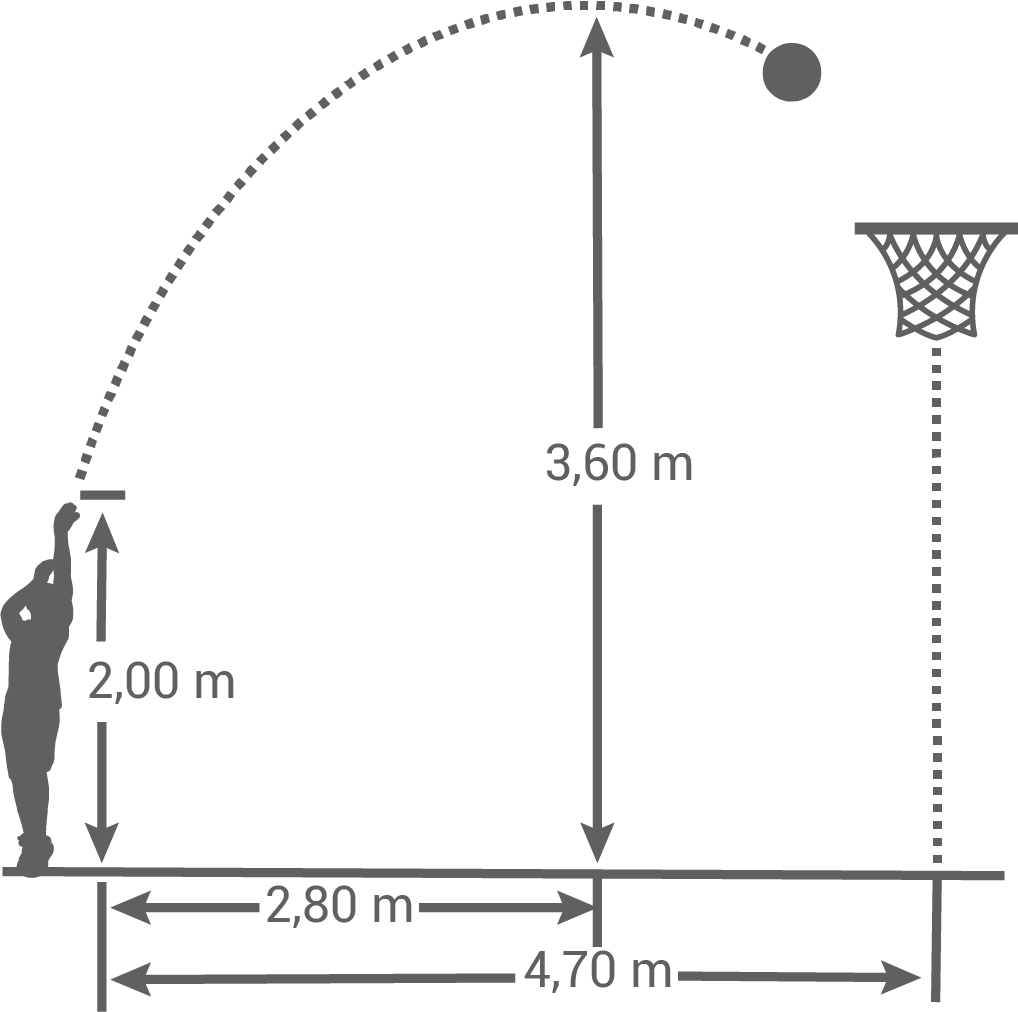 Die annähernd parabelförmige Flugkurve des Balles lässt sich mit der Gleichung
Die annähernd parabelförmige Flugkurve des Balles lässt sich mit der Gleichung  beschreiben.
beschreiben.
Gib eine mögliche Gleichung der zugehörigen Parabel an.
Trifft Theo bei diesem Wurf direkt in den Korb, der in einer Höhe von
an.
Trifft Theo bei diesem Wurf direkt in den Korb, der in einer Höhe von  hängt?
hängt?
Begründe durch Rechnung. Vor Theo steht der Abwehrspieler Dennis im Abstand von Mit nach oben gestreckten Armen erreicht Dennis eine Höhe von
Mit nach oben gestreckten Armen erreicht Dennis eine Höhe von 
Berührt er den Ball, ohne hochzuspringen?
Begründe durch Rechnung.

Gib eine mögliche Gleichung der zugehörigen Parabel
Begründe durch Rechnung. Vor Theo steht der Abwehrspieler Dennis im Abstand von
Berührt er den Ball, ohne hochzuspringen?
Begründe durch Rechnung.
4,5 P
Lösung W1
a)
b)
Lösung W2
a)
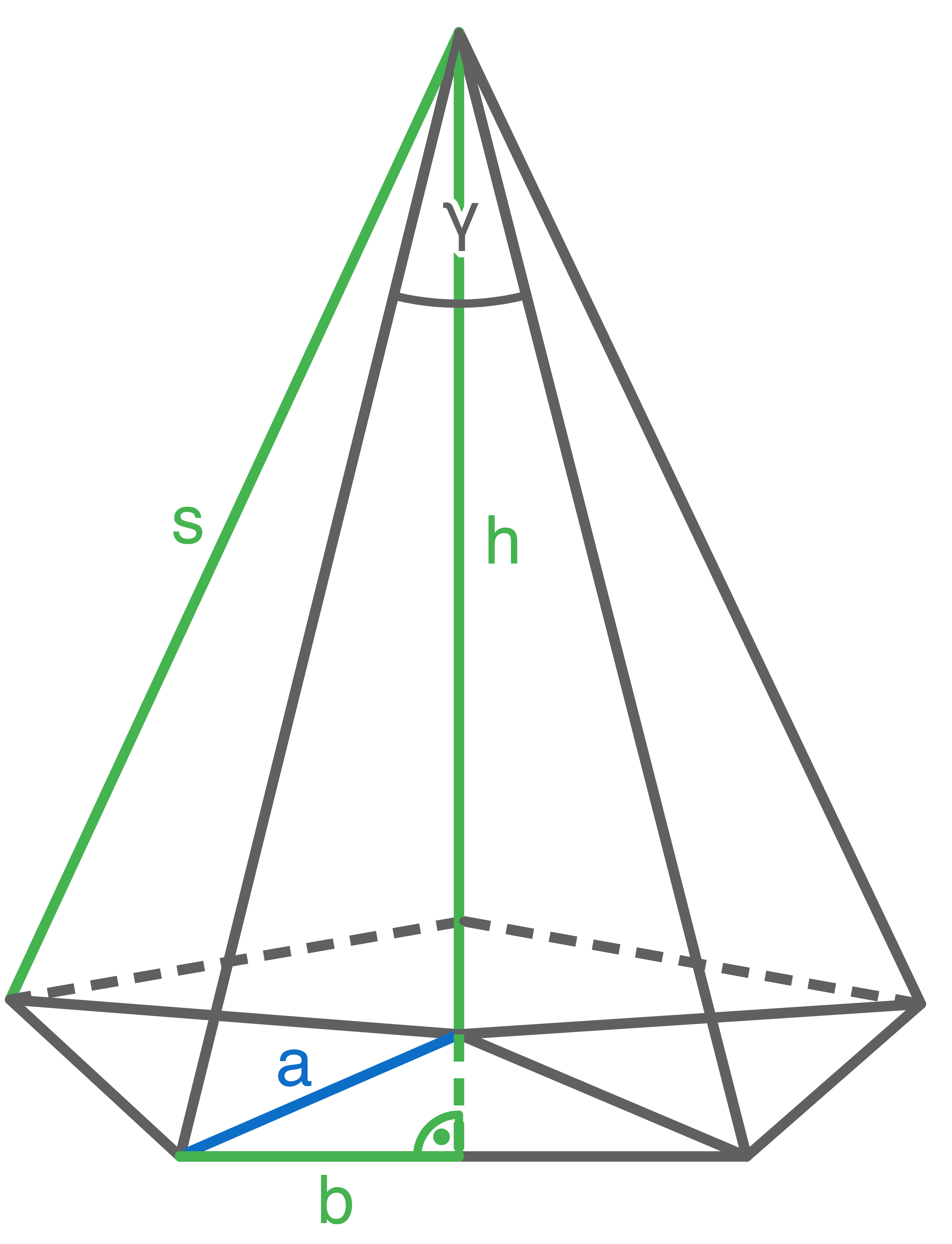
Skizze der Pyramide
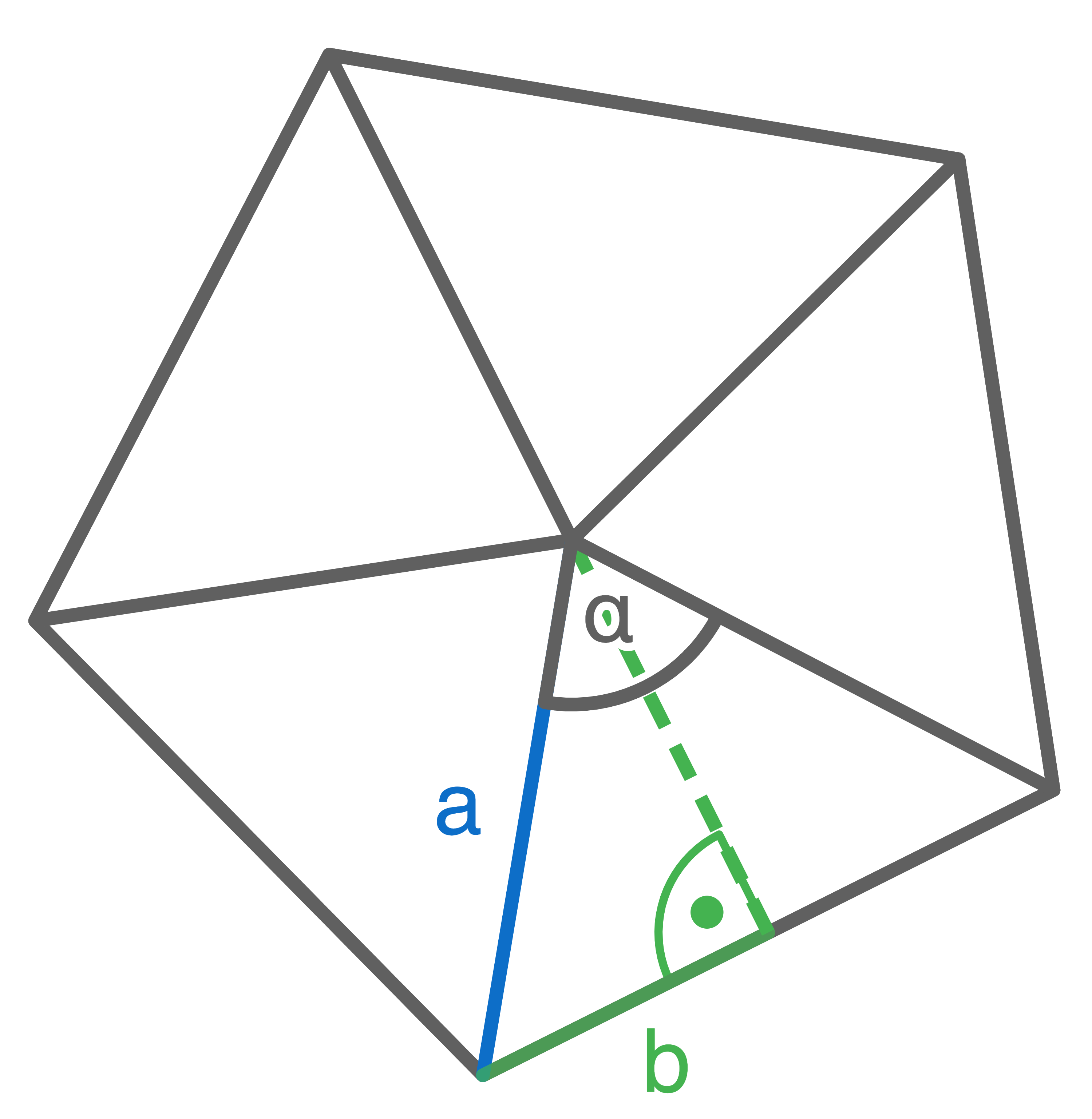
Skizze der Grundfläche
b)
Flächeninhalt des Dreiecks  berechnen
berechnen
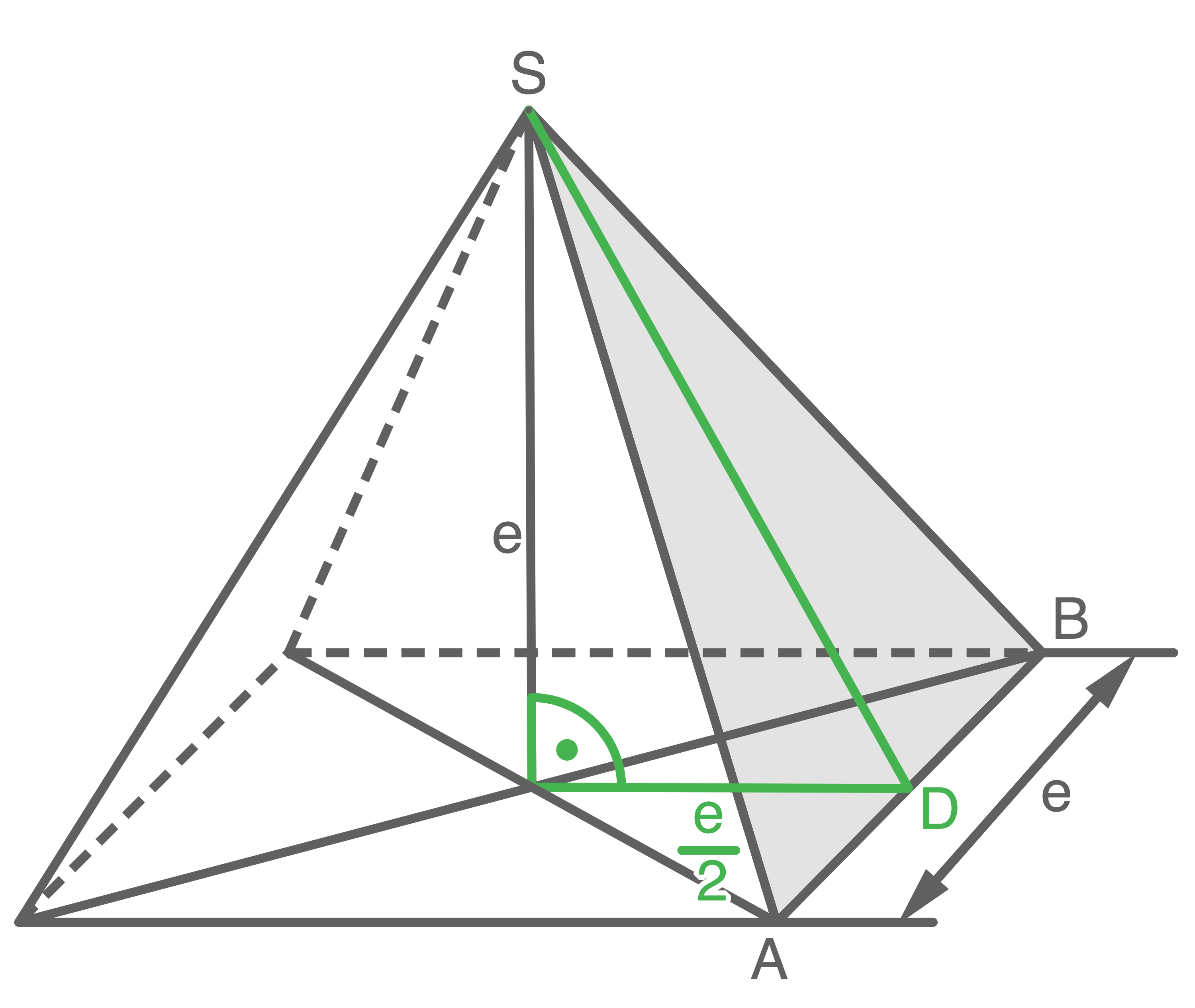 Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{SD}^2 &=& e^2+\left(\dfrac{e}{2}\right)^2\quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
\overline{SD} &=&\sqrt{e^2+\left(\dfrac{e}{2}\right)^2} \\[5pt]
\overline{SD} &=&\sqrt{e^2+\dfrac{e^2}{4}} \\[5pt]
\overline{SD} &=&\sqrt{\dfrac{5}{4}e^2} \\[5pt]
\overline{SD} &=&\underline{ \dfrac{e}{2}\sqrt{5}}
\end{array}\)](https://www.schullv.de/resources/formulas/12a394a7d6f087a119a3dd1f4e271076ec388557c32b6dcf4435d5debad8d277_light.svg) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{ABS}&=& \dfrac{1}{2}\cdot\text{e}\cdot \overline{SD}\\[5pt]
A_{ABS}&=&\dfrac{1}{2}\cdot e \cdot \dfrac{e}{2}\sqrt{5}\\[5pt]
A_{ABS}&=&\underline{ \dfrac{e^2}{4}\cdot\sqrt{5}}
\end{array}\)](https://www.schullv.de/resources/formulas/aa8b80280642055ac5a4223d1b86e63b7609df9a4f51f8c5fd5368d3c0d7dde5_light.svg) Somit gehört Formel (3) zur Dreiecksfläche
Somit gehört Formel (3) zur Dreiecksfläche  Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  berechnen
berechnen
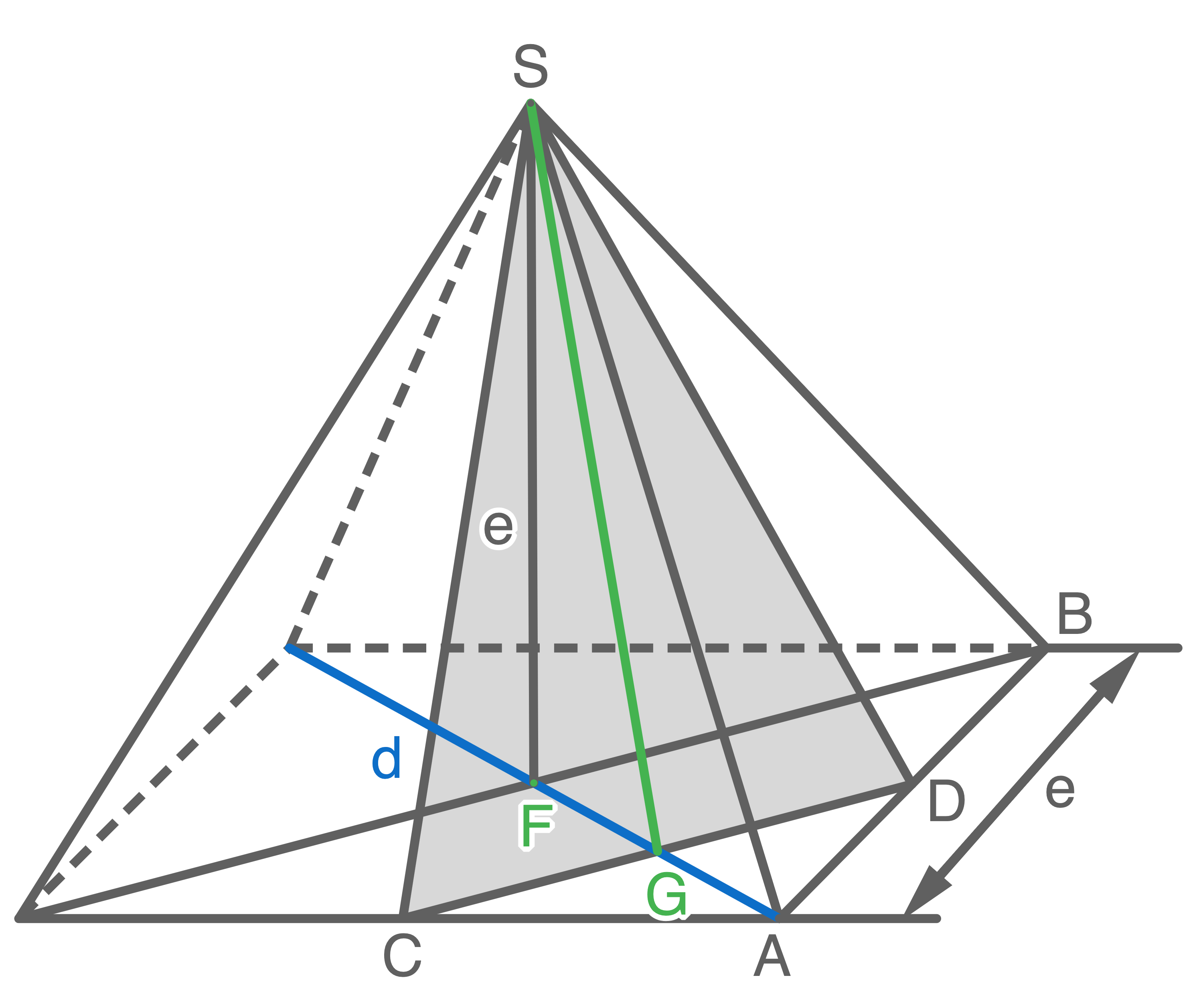 Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}^2&=& \overline{CA}^2+\overline{AD}^2 \quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
\overline{CD}&=& \sqrt{\overline{CA}^2+\overline{AD}^2} &\\[5pt]
\overline{CD}&=& \sqrt{\left(\dfrac{e}{2}\right)^2+\left(\dfrac{e}{2}\right)^2}\\[5pt]
\overline{CD}&=& \sqrt{\dfrac{e^2}{4}+\dfrac{e^2}{4}}\\[5pt]
\overline{CD}&=&\sqrt{\dfrac{2e^2}{4}}\\[5pt]
\overline{CD}&=&\underline{ \dfrac{1}{2}e\sqrt{2}}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4318de65099b154129b758720f10cd0a291acfdd2e5ebba6cd416001399c88c9_light.svg) Länge der Strecke
Länge der Strecke  mit der Diagonale
mit der Diagonale  berechnen
berechnen
![\(\begin{array}[t]{rll}
d^2&=&e^2+e^2 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
d&=& \sqrt{e^2+e^2} & \\[5pt]
d&=& \sqrt{2e^2} & \\[5pt]
d&=& e\sqrt{2} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0818433e5032bab639cf86d5c9245af2ef430586df0431a4f9f067507673dc68_light.svg) Daraus folgt:
Daraus folgt:  Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\dfrac{\overline{FG}}{\overline{FA}}&=&\dfrac{\overline{DB}}{\overline{AB}} &\quad \scriptsize \mid\;\cdot \overline{FA} \\[5pt]
\overline{FG}&=&\dfrac{\overline{DB}}{\overline{AB}}\cdot \overline{FA} & \\[5pt]
\overline{FG}&=&\dfrac{\dfrac{e}{2}}{e} \cdot \dfrac{1}{2}e\sqrt{2}& \\[5pt]
\overline{FG}&=&\dfrac{1}{2}\cdot \dfrac{1}{2}e\sqrt{2} &\quad \scriptsize \\[5pt]
\overline{FG}&=&\underline{ \dfrac{1}{4}e\sqrt{2}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/48d8ec9d1e4032e7b760731c8b21b031aaaf0dd06ddfd54a6e46b9811ddd4dc9_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{SG}^2&=&\overline{SF}^2+\overline{FG}^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\overline{SG}&=&\sqrt{\overline{SF}^2+\overline{FG}^2 }& \\[5pt]
\overline{SG}&=&\sqrt{e^2+\left(\dfrac{1}{4}e\sqrt{2}\right)^2 }& \\[5pt]
\overline{SG}&=&\sqrt{e^2+\dfrac{1}{16}e^2\cdot 2 }& \\[5pt]
\overline{SG}&=&\sqrt{\dfrac{9}{8}e^2}& \\[5pt]
\overline{SG}&=&\dfrac{3}{2\sqrt{2}}e \quad \scriptsize \mid\; \text{Nenner rational machen} \\[5pt]
\overline{SG}&=&\dfrac{3\sqrt{2}}{2\sqrt{2}\sqrt{2}}e&\\[5pt]
\overline{SG}&=&\dfrac{3\sqrt{2}}{2\cdot 2}e&\\[5pt]
\overline{SG}&=&\underline{ \dfrac{3\sqrt{2}}{4}e}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/19d56784f8c76b37751c80c16b27173d5d16cadf2a6f8bac09ae5d518335d3f4_light.svg) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{CDS}&=& \dfrac{1}{2}\cdot\overline{CD}\cdot \overline{SG}\\[5pt]
&=& \dfrac{1}{2}\cdot \dfrac{1}{2}e\sqrt{2}\cdot \dfrac{3\sqrt{2}}{4}e\\[5pt]
&=& \dfrac{1}{4}e^2\cdot \dfrac{3\cdot 2}{4}\\[5pt]
A_{CDS}&=& \underline{ \dfrac{3}{8}e^2}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ee02a7cd20900ea5cb8206457762ffe8b40202847da148a022cb0bef7f92bb37_light.svg) Somit gehört Formel (1) zur Dreiecksfläche
Somit gehört Formel (1) zur Dreiecksfläche 


Lösung W3
a)
Gleichung der Parabel  bestimmen
bestimmen
 und
und  in die allgemeine Form einer Normalparabel
in die allgemeine Form einer Normalparabel  einsetzen und ein lineares Gleichungssystem erstellen
einsetzen und ein lineares Gleichungssystem erstellen

 in
in  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
-1&=&1+2+c & \\[5pt]
-1&=&3+c &\quad \scriptsize \mid\;-3 \\[5pt]
c&=&-4 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b872c7694f2bbf2689159170a6e395b212e72286057577c548f7073c83b38c04_light.svg) Somit gilt:
Somit gilt:  Gleichung der Geraden
Gleichung der Geraden  berechnen
Koordinaten des Scheitelpunkts
berechnen
Koordinaten des Scheitelpunkts  der Parabel
der Parabel  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=&x^2+2x-4 &\\[5pt]
&=&x^2+2x+1^2-1^2-4 &\\[5pt]
&=&(x+1)^2-1-4 &\\[5pt]
y&=&(x+1)^2-5 &
\end{array}\)](https://www.schullv.de/resources/formulas/eaf256d6a46a52686f95cce52b433f059256002069b70622ac8c775d6e25347f_light.svg) Daraus folgt für den Scheitelpunkt:
Daraus folgt für den Scheitelpunkt:  Gleichung der Geraden
Gleichung der Geraden  ermitteln, die von den Punkten
ermitteln, die von den Punkten  und
und  festgelegt wird
festgelegt wird
 Eine mögliche Gleichung der Geraden
Eine mögliche Gleichung der Geraden  berechnen
Gleichung der Parabel
berechnen
Gleichung der Parabel  ermitteln
ermitteln
 Schnittpunkte von
Schnittpunkte von  und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
p_1&=& p_2&\\[5pt]
x^2+2x-4&=& -x^2+8&\quad \scriptsize \mid\;+x^2 \,\mid\,-8 \\[5pt]
2x^2+2x-12&=& 0 &\quad \scriptsize \mid\;:2 \\[5pt]
x^2+x-6&=& 0 &\quad \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7ffbc83240457a5ea8d0ae21d614257a29f8f58410bf409765b2d13be4b0c554_light.svg) Weiter mit der
Weiter mit der  -Formel:
-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2+6} \\[5pt]
x_{1/2}&=& -\dfrac{1}{2} \pm \dfrac{5}{2}& \\[5pt]
x_1&=& -\dfrac{1}{2}+\dfrac{5}{2}=2 \\[5pt]
x_2&=&-\dfrac{1}{2}-\dfrac{5}{2}=-3
\end{array}\)](https://www.schullv.de/resources/formulas/d6b69f78cd7605c9b2bbc01d13633289c68073d6fb7b86e3004887a4c479e43e_light.svg) Lösungsvorschlag 1:
Lösungsvorschlag 1:  verläuft durch den Punkt
verläuft durch den Punkt  mit der
mit der  -Koordinate
-Koordinate 
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&-x^2+8 \\[5pt]
y&=&-2^2+8\\[5pt]
y&=&4\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5ed58b68abefc2e0627279e8678bc3154bb7c307566a1072175598b9c7e5e0eb_light.svg) Daraus folgt für diesen Schnittpunkt:
Daraus folgt für diesen Schnittpunkt:  Gleichung der Gerade
Gleichung der Gerade  berechnen:
berechnen:
 Lösungsvorschlag 2:
Lösungsvorschlag 2:  verläuft durch den Punkt
verläuft durch den Punkt  mit der
mit der  -Koordinate
-Koordinate 
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&-x^2+8 \\[5pt]
y&=&-(-3)^2+8\\[5pt]
y&=&-1\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8b6a73baaf90115ca0e3dce4bc029dd985ac60b5b824594089048a10385a2c05_light.svg) Daraus folgt für diesen Schnittpunkt:
Daraus folgt für diesen Schnittpunkt:  Gleichung der Gerade
Gleichung der Gerade  berechnen:
berechnen:

- Allgemeine Geradengleichung:
- Für den Steigungsfaktor
gilt:
- Da
durch
verläuft und
auf der
-Achse liegt, gilt:
- Da
eine nach unten geöffnete Normalparabel ist und ihr Scheitelpunkt
auf der
-Achse liegt, gilt:
- Da der Scheitelpunkt
auf der
-Achse liegt, gilt auch:
- Allgemeine Geradengleichung:
- Da
und
parallel verlaufen, gilt für den Steigungsfaktor:
- Daraus folgt für
- Allgemeine Geradengleichung:
- Da
und
parallel verlaufen, gilt für den Steigungsfaktor:
- Daraus folgt für
b)
Koordinaten der Schnittpunkte  und
und  von
von  und
und  berechnen
Gleichung der Parabel
berechnen
Gleichung der Parabel  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=& \dfrac{1}{4}\cdot x^2+c\quad \scriptsize \mid\; R\,(4\mid0) \\[5pt]
0 &=&\dfrac{1}{4} \cdot 4^2+c \\[5pt]
0 &=&4+c \quad \scriptsize \mid\; -4\\[5pt]
c&=& -4\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/412d3ff47c230518d33ae93cb55119443b5fe3107a2b2a221e256847418a5069_light.svg)

 -Koordinaten der Schnittpunkte berechnen
-Koordinaten der Schnittpunkte berechnen
![\(\begin{array}[t]{rll}
p_1&=& p_2 \\[5pt]
\dfrac{1}{4}x^2-4&=& -x^2+1 &\quad \scriptsize \mid\; +4 \\[5pt]
\dfrac{1}{4}x^2&=& -x^2+5 &\quad \scriptsize \,\mid\, +x^2 \\[5pt]
\dfrac{5}{4}x^2&=& 5 &\quad \scriptsize \mid\;:\dfrac{5}{4} \\[5pt]
x^2&=& 4 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&=& \underline{ 2} \\[5pt]
x_2&=& \underline{ -2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7515e5c046a5c794e51ff5f6a711a0addaa447e4f751e7df0386b753c2801347_light.svg)
 -Koordinaten der Schnittpunkte berechnen
-Koordinaten der Schnittpunkte berechnen
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&-x^2+1 \\[5pt]
y&=& - 2^2+1 &\quad \scriptsize \\[5pt]
y&=& -4+1 \\[5pt]
y&=& -3
\end{array}\)](https://www.schullv.de/resources/formulas/59bc7c51933032d9b51ae6e8c376616362c5371cc035b59ba594377ede3682a7_light.svg) Schnittpunkt 1:
Schnittpunkt 1: 
 in
in  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
y&=&-x^2+1 \\[5pt]
y&=& - (-2)^2+1 &\quad \scriptsize \\[5pt]
y&=& -4+1 \\[5pt]
y&=& -3
\end{array}\)](https://www.schullv.de/resources/formulas/07f0bc9c56b7af556b3c4124ba18762c255d8e01fea00c8df112270fc8e1b5ea_light.svg) Schnittpunkt 2:
Schnittpunkt 2:  Hat Mia recht?
Koordinaten des Scheitelpunkts
Hat Mia recht?
Koordinaten des Scheitelpunkts  der Parabel
der Parabel  bestimmen
bestimmen
 Koordinaten des Scheitelpunkts
Koordinaten des Scheitelpunkts  der Parabel
der Parabel  bestimmen
bestimmen

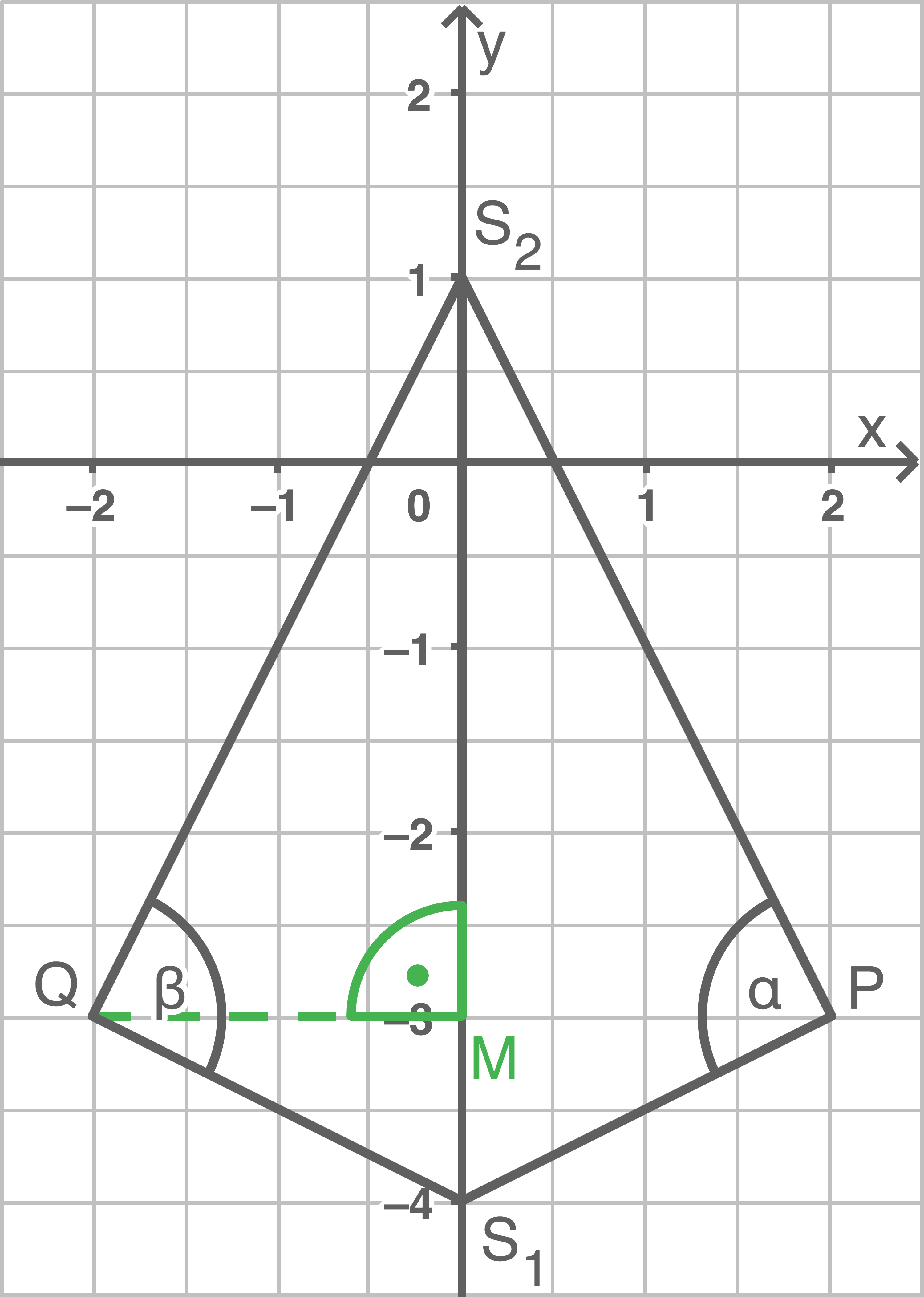 Gilt der Satz des Pythagoras im Dreieck
Gilt der Satz des Pythagoras im Dreieck  ?
?
 berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\overline{S_2Q}^2&=& \overline{S_2M} ^2+ \overline{MQ}^2 \\[5pt]
\overline{S_2Q}^2&=& (4\,\text{LE})^2+(2\,\text{LE})^2 \\[5pt]
\overline{S_2Q}^2&=&\underline{ 20\,\text{LE}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/ecf22ec65a801299116aaf65e0fb4da2457a65d82961cbbcc75e06610dc9cb77_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{S_1Q}^2&=& \overline{S_1M} ^2+ \overline{MQ}^2 \\[5pt]
\overline{S_1Q}^2&=& (1\,\text{LE})^2+(2\,\text{LE})^2 &\\[5pt]
\overline{S_1Q}^2&=&\underline{ 5\,\text{LE}^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/56c5c6c02e6c071b8d62cfb56203940a4e3f8f4dd7ce8291375da29dfb695e7a_light.svg) Satz des Pythagoras anwenden
Satz des Pythagoras anwenden
![\(\begin{array}[t]{rll}
\overline{S_1S_2}^2&=& \overline{S_1Q}^2+\overline{S_2Q}^2\\[5pt]
\overline{S_1S_2}^2&=& 5\,\text{LE}^2 + 20\,\text{LE}^2 \\[5pt]
\overline{S_1S_2}^2&=& 25\,\text{LE}^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
\overline{S_1S_2}&=& \underline{ 5\,\text{LE}}
\end{array}\)](https://www.schullv.de/resources/formulas/fd518a18678791abffab1bb88620ee5bd7c61f9a8040c0d7666d44a0e7125aff_light.svg) An der Abbildung kann man ablesen, dass die Länge der Strecke
An der Abbildung kann man ablesen, dass die Länge der Strecke  tatsächlich
tatsächlich  beträgt. Der Satz des Pythagoras gilt hier also. Somit ist
beträgt. Der Satz des Pythagoras gilt hier also. Somit ist  ein rechter Winkel. Gleiches gilt für den Winkel
ein rechter Winkel. Gleiches gilt für den Winkel  Mia hat also recht.
Mia hat also recht.

- Falls ja
Winkel
ist ein rechter Winkel
- Falls nein
Winkel
ist kein rechter Winkel
Lösung W4
a)
b)
Eine mögliche Gleichung der Parabel angeben
Es gilt:
 Somit gilt für den Vorfaktor
Somit gilt für den Vorfaktor 
![\(\begin{array}[t]{rll}
y&=&ax^2+c &\quad \scriptsize \mid\;-\,c \\[5pt]
ax^2&=&y-c &\quad \scriptsize \mid\;:x^2 \\[5pt]
a&=&\dfrac{y-c}{x^2} &\quad \scriptsize \mid\; c=3,6, \, D(-2,8|2)\\[5pt]
a&=&\dfrac{2-3,6}{(-2,8)^2} \\[5pt]
a&=& \underline{ -0,20}
\end{array}\)](https://www.schullv.de/resources/formulas/37e3af4b2974c31b68910e5d7d3afe93e5240317a140d14f3af3b31e84d04adb_light.svg) Eine mögliche Parabel lautet also
Eine mögliche Parabel lautet also  Trifft Theo bei diesem Wurf direkt in den Korb?
1. Schritt: Koordinaten des Korbringmittelpunkts ermitteln
Trifft Theo bei diesem Wurf direkt in den Korb?
1. Schritt: Koordinaten des Korbringmittelpunkts ermitteln
 2. Schritt: Punktprobe durchführen
2. Schritt: Punktprobe durchführen
![\(\begin{array}[t]{rll}
y &=& -0,2x^2+3,6\quad \scriptsize \mid\; K(1,9|3,5)\text{ einsetzen}\\[5pt]
3,05 &=& -0,2 \cdot (1,9)^2+3,6 \\[5pt]
3,05 &\neq& 2,878\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4c313d91118d6caeca14037026e4cbb0f52786953be49573fa98ead66279a0c9_light.svg) Der Punkt liegt nicht auf der Parabel. Theo trifft bei diesem Wurf also nicht in den Korb.
Berührt Dennis den Ball, ohne hochzuspringen?
1. Schritt: Koordinaten des Punktes ermitteln, den Dennis mit ausgestreckten Händen und ohne hochzuspringen, erreicht
Der Punkt liegt nicht auf der Parabel. Theo trifft bei diesem Wurf also nicht in den Korb.
Berührt Dennis den Ball, ohne hochzuspringen?
1. Schritt: Koordinaten des Punktes ermitteln, den Dennis mit ausgestreckten Händen und ohne hochzuspringen, erreicht
 2. Schritt: Flughöhe des Balls bei
2. Schritt: Flughöhe des Balls bei  berechnen
berechnen
![\(\begin{array}[t]{rll}
y &=& -0,2x^2+3,6\quad \scriptsize \mid\; x_\text{D}=-2,2\\[5pt]
y &=& -0,2 \cdot (-2,2)^2+3,6 \\[5pt]
y&=& \underline{ 2,63}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/67b9c3be27a47362da53de62ab9db9afe20ddec114303c9a4605a39ec08a7912_light.svg) Dennis kann den Ball mit ausgestreckten Händen nicht berühren, da der Ball
Dennis kann den Ball mit ausgestreckten Händen nicht berühren, da der Ball  höher fliegt.
höher fliegt.
- Der höchste Punkt (= Scheitelpunkt) liegt bei
- Der Abwurfpunkt liegt bei
-Koordinate:
-Koordinate: Korbhöhe
-Koordinate:
links vom Ursprung
-Koordinate: Höhe von Dennis mit nach oben gestreckten Armen