Pflichtteil A1

Von einem Dreieck Formula: ABC sind folgende Angaben bekannt:

Seite $Formula: c = 7 \ \text{cm}$ $Formula: c = 7 \ \text{cm}$
Seite $Formula: a = 6 \ \text{cm}$ $Formula: a = 6 \ \text{cm}$
Winkel $Formula: \gamma = 80^{\circ}$ $Formula: \gamma = 80^{\circ}$

Konstruiere das Dreieck und gib die Form des Dreiecks an.

1 P

Aus einer Tageszeitung:

„Im Jahr 2010 fuhr laut Polizeibericht jeder zehnte Autofahrer zu schnell. 2024 fuhr ,nur noch‘ jeder fünfte Autofahrer zu schnell. Für die Polizei sind fünf Prozent immer noch zu viel, sodass weiterhin kontrolliert wird.“

Nimm Stellung, ob der Polizeibericht mathematisch korrekt ist.

1 P

Gegeben ist die Funktionsgleichung Formula: y=-2 x^2-5.

Kreuze die richtige Aussage an.

 Die um $Formula: 5 \ \text{LE}$ $Formula: 5 \ \text{LE}$ nach unten verschobene Parabel ist breiter als die Normalparabel.

 Die Parabel ist nach unten geöffnet, breiter als eine Normalparabel und um $Formula: 5 \ \text{LE}$ $Formula: 5 \ \text{LE}$ nach oben verschoben.

 Die Parabel ist nach unten geöffnet, schmaler als die Normalparabel und um $Formula: 5 \ \text{LE}$ $Formula: 5 \ \text{LE}$ nach unten verschoben.

 Die Parabel ist schmaler als die Normalparabel, nach oben geöffnet und ist um $Formula: 5 \ \text{LE}$ $Formula: 5 \ \text{LE}$ nach unten verschoben.

1 P

Löse die Gleichung.

Formula: 2 x(x-2)-6 x=-10 x+32

1 P

An der Ostsee stehen viele Leuchttürme.

Wie hoch ist der abgebildete Leuchtturm ungefähr?

(Maße dürfen aus der Zeichnung entnommen werden.)

Beschreibe dein Vorgehen und begründe rechnerisch.

Weißer Leuchtturm bei Abenddämmerung, leuchtende Laterne sendet Lichtkegel vor Sternenhimmel

1 P

Eren soll folgende Textaufgabe lösen:

„Familie Semerak hat in ihrem Garten einen Apfelbaum mit einer Höhe von $Formula: 1,30 \ \text{m}$ $Formula: 1,30 \ \text{m}$ gepflanzt. Im ersten Jahr ist er um weitere $Formula: 1,10 \ \text{m}$ $Formula: 1,10 \ \text{m}$ gewachsen.

Wie hoch wird der Apfelbaum nach 80 Jahren sein?“

Eren löst die Textaufgabe mit Hilfe einer Gleichung:

$Formula: y=1,30+80 \cdot 1,10$ $Formula: y=1,30+80 \cdot 1,10$

Antwort: $Formula: 89,3 \ \text{m}$ $Formula: 89,3 \ \text{m}$

Erkläre, warum der Lösungsansatz (mit Lösung) nicht stimmen kann.

1 P

Das Säulendiagramm zeigt die Arbeitslosenzahlen in Deutschland von 2014 bis 2019 .

Balkendiagramm: sinkende Arbeitslosenzahlen in Deutschland 2014–2019, von ca. 2,9 auf 2,2 Millionen.

Kreuze richtige Aussagen an.

 Es ist sicher, dass die Zahl der Arbeitslosen 2020 weiter gesunken ist.

 Die Arbeitslosenzahlen sind von 2014 bis 2019 jährlich gesunken.

 Der Rückgang der jährlichen Arbeitslosenzahl ist von 2017 bis 2018 am stärksten.

 Von 2017 auf 2019 sinken die Arbeitslosenzahlen um über $Formula: 50 \, \%.$ $Formula: 50 \, \%.$

1 P

Gegeben sind eine Raute und ein Drachen mit den Diagonalen Formula: e und Formula: f.

Bei beiden Figuren ist die Diagonale Formula: f gleich lang.

Der Flächeninhalt der Raute beträgt $Formula: 60 \ \text{cm}^2.$ $Formula: 60 \ \text{cm}^2.$

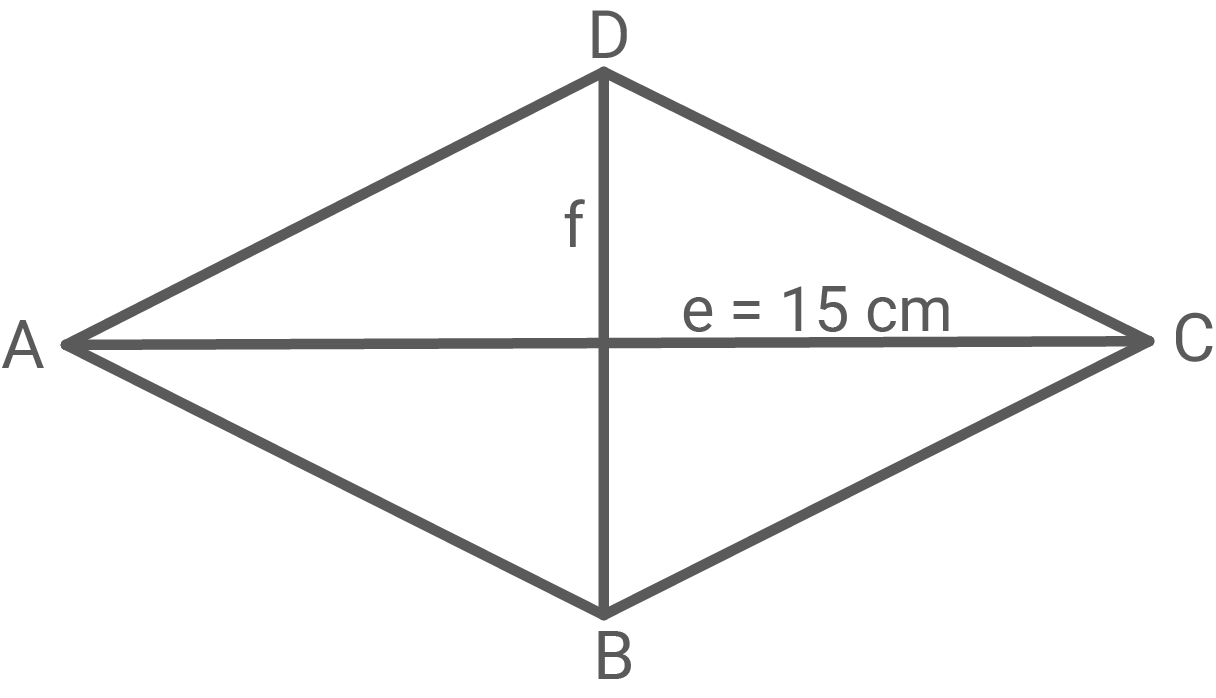
Raute mit horizontaler Diagonale AC = 15 cm und vertikaler Diagonale f, Punkte A links, B unten, C rechts, D oben

Drachenförmige Figur mit Punkten A,B,C,D; horizontale Diagonale AC = 45 cm und senkrechte Diagonale f.

(Skizzen nicht maßstabsgetreu)

Bestimme den Flächeninhalt des Drachens.

1 P

In den Bechern befinden sich rote Formula: (R), grüne Formula: ( G ) und blaue Formula: ( B ) Murmeln. Aus jedem Becher wird eine Murmel gezogen.

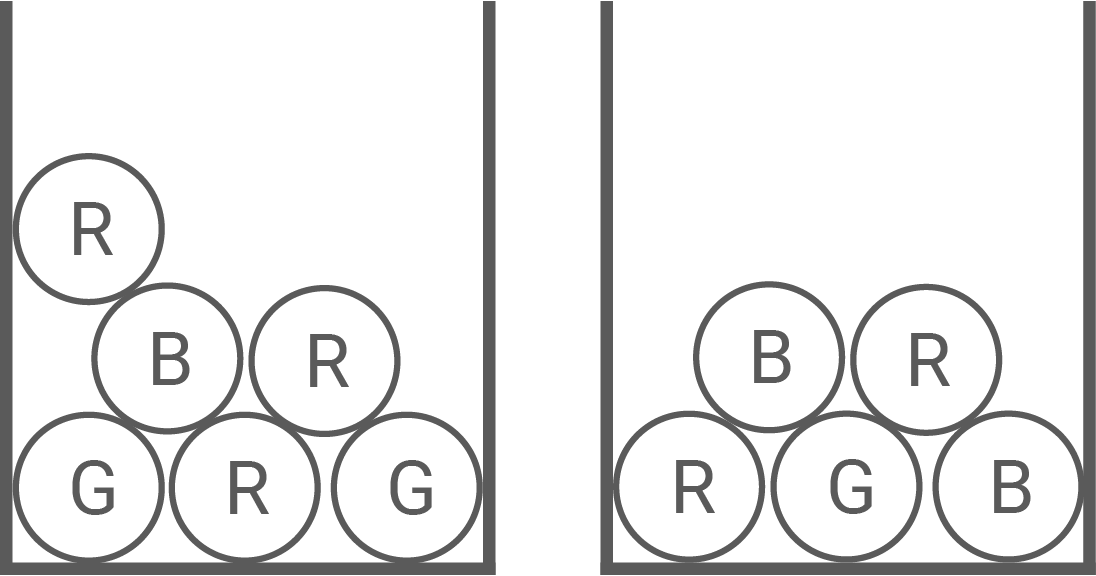
Zwei nebeneinander stehende Behälter mit gestapelten Kugeln, jeweils mit den Buchstaben R, B und G beschriftet.

Pia berechnet die Wahrscheinlichkeit eines Ereignisses wie folgt:

$Formula: P(x)=\frac{1}{2} \cdot \frac{1}{5}=\frac{1}{10}$ $Formula: P(x)=\frac{1}{2} \cdot \frac{1}{5}=\frac{1}{10}$

Ergänze, welche Farben die gezogenen Murmeln haben.

1. Zug: $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$ $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$ 2. Zug: $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$ $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$

1. Zug: $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$ $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$

2. Zug: $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$ $Formula: \_\_\_\_\_\_\_\_\_\_\_\_$

1 P

Gegeben ist ein Rechteck Formula: A und eine neue Figur Formula: B (dick umrandet).

Zwei Gitterrechtecke nebeneinander: links kleines Rasterquadrat (Rechteck A), rechts langes Rasterrechteck (Figur B).

Der Flächeninhalt der Figur B

(A) entspricht jetzt $Formula: 150 \, \%$ $Formula: 150 \, \%$ im Vergleich zu Rechteck Formula: A.

(B) nahm um $Formula: 150 \, \%$ $Formula: 150 \, \%$ im Vergleich zu Rechteck Formula: A zu.

(D) wurde um $Formula: 75 \, \%$ $Formula: 75 \, \%$ im Vergleich zu Rechteck Formula: A vergrößert.

Gib die richtige Aussage an und begründe deine Entscheidung.

1 P

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Dreieck ABC, Winkel C 80°, Seite a = 6 cm, Grundlinie AB, gestrichelte 7-cm-Strecke und grüne Kreislinie links.

Es handelt sich um ein spitzwinkliges Dreieck.

Erklärung zur Konstruktion:

Zeichne zuerst die Seite $Formula: a = 6 \ \text{cm}$ $Formula: a = 6 \ \text{cm}$ als Strecke $Formula: \overline{BC}.$ $Formula: \overline{BC}.$ Zeichne am Punkt Formula: C den Winkel $Formula: \gamma = 80^{\circ}$ $Formula: \gamma = 80^{\circ}$ und verlängere den Schenkel. Ziehe mit dem Zirkel einen Kreisbogen um den Punkt Formula: B als Mittelpunkt mit dem Radius $Formula: c = 7 \ \text{cm}.$ $Formula: c = 7 \ \text{cm}.$ Dort, wo sich der Schenkel des Winkels $Formula: \gamma$ $Formula: \gamma$ und der Kreisbogen schneiden, liegt der Punkt Formula: A.

Im Jahr 2010 fuhren $Formula: \tfrac{1}{10} = 10 \, \%$ $Formula: \tfrac{1}{10} = 10 \, \%$ (jeder zehnte) der Autofahrer zu schnell. Im Jahr 2024 fuhren aber $Formula: \tfrac{1}{5}= 20 \, \%$ $Formula: \tfrac{1}{5}= 20 \, \%$ (jeder fünfte) der Autofahrer zu schnell. Die Behauptung im Zeitungsartikel stimmt deshalb nicht.

Die Parabel ist nach unten geöffnet, schmaler als die Normalparabel und um $Formula: 5 \ \text{LE}$ $Formula: 5 \ \text{LE}$ nach unten verschoben.

$Formula: \begin{array}[t]{rll} 2x(x-2)-6x &=& -10x+32 &\quad \mid\; \text{ausmultiplizieren} \\ 2x^2-4x-6x &=& -10x+32 &\quad \mid\; \text{zusammenfassen} \\ 2x^2-10x &=& -10x+32 &\quad \mid\; +10x \\ 2x^2 &=& 32 &\quad \mid\; \div2 \\ x^2 &=& 16 &\quad \mid\; \sqrt{\ } \\ x_1 &=& 4 \ \\ \text{und} \ x_2 &=& -4 \end{array}$ $Formula: \begin{array}[t]{rll} 2x(x-2)-6x &=& -10x+32 &\quad \mid\; \text{ausmultiplizieren} \\ 2x^2-4x-6x &=& -10x+32 &\quad \mid\; \text{zusammenfassen} \\ 2x^2-10x &=& -10x+32 &\quad \mid\; +10x \\ 2x^2 &=& 32 &\quad \mid\; \div2 \\ x^2 &=& 16 &\quad \mid\; \sqrt{\ } \\ x_1 &=& 4 \ \\ \text{und} \ x_2 &=& -4 \end{array}$

Die Tür ist ungefähr $Formula: 2 \ \text{m}$ $Formula: 2 \ \text{m}$ hoch. Der Leuchtturm ist in der Zeichnung ungefähr Formula: 9 Türen hoch.

Damit ist der Leuchtturm in Wirklichkeit ungefähr $Formula: 9 \cdot 2 = 18 \ \text{m}$ $Formula: 9 \cdot 2 = 18 \ \text{m}$ hoch.

Ein Apfelbaum wächst nicht jedes Jahr gleichmäßig um $Formula: 1,10 \ \text{m}.$ $Formula: 1,10 \ \text{m}.$ Zudem kann ein Apfelbaum nicht knapp $Formula: 90 \ \text{m}$ $Formula: 90 \ \text{m}$ hoch werden. Es handelt sich hier nicht (durchgehend) um einen linearen Zusammenhang.

Die Arbeitslosenzahlen sind von 2014 bis 2019 jährlich gesunken.

Der Rückgang der jährlichen Arbeitslosenzahl ist von 2017 bis 2018 am stärksten.

Formel für den Flächeninhalt für Raute und Drachen: $Formula: A = \frac{e \cdot f}{2}.$ $Formula: A = \frac{e \cdot f}{2}.$

Aus dem Flächeninhalt der Raute folgt:

$Formula: \begin{array}[t]{rll} 60 &=& \dfrac{15 \cdot f}{2} &\quad \mid\; \cdot \, 2 \\ 120 &=& 15 \cdot f &\quad \mid\; \div 15 \\ 8 &=& f \\ \end{array}$ $Formula: \begin{array}[t]{rll} 60 &=& \dfrac{15 \cdot f}{2} &\quad \mid\; \cdot \, 2 \\ 120 &=& 15 \cdot f &\quad \mid\; \div 15 \\ 8 &=& f \\ \end{array}$

Damit gilt für den Flächeninhalt des Drachens:

$Formula: A = \dfrac{e \cdot f}{2} = \dfrac{45 \cdot 8}{2} = \dfrac{360}{2} = 180 \ \text{cm}^2$ $Formula: A = \dfrac{e \cdot f}{2} = \dfrac{45 \cdot 8}{2} = \dfrac{360}{2} = 180 \ \text{cm}^2$

Zug: rot
Zug: grün

Erklärung:

Im ersten Becher sind die Hälfte aller Murmeln rot, im zweiten Becher eine von insgesamt 5 Murmeln grün.

Der Flächeninhalt der Figur Formula: B nahm um $Formula: 150 \, \%$ $Formula: 150 \, \%$ im Vergleich zu Rechteck Formula: A zu.

Der Flächeninhalt des Rechtecks Formula: A beträgt $Formula: A_{A} = 4 \cdot 6 = 24 \ \text{FE},$ $Formula: A_{A} = 4 \cdot 6 = 24 \ \text{FE},$ der des Recktecks Formula: B beträgt $Formula: A_{B} = 4 \cdot 15 = 60 \ \text{FE}.$ $Formula: A_{B} = 4 \cdot 15 = 60 \ \text{FE}.$

Es gilt $Formula: \tfrac{A_{B}}{A_{A}} = \tfrac{60}{24} = 2,5 = 250 \, \% ,$ $Formula: \tfrac{A_{B}}{A_{A}} = \tfrac{60}{24} = 2,5 = 250 \, \% ,$ das heißt, der Flächeninhalt von Rechteck Formula: B entspricht $Formula: 250 \, \%$ $Formula: 250 \, \%$ des Flächeninhalts von Rechteck Formula: A.

Damit beträgt die Zunahme $Formula: 250 \, \% - 100 \, \% = 150 \, \% .$ $Formula: 250 \, \% - 100 \, \% = 150 \, \% .$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?