Wahlteil B

Der Durchmesser von Kugel Formula: A ist dreimal so groß wie der Durchmesser von Kugel Formula: B.

Überprüfe die Aussagen und kreuze entsprechend an.

Begründe jeweils deine Entscheidung.

Aussage	richtig	falsch
(1) Das Volumen von Kugel ist dreimal so groß wie das Volumen von Kugel
(2) Der Oberflächeninhalt von Kugel beträgt ein Neuntel des Oberflächeninhalts von Kugel
(3) Die Hälfte des Durchmessers von Kugel entspricht dem dreifachen Radius von Kugel

Folgende Verhältnisgleichung ist gegeben:

$Formula: \frac{x}{20}=\frac{x+40}{28}$ $Formula: \frac{x}{20}=\frac{x+40}{28}$

Beschrifte die Strahlensatzfigur so, dass diese zur Verhältnisgleichung passt.

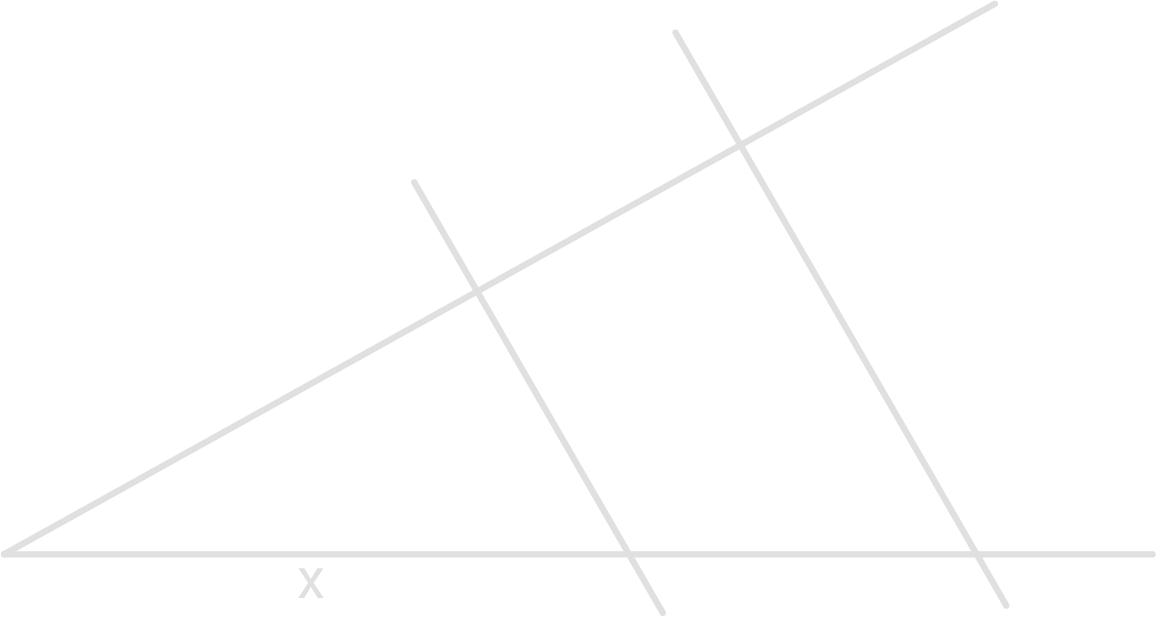
Geometrische Skizze: waagerechte Grundlinie mit "x", eine schräge Seite und zwei parallele schräge Linien, die sie schneiden.

Bestimme Formula: x.

5 P

Bei einem Schulfest verkauft die Klasse 5a Lose an einem Stand. Es gibt Hauptgewinne (HG), Trostpreise (TP) und Nieten (NT). Die Hälfte der Lose sind Nieten.

Vervollständige das Baumdiagramm.

Berechne die prozentuale Wahrscheinlichkeit für das Ereignis, einen Hauptgewinn und einen Trostpreis zu ziehen.

Die Klasse 5b betreibt beim gleichen Schulfest ein Glücksrad.

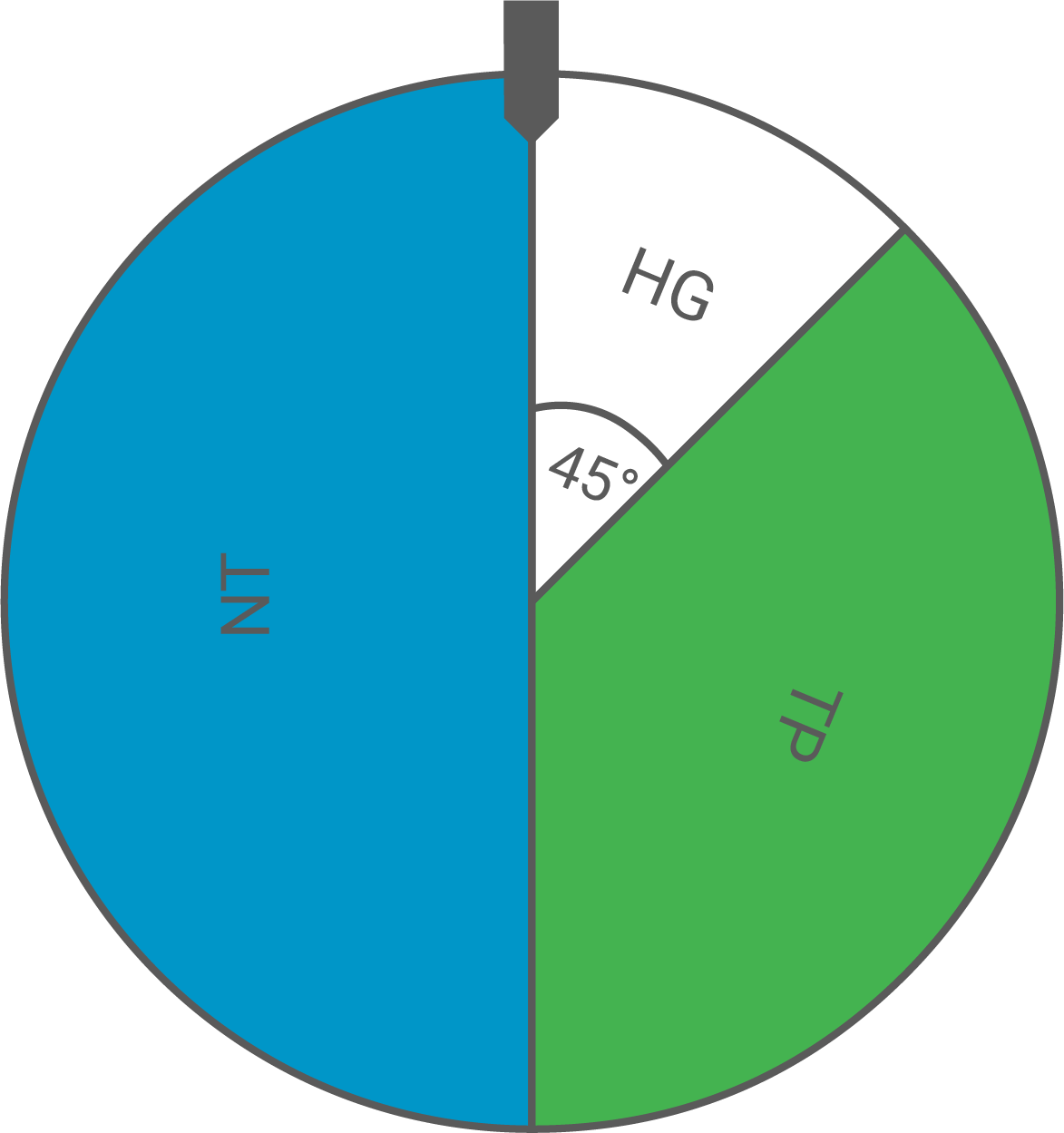
Kreisdiagramm: großer blauer Sektor (NT), großer grüner Sektor (TR) und kleiner weißer Sektor (HG, 45°) mit Markierung oben.

(Skizze nicht maßstabsgetreu)

Überprüfe, bei welchem Stand es wahrscheinlicher ist, zwei Hauptgewinne zu erzielen.

5 P

10 P

Die Abbildung zeigt einen Halbkreis mit Formula: M als Mittelpunkt. Die Punkte Formula: C und Formula: D liegen auf dem Halbkreis.

Halbkreis mit Punkten A, B, C, D, M, eingezeichnete Strecken und beschriftete Winkel 32°, 67°, α und ε.

(Skizze nicht maßstabsgetreu)

Begründe, dass der Winkel $Formula: \varepsilon=46^{\circ}$ $Formula: \varepsilon=46^{\circ}$ ist.

Berechne Winkel $Formula: \alpha.$ $Formula: \alpha.$ Markiere entsprechende Winkel in der Abbildung.

An einem Gruppentisch sitzen Formula: 5 Kinder, die sich zur Begrüßung untereinander die Hände schütteln. Insgesamt werden Formula: 10 Mal die Hände geschüttelt. Leo überlegt sich, wie oft die Hände bei $Formula: 2, \ 3, \ 4$ $Formula: 2, \ 3, \ 4$ und Formula: 6 Personen geschüttelt werden.

Anzahl der Personen	Anzahl des Händeschüttelns

Ergänze in der Tabelle die Anzahl des Händeschüttelns.

Beschreibe, wie man die Anzahl des Händeschüttelns bei Formula: 9 Personen ermitteln kann.

5 P

Gegeben ist die Parabel Formula: p_1 mit folgender Funktionsgleichung: $Formula: y=-\frac{3}{8} x^2+6.$ $Formula: y=-\frac{3}{8} x^2+6.$ Eine verschobene Normalparabel Formula: p_2 hat den Scheitelpunkt $Formula: S(0 \mid 6).$ $Formula: S(0 \mid 6).$

Beschreibe die Bedeutung des Faktors $Formula: a=-\frac{3}{8}$ $Formula: a=-\frac{3}{8}$ im Vergleich zum Faktor der Parabel Formula: p_2 hinsichtlich der Darstellung im Koordinatensystem.

Zeige, dass die Parabel Formula: p_1 und die Formula: x -Achse die Schnittpunkte $Formula: N_1(4 \mid 0)$ $Formula: N_1(4 \mid 0)$ und $Formula: N_2(-4 \mid 0)$ $Formula: N_2(-4 \mid 0)$ haben.

Die Parabel Formula: p_1 wird zuerst an der Formula: x -Achse gespiegelt und anschließend um zwei Einheiten nach oben verschoben. Es entsteht die Parabel Formula: p_3.

Überprüfe, ob der Punkt $Formula: P (4 \mid 2)$ $Formula: P (4 \mid 2)$ auf der Parabel Formula: p_3 liegt.

Der Scheitelpunkt der Parabel Formula: p_1 und die Schnittpunkte mit der Formula: x -Achse bilden das Dreieck $Formula: SN_{1}N_{2}.$ $Formula: SN_{1}N_{2}.$

Berechne die Innenwinkel des Dreiecks $Formula: SN_{1}N_{2}.$ $Formula: SN_{1}N_{2}.$

5 P

10 P

Gegeben ist ein rechtwinkliges Trapez.

Den Flächeninhalt des Trapezes kann man durch verschiedene Strategien bestimmen und mit unterschiedlichen Termen darstellen.

Zu jedem Term gehören eine Strategie und ein Bild.

Geometrische Zeichnung eines Trapezes: obere Seite 10 cm lang, untere Seite 8 cm lang, rechte Seite senkrecht mit einer Länge von 3 cm. An der rechten Seite sind oben und unten zwei gleich markierte Winkel eingezeichnet, die auf rechte Winkel hinweisen.

Gegeben ist ein rechtwinkliges Trapez.

Den Flächeninhalt des Trapezes kann man durch verschiedene Strategien bestimmen und mit unterschiedlichen Termen darstellen.

Zu jedem Term gehören eine Strategie und ein Bild.

Ordne die Darstellungen einander zu.

Ergänze die unvollständigen Darstellungen.

Strategien für Flächenberechnung von Trapez

5 P

Katja legt bei ihrer Hausbank ein Kapital von $Formula: 3200,00 \, €$ $Formula: 3200,00 \, €$ bei einem festen Zinssatz für vier Jahre an.

Die Bank stellt das Wachstum des Kapitals in einem Diagramm dar:

Säulendiagramm Kapital und Zinssatz über 4 Jahre

(Darstellung nicht maßstabsgetreu)

Überprüfe, ob die folgenden Aussagen zum Diagramm passen. Begründe jeweils deine Entscheidung.

(1) Das Kapital ist nach drei Jahren von $Formula: 3200,00 \, €$ $Formula: 3200,00 \, €$ auf $Formula: 3427,92 \, €$ $Formula: 3427,92 \, €$ gestiegen.

(2) Der jährliche Wachstumsfaktor beträgt $Formula: 1,035 \% .$ $Formula: 1,035 \% .$

(3) Nach zwei Jahren ist das Kapital um $Formula: 7 \, \%$ $Formula: 7 \, \%$ gestiegen.

(4) Die Zinsen sind jedes Jahr gleich.

Ergänze im Diagramm einen Prozentstreifen für das 4. Jahr und beschrifte diesen entsprechend.

Gegeben ist folgendes Gleichungssystem:

$Formula: \begin{array}[t]{rll} &(1)& \ \ \dfrac{15}{2} x &=& 3y+27 \\[5pt] &(2)& \ \ y-3 &=& \dfrac{1}{2} x\\[5pt] \end{array}$ $Formula: \begin{array}[t]{rll} &(1)& \ \ \dfrac{15}{2} x &=& 3y+27 \\[5pt] &(2)& \ \ y-3 &=& \dfrac{1}{2} x\\[5pt] \end{array}$

Löse das Gleichungssystem.

5 P

10 P

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aussage	richtig	falsch
(1) Das Volumen von Kugel ist dreimal so groß wie das Volumen von Kugel		x
(2) Der Oberflächeninhalt von Kugel beträgt ein Neuntel des Oberflächeninhalts von Kugel	x
(3) Die Hälfte des Durchmessers von Kugel entspricht dem dreifachen Radius von Kugel	x

Da der Durchmesser von Kugel Formula: A dreimal so groß wie der Durchmesser von Kugel Formula: B ist, ist auch der Radius von Kugel dreimal so groß wie der Radius von Kugel $Formula: B\text{:}$ $Formula: B\text{:}$

$Formula: \begin{array}[t]{rll} d_{A} &=& 3 \cdot d_{B} \\ 2 \cdot r_{A} &=& 3 \cdot 2 \cdot r_{B} &\quad \mid\; \div 2 \\ r_{A} &=& 3 \cdot r_{B} \end{array}$ $Formula: \begin{array}[t]{rll} d_{A} &=& 3 \cdot d_{B} \\ 2 \cdot r_{A} &=& 3 \cdot 2 \cdot r_{B} &\quad \mid\; \div 2 \\ r_{A} &=& 3 \cdot r_{B} \end{array}$

Überprüfung der 1. Aussage

$Formula: \begin{array}[t]{rll} V_{A} &=& \dfrac{4}{3} \cdot \pi \cdot r_{A}^{3} \\[5pt] &=& \dfrac{4}{3} \cdot \pi \cdot (3 \cdot r_{B})^{3} \\[5pt] &=& \dfrac{4}{3} \cdot \pi \cdot 27 \cdot r_{B}^{3} \\[5pt] &=& 27 \cdot \dfrac{4}{3} \pi \cdot r_{B}^{3} \\[5pt] &=& 27 \cdot V_{B} \end{array}$ $Formula: \begin{array}[t]{rll} V_{A} &=& \dfrac{4}{3} \cdot \pi \cdot r_{A}^{3} \\[5pt] &=& \dfrac{4}{3} \cdot \pi \cdot (3 \cdot r_{B})^{3} \\[5pt] &=& \dfrac{4}{3} \cdot \pi \cdot 27 \cdot r_{B}^{3} \\[5pt] &=& 27 \cdot \dfrac{4}{3} \pi \cdot r_{B}^{3} \\[5pt] &=& 27 \cdot V_{B} \end{array}$

Das Volumen von Kugel Formula: A ist Formula: 27 -mal so groß wie das Volumen von Kugel Formula: B. Die erste Aussage ist also falsch.

Überprüfung der 2. Aussage

$Formula: \begin{array}[t]{rll} O_{B} &=& 4 \cdot \pi \cdot r_{B}^{2} \\[5pt] &=& 4 \cdot \pi \cdot \left( \dfrac{1}{3} \cdot r_{A} \right)^{2} \\[5pt] &=& 4 \cdot \pi \cdot \dfrac{1}{9} \cdot r_{A}^{2} \\[5pt] &=& \dfrac{1}{9} \cdot 4 \cdot \pi \cdot r_{A}^{2} \\[5pt] &=& \dfrac{1}{9} \cdot O_{A} \end{array}$ $Formula: \begin{array}[t]{rll} O_{B} &=& 4 \cdot \pi \cdot r_{B}^{2} \\[5pt] &=& 4 \cdot \pi \cdot \left( \dfrac{1}{3} \cdot r_{A} \right)^{2} \\[5pt] &=& 4 \cdot \pi \cdot \dfrac{1}{9} \cdot r_{A}^{2} \\[5pt] &=& \dfrac{1}{9} \cdot 4 \cdot \pi \cdot r_{A}^{2} \\[5pt] &=& \dfrac{1}{9} \cdot O_{A} \end{array}$

Die zweite Aussage ist richtig.

Überprüfung der 3. Aussage:

$Formula: \dfrac{1}{2} \cdot d_{A} = r_{A} = 3 \cdot r_{B}$ $Formula: \dfrac{1}{2} \cdot d_{A} = r_{A} = 3 \cdot r_{B}$

Die dritte Aussage ist richtig.

Mögliche Strahlensatzfiguren:

$Formula: \begin{array}[t]{rll} \dfrac{x}{20} &=& \dfrac{x+40}{28} &\quad \mid\; \cdot\,28 \\[0.5em] \dfrac{28x}{20} &=& x+40 &\quad \mid\; \cdot\,20 \\[0.5em] 28x &=& 20x+800 &\quad \mid\; - 20x \\[0.5em] 8x &=& 800 &\quad \mid\; \div 8 \\[0.5em] x &=& 100 \end{array}$ $Formula: \begin{array}[t]{rll} \dfrac{x}{20} &=& \dfrac{x+40}{28} &\quad \mid\; \cdot\,28 \\[0.5em] \dfrac{28x}{20} &=& x+40 &\quad \mid\; \cdot\,20 \\[0.5em] 28x &=& 20x+800 &\quad \mid\; - 20x \\[0.5em] 8x &=& 800 &\quad \mid\; \div 8 \\[0.5em] x &=& 100 \end{array}$

Berechnung der Wahrscheinlichkeiten bei den Losen:

$Formula: \begin{array}[t]{rll} P( \text{1x HG + 1x TP}) &=& \dfrac{10}{80} \cdot \dfrac{30}{79} + \dfrac{30}{80} \cdot \dfrac{10}{79} \\[5pt]&\approx& 0,0949 \\[5pt] &=& 9,49 \, \% \end{array}$ $Formula: \begin{array}[t]{rll} P( \text{1x HG + 1x TP}) &=& \dfrac{10}{80} \cdot \dfrac{30}{79} + \dfrac{30}{80} \cdot \dfrac{10}{79} \\[5pt]&\approx& 0,0949 \\[5pt] &=& 9,49 \, \% \end{array}$

$Formula: \begin{array}[t]{rll} P(\text{2x HG}) &=& \dfrac{10}{80} \cdot \dfrac{9}{79} \\[5pt] &\approx& 0,0142 \\[5pt] &=& 1,42 \, \% \end{array}$ $Formula: \begin{array}[t]{rll} P(\text{2x HG}) &=& \dfrac{10}{80} \cdot \dfrac{9}{79} \\[5pt] &\approx& 0,0142 \\[5pt] &=& 1,42 \, \% \end{array}$

Berechnung der Wahrscheinlichkeit beim Glücksrad:

$Formula: \begin{array}[t]{rll} P( \text{2x HG}) &=& \dfrac{45}{360} \cdot \dfrac{45}{360} \\[5pt] &\approx& 0,0156 \\[5pt] &=& 1,56 \, \% \end{array}$ $Formula: \begin{array}[t]{rll} P( \text{2x HG}) &=& \dfrac{45}{360} \cdot \dfrac{45}{360} \\[5pt] &\approx& 0,0156 \\[5pt] &=& 1,56 \, \% \end{array}$

Beim Stand mit dem Glücksrad ist es wahrscheinlicher, zwei Hauptgewinne zu erzielen.

Berechnung der Winkel im Halbkreis:

Da die Strecken $Formula: \overline{MB}$ $Formula: \overline{MB}$ und $Formula: \overline{MC}$ $Formula: \overline{MC}$ beide dem Radius des Halbkreises entsprechen, ist das Dreieck $Formula: MBC \$ $Formula: MBC \$ gleichschenklig.

Demnach muss der Winkel $Formula: \gamma_{2}$ $Formula: \gamma_{2}$ beim Punkt Formula: C des Dreiecks $Formula: MBC \$ $Formula: MBC \$ ebenfalls $Formula: \gamma_{2} = 67^{\circ}$ $Formula: \gamma_{2} = 67^{\circ}$ betragen.

Da die Summe der Innenwinkel jedes Dreiecks $Formula: 180^{\circ}$ $Formula: 180^{\circ}$ beträgt, folgt $Formula: \varepsilon = 180^{\circ} - 2 \cdot 67^{\circ} = 46^{\circ}.$ $Formula: \varepsilon = 180^{\circ} - 2 \cdot 67^{\circ} = 46^{\circ}.$

Nach dem Satz des Thales beträgt Winkel $Formula: \gamma$ $Formula: \gamma$ bei dem Punkt Formula: C des Dreiecks Formula: ABC $Formula: \gamma = 90^{\circ}.$ $Formula: \gamma = 90^{\circ}.$

Damit gilt $Formula: \gamma_{1} = \gamma - \gamma_{2} = 90^{\circ} - 67^{\circ} = 23^{\circ}.$ $Formula: \gamma_{1} = \gamma - \gamma_{2} = 90^{\circ} - 67^{\circ} = 23^{\circ}.$

Da auch die Strecke $Formula: \overline{MD}$ $Formula: \overline{MD}$ dem Radius des Halbkreises entspricht, ist das Dreieck $Formula: MCD \$ $Formula: MCD \$ ebenfalls gleichschenklig und es folgt:

$Formula: \begin{array}[t]{rll} \alpha + \gamma_{1} &=& 32^{\circ} \\ \alpha + 23^{\circ} &=& 32^{\circ} &\quad \mid\; -23^{\circ} \\ \alpha &=& 9^{\circ} \end{array}$ $Formula: \begin{array}[t]{rll} \alpha + \gamma_{1} &=& 32^{\circ} \\ \alpha + 23^{\circ} &=& 32^{\circ} &\quad \mid\; -23^{\circ} \\ \alpha &=& 9^{\circ} \end{array}$

Berechnung der Anzahl des Händeschüttelns:

Anzahl der Personen
Anzahl des Händeschüttelns

Anzahl der Personen	Anzahl des Händeschüttelns

Die erste Person schüttelt 9 Personen die Hand.

Die zweite Person hat der ersten Person bereits die Hand gegeben. Sie schüttelt also nur noch 8 weiteren Personen die Hand.

Die dritte Person hat schon mit der ersten und zweiten Person Hände geschüttelt und gibt nur noch 7 weiteren Personen die Hand.

Fortsetzend erhält man mit Formula: 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 die Anzahl des Händeschüttelns bei 9 Personen.

Die Parabel $Formula: p_{1}$ $Formula: p_{1}$ ist nach unten geöffnet und breiter als die Parabel $Formula: p_{2}.$ $Formula: p_{2}.$

Der Betragswert des Vorfaktors $Formula: \left( 0 < \left| \tfrac{3}{8} \right| < 1 \right)$ $Formula: \left( 0 < \left| \tfrac{3}{8} \right| < 1 \right)$ führt zu einer vertikalen Stauchung der Parabel Formula: p_2. Durch das negative Vorzeichen wird sie zudem an der Formula: x -Achse gespiegelt.

$Formula: \begin{array}[t]{rll} - \dfrac{3}{8} x^2 + 6 &=& 0 &\quad \mid\; -6 \\ - \dfrac{3}{8} x^2 &=& -6 &\quad \mid\; \div \left( - \dfrac{3}{8} \right) \\ x^2 &=& 16 &\quad \mid\; \sqrt{\ } \\ x_{1} &=& 4 \\ x_{2} &=& -4 \end{array}$ $Formula: \begin{array}[t]{rll} - \dfrac{3}{8} x^2 + 6 &=& 0 &\quad \mid\; -6 \\ - \dfrac{3}{8} x^2 &=& -6 &\quad \mid\; \div \left( - \dfrac{3}{8} \right) \\ x^2 &=& 16 &\quad \mid\; \sqrt{\ } \\ x_{1} &=& 4 \\ x_{2} &=& -4 \end{array}$

Damit hat die Parabel $Formula: p_{1}$ $Formula: p_{1}$ mit der Formula: x -Achse die Schnittpunkte $Formula: N_{1}(4 \mid 0)$ $Formula: N_{1}(4 \mid 0)$ und $Formula: N_{2}(-4 \mid 0).$ $Formula: N_{2}(-4 \mid 0).$

Die Funktionsgleichung der Parabel $Formula: p_{3}$ $Formula: p_{3}$ lautet:

$Formula: \begin{array}[t]{rll} y &=& (-1) \cdot \left( - \dfrac{3}{8} x^2 + 6 \right) + 2 \\&=& \dfrac{3}{8} x^2 - 6 + 2 \\ &=& \dfrac{3}{8} x^2 - 4 \end{array}$ $Formula: \begin{array}[t]{rll} y &=& (-1) \cdot \left( - \dfrac{3}{8} x^2 + 6 \right) + 2 \\&=& \dfrac{3}{8} x^2 - 6 + 2 \\ &=& \dfrac{3}{8} x^2 - 4 \end{array}$

Es gilt:

$Formula: \dfrac{3}{8} \cdot 4^2 - 4 = \dfrac{3}{8} \cdot 16 - 4 = 6 - 4 = 2$ $Formula: \dfrac{3}{8} \cdot 4^2 - 4 = \dfrac{3}{8} \cdot 16 - 4 = 6 - 4 = 2$

Damit liegt der Punkt $Formula: P( 4 \mid 2)$ $Formula: P( 4 \mid 2)$ auf der Parabel $Formula: p_{3}.$ $Formula: p_{3}.$

Der Scheitelpunkt der Parabel $Formula: p_{1}$ $Formula: p_{1}$ ist $Formula: S(0 \mid 6).$ $Formula: S(0 \mid 6).$

Aufgrund der Symmetrie ist das Dreieck $Formula: SN_{1}N_{2}$ $Formula: SN_{1}N_{2}$ gleichschenklig.

Durch Einzeichnen der Höhe wird das Dreieck in zwei gleichgroße rechtwinklige Dreiecke geteilt.

Für einen mit einem der Schenkel eingeschlossenen Winkel gilt:

$Formula: \begin{array}[t]{rll} \tan(\alpha) &=& \dfrac{\text{Gegenkathete von} \ \alpha}{\text{Ankathete von} \ \alpha} \\[0.5em] &=& \dfrac{\overline{MS}}{\overline{MN_{1}}} \\[0.5em] &=& \dfrac{6}{4} \\[0.5em] &=& 1,5 \end{array}$ $Formula: \begin{array}[t]{rll} \tan(\alpha) &=& \dfrac{\text{Gegenkathete von} \ \alpha}{\text{Ankathete von} \ \alpha} \\[0.5em] &=& \dfrac{\overline{MS}}{\overline{MN_{1}}} \\[0.5em] &=& \dfrac{6}{4} \\[0.5em] &=& 1,5 \end{array}$

$Formula: \alpha = \tan^{-1}(1,5) \approx 56,31^{\circ}$ $Formula: \alpha = \tan^{-1}(1,5) \approx 56,31^{\circ}$

und somit $Formula: \alpha = \beta \approx 56,31^{\circ}.$ $Formula: \alpha = \beta \approx 56,31^{\circ}.$

Aus dem Innenwinkelsummensatz von Dreiecken folgt:

$Formula: \gamma=180^{\circ} - 2 \cdot 56,31^{\circ}\approx67,38^{\circ}$ $Formula: \gamma=180^{\circ} - 2 \cdot 56,31^{\circ}\approx67,38^{\circ}$

Zuordnung der Darstellungen:

A-2-y

B-1-z

C-3-x

Ergänzung der Darstellung C:

Strategie zur Bestimmung des Flächeninhalts eines Trapezes

Ergänzung der Darstellung 1:

Zuerst zerlegen und dann verschieben, sodass ein Rechteck entsteht.

Ergänzung der Darstellung y:

$Formula: ((10+8)\cdot3)\div2$ $Formula: ((10+8)\cdot3)\div2$

Aussage (1) ist falsch, da der Betrag von $Formula: 3427,92 \, €$ $Formula: 3427,92 \, €$ den $Formula: 100 \, \%$ $Formula: 100 \, \%$ zu Beginn des dritten Jahres entsprechen.

Aussage (2) ist richtig. Jedes Jahr wird das Kapital um $Formula: 103,5 \, \%$ $Formula: 103,5 \, \%$ erhöht. Das entspricht einem Faktor von Formula: 1,035.

Aussage (3) ist falsch, da eine zweimalige Erhöhung von $Formula: 3,5 \, \%$ $Formula: 3,5 \, \%$ einer Erhöhung von $Formula: 7,12 \, \%$ $Formula: 7,12 \, \%$ entspricht.

Aussage (4) ist falsch. Die Zinsen im ersten Jahr betragen $Formula: 112 \, €,$ $Formula: 112 \, €,$ im zweiten Jahr $Formula: 115,92 \, €.$ $Formula: 115,92 \, €.$

Stelle die zweite Gleichung nach Formula: y um:

$Formula: \begin{array}[t]{rll} y-3 &=& \dfrac{1}{2}x &\quad \mid\; + 3 \\ y &=& \dfrac{1}{2}x + 3 \\ \end{array}$ $Formula: \begin{array}[t]{rll} y-3 &=& \dfrac{1}{2}x &\quad \mid\; + 3 \\ y &=& \dfrac{1}{2}x + 3 \\ \end{array}$

Setze den Term für Formula: y in die zweite Gleichung ein:

$Formula: \begin{array}[t]{rll} \dfrac{15}{2} x &=& 3y + 27 \\ \dfrac{15}{2} x &=& 3 \cdot \left( \dfrac{1}{2} x + 3 \right) + 27 \\ \dfrac{15}{2} x &=& \dfrac{3}{2} x + 9 + 27 \\ \dfrac{15}{2} x &=& \dfrac{3}{2} x + 36 &\quad \mid\; - \dfrac{3}{2} x \\ \dfrac{12}{2} x &=& 36 \\ 6 x &=& 36 &\quad \mid\; \div 6 \\ x &=& 6\\ \end{array}$ $Formula: \begin{array}[t]{rll} \dfrac{15}{2} x &=& 3y + 27 \\ \dfrac{15}{2} x &=& 3 \cdot \left( \dfrac{1}{2} x + 3 \right) + 27 \\ \dfrac{15}{2} x &=& \dfrac{3}{2} x + 9 + 27 \\ \dfrac{15}{2} x &=& \dfrac{3}{2} x + 36 &\quad \mid\; - \dfrac{3}{2} x \\ \dfrac{12}{2} x &=& 36 \\ 6 x &=& 36 &\quad \mid\; \div 6 \\ x &=& 6\\ \end{array}$

Setze Formula: x = 6 in die nach Formula: y umgestellte erste Gleichung ein:

$Formula: \begin{array}[t]{rll} y &=& \dfrac{1}{2} x + 3 \\[5pt] &=& \dfrac{1}{2} \cdot 6 + 3 \\[5pt] &=& 3 + 3 \\[5pt] &=& 6 \end{array}$ $Formula: \begin{array}[t]{rll} y &=& \dfrac{1}{2} x + 3 \\[5pt] &=& \dfrac{1}{2} \cdot 6 + 3 \\[5pt] &=& 3 + 3 \\[5pt] &=& 6 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?