Prüfungsteil B: Mit Hilfsmittel

Aufgabe 3

Gegeben ist die ganzrationale Funktion $f$ mit
$f(x)=4\cdot x^3 -4\cdot x^2, \, x \in \mathbb{R}.$

(1)

Begründe mit Hilfe des Funktionsterms, dass der Graph von $f$ weder achsensymmetrisch zur $y$ -Achse noch punktsymmetrisch zum Ursprung ist.

(2)

Gib $\lim\limits_{x\to+\infty}f(x)$ an.

(3)

Berechne die Koordinaten der lokalen Extrempunkte und die Art der lokalen Extrempunkte des Graphen von $f.$

(1 + 1 + 7 Punkte)

Bei der Lösung einer Aufgabenstellung zur gegebenen Funktion $f$ wurden Berechnungen durchgeführt, die im Folgenden dokumentiert sind:

$\(\begin{array}{rll} & \left. \begin{array}{l} &\bullet& t(x)=m\cdot x+b \\[5pt] &\bullet& m=f$

(1)

(i)

Gib eine zu den angegebenen Berechnungen passende Aufgabenstellung an.

(ii)

Erläutere den dargestellten Lösungsweg.

(2)

Der Graph von $t$ mit $t(x)=7\cdot x+2$ ist eine Gerade.

Berechne den Steigungswinkel $\alpha$ dieser Gerade.

(3)

Für einen Wert $a \in \mathbb{R}$ ist durch $h(x)=f(a\cdot x)+4 \, , \, x\in \mathbb{R},$ eine Funktion $h$ gegeben.

Der Graph von $h$ entsteht durch Transformationen aus dem Graph $f.$

Wenn diese Transformationen auch auf den Graphen von $t$ angewendet werden, dann entsteht eine Gerade mit der Steigung $-7.$

Gib den passenden Wert von $a$ an.

(5 + 2 + 2 Punkte)

Aufgabe 4

St. Michaels Mount ist eine Insel an der Küste vor Cornwall (Großbritannien). Durch Ebbe und Flut ändert sich regelmäßig der Wasserstand im Meer. Bei niedrigen Wasserständen ist St. Michaels Mount vom Festland aus über einen Landweg erreichbar. Bei hohen Wasserständen hingegen gibt es keine Landverbindung. $^1$

Eine Insel mit einem Schloss, umgeben von Wasser und Land, mit einigen Menschen auf einem Weg.

Abbildung 1: St Michael's Mount - geograph.org.uk - 6443144, CC BY-SA 2.0

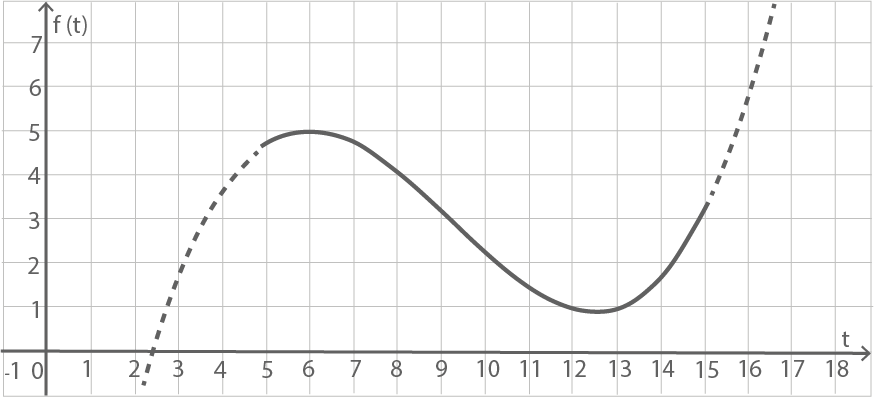
Der Wasserstand an einer Messstation bei St. Michaels Mount zwischen 5:00 Uhr und 15:00 Uhr an einem bestimmten Tag kann für $5\leq t\leq 15$ näherungsweise mit der folgenden Funktion $f$ modelliert werden:

$f(t)=0,03\cdot t^3-0,8325\cdot t^2+6,75\cdot t-12 \, , \, t \in \mathbb{R}.$

Dabei steht $t$ für die Uhrzeit in Stunden und $f(t)$ für den Wasserstand in Metern $(\text{m}).$
$f(8)$ beschreibt z. B. den Wasserstand um 8:00 Uhr.

Graph einer Funktion f(t) über der Zeit t, zeigt verschiedene Werte und Trends.

Abbildung 2

(1)

Berechne den Wasserstand um 8:30 Uhr.

(2)

Es gilt: $f(11)-f(7)=-3,3.$
Gib die Bedeutung des Wertes $-3,3$ im Sachzusammenhang an.

(2 + 1 Punkte)

Die Insel St. Michaels Mount kann über einen gepflasterten Weg erreicht werden, der bei Wasserständen unter $2\;\text{m}$ begehbar ist.

Ermittle mithilfe der Abbildung 2, zwischen welchen Uhrzeiten die Insel zu Fuß erreicht werden kann.

(3 Punkte)

Bei der Lösung einer Aufgabenstellung im gegebenen Sachzusammenhang wurden Berechnungen durchgeführt. Dabei ergab sich:

$\(\bullet \; \;f$

$\bullet \; \;f(5)\approx4,688,\,f(6)=5,01, \, f(12,5)\approx 0,891, \, f(15)\approx3,188.$

Gib unter Berücksichtigung aller Ergebnisse der obigen Berechnungen an, welche Bedeutung im Sachzusammenhang die Koordinaten des Punktes $(6\mid5,01)$ haben, und erläutere anhand der Berechnungen deine Angabe.

(5 Punkte)

(1)

Berechnen Sie die Wendestelle von $f.$

(2)

Interpretiere die Bedeutung der Wendestelle für den vorliegenden Sachzusammenhang.

(3 + 2 Punkte)

Die Zeitpunkte, zu denen der höchste bzw. niedrigste Wasserstand gemessen werden, sowie die höchsten und niedrigsten Wasserstände selbst, ändern sich im Laufe eines Jahres.

Der Wasserstand kann für einen anderen Tag für $5\leq t \leq 15$ durch eine Funktion $g$ beschrieben werden, deren Graph durch Verschiebungen aus dem Graphen von $f$ hervorgeht.

Im Vergleich zu dem Wasserstand, der durch $f$ beschrieben wird, gilt an dem anderen Tag:

Der höchste und der niedrigste Wasserstand werden jeweils eine Stunde später erreicht.
Der höchste und der niedrigste Wasserstand liegen jeweils $0,5$ Meter höher.

Gib eine Gleichung von $g$ an.

[Hinweis: Eine Vereinfachung der Gleichung von $g$ ist nicht erforderlich.]

(2 Punkte)

^[1]Der Wasserstand ist die Höhe des Wassers über einem festgelegten Meeresniveau.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 3

(1)

Der Graph ist nur dann achsensymmetrisch zur $y$ -Achse, wenn die folgende Gleichung erfüllt ist:
$f(-x)=f(x)$

$\begin{array}[t]{rlll} f(-x)&=&4(-x)^3-4(-x)^2 \\[5pt] &=&-4x^3-4x^2 \\[5pt] &\neq&f(x) \end{array}$

Der Graph ist nur dann punktsymmetrisch zum Ursprung, wenn die folgende Gleichung erfüllt ist:
$-f(x) = f(-x)$

$\begin{array}[t]{rlll} -f(x)&=&-(4x^3-4x^2)\\[5pt] &=&-4x^3+4x^2 \\[5pt] &\neq& f(-x) \end{array}$

Somit ist der Graph von $f$ weder achsensymmetrisch zur $y$ -Achse noch punktsymmetrisch zum Ursprung.

(2)

Bei Polynomen dominiert der höchste Exponent.
Hier ist das: $4x^3.$

Für $x \to +\infty$ gilt: $x^3\to +\infty$ und wegen des positiven Vorfaktors strebt der Term nach $+\infty.$

$\lim\limits_{x\to+\infty}f(x)=+\infty$

(3)

1. Ableitung bilden
$\(f$

Extremstellen von $f$ sind Nullstellen von $\(f$ daher gilt: $\(f$
$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt $x_1=0$ und $x_2=\frac{2}{3}.$

2. Ableitung bilden
$\(f$

$\boldsymbol{x}$ -Werte in $\(\boldsymbol{f$ einsetzen und Extrempunkte bestimmen

$\(f$
Bei $x=0$ ist ein lokales Maximum.
$f(0)=4\cdot 0^3-4\cdot 0^2=0$
Also ist der lokale Hochpunkt bei $H(0\mid 0).$

$\(f$
Bei $x=\tfrac{2}{3}$ ist ein lokales Minimum.
$f\left(\frac{2}{3}\right)=4\cdot \left(\frac{8}{27}\right)-4\cdot \left(\frac{4}{9}\right)=-\frac{16}{27}$
Also ist der lokale Hochpunkt bei $H\left(\tfrac{2}{3}\mid -\tfrac{16}{27}\right).$

(1)

(i)

Mögliche Aufgabenstellung:
Bestimme die Tangente an den Graphen von $f$ im Punkt mit der $x$ -Koordinate $x=-0,5.$
Berechne die Schnittpunkte dieser Tangente mit dem Graphen von $f.$

(ii)

Erläuterung des Lösungswegs:

1. Allgemeine Form der Tangente bestimmen
$t(x)=m\cdot x+b$
2. Steigung der Tangente durch Ableitung bestimmen
$\(m=f$

3. Achsenabschnitt $\boldsymbol{b}$ berechnen
Die Steigung $m=7$ und der Berührpunkt $(-0,5\mid f(-0,5))$ werden in die Tangentengleichung $t(x) = m \cdot x + b$ eingesetzt, um den Achsenabschnitt $b=2$ zu bestimmen.

4. Schnittpunkte von $\boldsymbol{t(x)}$ und $\boldsymbol{f(x)}$ berechnen
Tangentengleichung $t(x)$ wird mit der Funktionsgleichung $f(x)$ gleichgesetzt:
$t(x) = f(x)$

Die Lösungen dieser Gleichung sind die $x$ -Werte der Schnittpunkte:
$x = -0,5$ ist der Berührpunkt der Tangente mit dem Graphen.
$x = 2$ ist die $x$ -Koordinate des zweiten Schnittpunkts der Tangente mit dem Graphen.

(2)

Steigungswinkel $\alpha$ mit $\alpha= \arctan(m)$ berechnen:
$m=7$
$\alpha= \arctan(7)\approx 82^\circ$

Der Steigungswinkel von $\alpha$ beträgt etwa $48^\circ.$

(3)

Transformation von $\boldsymbol{f(x)}$ zu $\boldsymbol{h(x)}$
$h(x) = t(a \cdot x) + 4$
Horizontalstauchung/Streckung und Spiegelung ( $\boldsymbol{t(a \cdot x)}$ )
$x$ wird in der Tangentengleichung durch $(a \cdot x)$ ersetzt:
$t(a \cdot x) = 7 \cdot a \cdot x + 2$
Die neue Steigung nach dieser Transformation ist $m = 7a.$
Vertikale Verschiebung ( $+4$ )
$t_h(x) = 7\cdot a\cdot x + 6$
Wert von $a$ bestimmen
$7a = -7$
Nach $a$ auflösen: $a=-1$
Der passende Wert von $a$ ist $-1.$

Lösung 4

(1)

Berechnung des Wasserstands um 8:30 Uhr

Rechenweg anzeigen

$3,64\;\text{m}$

Der Wasserstand um 8:30 Uhr beträgt etwa $3,64$ Meter.

(2)

Bedeutung des Wertes $-3,3$ im Sachzusammenhang
Die Differenz $f(11) - f(7)$ ist die Veränderung des Wasserstands zwischen 7:00 Uhr und 11:00 Uhr.

Der Wert $-3,3$ bedeutet, dass der Wasserstand zwischen 7:00 Uhr und 11:00 Uhr um $3,3$ Meter gesunken ist (Das negative Vorzeichen zeigt eine Abnahme an).

Begehbarkeit der Insel
$t \approx 10,3$ entspricht $10$ Uhr und $0,3 \times 60 \approx 18$ Minuten, also 10:18 Uhr.

Die Insel kann zwischen etwa 10:18 Uhr und 14:24 Uhr zu Fuß erreicht werden.

Bedeutung des Punktes $\boldsymbol{(6\mid5,01)}$

Der Punkt $(6\mid 5,01)$ repräsentiert den lokalen Höchststand des Wassers (Flut) am Morgen. Die $t$ -Koordinate $t=6$ bedeutet, dass dieser Höchststand um 6:00 Uhr erreicht wird, und die $y$ -Koordinate $5,01$ Meter gibt die Höhe dieses maximalen Wasserstands an.
Dies wird durch die Berechnung von $\(f$ bestätigt, die $t=6$ als Extremstelle liefert, und durch den Funktionswert $f(6)=5,01,$ der im Vergleich zu den anderen berechneten Werten der höchste ist.

(1)

Berechnung der Wendestelle von $f$
1. Erste Ableitung $\(f$ bestimmen
$\(f$
2. Zweite Ableitung $\(f$ bestimmen
$\(f$
3. Wendestelle $t_W$ berechnen ( $\(f$ )
$\begin{array}[t]{rlll} 0,18\cdot t-1,665&=&0 &\mid\;+1,665 \\[5pt] 0,18\cdot t&=&1,665&\mid\;:0,18 \\[5pt] t&=&9,25 \end{array}$

Die Wendestelle der Funktion $f$ liegt bei $t = 9,25.$

(2)

Interpretation der Wendestelle
Die Wendestelle markiert den Zeitpunkt der maximalen Änderungsrate des Wasserstands. Der Wasserstand sinkt nach der Flut (ca. 6:00 Uhr) stark ab und steuert auf die Ebbe (ca. 12:30 Uhr) zu.
Bedeutung: Zur Zeit $t = 9,25$ Uhr (9:15 Uhr) fällt der Wasserstand am schnellsten. Die Geschwindigkeit, mit der das Wasser sinkt, ist zu diesem Zeitpunkt am größten.

Die Funktion $g(t)$ entsteht aus $f(t)$ durch zwei Verschiebungen:
1. Horizontale Verschiebung (Zeit)

Eine Stunde später: Verschiebung um $1$ nach rechts.
Transformation: Ersetze $t$ durch $(t-1).$

2. Vertikale Verschiebung (Höhe)

$0,5$ Meter höher: Verschiebung um $0,5$ nach oben.
Transformation: Addiere $+0,5.$

3. Gleichung für $\boldsymbol{g(t)}$ aufstellen

Rechenweg anzeigen

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?