Wahlaufgaben

Wahlaufgabe Stochastik

6.1

Beim Schlagballwurf wurden die Weiten der Schülerinnen notiert.

Schülerin	Weite $\;\text{(m)}$
Ina
Mia
Lea
Sara
Leni
Ria
Ida
Erna
Ella
Jule

Das arithmetische Mittel aller Weiten beträgt $25,0\;\text{m}.$
Berechne die Wurfweite von Jule.

(3 BE)

6.2

In einer Zoohandlung sitzen zwei weiße, fünf gescheckte und drei braune Meerschweinchen im Gehege. Die Meerschweinchen werden ausschließlich paarweise verkauft. Der Verkäufer entnimmt zufällig zwei Meerschweinchen.

Erstelle hierfür ein vollständiges und beschriftetes Baumdiagramm.

(3 BE)

Betrachtet wird nun folgendes Ereignis:
"Zwei gleichfarbige Meerschweinchen werden zufällig entnommen".

Bestimme die Wahrscheinlichkeit für dieses Ereignis.
Gib die Wahrscheinlichkeit in Prozent an.

(4 BE)

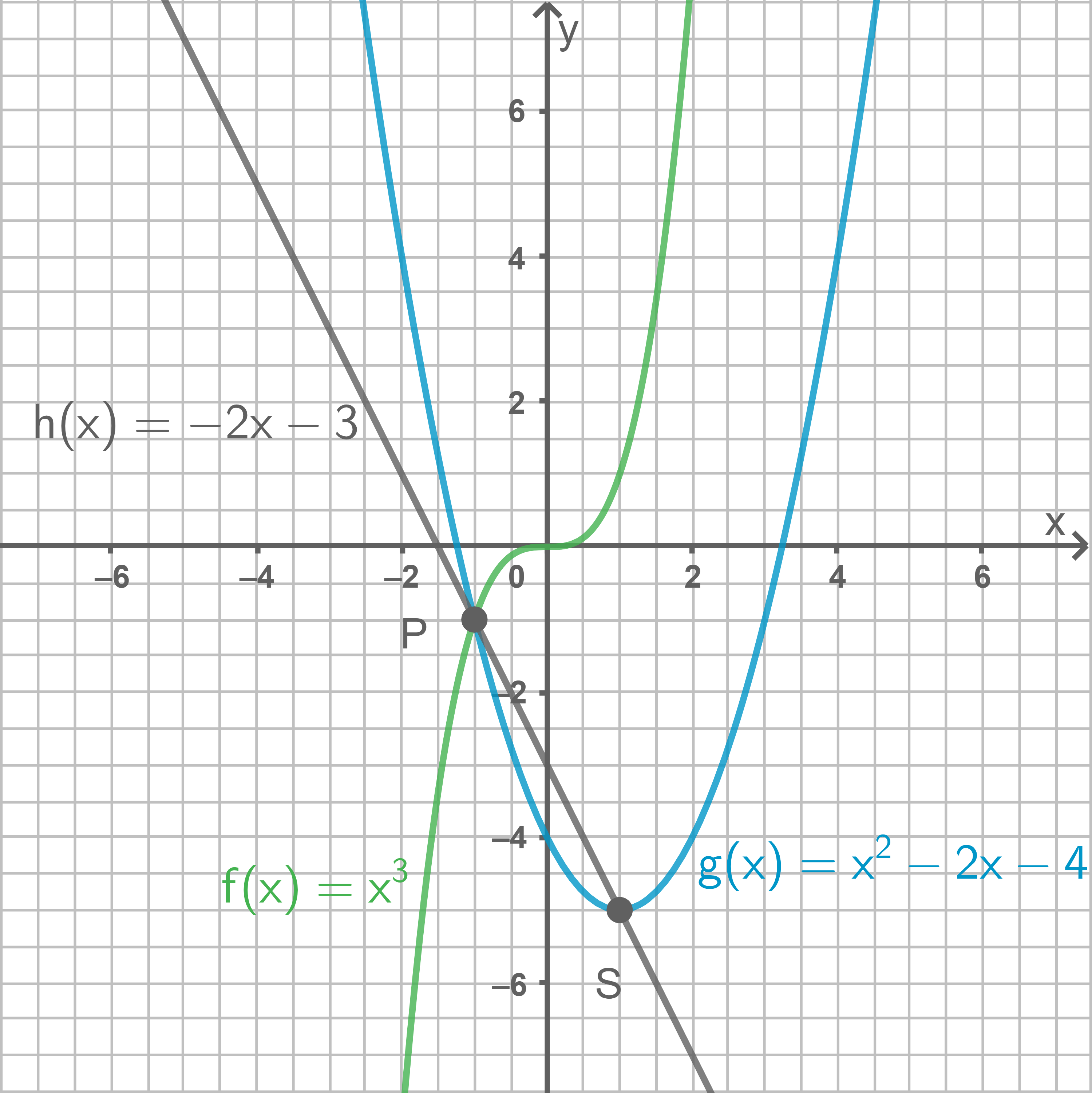
Wahlaufgabe Funktionen 1

Gegeben sind die Gleichungen der Funktionen $f(x)$ und $g(x).$

$y=f(x)=x^{3} \quad(x \in \mathbb{R})$ und

$y=g(x)=x^{2}-2x-4 \quad(x \in \mathbb{R})$

Stelle den Graph der Funktion $f(x)$ mindestens im Intervall $-1,5 \leq x \leq 1,5$ dar.

(3 BE)

Ermittle die Koordinaten des Scheitelpunktes der Funktion $g(x).$
Zeichnne den Graph der Funktion $g(x)$ in dasselbe Koordinatensystem.

(3 BE)

Berechne die Nullstellen der Funktion $g(x).$

(2 BE)

Durch die Punkte $P (-1 \mid- 1)$ und $S (1 \mid -5)$ verläuft der Graph der linearen Funktion $h(x).$

Gib die Funktionsgleichung für $h(x)$ an.

(2 BE)

Wahlaufgabe Geometrie

8.1

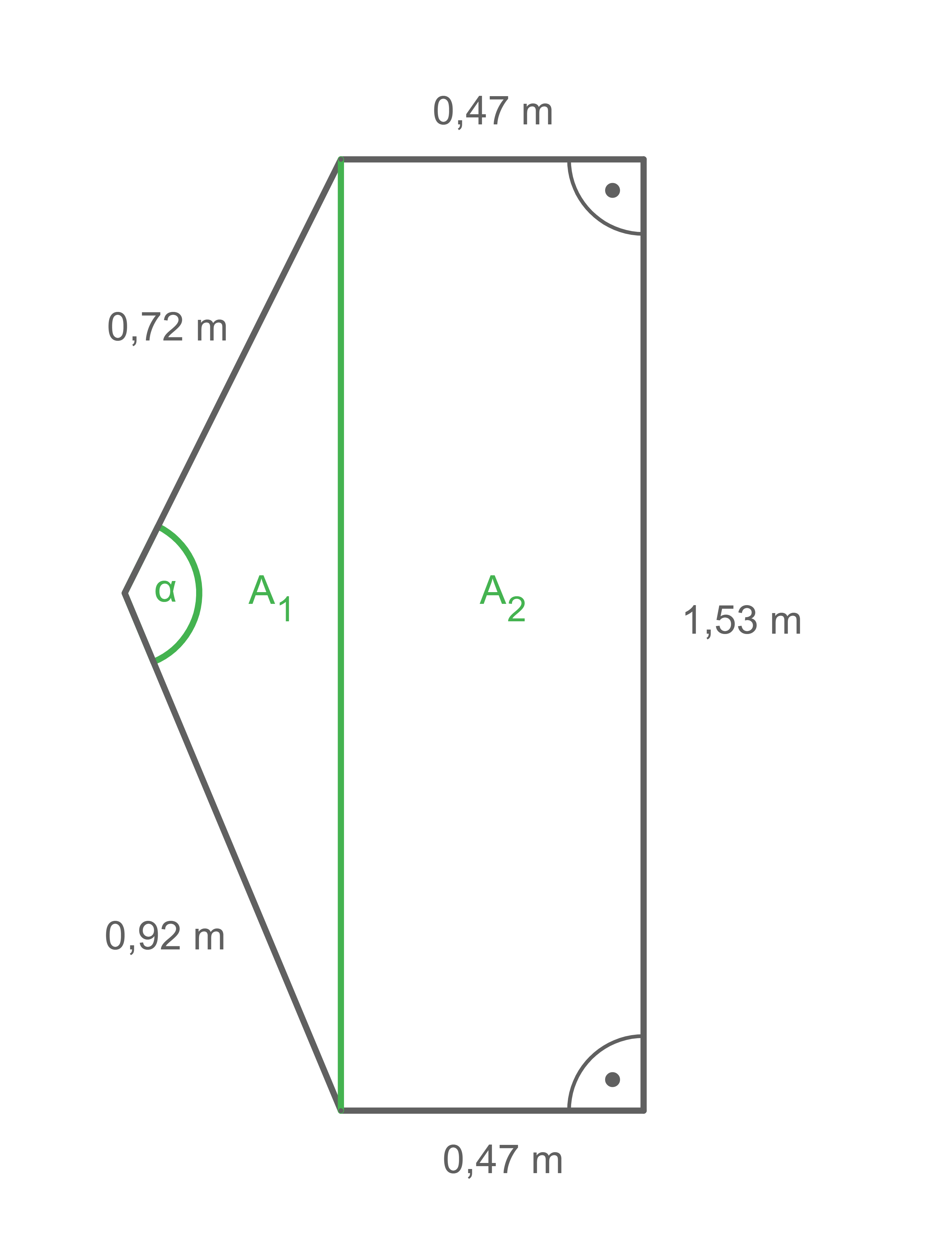
Gegeben ist ein Spiegel und seine Maße.
(siehe Abbildung und Skizze)

Foto: ChatGPT

Skizze nicht maßstäblich

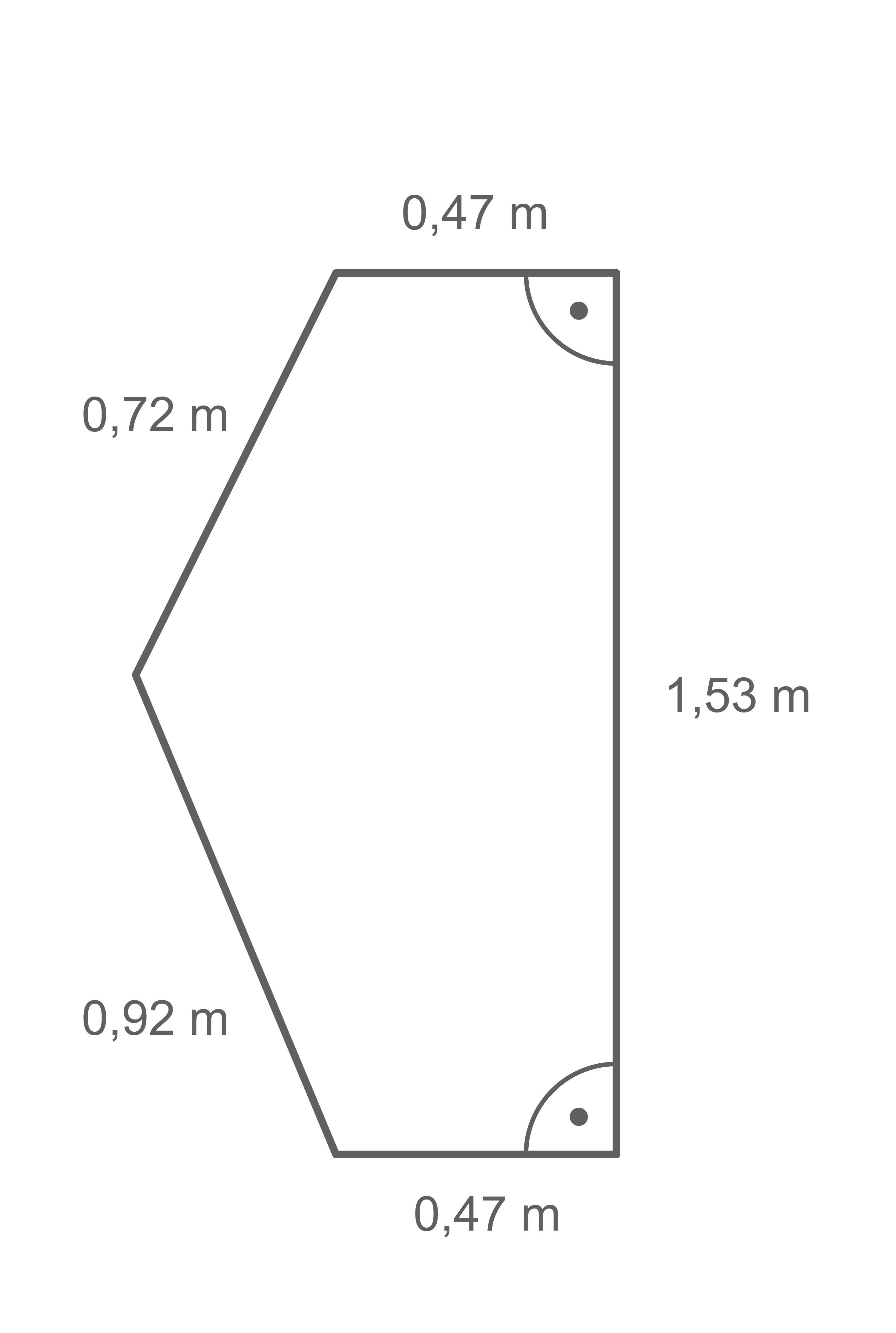
Berechne den Flächeninhalt des Spiegels.

(6 BE)

8.2

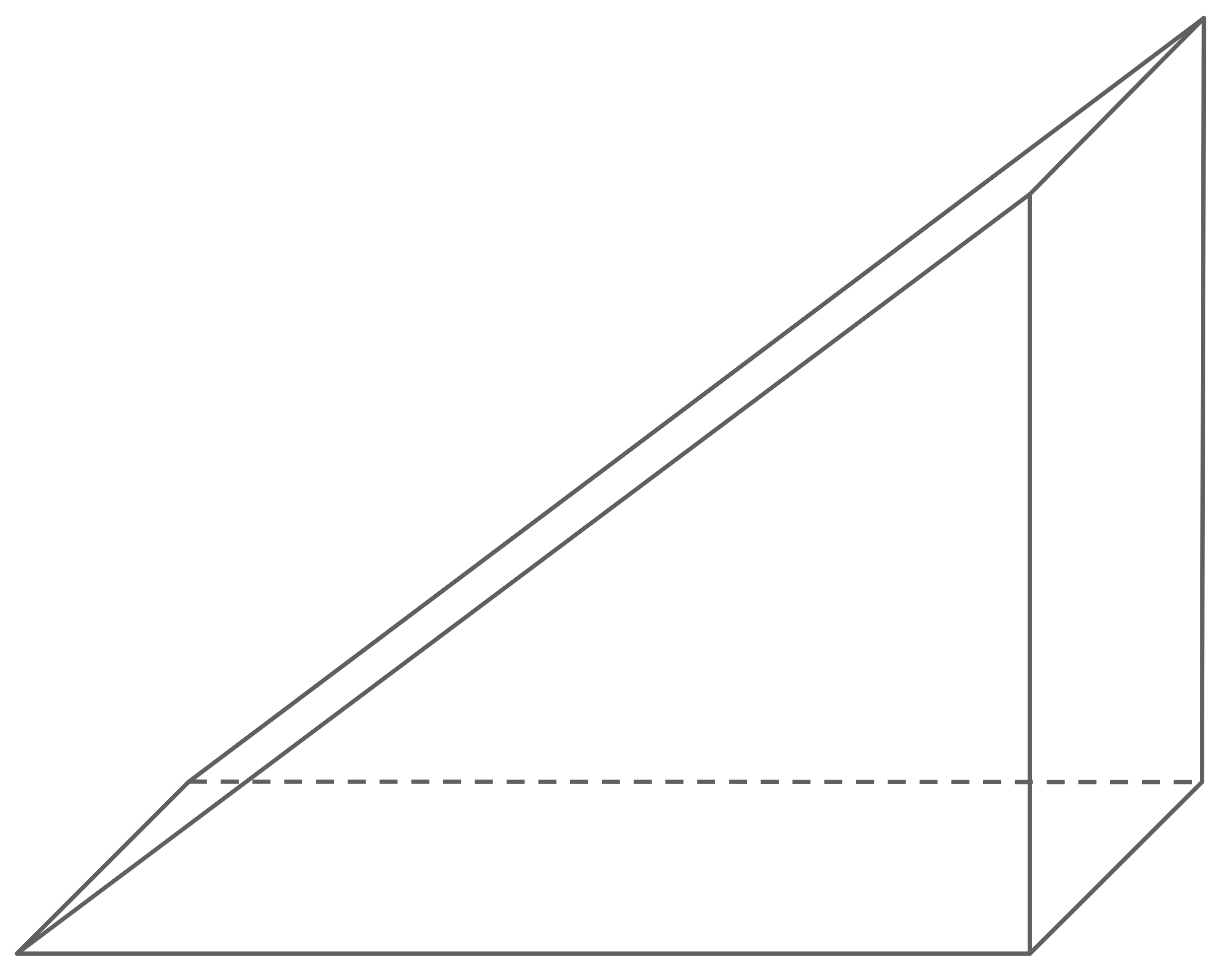
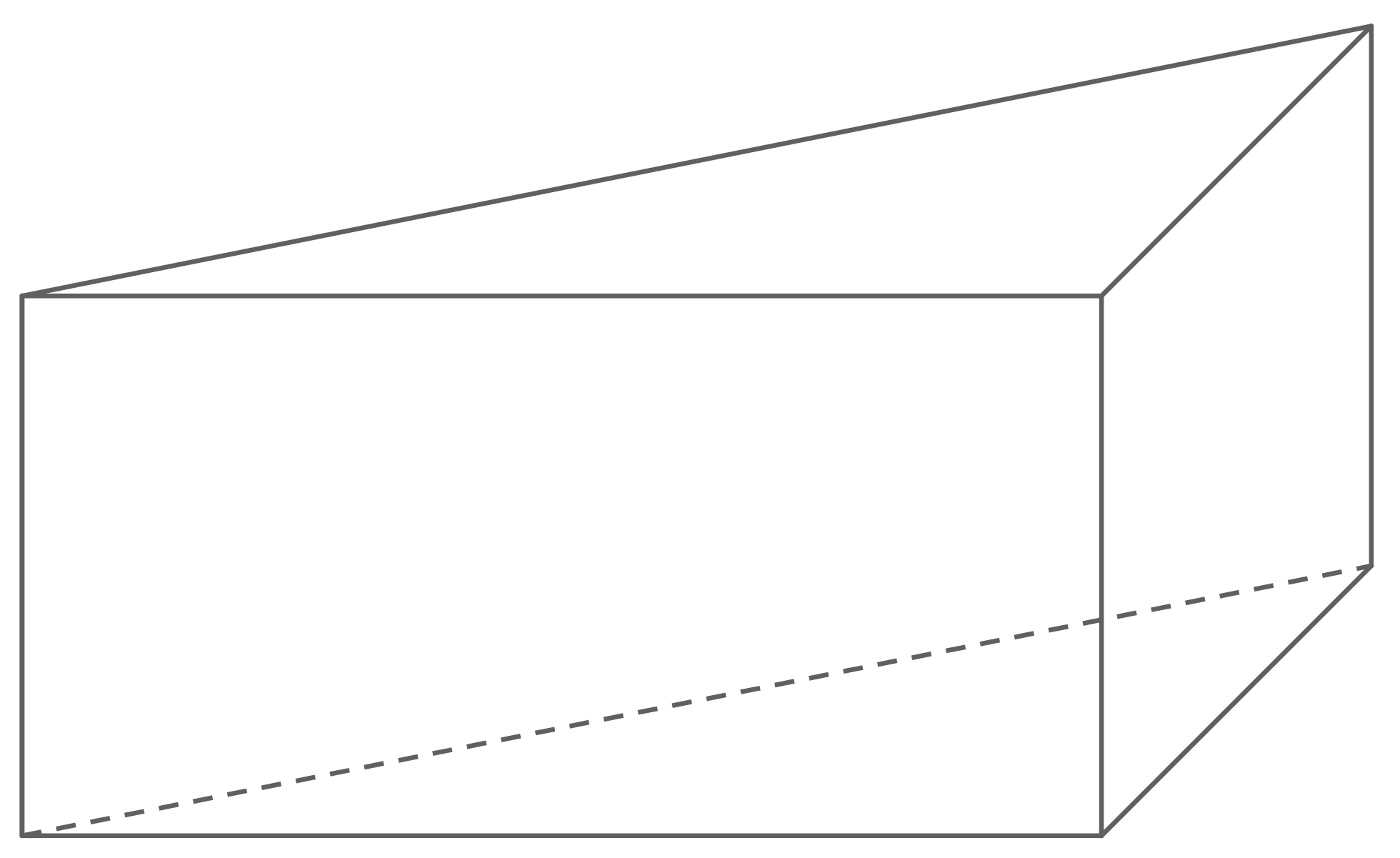
Gegeben ist das Netz eines Prismas mit dreieckiger Grundfläche.

Skizze nicht maßstäblich

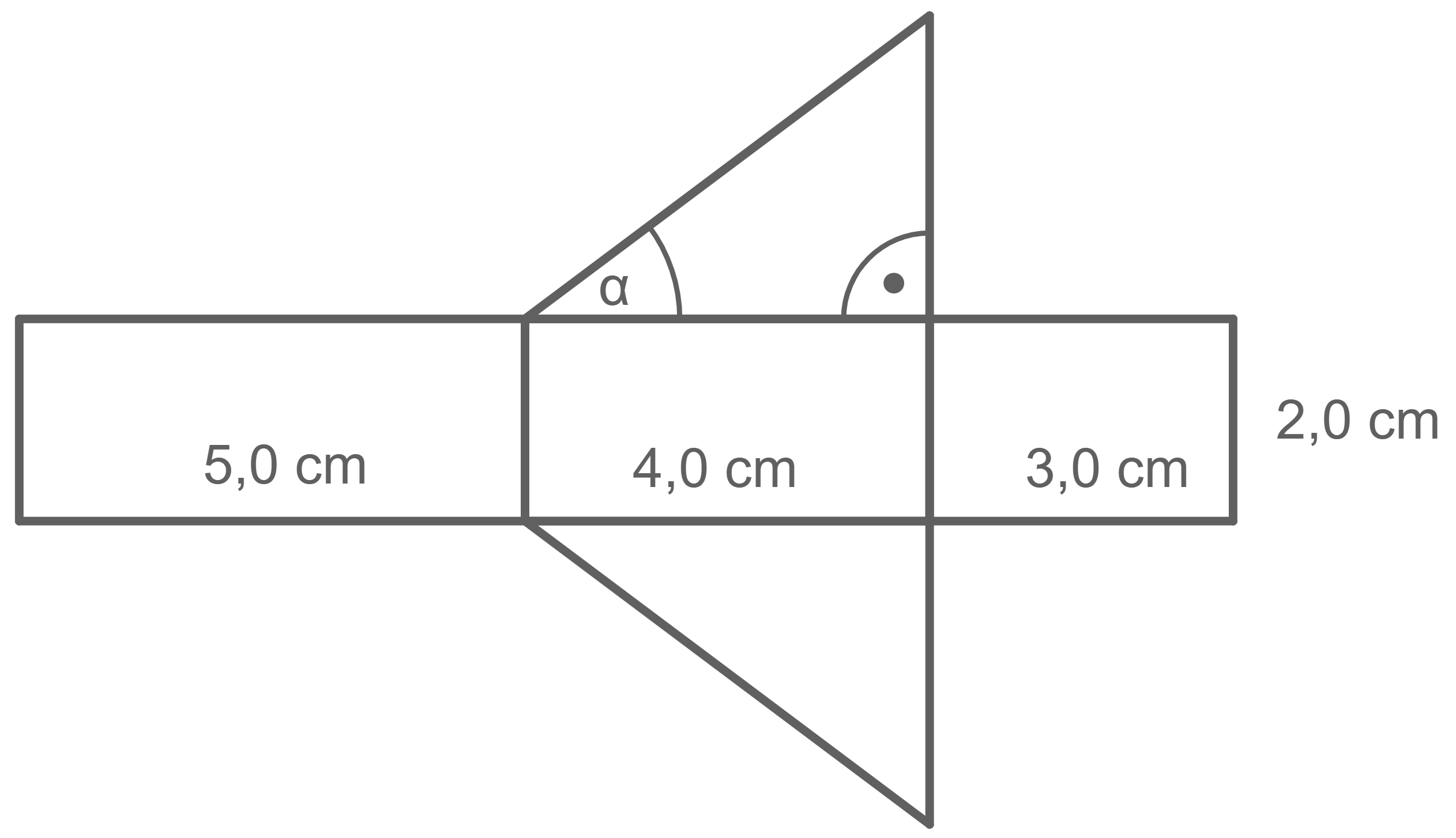
Berechne die Größe des Winkels $\alpha.$

(2 BE)

Stelle dieses Prisma im Schrägbild unter Verwendung der angegeben Maße auf unliniertem Papier dar.

(2 BE)

Wahlaufgabe Funktionen 2

9.1

$x$	$f(x)$
$-3$	$10$
$-2$	$5$
$-1$	$2$
$-0,5$	$1,25$
$0$	$1$
$0,5$	$1,25$
$1$	$2$
$2$	$5$
$3$	$10$

Zeichne den Graph der Funktion $f(x)$ in ein geeignetes Koordinatensystem und gib die Funktionsgleichung an.

(3 BE)

Eine zweite Funktion ist gegeben durch $y=g(x)=a x^{2}+1 \quad(x \in \mathbb{R}).$

Nenne drei mögliche Auswirkungen des Faktors $a$ auf den Verlauf des Graphen von $g(x).$

(3 BE)

9.2

Die Form eines Tunnels in Solingen entspricht ungefähr einer nach unten geöffneten Parabel mit der Gleichung

$y=f(x)=-0,64x^2+4 \quad(x \in \mathbb{R}).$

(Eine Längeneinheit entspricht einem Meter.)

Steinerner Tunnel in einem Wald, dunkler Durchgang mit Blick auf Bäume am Ende

SolingenFan95, Solingen, Unterführung Bodlenberg der Bahnstrecke Gruiten–Köln-Deutz, Cropped, CC BY-SA 4.0

Gib die Höhe des Tunnels an.

(1 BE)

Zeige rechnerisch, dass die Fahrbahnbreite $5,00\;\text{m}$ beträgt.

(3 BE)

Wahlaufgabe Arithmetik/Algebra 1

10.1

Charlotte hat beim Frühstück auf ihre Hausaufgaben gekleckert:

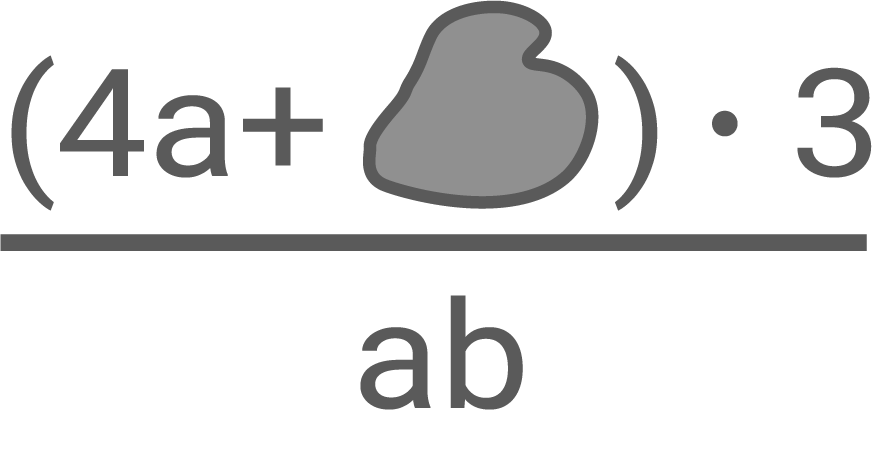
Sie weiß noch, dass der Term für $a = 5$ und $b = 8$ einen Wert von $6,3$ hatte und unter dem Fleck die Potenz einer der beiden Variablen stand.

Berechne den fehlenden Teil des Terms.

(4 BE)

10.2

Ein Mann hat sein Vermögen gleichmäßig auf zwei Safes bei unterschiedlichen Banken aufgeteilt. Von einem Teil seines Geldes hat er Goldbarren mit gleichem Wert gekauft. Das restliche Geld liegt jeweils als Bargeld in dem Safe daneben.
(siehe Abbildung)

Gib je eine Gleichung für das in jedem Safe hinterlegte Vermögen in der Form $y = mx + n$ an.

(3 BE)

Ermittle das Gesamtvermögen des Mannes.

(3 BE)

Wahlaufgabe Arithmetik/Algebra 2

11.1

Im ersten Quartal des Jahres 2023 haben die Thüringer Energieversorger in das Stromnetz $2848 \;\text{Gigawattstunden} \;\text{(GWh)}$ Energie eingespeist. Davon betrug der Anteil der erneuerbaren Energien $62,3\,\text{%}.$ Durch Windkraftanlagen wurden in diesem Zeitraum $1155 \;\text{GWh}$ bereitgestellt.

dpa: Weniger Strom aus Windkrafty. In: TLZ, 07.06.2023, Seite 8.

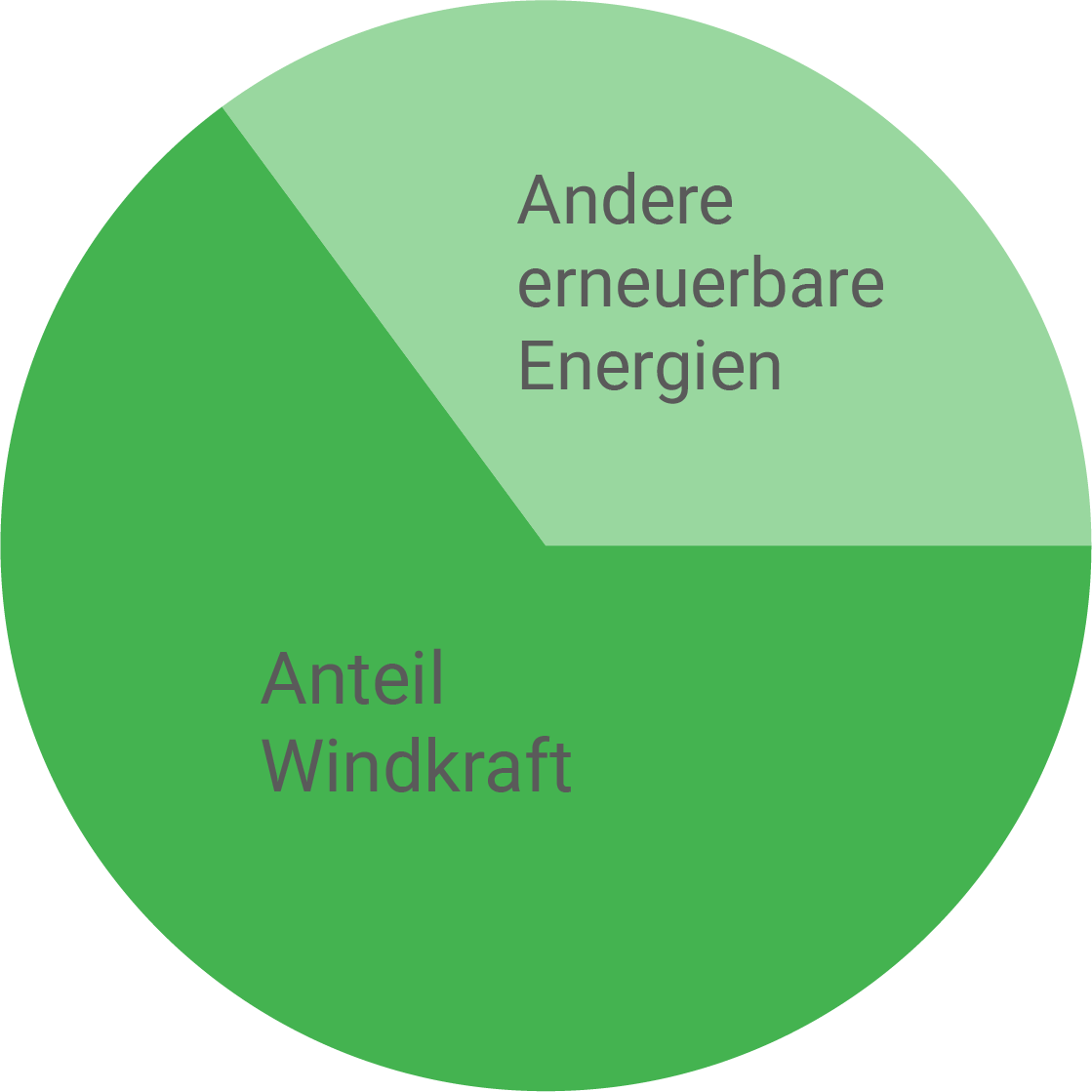
Stelle den Anteil der durch Windkraftanlagen erzeugten Energie an den erneuerbaren Energien in einem Kreisdiagramm dar.

(5 BE)

11.2

Im Eingangsbereich des Dresdener Stadtschlosses steht ein Modell des Schlosses im Maßstab $1: 125.$

Der Turm ist im Modell $0,80\;\text{m}$ hoch.

SchiDD, DD-Schloss-Modell-2, CC BY-SA 4.0

Hajotthu, Schloss Dresden Hausmannsturm, CC BY-SA 3.0

Berechne die tatsächliche Höhe des Turmes des Stadtschlosses.

(2 BE)

11.3

Löse die Gleichung.

$-10x-(92-2x)=7(7+x)+84 \quad(x \in \mathbb{R}).$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?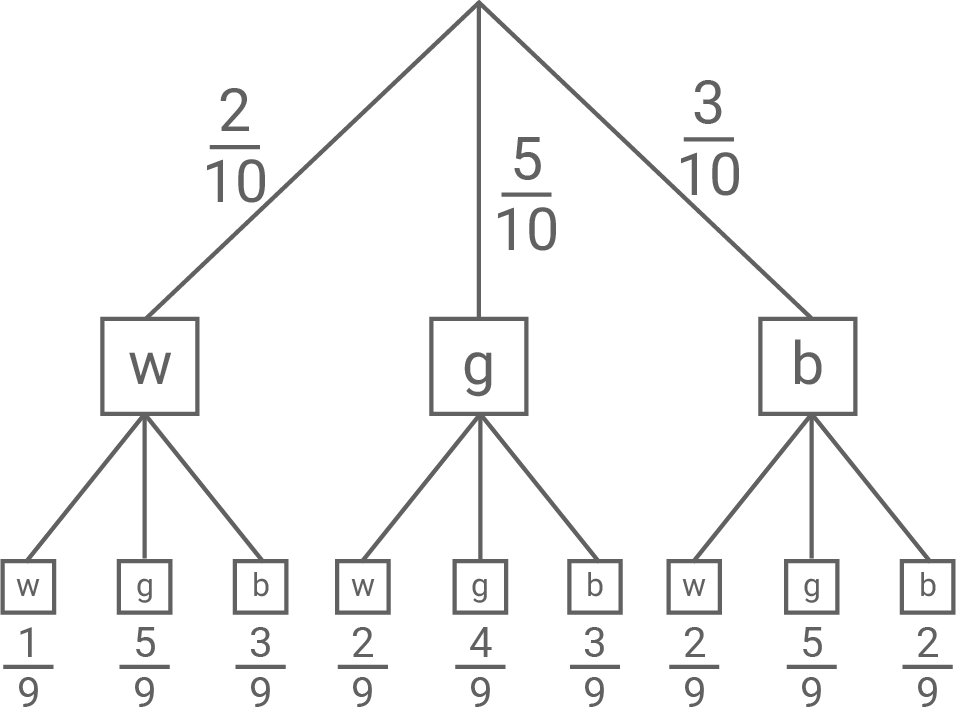

6.1

Rechenweg anzeigen

$x=26,0\;\text{m}$

6.2

$w=\text{weiß},\,\,g=\text{gescheckt},\,\,b=\text{braun}\,$

Wahrscheinlichkeitsbaum: drei Hauptzweige 2/10, 5/10, 3/10 zu Knoten w, g, b; darunter weitere Verzweigungen mit Bruch-Wahrscheinlichkeiten.

$P(ww)=\frac{2}{10}\cdot \frac{1}{9}=\frac{2}{90}=\frac{1}{45};$

$P(wg)=\frac{2}{10}\cdot \frac{1}{5}=\frac{10}{90}=\frac{1}{9};$

$P(wb)=\frac{2}{10}\cdot \frac{3}{9}=\frac{6}{90}=\frac{1}{15};$

$P(gw)=\frac{5}{10}\cdot \frac{2}{9}=\frac{10}{90}=\frac{1}{9};$

$P(gg)=\frac{5}{10}\cdot \frac{4}{9}=\frac{20}{90}=\frac{2}{9};$

$P(gb)=\frac{5}{10}\cdot \frac{3}{9}=\frac{15}{90}=\frac{1}{6};$

$P(bw)=\frac{2}{10}\cdot \frac{2}{9}=\frac{6}{90}=\frac{1}{15}$

$P(bg)=\frac{2}{10}\cdot \frac{5}{9}=\frac{15}{90}=\frac{1}{6}$

$P(bb)=\frac{2}{10}\cdot \frac{2}{9}=\frac{6}{90}=\frac{1}{15}$

Rechenweg anzeigen

$P(\text{Zwei gleichfarbige})= 31,1\,\text{%}$

Koordinatensystem mit Gitter, drei Funktionen (grüne Kubik, blaue Parabel, graue Gerade) und zwei markierten Punkten P und S.

$g(x)=x^2-2x-4=(x-1)^2-5$

$S(1\mid -5)$

Rechenweg anzeigen

$x_1\approx 3,23, \quad x_2\approx -1,23$

$h(x)=-2x-3$

8.1

$A=A_1+A_2$

Der Flächeninhalt des Rechtecks $A_2$ lässt sich wie folgt berechnen:

$A_2=1,53\;\text{m}\cdot 0,47\;\text{m}=0,72\;\text{m}^{2}$

Da es sich bei $A_1$ um ein ungleichseitiges Dreieck handelt, dessen Höhe unbekannt ist, lautet die Formel für die Berechnung von $A_1:$

$A_1=\frac{1}{2}\cdot 0,72\cdot 0,92\cdot \sin\alpha$

Der Winkel $\alpha$ lässt sich durch den Kosinussatz berechnen:

$\cos\alpha=\frac{a^2+b^2-c^2}{2ab}$

Werte einsetzen:

Rechenweg anzeigen

$\alpha=137,5^\circ$

Nun kann $A_1$ ausgerechnet werden:

$A_1=\dfrac{1}{2}\cdot 0,72\;\text{m}\cdot 0,92\;\text{m}\cdot \sin(137,5^\circ)$

$A_1=0,22\;\text{m}^2$

$\rightarrow A_1+A_2=0,22\;\text{m}^2+0,72\;\text{m}^2=0,94\;\text{m}^2$

8.2

Um $\alpha$ zu berechnen können verschiedene Trigonometrische Beziehungen verwendet werden. Zum Beispiel:

$\sin\alpha=\dfrac{3\;\text{cm}}{5\;\text{cm}} \quad\quad\quad$ oder

$\alpha=36,9^\circ$

$\cos\alpha=\dfrac{4\;\text{cm}}{5\;\text{cm}}\quad\quad\quad$ oder

$\alpha=36,9^\circ$

$\tan\alpha=\dfrac{3\;\text{cm}}{4\;\text{cm}}$

$\alpha=36,9^\circ$

Denn wenn man das Netz des Prismas gedanklich wieder zusammenklappt, ergibt sich eine Hypotenuse mit einer Länge von $5\;\text{cm}$ , eine Gegenkathete mit $3\;\text{cm}$ und eine Ankathete mit $4\;\text{cm}$ .

Für diese Aufgabe gibt es zwei Verschiedene Lösungswege, die beide korrekt sind:

1. Das Prisma liegt auf seiner Mantelfläche:

2. Das Prisma liegt auf seiner Grundfläche:

9.1

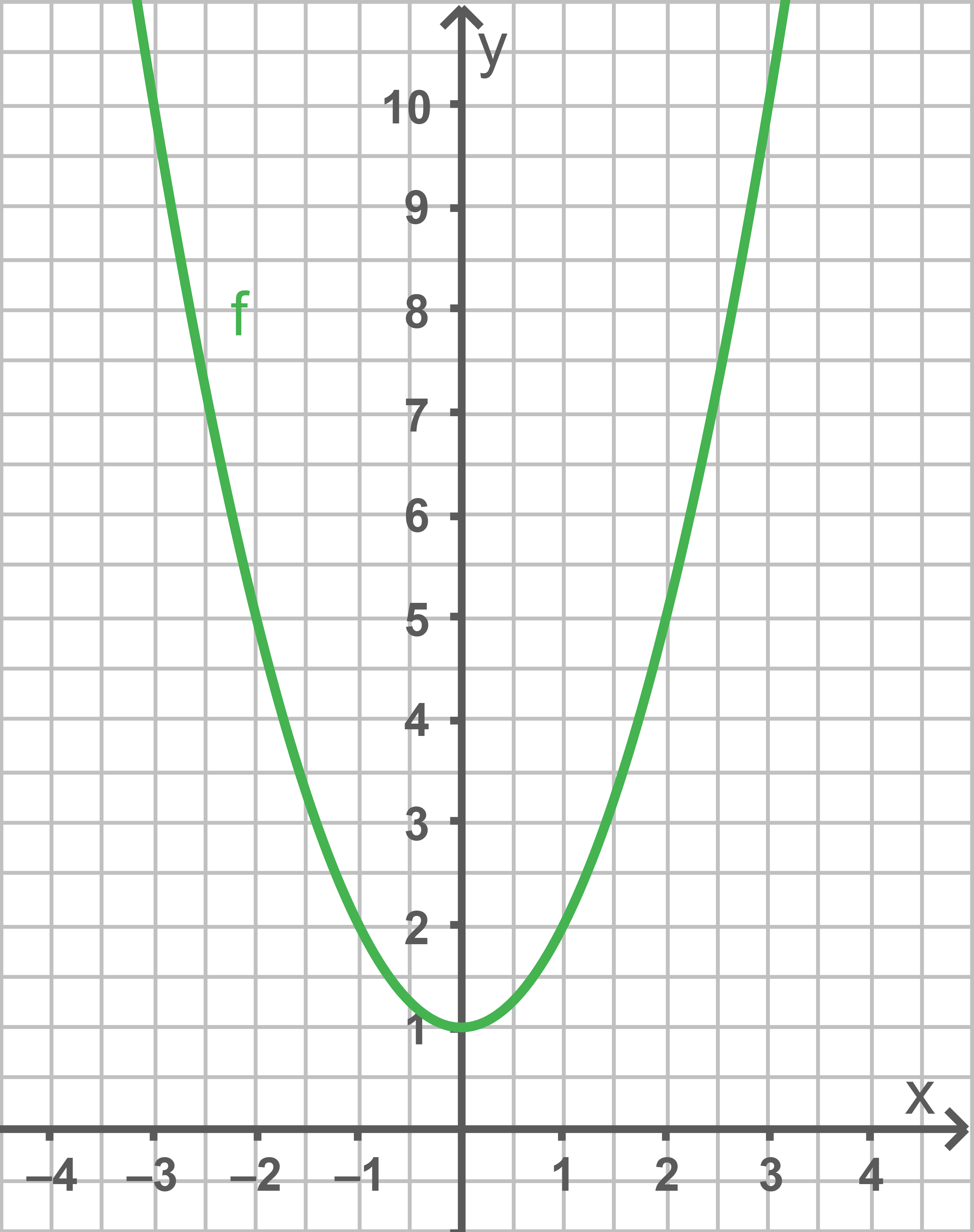
Der Graph kann gestreckt werden.
Der Graph kann gestaucht werden.
Der Graph kann an der $x-$ Achse gespiegelt werden/ nach unten geöffnet sein.

9.2

Die Höhe des Tunnels lässt sich einfach aus der Funktionsgleichung der Parabel ablesen, denn die Verschiebung auf der $y-$ Achse entspricht der Höhe des Tunnels. Also:

$h=4\;\text{m}$

Um Nachweisen zu können, dass die Fahrbahnbreite $5,00\;\text{m}$ beträgt, müssen zuerst die Schnittpunkte der Parabel mit der $x-$ Achse und dann der Abstand zwischen diesen berechnet werden:

$\begin{array}[t]{rlll} 0&=&-0,64x^2+4 &\mid\; +0,64x^2\\[5pt] 0,64x^2&=&4 &\mid\; :0,64 \\[5pt] x^2&=&6,25 &\mid\; \sqrt{\;} \\[5pt] x_1&=&2,5 \\[5pt] x_2&=&-2,5 \\[5pt] \end{array}$

Fahrbahnbereich = $2\cdot 2,5\;\text{m}=5\;\text{m}$

10.1

$\dfrac{(4a+x)\cdot 3}{ab}$

$a=5, \quad$ $b=8$

$\begin{array}[t]{rlll} \dfrac{(20+x)\cdot 3}{40}&=&6,3 &\mid\;\ \cdot 40 \\[5pt] (20+x)\cdot 3&=&252 \\[5pt] 60+3x&=&252 &\mid\;\ -60 \\[5pt] 3x&=&192 &\mid\;\ :3 \\[5pt] x&=&64 \\[5pt] \end{array}$