Pflichtteil 2
Pflichtaufgabe 1
a)
Ein Zug fährt mit einer Durchschnittsgeschwindigkeit von 
Ermittle die Zeit, die der Zug für eine Strecke von benötigt.
benötigt.
Ermittle die Zeit, die der Zug für eine Strecke von
b)
Die Abbildung zeigt ein Glücksrad mit fünf gleich großen Sektoren. Das Glücksrad wird zweimal gedreht. Ermittelt wird die Summe der beiden angezeigten Zahlen.
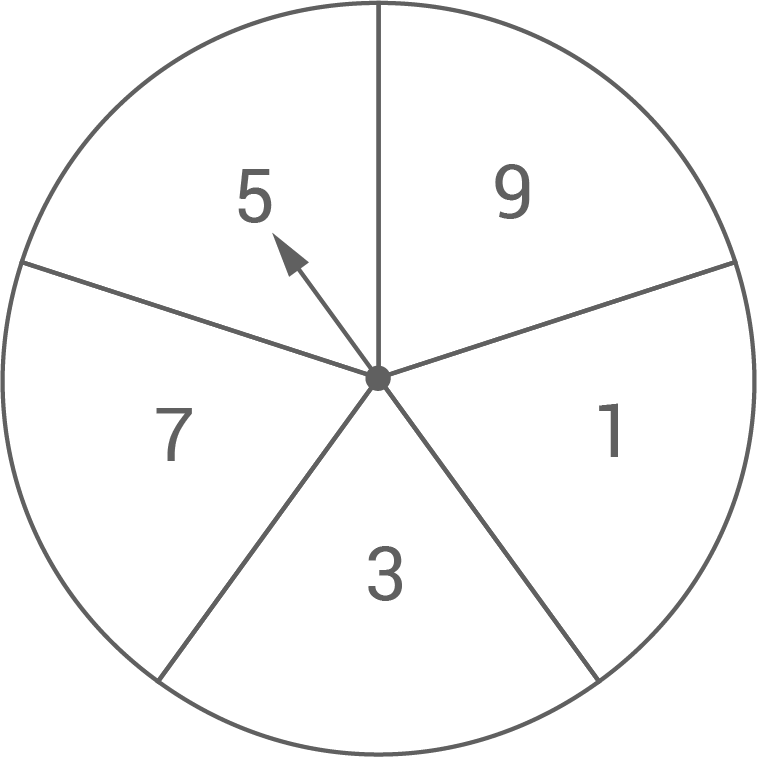
Berechne die Wahrscheinlichkeit dafür, dass die Summe der beiden angezeigten Zahlen  ist.
ist.

Abbildung 1
c)
Fotos werden in den Bildformaten 9x13, 10x15, 13x18 und 20x30 angeboten.
Gib die zwei zueinander ähnlichen Bildformate an und begründe deine Angabe.
Gib die zwei zueinander ähnlichen Bildformate an und begründe deine Angabe.
d)
Abbildung 2 zeigt ein gerades Prisma mit einem gleichseitigen Dreieck als Grundfläche.
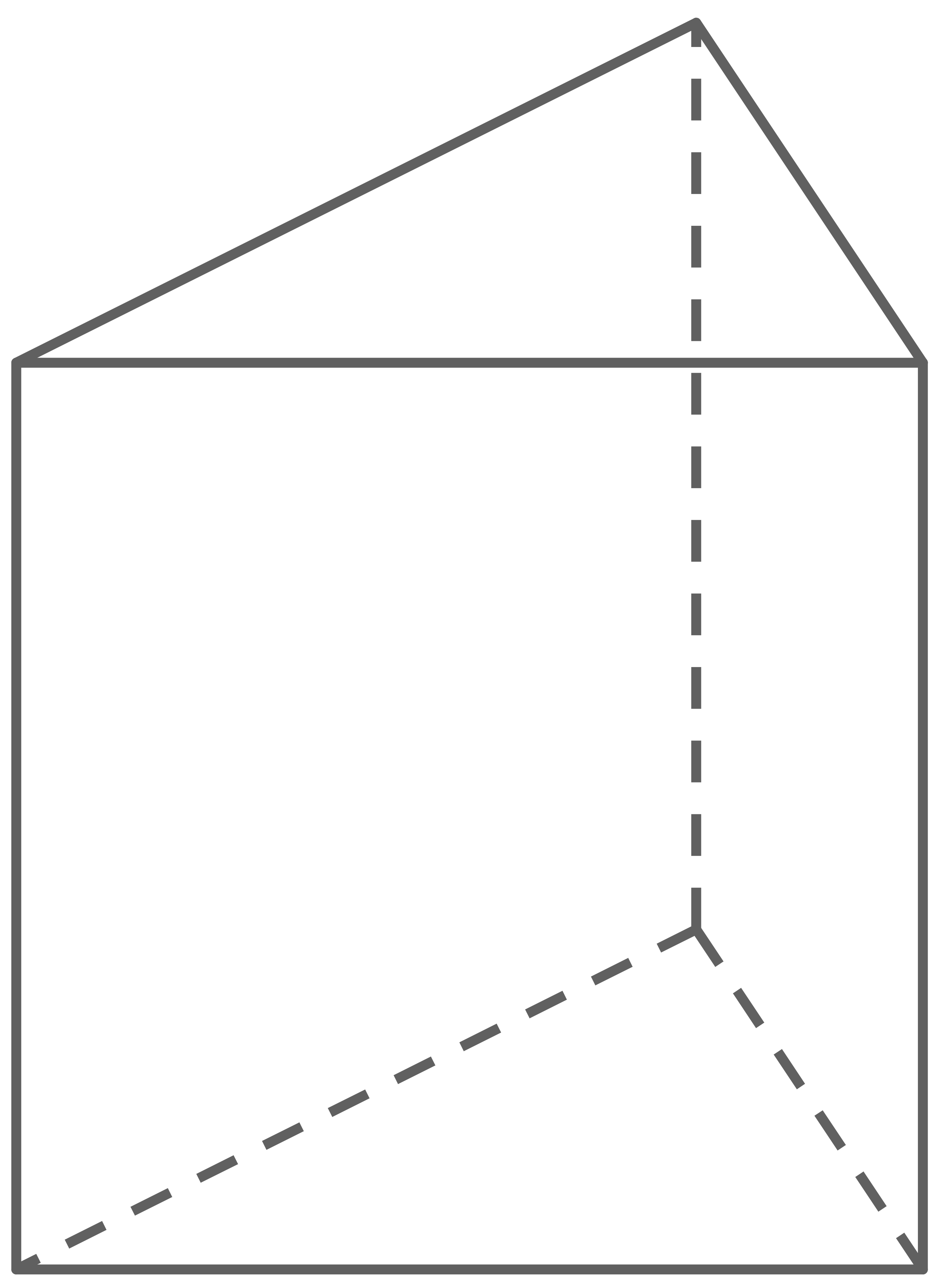 Die Höhe des Prismas beträgt
Die Höhe des Prismas beträgt  eine Dreiecksseite hat eine Länge von
eine Dreiecksseite hat eine Länge von  Berechne den Oberflächeninhalt des Prismas.
Berechne den Oberflächeninhalt des Prismas.

Abbildung 2
(nicht maßstäblich)
(nicht maßstäblich)
e)
Gegeben ist die Funktion  durch
durch  und
und 
Gib die Scheitelpunktkoordinaten des Graphen der Funktion an.
an.
Zeichne den Graphen von mindestens im Intervall
mindestens im Intervall  in ein Koordinatensystem.
in ein Koordinatensystem.
Gib die Scheitelpunktkoordinaten des Graphen der Funktion
Zeichne den Graphen von
f)
Gib eine Größe für den Winkel  an, so dass gilt:
an, so dass gilt:

11 BE erreichbar
Pflichtaufgabe 2
Gegeben ist das Fünfeck  (siehe Abbildung) mit:
(siehe Abbildung) mit:


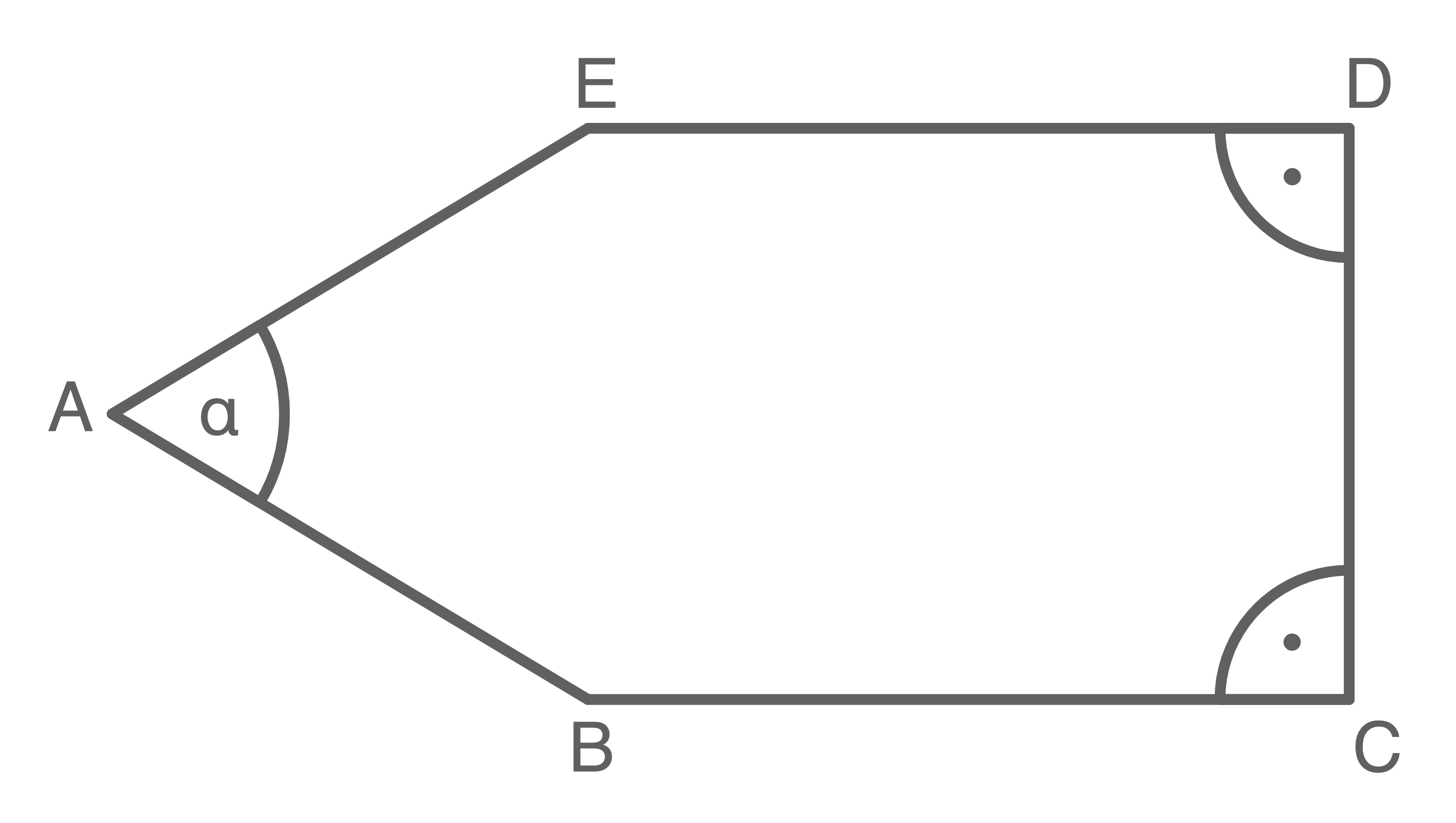
Abbildung (nicht maßstäblich)
a)
Konstruiere das Fünfeck 
b)
Berechne die Größe des Winkels 
c)
Beurteile die Aussage:
Der Flächeninhalt des Dreiecks  ist halb so groß wie der Flächeninhalt des Vierecks
ist halb so groß wie der Flächeninhalt des Vierecks 
7 BE erreichbar
Pflichtaufgabe 3
In einem Tabellenkalkulationsprogramm sind die Zuckerrübenerträge in Tonnen je Hektar von zehn landwirtschaftlichen Betrieben erfasst.


a)
Veranschauliche die Erträge der Betriebe I, II, und III in einem Säulendiagramm.
b)
Gib die Bedeutung des Wertes in Zelle B4 im Sachzusammenhang an.
c)
Durchschnittlich hat eine Zuckerrübe eine Masse von  und einen Zuckergehalt von
und einen Zuckergehalt von  .
.
Ermittle die Anzahl der Zuckerrüben, die für die Herstellung von einem Kilogramm Zucker mindestens benötigt wird.
Ermittle die Anzahl der Zuckerrüben, die für die Herstellung von einem Kilogramm Zucker mindestens benötigt wird.
6 BE erreichbar
Lösung 1
a)
b)
Um  als Summe zu erhalten, muss beim ersten und zweiten Drehen die Zahl
als Summe zu erhalten, muss beim ersten und zweiten Drehen die Zahl  angezeigt werden.
Für die Wahrscheinlichkeit, dass beim Drehen des Glücksrads die Zahl
angezeigt werden.
Für die Wahrscheinlichkeit, dass beim Drehen des Glücksrads die Zahl  angezeigt wird, gilt:
angezeigt wird, gilt:  Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{rll}
P(18)&=&P(9)\cdot P(9) \\[5pt]
P(18)&=&\dfrac{1}{5}\cdot \dfrac{1}{5} \\[5pt]
P(18)&=&\dfrac{1}{25}\\[5pt]
P(18)&=&0,04=4\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/58af2552da1267be5b3b94c25deaf304514917f6bc6b6a5d37a61aa6ce1f52b9_light.svg) Die Wahrscheinlichkeit beträgt
Die Wahrscheinlichkeit beträgt 
c)
Zueinander ähnliche Bildformate angeben
10x15 und 20x30
Begründung
Die Bildformate haben jeweils die gleichen Längenverhältnisse. Sie entsprechen dem Faktor 
d)
Höhe des gleichseitigen Dreiecks berechnen:
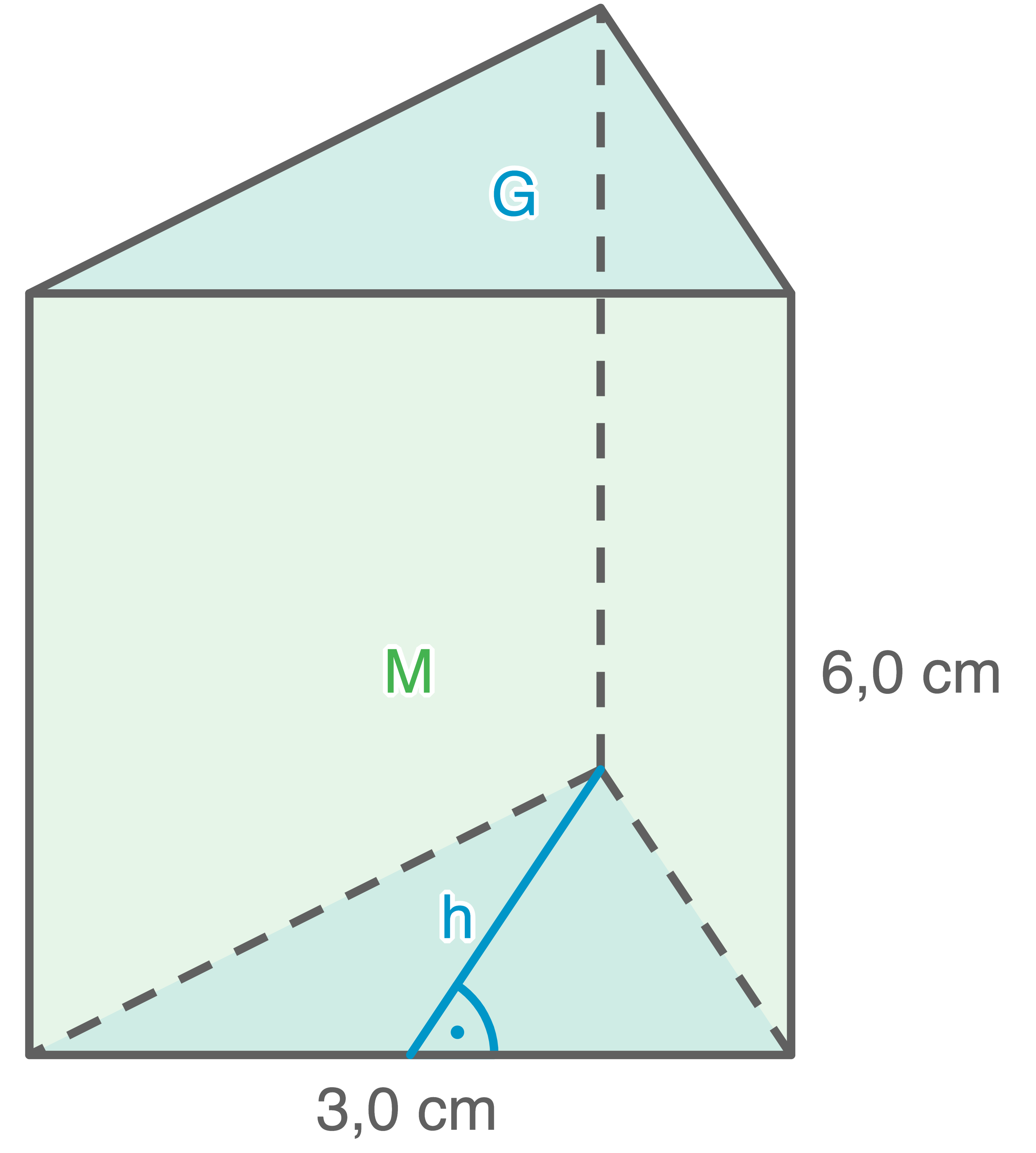
![\(\begin{array}[t]{rll}
h^2+ \left(\dfrac{3,0\,\text{cm}}{2} \right)^2&=& (3,0\,\text{cm})^2&\quad \scriptsize \mid\;-\left(\dfrac{3,0\,\text{cm}}{2} \right)^2
\end{array}\)](https://www.schullv.de/resources/formulas/5a13989d47f36ff845c2d57a8046e0ce58d8b98ec9b1c6bb8dc716017db8552c_light.svg)
![\(\begin{array}[t]{rll}
h^2&=& (3,0\,\text{cm})^2-\left(\dfrac{3,0\,\text{cm}}{2} \right)^2&\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h&=& \sqrt{(3,0\,\text{cm})^2-\left(\dfrac{3,0\,\text{cm}}{2}
\right)^2} \\[5pt]
h&\approx& 2,6\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/4bfc05f7155e8d247938500e1558ba59f7dd59bc0e847d451e3c53c47e910925_light.svg) Grundflächeninhalt berechnen:
Grundflächeninhalt berechnen:
![\(\begin{array}[t]{rll}
G&=&\dfrac{1}{2}\cdot g\cdot h \\[5pt]
G&=&\dfrac{1}{2}\cdot 3,0\,\text{cm}\cdot 2,6\,\text{cm} \\[5pt]
G&=&3,9\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/af4f6c1cc51bd376e1496fa99cfbcc3d7c64c753b133ac11e202eaafbf099bbf_light.svg) Mantelflächeninhalt berechnen:
Mantelflächeninhalt berechnen:
![\(\begin{array}[t]{rll}
M&=&u_G\cdot h \\[5pt]
M&=&3\cdot 3,0\,\text{cm}\cdot h \\[5pt]
M&=&3\cdot 3,0\,\text{cm}\cdot 6\,\text{cm} \\[5pt]
M&=&54\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/236bec7428ca8d2f9c6f27c7d22fa6f96733f11e6e13b652ed61292b423616df_light.svg) Oberflächeninhalt berechnen:
Oberflächeninhalt berechnen:
![\(\begin{array}[t]{rll}
O&=&2\cdot G+M \\[5pt]
O&=&2\cdot 3,9\,\text{cm}^2+54\,\text{cm}^2 \\[5pt]
O&=&61,8\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c9dc726b0326125aed2aa28d1b36cfbcd7ed6936ae658722633da54d50f31a05_light.svg)

e)
Scheitelpunktkoordinaten angeben
 Graphen von
Graphen von  zeichnen
zeichnen
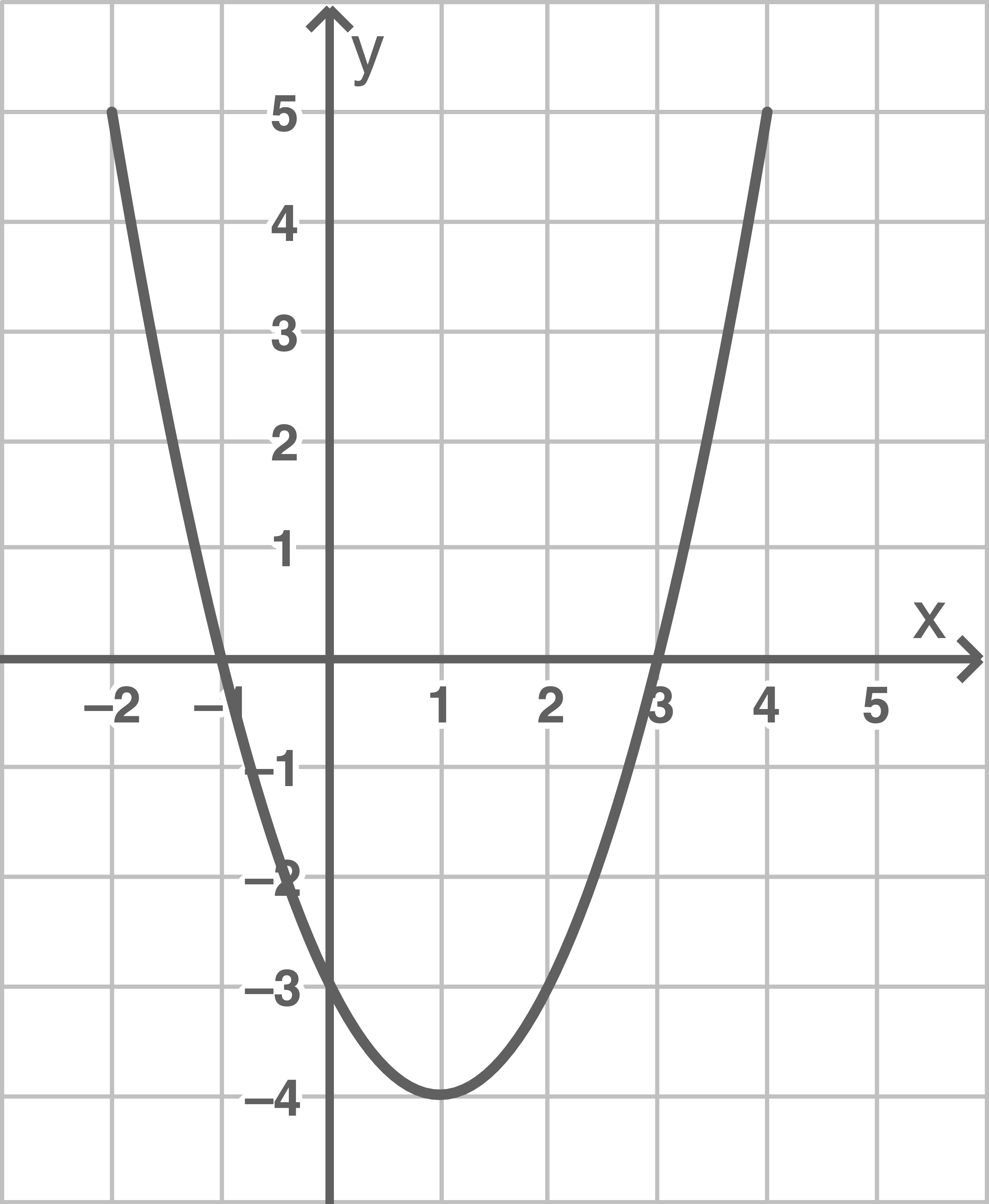

f)
Lösung 2
a)
- Strecke
zeichnen.
- Strecke
zeichnen.
- Strecke
zeichnen.
- Kreisbogen um
mit dem Radius
zeichnen.
- Kreisbogen um
mit dem Radius
zeichnen. Es entsteht Punkt
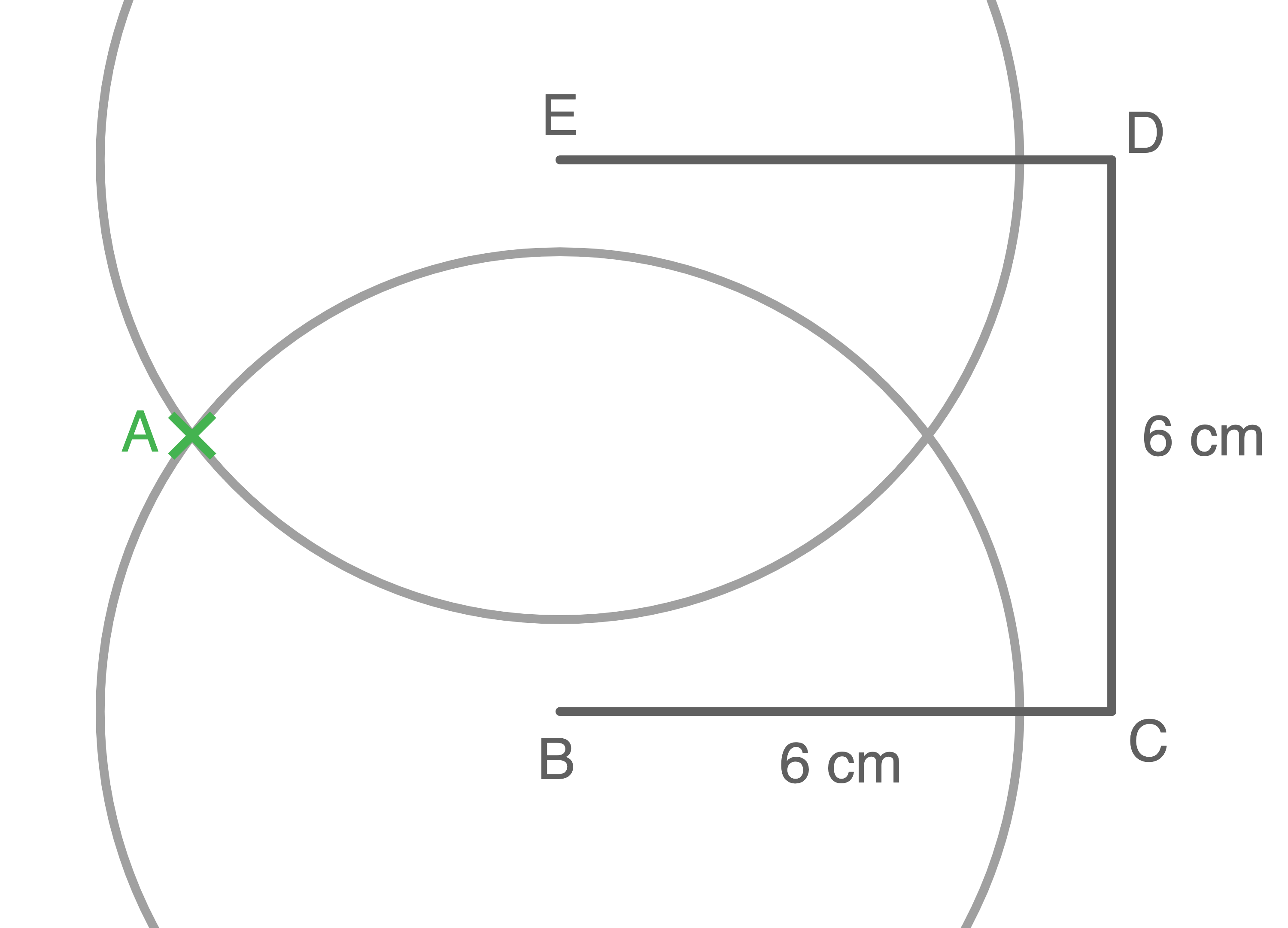
- Punkte
und
sowie
und
verbinden.
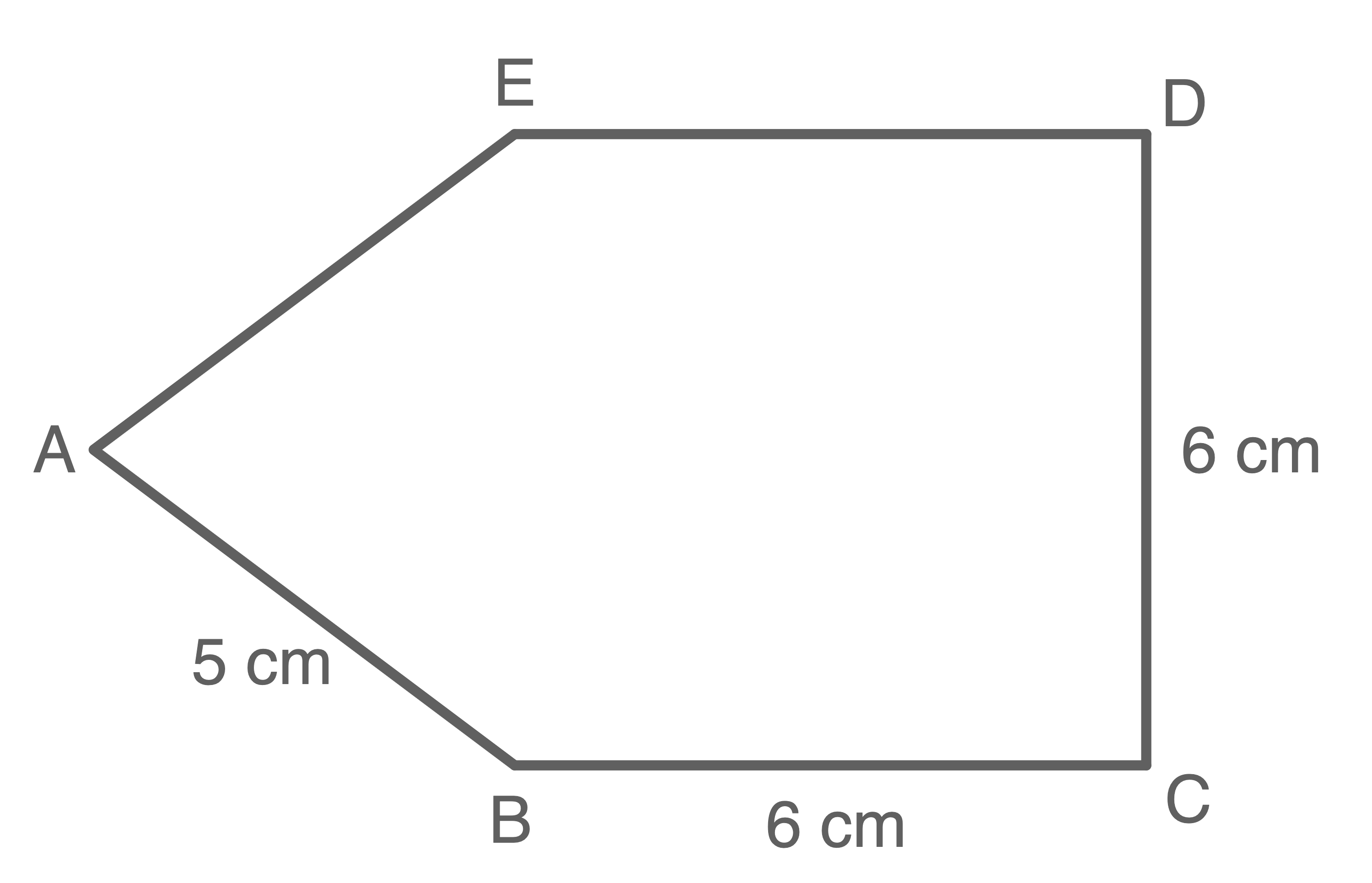
b)
Kosinussatz anwenden:
![\(\begin{array}[t]{rll}
a^2&=&b^2+c^2-2bc\cdot \cos(\alpha) &\scriptsize \mid\;-b^2 \\[5pt]
a^2-b^2&=&c^2-2bc\cdot \cos(\alpha) & \scriptsize \mid\;-c^2 \\[5pt]
a^2-b^2-c^2&=&-2bc\cdot \cos(\alpha) & \scriptsize \mid\;:(-2bc) \\[5pt]
\dfrac{a^2-b^2-c^2}{-2bc}&=&\cos(\alpha)
\end{array}\)](https://www.schullv.de/resources/formulas/338dfd1efc0ad398d5aa0fca66a5f881b035c3c73bca13a61068b3f1549593d4_light.svg)
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{a^2-b^2-c^2}{-2bc} &\\[5pt]
\cos(\alpha)&=&\dfrac{(6\,\text{cm})^2-(5\,\text{cm})^2-(5\,\text{cm})^2}{-2\cdot 5\,\text{cm}\cdot 5\,\text{cm}} &\\[5pt]
\cos(\alpha)&=&0,28 & \scriptsize \mid\;\cos^{-1} \\[5pt]
\alpha&\approx &74^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/2890dd06452a8f18316812911c0a898eeb0ef6546cd7be95d59b18e681170068_light.svg) Die Größe des Winkels beträgt
Die Größe des Winkels beträgt 
c)
Formel zur Berechnung des Flächeninhalts eines Rechtecks: 
Formel zur Berechnung des Flächeninhalts eines Dreiecks: Für die gegebenen Flächeninhalte gilt:
Für die gegebenen Flächeninhalte gilt:
 Höhe des Dreiecks berechnen:
Höhe des Dreiecks berechnen:
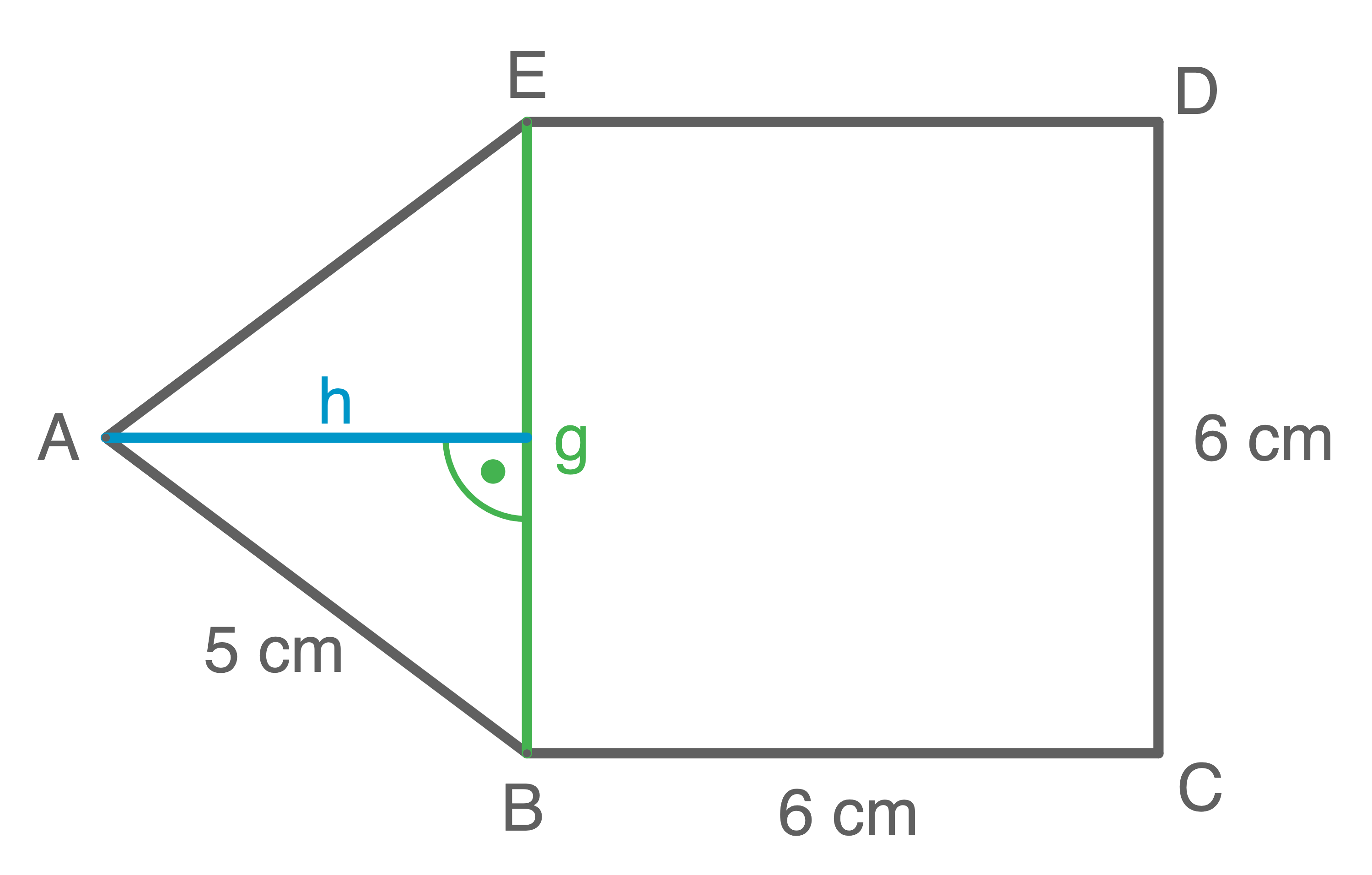
![\(\begin{array}[t]{rll}
h^2+\left(\dfrac{g}{2}\right)^2&=& \left(\overline{AB}\right)^2& \scriptsize \mid\;-\left(\dfrac{g}{2}\right)^2 \\[5pt]
h^2&=& \left(\overline{AB}\right)^2-\left(\dfrac{g}{2}\right)^2& \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
h&=& \sqrt{\left(\overline{AB}\right)^2-\left(\dfrac{g}{2}\right)^2} \\[5pt]
h&=& \sqrt{(5\,\text{cm})^2-\left(\dfrac{6\,\text{cm}}{2}\right)^2} \\[5pt]
h&=& \sqrt{(5\,\text{cm})^2-(3\,\text{cm})^2} \\[5pt]
h&=& 4\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/84ed244f4f8722f4d1d9365cee093141681e84b7e0ff56e7b502a3996b40becf_light.svg) Somit gilt:
Somit gilt:
 ist nicht halb so groß wie der Flächeninhalt des Vierecks
ist nicht halb so groß wie der Flächeninhalt des Vierecks 
Formel zur Berechnung des Flächeninhalts eines Dreiecks:

Lösung 3
a)
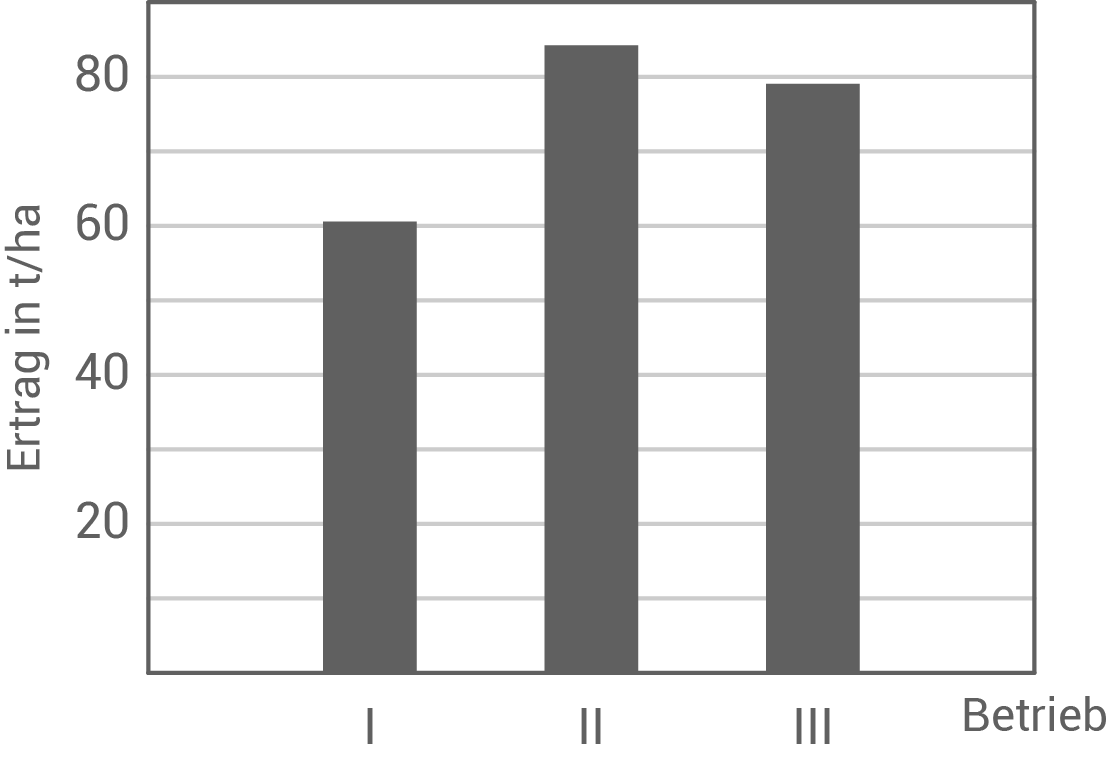
b)
Die Zelle B4 gibt den Durchschnitt bzw. Mittelwert der Erträge aller Betriebe an.
c)
Zuckergehalt einer Zuckerrübe berechnen:




![\(\begin{array}{rcl}
920\,\text{g} & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
9,2\,\text{g} & \mathrel{\widehat{=}}& 1\,\%\\[5pt]
174,8\,\text{g} & \mathrel{\widehat{=}}& 19\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1e89cc41db016017f2928ecf6d6d9c2bda0b38a5bc9d2c642b84c45be27fc2b1_light.svg)



 Daraus folgt für die Anzahl der Zuckerrüben:
Daraus folgt für die Anzahl der Zuckerrüben:
 Für die Herstellung von einem Kilogramm Zucker werden mindestens 6 Zuckerrüben benötigt.
Für die Herstellung von einem Kilogramm Zucker werden mindestens 6 Zuckerrüben benötigt.