Pflichtteil 1
1.
Berechne.



 von
von 
a)
b)
c)
d)
2.
Vergleiche und setze das richtige Relationszeichen 


3.
Runde auf Hundertstel.

4.
Die Abbildung zeigt ein Dreieck 
a)
Gib die Größe des Winkels  im Dreieck
im Dreieck  an.
an.
b)
Begründe, dass die Seite  die längste Seite im Dreieck
die längste Seite im Dreieck  ist.
ist.
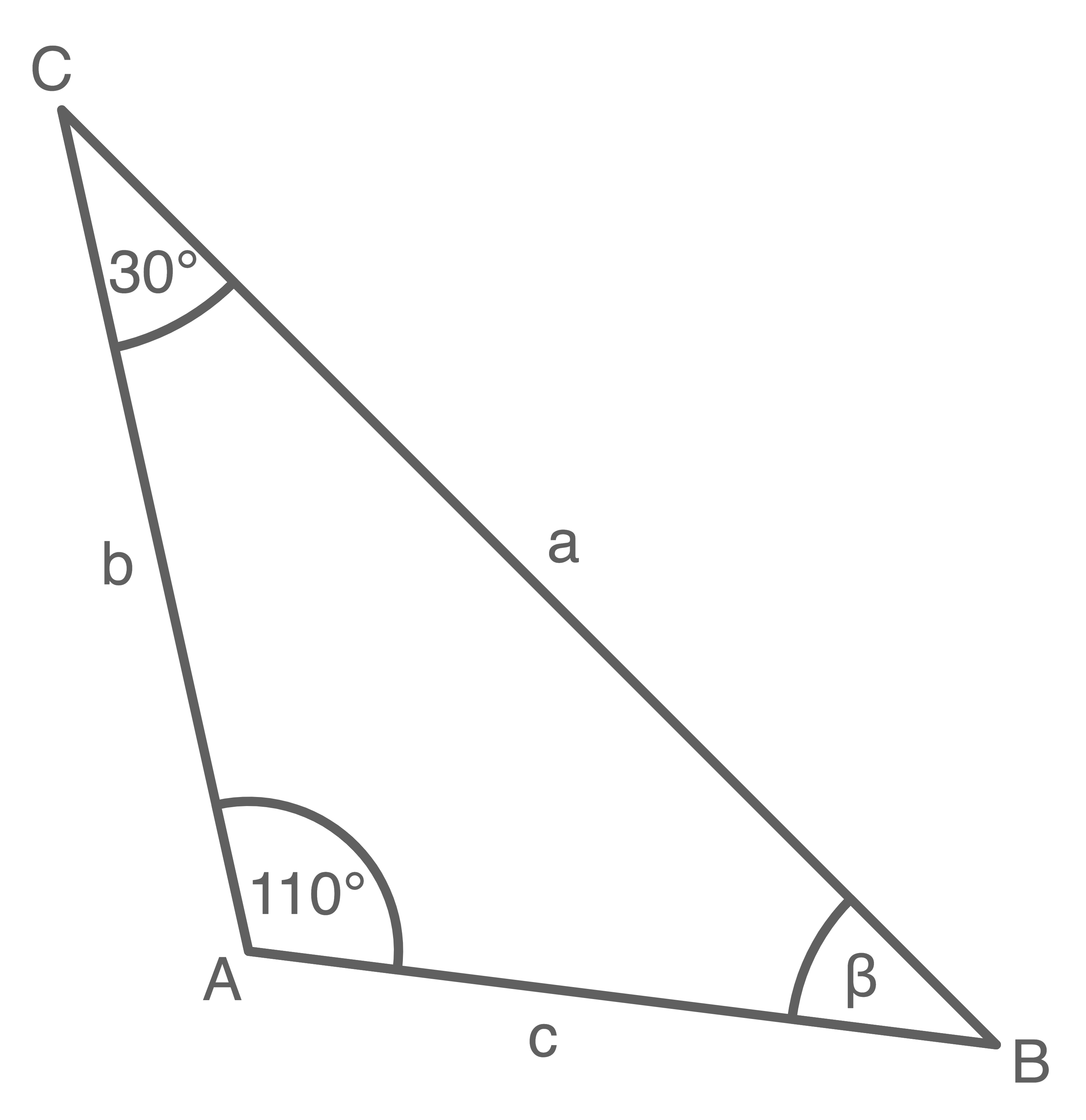
Abbildung (nicht maßstäblich)
5.
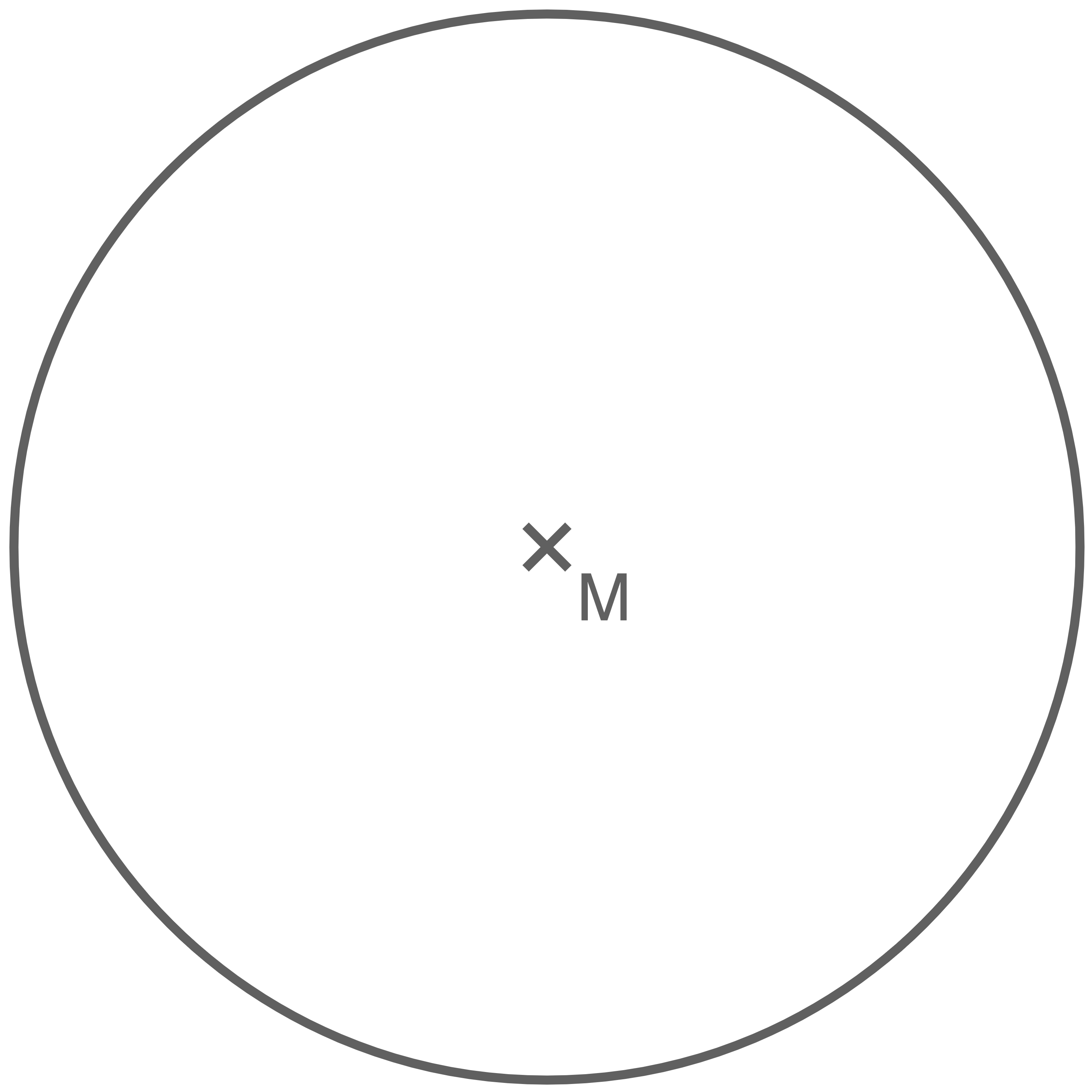
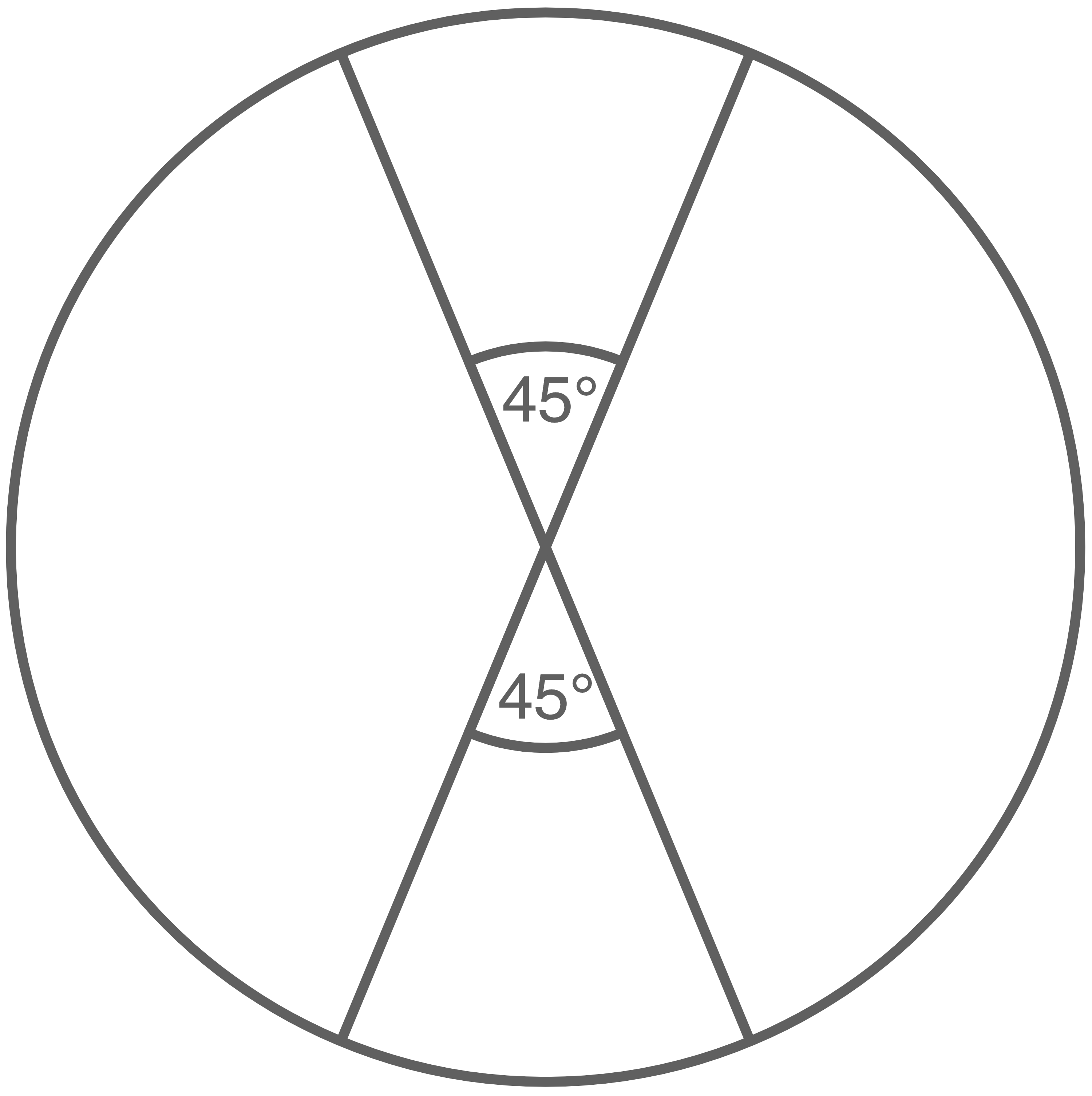
Zeichne in den Kreis zwei Durchmesser ein, die einen Winkel von  einschließen.
einschließen.
6.
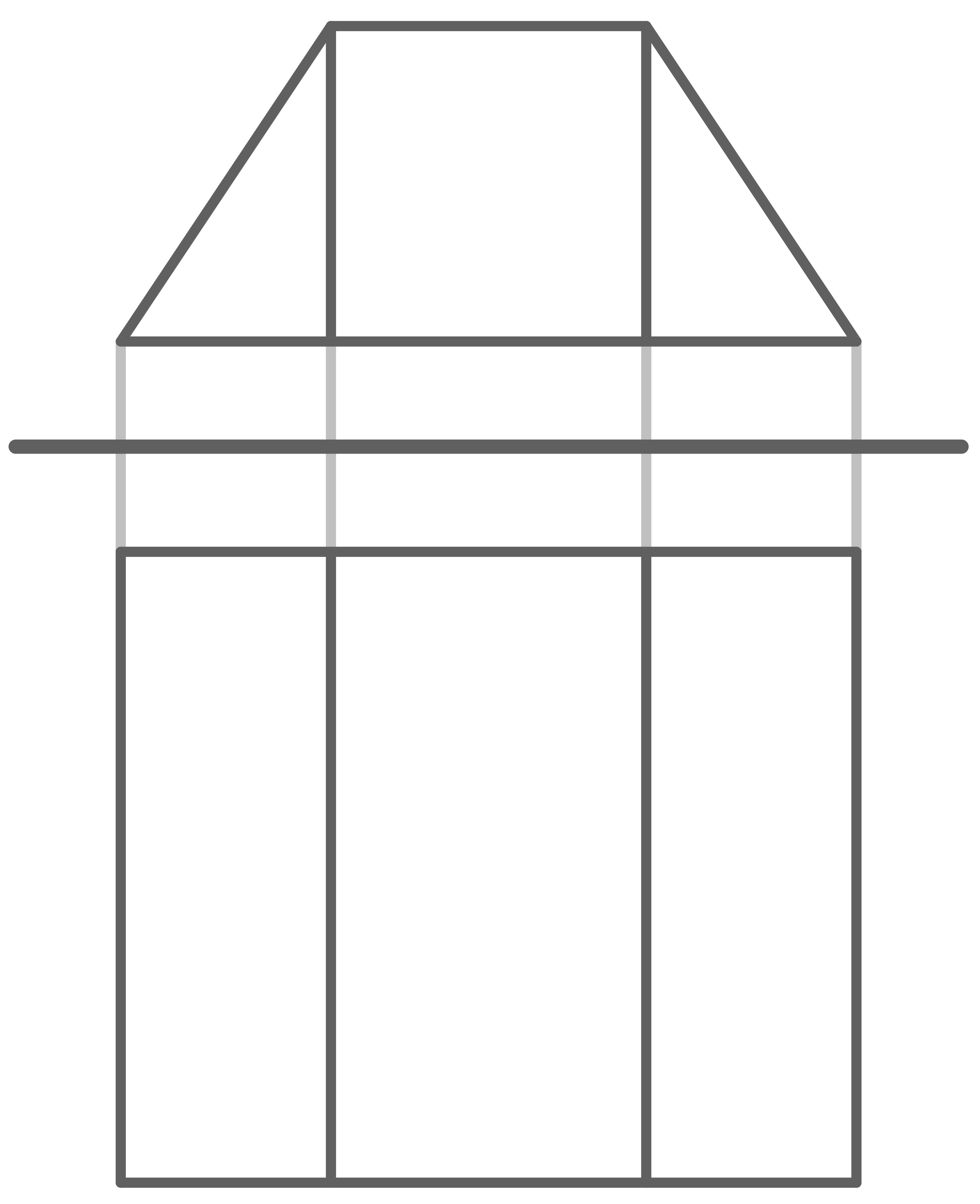
Gib den Körper an, der im Zweitafelbild dargestellt ist.
7.
Gegeben ist die lineare Funktion  mit der Gleichung
mit der Gleichung 
a)
Der Punkt  ist ein Punkt des Graphen der Funktion
ist ein Punkt des Graphen der Funktion 
Ergänze die fehlende Koordinate.

Ergänze die fehlende Koordinate.
b)
Zeige, dass  keine Nullstelle der Funktion
keine Nullstelle der Funktion  ist.
ist.
8.
Gib durch Ankreuzen die Lösungsmenge der Gleichung  an.
an.
9.
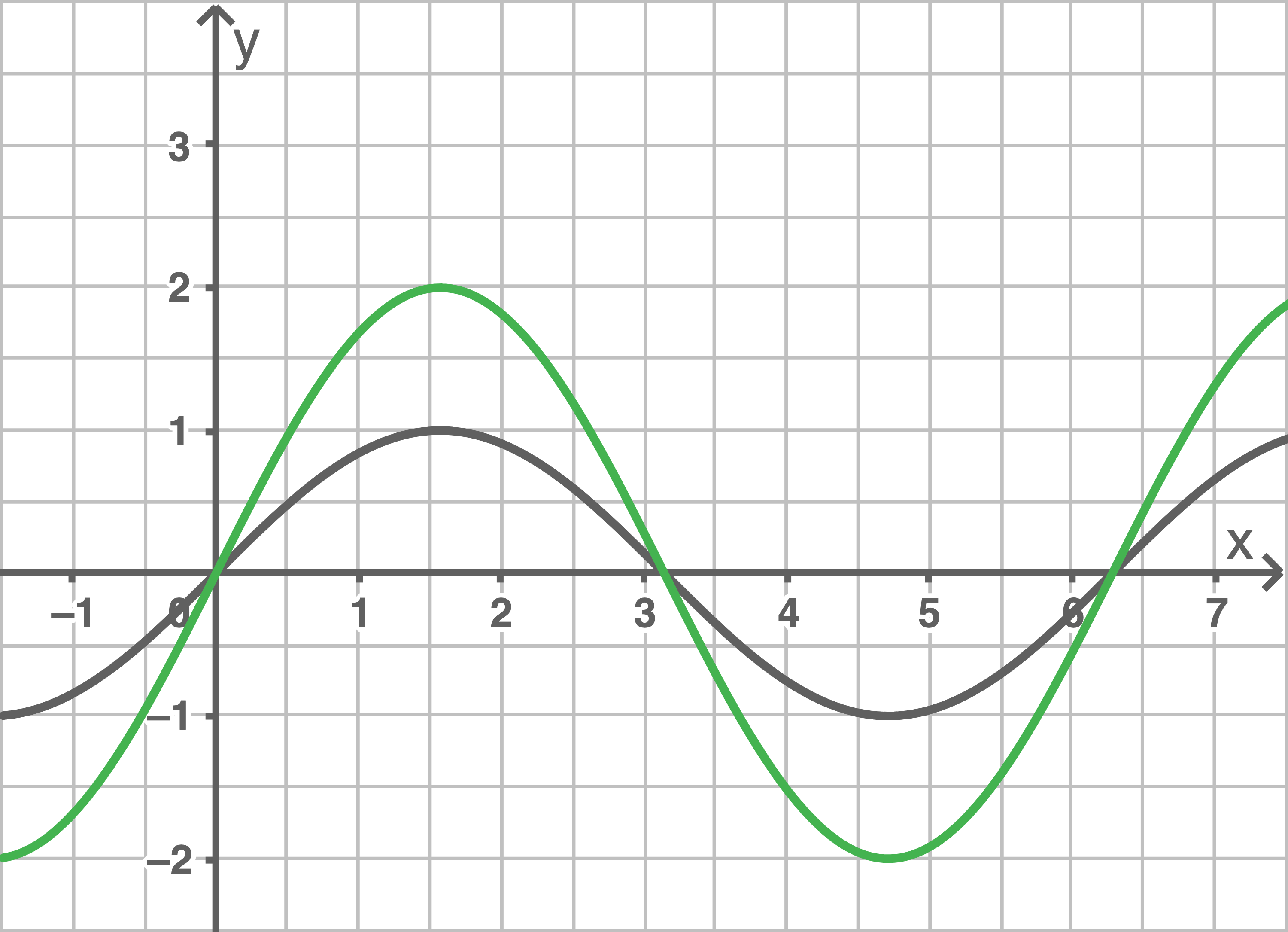
Im Koordinatensystem ist der Graph einer Funktion  mit der Gleichung
mit der Gleichung  dargestellt.
dargestellt.
Skizziere in dieses Koordinatensystem den Graphen einer Funktion mit der Gleichung
mit der Gleichung  .
.
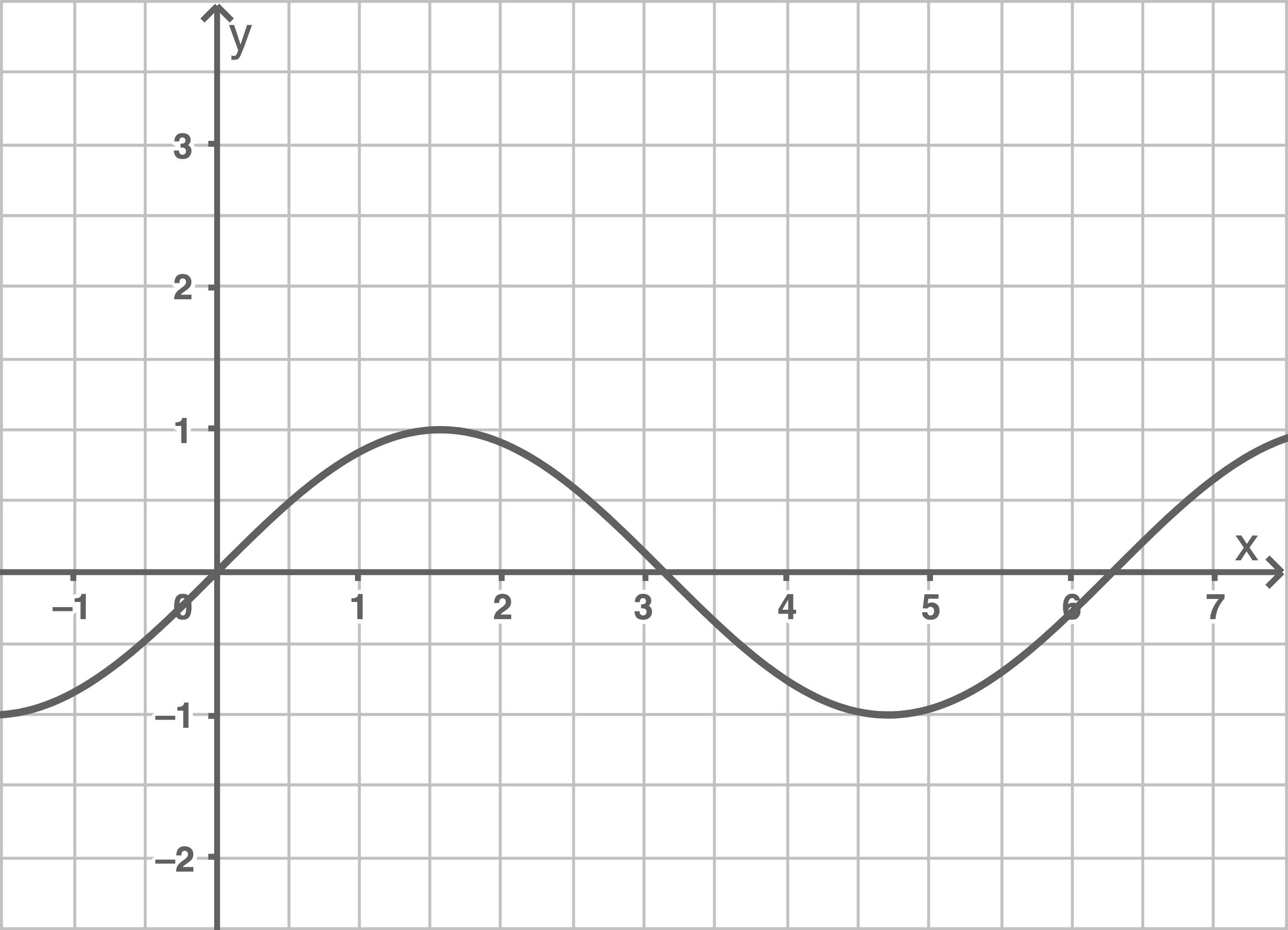
Skizziere in dieses Koordinatensystem den Graphen einer Funktion

10.
Zeichne eine zum gegebenen Viereck ähnliche Figur.


8 BE erreichbar
1.
a)
b)
c)
d)
Lösung mit Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 600\,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 6\,€\\[5pt]
5\,\% & \mathrel{\widehat{=}}& 30\,€
\end{array}\)](https://www.schullv.de/resources/formulas/a0382229b6e2c5475b0d73d6a44c6355a560da65de5193f8183adabdaec5bfa5_light.svg)



 Lösung mit Prozentformel
Lösung mit Prozentformel


![\(\begin{array}[t]{rll}
W&=& \dfrac{p\,\%}{100\,\%}\cdot G \\[5pt]
W&=& \dfrac{5\,\%}{100\,\%}\cdot 600\,€ \\[5pt]
W&=& 30\,€
\end{array}\)](https://www.schullv.de/resources/formulas/c964410ccb0c0adfdc6d8eb7e10ee203c99ed754c9679c53c60f226887b3b2fb_light.svg)
 von
von  entsprechen
entsprechen 
2.
Es gilt  . Somit folgt:
. Somit folgt:

3.
4.
a)
Mit der Winkelsumme im Dreieck  folgt:
folgt:

b)
Da ein Winkel in dem Dreieck  größer als
größer als  ist, ist das Dreieck
ist, ist das Dreieck  ein stumpfwinkliges Dreieck. In einem stumpfwinkligen Dreieck gilt, dass die längste Seite immer gegenüber des stumpfen Winkels liegt.
Der stumpfe Winkel ist hierbei mit
ein stumpfwinkliges Dreieck. In einem stumpfwinkligen Dreieck gilt, dass die längste Seite immer gegenüber des stumpfen Winkels liegt.
Der stumpfe Winkel ist hierbei mit  gegeben. Somit ist die längste Seite die Seite
gegeben. Somit ist die längste Seite die Seite 
5.
6.
In der Vorderansicht ist ein Trapez dargestellt. Bei dem Körper im Zweitafelbild handelt es sich somit um ein Trapezprisma.
7.
a)
Durch Einsetzen der  -Koordinate in die Funktionsgleichung der linearen Funktion
-Koordinate in die Funktionsgleichung der linearen Funktion  folgt für die
folgt für die  -Koordinate:
-Koordinate:
![\(\begin{array}[t]{rll}
14&=& x+4 &\quad \scriptsize \mid\; -4\\[5pt]
10&=& x
\end{array}\)](https://www.schullv.de/resources/formulas/912873a276eb96543ca79a94ccd1394f6b5236874c26d8897657976e2a7c0b62_light.svg) Daraus folgt:
Daraus folgt: 
b)
8.
9.
10.
Zwei Figuren sind ähnlich, wenn sie durch zentrische Streckung vergrößert oder verkleinert werden oder gedreht werden. Eine mögliche ähnliche Figur zum gegebenen Viereck ist also die folgende: