Pflichtteil 2
Pflichtaufgabe 1
a)
Die nebenstehende Gleichung wurde falsch gelöst. Gib den fehlerhaften Umformungsschritt an und ermittle die Lösung der Gleichung.
b)
Ein See hat an seiner breitesten Stelle eine Ausdehung von  Auf einer Landkarte wird diese Ausdehnung mit
Auf einer Landkarte wird diese Ausdehnung mit  dargestellt. Gib den verwendeten Maßstab an.
dargestellt. Gib den verwendeten Maßstab an.
c)
Konstruiere ein Viereck  nach folgender Konstruktionsbeschreibung:
nach folgender Konstruktionsbeschreibung:
(1)
Strecke  zeichnen,
zeichnen,
(2)
Winkel 
 an die Strecke
an die Strecke  im Punkt
im Punkt  antragen,
antragen,
(3)
Strecke  auf dem freien Schenkel des Winkels
auf dem freien Schenkel des Winkels  vom Punkt
vom Punkt  aus abtragen und Endpunkt mit
aus abtragen und Endpunkt mit  bezeichnen,
bezeichnen,
(4)
parallele Gerade  zur Strecke
zur Strecke  durch Punkt
durch Punkt  zeichnen,
zeichnen,
(5)
Kreisbogen um Punkt  mit dem Radius
mit dem Radius  zeichnen und einen Schnittpunkt mit der Geraden
zeichnen und einen Schnittpunkt mit der Geraden  mit
mit  bezeichnen,
bezeichnen,
(6)
Punkte  und
und  verbinden.
verbinden.
d)
Von einem Kreiskegel mit einem Grundkreisradius von  und einer Höhe von
und einer Höhe von  wird eine kegelförmige Spitze mit einer Höhe von
wird eine kegelförmige Spitze mit einer Höhe von  und einem Radius von
und einem Radius von  abgeschnitten. Dabei entsteht ein Restkörper. Dieser ist in der Abbildung grün dargestellt. Berechne das Volumen des Restkörpers.
abgeschnitten. Dabei entsteht ein Restkörper. Dieser ist in der Abbildung grün dargestellt. Berechne das Volumen des Restkörpers.

Abbildung nicht maßstäblich
e)
Bei einem Räumungsverkauf wurde der Preis einer Tasche um  gesenkt. Eine Woche später erfolgte noch einmal eine Preisreduzierung um
gesenkt. Eine Woche später erfolgte noch einmal eine Preisreduzierung um  Zeige, dass dadurch der ursprüngliche Preis nicht um
Zeige, dass dadurch der ursprüngliche Preis nicht um  gesenkt wurde.
gesenkt wurde.
10 BE erreichbar
Pflichtaufgabe 2
Gegeben ist ein gleichschenkliges Dreieck  wie in der Abbildung mit:
wie in der Abbildung mit:
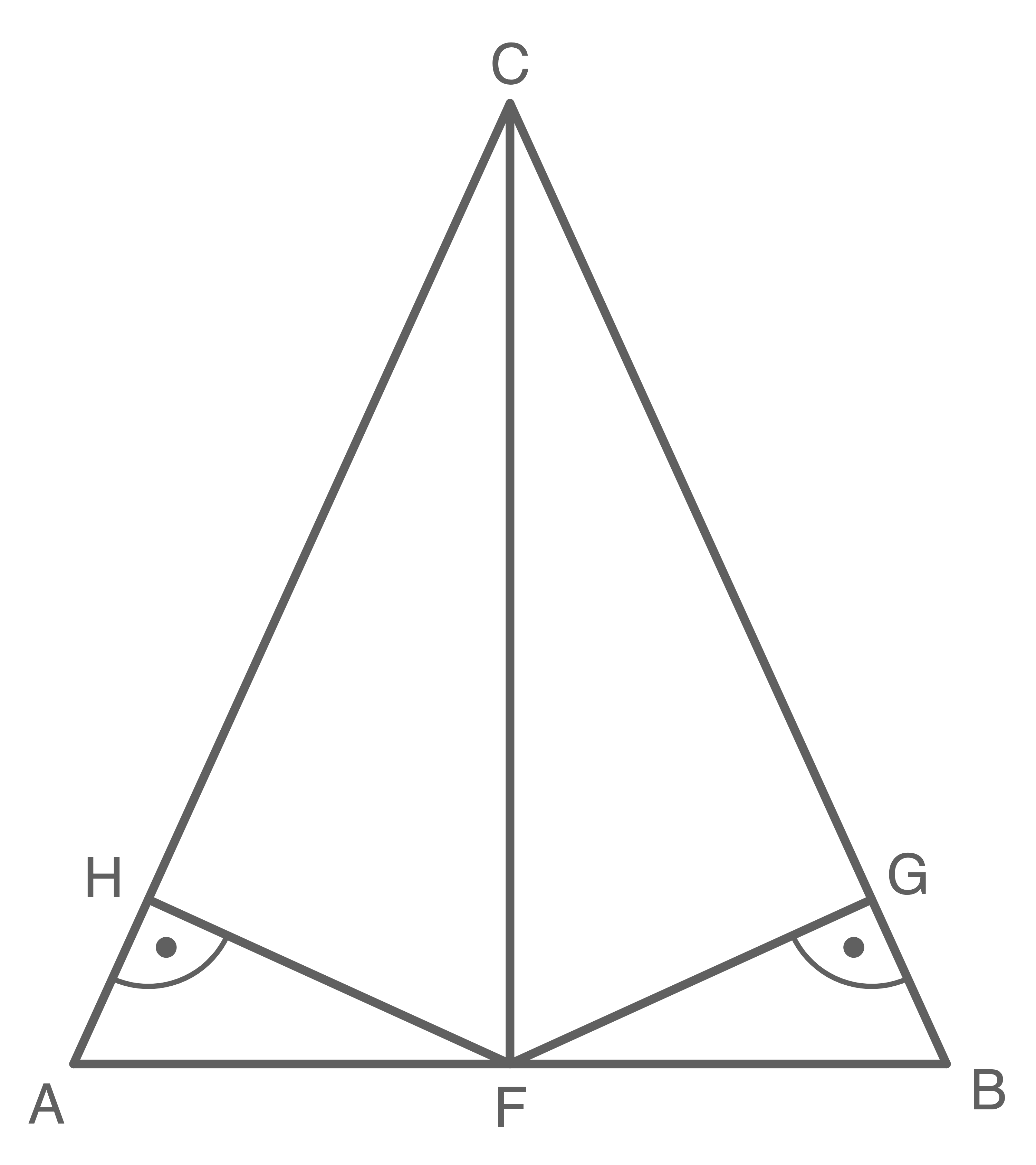
Abbildung nicht maßstäblich
a)
Berechne die Größe des Winkels  und die Länge der Strecke
und die Länge der Strecke  .
.
b)
Berechne den Flächeninhalt des Vierecks 
c)
Begründe, dass die Winkel  und
und  gleich groß sind.
gleich groß sind.
8 BE erreichbar
Pflichtaufgabe 3
Bei einer Gebäudezählung werden Daten erhoben, um einen Überblick zu ermöglichen, wie Menschen in Sachsen-Anhalt leben. Für den Salzlandkreis sind für eine Gesamtzahl von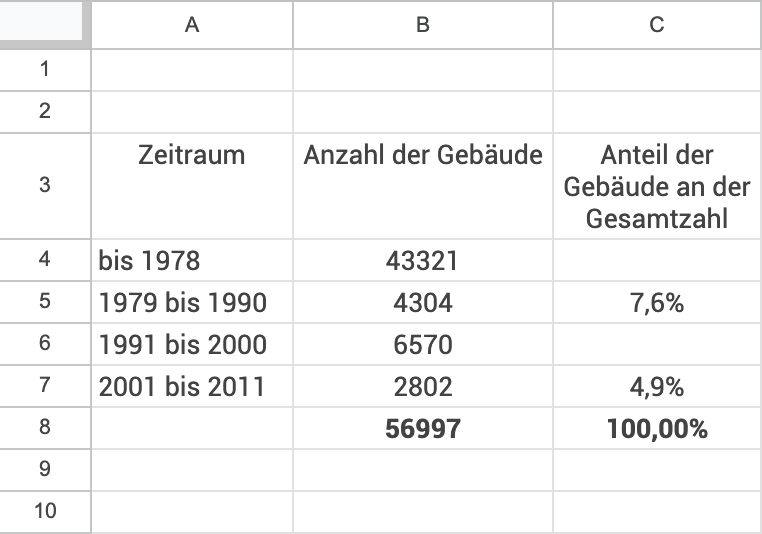
a)
Stelle die Anzahl der Gebäude für die Zeiträume nach 1978 in einem Säulendiagramm dar.
b)
In der Spalte C der Tabelle wurde mit einem Tabellenkalkulationsprogramm jeweils der prozentuale Anteil der in den angegebenen Zeiträumen erfassten Gebäude an der Gesamtzahl der Gebäude ermittelt.
Gib eine Formel für Zelle C4 an, mit der dieser Anteil ermittelt werden kann, und berechne diese. Hinweis: In der Formel sind Zellbezüge zu verwenden.
Gib eine Formel für Zelle C4 an, mit der dieser Anteil ermittelt werden kann, und berechne diese. Hinweis: In der Formel sind Zellbezüge zu verwenden.
c)
Zeige, dass sich der Anteil der Gebäude an der Gesamtzahl im Zeitraum von 1991 bis 2000 gegenüber 1979 bis 1990 etwa um  erhöht hat.
erhöht hat.
6 BE erreichbar
Lösung 1
a)
Der Fehler in der Rechnung liegt an der Stelle, an der die Zahl  addiert wird. Die richtige Rechnung ist die folgende:
addiert wird. Die richtige Rechnung ist die folgende:
![\(\begin{array}[t]{rll}
5 - 2x&=& 6x + 3 &\quad \scriptsize \mid\; -5 \\[5pt]
-2x&=& 6 x - 2 &\quad \scriptsize \mid\; -6\,x \\[5pt]
-8x&=& -2 &\quad \scriptsize \mid\; : (-8) \\[5pt]
x&=& \dfrac{2}{8} \\[5pt]
&=& \dfrac{1}{4}
\end{array}\)](https://www.schullv.de/resources/formulas/9a45f738b8193a5e6f0334f0e6f54c6592d4933721954d6ba0467ff30beb4896_light.svg) Die richtige Lösung beträgt
Die richtige Lösung beträgt 
b)
c)
Es gibt zwei verschiedene Möglichkeiten:
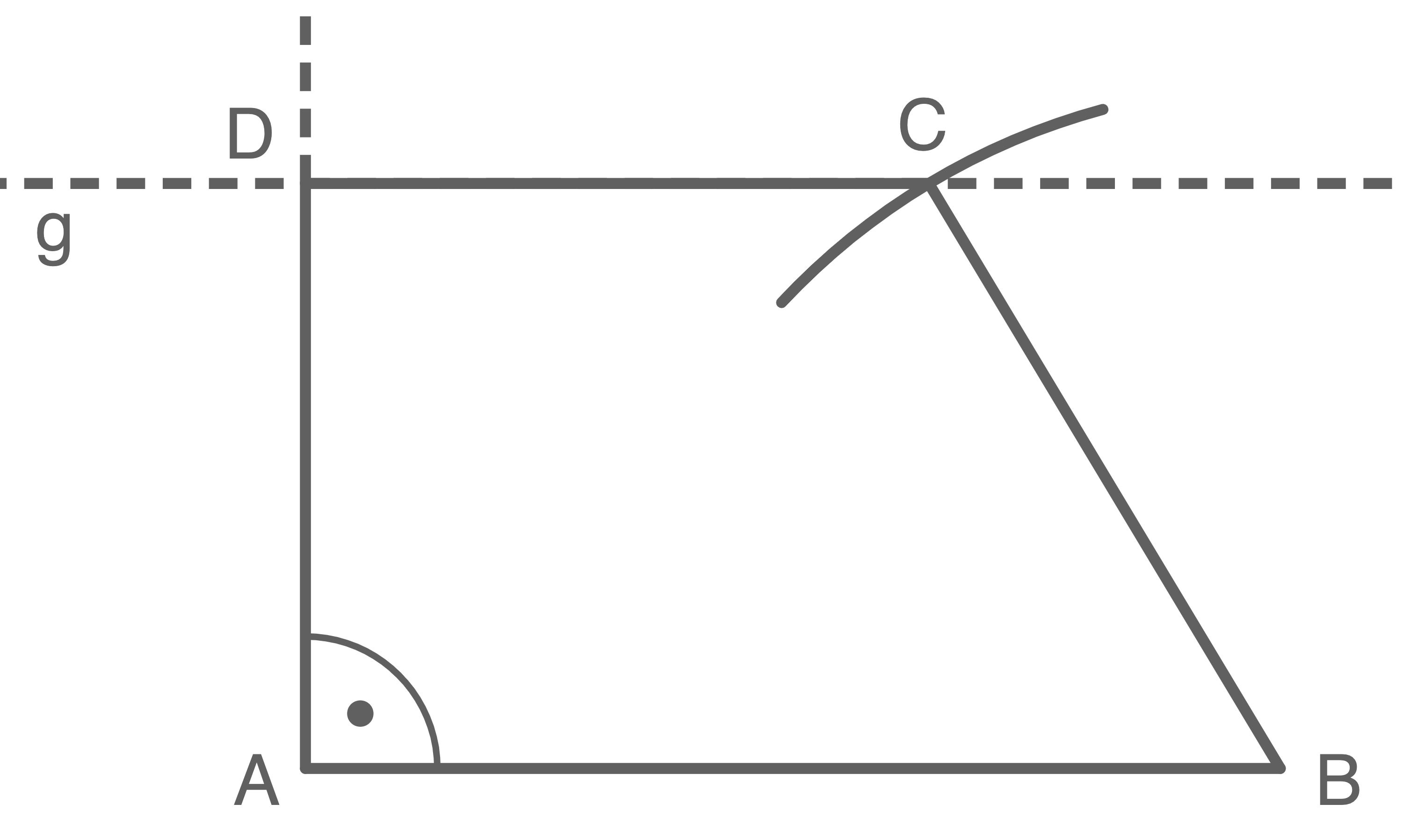
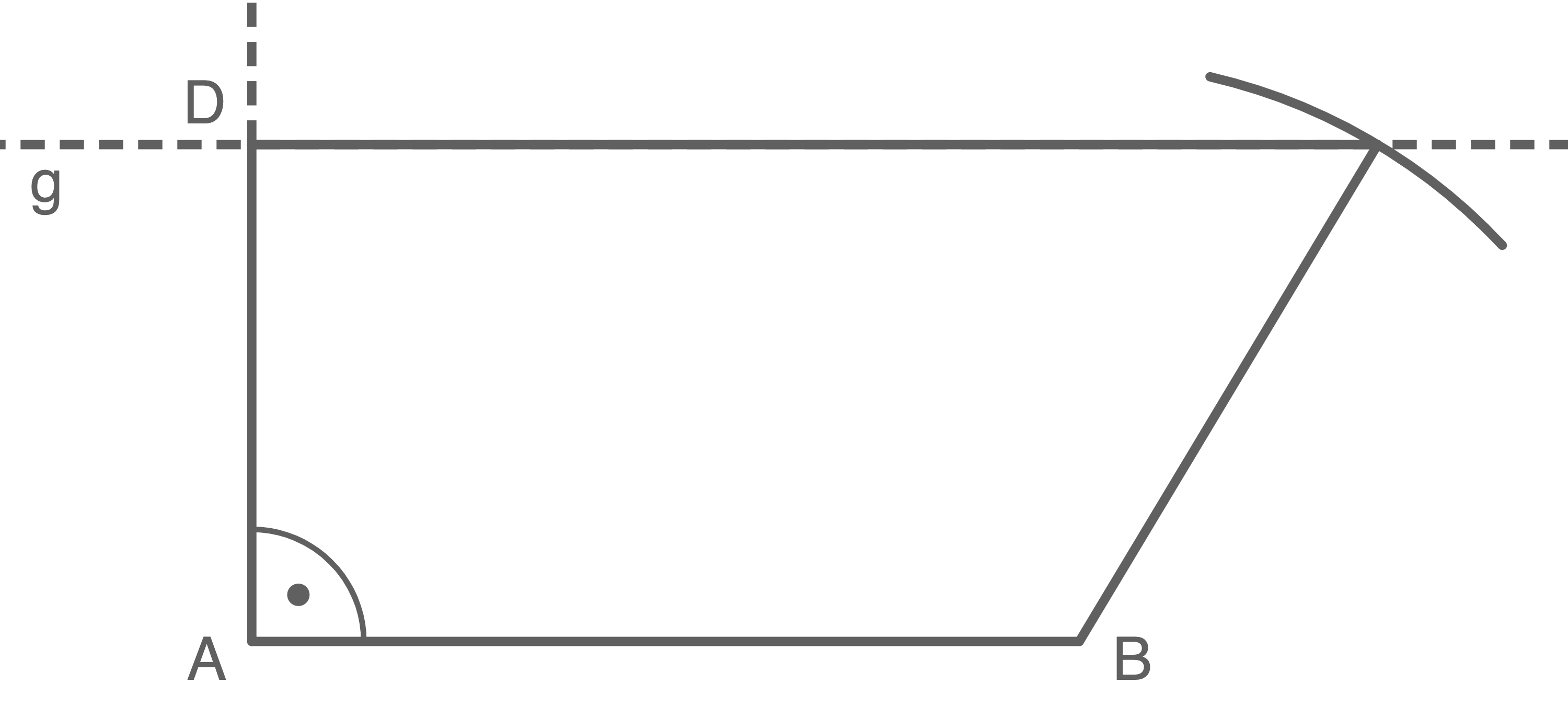 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.


d)
Gesamtes Volumen des Kegels:
![\(\begin{array}[t]{rll}
V_{\text{ges}}&=& \dfrac{1}{3} \cdot \pi \cdot (4 \, \text{cm})^2 \cdot 8 \, \text{cm} \\[5pt]
&\approx& 134,04 \, \text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/4be9bd8ce3ad7b6cc9ab4b9cd110980260c8eaf230dfc394a0505ee173c4877f_light.svg) Volumen der abgeschnittenen, kegelförmigen Spitze:
Volumen der abgeschnittenen, kegelförmigen Spitze:
![\(\begin{array}[t]{rll}
V_{\text{Spitze}}&=& \dfrac{1}{3} \cdot \pi \cdot (3 \, \text{cm})^2 \cdot 6 \, \text{cm} \\[5pt]
&\approx& 56,55 \, \text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/b36262b4f4978669199a9982ed38c51d7085071ddb33eddec3ebf87b0764c7a0_light.svg) Volumen des Restkörpers:
Volumen des Restkörpers:
![\(\begin{array}[t]{rll}
V_{\text{Rest}}&=& V_{\text{ges}} - V_{\text{Spitze}} \\[5pt]
&\approx& 134,04 \, \text{cm}^3 - 56,55 \, \text{cm}^3 \\[5pt]
&=& 77,49 \, \text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/0f22befee27ab2c4bef490687ac5fe9d8c4f91f07b0dadc5057a819e4e56bafc_light.svg) Das Volumen des Restkörpers beträgt ungefähr
Das Volumen des Restkörpers beträgt ungefähr 
e)
Wird der ursprüngliche Preis  zweimal um
zweimal um  gesenkt, so ergibt sich für den reduzierten Preis
gesenkt, so ergibt sich für den reduzierten Preis 
![\(\begin{array}[t]{rll}
P&=& (1 - 0,5 \cdot 0,5)\cdot G \\[5pt]
&=& (1 - 0,25)\cdot G \\[5pt]
&=& 0,75\cdot G
\end{array}\)](https://www.schullv.de/resources/formulas/4a72ea72948da010545bdba95ad36a960384807d99f2d11abb410eb9a3bde072_light.svg) Der Preis wurde nicht um
Der Preis wurde nicht um  sondern um
sondern um  gesenkt.
gesenkt.
Lösung 2
a)
Größe des Winkels berechnen
Die Höhe  des Dreiecks kann mit dem Satz des Pythagoras berechnet werden:
des Dreiecks kann mit dem Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
h^2+\overline{AF}^2&=& \overline{AC}^2 \quad \scriptsize \mid\; -\overline{AF}^2\\[5pt]
h^2&=& \overline{AC}^2 -\overline{AF}^2 \\[5pt]
h^2 &=& (5,6 \, \text{cm})^2 - \left(\dfrac{5,0\, \text{cm}}{2}\right)^2 \\[5pt]
h^2&=& 25,11 \, \text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
h &\approx& 5,01 \, \text{cm} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1a1d855653f550aa71a11c80e9bbb90064fd896070046920c6dc7fb01317987b_light.svg) Der Winkel
Der Winkel  lässt sich nun mit dem Sinus im rechtwinkligen Dreieck
lässt sich nun mit dem Sinus im rechtwinkligen Dreieck  berechnen.
berechnen.
![\(\begin{array}[t]{rll}
\sin (\alpha)&=& \left(\dfrac{h}{\overline{AC}}\right) \\[5pt]
\sin (\alpha)&\approx& \dfrac{5,01 \, \text{cm}}{5,6 \, \text{cm}} \\[5pt]
\sin (\alpha)&\approx& 0,89 \quad \scriptsize \mid\; \sin^{-1} \\[15pt]
\alpha &\approx& 62,87^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/5127ab644fb397df3dcd573f231be8c7a10cdfdcac34cc90907452151560f06b_light.svg) Die Größe des Winkels
Die Größe des Winkels  beträgt ungefähr
beträgt ungefähr  .
Länge der Strecke berechnen
Die Länge der Strecke
.
Länge der Strecke berechnen
Die Länge der Strecke  kann über den Kosinus im rechtwinkligen Dreieck
kann über den Kosinus im rechtwinkligen Dreieck  berechnet werden.
berechnet werden.
![\(\begin{array}[t]{rll}
\cos (\alpha)&=& \dfrac{\overline{AH}}{\overline{AF}} \quad \scriptsize \mid\; \cdot \overline{AF} \\[5pt]
\overline{AF} \cdot \cos \, (\alpha) &=& \overline{AH} \\[5pt]
2,5 \, \text{cm} \cdot \cos \, (62,87 \, ^{\circ})&=& \overline{AH} \\[5pt]
1,14 \, \text{cm} &\approx& \overline{AH}
\end{array}\)](https://www.schullv.de/resources/formulas/cd45016f6c771a5a8eb0e8d817864027bd900f3468ad82f295e76cf5b9035af4_light.svg) Die Länge der Strecke
Die Länge der Strecke  beträgt ca.
beträgt ca.  .
.
b)
Flächeninhalt des Dreiecks  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
A_{ABC}&=& \dfrac{1}{2}\cdot \overline{AB} \cdot \overline{AC} \cdot \sin \alpha \\[5pt]
&=& \dfrac{1}{2}\cdot 5,0\,\text{cm} \cdot 5,6\,\text{cm} \cdot \sin 63° \\[5pt]
&\approx& 12,47\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/64fa7e1992b9646fd316d80a9413d98ea14db40c89600d14c1693411ec9face4_light.svg) Länge der Strecke
Länge der Strecke  mit dem Satz des Pythagoras berechnen:
Flächeninhalt des Dreiecks
mit dem Satz des Pythagoras berechnen:
Flächeninhalt des Dreiecks  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
A_{AFH}&=& \dfrac{1}{2}\cdot \overline{AH} \cdot \overline{FH} \\[5pt]
&=& \dfrac{1}{2}\cdot 1,14\,\text{cm} \cdot 2,22\,\text{cm} \\[5pt]
&\approx& 1,27\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/27a05eb58a6dd8dcaa60c80a2d8c2318a41a1382d10ca0ac4811783e7ffdae61_light.svg) Da das Dreieck
Da das Dreieck  gleichschenklig ist, lässt sich der gesuchte Flächeninhalt wie folgt berechnen:
gleichschenklig ist, lässt sich der gesuchte Flächeninhalt wie folgt berechnen:
![\(\begin{array}[t]{rll}
A_{HFGC}&=& A_{ABC}-2\cdot A_{AFH} \\[5pt]
&=& 12,47\,\text{cm}^2-2\cdot 1,27\,\text{cm}^2 \\[5pt]
&=& 9,93\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/b0ad76e3d292fe1317b02c00b149f7237dc6c8a0138a93db10c779db5d21778f_light.svg) Der Flächeninhalt des Vierecks
Der Flächeninhalt des Vierecks  beträgt ungefähr
beträgt ungefähr 
c)
Die beiden Dreiecke  und
und  haben den Winkel
haben den Winkel  gemeinsam. Außerdem sind beide Dreiecke rechtwinklig: Das Dreieck
gemeinsam. Außerdem sind beide Dreiecke rechtwinklig: Das Dreieck  hat den rechten Winkel
hat den rechten Winkel  , das Dreieck
, das Dreieck  hat den rechten Winkel
hat den rechten Winkel  Damit müssen die jeweils übrigen Winkel
Damit müssen die jeweils übrigen Winkel  und
und  ebenfalls gleich groß sein.
ebenfalls gleich groß sein.
Lösung 3
a)
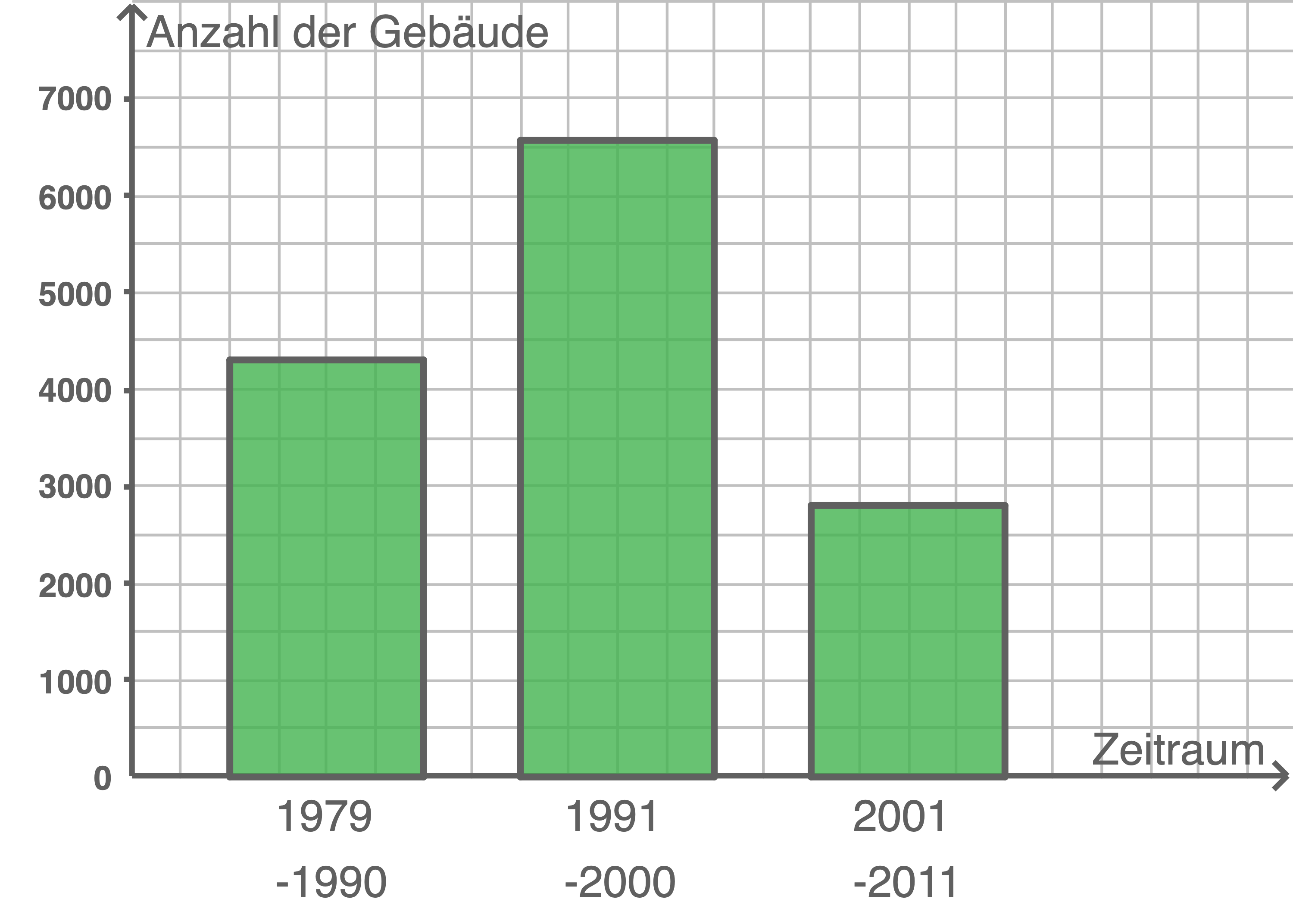
b)
Formel angeben
Es ist der Anteil der Gebäude für den Zeitraum bis 1978 gefragt. Die Anzahl der Gebäude, die bis  gebaut worden sind, steht in Zelle
gebaut worden sind, steht in Zelle  die Gesamtanzahl der Gebäude in Zelle
die Gesamtanzahl der Gebäude in Zelle  Die Formel mit Zellbezügen für die Zelle
Die Formel mit Zellbezügen für die Zelle  lautet daher
lautet daher  Wert berechnen
Der Anteil für den Zeitraum bis
Wert berechnen
Der Anteil für den Zeitraum bis  berechnet sich wie folgt:
berechnet sich wie folgt:
![\(\begin{array}[t]{rll}
C\,4&=& \dfrac{B\,4}{B\,8} \cdot 100\,\% \\[5pt]
&=& \dfrac{43\,321}{56\,997} \cdot 100\,\% \\[5pt]
&\approx& 76,0 \, \%
\end{array}\)](https://www.schullv.de/resources/formulas/20f93847a87b4bb4880ff86fa907480161cf0363d105c72c60f530957f3cb194_light.svg) Der Anteil an der Gesamtzahl der Gebäude für den Zeitraum bis
Der Anteil an der Gesamtzahl der Gebäude für den Zeitraum bis  beträgt
beträgt  .
.
c)
Anteil an Gebäuden für den Zeitraum 1991 bis 2000:
 Anteil an Gebäuden für den Zeitraum 1979 bis 1990 um
Anteil an Gebäuden für den Zeitraum 1979 bis 1990 um  erhöht:
erhöht:
 Die beiden Anteile sind ungefähr gleich groß. Der Anteil der Gebäude an der Gesamtzahl im Zeitraum 1991 bis 2000 erhöht sich gegenüber dem Zeitraum 1979 bis 1990 also um etwa
Die beiden Anteile sind ungefähr gleich groß. Der Anteil der Gebäude an der Gesamtzahl im Zeitraum 1991 bis 2000 erhöht sich gegenüber dem Zeitraum 1979 bis 1990 also um etwa 