SchulLV Logo
Lerninhalte in Mathe
Inhaltsverzeichnis

Pflichtteil 2

Pflichtaufgabe 1

a)

Eine Vollmilchschokolade mit einer Masse von \(250 \: \text{g}\) hat einen Kakao-Anteil von \(36 \, \%.\)

Berechne die Masse an Kakao in der Vollmilchschokolade.

(2 BE)
b)

Löse das lineare Gleichungssystem.

\(\begin{array}{lrll} \text{I}\quad&2x+y&=& 2\\ \text{II}\quad&y-5&=& x \end{array}\)

(3 BE)
c)

Gegeben ist die Datenreihe \(20 ; 7 ; 12 ; 9 ; 13 ; 8 ; 10 ; 4 ; 7.\)

\((1)\)

Berechne das arithmetische Mittel.

\((2)\)

Gib die Spannweite der Daten an.

(2 BE)
d)

Untersuche, ob der Punkt \(P(1 \mid -2)\) auf dem Graphen der quadratischen Funktion \(f\) mit \(y=f(x)=x^2 +2x- 5\) liegt.

(2 BE)
e)

Ein Lichtjahr ist die Strecke, die das Licht in einem Jahr zurücklegt.
Der Stern Proxima Centauri ist von der Erde \(4,24\) Lichtjahre entfernt.

Geben Sie die Entfernung von Proxima Centauri zur Erde in Kilometern an.
Hinweis: \(1\) Lichtjahr \(= 9,46 \cdot10^{12} \: \text{km}\)

(1 BE)
f)

Betrachtet wird die Aussage:
Die dritte Potenz einer ganzen Zahl \(z\) ist stets größer als das Quadrat von \(z.\)

Gib eine Bedingung für \(z\) an, so dass die Aussage wahr ist.

(1 BE)

Pflichtaufgabe 2

Gegeben ist ein gerader Kreiszylinder mit der Höhe \(h=12,0 \: \text{cm}.\)
Der Radius der Grundfläche beträgt \(r=5,0 \: \text{cm}.\)

a)

Berechne das Volumen des Kreiszylinders.

(2 BE)
b)

Zeichne ein Netz des Kreiszylinders im Maßstab \(1:5.\)

(3 BE)
c)

Beurteilen Sie folgende Aussage.
Für alle Kreiszylinder mit gleicher Höhe gilt:
Wird der Radius verdoppelt, vervierfacht sich das Volumen.

(2 BE)

Pflichtaufgabe 3

Im Koordinatensystem ist der Graph der Funktion \(g\) dargestellt.
Der Graph schneidet die Koordinatenachsen in den Punkten \(A\) und \(B.\)

Eine Einheit im Koordinatensystem entspricht \(1 \: \text{cm}.\)

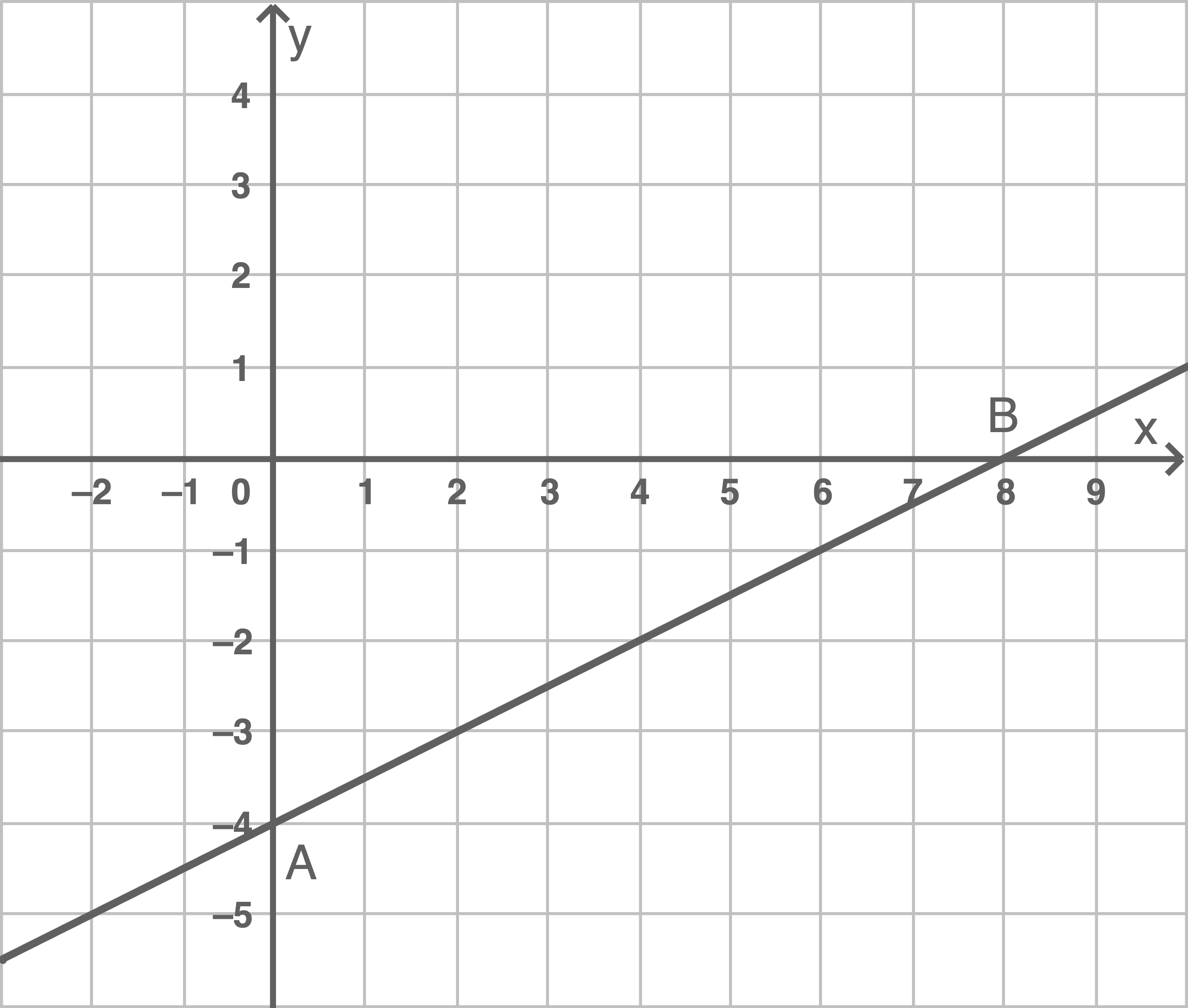
Abbildung

a)

Gib die Nullstelle der Funktion \(g\) an.

(1 BE)
b)

Gib eine Gleichung der Funktion \(g\) an.

(1 BE)
c)

Berechne die Länge der Strecke \(\overline{AB}.\)

(2 BE)
d)

Gegeben ist der Punkt \(C(0 \mid 4).\) Der Koordinatenursprung wird mit \(O\) bezeichnet.

Begründe, dass das Dreieck \(ABO\) kongruent zum Dreieck \(BCO\) ist.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?