Wahlpflichtteil

Wahlpflichtaufgabe 1

Die Tabelle zeigt den Wert der Innenwinkelsumme für ausgewählte $n$ -Ecke $(n \geq 3).$

	$\color{#fff}{A}$	$\color{#fff}{B}$
$\color{#fff}{1}$	$n$ -Eck	Innenwinkelsumme in Grad
$\color{#fff}{2}$	$n$ -Eck	Innenwinkelsumme in Grad
$\color{#fff}{3}$	$3$	$180$
$\color{#fff}{4}$	$4$	$360$
$\color{#fff}{5}$	$5$	$540$
$\color{#fff}{6}$	$6$
$\color{#fff}{7}$	$7$
$\color{#fff}{8}$	$8$
$\color{#fff}{9}$	$9$
$\color{#fff}{10}$	$10$

Tabelle

Gib den Wert der Innenwinkelsumme in der Zelle $B8$ an.

(1 BE)

Die Innenwinkelsumme kann mit der Gleichung $(n-2)\cdot180^\circ$ berechnet werden.
Gib eine Formel zur Berechnung für die Zelle $B8$ an.

Hinweis: In der Formel sind Zellbezüge zu verwenden.

(1 BE)

Jedem regelmäßigen $n$ -Eck lässt sich ein Kreis umschreiben. Verbindet man den Mittelpunkt dieses Kreises mit jedem Eckpunkt, so wird das $n$ -Eck in $n$ gleichschenklige, kongruente Dreiecke zerlegt.

Die Abbildung zeigt ein regelmäßiges Achteck. Die Eckpunkte des Achtecks liegen auf einem Kreis mit dem Radius $r.$

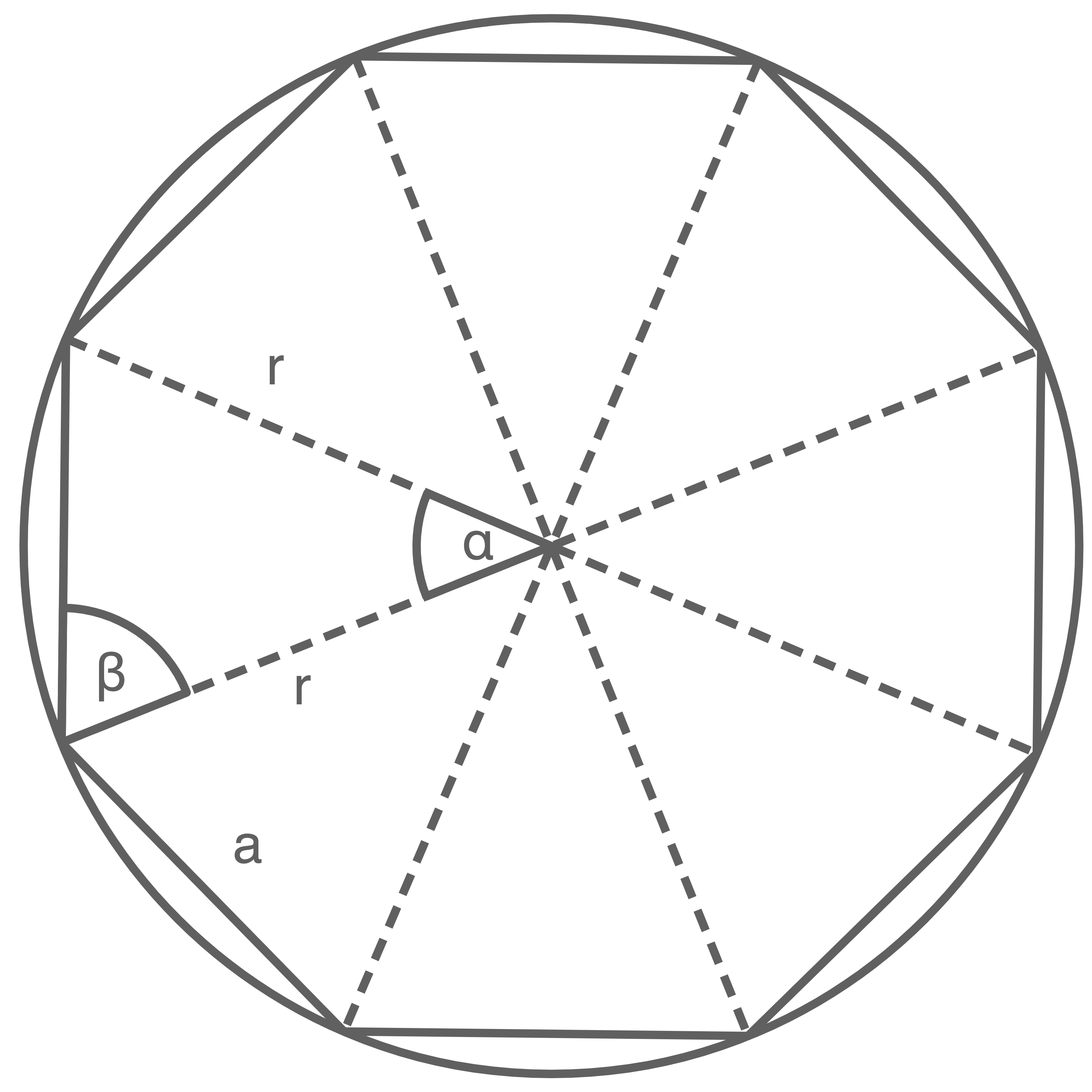
Abbildung

Abbildung
(nicht maßstäblich)

Begründe, dass die Größe des Winkels $\beta$ mit der folgenden Formel berechnet werden kann.
$\beta=90^\circ-\dfrac{\alpha}{2}$

(2 BE)

Weise rechnerisch nach, dass der Flächeninhalt des Achtecks mit $a = 3,0 \:\text{cm}$ ca. $90 \,\text{%}$ des Flächeninhalts des Kreises einnimmt.

(4 BE)

Wahlpflichtaufgabe 2

Das Containerschiff „Ever Given“ war im März 2021 im Suezkanal auf Grund gelaufen, hatte sich unter einem Winkel von ca. $52^\circ$ schräg gestellt und so den Kanal blockiert (siehe Abbildung 1).
Während des gesamten Zeitraumes der Blockade mussten viele Schiffe im oder vor dem Suezkanal warten.

Der Suezkanal ist ungefähr $313 \: \text {m}$ breit.
Weise rechnerisch nach, dass das Containerschiff „Ever Given“ etwa $400 \: \text {m}$ lang ist.

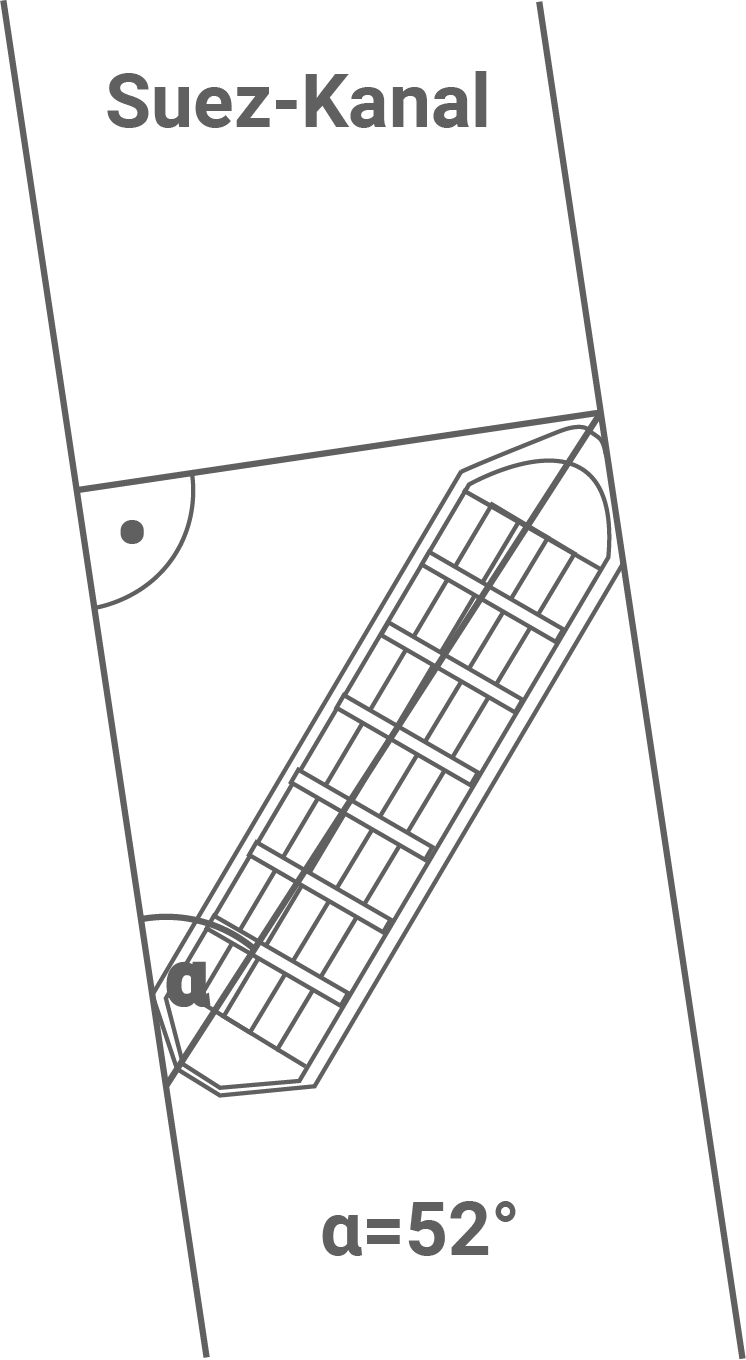
Abbildung

Abbildung 1
(nicht maßstäblich)

(2 BE)

Der Suezkanal verkürzt den Seeweg von Europa nach Indien um etwa $7000 \: \text {km}.$

Das Containerschiff „Ever Given“ kann $20124$ Container laden. Es benötigt ca. $3$ Liter Treibstoff pro geladenem Container auf einer Strecke von $100 \: \text{km}.$ Ein Liter Treibstoff kostet $0,26$ Euro.

Berechne die zusätzlichen Treibstoffkosten, die entstehen würden, wenn das Schiff von Europa nach Indien nicht durch den Suezkanal fahren würde.

(2 BE)

Die Querschnittsfläche des Kanals hat die Form eines Trapezes und beträgt ca. $5200 \: \text{m}^2.$ Die Abbildung 2 zeigt den Querschnitt des Suezkanals inklusive des Schiffs „Ever Given“. Alle Angaben sind in Metern gegeben. Der Tiefgang $t$ eines Schiffs ist die Entfernung von der Wasseroberfläche bis zum tiefsten Punkt des Schiffs (siehe Abbildung 2).

Ermittle den Tiefgang $t$ der „Ever Given“.

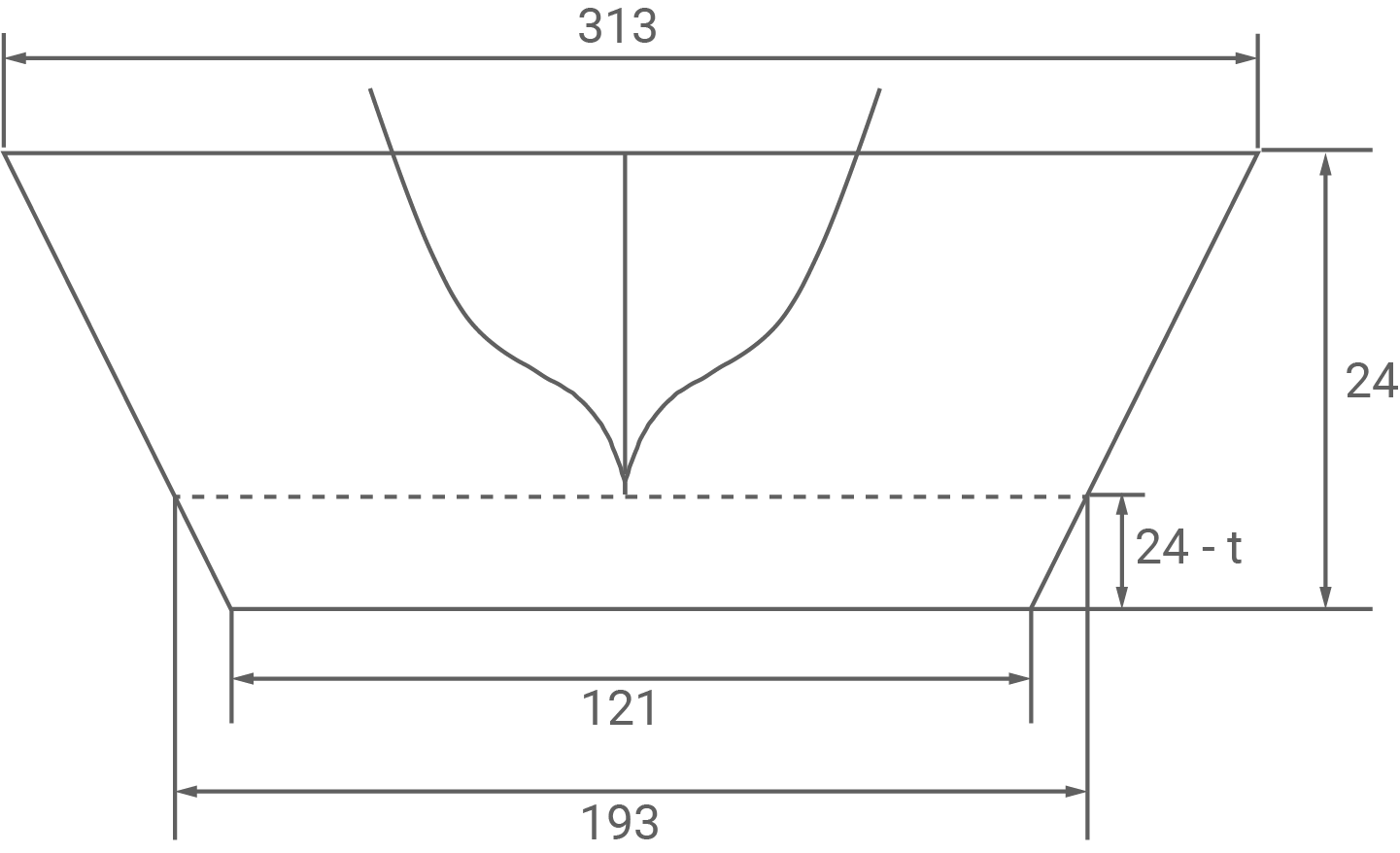
Abbildung 2
(nicht maßstäblich)

(4 BE)

Wahlpflichtaufgabe 3

Die Dachkante des abgebildeten baufälligen Gebäudes (siehe Abbildung 1) kann vereinfacht durch den Graphen einer Funktion beschrieben werden.

Abbildung

Abbildung 1

Gib einen möglichen Funktionstyp an, mit dem die Dachkante geeignet beschrieben werden kann.

(1 BE)

Die Dachkante kann modellhaft durch den Graphen der Funktion $g$ mit $y=g(x)=\frac{1}{4}x^2-1$ beschrieben werden (siehe Abbildung 2).

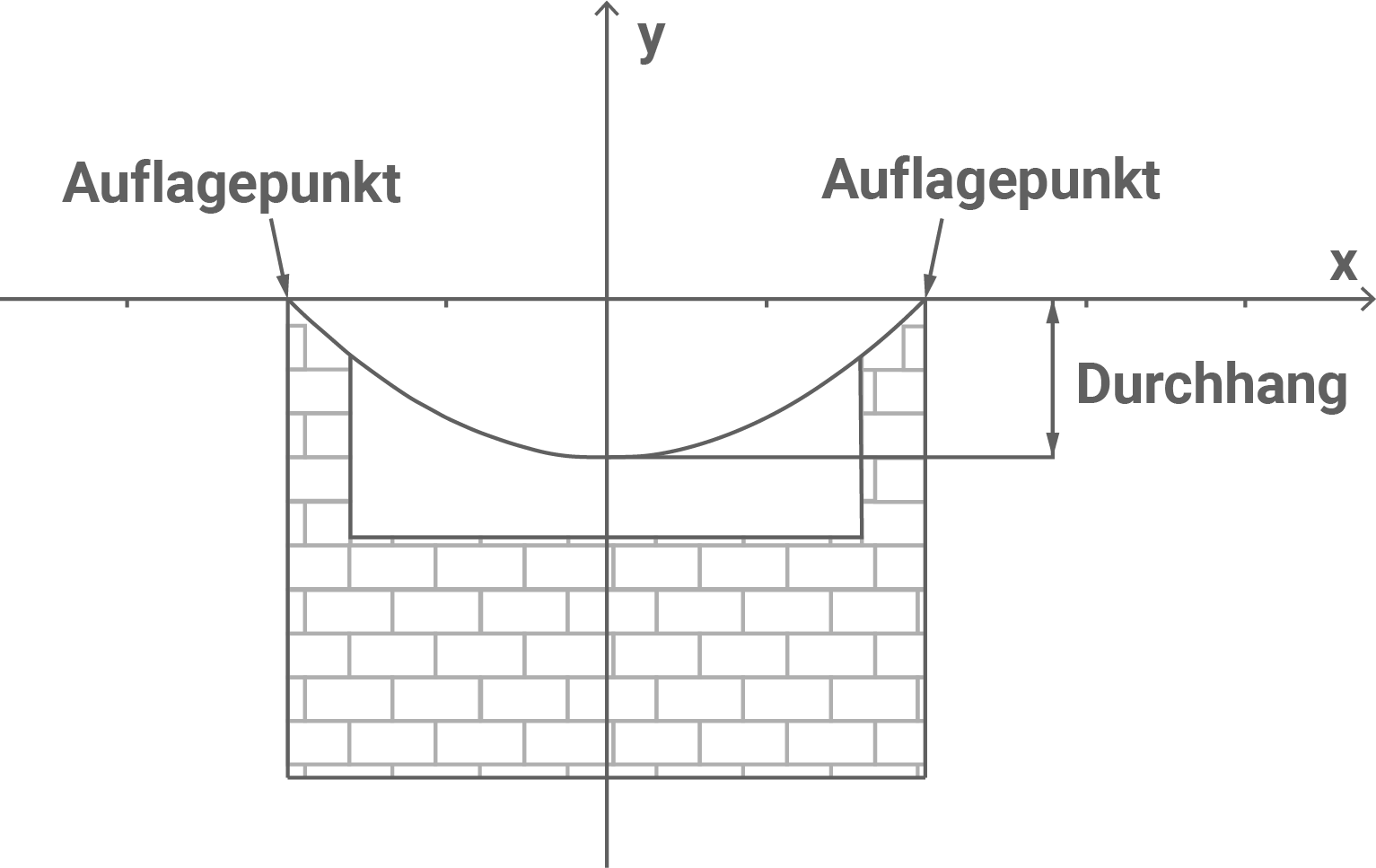
Abbildung

Abbildung 2
(nicht maßstäblich)

Zeige rechnerisch, dass der Abstand der Auflagepunkte $4 \: \text{m}$ beträgt.

Hinweis: Eine Längeneinheit im Koordinatensystem entspricht $1 \: \text{m}.$

(3 BE)

Beurteile die Aussage:
Die Dachkante hat eine Länge von $4 \: \text{m}.$

(2 BE)

Eine andere Dachkante hat den doppelten Durchhang. Die Auflagepunkte sind gleich.

Begründe rechnerisch, dass der Graph der Funktion $h$ mit $y=h(x)=\dfrac{1}{2}x^2-2$ diese Dachrinne mit den gegebenen Eigenschaften beschreibt.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wahlpflichtaufgabe 1

$1080$

$B8 = (A8-2)\cdot180^\circ$

Das Dreieck ist ein gleichschenkliges Dreieck. Somit kommt der Winkel $\beta$ zweimal vor. Da ein Dreieck immer eine Innenwinkelsumme von $180^\circ$ besitzt, folgt:

$\begin{array}[t]{rlll} \alpha+2\cdot \beta &=& 180^\circ &\mid\; -\alpha \\[5pt] 2\cdot \beta &=& 180^\circ-\alpha &\mid\; :2 \\[5pt] \beta &=& 90^\circ-\dfrac{\alpha}{2} \end{array}$

Radius eines Dreiecks berechnen

$\begin{array}[t]{rlll} r &=& \dfrac{a}{2\cdot \sin\left(\dfrac{180^\circ}{n}\right)} \\[5pt] r &=& \dfrac{3 \; \text{cm}}{2\cdot \sin\left(\dfrac{180^\circ}{8}\right)} \\[5pt] r &\approx& 3,9 \; \left[\text{cm}\right] \end{array}$

Flächeninhalt eines Dreiecks berechnen

$A =\dfrac{1}{2}\cdot r^2 \cdot \sin(\alpha)$

Flächeninhalt des Achtecks berechnen

Für den Winkel $\alpha$ gilt:

$\dfrac{360^\circ}{8} = 45^\circ$

$\begin{array}[t]{rlll} A_1 &=& 8\cdot \dfrac{1}{2}\cdot r^2 \cdot \sin(\alpha) \\[5pt] A_1 &=& 8\cdot \dfrac{1}{2}\cdot 3,9^2 \cdot \sin(45^\circ) \\[5pt] A_1 &=& 43,0 \; \left[\text{cm}^2\right] \end{array}$

Flächeninhalt des Kreises berechnen

$\begin{array}[t]{rlll} A_2 &=& \pi \cdot r^2 \\[5pt] A_2 &=& \pi \cdot 3,9^2 \\[5pt] A_2 &=& 47,8 \; \left[\text{cm}^2\right] \end{array}$

Vergleich als Prozentwert angeben

$\dfrac{43,0 \: \text{cm}^2}{47,8 \: \text{cm}^2} \cdot 100 \approx 90 \: \left[\text{%}\right]$

Wahlpflichtaufgabe 2

Für die Länge $a$ der „Ever Given“ folgt:

$\begin{array}[t]{rlll} \sin(52^\circ) &=& \dfrac{313 \; \text{m}}{a} &\mid\; \cdot \ a \\[5pt] a \cdot \sin(52^\circ) &=& 313 \; \text{m} &\mid\; : \sin(52^\circ) \\[5pt] a &=& \dfrac{313 \; \text{m}}{\sin(52^\circ)} \\[5pt] 397 \; \text{m} &\approx& \dfrac{313 \; \text{m}}{\sin(52^\circ)} \end{array}$

Das Containerschiff „Ever Given“ ist ca. $400 \;\text{m}$ lang.

$\dfrac{20124 \cdot 3 \cdot 7000 \cdot 0,26}{100} \approx 1.098.770 \, \left[\text{€}\right]$

Die zusätzlich entstehenden Treibstoffkosten betragen $1.098.770 \, \text{€}.$

Da die zwei Dreiecke (s. Hilfsskizze) kongruent sind, folgt durch Gleichsetzen:

$\begin{array}[t]{rlll} \dfrac{a_1}{a_2} &=& \dfrac{h_1}{h_2} \\[5pt] \dfrac{96}{36} &=& \dfrac{24}{24-t} &\mid\; \cdot 36 \\[5pt] 96 &=& \dfrac{24}{24-t} \cdot 36 &\mid\; \cdot 24-t \\[5pt] 96 \cdot (24-t) &=& 24 \cdot 36 \\[5pt] 2304 -96\cdot t &=& 864 &\mid\; + 96 \cdot t \\[5pt] 2304 &=& 864 + 96 \cdot t &\mid\; -864 \\[5pt] 1440 &=& 96 \cdot t &\mid\; :96 \\[5pt] 15 &=& t \end{array}$

Der Tiefgang $t$ des Schiffes beträgt $15 \; \text{m}.$

Hilfskizze
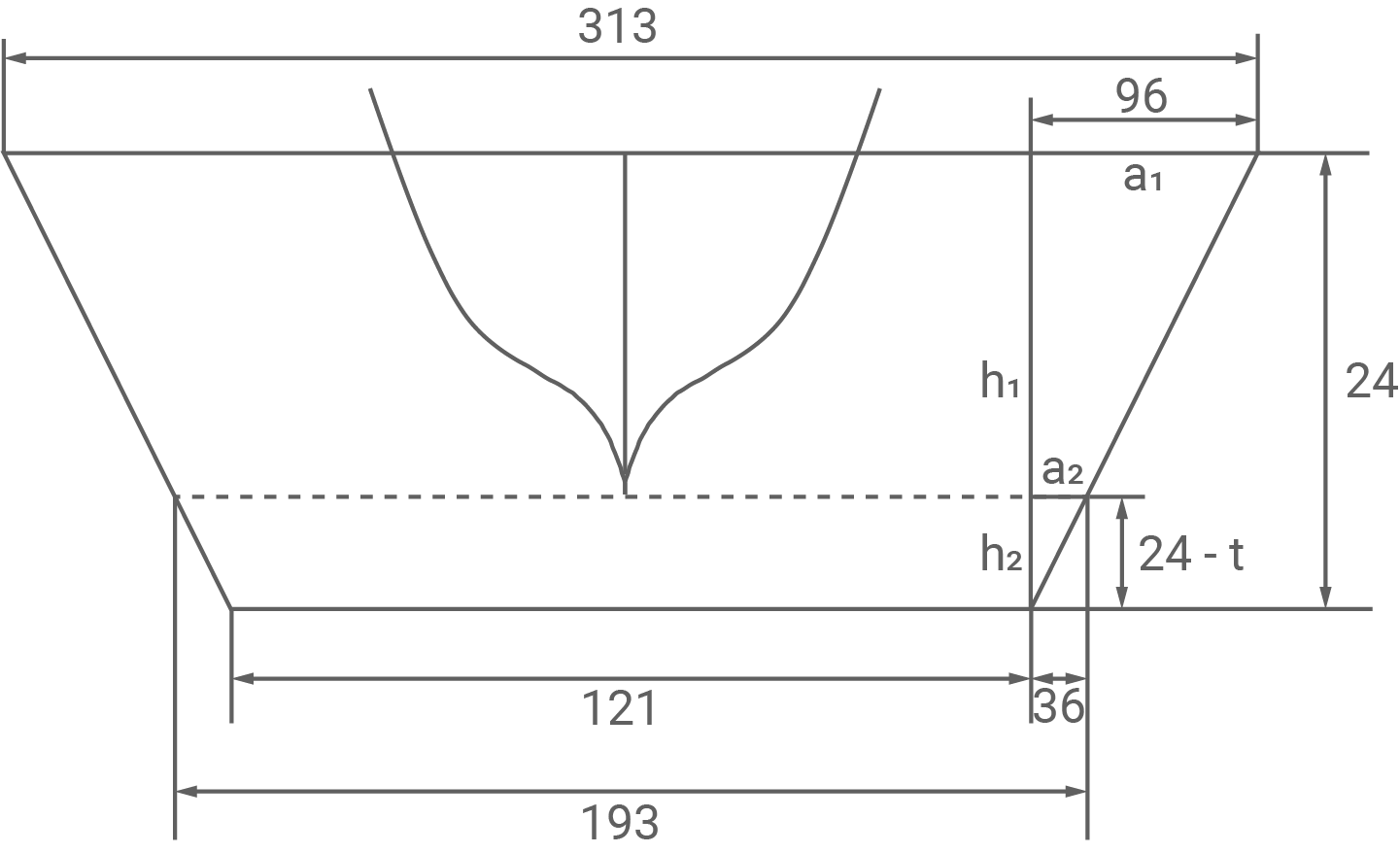
(nicht maßstäblich)

Wahlpflichtaufgabe 3

Ein möglicher Funktionstyp ist die quadratische Funktion.

Nullstellen berechnen

$\begin{array}[t]{rlll} g(x) &=& 0 \\[5pt] \dfrac{1}{4}x^2 - 1 &=& 0 &\mid\; + 1 \\[5pt] \dfrac {1}{4} x^2 &=& 1 &\mid\; \cdot 4 \\[5pt] x^2 &=& 4 &\mid\; \sqrt{\;} \\[5pt] x_{1} &=& 2 \\[5pt] x_{2} &=& -2 \end{array}$

Abstand der Auflagepunkte angeben

$\vert-2 \vert + 2=4$

Der Abstand der Auflagepunkte beträgt $4 \; \text{m}.$

Die Aussage ist falsch. Der Abstand zwischen den Auflagepunkten beträgt $4 \; \text{m}.$ Da dieser Abstand kürzer ist als die Dachrinne, kann die Dachrinne nicht $4 \; \text{m}$ lang sein.

Bedingung 1: Doppelter Durchhang

Die Funktion $g$ schneidet die $y$ -Achse bei $-1.$ Somit muss eine Funktion mit doppeltem Durchhang die $y$ -Achse bei $y=-2$ schneiden.

$h(0) = -2$

Bedingung 2: Gleiche Auflagepunkte

$h(-2) = 2-2 = 0$

$h(2) = 2-2 = 0$

Da die Funktion $h(x)$ die beiden notwendigen Bedingungen erfüllt, ist es die richtige Funktion.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?