Pflichtteil 2
Pflichtaufgabe 1
a)
In einer Umfrage wurden 340 Jugendliche zu ihrem Einkaufsverhalten befragt. Davon gaben 24 Jugendliche an, beim Einkaufen auf Nachhaltigkeit zu achten.
Berechne den prozentualen Anteil der Jugendlichen, die beim Einkaufen auf Nachhaltigkeit achten.
Berechne den prozentualen Anteil der Jugendlichen, die beim Einkaufen auf Nachhaltigkeit achten.
(2 BE)
b)
Zeichne ein Schrägbild einer Pyramide mit quadratischer Grundfläche. Die Höhe der Pyramide beträgt  und eine Grundkante hat eine Länge von
und eine Grundkante hat eine Länge von 
(2 BE)
c)
Bei einem Turnier geht aus mehreren Spielern in mehreren Runden ein Gewinner hervor.
In der ersten Runde treten pro Spiel je zwei zufällig ausgewählte Spieler gegeneinander an. Der Gewinner des Spiels kommt in die nächste Runde. Ein Unentschieden ist nicht möglich. Es werden so viele Runden gespielt, bis ein Gewinner des Turniers feststeht. Die Abbildung zeigt beispielhaft ein solches Turnier mit acht Spielern, in dem Spieler drei Runden spielen musste, um das Turnier zu gewinnen.
drei Runden spielen musste, um das Turnier zu gewinnen.
In der ersten Runde treten pro Spiel je zwei zufällig ausgewählte Spieler gegeneinander an. Der Gewinner des Spiels kommt in die nächste Runde. Ein Unentschieden ist nicht möglich. Es werden so viele Runden gespielt, bis ein Gewinner des Turniers feststeht. Die Abbildung zeigt beispielhaft ein solches Turnier mit acht Spielern, in dem Spieler
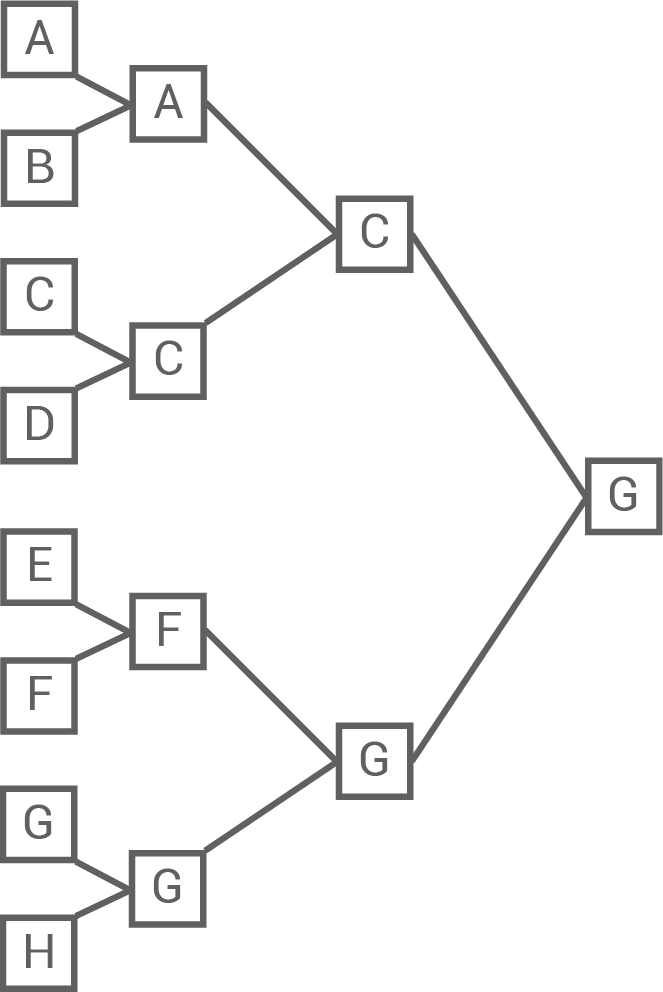
Abbildung
(1)
Gib an, wie viele Runden Spieler  gewonnen hat.
gewonnen hat.
(2)
Ermittle die Anzahl der Runden, die gespielt werden muss, um aus 32 Spielern einen Gewinner zu erhalten.
(3)
Die Funktion  mit
mit  beschreibt den Sachzusammenhang.
beschreibt den Sachzusammenhang.
Gib die Bedeutung von und
und  im Sachzusammenhang an.
im Sachzusammenhang an.
Gib die Bedeutung von
(5 BE)
d)
Der Eiffelturm in Paris ist etwa 330 Meter hoch. Ein Modell des Eiffelturms wird im Maßstab 1:300 angefertigt.
Berechne die Höhe des Modells.
Berechne die Höhe des Modells.
(2 BE)
e)
Gegeben ist die quadratische Funktion  durch
durch 
(1)
Gib die Koordinaten des Scheitelpunkts des Graphen der Funktion an.
(2)
Zeichne den Graphen der Funktion mindestens im Intervall  in ein Koordinatensystem.
in ein Koordinatensystem.
(2 BE)
Pflichtaufgabe 2
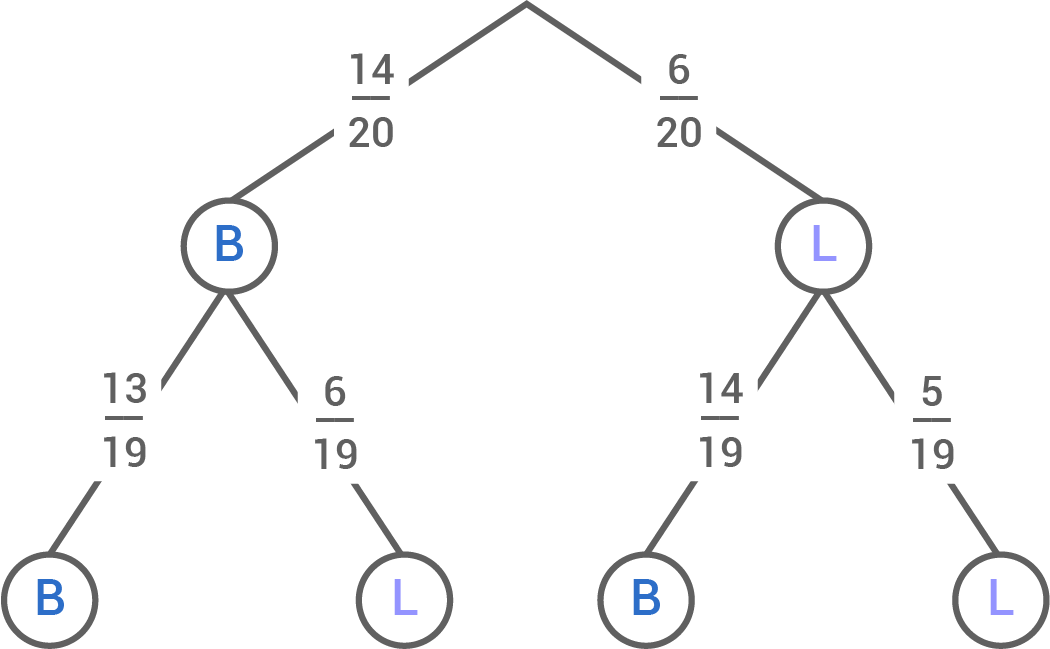
In einer Schachtel befinden sich 20 Schokolinsen. Davon sind 14 Schokolinsen blau. Die übrigen Schokolinsen sind lila.Es wird zweimal nacheinander eine Schokolinse zufällig entnommen und nicht zurückgelegt.
a)
Zeichne für diesen zweistufigen Zufallsversuch ein Baumdiagramm und trage die Wahrscheinlichkeiten an allen Pfaden an.
(3 BE)
b)
Zeige, dass die Wahrscheinlichkeit, dass beide Schokolinsen blau sind, ca.  beträgt.
beträgt.
(1 BE)
c)
Berechne die Wahrscheinlichkeit, eine blaue und eine lila Schokolinse zu entnehmen.
(2 BE)
Pflichtaufgabe 3
Die Abbildung zeigt das DreieckEine Längeneinheit im Koordinatensystem entspricht
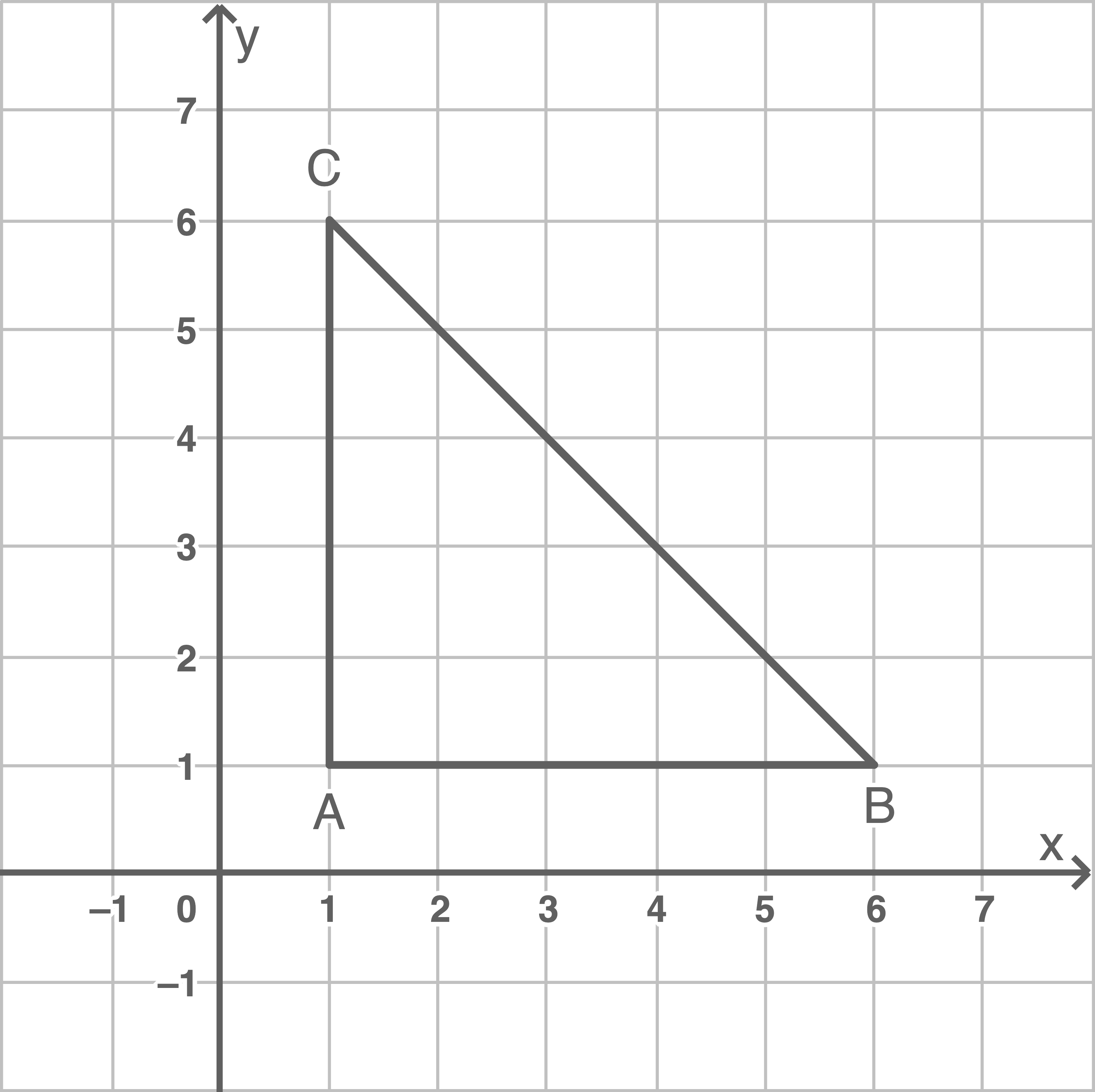
Abbildung
a)
Gib die Art des Dreiecks nach Seiten an.
(1 BE)
b)
Bestimme den Flächeninhalt des Dreiecks 
(2 BE)
c)
Der Punkt  ist der Mittelpunkt eines Kreises. Die Punkte
ist der Mittelpunkt eines Kreises. Die Punkte  und
und  liegen auf diesem Kreis.
liegen auf diesem Kreis.
Begründe rechnerisch, dass der Punkt ebenfalls auf dem Kreis um
ebenfalls auf dem Kreis um  liegt.
liegt.
Begründe rechnerisch, dass der Punkt
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
b)
c)
(1)
Spieler  hat 2 Runden gewonnen.
hat 2 Runden gewonnen.
(2)
| Anzahl Runden | Anzahl Spieler |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
(3)
d)
e)
(1)
Aus der Funktionsgleichung in Scheitelpunktform lässt sich der Scheitelpunkt direkt ablesen:

(2)
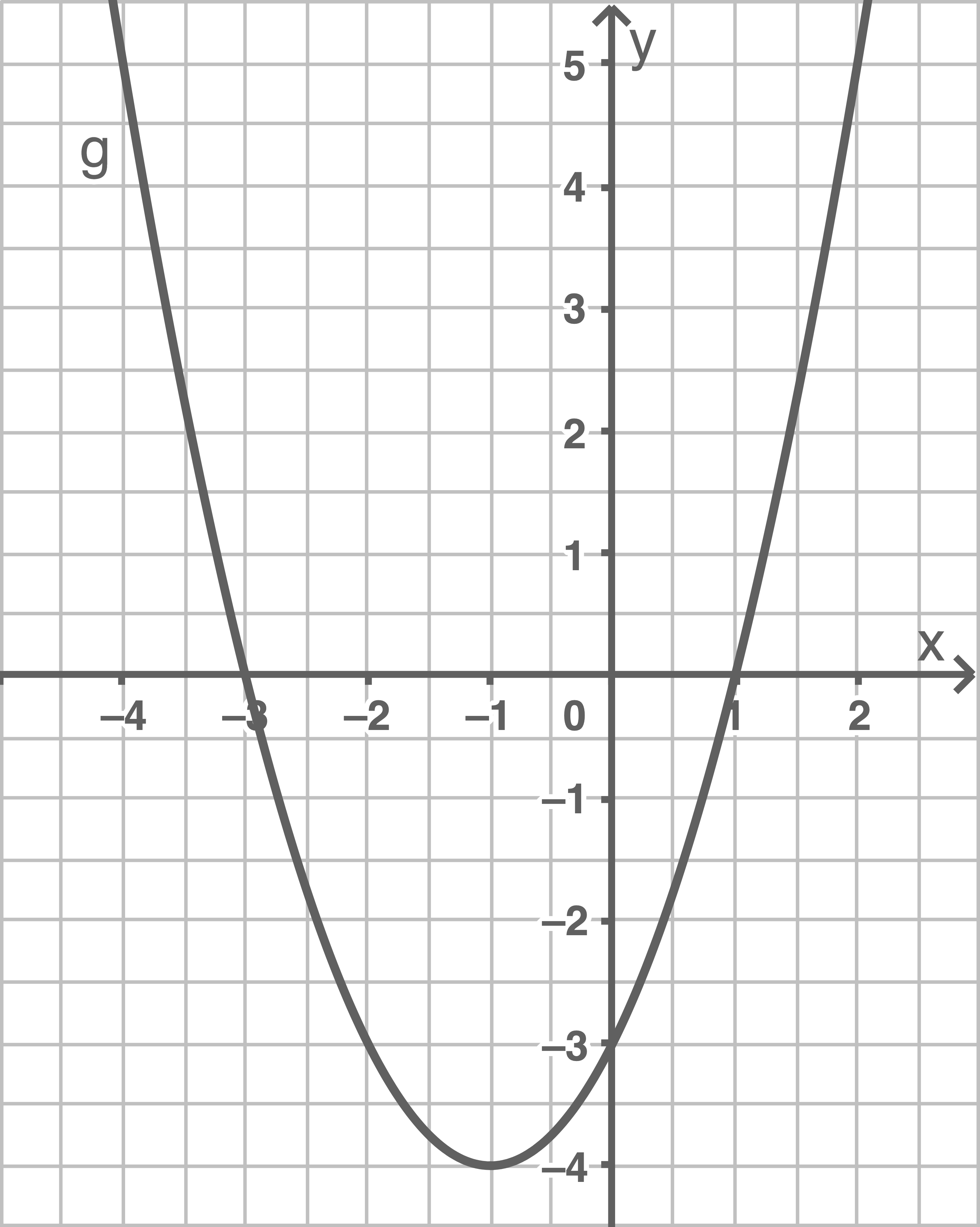
Lösung 2
a)
b)
c)
Lösung 3
a)
Es handelt sich um ein gleichschenkliges Dreieck.
b)
c)