HT 1
Zerfall atmosphärischer Myonen
Albert Einstein begründete im Jahre 1905 die Spezielle Relativitätstheorie (SRT), eine Erweiterung der Newtonschen Mechanik mit wichtigen Konsequenzen für Kinematik und Dynamik wie auch eine Revolution des wissenschaftlichen Weltbilds insgesamt. Die Voraussagen der SRT lassen sich mit vielen Experimenten bestätigen. Einen besonders eindrucksvollen Beleg liefert die Analyse des Zerfalls atmosphärischer Myonen. Teilaufgabe 1: Zeitdilatation und Längenkontraktion Um den Zerfall atmosphärischer Myonen untersuchen zu können, ist ein Verständnis von Zeitdilatation und Längenkontraktion notwendig.
a)
Eine Rakete besitzt an ihrer Spitze eine Lampe, die in regelmäßigen Abständen kurz aufleuchtet. Im Raketenbezugssystem wird dabei zwischen zwei aufeinanderfolgenden Leuchtereignissen die Zeit  gemessen. Im Erdbezugssystem, in dem sich die Rakete geradlinig-gleichförmig mit hoher Geschwindigkeit
gemessen. Im Erdbezugssystem, in dem sich die Rakete geradlinig-gleichförmig mit hoher Geschwindigkeit  bewegt, wird stattdessen zwischen zwei aufeinanderfolgenden Leuchtereignissen die Zeit
bewegt, wird stattdessen zwischen zwei aufeinanderfolgenden Leuchtereignissen die Zeit  gemessen. Unter der Voraussetzung, dass es sich bei den Bezugssystemen um Inertialsysteme im Sinne der SRT handelt, gilt folgender Zusammenhang:
gemessen. Unter der Voraussetzung, dass es sich bei den Bezugssystemen um Inertialsysteme im Sinne der SRT handelt, gilt folgender Zusammenhang:
 Dabei ist der sogenannte Lorentzfaktor
Dabei ist der sogenannte Lorentzfaktor  definiert durch
definiert durch

 ist die Vakuumlichtgeschwindigkeit.
Es wird nun eine Rakete betrachtet, die sich mit einer Geschwindigkeit von
ist die Vakuumlichtgeschwindigkeit.
Es wird nun eine Rakete betrachtet, die sich mit einer Geschwindigkeit von  relativ zur Erde bewegt und deren Raketenlampe im Raketenbezugssystem zweimal pro Sekunde blinkt. Die Zeit zwischen zwei aufeinanderfolgenden Leuchtereignissen ist also in diesem Bezugssystem
relativ zur Erde bewegt und deren Raketenlampe im Raketenbezugssystem zweimal pro Sekunde blinkt. Die Zeit zwischen zwei aufeinanderfolgenden Leuchtereignissen ist also in diesem Bezugssystem 
- Berechne den Lorentzfaktor
und die im Erdbezugssystem gemessene Zeit
zwischen zwei aufeinanderfolgenden Leuchtereignissen.
- Entscheide begründet, ob die Blinkfrequenz der Raketenlampe im Raketenbezugssystem oder im Erdbezugssystem größer ist.
- Erkläre, wieso die Bestimmung von
und
nicht mit insgesamt nur einer einzigen Uhr während der gleichen Messung durchgeführt werden kann.
b)
Die Entfernung zwischen dem vorderen und hinteren Ende einer Rakete wird gemessen. Im Raketenbezugssystem wird eine Entfernung  , die sogenannte Ruhelänge, gemessen. Im Erdbezugssystem, in dem sich die Rakete geradlinig-gleichförmig mit hoher Geschwindigkeit
, die sogenannte Ruhelänge, gemessen. Im Erdbezugssystem, in dem sich die Rakete geradlinig-gleichförmig mit hoher Geschwindigkeit  bewegt, wird stattdessen zwischen dem vorderen und hinteren Ende eine Entfernung
bewegt, wird stattdessen zwischen dem vorderen und hinteren Ende eine Entfernung  gemessen. Unter der Voraussetzung, dass es sich bei den Bezugssystemen um Inertialsysteme im Sinne der SRT handelt, gilt ein Zusammenhang zwischen beiden Größen:
gemessen. Unter der Voraussetzung, dass es sich bei den Bezugssystemen um Inertialsysteme im Sinne der SRT handelt, gilt ein Zusammenhang zwischen beiden Größen:
 Dabei ist
Dabei ist  der bereits oben definierte Lorentzfaktor. Eine Rakete der Länge
der bereits oben definierte Lorentzfaktor. Eine Rakete der Länge  kann somit in einem Inertialsystem, in dem die Rakete eine ausreichend hohe Geschwindigkeit
kann somit in einem Inertialsystem, in dem die Rakete eine ausreichend hohe Geschwindigkeit  besitzt, die Länge
besitzt, die Länge  besitzen.
besitzen.
- Berechne die dafür notwendige Geschwindigkeit
(als Vielfaches der Lichtgeschwindigkeit c).
- Entscheide begründet, ob es ein Inertialsystem gibt, in dem die gemessene Länge der Rakete größer ist als im Raketenbezugssystem.
c)
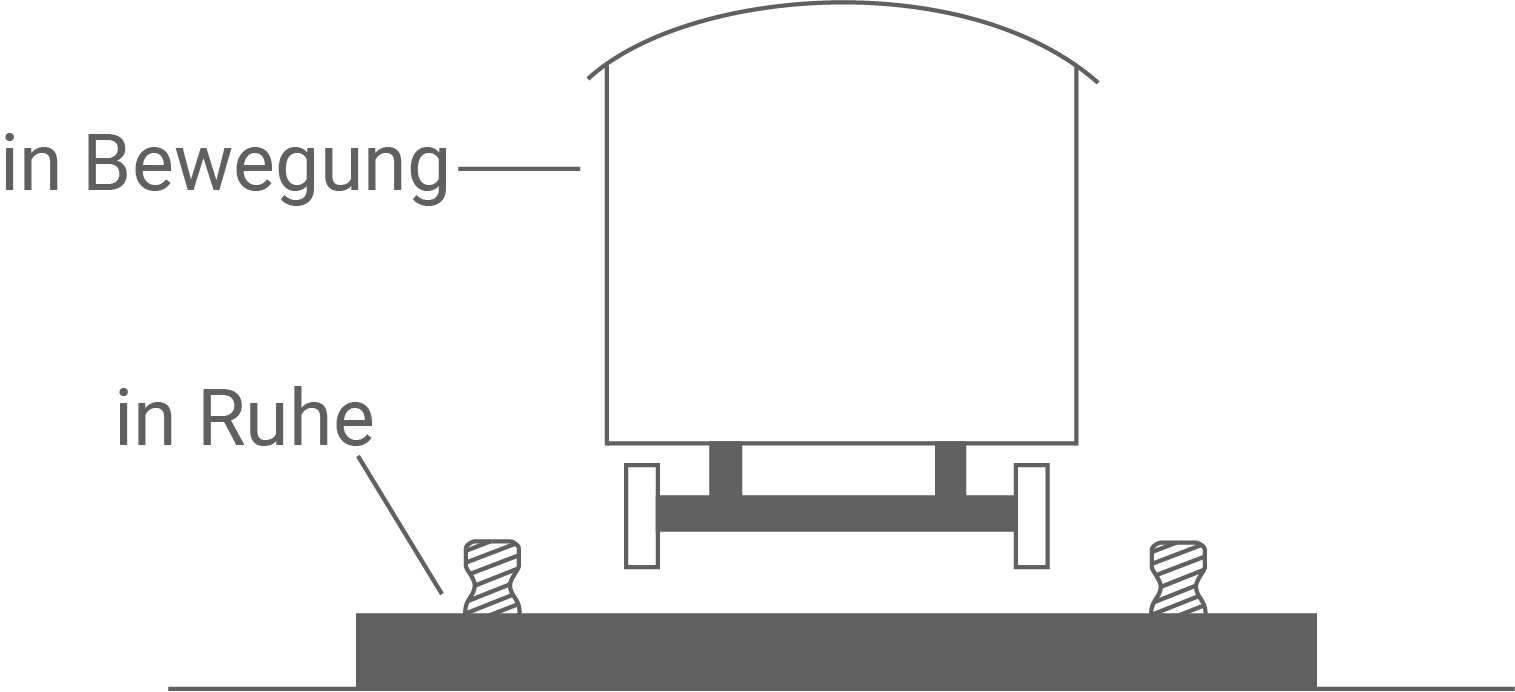
Ein Zug bewegt sich geradlinig gleichförmig entlang eines Gleises vorwärts. Dabei wird vorhergesagt, dass es bei einer relativistisch bedeutsamen Geschwindigkeit zum Entgleisen des Zuges kommen würde, da die Radachse des Zuges so stark kontrahiert wird, dass die Räder nicht mehr auf den Gleisen aufliegen (siehe Abbildung 1).
Erkläre, warum diese Vorhersage falsch ist. Hinweis: Dies ist ein Gedankenexperiment, bei dem die tatsächliche technische Realisierbarkeit (Zug mit relativistischer Geschwindigkeit) für die Diskussion belanglos ist.
Teilaufgabe 2: Relativistische Phänomene atmosphärischer Myonen
Die Teilchenart der sogenannten Myonen wurde in den Jahren 1936/1937 von C. D. Anderson und S. Neddermeyer sowie von J. C. Street und E. C. Stevenson entdeckt.
Erkläre, warum diese Vorhersage falsch ist. Hinweis: Dies ist ein Gedankenexperiment, bei dem die tatsächliche technische Realisierbarkeit (Zug mit relativistischer Geschwindigkeit) für die Diskussion belanglos ist.

Abbildung 1: Zug und Gleis im Querschnitt
(9 + 9 + 4 Punkte)
a)
Myonen unterscheiden sich von ihren „Verwandten“, den Elektronen, insbesondere durch ihre größere Masse. Zudem sind Myonen im Gegensatz zu Elektronen instabil, mit einer Halbwertszeit von  . Aufgrund ihrer Instabilität werden beispielsweise von einer anfänglichen Menge von 1000 Myonen nach kurzer Zeit nur noch wenige Myonen vorhanden sein. Berechne, wie lange es dauert, bis nur noch etwa 125 Myonen vorhanden sind, unter der Annahme, dass alle Myonen als ruhend betrachtet werden können.
. Aufgrund ihrer Instabilität werden beispielsweise von einer anfänglichen Menge von 1000 Myonen nach kurzer Zeit nur noch wenige Myonen vorhanden sein. Berechne, wie lange es dauert, bis nur noch etwa 125 Myonen vorhanden sind, unter der Annahme, dass alle Myonen als ruhend betrachtet werden können.
b)
Die Erdatmosphäre wird beständig von kosmischer Strahlung getroffen. In den höheren Schichten der Atmosphäre entstehen dabei zahlreiche Myonen, von denen viele Richtung Erdoberfläche fliegen. Zur Analyse dieses Flugs wird nachfolgend von einigen vereinfachenden Annahmen ausgegangen (siehe Abbildung 2):
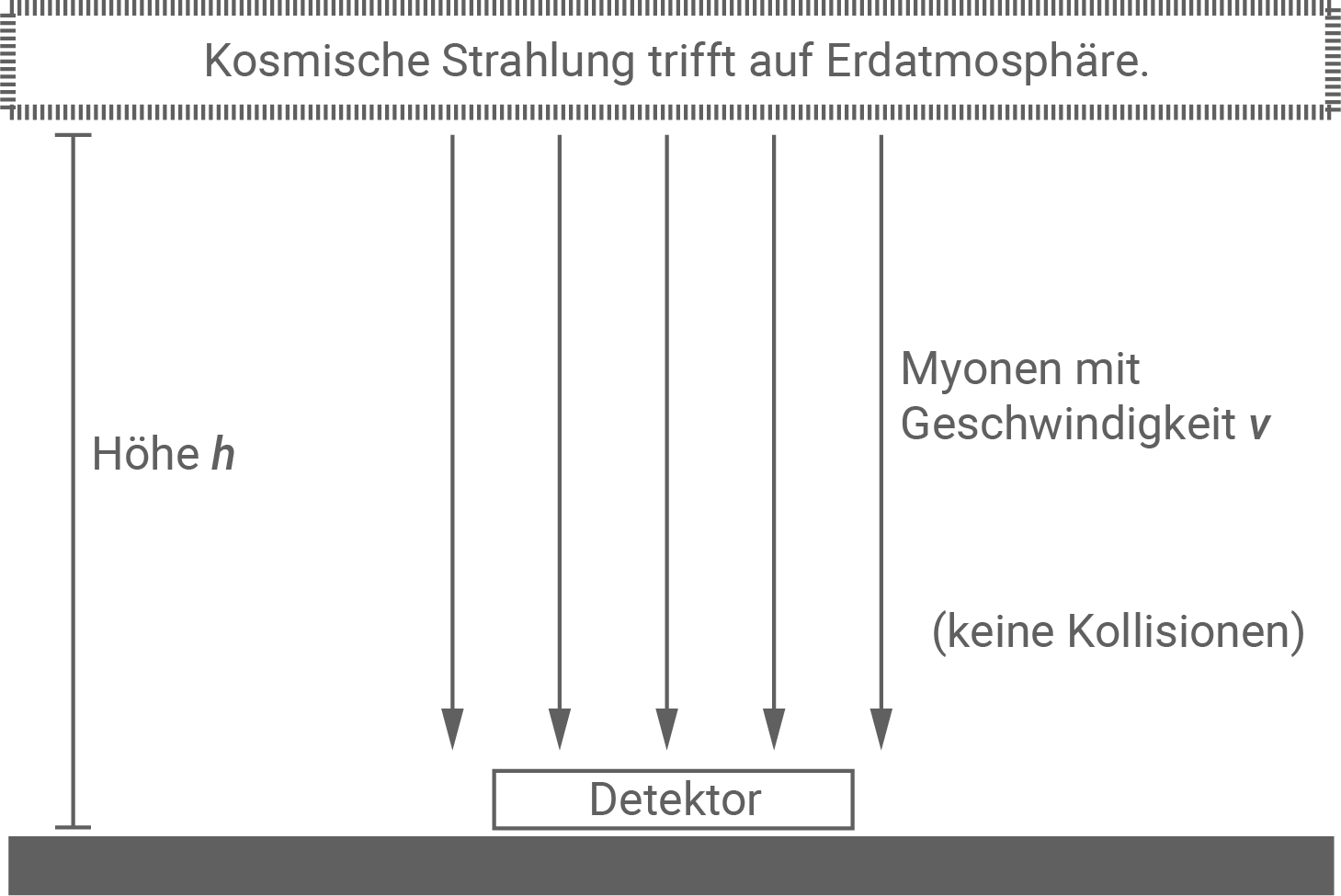 Bei ihrem Flug Richtung Erdoberfläche zerfallen so viele Myonen, dass mittels eines Detektors auf der Erdoberfläche (Höhe
Bei ihrem Flug Richtung Erdoberfläche zerfallen so viele Myonen, dass mittels eines Detektors auf der Erdoberfläche (Höhe  ) nur ein kleiner Prozentsatz derjenigen Teilchen registriert wird, der in den höheren Schichten der Atmosphäre erzeugt worden ist.
) nur ein kleiner Prozentsatz derjenigen Teilchen registriert wird, der in den höheren Schichten der Atmosphäre erzeugt worden ist.
- Alle Myonen entstehen in der gleichen Höhe
- Alle Myonen haben die gleiche Geschwindigkeit
- Alle Myonen bewegen sich senkrecht zur Erdoberfläche.
- Bei ihrem Flug kommt es zu keinen Kollisionen mit Teilchen der Atmosphäre.

Abbildung 2: Atmosphärische Myonen
- Zeige unter Nichtberücksichtigung relativistischer Effekte, dass von anfänglich jeweils
Myonen mittels eines Detektors auf der Erdoberfläche rechnerisch gesehen nur ein einziges Myon registriert wird.
- Erkläre diesen experimentellen Befund, einmal aus Sicht eines mitbewegten Bezugssystems (in dem das Myon ruht) und einmal aus Sicht des Erdbezugssystems.
- Bestimme, diesmal unter Berücksichtigung des entsprechenden relativistischen Effekts, wie viele von anfänglich jeweils
Myonen mittels eines Detektors auf der Erdoberfläche rechnerisch gesehen registriert werden.
c)
Als massebehaftete Teilchen bewegen sich die Myonen stets langsamer als Licht.
Teilaufgabe 3: Zeitdilatation in Spezieller und Allgemeiner Relativitätstheorie
Neben dem Zerfall atmosphärischer Myonen gibt es viele weitere Experimente, die zu ihrer Erklärung der speziell-relativistischen Zeitdilatation bedürfen, so etwa die Lebensdauer instabiler Teilchen in Teilchenbeschleunigern, das Hafele-Keating-Experiment und auch das nachfolgend beschriebene Experiment.
- Erkläre, wie viele Myonen registriert werden würden, wenn die Fluggeschwindigkeit der Teilchen näherungsweise Lichtgeschwindigkeit betragen würde.
- Begründe qualitativ und mit Bezug auf den oben beschriebenen Entstehungsprozess der Myonen, warum Annahme 3 eine sehr grobe Vereinfachung darstellt.
- Begründe diese Aussage qualitativ.
- Beurteile qualitativ und mit Bezug auf die Wechselwirkung während der Kollision, wie sich die berechnete Zahl der detektierten Myonen verändern würde, wenn die obige Vereinfachung 4 nicht vorgenommen werden würde.
(4 + 17 + 11 Punkte)
a)
Im Jahr 1975 wurden Atomuhren 15 Stunden lang in einem kreisenden Flugzeug transportiert, in einer Höhe von  bis
bis  [1] Der Stand dieser Uhren wurde mittels Laserimpulsen mit dem Stand gleichartiger Uhren auf dem Erdboden verglichen.
[1] Der Stand dieser Uhren wurde mittels Laserimpulsen mit dem Stand gleichartiger Uhren auf dem Erdboden verglichen.
Für einen fünfzehnstündigen Flug sagt die SRT voraus, dass die kreisende Uhr im Vergleich zur Erduhr „nachgeht“, nämlich 5,7 Nanosekunden. (Die zeitliche Differenz fällt vergleichsweise gering aus, da die Geschwindigkeit des Flugzeugs in Relation zur Lichtgeschwindigkeit sehr klein ist.) Tatsächlich wurde jedoch gemessen, dass die kreisende Uhr „vorgeht“, nämlich 47,2 Nanosekunden. Die SRT kann also diesen Unterschied zwischen Theorie und Experiment von 52,9 Nanosekunden nicht erklären. Die Allgemeine Relativitätstheorie (ART) dagegen kann diesen Unterschied auf die Höhendifferenz zwischen kreisender Uhr und Erduhr zurückführen. Begründe qualitativ, warum die ART den Gegensatz zwischen SRT und Experiment auf die Höhendifferenz zwischen kreisender Uhr und Erduhr zurückzuführen vermag.
Für einen fünfzehnstündigen Flug sagt die SRT voraus, dass die kreisende Uhr im Vergleich zur Erduhr „nachgeht“, nämlich 5,7 Nanosekunden. (Die zeitliche Differenz fällt vergleichsweise gering aus, da die Geschwindigkeit des Flugzeugs in Relation zur Lichtgeschwindigkeit sehr klein ist.) Tatsächlich wurde jedoch gemessen, dass die kreisende Uhr „vorgeht“, nämlich 47,2 Nanosekunden. Die SRT kann also diesen Unterschied zwischen Theorie und Experiment von 52,9 Nanosekunden nicht erklären. Die Allgemeine Relativitätstheorie (ART) dagegen kann diesen Unterschied auf die Höhendifferenz zwischen kreisender Uhr und Erduhr zurückführen. Begründe qualitativ, warum die ART den Gegensatz zwischen SRT und Experiment auf die Höhendifferenz zwischen kreisender Uhr und Erduhr zurückzuführen vermag.
b)
Im Falle von kreisenden Flugzeugen ist die genaue Berechnung zeitlicher Differenzen vergleichsweise kompliziert. Der Einfachheit halber soll die allgemein-relativistische Zeitdilatation im Folgenden an einem anderen Beispiel diskutiert werden. In der Nähe eines massereichen Körpers, beispielsweise in geringer Entfernung zu einem Stern, kann die allgemein-relativistische Zeitdilatation näherungsweise durch die folgende Formel beschrieben werden:[2]
 Dabei ist
Dabei ist  diejenige Zeit, die auf einer relativ zur Masse
diejenige Zeit, die auf einer relativ zur Masse  ruhenden Uhr
ruhenden Uhr  verstreicht, die sehr weit von dieser Masse entfernt ist, und
verstreicht, die sehr weit von dieser Masse entfernt ist, und  ist diejenige Zeit, die auf einer relativ zur Masse
ist diejenige Zeit, die auf einer relativ zur Masse  ruhenden Uhr
ruhenden Uhr  verstreicht, die dieser Masse sehr nahe ist (mit Abstand
verstreicht, die dieser Masse sehr nahe ist (mit Abstand  zwischen Uhr und Massenmittelpunkt (siehe Abbildung 3)).
zwischen Uhr und Massenmittelpunkt (siehe Abbildung 3)).  ist die Vakuumlichtgeschwindigkeit und
ist die Vakuumlichtgeschwindigkeit und  die Gravitationskonstante.
die Gravitationskonstante.
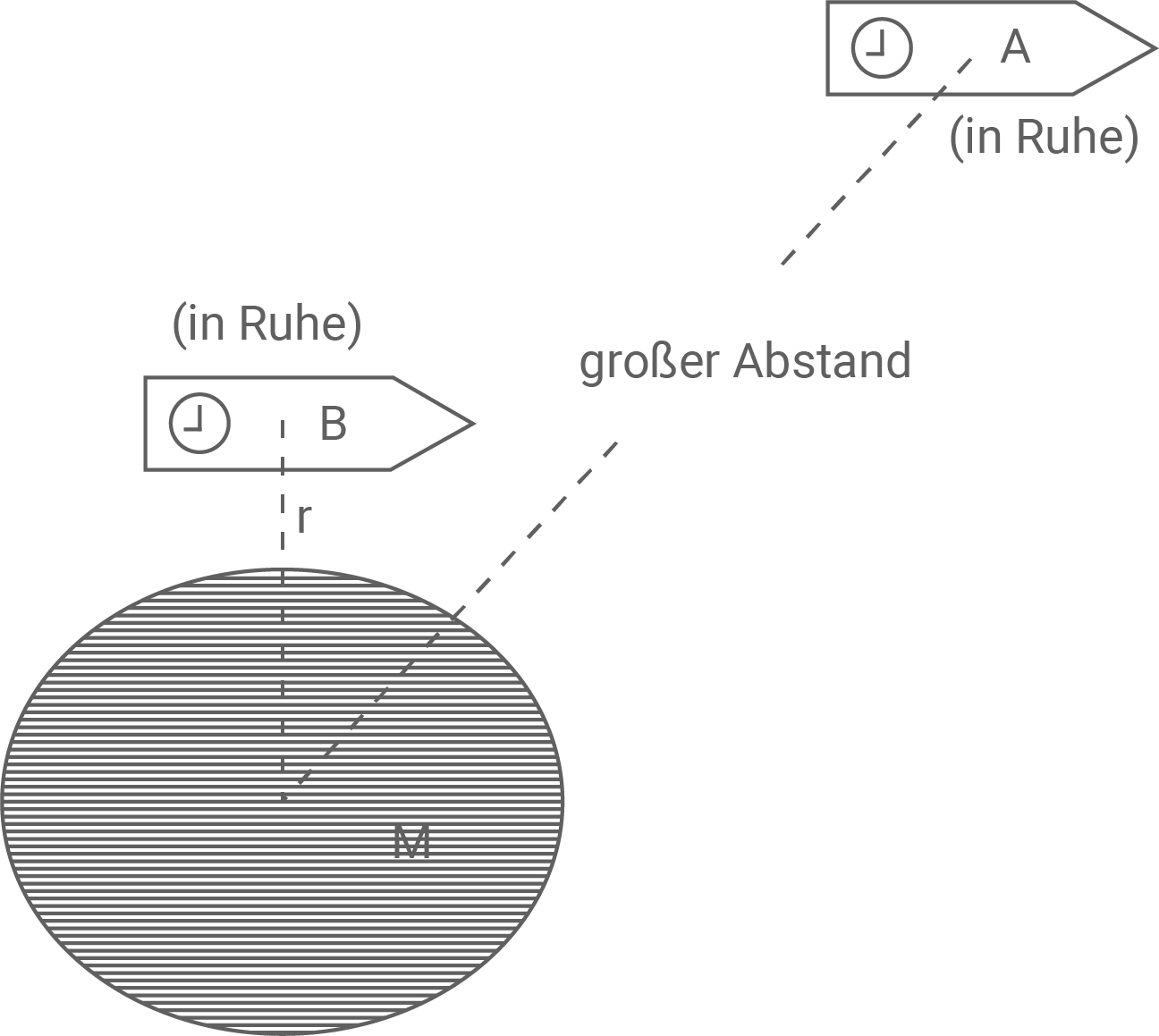 Der Pilot der Rakete
Der Pilot der Rakete  sieht auf seiner Uhr die Zeit
sieht auf seiner Uhr die Zeit  verstreichen.
verstreichen.


Abbildung 3: Zeitdilatation in der ART
- Berechne mit einer Genauigkeit von einer hundertstel Millisekunde, wie viel Zeit
der Pilot der Rakete
in einer Entfernung von
vom Mittelpunkt der Sonne auf seiner Uhr verstreichen sieht (Sonnenmasse
).
- Beurteile qualitativ die Bedeutung der von der Sonnenmasse verursachten allgemein-relativistischen Zeitdilatation für das Verstreichen der Zeit auf einer Uhr, die sich auf der Erdoberfläche befindet.
- Erkläre, welche Eigenschaften ein Himmelskörper im Vergleich zu unserer Sonne besitzen muss, damit auf seiner Oberfläche eine sehr viel stärkere allgemein-relativistische Zeitdilatation herrschen wird als auf der Oberfläche der Sonne.
(2 + 9 Punkte)
[1] E. F. Taylor & J. A. Wheeler: Physik der Raumzeit. Eine Einführung in die spezielle Relativitätstheorie. Spektrum Akademischer Verlag, Heidelberg, 1994, S. 210 f.
[2] Der massereiche Körper muss kugelsymmetrisch sein und darf nicht rotieren. Diese Bedingungen sind für viele Planeten und Sterne nicht exakt erfüllt, sie sind beispielsweise im Falle der Erde und der Sonne näherungsweise erfüllt.
Teillösung 1: Zeitdilatation und Längenkontraktion
a)
Lorentzfaktor  und die im Erdbezugssystem gemessene Zeit
und die im Erdbezugssystem gemessene Zeit  zwischen zwei aufeinanderfolgenden Leuchtereignissen
Der Lorentzfaktor
zwischen zwei aufeinanderfolgenden Leuchtereignissen
Der Lorentzfaktor  ergibt sich zu:
ergibt sich zu:
![\(\begin{array}[t]{rll}
\gamma&=& \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}} &\quad \scriptsize \\[5pt]
&=& \dfrac{1}{\sqrt{1-\dfrac{(0,7 c)^2}{c^2}}}&\quad \scriptsize \\[5pt]
&=& \dfrac{1}{\sqrt{1-0,49}}&\quad \scriptsize \\[5pt]
&=& 1,4
\end{array}\)](https://www.schullv.de/resources/formulas/393efac19f47723232c16d23b89b5eaaf3598b8ee19b816ed9b80851a26f4643_light.svg) Damit ergibt sich
Damit ergibt sich  zu:
zu:
![\(\begin{array}[t]{rll}
\Delta t_2&=&\gamma \cdot \Delta t_1&\quad \scriptsize \\[5pt]
&=& 1,4 \cdot 0,5 \;\text{s}&\quad \scriptsize \\[5pt]
&=& 0,7 \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/4966f4371ef194a8127a69587bf06d5c6a1485b58202f0f55ac1ea57143c6cb8_light.svg) Unterschied Blinkfrequenz der Raketenlampe im Raketenbezugssystem und im Erdbezugssystem
Die Periodendauer
Unterschied Blinkfrequenz der Raketenlampe im Raketenbezugssystem und im Erdbezugssystem
Die Periodendauer  im Erdbezugssystem ist größer als die Periodendauer
im Erdbezugssystem ist größer als die Periodendauer  im Raketenbezugssystem. Da die Frequenz umgekehrt proportional zur Periodendauer ist, muss die Blinkfrequenz im Erdbezugssystem kleiner sein.
Erklärung, wieso die Bestimmung von
im Raketenbezugssystem. Da die Frequenz umgekehrt proportional zur Periodendauer ist, muss die Blinkfrequenz im Erdbezugssystem kleiner sein.
Erklärung, wieso die Bestimmung von  und
und  nicht mit insgesamt nur einer einzigen Uhr während der gleichen Messung durchgeführt werden kann
Auf einer Uhr, die sich relativ zum Beobachter mit hoher Geschwindigkeit bewegt, erscheint das Verstreichen der Zeit dilatiert. Messungen innerhalb eines Bezugssystems können daher nur mit Uhren durchgeführt werden, die in diesem Bezugssystem in Ruhe verharren. Da sich die Rakete mit hoher Geschwindigkeit relativ zur Erde bewegt, kann eine im Raketenbezugssystem genutzte (also dort ruhende) Uhr nicht während der gleichen Messung im Erdbezugssystem genutzt werden (da sie dort nicht ruht).
nicht mit insgesamt nur einer einzigen Uhr während der gleichen Messung durchgeführt werden kann
Auf einer Uhr, die sich relativ zum Beobachter mit hoher Geschwindigkeit bewegt, erscheint das Verstreichen der Zeit dilatiert. Messungen innerhalb eines Bezugssystems können daher nur mit Uhren durchgeführt werden, die in diesem Bezugssystem in Ruhe verharren. Da sich die Rakete mit hoher Geschwindigkeit relativ zur Erde bewegt, kann eine im Raketenbezugssystem genutzte (also dort ruhende) Uhr nicht während der gleichen Messung im Erdbezugssystem genutzt werden (da sie dort nicht ruht).
b)
notwendige Geschwindigkeit 
![\(\begin{array}[t]{rll}
\gamma&=& \dfrac{\Delta x_1}{\Delta x_2}&\quad \scriptsize \\[5pt]
&=& \dfrac{100 \;\text{m}}{50 \;\text{m}}&\quad \scriptsize \\[5pt]
&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/069b9143a40f93dd96e56a2c3902aed0290687f8d4a8f16dd6ddb28b11fed170_light.svg) Umstellen von
Umstellen von  nach
nach  ergibt:
Einsetzen der Werte liefert:
ergibt:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
v &=& c\cdot \sqrt{1 -\dfrac{1}{\gamma^2}}&\quad \scriptsize \\[5pt]
&=& c \cdot \sqrt{1-\dfrac{1}{2^2}} &\quad \scriptsize \\[5pt]
&=& 0,87 \; c
\end{array}\)](https://www.schullv.de/resources/formulas/012a170153130c1dd329d37a4a285a8f54ad5e5363f8fad511651f543ceb0a95_light.svg) Existenz eines Inertialsystems, in dem die gemessene Länge der Rakete größer ist als im Raketenbezugssystem
Da der Lorentzfaktor stets größer oder gleich 1 ist, ist die Länge der Rakete in anderen Inertialsystemen stets kleiner oder genauso groß wie im Raketenbezugssystem.
Existenz eines Inertialsystems, in dem die gemessene Länge der Rakete größer ist als im Raketenbezugssystem
Da der Lorentzfaktor stets größer oder gleich 1 ist, ist die Länge der Rakete in anderen Inertialsystemen stets kleiner oder genauso groß wie im Raketenbezugssystem.
b)
Der Vorhersage des Gedankenexperiments liegt die zutreffende Annahme zugrunde, dass es bei einer sehr hohen Relativgeschwindigkeit zwischen Gleis und Zug zur Längenkontraktion kommen würde. Allerdings findet die Längenkontraktion immer nur in Längsrichtung statt, also in Fahrtrichtung des Zugs, niemals in den Querdimensionen, also in Richtungen quer zur Fahrtrichtung des Zugs.
Teillösung 2: Relativistische Phänomene atmosphärischer Myonen
a)
Nach jeder Halbwertszeit wird sich die Zahl der Myonen statistisch gesehen halbiert haben. Aus 1000 Myonen werden so zunächst etwa 500, dann etwa 250 und schließlich etwa 125 Myonen. Drei Halbwertszeiten entsprechen dem Zeitraum:
![\(\begin{array}[t]{rll}
3 \cdot T_{1 / 2}&=& 3 \cdot 1,523 \cdot 10^{-6} \,\text{s}&\quad \scriptsize \\[5pt]
&=& 4,569 \cdot 10^{-6} \;\text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/71621ff51a2668e5581086984ee152d99093ddcb6e62236453f5590db819f9d5_light.svg)
b)
Unter Nichtberücksichtigung relativistischer Effekte wird auf der Erdoberfläche nur ein einziges Myon registriert
Zeit  , die das Myon zum Erreichen der Erdoberfläche benötigt:
, die das Myon zum Erreichen der Erdoberfläche benötigt:
![\(\begin{array}[t]{rll}
\Delta t&=& \dfrac{h}{v} &\quad \scriptsize \\[5pt]
&=& \dfrac{10 \;\text{km}}{0,995 \;c} &\quad \scriptsize \\[5pt]
&=& 3,352 \cdot 10^{-5} \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/1065bed8056e428fc1013cdcf1b1854c7401f20dc24afe77531a2595b8a5c849_light.svg) Anzahl
Anzahl  der Halbwertszeiten, die das Myon in dieser Zeit durchläuft:
der Halbwertszeiten, die das Myon in dieser Zeit durchläuft:
![\(\begin{array}[t]{rll}
n &=& \dfrac{\Delta t}{T_{1 / 2}}&\quad \scriptsize \\[5pt]
&=& \dfrac{3,352 \cdot 10^{-5} \;\text{s}}{1,523 \cdot 10^{-6} \;\text{s}}&\quad \scriptsize \\[5pt]
&\approx& 22
\end{array}\)](https://www.schullv.de/resources/formulas/4e87d151b89f6a2d4ec24791da2e6b52669eb5463c3951ce31926e901a0f1a64_light.svg) Anzahl der registrierten Myonen auf der Erdoberfläche aus klassischer Sicht von anfänglich jeweils
Anzahl der registrierten Myonen auf der Erdoberfläche aus klassischer Sicht von anfänglich jeweils  Myonen:
Myonen:
![\(\begin{array}[t]{rll}
\dfrac{N_0}{2^n}&=& \dfrac{4,229 \cdot 10^6}{2^{22}}&\quad \scriptsize \\[5pt]
&=& \dfrac{4,229 \cdot 10^6}{4,194 \cdot 10^6}&\quad \scriptsize \\[5pt]
&=& 1,008
\end{array}\)](https://www.schullv.de/resources/formulas/6675316ae48501d25a0cda20e0c9303367604c934584c4ae547946c9af85fab0_light.svg) Es wird folglich aus klassischer Sicht rein rechnerisch nur ein einziges Myon registriert.
Erlärung des experimentellen Befrundes aus Sicht eines mitbewegten Bezugssystems und aus Sicht des Erdbezugssystems
Aus Sicht eines mitbewegten Bezugssystems, in dem das Myon ruht, wird die Flugstrecke der Myonen, die im Erdbezugssystem
Es wird folglich aus klassischer Sicht rein rechnerisch nur ein einziges Myon registriert.
Erlärung des experimentellen Befrundes aus Sicht eines mitbewegten Bezugssystems und aus Sicht des Erdbezugssystems
Aus Sicht eines mitbewegten Bezugssystems, in dem das Myon ruht, wird die Flugstrecke der Myonen, die im Erdbezugssystem  beträgt, kontrahiert (relativistischer Effekt der Längenkontraktion), sodass es den Myonen gelingt, in kürzerer Zeit den Erdboden zu erreichen. Es zerfallen also weniger Myonen, als nach klassischer Rechnung zu erwarten ist. Aus Sicht des Erdbezugssystems dagegen fliegen die Myonen mit hoher Geschwindigkeit, sodass die Halbwertszeit der Myonen (die als bewegte Uhren interpretiert werden können) aus Sicht des Erdbezugssystems größer ist (relativistischer Effekt der Zeitdilatation), also weniger Myonen zerfallen, als nach klassischer Rechnung zu erwarten ist.
Anzahl der registrierten Myonen auf der Erdoberfläche unter Berücksichtigung des entsprechenden relativistischen Effekts
Bei einer Geschwindigkeit von
beträgt, kontrahiert (relativistischer Effekt der Längenkontraktion), sodass es den Myonen gelingt, in kürzerer Zeit den Erdboden zu erreichen. Es zerfallen also weniger Myonen, als nach klassischer Rechnung zu erwarten ist. Aus Sicht des Erdbezugssystems dagegen fliegen die Myonen mit hoher Geschwindigkeit, sodass die Halbwertszeit der Myonen (die als bewegte Uhren interpretiert werden können) aus Sicht des Erdbezugssystems größer ist (relativistischer Effekt der Zeitdilatation), also weniger Myonen zerfallen, als nach klassischer Rechnung zu erwarten ist.
Anzahl der registrierten Myonen auf der Erdoberfläche unter Berücksichtigung des entsprechenden relativistischen Effekts
Bei einer Geschwindigkeit von  c beträgt der Lorentzfaktor :
c beträgt der Lorentzfaktor :
![\(\begin{array}[t]{rll}
\gamma&=& \dfrac{1}{\sqrt{1-\dfrac{v^2}{\text{c}^2}}}&\quad \scriptsize \\[5pt]
\gamma&=& \dfrac{1}{\sqrt{1-\dfrac{(0,995 \text{c})^2}{\mathrm{c}^2}}}&\quad \scriptsize \\[5pt]
\gamma&=& \dfrac{1}{\sqrt{1-0,990 \ldots}}&\quad \scriptsize \\[5pt]
&\approx& 10,013
\end{array}\)](https://www.schullv.de/resources/formulas/77c1c69e386f1ccd94781358d027ad1c4d4e5fe054faef45106fb2622225ac5d_light.svg) Anzahl
Anzahl  der Halbwertszeiten aus relativistischer Sicht, die das Myon in dieser Zeit durchläuft:
der Halbwertszeiten aus relativistischer Sicht, die das Myon in dieser Zeit durchläuft:
![\(\begin{array}[t]{rll}
n](https://www.schullv.de/resources/formulas/bec3796aaf4011450ebdad623ff4437b823fb2bfa05573aff69d5a6198389344_light.svg) Anzahl der registrierten Myonen auf der Erdoberfläche aus relativistischer Sicht von anfänglich jeweils
Anzahl der registrierten Myonen auf der Erdoberfläche aus relativistischer Sicht von anfänglich jeweils  Myonen:
Myonen:
![\(\begin{array}[t]{rll}
\dfrac{N_0}{2^n}&=& \dfrac{4,229 \cdot 10^6}{2^{2,197}}&\quad \scriptsize \\[5pt]
&=& \dfrac{4,229 \cdot 10^6}{4,585}&\quad \scriptsize \\[5pt]
&=& 9,223 \cdot 10^5
\end{array}\)](https://www.schullv.de/resources/formulas/f2999b554ba642477287b2b25ccbd38afc6c547fcd0f335acb89487101f95428_light.svg) Es werden folglich aus relativistischer Sicht rein rechnerisch etwa 9 Myonen auf der Erdoberfläche registriert.
Es werden folglich aus relativistischer Sicht rein rechnerisch etwa 9 Myonen auf der Erdoberfläche registriert.
c)
Erklärung, wie viele Myonen registriert werden würden, wenn die Fluggeschwindigkeit der Teilchen näherungsweise Lichtgeschwindigkeit betragen würde.
Wenn sich die Teilchengeschwindigkeit immer mehr der Lichtgeschwindigkeit annähert, wird sich die Zeit ![\(\begin{array}[t]{rll}
\Delta t&=&\frac{h}{v} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/38d376f4b30bf8ded190be8f17245e63d7eb8f88d424cb8da1fcb7fba3e63b6c_light.svg) zum Erreichen der Erdoberfläche im Erdbezugssystem nur noch geringfügig verringern, allerdings wird der Lorentzfaktor
zum Erreichen der Erdoberfläche im Erdbezugssystem nur noch geringfügig verringern, allerdings wird der Lorentzfaktor  alle Grenzen überschreiten, sodass bei ausreichend hoher Geschwindigkeit nahezu alle in der Erdatmosphäre erzeugten Myonen den Detektor erreichen werden.
Begründung,der sehr groben Vereinfachung von Annahme 3
Die in der Aufgabenstellung genannte Bedingung Nr. 3 ist eine grobe Vereinfachung: Die Myonen entstehen durch Zerfälle in der Atmosphäre, und diese Zerfälle wiederum werden durch das Zusammentreffen hochenergetischer Teilchen (Protonen) mit Atomkernen der Atmosphäre verursacht. Da die hochenergetischen Teilchen in vielfältigen Winkeln auf die Erdatmosphäre treffen, fliegen nur wenige Myonen senkrecht zur Erdoberfläche.
Begründen der Aussage
Wenn ein Teil der Myonen nicht senkrecht zur Erdoberfläche fliegt, werden weniger Myonen den Detektor erreichen, da die Myonen dann im Durchschnitt längere Wege vom Entstehungsort bis zum Detektor zurücklegen müssen und somit ein größerer Prozentsatz der Myonen zerfallen wird.
Beurteilung,wie sich die berechnete Zahl der detektierten Myonen verändern würde, wenn die obige Vereinfachung 4 nicht vorgenommen werden würde
Treffen einige der Myonen zudem auf Teilchen der Erdatmosphäre, können diese Myonen, je nach Charakter der dabei stattfindenden Wechselwirkung, in andere Teilchenarten umgewandelt, zumindest aber ihre Flugrichtungen geändert bzw. ihre Geschwindigkeiten durch Ionisation der Luftmoleküle verringert werden. Es ist also auch in diesem Fall anzunehmen, dass sich die Zahl der detektierten Myonen verringern wird (vorausgesetzt, dass bei den Kollisionen nicht in großer Zahl neue Myonen entstehen).
alle Grenzen überschreiten, sodass bei ausreichend hoher Geschwindigkeit nahezu alle in der Erdatmosphäre erzeugten Myonen den Detektor erreichen werden.
Begründung,der sehr groben Vereinfachung von Annahme 3
Die in der Aufgabenstellung genannte Bedingung Nr. 3 ist eine grobe Vereinfachung: Die Myonen entstehen durch Zerfälle in der Atmosphäre, und diese Zerfälle wiederum werden durch das Zusammentreffen hochenergetischer Teilchen (Protonen) mit Atomkernen der Atmosphäre verursacht. Da die hochenergetischen Teilchen in vielfältigen Winkeln auf die Erdatmosphäre treffen, fliegen nur wenige Myonen senkrecht zur Erdoberfläche.
Begründen der Aussage
Wenn ein Teil der Myonen nicht senkrecht zur Erdoberfläche fliegt, werden weniger Myonen den Detektor erreichen, da die Myonen dann im Durchschnitt längere Wege vom Entstehungsort bis zum Detektor zurücklegen müssen und somit ein größerer Prozentsatz der Myonen zerfallen wird.
Beurteilung,wie sich die berechnete Zahl der detektierten Myonen verändern würde, wenn die obige Vereinfachung 4 nicht vorgenommen werden würde
Treffen einige der Myonen zudem auf Teilchen der Erdatmosphäre, können diese Myonen, je nach Charakter der dabei stattfindenden Wechselwirkung, in andere Teilchenarten umgewandelt, zumindest aber ihre Flugrichtungen geändert bzw. ihre Geschwindigkeiten durch Ionisation der Luftmoleküle verringert werden. Es ist also auch in diesem Fall anzunehmen, dass sich die Zahl der detektierten Myonen verringern wird (vorausgesetzt, dass bei den Kollisionen nicht in großer Zahl neue Myonen entstehen).
Teillösung 3: Zeitdilatation in Spezieller und Allgemeiner Relativitätstheorie
a)
Die kreisende Uhr bewegt sich in einer größeren Höhe, also einem größeren Abstand zum Erdmittelpunkt, als die Erduhr. Deshalb unterliegt die Erduhr aufgrund der größeren Gravitation einer stärkeren allgemein-relativistischen Zeitdilatation, d. h. die Zeit auf der kreisenden Uhr müsste schneller vergehen als auf der Erduhr. Da die kreisende Uhr im Experiment tatsächlich vorgeht, überwiegt der allgemein-relativistische Effekt den speziell-relativistischen Effekt.
b)
Berechnung der Zeit  , die der Pilot der Rakete B auf seiner Uhr verstreichen sieht
Für die Zeit
, die der Pilot der Rakete B auf seiner Uhr verstreichen sieht
Für die Zeit  des Piloten der Rakete B ergibt sich mit dem gegeben Zusammenhang:
des Piloten der Rakete B ergibt sich mit dem gegeben Zusammenhang:
![\(\begin{array}[t]{rll}
\Delta t&=& \sqrt{1-\frac{2 \cdot \mathrm{G} \cdot M}{\mathrm{c}^2 \cdot r}} \Delta t_{\text {entfernt }} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5a7b3af3a896fd488f5fab6a998127bac26b1adfb5f894f48d9f332134d76244_light.svg) Einsetzen der Werte liefert:
Beurteilung der von der Sonnenmasse verursachten allgemein-relativistischen Zeitdilatation für das Verstreichen der Zeit auf einer Uhr, die sich auf der Erdoberfläche befindet.
Der bei dieser Rechnung benutzte Abstand vom Mittelpunkt der Sonne ist sehr viel kleiner als der Radius der Erdumlaufbahn, und selbst in dieser viel kleineren Entfernung ist die durch die Gravitation hervorgerufene Zeitdilatation der Sonne sehr gering. Da sich der Wurzelterm mit steigendem Radius
Einsetzen der Werte liefert:
Beurteilung der von der Sonnenmasse verursachten allgemein-relativistischen Zeitdilatation für das Verstreichen der Zeit auf einer Uhr, die sich auf der Erdoberfläche befindet.
Der bei dieser Rechnung benutzte Abstand vom Mittelpunkt der Sonne ist sehr viel kleiner als der Radius der Erdumlaufbahn, und selbst in dieser viel kleineren Entfernung ist die durch die Gravitation hervorgerufene Zeitdilatation der Sonne sehr gering. Da sich der Wurzelterm mit steigendem Radius  weiter verringert, ist der Einfluss der durch die Gravitation der Sonne hervorgerufenen Zeitdilatation für Prozesse auf der Erde, die einen vergleichsweise großen Abstand zum Zentralgestirn besitzt, vernachlässigbar. Eine auf der Erdoberfläche befindliche Uhr wird daher keine bedeutsame Zeitdilatation aufgrund der Sonnenmasse erfahren.
Erklärung, welche Eigenschaften ein Himmelskörper im Vergleich zu der Sonne besitzen muss, damit auf seiner Oberfläche eine sehr viel stärkere allgemein-relativistische Zeitdilatation herrschen wird als auf der Oberfläche der Sonne.
Eine stärkere allgemein-relativistische Zeitdilatation ist auf der Oberfläche solcher Himmelskörper zu erwarten, die im Vergleich zur Sonne eine größere Masse oder einen geringeren Radius (oder beides) besitzen.
weiter verringert, ist der Einfluss der durch die Gravitation der Sonne hervorgerufenen Zeitdilatation für Prozesse auf der Erde, die einen vergleichsweise großen Abstand zum Zentralgestirn besitzt, vernachlässigbar. Eine auf der Erdoberfläche befindliche Uhr wird daher keine bedeutsame Zeitdilatation aufgrund der Sonnenmasse erfahren.
Erklärung, welche Eigenschaften ein Himmelskörper im Vergleich zu der Sonne besitzen muss, damit auf seiner Oberfläche eine sehr viel stärkere allgemein-relativistische Zeitdilatation herrschen wird als auf der Oberfläche der Sonne.
Eine stärkere allgemein-relativistische Zeitdilatation ist auf der Oberfläche solcher Himmelskörper zu erwarten, die im Vergleich zur Sonne eine größere Masse oder einen geringeren Radius (oder beides) besitzen.