HT 1
Experimentelle und theoretische Untersuchung von induktiven Vorgängen
Das Induktionsgesetz kann mit Differenzquotienten gemäß
a)
- Erläutere jeweils, welche Ursache für das Auftreten einer Induktionsspannung mit dem 1. bzw. 2. Term beschrieben wird.
- Beschreibe jeweils ein Experiment, mit dem das Auftreten einer Induktionsspannung gemäß dem 1. bzw. 2. Term demonstriert werden kann.
b)
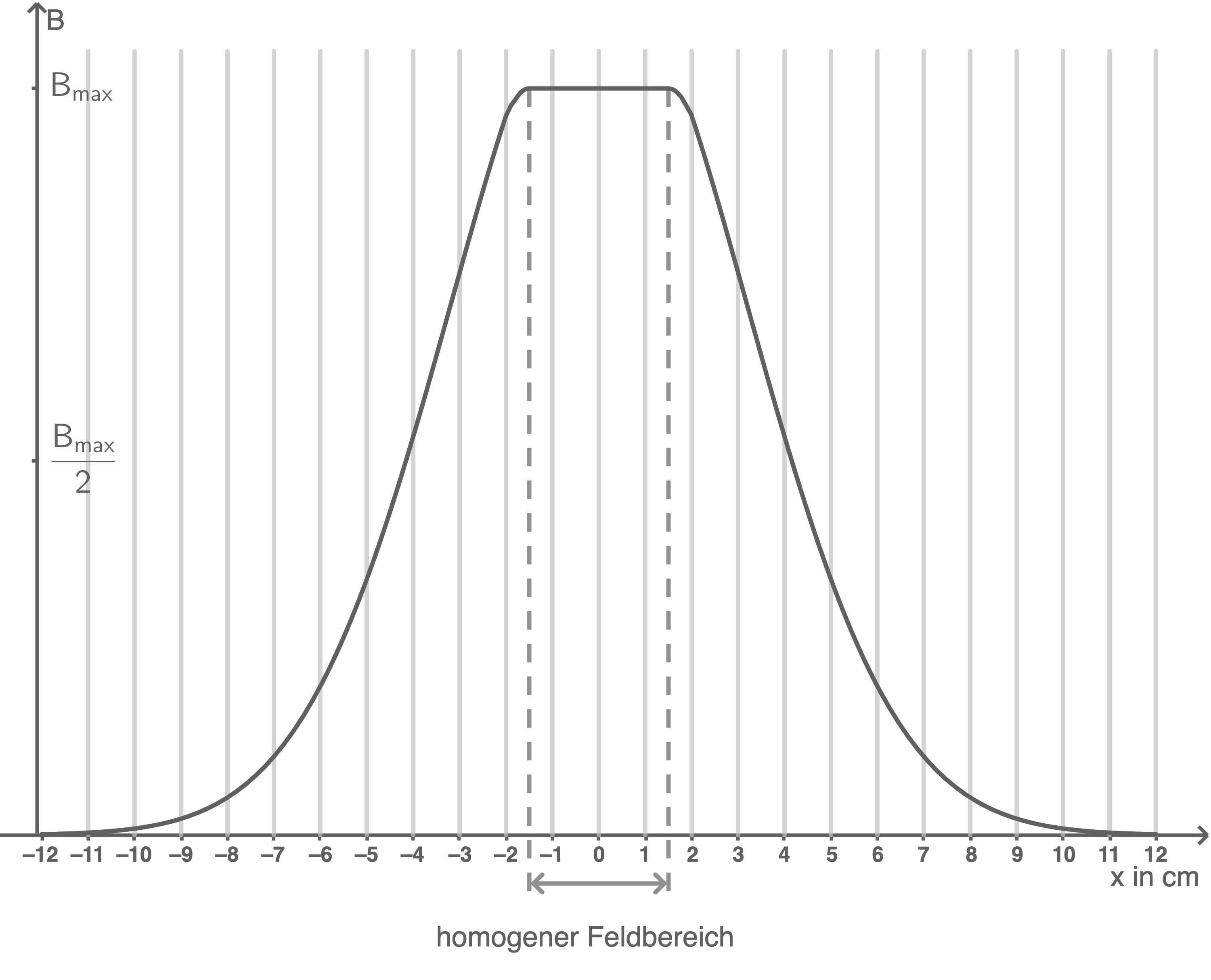
In einem Gedankenexperiment gemäß Abbildung 1 bewegt sich eine rechteckige, mit einem Voltmeter verbundene Leiterschleife der Breite  mit konstanter Geschwindigkeit
mit konstanter Geschwindigkeit  von links nach rechts vollständig durch ein räumlich begrenztes homogenes Magnetfeld der Stärke
von links nach rechts vollständig durch ein räumlich begrenztes homogenes Magnetfeld der Stärke 
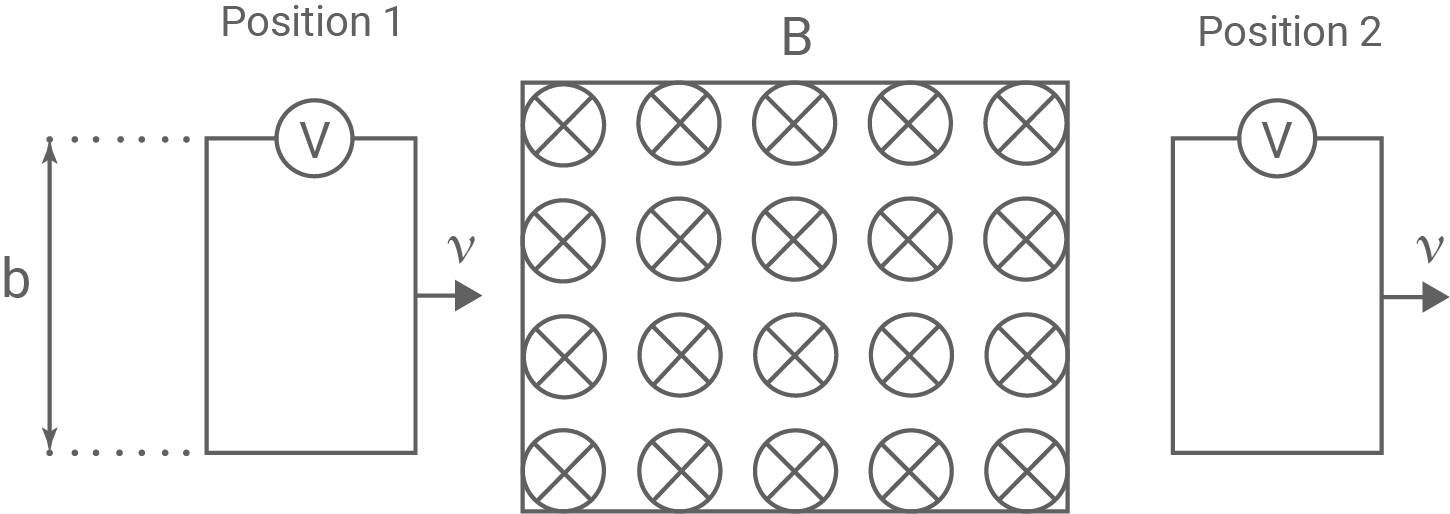 Abbildung 1 zeigt sowohl den Beginn des Gedankenexperiments zum Zeitpunkt
Abbildung 1 zeigt sowohl den Beginn des Gedankenexperiments zum Zeitpunkt  (Position 1) sowie das Ende (Position 2) der zu betrachtenden Bewegung.
(Position 1) sowie das Ende (Position 2) der zu betrachtenden Bewegung.
Zeichne ein qualitatives -
-  -Diagramm dieses Gedankenexperiments.
-Diagramm dieses Gedankenexperiments.

Abbildung 1: Schema des Gedankenexperiments
Zeichne ein qualitatives
c)
Das Auftreten einer von null verschiedenen Induktionsspannung beim Eintritt einer Leiterschleife in ein räumlich begrenztes homogenes Magnetfeld gemäß Abbildung 1 kann quantitativ mithilfe des oben angegebenen Induktionsgesetzes beschrieben werden.
Teilaufgabe 2: Fahrbahn-Versuche zum Induktionsgesetz
Im Folgenden wird das Gedankenexperiment gemäß Abbildung 1 in einem Realexperiment untersucht (siehe Abbildung 2a).
- Begründe, dass dafür eine Vereinfachung des angegebenen Induktionsgesetzes zu
verwendet werden kann.
- Zeige, dass sich daraus
herleiten lässt.
(6 + 4 + 5 Punkte)
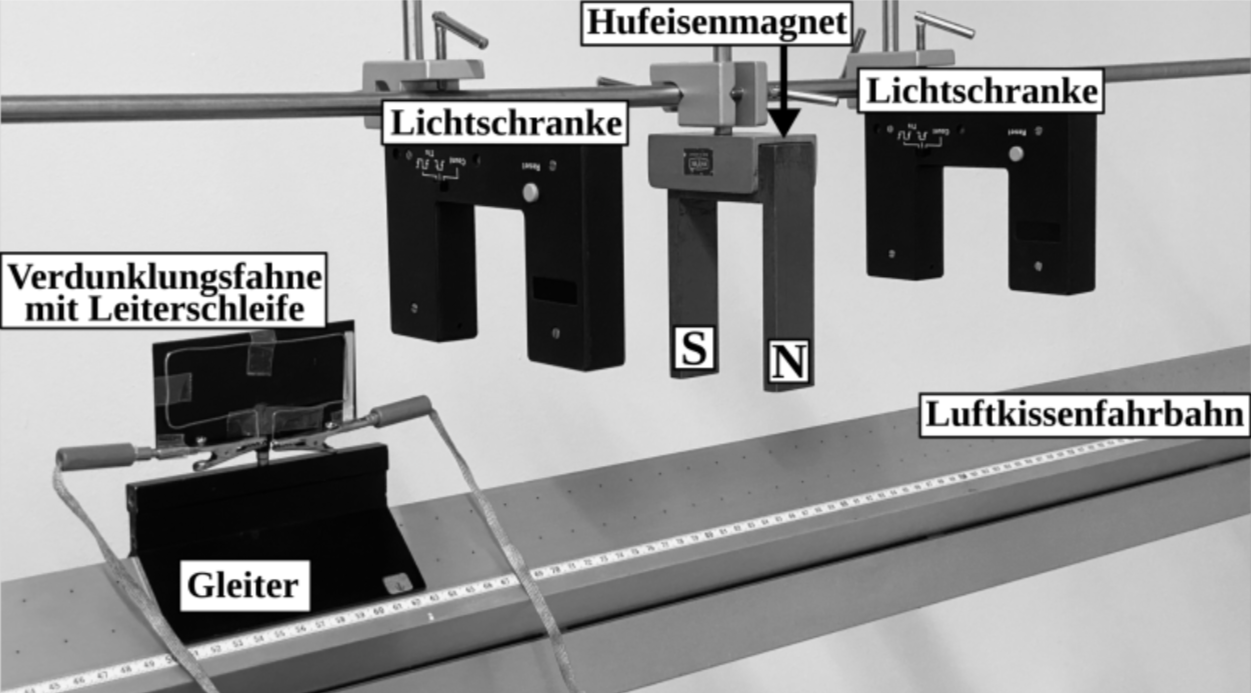
Abbildung 2a: Aufbau des Realexperiments mit einer Leiterschleife
Abbildung 2b zeigt den Gleiter samt Verdunklungsfahne der Länge

Abbildung 2b: Gleiter mit Verdunklungsfahne und Leiterschleife
a)
Die Leiterschleife ist an ein Messwerterfassungssystem angeschlossen, sodass der zeitliche Verlauf der elektrischen Spannung aufgezeichnet werden kann. Abbildung 3 stellt das aufgenommene Spannungssignal dar, wobei die Verdunklungszeiten der beiden Lichtschranken gleich gemessen werden.
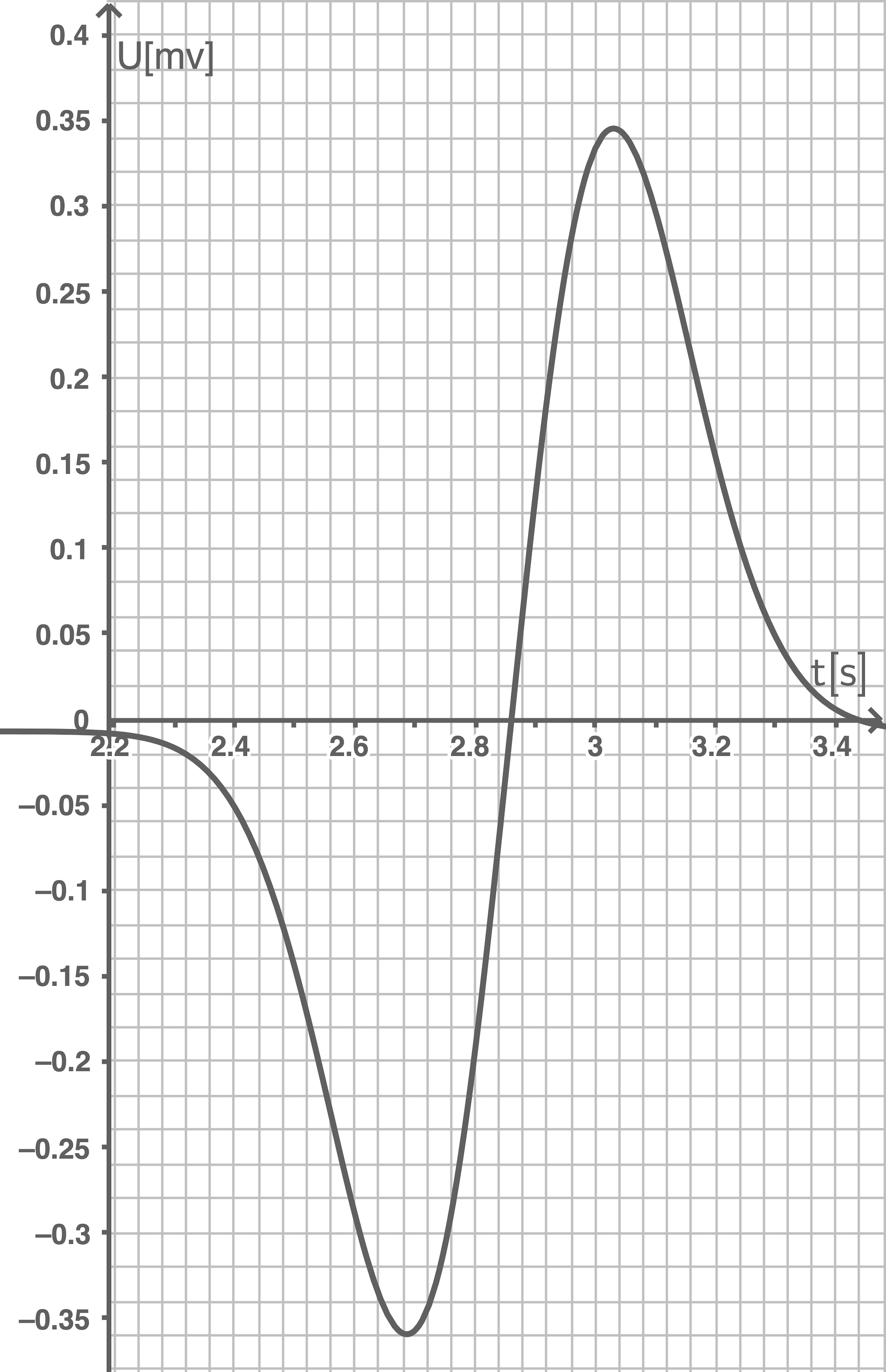 Beschreibe das Diagramm in Abbildung 3.
Beschreibe das Diagramm in Abbildung 3.

b)
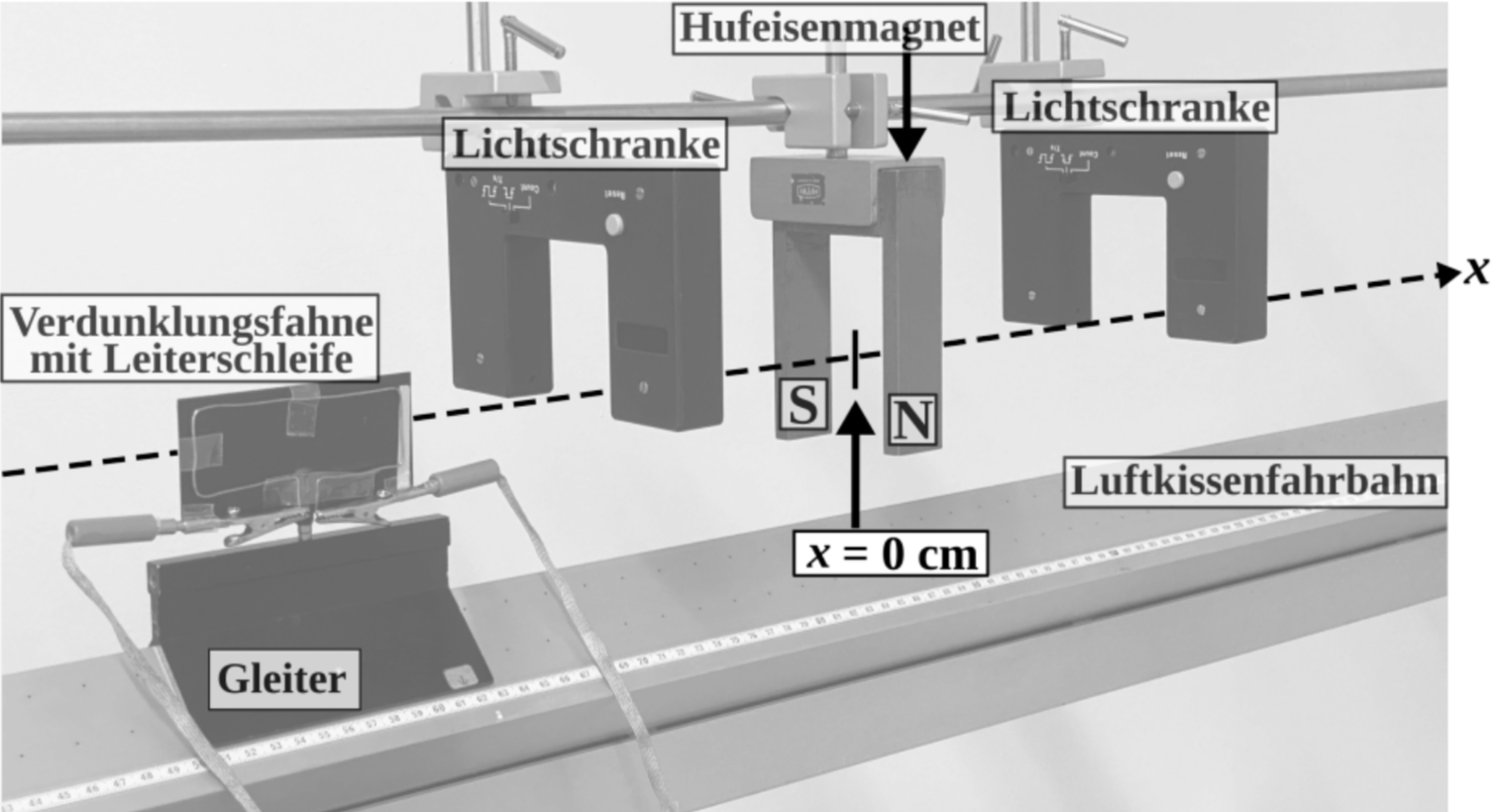
Die Leiterschleife bewegt sich entlang der  -Achse (vgl. Abbildung 4), wobei die Ortskoordinate
-Achse (vgl. Abbildung 4), wobei die Ortskoordinate  genau mittig zwischen den Schenkeln des Hufeisenmagneten liegt.
genau mittig zwischen den Schenkeln des Hufeisenmagneten liegt.
 Das Magnetfeld des Hufeisenmagneten wird im Folgenden zwischen den Schenkeln
Das Magnetfeld des Hufeisenmagneten wird im Folgenden zwischen den Schenkeln  näherungsweise als homogen angenommen. Außerhalb der Schenkel ist das Magnetfeld inhomogen. Abbildung 5a stellt die Stärke
näherungsweise als homogen angenommen. Außerhalb der Schenkel ist das Magnetfeld inhomogen. Abbildung 5a stellt die Stärke  des Magnetfeldes in Abhängigkeit vom Ort
des Magnetfeldes in Abhängigkeit vom Ort  dar.
dar.
 Die Abbildungen 5b und 5c zeigen die sich von links naxch rechts bewegende Leiterschleifen an zwei verschiedenen Positionen.
Die Abbildungen 5b und 5c zeigen die sich von links naxch rechts bewegende Leiterschleifen an zwei verschiedenen Positionen.
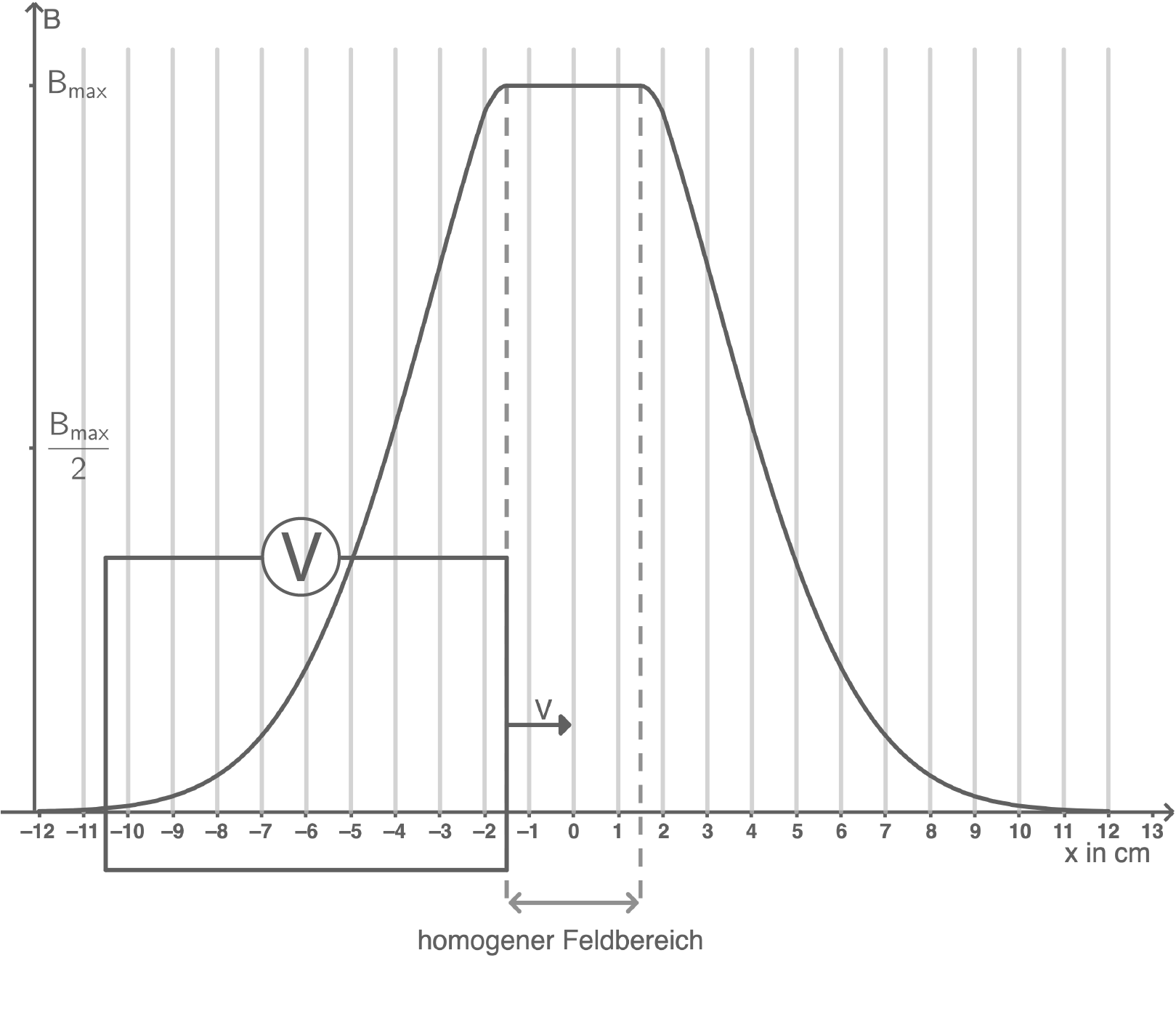
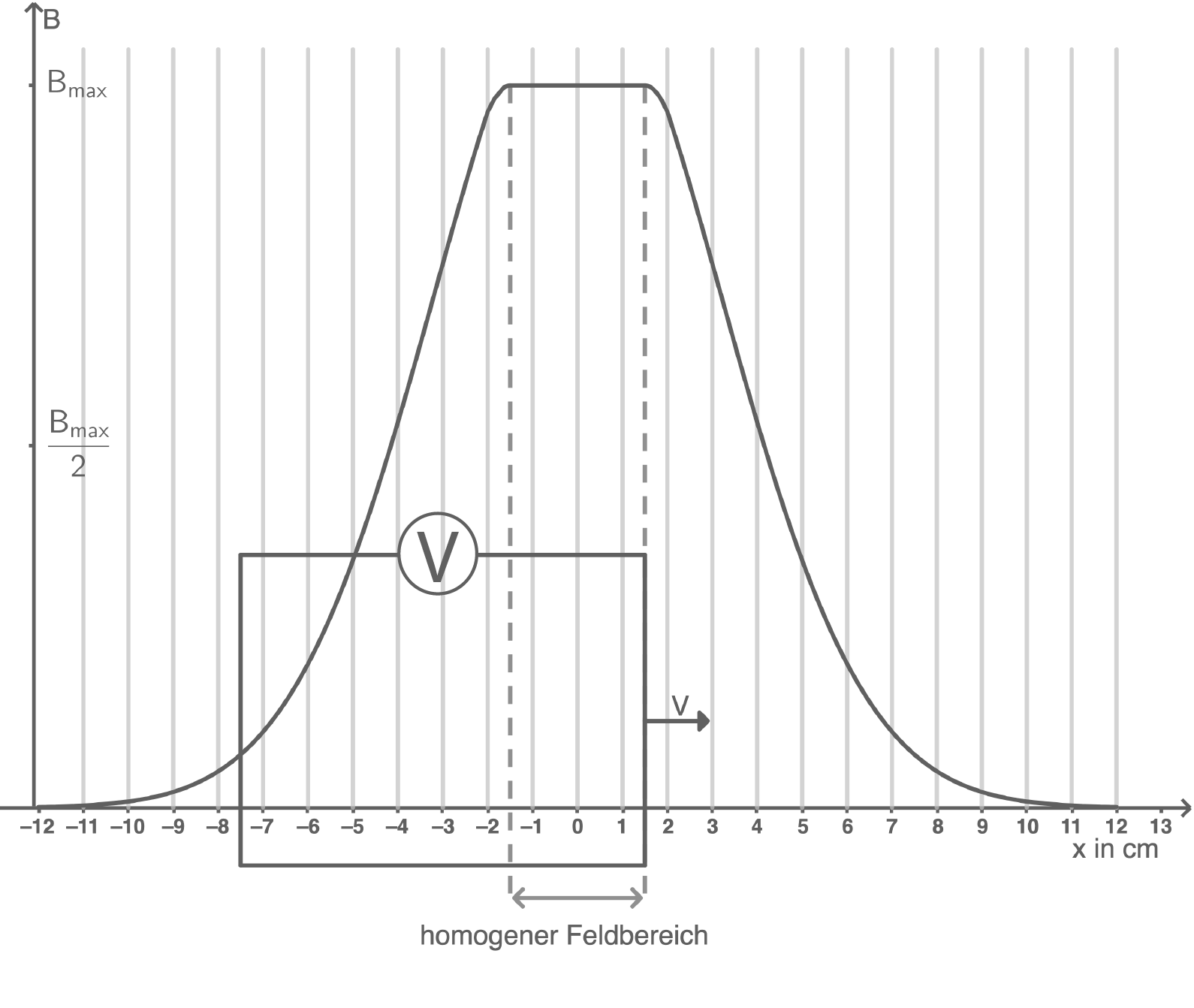 Bei der Bewegung der Leiterschleife von links nach rechts (vgl. Abbildungen 5b und 5c) wirkt jeweils im rechten und linken Leiterstück eine Lorentzkraft. Damit kann die Stärke des gemessenen Spannungssignals erklärt werden.
Bei der Bewegung der Leiterschleife von links nach rechts (vgl. Abbildungen 5b und 5c) wirkt jeweils im rechten und linken Leiterstück eine Lorentzkraft. Damit kann die Stärke des gemessenen Spannungssignals erklärt werden.
 (statt
(statt  ) verwendet wird. Dabei kann davon ausgegangen werden, dass die Breite
) verwendet wird. Dabei kann davon ausgegangen werden, dass die Breite  gleich ist, die Lichtschranken weiterhin die gleichen Verdunklungszeiten wie in 2a) messen und sich die Mitte der kürzeren Leiterschleife zum selben Zeitpunkt in der Mitte des homogenen Feldbereichs befindet.
gleich ist, die Lichtschranken weiterhin die gleichen Verdunklungszeiten wie in 2a) messen und sich die Mitte der kürzeren Leiterschleife zum selben Zeitpunkt in der Mitte des homogenen Feldbereichs befindet.

Abbildung 4: Realexperiment mit  -Achse
-Achse



- Erkläre mithilfe eines Vergleichs der Lorentzkraft im rechten und linken Leiterstück, dass in Abbildung 5b das gemessene Spannungssignal höher ist als in Abbildung 5c.
- Begründe, dass die gemessene Spannung kleiner wird, wenn sich das rechte Leiterstück durch den homogenen Feldbereich bewegt.
- Erläutere, dass die Spannung mit
gemessen wird, wenn sich die Mitte der Leiterschleife genau in der Mitte des homogenen Feldbereichs befindet.
- Skizziere in Abbildung 3 das veränderte Spannungssignal.
c)
In Abbildung 6 sind vier  -
-  -Diagramme und die dazugehörigen Verdunklungszeiten
-Diagramme und die dazugehörigen Verdunklungszeiten  dargestellt. Dabei hat sich die Leiterschleife jeweils gleichförmig durch den Hufeisenmagneten bewegt.
dargestellt. Dabei hat sich die Leiterschleife jeweils gleichförmig durch den Hufeisenmagneten bewegt.
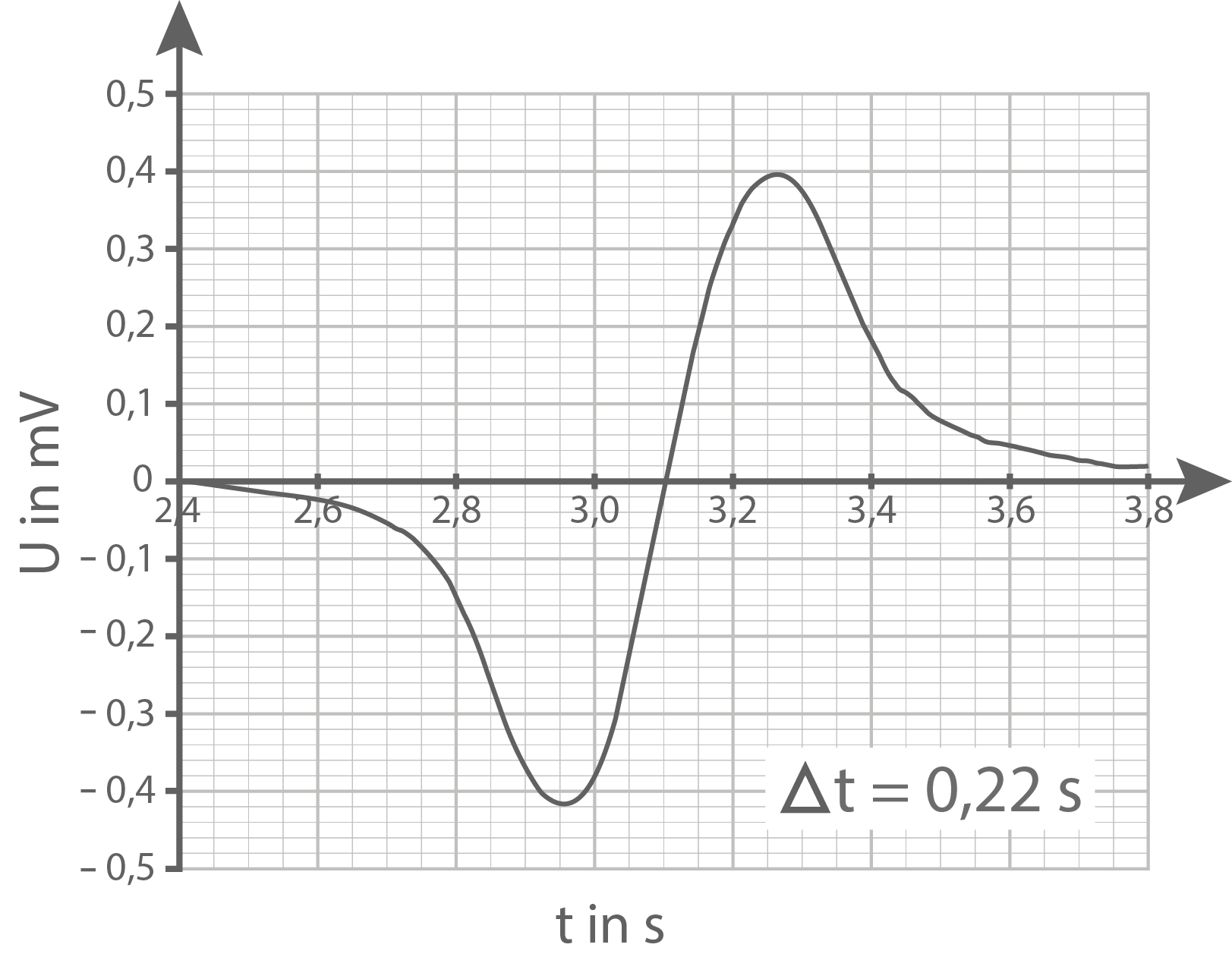
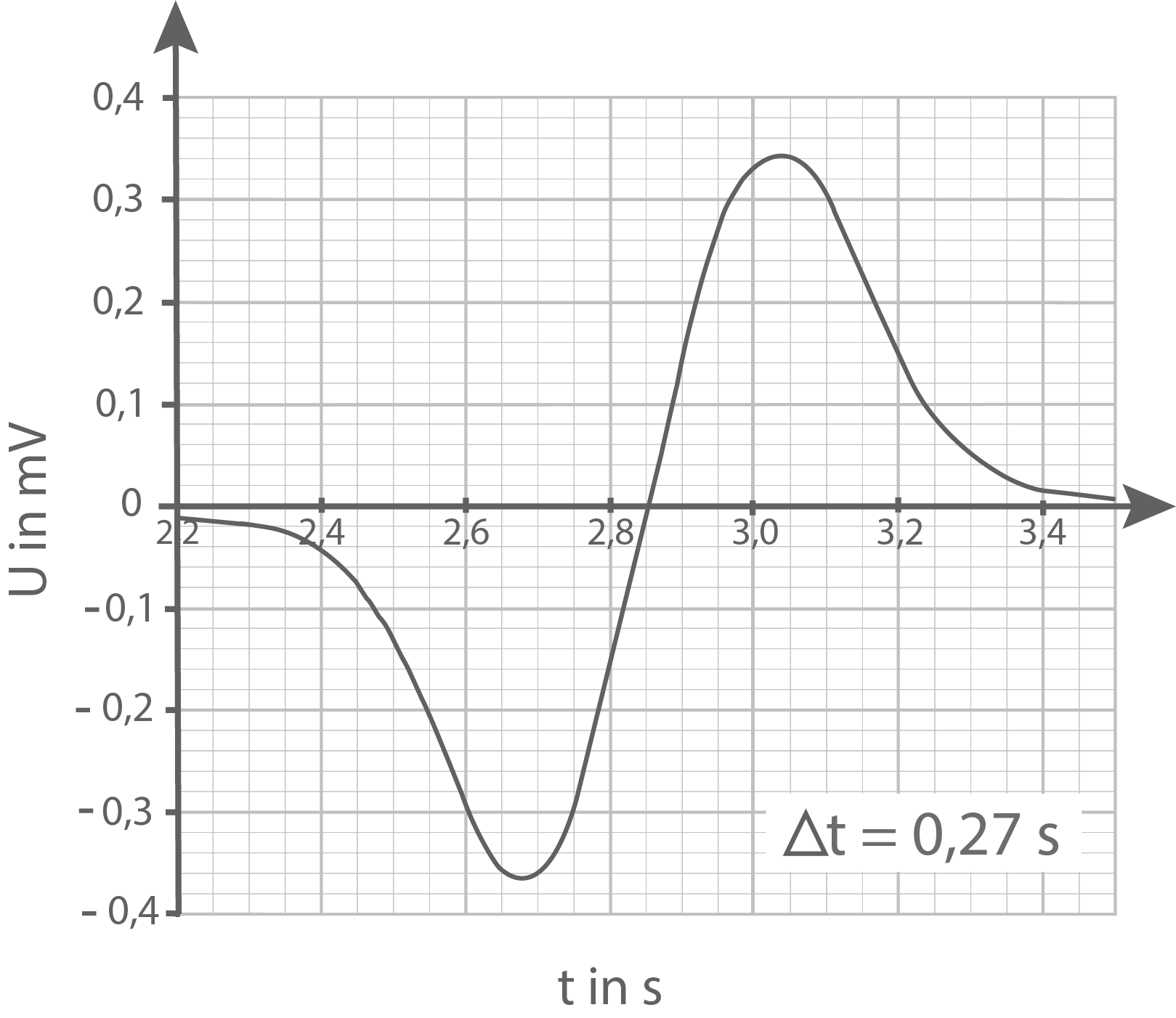
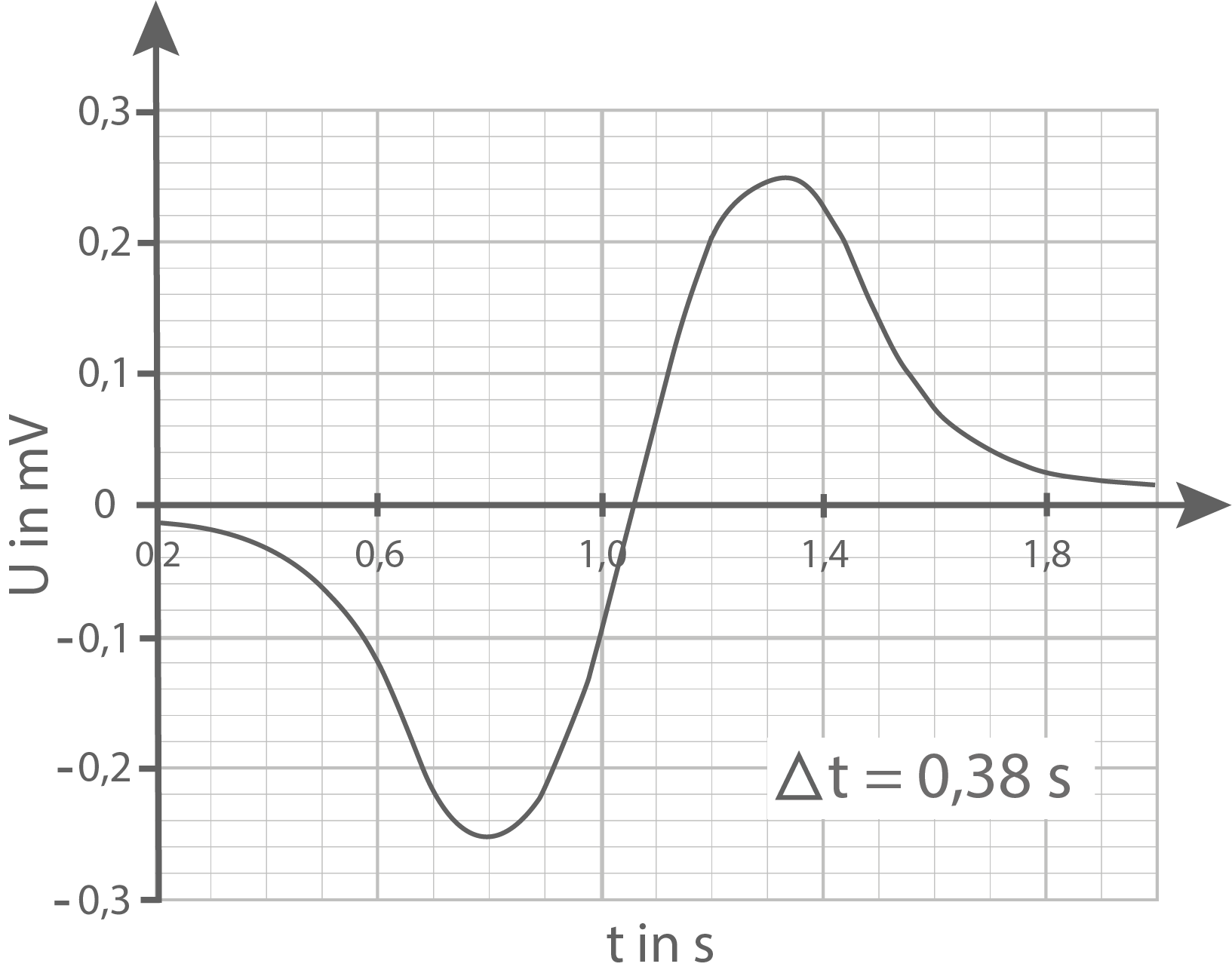
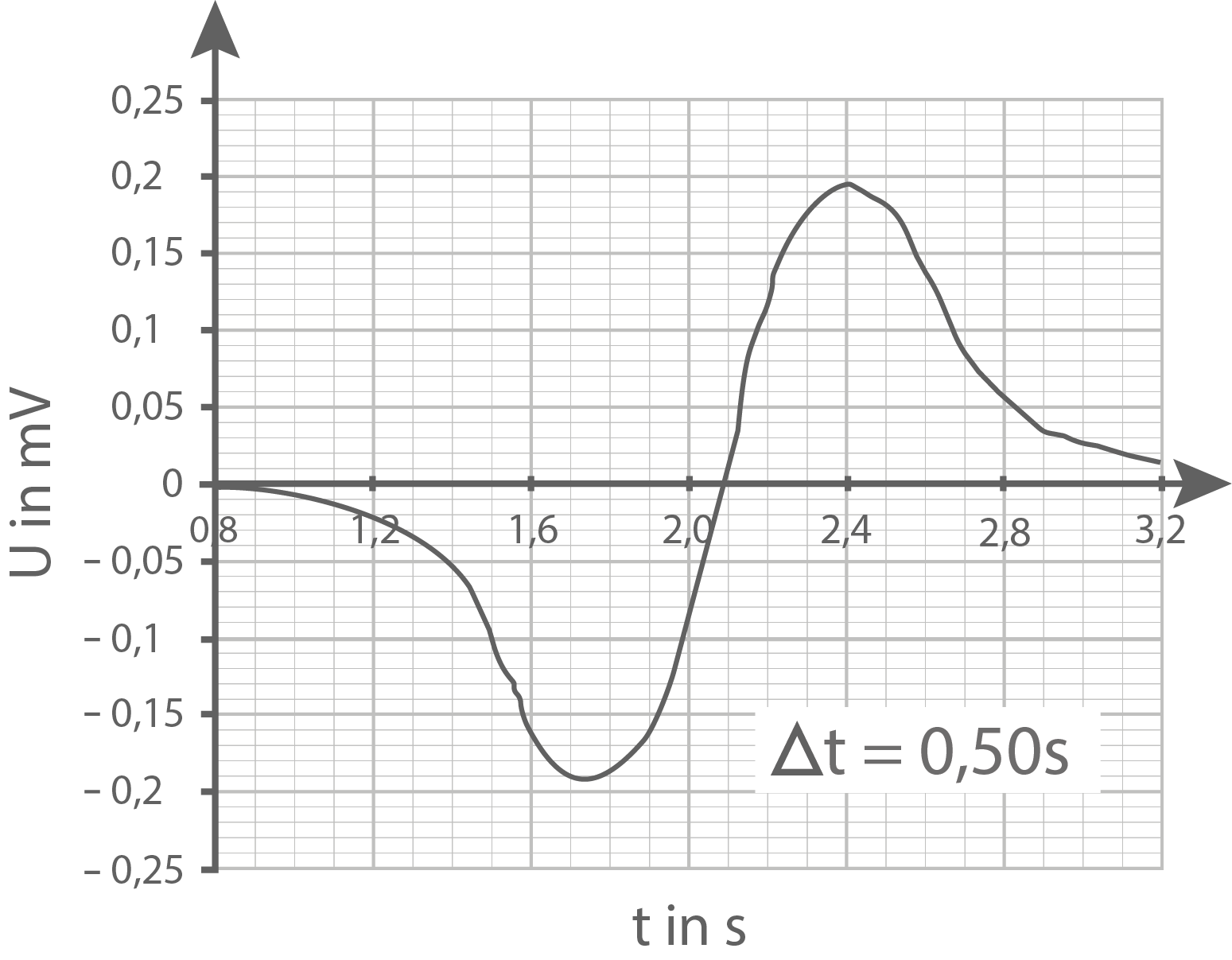
 beschreibt den maximalen Betrag des Spannungssignals ohne Berücksichtigung des Vorzeichens. Die maximale Stärke
beschreibt den maximalen Betrag des Spannungssignals ohne Berücksichtigung des Vorzeichens. Die maximale Stärke  des magnetischen Feldes im homogenen Bereich kann für die verwendete Leiterschleife näherungsweise mittels
des magnetischen Feldes im homogenen Bereich kann für die verwendete Leiterschleife näherungsweise mittels  ermittelt werden. Die Breite der Leiterschleife beträgt dabei
ermittelt werden. Die Breite der Leiterschleife beträgt dabei  und die Länge der Verdunklungsfahne
und die Länge der Verdunklungsfahne 




- Bestimme für jedes Diagramm gemäß Abbildung 6 den Betrag der maximalen Induktionsspannung
sowie den Geschwindigkeitsbetrag
des Gleiters.
Hinweis: Berücksichtigen Sie dabei die unterschiedlichen Skalierungen der-Achsen.
- Zeichne ein
-Diagramm.
- Ermittle anhand einer grafischen Auswertung des
-
-Diagramms die Stärke
des magnetischen Feldes.
d)
Der Versuchsaufbau wird gemäß Abbildung 7a durch einen weiteren Hufeisenmagneten ergänzt. Die zweite Lichtschranke ist dabei der Übersichtlichkeit halber nicht mehr dargestellt. Der Gleiter samt rechteckiger Leiterschleife bewegt sich gleichförmig von links nach rechts. Abbildung 7b zeigt das dabei aufgenommene  -
-  -Diagramm.
-Diagramm.
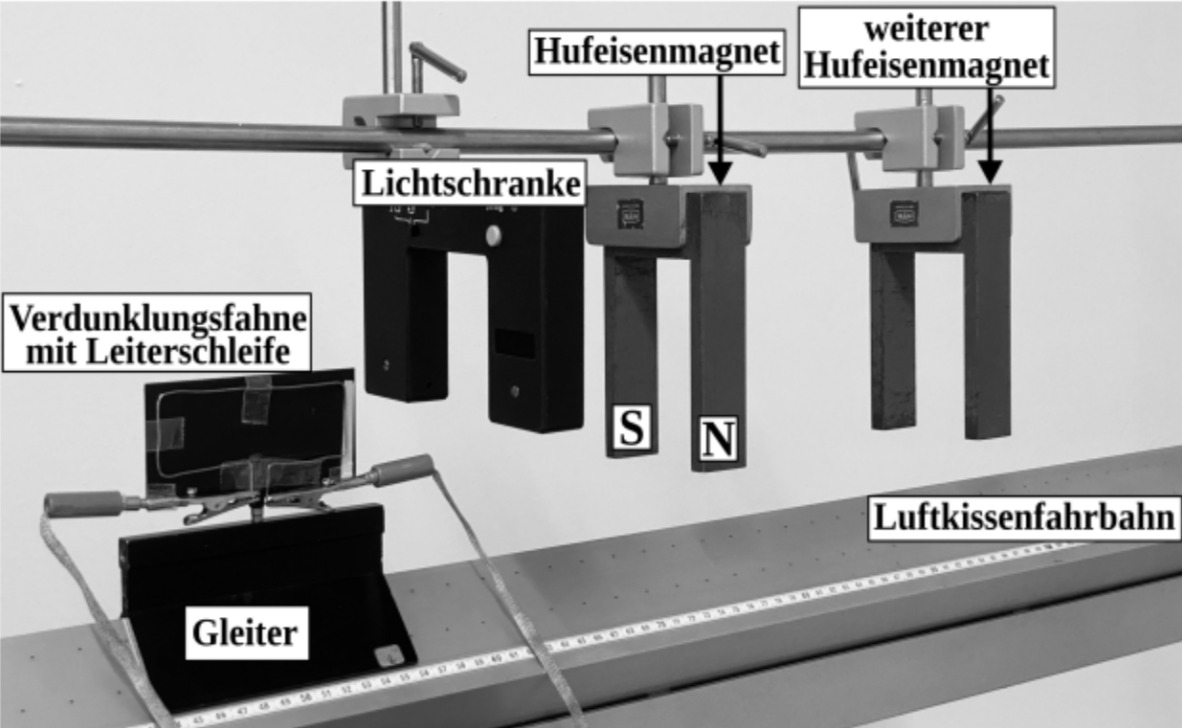
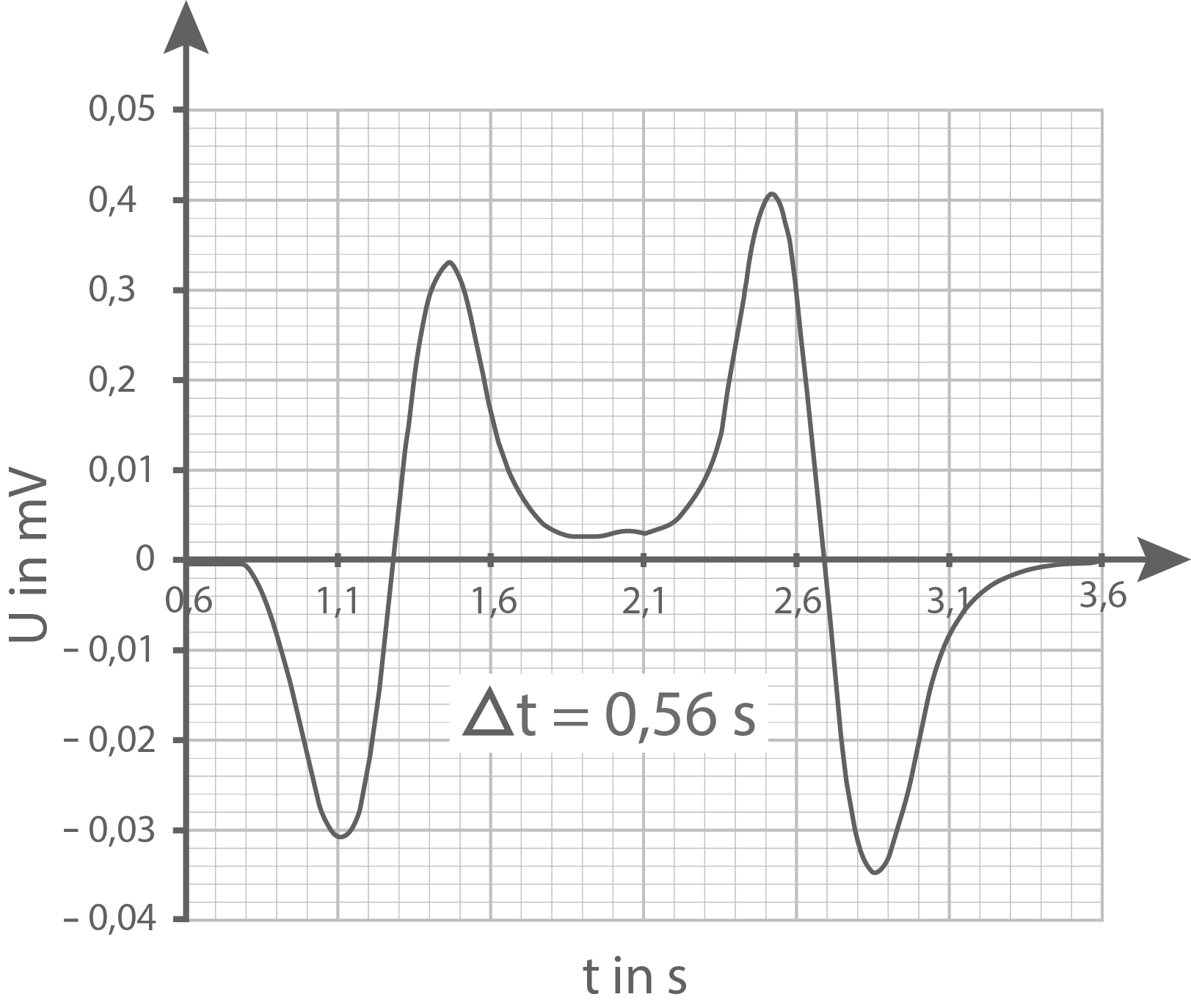

Abbildung 7a: Versuchsaufbau inklusive eines weiteren Hufeisenmagneten

- Erläutere mithilfe von Abbildung 7b, wie der ergänzte Magnet gepolt ist und welcher der beiden Magnete eine größere Stärke
des magnetischen Feldes aufweist.
- Bestimme mithilfe von Abbildung 7b den Abstand
zwischen den Mitten der beiden Hufeisenmagneten.
e)
Nachfolgend wird das Experiment abermals verändert. Unter den gleichnamigen Polen der beiden Hufeisenmagneten werden jeweils quaderförmige Eisenkerne so angebracht, dass zwischen ihnen ein Spalt ist (vgl. Abbildung 8a). Abbildung 8b zeigt das aufgenommene  -
-  -Diagramm, wenn sich der Gleiter abermals gleichförmig von links nach rechts bewegt.
-Diagramm, wenn sich der Gleiter abermals gleichförmig von links nach rechts bewegt.
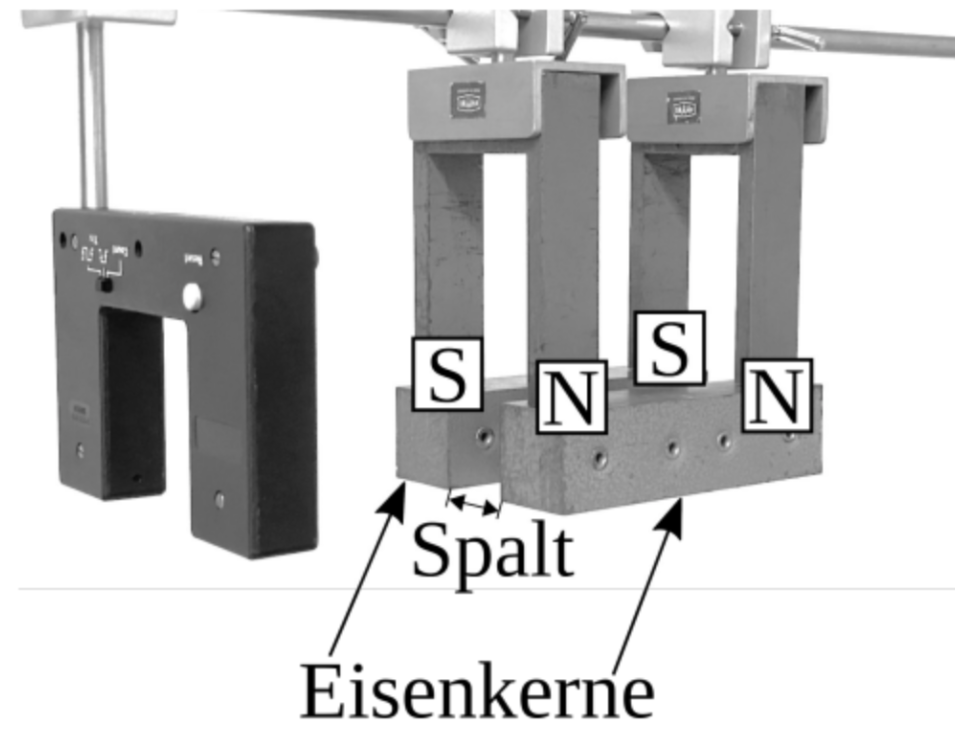 Die Leiterschleife bewegt sich dabei durch den Spalt zwischen den beiden Eisenkernen.
Die Leiterschleife bewegt sich dabei durch den Spalt zwischen den beiden Eisenkernen.

Abbildung 8a: Versuchsaufbau mit Eisenkern
- Vergleiche den zeitlichen Verlauf der Spannung in Abbildung 3 und Abbildung 8b.
- Erkläre die mit annähernd
gemessene Spannung im Zeitintervall von
bis
in Abbildung 8b.
(4 + 16 + 15 + 8 + 7 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Teillösung 1: Grundlagen zum Induktionsgesetz
a)
Erläuterung der Ursache für das Auftreten einer Induktionsspannung
Der 1. Term beschreibt das Auftreten einer Induktionsspannung, wenn sich die vom Magnetfeld senkrecht durchsetzte Fläche eines Leiterkreises (z.B. einer Leiterschleife) zeitlich ändert. Der 2. Term beschreibt das Auftreten einer Induktionsspannung, wenn sich die Stärke  des magnetischen Feldes, das die Fläche eines Leitkreises (z.B. einer Leiterschleife) senkrecht durchsetzt, zeitlich ändert.
Beschreibung eines Experimentes
Für den 1. Term demonstriert beispielsweise das Rotieren einer Leiterschleife in einem Magnetfeld das Auftreten einer Induktionsspannung. Ein geeignetes Experiment, um das Auftreten einer Induktionsspanung gemäß des 2. Terms zu demonstrieren, wäre beispielsweise das Legen einer Induktionsspule in eine Feldspule und die zeitliche Änderung der Stärke
des magnetischen Feldes, das die Fläche eines Leitkreises (z.B. einer Leiterschleife) senkrecht durchsetzt, zeitlich ändert.
Beschreibung eines Experimentes
Für den 1. Term demonstriert beispielsweise das Rotieren einer Leiterschleife in einem Magnetfeld das Auftreten einer Induktionsspannung. Ein geeignetes Experiment, um das Auftreten einer Induktionsspanung gemäß des 2. Terms zu demonstrieren, wäre beispielsweise das Legen einer Induktionsspule in eine Feldspule und die zeitliche Änderung der Stärke  des magnetischen Feldes der Feldspule.
des magnetischen Feldes der Feldspule.
b)
Beim Zeichnen eines  -
- -Diagramms dieses Gedankenexperiments ist der Vorzeichenwechsel genauso zu beachten wie derselbe Betrag der Induktionsspannung. Auch die Dauer beim Auftreten einer von null verschiedenen Induktionsspannung muss gleich sein. Außerdem soll das Zeitintervall für die vollständig im Magnetfeld befindliche Leiterschleife länger sein als die beiden Zeitintervalle beim Ein- und Austreten.
-Diagramms dieses Gedankenexperiments ist der Vorzeichenwechsel genauso zu beachten wie derselbe Betrag der Induktionsspannung. Auch die Dauer beim Auftreten einer von null verschiedenen Induktionsspannung muss gleich sein. Außerdem soll das Zeitintervall für die vollständig im Magnetfeld befindliche Leiterschleife länger sein als die beiden Zeitintervalle beim Ein- und Austreten.
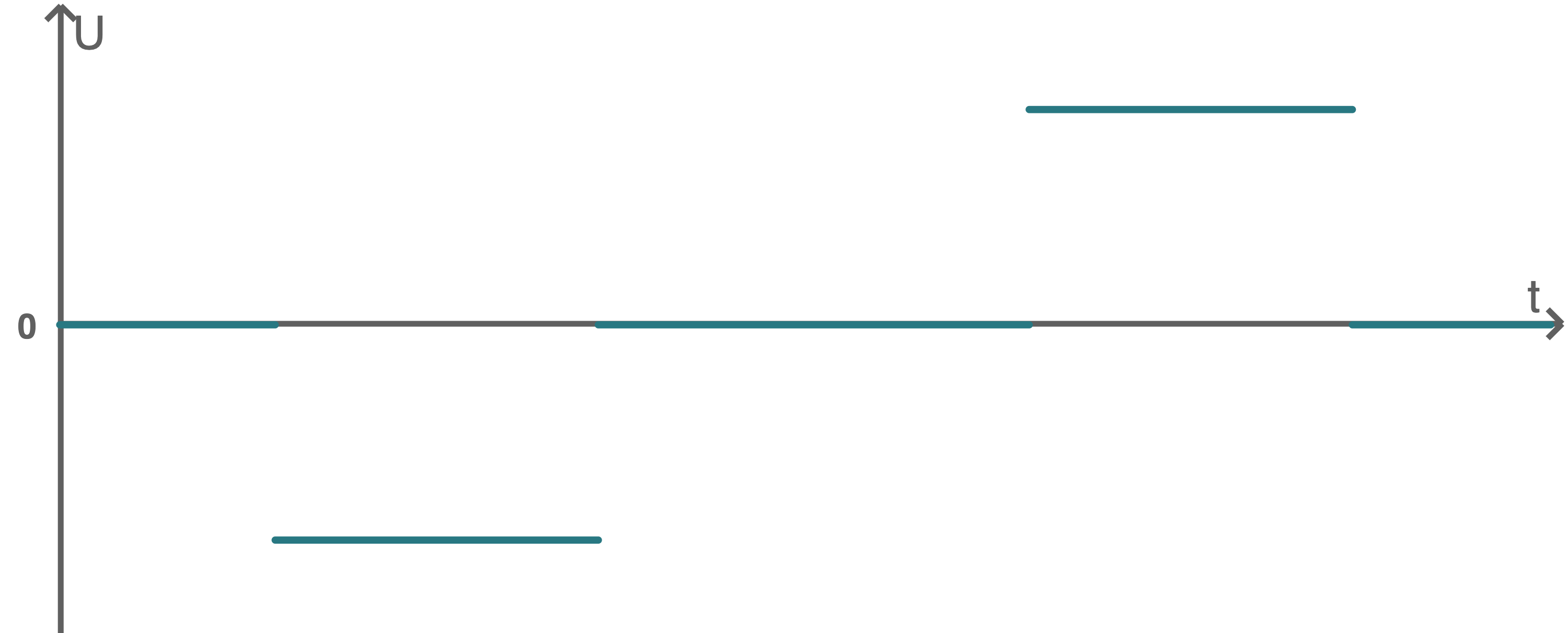
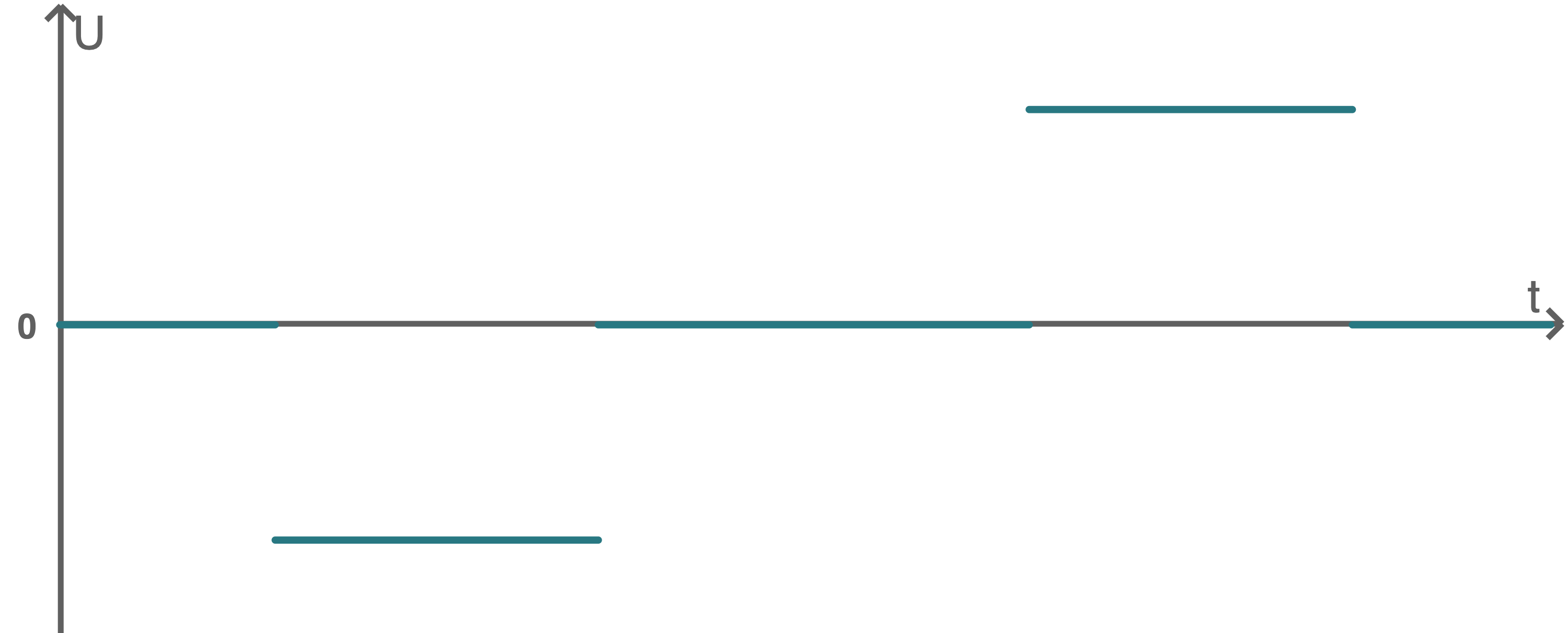
ein mögliches, qualitatives  -
- -Diagramm
-Diagramm
c)
Begründung der Vereinfachung des Induktionsgesetzes
Beim Eintritt der Leiterschleife mit der Windungszahl  in das Magnetfeld ändert sich zeitlich die senkrecht von den Feldlinien durchsetzte Fläche, wobei die Stärke
in das Magnetfeld ändert sich zeitlich die senkrecht von den Feldlinien durchsetzte Fläche, wobei die Stärke  des Magnetfeldes konstant ist. Damit ist der 1. Term des in der Aufgabenstellung angegebenen Induktionsgesetzes mit der Windungszahl
des Magnetfeldes konstant ist. Damit ist der 1. Term des in der Aufgabenstellung angegebenen Induktionsgesetzes mit der Windungszahl  zu verwenden, wohingegen der 2. Term stets null ist, da sich die Stärke
zu verwenden, wohingegen der 2. Term stets null ist, da sich die Stärke  des Magnetfeldes zeitlich nicht ändert.
Herleitung des Zusammenhangs
des Magnetfeldes zeitlich nicht ändert.
Herleitung des Zusammenhangs
 beschreibt die Längenänderung während der Zeit
beschreibt die Längenänderung während der Zeit  des sich im Magnetfeld befindlichen Teils der Leiterschleife. Daraus folgt der Zusammenhang
des sich im Magnetfeld befindlichen Teils der Leiterschleife. Daraus folgt der Zusammenhang  und es ergibt sich:
und es ergibt sich:
![\(\begin{array}[t]{rll}
U_{\text {ind }}&=& -B \cdot \dfrac{\Delta A}{\Delta t} &\quad \scriptsize \\[5pt]
&=& -B \cdot \dfrac{\Delta s \cdot b}{\Delta t} &\quad \scriptsize \\[5pt]
&=& -B \cdot b \cdot \dfrac{\Delta s}{\Delta t} &\quad \scriptsize \\[5pt]
&=& -B \cdot b \cdot v
\end{array}\)](https://www.schullv.de/resources/formulas/6ca7fe2dc59ccb5bb672c731f828da42ba269240f51cec5bce23baa9c12fa3cd_light.svg) Dabei ist
Dabei ist  der Geschwindigkeitsbetrag der Leiterschleife.
der Geschwindigkeitsbetrag der Leiterschleife.
Teillösung 2: Fahrbahn-Versuche zum Induktionsgesetz
a)
Die gemessene Spannung ist zunächst nahe null und negativ. Sie wird mit zunehmender Zeit immer kleiner, bis sie bei etwa  ihr Minimum mit
ihr Minimum mit  erreicht. Danach steigen die Spannungswerte, bis bei etwa
erreicht. Danach steigen die Spannungswerte, bis bei etwa  der Wert null gemessen wird. Von nun an sind die Spannungswerte positiv und steigen zunächst bis etwa
der Wert null gemessen wird. Von nun an sind die Spannungswerte positiv und steigen zunächst bis etwa  mit einer maximalen Spannung von etwa
mit einer maximalen Spannung von etwa  . Danach fallen die Spannungswerte und nähern sich wieder null an.
. Danach fallen die Spannungswerte und nähern sich wieder null an.
b)
Erklärung mithilfe eines Vergleichs der Lorentzkraft
Die Lorentzkraft wirkt im gesamten Leiter aufgrund der Drei-Finger-Regel der linken Hand stets nach unten und ist proportional zur Stärke  des magnetischen Feldes am entsprechenden Ort. Da das rechte Leiterstück in beiden Abbildungen im homogenen Feldbereich ist und dort die gleiche Feldstärke
des magnetischen Feldes am entsprechenden Ort. Da das rechte Leiterstück in beiden Abbildungen im homogenen Feldbereich ist und dort die gleiche Feldstärke  vorliegt, wirkt im rechten Leiterstück die gleiche Lorentzkraft. Das linke Leiterstück ist in beiden Abbildungen jeweils einer Feldstärke
vorliegt, wirkt im rechten Leiterstück die gleiche Lorentzkraft. Das linke Leiterstück ist in beiden Abbildungen jeweils einer Feldstärke  ausgesetzt. Gemäß einem Vergleich der Feldstärken für das linke Leiterstück ist die Lorentzkraft in Abbildung 5c größer als in Abbildung 5b. Größere Unterschiede zwischen den Lorentzkräften im rechten und linken Leiterstück bewirken höhere Spannungen. Somit ist das zu messende Spannungssignal in Abbildung 5b höher als in Abbildung 5c.
Begründung der kleiner werdenden Spannung
Da das rechte Leiterstück im homogenen Feldbereich einer konstanten Stärke
ausgesetzt. Gemäß einem Vergleich der Feldstärken für das linke Leiterstück ist die Lorentzkraft in Abbildung 5c größer als in Abbildung 5b. Größere Unterschiede zwischen den Lorentzkräften im rechten und linken Leiterstück bewirken höhere Spannungen. Somit ist das zu messende Spannungssignal in Abbildung 5b höher als in Abbildung 5c.
Begründung der kleiner werdenden Spannung
Da das rechte Leiterstück im homogenen Feldbereich einer konstanten Stärke  des magnetischen Feldes ausgesetzt ist, ist im rechten Leiterstück die Lorentzkraft maximal und konstant. Das linke Leiterstück ist bei der beschriebenen Bewegung einer zunehmend größeren Stärke
des magnetischen Feldes ausgesetzt ist, ist im rechten Leiterstück die Lorentzkraft maximal und konstant. Das linke Leiterstück ist bei der beschriebenen Bewegung einer zunehmend größeren Stärke  des magnetischen Feldes ausgesetzt, weshalb die Lorentzkraft im linken Leiterstück zunehmend größer wird. Damit ist der Unterschied der Lorentzkraft im rechten und linken Leiterstück zunehmend kleiner, weshalb die gemessene Spannung zunehmend kleiner wird.
Erläuterung der Spannung
des magnetischen Feldes ausgesetzt, weshalb die Lorentzkraft im linken Leiterstück zunehmend größer wird. Damit ist der Unterschied der Lorentzkraft im rechten und linken Leiterstück zunehmend kleiner, weshalb die gemessene Spannung zunehmend kleiner wird.
Erläuterung der Spannung  , wenn sich die Mitte der Leiterschleife genau in der Mitte des homogenen Feldbereichs befindet
Wenn die Mitte der Leiterschleife genau mittig im homogenen Bereich ist, sind beide äußeren Leiterstücke den gleichen Stärken
, wenn sich die Mitte der Leiterschleife genau in der Mitte des homogenen Feldbereichs befindet
Wenn die Mitte der Leiterschleife genau mittig im homogenen Bereich ist, sind beide äußeren Leiterstücke den gleichen Stärken  des magnetischen Feldes ausgesetzt. Die Lorentzkräfte weisen also den gleichen Betrag auf und zeigen in die gleiche Richtung, damit wird eine Spannung von
des magnetischen Feldes ausgesetzt. Die Lorentzkräfte weisen also den gleichen Betrag auf und zeigen in die gleiche Richtung, damit wird eine Spannung von  gemessen.
Skizzierung des veränderten Spannungssignals
gemessen.
Skizzierung des veränderten Spannungssignals
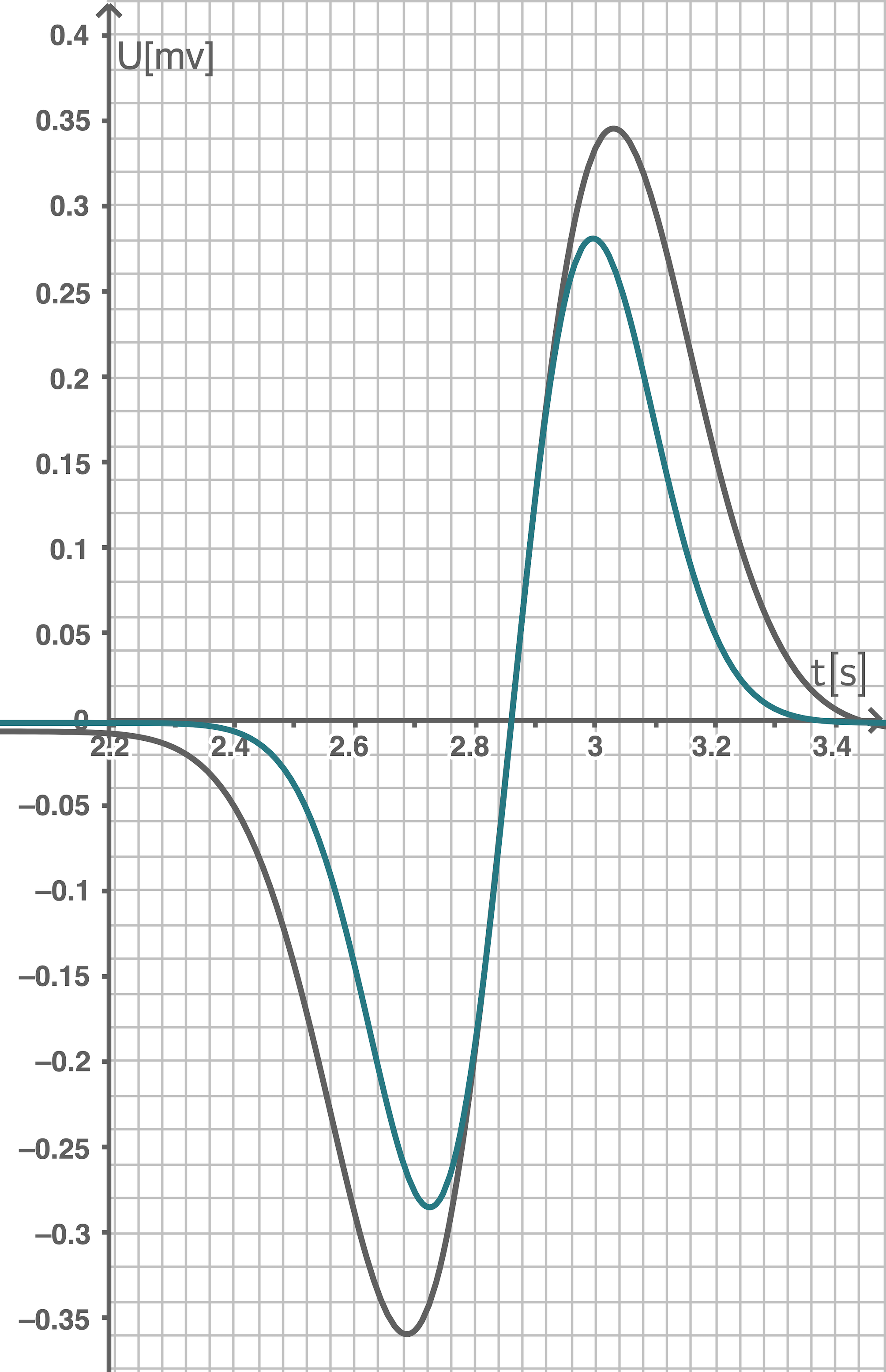

c)
Bestimmung der Beträge der maximalen Induktionsspannungen  und der Geschwindigkeitsbeträge
und der Geschwindigkeitsbeträge  In der folgenden Tabelle sind die Werte eingetragen, wobei die aufgeführten Spannungen gemittelte und gerundete Werte der Spannungsextrema sind: In der folgenden Tabelle sind die Werte eingetragen, wobei die aufgeführten Spannungen gemittelte und gerundete Werte der Spannungsextrema sind:
In der folgenden Tabelle sind die Werte eingetragen, wobei die aufgeführten Spannungen gemittelte und gerundete Werte der Spannungsextrema sind: In der folgenden Tabelle sind die Werte eingetragen, wobei die aufgeführten Spannungen gemittelte und gerundete Werte der Spannungsextrema sind:
 -
- Diagramm
Diagramm
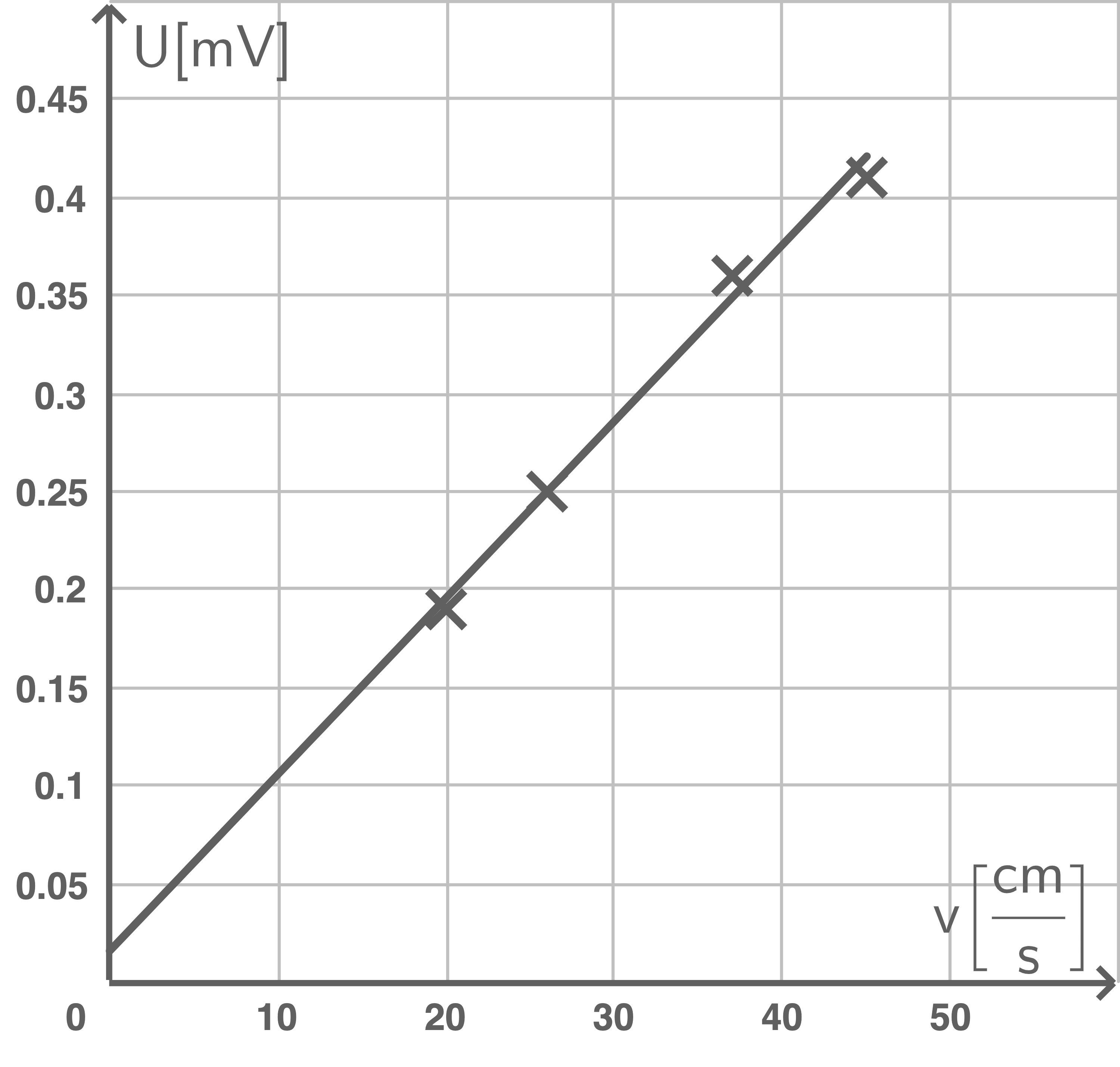 Ermittlung der Stärke
Ermittlung der Stärke  des magnetischen Feldes
Eine grafische Auswertung der eingezeichneten Messdaten zeigt den Zusammenhang
des magnetischen Feldes
Eine grafische Auswertung der eingezeichneten Messdaten zeigt den Zusammenhang  . Mit
. Mit  und mit der Steigung
und mit der Steigung  folgt:
folgt:
![\(\begin{array}[t]{rll}
v \cdot B_{\text {max }} \cdot b &=& U_{\text {max }}&\quad \scriptsize \mid\; \cdot \frac{1}{v} \\[5pt]
B_{\text {max }} \cdot b&=& \dfrac{U_{\text {max }}}{v} &\quad \scriptsize \mid\; U_{\text {max }} \sim v \\[5pt]
B_{\text {max }} \cdot b&=& m &\quad \scriptsize \mid\; \dfrac{1}{b}\\[5pt]
B_{\text {max }} &=& \dfrac{m}{b} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0ed55e0c1707ad6213a1d445f8984a035e976a7ebd86ba04fb660a4b50725c34_light.svg) Einsetzen der Werte für
Einsetzen der Werte für  und für
und für  liefert:
liefert:
![\(\begin{array}[t]{rll}
B_{\text {max }} &=& \dfrac{0,0090 \;\dfrac{\text{mV}}{\dfrac{\text{cm}}{\text{s}}}}{3,2 \;\text{cm}} &\quad \scriptsize \\[5pt]
B_{\text {max }}&=& \dfrac{9,0 \;\dfrac{\mu \text{V}}{\dfrac{\text{cm}}{\text{s}}}}{3,2 \;\text{cm}} &\quad \scriptsize \\[5pt]
B_{\text {max }}&\approx& 28 \text{mT}
\end{array}\)](https://www.schullv.de/resources/formulas/1903e5d731c3b0b454053f9a050c671e064d180610e0ae48acce6d24cd7262ba_light.svg)
| Messungen | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0,22 | 0,27 | 0,38 | 0,50 | |
| 0,41 | 0,36 | 0,25 | 0,19 | |
| 45 | 37 | 26 | 20 | |

d)
Erläuterung der Polung des ergänzten Magneten und Erläuterung des Magneten mit der größeren Stärke  des magnetischen Feldes
Die Messdaten und die Abbildung zeigen, dass der linke Hufeisenmagnet, der zuerst von dem Gleiter erreicht wird, weiterhin so ausgerichtet ist wie bei den vorherigen Experimenten (Nordpol vorne, Südpol hinten; Spannungsverlauf ähnlich zu Abbildung 3). Beim zweiten Magneten sind die Pole jedoch genau andersherum orientiert, da das Spannungssignal beim zweiten Hufeisenmagneten bezüglich des Vorzeichens genau invers zum ersten ist. Also hat der rechte Hufeisenmagnet vorne seinen Süd- und hinten seinen Nordpol. Außerdem sind die Spannungsextrema beim zweiten Hufeisenmagneten größer, weshalb wegen der Gleichförmigkeit der Bewegung auf einen Magneten mit einer größeren Feldstärke
des magnetischen Feldes
Die Messdaten und die Abbildung zeigen, dass der linke Hufeisenmagnet, der zuerst von dem Gleiter erreicht wird, weiterhin so ausgerichtet ist wie bei den vorherigen Experimenten (Nordpol vorne, Südpol hinten; Spannungsverlauf ähnlich zu Abbildung 3). Beim zweiten Magneten sind die Pole jedoch genau andersherum orientiert, da das Spannungssignal beim zweiten Hufeisenmagneten bezüglich des Vorzeichens genau invers zum ersten ist. Also hat der rechte Hufeisenmagnet vorne seinen Süd- und hinten seinen Nordpol. Außerdem sind die Spannungsextrema beim zweiten Hufeisenmagneten größer, weshalb wegen der Gleichförmigkeit der Bewegung auf einen Magneten mit einer größeren Feldstärke  geschlossen werden kann.
Bestimmung des Abstandes
geschlossen werden kann.
Bestimmung des Abstandes  Die Verdunklungszeit beträgt
Die Verdunklungszeit beträgt  . Damit ergibt sich folgender Geschwindigkeitsbetrag:
. Damit ergibt sich folgender Geschwindigkeitsbetrag:
![\(\begin{array}[t]{rll}
v &=& \dfrac{\Delta s}{\Delta t}&\quad \scriptsize \\[5pt]
&=& \dfrac{10 \text{cm}}{0,56 \text{s}} \quad \scriptsize \\[5pt]
&\approx& 18 \dfrac{\text{cm}}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/74db4dd8d86d097becddcfe2e72115072ae42f8267fb1140500ecd9b7e4d75ef_light.svg) Die Nulldurchgänge liegen bei
Die Nulldurchgänge liegen bei  und
und  , sodass sich der zeitliche Abstand von
, sodass sich der zeitliche Abstand von  in einen räumlichen Abstand
in einen räumlichen Abstand  umrechnen lässt:
umrechnen lässt:
![\(\begin{array}[t]{rll}
D&=& 1,4 \;\text{s} \cdot\dfrac{\Delta s}{\Delta t}&\quad \scriptsize \\[5pt]
&=& 1,4 \;\text{s} \cdot 18 \;\dfrac{\text{cm}}{\text{s}}& \quad \scriptsize \\[5pt]
&\approx& 25 \text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/66a19795bf655b1476fa9462bd56a35575d2326449074e7708a7e1e8db44a88c_light.svg) Die Mitten der Hufeisenmagnete sind folglich etwa
Die Mitten der Hufeisenmagnete sind folglich etwa  voneinander entfernt.
voneinander entfernt.
e)
Vergleich der zeitlichen Verläufe der Spannungen
Sowohl in Abbildung 3 als auch in Abbildung 8b ist das erste Spannungsextremum im negativen, das zweite Spannungsextremum im positiven Bereich. Auch beginnt und endet die Spannungskurve nahe null. Im Gegensatz zu Abbildung 3 ist der Verlauf der Spannung zwischen den Extrema in Abbildung 8b anders. Erstens ist zwischen  und
und  eine Plateauphase mit nahezu
eine Plateauphase mit nahezu  . Zweitens verläuft das Spannungssignal kurz vor und kurz hinter der Plateauphase zunehmend weniger steil.
Erklärung der gemessenen Spannung
. Zweitens verläuft das Spannungssignal kurz vor und kurz hinter der Plateauphase zunehmend weniger steil.
Erklärung der gemessenen Spannung  Dies kann dadurch erklärt werden, dass sich durch das Anbringen der Eisenkerne ein deutlich breiterer Bereich, in dem das Magnetfeld homogen ist, ausbildet, sodass an der komplett darin bewegten Leiterschleife keine Induktionsspannung messbar ist.
Dies kann dadurch erklärt werden, dass sich durch das Anbringen der Eisenkerne ein deutlich breiterer Bereich, in dem das Magnetfeld homogen ist, ausbildet, sodass an der komplett darin bewegten Leiterschleife keine Induktionsspannung messbar ist.