HT 3
Neutrinomassenbestimmung
Die experimentelle Untersuchung von Neutrinos stellt ein schwieriges Unterfangen dar. Es gilt heute als sicher, dass Neutrinos eine endliche Masse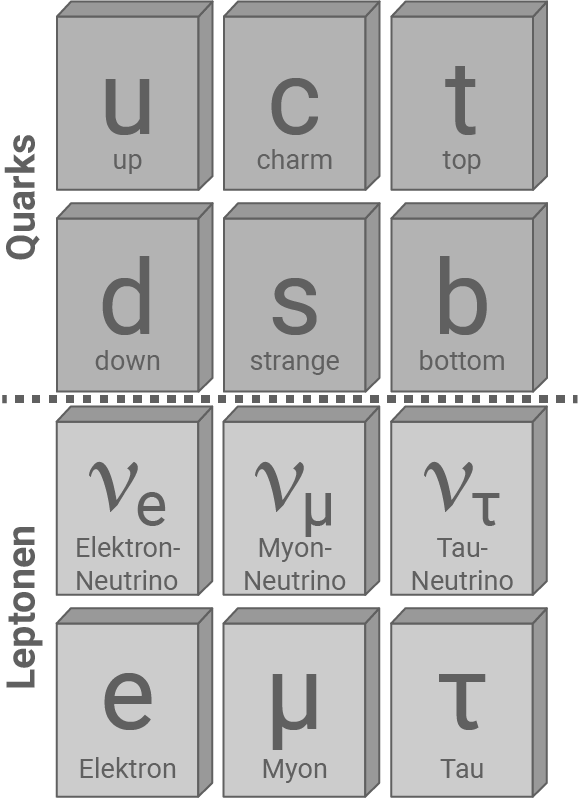
Abbildung 1: Überblick über die elementaren Teilchen des Standardmodells
a)
Die drei unterschiedlichen Neutrinosorten gehören zur Teilchenart der Leptonen.
- Gib die elektrische Ladung
des Elektrons, des Myons und des Tauons sowie der jeweiligen zugehörigen Neutrinos an.
- Erläutere, warum ein direkter Nachweis von Neutrinos erheblich schwieriger ist als der Nachweis der anderen Leptonen.
b)
Alle aus Atomen aufgebaute Materie besteht lediglich aus drei der in Abbildung 1 dargestellten elektrisch geladenen Elementarteilchen.
 (Deuterium).
(Deuterium).
- Erläutere, warum alle anderen elektrisch geladenen Elementarteilchen aus Abbildung 1 nicht in der heute existierenden atomaren Materie vorkommen.
- Gib an, aus wie vielen und welchen Elementarteilchen aus Abbildung 1 das Deuteriumatom
aufgebaut ist.
- Beschreibe, welche elementaren Wechselwirkungen für die Stabilität des
-Atoms verantwortlich sind.
c)
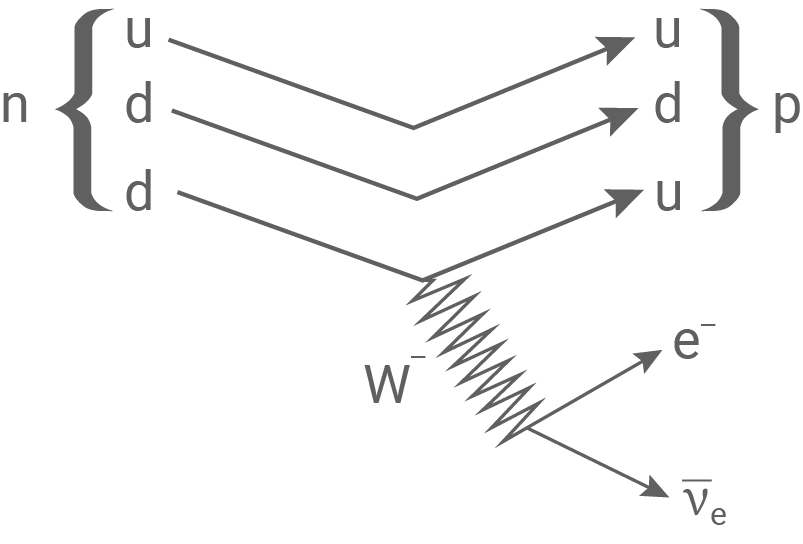
Neutrinos und ihre Antiteilchen treten ausschließlich bei Prozessen unter Beteiligung der schwachen Wechselwirkung auf. Ein typisches Beispiel für einen solchen Prozess ist der  -Zerfalls eines Neutrons in ein Proton. Dieser Umwandlungsprozess ist auf Quarkebene in Abbildung 2 dargestellt.
-Zerfalls eines Neutrons in ein Proton. Dieser Umwandlungsprozess ist auf Quarkebene in Abbildung 2 dargestellt.
Teilaufgabe 2: Die Zerfallseigenschaften des Tritiums und das Energiespektrum seiner 
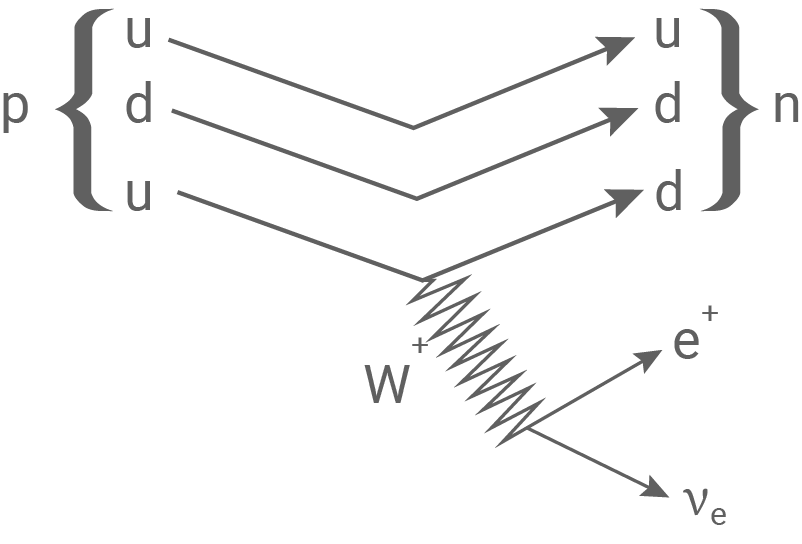
Abbildung 2: Prozess der  -Umwandlung aufgrund der schwachen Wechselwirkung
-Umwandlung aufgrund der schwachen Wechselwirkung
- Beschreibe den in Abbildung 2 dargestellten Vorgang und gehen Sie dabei insbesondere auf die Bedeutung des
-Teilchens ein.
- Gib an, was sich an Abbildung 2 ändert, wenn anstelle des
-Zerfalls ein
-Zerfall dargestellt wird.
(5 + 8 + 5 Punkte)
a)
Das Wasserstoffisotop  (Tritium) ist ein
(Tritium) ist ein  -Strahler mit der Zerfallsgleichung:
-Strahler mit der Zerfallsgleichung:
 Die Abnahme der Anzahl
Die Abnahme der Anzahl  der Tritiumkerne in einer Probe als Funktion der Zeit wird durch das Zerfallsgesetz
der Tritiumkerne in einer Probe als Funktion der Zeit wird durch das Zerfallsgesetz  beschrieben. Dabei bezeichnet
beschrieben. Dabei bezeichnet  die Anfangszahl der Tritiumkerne und
die Anfangszahl der Tritiumkerne und  die Zerfallskonstante des Tritiums.
die Zerfallskonstante des Tritiums.
Die Aktivität der Probe ergibt sich aus der Ableitung von
der Probe ergibt sich aus der Ableitung von  nach der Zeit, also der Änderungsrate der Tritiumkerne
nach der Zeit, also der Änderungsrate der Tritiumkerne  . Für die Aktivität
. Für die Aktivität  gilt das Abnahmegesetz
gilt das Abnahmegesetz 
 bestimmt und dann nach
bestimmt und dann nach  erneut. Es zeigt sich, dass sich die Aktivität
erneut. Es zeigt sich, dass sich die Aktivität  der Probe um
der Probe um  gegenüber der ersten Messung reduziert hat.
gegenüber der ersten Messung reduziert hat.
Die Aktivität
- Zeige, dass für die Anfangsaktivität
der Probe folgender Zusammenhang gilt:
- Zeige, dass die Halbwertszeit
eines radioaktiven Nuklids wie folgt von dessen Zerfallskonstante
abhängt:
.
- Bestimme aus dieser Messung die Halbwertszeit
des Tritiums in Jahren.
b)
Da der  -Zerfall des Tritiums direkt in den Grundzustand des Tochternuklids
-Zerfall des Tritiums direkt in den Grundzustand des Tochternuklids  erfolgt, tritt bei diesem Prozess keine
erfolgt, tritt bei diesem Prozess keine  -Strahlung auf. Somit verteilt sich bei diesem
-Strahlung auf. Somit verteilt sich bei diesem  -Zerfall die gesamte frei werdende Energie
-Zerfall die gesamte frei werdende Energie  auf die entstehenden Teilchen. Für die Gesamtenergie
auf die entstehenden Teilchen. Für die Gesamtenergie  des
des  -Zerfalls gilt dabei der folgende Zusammenhang:
-Zerfalls gilt dabei der folgende Zusammenhang:
![\(E_{\text {ges }}=\left[m_{3_\text H }-\left(m_{3_{\text{He}}} +m_{ e }+m_{\bar{v}}\right)\right] \cdot c ^2\)](https://www.schullv.de/resources/formulas/154f5a710be01d702283f4cb1a5fe78b3822969f45d88d745ef75dcf93dd27de_light.svg) .
Erläutere den angegebenen Zusammenhang zwischen den Massen und der Gesamtenergie des
.
Erläutere den angegebenen Zusammenhang zwischen den Massen und der Gesamtenergie des  -Zerfalls
-Zerfalls  .
.
c)
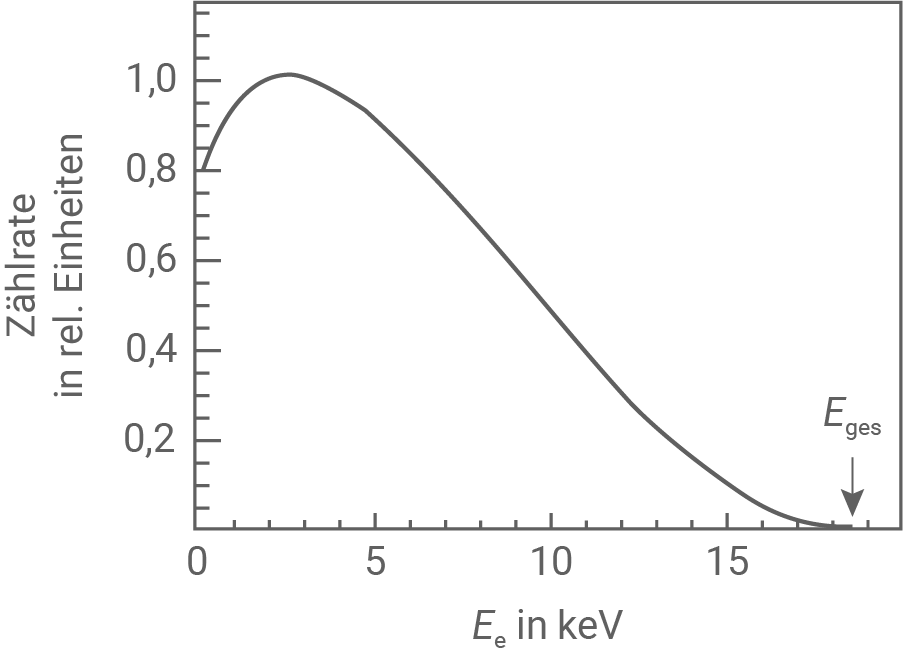
Ein gemessenes Energiespektrum der beim  -Zerfall des Tritiums entstehenden Elektronen ist in Abbildung 3 dargestellt.
-Zerfall des Tritiums entstehenden Elektronen ist in Abbildung 3 dargestellt.
 Aufgrund des großen Massenunterschieds zwischen Elektron und Tochterkern kann der
Aufgrund des großen Massenunterschieds zwischen Elektron und Tochterkern kann der  -Kern aus dem
-Kern aus dem  -Zerfall aufgrund der Impulserhaltung maximal
-Zerfall aufgrund der Impulserhaltung maximal  der kinetischen Energie des Elektrons
der kinetischen Energie des Elektrons  erhalten.
erhalten.
Teilaufgabe 3: Das KATRIN-Experiment und die Masse des Neutrinos
Für das Elektron-Antineutrino 
Abbildung 3: Energiespektrum der Elektronen des Tritium  -Zerfalls
-Zerfalls
- Beschreibe den Verlauf des Energiespektrums der Elektronen in Abbildung 3.
- Begründe, dass das ansonsten nicht nachweisbare Antineutrino
erforderlich ist, um das Spektrum in Abbildung 3 zu erklären.
(11 + 4 + 6 Punkte)
a)
Berechnen Sie die bislang gültige obere Grenze für die Neutrinomasse  in der Maßeinheit „
in der Maßeinheit „ “.
“.
b)
Das Ziel des KATRIN-Experiments ist es, das hochenergetische Ende des Energiespektrums beim  -Zerfall des Tritiums sehr genau zu messen. Die Masse des zerfallenden Tritiumkerns
-Zerfall des Tritiums sehr genau zu messen. Die Masse des zerfallenden Tritiumkerns  , die Masse des
, die Masse des  -Kerns
-Kerns  sowie die Masse des Elektrons
sowie die Masse des Elektrons  sind sehr genau bekannt. Für die Annahme, dass das Antineutrino
sind sehr genau bekannt. Für die Annahme, dass das Antineutrino  masselos ist
masselos ist  , kann damit die Gesamtenergie des
, kann damit die Gesamtenergie des  -Zerfalls des Tritiums sehr genau bestimmt werden und sie ergibt sich zu
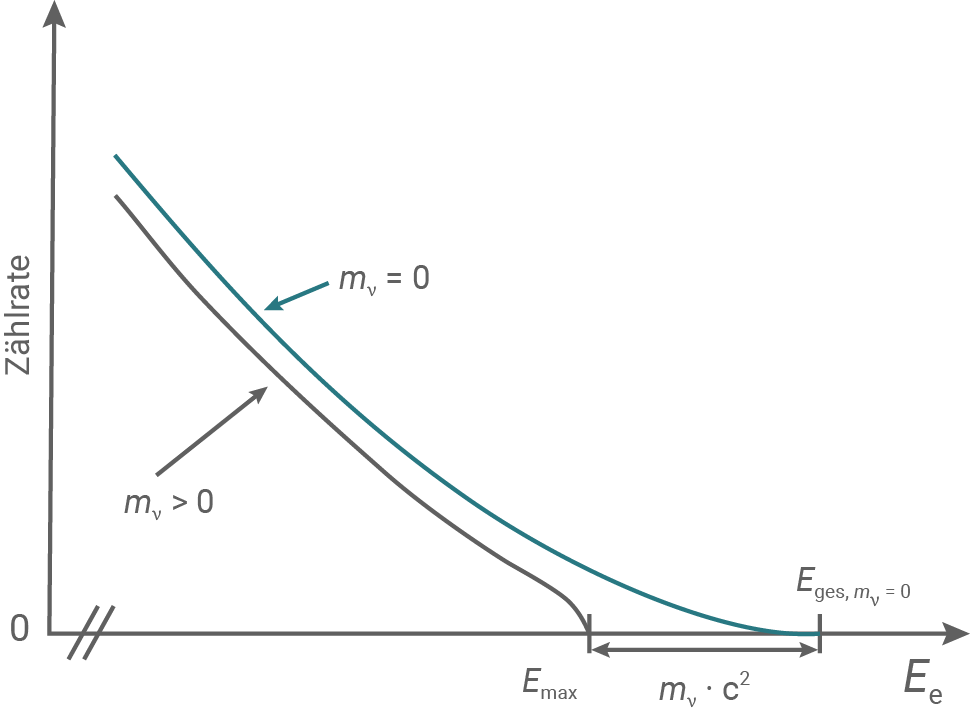
-Zerfalls des Tritiums sehr genau bestimmt werden und sie ergibt sich zu  Abbildung 4 zeigt die Verläufe des Elektronen-Energiespektrums des
Abbildung 4 zeigt die Verläufe des Elektronen-Energiespektrums des  -Zerfalls im Bereich der Gesamtenergie
-Zerfalls im Bereich der Gesamtenergie  für die Annahme eines masselosen Antineutrinos
für die Annahme eines masselosen Antineutrinos  sowie für den Fall
sowie für den Fall  . Bei einer Neutrinomasse
. Bei einer Neutrinomasse  gilt für die maximal mögliche Energie
gilt für die maximal mögliche Energie  der Elektronen aus dem
der Elektronen aus dem  -Zerfall
-Zerfall 
 der dabei entstehenden Elektronen bestimmt werden.
der dabei entstehenden Elektronen bestimmt werden.
Die Elektronen des 
Abbildung 4: Einfluss der Neutrinomasse  auf das hochenergetische Ende des Elektronenspektrums beim
auf das hochenergetische Ende des Elektronenspektrums beim  -Zerfall in der Nähe der Gesamtenergie
-Zerfall in der Nähe der Gesamtenergie 
- Begründe den in Abbildung 4 dargestellten Unterschied zwischen der maximalen Elektronenenergie
beim
-Zerfall und
- Gib an, in welchem Energieintervall die maximale Energie
der Elektronen beim
-Zerfall des Tritiums zu erwarten ist.

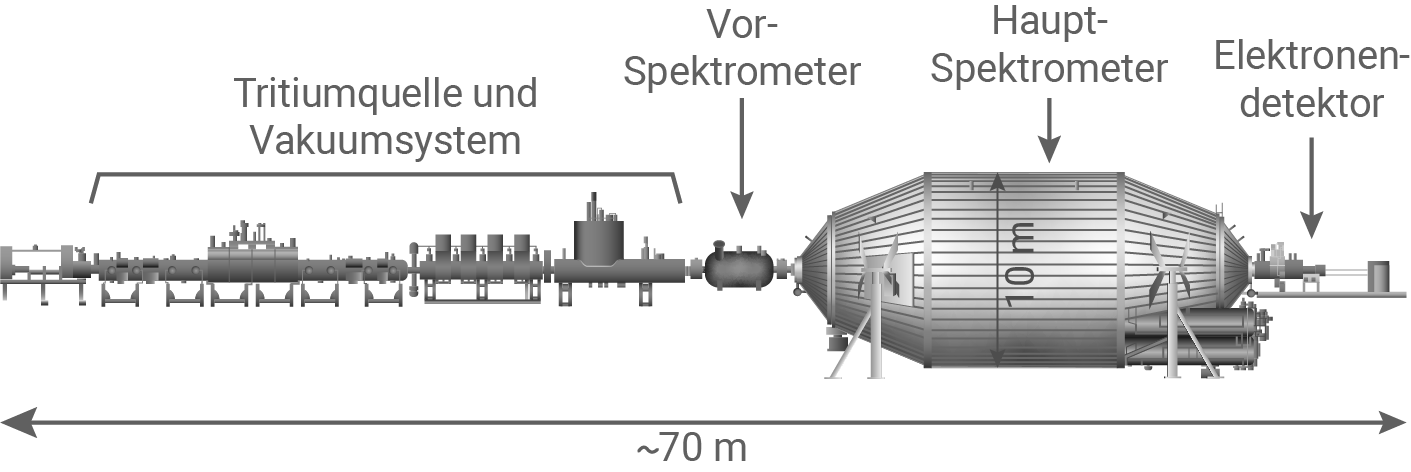
Abbildung 5: Komponenten des KATRIN-Experiments
c)
Aus messtechnischen Gründen werden die Elektronen im Innern des Haupt-Spektrometers zudem durch ein stark inhomogenes Magnetfeld zum Elektronendetektor geführt.
 weiter abgebremst und nur nach Überwinden dieser Gegenspannung im Elektronendetektor nachgewiesen. Die Gegenspannung im Haupt-Spektrometer kann zum jetzigen Zeitpunkt in Schritten von
weiter abgebremst und nur nach Überwinden dieser Gegenspannung im Elektronendetektor nachgewiesen. Die Gegenspannung im Haupt-Spektrometer kann zum jetzigen Zeitpunkt in Schritten von  stabilisiert eingestellt werden und soll in den nächsten Jahren durch weitere Verbesserungen am Experiment in Schritten von
stabilisiert eingestellt werden und soll in den nächsten Jahren durch weitere Verbesserungen am Experiment in Schritten von  variierbar sein.
variierbar sein.
- Begründe qualitativ, warum die kinetische Energie der Elektronen durch statische Magnetfelder prinzipiell nicht beeinflusst wird.
- Erläutere, warum diese Verbesserung der Einstellgenauigkeit der Gegenspannung
bei der Gegenfeldmethode zu genaueren Messergebnissen führt.
d)
Bereits heute grenzen die ersten vorläufigen Ergebnisse des KATRIN-Experiments die Ruheenergie des Elektron-Neutrinos auf  ein.
Beurteile diesen Erkenntnisfortschritt gegenüber dem Kenntnisstand vor dem KATRIN-Experiment.
ein.
Beurteile diesen Erkenntnisfortschritt gegenüber dem Kenntnisstand vor dem KATRIN-Experiment.
Teilaufgabe 4: Die Bedeutung der Neutrinomasse für die Kosmologie
Nach heutigem Kenntnisstand der Kosmologie besitzt das kugelförmige Universum einen Radius von mindestens
(2 + 8 + 7 + 3 Punkte)
Weitere Optimierungen am KATRIN-Experiment werden zukünftig zu einer höheren Messgenauigkeit führen. Es besteht die Aussicht, dass es dann auch einen Messwert für die Neutrinomasse
(6 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Teillösung 1
Neutrinos durchqueren Materie leicht, ohne dabei signifikante Energieverluste oder Ablenkungen zu erfahren. Ihre Interaktion erfolgt dabei ausschließlich über die schwache Wechselwirkung. Da sie keine elektrische Ladung besitzen, werden sie weder von elektrischen Feldern noch von magnetischen Feldern beeinflusst.
a)
| Leptonen | Ladung q |
|---|---|
| Elektron | -e |
| Myon | -e |
| Tauon | -e |
| Elektron-Neutrino | 0 |
| Myon-Neutrino | 0 |
| Tauon-Neutrino | 0 |
b)
Alle anderen elektrisch geladenen Elementarteilchen sind viel massiver. Die schwereren Teilchen sind instabil und zerfallen durch die starke oder schwache Wechselwirkung in leichtere Teilchen wie Elektronen, u-Quarks und d-Quarks. Daher sind sie nicht langfristig in der Materie vorhanden.
Das Deuteriumatom  besteht aus einem Proton und einem Neutron. Das Proton ist zusammengesetzt aus zwei Up-Quarks und einem Down-Quark, das Neutron besteht aus einem Up-Quark und zwei Down-Quarks. In der Atomhülle befindet sich ein Elektron.
Für die Stabilität des Deuteriumatoms
besteht aus einem Proton und einem Neutron. Das Proton ist zusammengesetzt aus zwei Up-Quarks und einem Down-Quark, das Neutron besteht aus einem Up-Quark und zwei Down-Quarks. In der Atomhülle befindet sich ein Elektron.
Für die Stabilität des Deuteriumatoms  sind die starke Wechselwirkung und die elektromagnetische Wechselwirkung verantwortlich. Die starke Wechselwirkung hält die Quarks im Proton und im Neutron zusammen und überwindet die elektrostatische Abstoßung der positiv geladenen Protonen im Atomkern. Die elektromagnetische Wechselwirkung sorgt für die Abstoßung zwischen den positiv geladenen Protonen im Kern, sodass diese nicht in einander fallen und bindet das Hüllenelektron an den Atomkern.
sind die starke Wechselwirkung und die elektromagnetische Wechselwirkung verantwortlich. Die starke Wechselwirkung hält die Quarks im Proton und im Neutron zusammen und überwindet die elektrostatische Abstoßung der positiv geladenen Protonen im Atomkern. Die elektromagnetische Wechselwirkung sorgt für die Abstoßung zwischen den positiv geladenen Protonen im Kern, sodass diese nicht in einander fallen und bindet das Hüllenelektron an den Atomkern.
c)
Beim abgebildeten  wird ein Neutron in ein Proton umgewandelt, wobei ein Elektron und ein Antineutrino emittiert werden. Zuerst wird ein Down-Quark im Neutron in ein Up-Quark umgewandelt, wobei ein
wird ein Neutron in ein Proton umgewandelt, wobei ein Elektron und ein Antineutrino emittiert werden. Zuerst wird ein Down-Quark im Neutron in ein Up-Quark umgewandelt, wobei ein  Boson ausgetauscht wird. Das
Boson ausgetauscht wird. Das  Boson ist ein Vermittler der schwachen Wechselwirkung und ermöglicht die Umwandlung eines Down-Quarks in ein Up-Quark. Das
Boson ist ein Vermittler der schwachen Wechselwirkung und ermöglicht die Umwandlung eines Down-Quarks in ein Up-Quark. Das  Boson ist instabil und zerfällt in ein Elektron und ein Antineutrino.
Beim
Boson ist instabil und zerfällt in ein Elektron und ein Antineutrino.
Beim  wird ein Proton in ein Neutron umgewandelt, wobei ein Positron und ein Elektron-Neutrino emittiert werden. Das
wird ein Proton in ein Neutron umgewandelt, wobei ein Positron und ein Elektron-Neutrino emittiert werden. Das  Boson ist auch bei diesem Zerfall der Vermittler der schwachen Wechselwirkung und ermöglicht die Umwandlung eines Up-Quarks in ein Down-Quark. Das
Boson ist auch bei diesem Zerfall der Vermittler der schwachen Wechselwirkung und ermöglicht die Umwandlung eines Up-Quarks in ein Down-Quark. Das  Boson ist ebenfalls instabil und zerfällt in ein Positron und in ein Elektron-Neutrino.
Boson ist ebenfalls instabil und zerfällt in ein Positron und in ein Elektron-Neutrino.
Teillösung 2:

a)
Für die Akivität A der Probe gilt:
Für die Halbwertszeit  der Probe gilt:
Die verbliebene Aktivität des Tritiums nach
der Probe gilt:
Die verbliebene Aktivität des Tritiums nach  beträgt:
Einsetzen in die Gleichung für die Halbwertszeit liefert:
beträgt:
Einsetzen in die Gleichung für die Halbwertszeit liefert:
![\(\begin{array}[t]{rll}
T_{1/2}&=& \dfrac{\ln(2)}{\lambda}&\quad \scriptsize \mid\;\lambda=\dfrac{\ln \left(0,919 \right)}{-t_{\text{mess}}} \\[5pt]
&=& \dfrac{\ln(2)}{\dfrac{\ln \left(0,919 \right)}{-t_{\text{mess}}}} &\quad \scriptsize \\[5pt]
&=& -\dfrac{\ln(2)\cdot t_{\text{mess}} }{\ln \left(0,919 \right)} &\quad \scriptsize \mid\; t_{\text{mess}}= 548\,\text{d} \\[5pt]
&=& -\dfrac{\ln(2)\cdot 548\,\text{d} }{\ln \left(0,919 \right)} &\quad \scriptsize \\[5pt]
&=& 4,5\cdot 10^3 \;\text{d}&\quad \scriptsize \\[5pt]
&=& 12,3 \;\text{a}
\end{array}\)](https://www.schullv.de/resources/formulas/1005b7b9d906b6dcbc8d64ebe08cbd82dd448e4000ba2140e5cfee8eda7e4349_light.svg)
b)
Es gilt  Hierbei entspricht
Hierbei entspricht  der Differenz zwischen der Masse des Anfangszustandes und der Masse der Endzustände des Zerfalls. Dies entspricht der Masse, die während des Zerfalls in Energie umgewandelt wird, wenn sich die Masse der beteiligten Teilchen ändert. Multipliziert mit
der Differenz zwischen der Masse des Anfangszustandes und der Masse der Endzustände des Zerfalls. Dies entspricht der Masse, die während des Zerfalls in Energie umgewandelt wird, wenn sich die Masse der beteiligten Teilchen ändert. Multipliziert mit  ergibt dies die Gesamtenergie, die in Form von kinetischer Energie der Teilchen und anderen Energien freigesetzt wird.
ergibt dies die Gesamtenergie, die in Form von kinetischer Energie der Teilchen und anderen Energien freigesetzt wird.
c)
Energiespektrum
Das Energiespektrum zeigt eine kontinuierliche Verteilung der Elektronenenergien im Bereich von  bis
bis  Die y-Achse repräsentiert die Anzahl der detektierten Elektronen im Verhältnis zur maximal möglichen Anzahl.
Die rasche Erhöhung der Kurve auf den Wert 1 bei etwa
Die y-Achse repräsentiert die Anzahl der detektierten Elektronen im Verhältnis zur maximal möglichen Anzahl.
Die rasche Erhöhung der Kurve auf den Wert 1 bei etwa  zeigt, dass die meisten Elektronen eine Energie von ungefähr
zeigt, dass die meisten Elektronen eine Energie von ungefähr  haben und die Zählrate ihr Maximum erreicht. Dies deutet darauf hin, dass Elektronen in diesem Energiebereich nahezu vollständig erfasst werden.
Die Kurve fällt nach dem Maximum zuerst steiler und dann gleichmäßiger ab, und ab etwa
haben und die Zählrate ihr Maximum erreicht. Dies deutet darauf hin, dass Elektronen in diesem Energiebereich nahezu vollständig erfasst werden.
Die Kurve fällt nach dem Maximum zuerst steiler und dann gleichmäßiger ab, und ab etwa  nimmt die Zählrate für höhere Energien weniger stark ab.
Der Abfall der Kurve auf 0 bei
nimmt die Zählrate für höhere Energien weniger stark ab.
Der Abfall der Kurve auf 0 bei  zeigt, dass Elektronen mit noch höheren Energien selten auftreten und die Zählrate für diese Energien stark abnimmt.
Erforderlichkeit des Antineutrinos
Das Energiespektrum in Abbildung 3 zeigt, dass die Elektronen aus dem
zeigt, dass Elektronen mit noch höheren Energien selten auftreten und die Zählrate für diese Energien stark abnimmt.
Erforderlichkeit des Antineutrinos
Das Energiespektrum in Abbildung 3 zeigt, dass die Elektronen aus dem  -Zerfall des Tritiums eine kontinuierliche Verteilung von Energien haben, die von
-Zerfall des Tritiums eine kontinuierliche Verteilung von Energien haben, die von  bis
bis  reicht. Aufgrund der Energieerhaltung und Impulserhaltung sollten die Elektronen jedoch einen breiteren Bereich kinetischer Energien haben, wenn die gesamte Energie des Zerfalls auf sie übertragen würde. Da der Tochterkern
reicht. Aufgrund der Energieerhaltung und Impulserhaltung sollten die Elektronen jedoch einen breiteren Bereich kinetischer Energien haben, wenn die gesamte Energie des Zerfalls auf sie übertragen würde. Da der Tochterkern  nur einen sehr kleinen Anteil, nämlich
nur einen sehr kleinen Anteil, nämlich  der kinetischen Energie des Elektrons erhalten kann, bleibt ein Teil der Energie im Spektrum unsichtbar. Das Antineutrino trägt diese fehlende Energie und ist daher erforderlich, um das Spektrum in Abbildung 3 zu erklären.
der kinetischen Energie des Elektrons erhalten kann, bleibt ein Teil der Energie im Spektrum unsichtbar. Das Antineutrino trägt diese fehlende Energie und ist daher erforderlich, um das Spektrum in Abbildung 3 zu erklären.
Teillösung 3
a)
b)
Bei  wird die Gesamtenergie des Zerfalls aufgrund der kinetischen Energie, die dem Neutrino zugeführt wird, verringert. Diese kinetische Energie steht den Elektronen nicht mehr zur Verfügung, wodurch die maximal mögliche Energie
wird die Gesamtenergie des Zerfalls aufgrund der kinetischen Energie, die dem Neutrino zugeführt wird, verringert. Diese kinetische Energie steht den Elektronen nicht mehr zur Verfügung, wodurch die maximal mögliche Energie  der Elektronen geringer ist als die Gesamtenergie
der Elektronen geringer ist als die Gesamtenergie  Für
Für  gilt:
Die maximale Energie
gilt:
Die maximale Energie  der Elektronen ist in dem Intervall
der Elektronen ist in dem Intervall
c)
Die Elektronen erfahren in magnetischen Feldern die Lorentzkraft  Diese Kraft wirkt stets senkrecht zur Bewegungsrichtung der Elektronen. Die Lorentzkraft kann daher nur die Richtung ihrer Bewegung ändern, jedoch keine Arbeit an ihnen verrichten. Die Geschwindigkeit und damit die kinetische Energie des Elektrons im statischen Magnetfeld bleibt somit unverändert.
Die Verbesserung der Einstellgenauigkeit der Gegenspannung
Diese Kraft wirkt stets senkrecht zur Bewegungsrichtung der Elektronen. Die Lorentzkraft kann daher nur die Richtung ihrer Bewegung ändern, jedoch keine Arbeit an ihnen verrichten. Die Geschwindigkeit und damit die kinetische Energie des Elektrons im statischen Magnetfeld bleibt somit unverändert.
Die Verbesserung der Einstellgenauigkeit der Gegenspannung  führt zu genaueren Messergebnissen, da die abgebremsten Elektronen präziser kontrolliert werden können. Im Detektor werden nur Elektronen nachgewiesen, die über ausreichend hohe Maximalenergie verfügen, um das durch die Gegenspannung erzeugte Gegenfeld zu überwinden. Wenn die Gegenspannung groß genug ist und keine Elektronen mehr dieses Feld überwinden können, entspricht dies der maximalen Gegenspannung und somit der maximalen Energie der Elektronen. Je genauer die Einstellung der Gegenspannung ist, desto präziser kann folglich die maximale Energie der Elektronen ermittelt werden.
führt zu genaueren Messergebnissen, da die abgebremsten Elektronen präziser kontrolliert werden können. Im Detektor werden nur Elektronen nachgewiesen, die über ausreichend hohe Maximalenergie verfügen, um das durch die Gegenspannung erzeugte Gegenfeld zu überwinden. Wenn die Gegenspannung groß genug ist und keine Elektronen mehr dieses Feld überwinden können, entspricht dies der maximalen Gegenspannung und somit der maximalen Energie der Elektronen. Je genauer die Einstellung der Gegenspannung ist, desto präziser kann folglich die maximale Energie der Elektronen ermittelt werden.
d)
Dieser Fortschritt in der Erkenntnis liefert eine wesentlich präzisere Obergrenze für die Neutrinomasse  Dadurch ist es möglich, den möglichen Massenbereich der Neutrinos genauer einzuschränken. Im Vergleich zur vorherigen Obergrenze für die Ruhemasse von Neutrinos von
Dadurch ist es möglich, den möglichen Massenbereich der Neutrinos genauer einzuschränken. Im Vergleich zur vorherigen Obergrenze für die Ruhemasse von Neutrinos von  hat sich die Messgenauigkeit um den Faktor 2 verbessert.
hat sich die Messgenauigkeit um den Faktor 2 verbessert.
Teillösung 4
Für die Masse  der Neutrinos in einem Kubikzentimeter
der Neutrinos in einem Kubikzentimeter  gilt:
Die Berechnung der Anzahl der
gilt:
Die Berechnung der Anzahl der  aus denen das Universum besteht, ergibt:
Für die Neutrinonmasse
aus denen das Universum besteht, ergibt:
Für die Neutrinonmasse  im Universum gilt:
im Universum gilt:
![\(\begin{array}[t]{rll}
M_U&=& \dfrac{M_1}{1\;\text{cm}^3}\cdot \text{Volumen des Universums} &\quad \scriptsize \\[5pt]
&=& \dfrac{1,8\cdot 10^{-34}\;\text{kg}}{1\;\text{cm}^3}\cdot 3,3 \cdot 10^{86} \;\text{cm}^3 &\quad \scriptsize \\[5pt]
&=& 1,8\cdot3,3 \cdot 10^{52} \;\text{kg} &\quad \scriptsize \\[5pt]
&=& 5,8\cdot 10^{52} \;\text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/7f0fc87a939449c6b048955ffd423e916a9c93ca97d8ff288eed54678c8dc4b7_light.svg) Für den prozentualen Anteil der Neutrinomasse
Für den prozentualen Anteil der Neutrinomasse  von
von  gilt:
gilt:
![\(\begin{array}[t]{rll}
p&=&\dfrac{M_U}{m_U} &\quad \scriptsize \\[5pt]
&=&\dfrac{5,8\cdot 10^{52} \;\text{kg}}{1\cdot 10^{53}\;\text{kg} } &\quad \scriptsize \\[5pt]
&=& 5,8 \cdot 10^{-1} &\quad \scriptsize \\[5pt]
&=& 0,58 &\quad \scriptsize \\[5pt]
&=& 58 \,\% &\quad \scriptsize \\[5pt]
&>& 10 \;\%
\end{array}\)](https://www.schullv.de/resources/formulas/6d8311182d639657127d4ccd357c43a15c5fcc086971567385cacf4b8c844422_light.svg) Die Neutrinos machen einen relevanten Anteil an der Masse des Universums aus.
Die Neutrinos machen einen relevanten Anteil an der Masse des Universums aus.