HT 2
Experimentelle und theoretische Untersuchungen zu induktiven Vorgängen
Viele Hersteller elektronischer Geräte bieten die Möglichkeit, den Akku eines Gerätes auch kabellos aufzuladen. Im Folgenden soll der Ladevorgang eines Smartphones untersucht werden, das zum Laden auf eine induktive Ladestation gelegt wird (siehe Abbildung 1).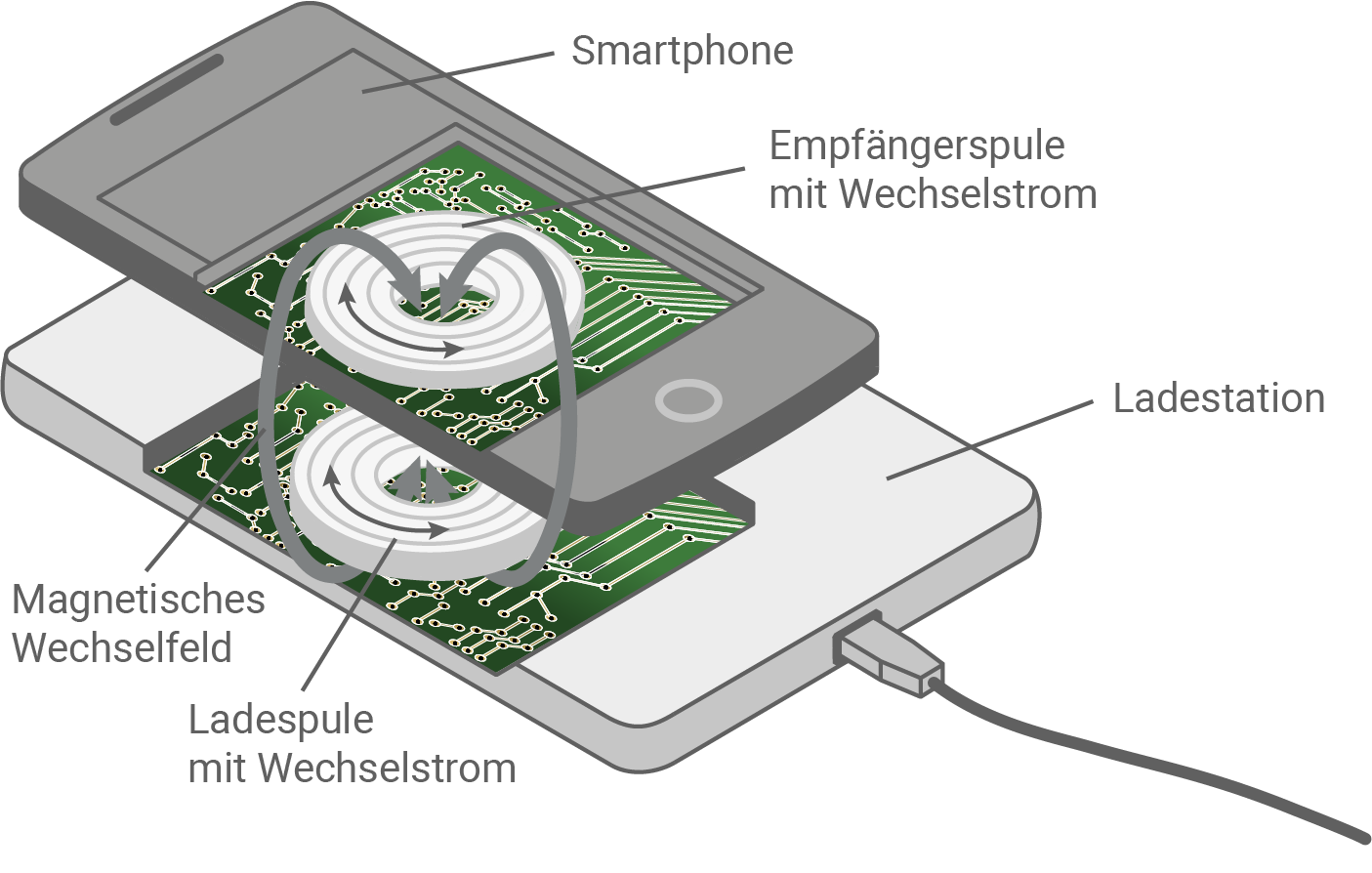
Abbildung 1: Grundprinzip des induktiven Ladevorgangs eines Smartphones (eine Skizze der Ladespule, hier einfachheitshalber baugleich mit der Empfängerspule, ist in Abbildung 3 dargestellt)
a)
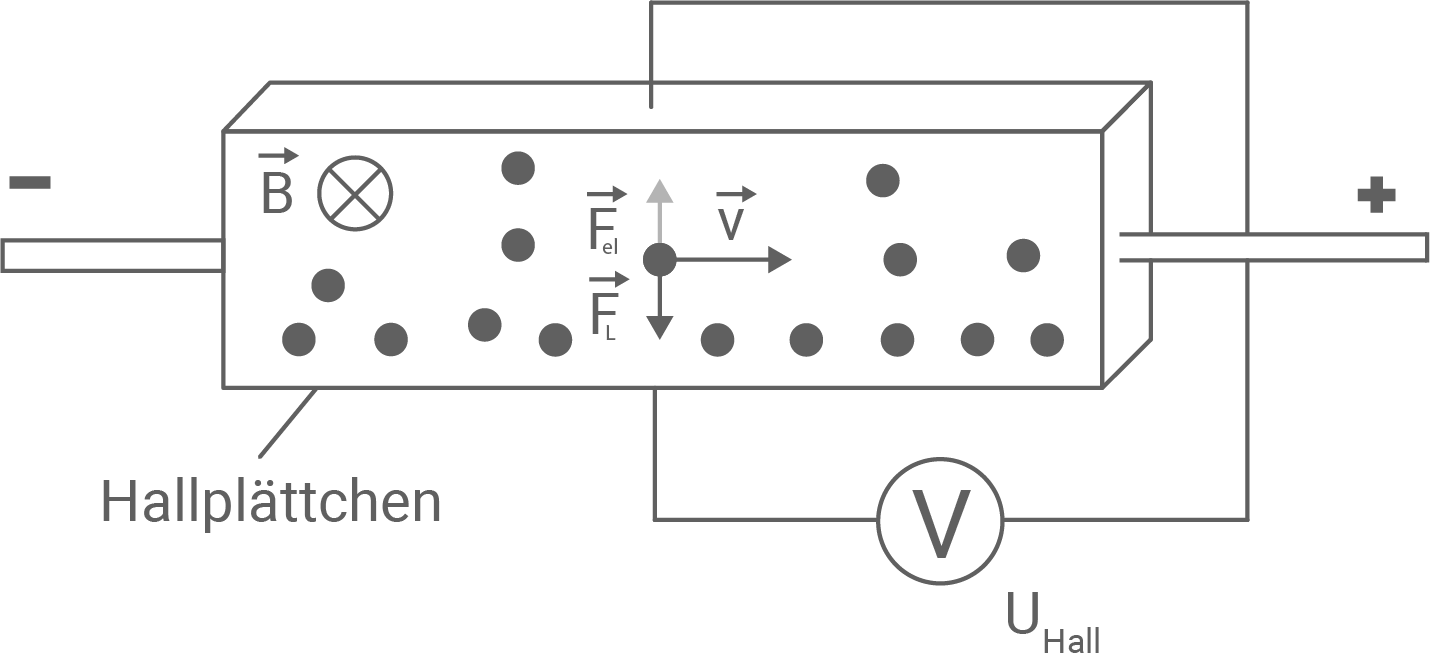
Zur Messung der Stärke  eines magnetischen Feldes kann eine Hallsonde verwendet werden, deren Funktionsprinzip auf dem Halleffekt beruht. Der schematische Aufbau einer Hallsonde ist in Abbildung 2 dargestellt.
eines magnetischen Feldes kann eine Hallsonde verwendet werden, deren Funktionsprinzip auf dem Halleffekt beruht. Der schematische Aufbau einer Hallsonde ist in Abbildung 2 dargestellt.
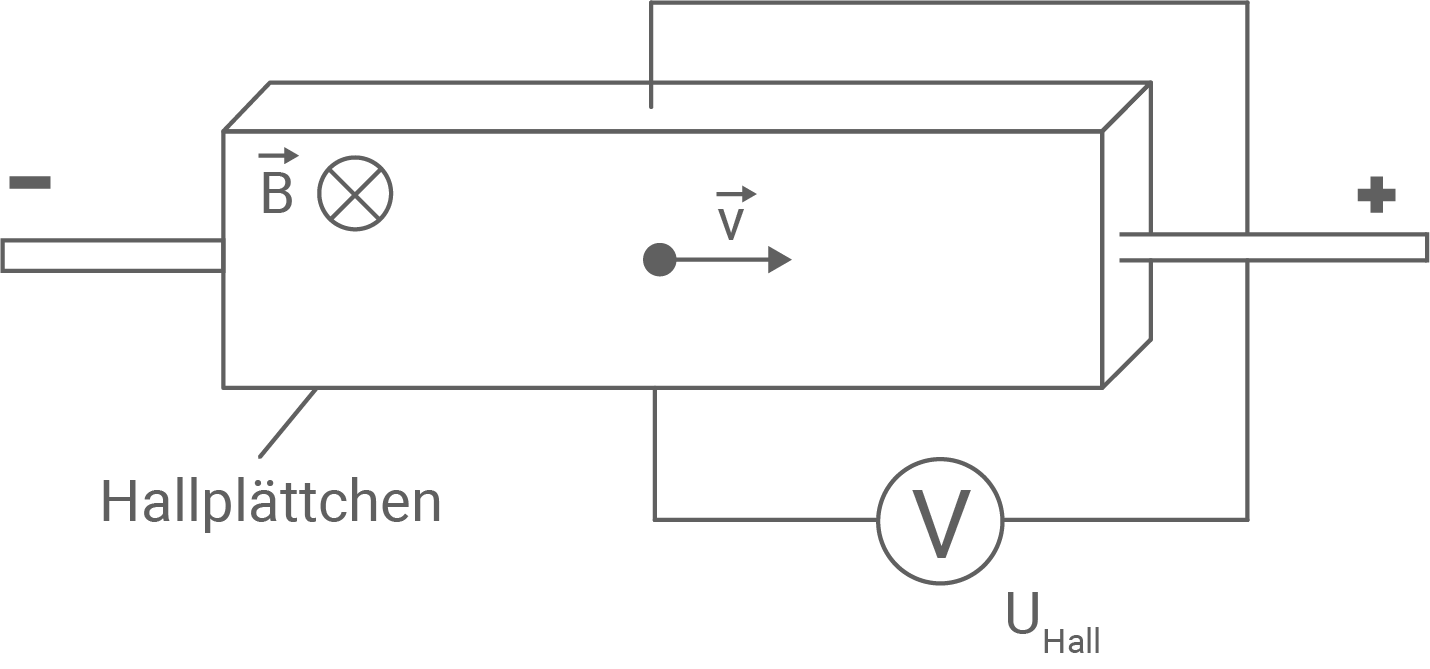 Vereinfachend wird angenommen, dass das magnetische Feld im Bereich des Hallplättchens homogen ist und dieses vollständig senkrecht durchsetzt. Direkt gemessen wird die Hallspannung
Vereinfachend wird angenommen, dass das magnetische Feld im Bereich des Hallplättchens homogen ist und dieses vollständig senkrecht durchsetzt. Direkt gemessen wird die Hallspannung  zwischen der oberen und unteren Seite des Hallplättchens. Zur Veranschaulichung des Halleffekts ist bereits ein Elektron mit der Driftgeschwindigkeit
zwischen der oberen und unteren Seite des Hallplättchens. Zur Veranschaulichung des Halleffekts ist bereits ein Elektron mit der Driftgeschwindigkeit  im Hallplättchen dargestellt.
im Hallplättchen dargestellt.
 muss nicht hergeleitet werden.
muss nicht hergeleitet werden.

Abbildung 2: Schematischer Aufbau einer Hallsonde
- Skizziere in Abbildung 2 zusätzlich die sich im Gleichgewicht einstellende Elektronenverteilung sowie die dann auf das bereits dargestellte Elektron wirkenden Kräfte.
- Erläutere deine Ergänzungen in der Skizze.
- Erkläre das Funktionsprinzip einer Hallsonde im Hinblick auf die Messung der Stärke
des magnetischen Feldes.
b)
Für eine konkrete Ladespule wird der Zusammenhang zwischen der Stärke  des magnetischen Feldes und einer jeweils konstanten Stromstärke
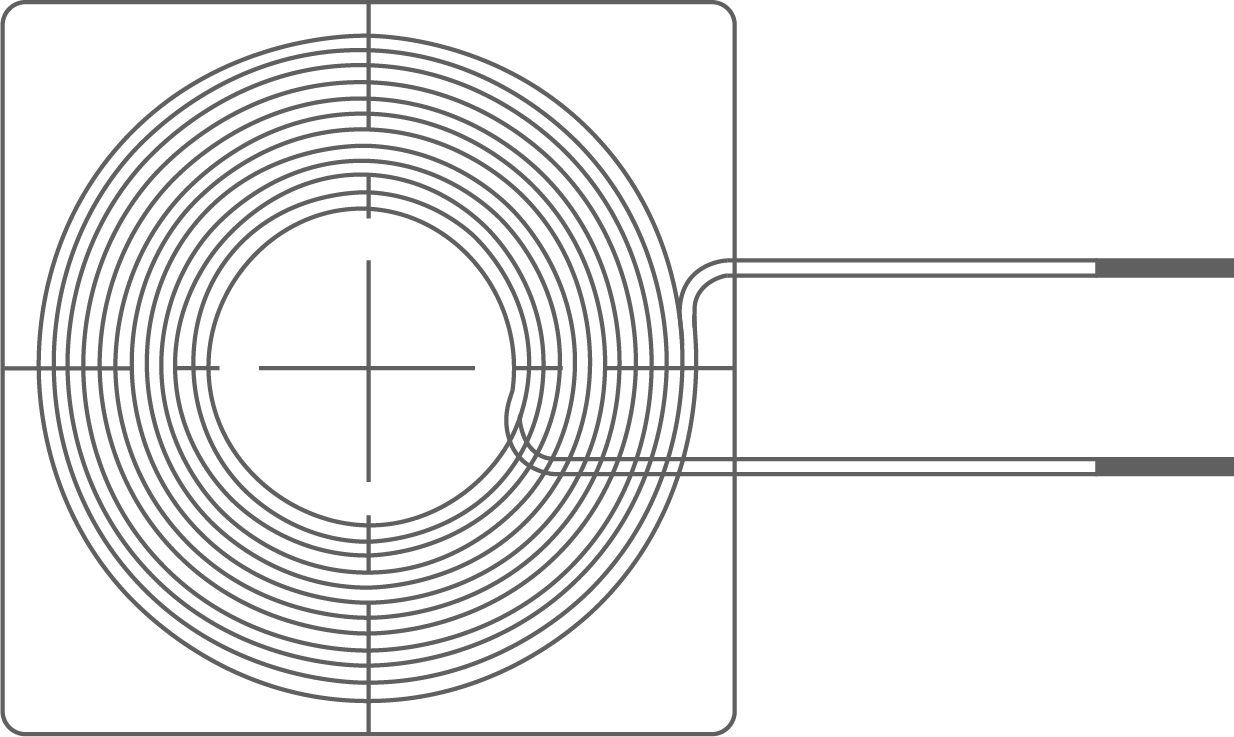
des magnetischen Feldes und einer jeweils konstanten Stromstärke  experimentell bestimmt. Für die Untersuchung wird eine Hallsonde, wie in Abbildung 3 dargestellt, genau in der Mitte der Spule so platziert, dass deren magnetisches Feld die Sonde (annähernd) homogen durchsetzt.
experimentell bestimmt. Für die Untersuchung wird eine Hallsonde, wie in Abbildung 3 dargestellt, genau in der Mitte der Spule so platziert, dass deren magnetisches Feld die Sonde (annähernd) homogen durchsetzt.
 Bei der Durchführung des Experiments wird die Stärke
Bei der Durchführung des Experiments wird die Stärke  des magnetischen Feldes für verschiedene Stromstärken
des magnetischen Feldes für verschiedene Stromstärken  in der Ladespule gemessen. Es ergeben sich die Messwerte in der folgenden Tabelle.
in der Ladespule gemessen. Es ergeben sich die Messwerte in der folgenden Tabelle.
Die Messergebnisse sollen im Folgenden ausgewertet werden.
 ]
]

Abbildung 3: Skizze der Ladespule mit der Position der Hallsonde in der Mitte des Kreuzes
| 0,00 | 0,0 |
| 0,05 | 46,5 |
| 0,15 | 115,2 |
| 0,25 | 221,8 |
| 0,35 | 256,3 |
| 0,45 | 381,3 |
| 0,55 | 460,5 |
- Zeige anhand einer Auswertung aller Messwerte in der Tabelle, dass die Stärke
des Feldes näherungsweise proportional zur Stromstärke
zunimmt, d.h.
mit dem Proportionalitätsfaktor
- Ermittle mithilfe aller Messwerte in der Tabelle einen Wert für den Proportionalitätsfaktor
c)
Die in Aufgabenteil b) verwendete Ladespule besteht aus kreisförmigen Windungen und ist luftgefüllt. Konkret soll sie im Folgenden eine Windungszahl von  , einen (mittleren) Radius von
, einen (mittleren) Radius von  und eine Länge von
und eine Länge von  aufweisen. Somit ist die Länge der Spule im Vergleich zum Radius gering. Aufgrund theoretischer Überlegungen kann die Abhängigkeit der Stärke
aufweisen. Somit ist die Länge der Spule im Vergleich zum Radius gering. Aufgrund theoretischer Überlegungen kann die Abhängigkeit der Stärke  des von dieser Spule erzeugten Feldes von der Stromstärke
des von dieser Spule erzeugten Feldes von der Stromstärke  mit folgendem Zusammenhang angegeben werden:
mit folgendem Zusammenhang angegeben werden:
 Hierbei ist
Hierbei ist  die sogenannte magnetische Feldkonstante. Die Gleichung für die Stärke des Feldes muss nicht hergeleitet werden.
die sogenannte magnetische Feldkonstante. Die Gleichung für die Stärke des Feldes muss nicht hergeleitet werden.
 wird durch die einfachere Gleichung
wird durch die einfachere Gleichung  beschrieben.
beschrieben.
Teilaufgabe 2: Untersuchung der Spannung an der Empfängerspule
Das Grundprinzip der kontaktlosen, induktiven Energieübertragung zwischen der Ladespule - Berechne den Proportionalitätsfaktor
für den theoretisch geltenden Zusammenhang.
- Bestimme die prozentuale Abweichung des Wertes
aus Aufgabenteil 1b) von dem Wert für
.
- Beurteile, inwieweit die Vereinfachung der Gleichung im hier vorliegenden Fall zu rechtfertigen ist.
(10 + 6 + 8 Punkte)
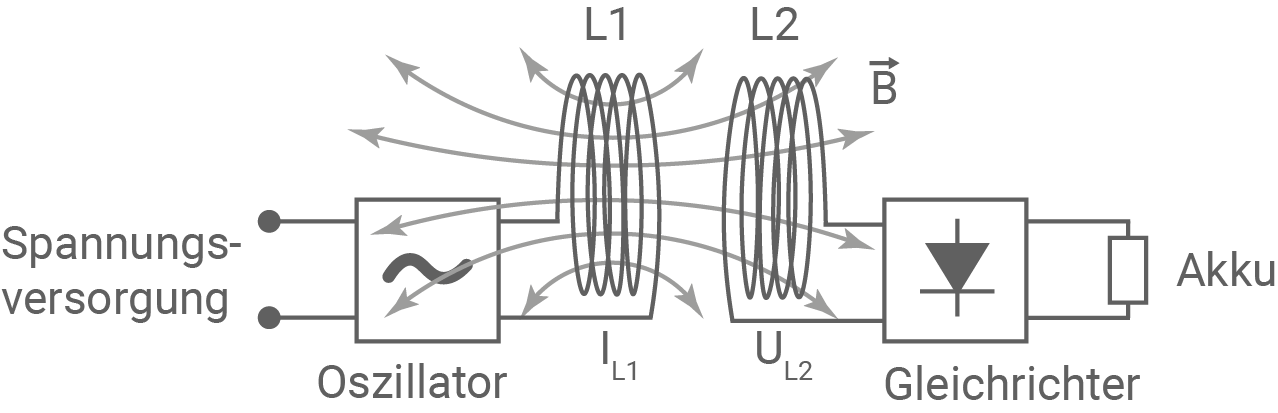
Abbildung 4: Prinzip der induktiven Energieübertragung
a)
- Erkläre ausgehend von einem möglichst allgemeinen Induktionsprinzip, warum eine Spannung
an der Empfängerspule
messbar ist.
- Begründe, warum eine induktive Energieübertragung mit einem zeitlich konstanten magnetischen Feld in der Ladespule
nicht möglich ist.
- Erkläre die in der Gleichung vorkommenden physikalischen Größen in Bezug auf Abbildung 4.
b)
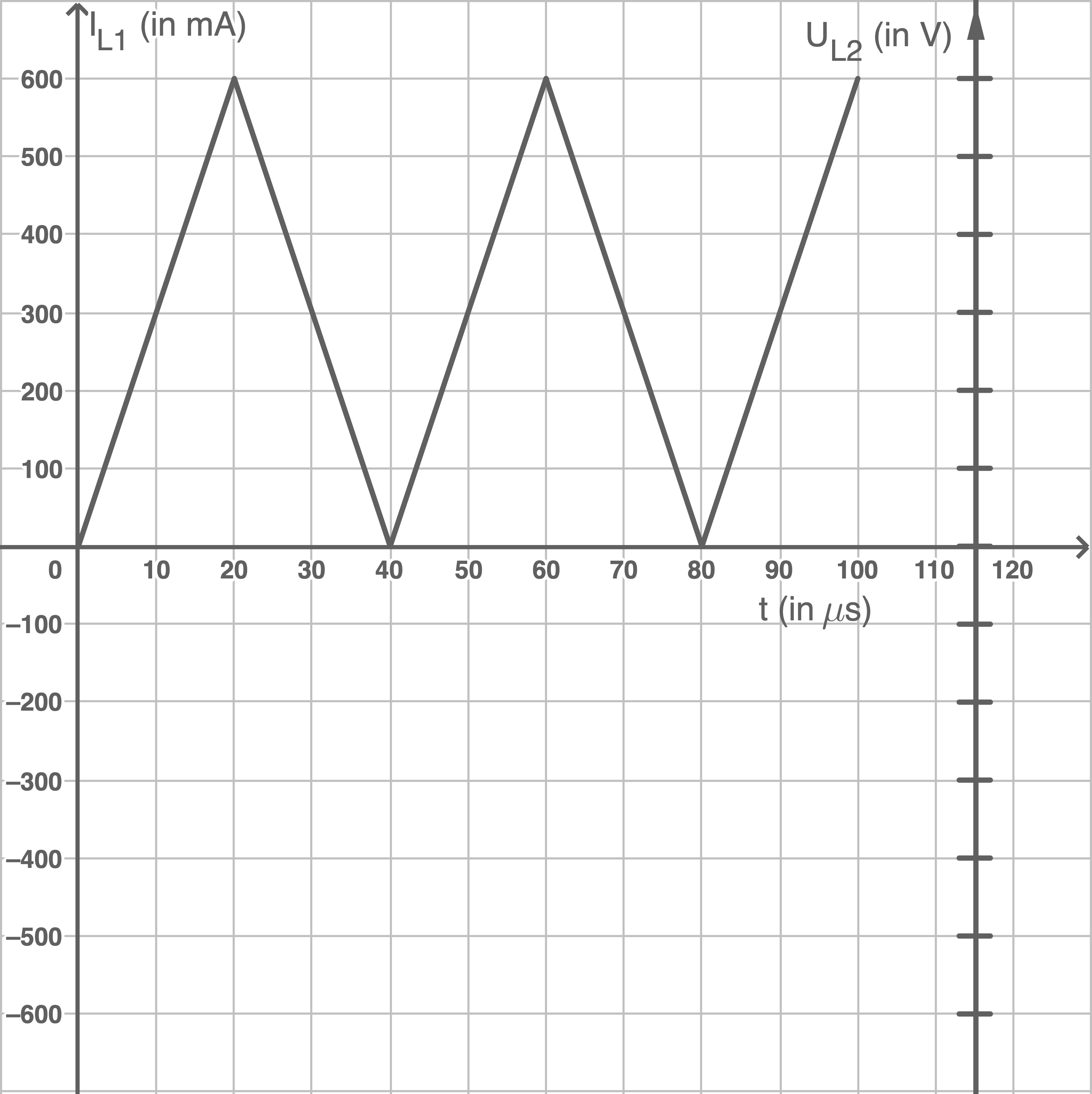
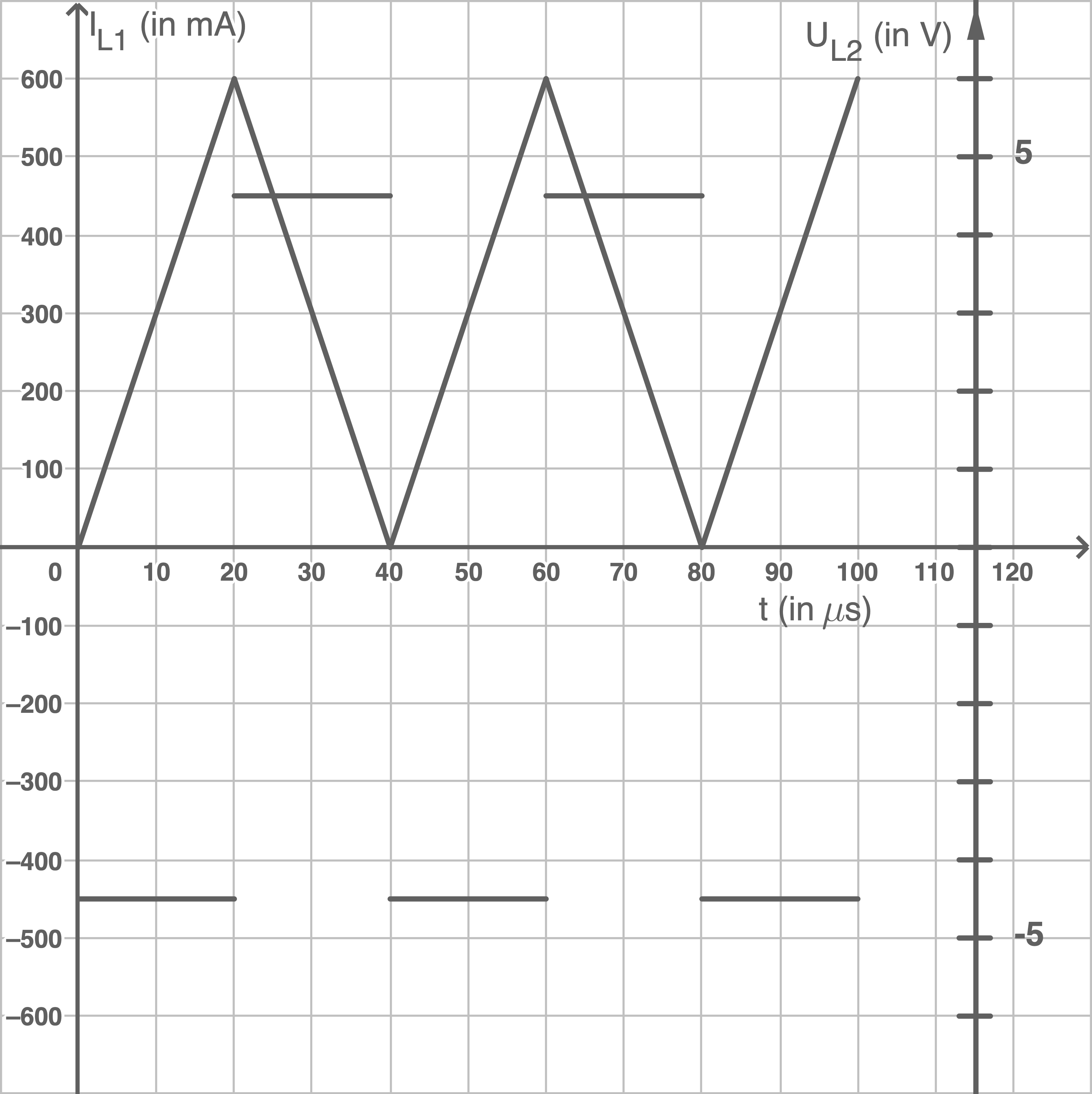
In der Ladespule  gemäß Abbildung 4 können verschiedene zeitliche Stromstärkeverläufe realisiert werden. In Abbildung 5 ist ein dreieckförmiger Verlauf der Stromstärke
gemäß Abbildung 4 können verschiedene zeitliche Stromstärkeverläufe realisiert werden. In Abbildung 5 ist ein dreieckförmiger Verlauf der Stromstärke  in der Ladespule dargestellt.
in der Ladespule dargestellt.
 Hieraus resultiere die Stärke
Hieraus resultiere die Stärke  des magnetischen Feldes in der Ladespule L1 entsprechend den Angaben in Aufgabenteil 1b). Die Empfängerspule L2 besitzt
des magnetischen Feldes in der Ladespule L1 entsprechend den Angaben in Aufgabenteil 1b). Die Empfängerspule L2 besitzt  Windungen und eine Querschnittsfläche mit einem Inhalt von
Windungen und eine Querschnittsfläche mit einem Inhalt von  .
.

Abbildung 5: Dreieckförmiger Verlauf der Stromstärke  in der Ladespule
in der Ladespule
- Berechne mithilfe der in Aufgabenteil a) angegebenen Gleichung die Spannung
an der Empfängerspule
für eine steigende Flanke in Abbildung 5.
- Zeichne unter Berücksichtigung der in Abbildung 5 rechts vorgegebenen Achse den zeitlichen Verlauf der Spannung
in das Diagramm ein. Hinweis: Die Achse rechts muss passend skaliert werden.
c)
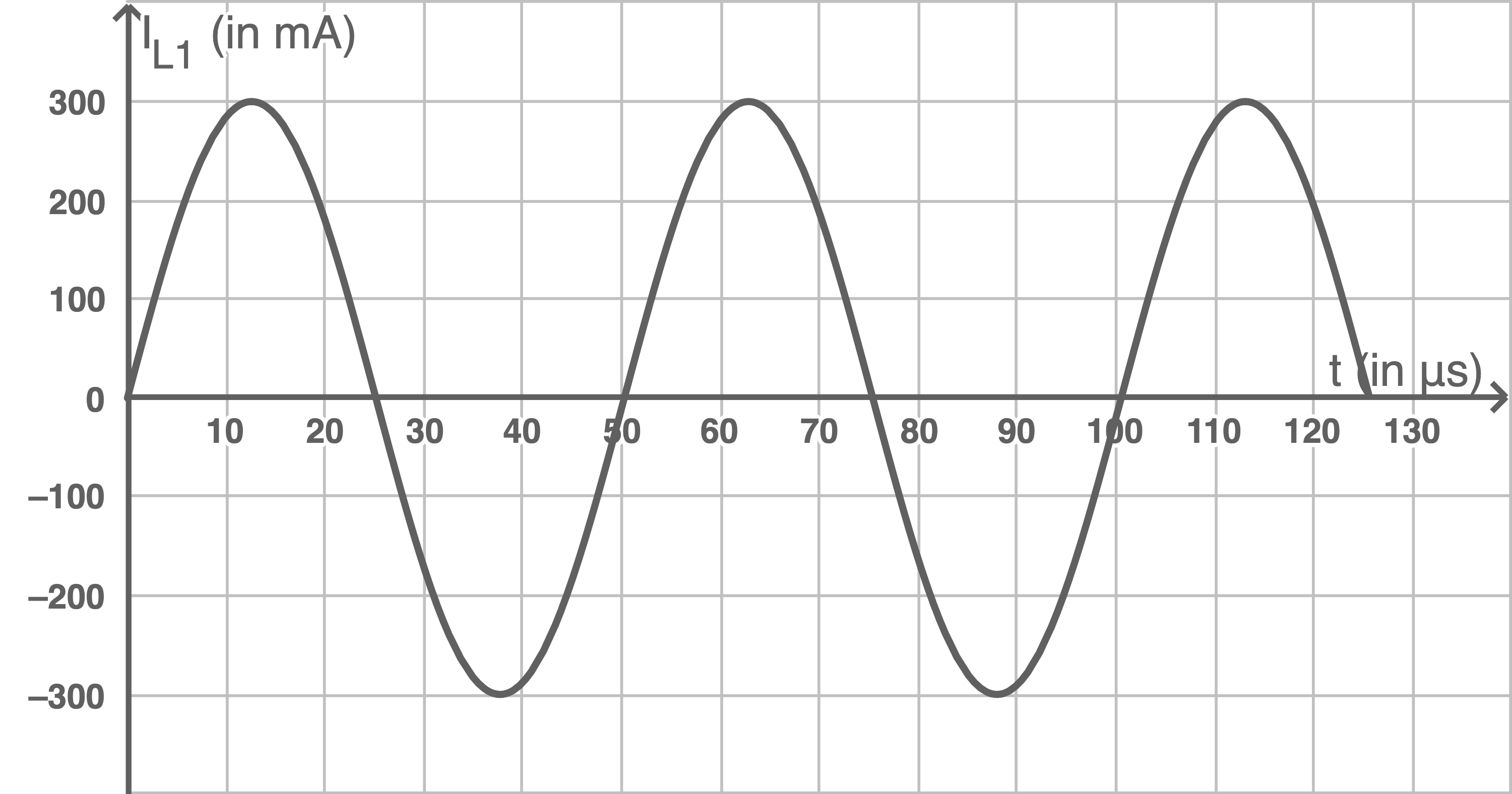
In Abbildung 6 ist ein sinusförmiger Verlauf der Stromstärke  in der Ladespule
in der Ladespule  dargestellt.
dargestellt.
 Die Periodendauer des sinusförmigen Stromstärkesignals in Abbildung 6 werde mit
Die Periodendauer des sinusförmigen Stromstärkesignals in Abbildung 6 werde mit  bezeichnet, die Amplitude der Stromstärke mit
bezeichnet, die Amplitude der Stromstärke mit  . Aus der Stromstärke resultiere die Stärke
. Aus der Stromstärke resultiere die Stärke  des magnetischen Feldes in der Ladespule
des magnetischen Feldes in der Ladespule  entsprechend den Angaben in Aufgabenteil 1c).
entsprechend den Angaben in Aufgabenteil 1c).

Abbildung 6: Sinusförmiger Verlauf der Stromstärke  in der Ladespule
in der Ladespule
- Zeige, dass sich die Spannung an der Empfängerspule L2 durch die Gleichung beschreiben lässt.
- Bestimme anhand des Diagramms in Abbildung 6 die Werte für
und
.
- Berechne die Amplitude
der Spannung an der Empfängerspule
d)
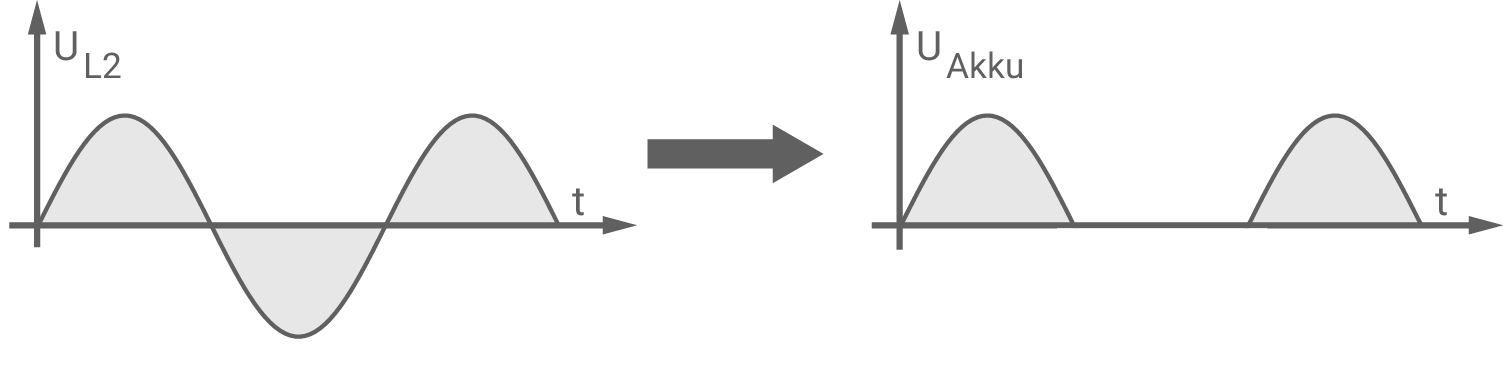
Mit dem Gleichrichter (siehe Abbildung 4) bleiben alle negativen Spannungen  ohne Einfluss, d.h. die am Akku anliegende Spannung
ohne Einfluss, d.h. die am Akku anliegende Spannung  beträgt dann jeweils Null, während alle positiven Spannungen nicht beeinflusst werden (siehe Abbildung 7).
beträgt dann jeweils Null, während alle positiven Spannungen nicht beeinflusst werden (siehe Abbildung 7).
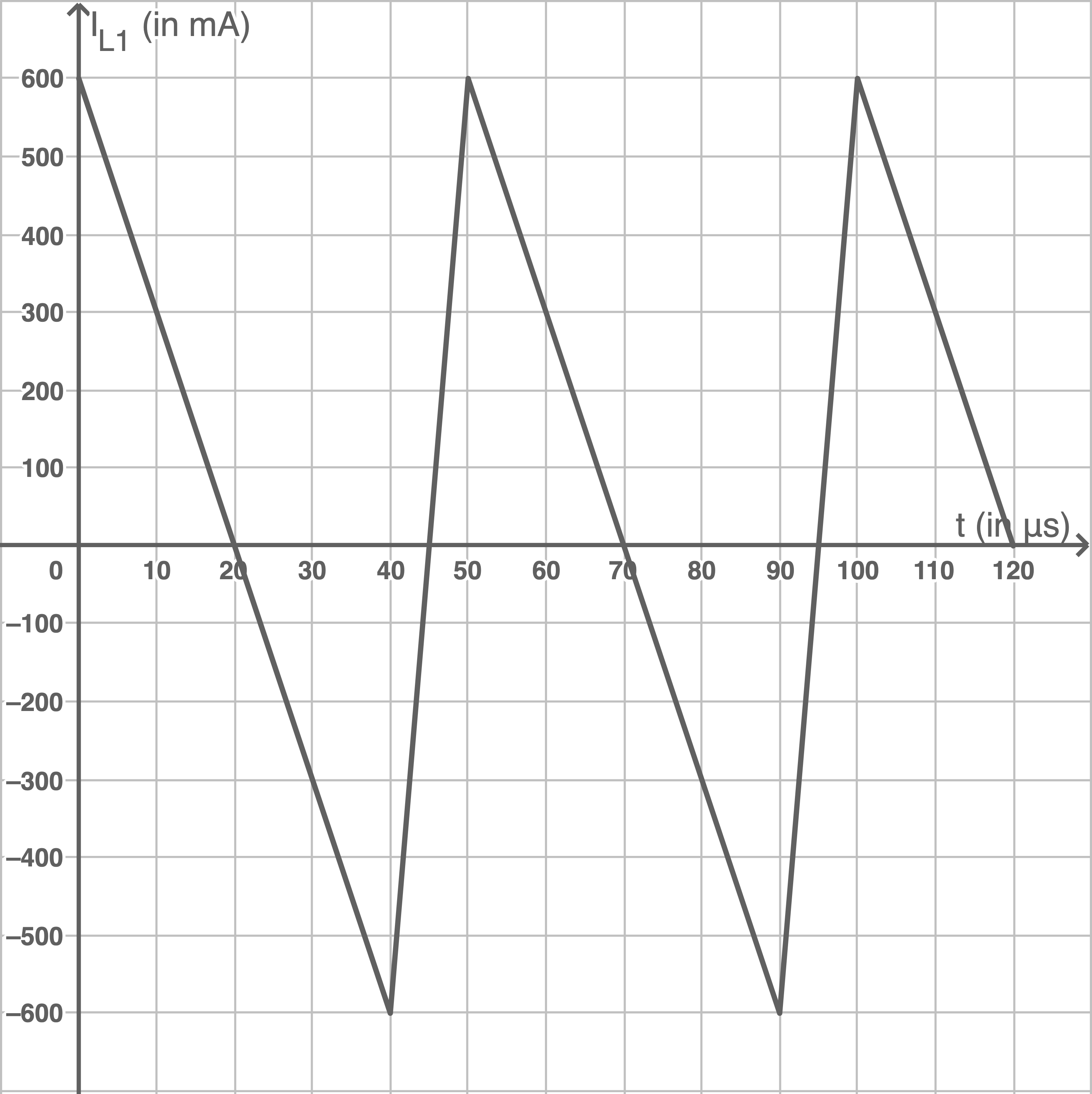
 Im Folgenden soll der dreieckförmige Verlauf der Stromstärke in Abbildung 5 mit dem sägezahnförmigen Verlauf in Abbildung 8 verglichen werden.
Im Folgenden soll der dreieckförmige Verlauf der Stromstärke in Abbildung 5 mit dem sägezahnförmigen Verlauf in Abbildung 8 verglichen werden.
 Gehe davon aus, dass eine fallende Flanke in den Abbildungen 5 und 8 jeweils zu einer positiven Induktionsspannung führt und dass ein Gleichrichter wie oben beschrieben auf die induzierte Spannung
Gehe davon aus, dass eine fallende Flanke in den Abbildungen 5 und 8 jeweils zu einer positiven Induktionsspannung führt und dass ein Gleichrichter wie oben beschrieben auf die induzierte Spannung  angewendet wird.
angewendet wird.
Teilaufgabe 3: Einfluss der Position des Smartphones auf der Ladestation
Bei der alltäglichen Verwendung induktiver Ladestationen kann es geschehen, dass das Smartphone nicht immer genau mittig auf die Ladestation gelegt wird. Viele Nutzerinnen und Nutzer verwenden außerdem zum Schutz ihres Smartphones eine mehr oder weniger dicke Schutzhülle. Beides trägt zu einer nicht mehr optimalen Positionierung des Smartphones auf der Ladestation bei.

Abbildung 7: Zur Wirkungsweise eines Gleichrichters

Abbildung 8: Weiterer Verlauf der Stromstärke IL1 in der Ladespule, sägezahnförmig
- Vergleiche die beiden zeitlichen Verläufe in den Abbildungen 5 und 8 im Hinblick auf die zum Laden eines Smartphones zur Verfügung stehende Spannung
- Entscheide anhand einer quantitativen Betrachtung, welcher der beiden zeitlichen Verläufe besser zum Laden eines Smartphones geeignet ist.
(8 + 7 + 9 + 6 Punkte)
a)
Erläutere anhand des (allgemeinen) Induktionsprinzips, welche Auswirkungen dieser Umstand auf den Ladevorgang des Smartphones haben kann.
b)
Intelligente Ladestationen erkennen eine nicht optimale Positionierung des Smartphones auf der Ladestation und können darauf reagieren. Betrachte im Folgenden das Beispiel des sägezahnförmigen Verlaufs der Stromstärke in der Ladespule in Abbildung 8 und gehe davon aus, dass sich die Empfängerspule in einem Bereich mit nur  der maximal möglichen Stärke des magnetischen Feldes befindet.
der maximal möglichen Stärke des magnetischen Feldes befindet.
- Ermittle mithilfe von Abbildung 8 den Wert, auf den die maximale Stromstärke
in der Ladespule erhöht werden muss, um den Effekt der nicht optimalen Positionierung auszugleichen.
- Nenne eine weitere Größe, die zur Optimierung des Ladevorgangs durch die zeitliche, elektronische Steuerung der Ladestation beeinflusst werden kann.
- Ermittle mithilfe von Abbildung 8 einen Wert für diese Größe, um den Effekt der nicht optimalen Positionierung auszugleichen.
(4 + 7 Punkte)
Teillösung 1: experimentelle und theoretische Untersuchungen zu induktiven Vorgängen
a)
Skizzierung der Elektronenverteilung sowie die auf das Elektron wirkenden Kräfte
 Erläutereung der Ergänzungen
Die Elektronen erfahren im Hallplättchen senkrecht zum magnetischen Feld anhand der Drei-Finger-Regel der linken Hand eine Lorentzkraft
Erläutereung der Ergänzungen
Die Elektronen erfahren im Hallplättchen senkrecht zum magnetischen Feld anhand der Drei-Finger-Regel der linken Hand eine Lorentzkraft  nach unten und werden so von ihrer ursprünglichen Bahn abgelenkt. Da hierdurch die obere Seite des Hallplättchens positiv und die untere Seite negativ geladen wird, erfahren die Leitungselektronen im Plättchen zusätzlich zur Lorentzkraft auch noch eine elektrische Kraft
nach unten und werden so von ihrer ursprünglichen Bahn abgelenkt. Da hierdurch die obere Seite des Hallplättchens positiv und die untere Seite negativ geladen wird, erfahren die Leitungselektronen im Plättchen zusätzlich zur Lorentzkraft auch noch eine elektrische Kraft  , welche der Lorentzkraft genau entgegengerichtet ist. Die Verschiebung der Leitungselektronen erfolgt so lange, bis die elektrische Kraft so groß ist, dass sie die Lorentzkraft gerade kompensiert, bis sich also das Kräftegleichgewicht
, welche der Lorentzkraft genau entgegengerichtet ist. Die Verschiebung der Leitungselektronen erfolgt so lange, bis die elektrische Kraft so groß ist, dass sie die Lorentzkraft gerade kompensiert, bis sich also das Kräftegleichgewicht  einstellt.
Erklärung des Funktionsprinzipes einer Hallsonde im Hinblick auf die Messung der Stärke
einstellt.
Erklärung des Funktionsprinzipes einer Hallsonde im Hinblick auf die Messung der Stärke  des magnetischen Feldes
Eine Hallsonde besteht aus einem stromdurchflossenem Leiter, der einem magnetischen Feld ausgesetzt wird. Wie oben beschrieben führt der Elektronenüberschuss auf der einen Leiterseite bzw. der Elektronenmangel auf der anderen zur messbaren Hallspannung
des magnetischen Feldes
Eine Hallsonde besteht aus einem stromdurchflossenem Leiter, der einem magnetischen Feld ausgesetzt wird. Wie oben beschrieben führt der Elektronenüberschuss auf der einen Leiterseite bzw. der Elektronenmangel auf der anderen zur messbaren Hallspannung  zwischen den gegenüberliegenden Seiten, die ein Maß für die Stärke
zwischen den gegenüberliegenden Seiten, die ein Maß für die Stärke  des magnetischen Feldes ist.
des magnetischen Feldes ist.

b)
Zeigen der Proportionalität der Stärke  des Feldes zur Stromstärke
des Feldes zur Stromstärke 
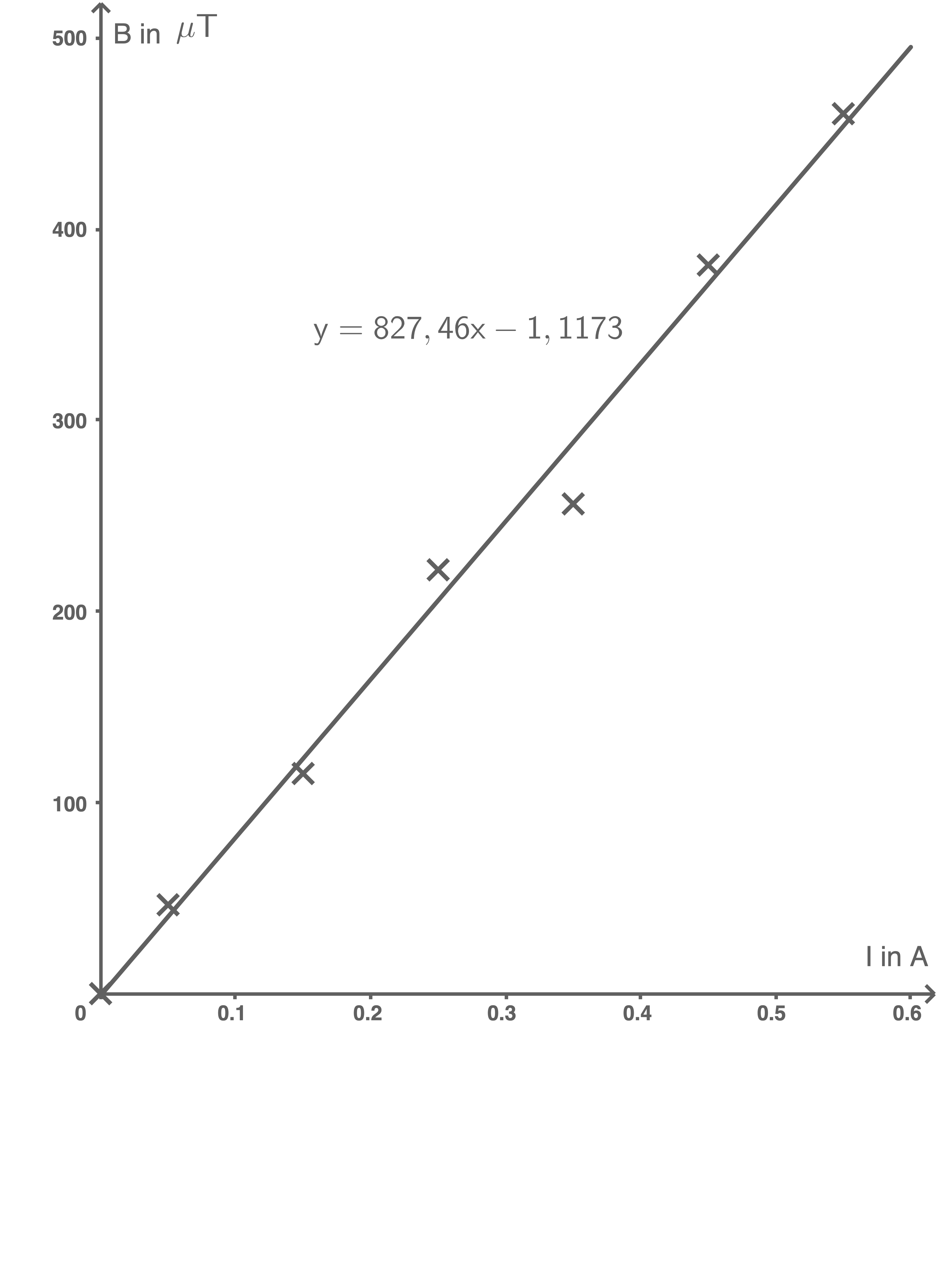 Es ist zu erkennen, dass die Messpunkte in guter Näherung auf einer Geraden durch den Ursprung liegen. (Die Regressionsgerade weist ein relativ hohes Bestimmtheitsmaß auf und verläuft ziemlich genau durch den Ursprung.) Damit ist der proportionale Zusammenhang zwischen der Stärke
Es ist zu erkennen, dass die Messpunkte in guter Näherung auf einer Geraden durch den Ursprung liegen. (Die Regressionsgerade weist ein relativ hohes Bestimmtheitsmaß auf und verläuft ziemlich genau durch den Ursprung.) Damit ist der proportionale Zusammenhang zwischen der Stärke  des magnetischen Feldes und der elektrischen Stromstärke
des magnetischen Feldes und der elektrischen Stromstärke  näherungsweise nachgewiesen.
Ermittlung des Proportionalitätsfaktor
näherungsweise nachgewiesen.
Ermittlung des Proportionalitätsfaktor  Die Steigung der Ausgleichsgeraden entspricht unter Berücksichtigung der Maßeinheiten dem Proportionalitätsfaktor
Die Steigung der Ausgleichsgeraden entspricht unter Berücksichtigung der Maßeinheiten dem Proportionalitätsfaktor  :
:
![\(\begin{array}[t]{rll}
k_{\exp }&=& 827 \;\dfrac{\mu\text{T}}{\text{A}}&\quad \scriptsize \\[5pt]
&=& 8,27 \cdot 10^{-4} \;\dfrac{\text{T}}{\text{A}}
\end{array}\)](https://www.schullv.de/resources/formulas/00b0f0a566173e3f256739ae7cb9197676140cdcd6b1d681e7087dc62417c950_light.svg)

c)
Berechnung des Proportionalitätsfaktor  Bestimmung der prozentualen Abweichung des Wertes
Bestimmung der prozentualen Abweichung des Wertes  Die Prozentuale Abweichung beträgt
Die Prozentuale Abweichung beträgt
![\(\begin{array}[t]{rll}
\dfrac{k_{\text{exp}}-k_{\text{theo}}}{k_{\text{theo}}}&=& \dfrac{8,27-7,84}{7,84}&\quad \scriptsize \\[5pt]
&=& 0.055 \quad \scriptsize \\[5pt]
&=& 5,5 \,\%
\end{array}\)](https://www.schullv.de/resources/formulas/81efa53a8a43a019c2bb57f8440a7b0a66374862667f6d7d2f85e17824e23fdf_light.svg) Der experimentell ermittelte Wert weicht um etwa
Der experimentell ermittelte Wert weicht um etwa  vom erwarteten theoretischen Wert ab.
Beurteilung der Vereinfachung der Gleichung
Für die flache Spule gilt:
vom erwarteten theoretischen Wert ab.
Beurteilung der Vereinfachung der Gleichung
Für die flache Spule gilt:
![\(\begin{array}[t]{rll}
B&=& \mu_0 \cdot \dfrac{n_1}{2 R} \cdot I &\quad \scriptsize \\[5pt]
&=& k_{\text{theo}} \cdot I
\end{array}\)](https://www.schullv.de/resources/formulas/9861b6a9039334684aa46c666979d6f501652a9ffa6e49d50edd1dec8ef916fd_light.svg) Der Poportionalitätsfaktor der flachen Spule beträgt:
Der Poportionalitätsfaktor der flachen Spule beträgt:
![\(\begin{array}[t]{rll}
k_{\text{theo}}&=& \mu_0 \cdot \dfrac{n_1}{2 R}&\quad \scriptsize \\[5pt]
&=& 4 \pi \cdot 10^{-7} \;\dfrac{\text{N}}{\text{A}^2} \cdot \dfrac{50}{2 \cdot 0,0400 \;\text{m}} &\quad \scriptsize \\[5pt]
&=& 7,85 \cdot 10^{-4} \;\dfrac{\text{T}}{\text{A}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/61fa225438341c92a08f47337acc282b9f1c591c7a105e4af79232dc56b8bfad_light.svg) Dies entspricht einer sehr geringen Abweichung von dem obigen Wert. Die einfachere Gleichung kann hier somit in geeigneter Weise verwendet werden.
Dies entspricht einer sehr geringen Abweichung von dem obigen Wert. Die einfachere Gleichung kann hier somit in geeigneter Weise verwendet werden.
Teillösung 2: Untersuchung der Spannungen an der Empfängerspule
a)
Erklärung , warum eine Spannung  an der Empfängerspule
an der Empfängerspule  messbar ist.
Grundlage der induktiven Energieübertragung ist das (Faraday'sche) Induktionsgesetz, welches besagt, dass Induktionsspannungen auftreten, wenn sich das Produkt aus der Stärke des (homogenen) magnetischen Feldes und dem Inhalt der senkrecht vom Feld durchsetzten Fläche zeitlich ändert. Das Produkt kann sich ändern, wenn sich mindestens eine der beiden eingehenden Größen ändert. Aufgrund der Verwendung des Oszillators wird ein zeitlich veränderliches magnetisches Feld erzeugt, das somit eine Induktionsspannung in der Empfängerspule
messbar ist.
Grundlage der induktiven Energieübertragung ist das (Faraday'sche) Induktionsgesetz, welches besagt, dass Induktionsspannungen auftreten, wenn sich das Produkt aus der Stärke des (homogenen) magnetischen Feldes und dem Inhalt der senkrecht vom Feld durchsetzten Fläche zeitlich ändert. Das Produkt kann sich ändern, wenn sich mindestens eine der beiden eingehenden Größen ändert. Aufgrund der Verwendung des Oszillators wird ein zeitlich veränderliches magnetisches Feld erzeugt, das somit eine Induktionsspannung in der Empfängerspule  des Smartphones hervorruft.
Begründung, warum eine induktive Energieübertragung mit einem zeitlich konstanten magnetischen Feld in der Ladespule
des Smartphones hervorruft.
Begründung, warum eine induktive Energieübertragung mit einem zeitlich konstanten magnetischen Feld in der Ladespule  nicht möglich ist.
Ist das magnetische Feld zeitlich konstant, so liegt bei unveränderlicher Fläche der Spule keine zeitliche Änderung der Stärke des Feldes vor, und es entsteht keine Induktionsspannung.
Erklärung der physikalischen Größen
Im angegebenen Induktionsgesetz sind
nicht möglich ist.
Ist das magnetische Feld zeitlich konstant, so liegt bei unveränderlicher Fläche der Spule keine zeitliche Änderung der Stärke des Feldes vor, und es entsteht keine Induktionsspannung.
Erklärung der physikalischen Größen
Im angegebenen Induktionsgesetz sind  und
und  die Windungszahl bzw. der Inhalt der Querschnittsfläche der Empfängerspule
die Windungszahl bzw. der Inhalt der Querschnittsfläche der Empfängerspule 
 ist die Änderungsrate der Stärke des magnetischen Feldes, das von der Ladespule
ist die Änderungsrate der Stärke des magnetischen Feldes, das von der Ladespule  erzeugt wird.
erzeugt wird.
b)
Berechnung der Spannung  Für die induzierte Spannung gilt nach Aufgabenteil a) die Gleichung:
Für die induzierte Spannung gilt nach Aufgabenteil a) die Gleichung:
![\(\begin{array}[t]{rll}
U_{\text{L} 2}&=& -n_2 \cdot A \cdot \dot{B} &\quad \scriptsize \\[5pt]
&=& -n_2 \cdot A \cdot k_{\exp } \cdot \dot{I}_{\text{L} 1}
\end{array}\)](https://www.schullv.de/resources/formulas/c3cce512aca838ce86c8f7c417ef6d311a30f81bdf409323d9badeba76e7e0c0_light.svg) Bei einem dreieckförmigen Verlauf besitzt die steigende Flanke eine konstante Steigung. Für die Induktionsspannung gilt daher im gesamten Intervall:
Zeichnung des zeitlichen Verlaufs der Spannung
Bei einem dreieckförmigen Verlauf besitzt die steigende Flanke eine konstante Steigung. Für die Induktionsspannung gilt daher im gesamten Intervall:
Zeichnung des zeitlichen Verlaufs der Spannung  Die Flanken besitzen betragsmäßig jeweils die gleiche Steigung, allerdings mit aufeinanderfolgend abwechselndem Vorzeichen. Im
Die Flanken besitzen betragsmäßig jeweils die gleiche Steigung, allerdings mit aufeinanderfolgend abwechselndem Vorzeichen. Im  -Diagramm ergibt sich damit das folgende Rechtecksignal:
-Diagramm ergibt sich damit das folgende Rechtecksignal:

c)
Gleichung der Spannung an der Empfängerspule  Für die induzierte Spannung gilt:
Für die induzierte Spannung gilt:
![\(\begin{array}[t]{rll}
U_{\text{L} 2}&=& -n_2 \cdot A \cdot \dot{B} &\quad \scriptsize \\[5pt]
&=& -n_2 \cdot A \cdot k_{\text {theo }} \cdot \dot{I}_{\text{L} 1}
\end{array}\)](https://www.schullv.de/resources/formulas/7c1cc58c211400107b50c9ac5a5176eddd8c4248b72bab04bd73001077c2c8ac_light.svg) Bei einem sinusförmigen Verlauf gilt hier für
Bei einem sinusförmigen Verlauf gilt hier für 
![\(\begin{array}[t]{rll}
I_{\text{L} 1}(t)&=& I_{\text{L} 1,0} \cdot \sin (\omega \cdot \text{t})&
\end{array}\)](https://www.schullv.de/resources/formulas/a0773c00dccd0e7f954978a62cad27fc8615c5083babae6de4de0984457aaa5a_light.svg) Für die Ableitung der Stromstärke gilt:
Es gilt außerdem für
Für die Ableitung der Stromstärke gilt:
Es gilt außerdem für 
![\(\begin{array}[t]{rll}
k_{\text {theo }}&=& \mu_0 \cdot \dfrac{n_1}{\sqrt{(2 R)^2+l^2}} &
\end{array}\)](https://www.schullv.de/resources/formulas/311a2862e7fd8ac8eeee4b7bf3295f15014b97a21be7913750f31ee39299907e_light.svg) Einsetzen in
Einsetzen in  liefert die Gleichung:
Einsetzen liefert die gegebene Gleichung:
Bestimmung der Werte für
liefert die Gleichung:
Einsetzen liefert die gegebene Gleichung:
Bestimmung der Werte für  und
und  Durch Ablesen der Werte im Diagramm in Abbildung 6 erhält man
Durch Ablesen der Werte im Diagramm in Abbildung 6 erhält man  und
und  Berechnung der Amplitude
Berechnung der Amplitude  Die Amplitude berechnet zu:
Die Amplitude berechnet zu:
d)
Vergleiche der beiden zeitlichen Verläufe
Durch den Gleichrichter ist die Spannung am Akku bei negativer Induktionsspannung an der Empfängerspule gleich Null. Durch einen Vergleich der beiden Stromverläufe erkennt man, dass in den für die Aufladung des Akkus relevanten Zeitintervallen die Änderungsraten der Stromstärke und dadurch auch die Änderungsraten der Stärke des magnetischen Feldes vom Betrage gleich sind, sodass die gleiche Spannung  induziert wird und damit die gleiche Akkuspannung
induziert wird und damit die gleiche Akkuspannung  zur Verfügung steht.
Entscheidung für den besser geeignten zeitlichen Verlauf
Aufgrund der gleichen Akkuspannung
zur Verfügung steht.
Entscheidung für den besser geeignten zeitlichen Verlauf
Aufgrund der gleichen Akkuspannung  ist dann derjenige Verlauf der effektivere, bei dem diese Spannung im Verhältnis zur Periodendauer über die längere Zeitspanne anliegt. Durch Ablesen erhält man für dieses Verhältnis
ist dann derjenige Verlauf der effektivere, bei dem diese Spannung im Verhältnis zur Periodendauer über die längere Zeitspanne anliegt. Durch Ablesen erhält man für dieses Verhältnis  folgende Werte:
Für den Dreieckförmigen Verlauf aus Abbildung 5 gilt:
Für den Sägezahnförmigen Verlauf in Abbildung 8 gilt:
Der sägezahnförmige Verlauf in Abbildung 8 ist somit besser geeignet, da
folgende Werte:
Für den Dreieckförmigen Verlauf aus Abbildung 5 gilt:
Für den Sägezahnförmigen Verlauf in Abbildung 8 gilt:
Der sägezahnförmige Verlauf in Abbildung 8 ist somit besser geeignet, da  statt nur
statt nur  der Ladezeit tatsächlich zum Laden des Smartphones verwendet werden.
der Ladezeit tatsächlich zum Laden des Smartphones verwendet werden.
Teillösung 3: Einfluss der Position des Smartphones auf der Ladestation
a)
Aufgrund der Geometrie der Ladespule ist das magnetische Feld nicht homogen und nimmt (räumlich) sowohl in vertikaler als auch in horizontaler Richtung (stark) ab. Liegen Lade und Empfängerspule genau übereinander, so ist der Einfluss der induktionsrelevanten Größen, d. h. die Änderungsrate der Stärke des magnetischen Feldes und die vom Feld senkrecht durchsetzte Fläche, maximal und damit auch gemäß dem Induktionsgesetz die entstehende Induktionsspannung. Liegt das Smartphone horizontal bzw. vertikal verschoben auf der Ladestation, so ist dieser Einfluss kleiner, was zu einer kleineren Induktionsspannung führt und damit einen längeren Ladevorgang bzw. ein unvollständiges Laden des Smartphones bedeuten kann.
b)
Ermittlung des Wertes zum Ausfleich des Effektes der nicht optimalen Positionierung
Nimmt die Stärke des magnetischen Feldes im Bereich der Empfängerspule auf  ab, so reduziert sich auch die Änderungsrate des magnetischen Feldes und damit die Induktionsspannung um denselben Wert. Mit der Formel zur Grundwertberechnung gilt:
ab, so reduziert sich auch die Änderungsrate des magnetischen Feldes und damit die Induktionsspannung um denselben Wert. Mit der Formel zur Grundwertberechnung gilt:
![\(\begin{array}[t]{rll}
G &=& \dfrac{100\cdot W}{p}&\quad \scriptsize \mid\; G = I_{\text{L} 1, \max } \\[5pt]
I_{\text{L} 1, \max }&=& \dfrac{100\cdot 600 \;\text{mA} }{75} &\quad \scriptsize \\[5pt]
&=& \dfrac{4}{3} \cdot 600 \;\text{mA} &\quad \scriptsize \\[5pt]
&=& 800 \;\text{mA}
\end{array}\)](https://www.schullv.de/resources/formulas/9cefb7d8689196e6c8d88fdf244bd95ff93c11fc59657c77752396d1eba63b8c_light.svg) Die Abnahme der Stärke des magnetischen Feldes im Bereich der Empfängerspule auf
Die Abnahme der Stärke des magnetischen Feldes im Bereich der Empfängerspule auf  lässt sich dadurch kompensieren, dass die maximale Stärke des Feldes der Ladespule um den Faktor
lässt sich dadurch kompensieren, dass die maximale Stärke des Feldes der Ladespule um den Faktor  erhöht wird. Dies ist durch eine Erhöhung der maximalen Stromstärke um denselben Faktor zu erreichen, d. h. die maximale Stromstärke bei dem sägezahnförmigen Verlauf in Abbildung 8 beträgt dann
erhöht wird. Dies ist durch eine Erhöhung der maximalen Stromstärke um denselben Faktor zu erreichen, d. h. die maximale Stromstärke bei dem sägezahnförmigen Verlauf in Abbildung 8 beträgt dann  Nennung weiterer Größen
Eine größere Induktionsspannung kann bei unveränderter maximaler Stromstärke
Nennung weiterer Größen
Eine größere Induktionsspannung kann bei unveränderter maximaler Stromstärke  auch durch eine Erhöhung der Frequenz
auch durch eine Erhöhung der Frequenz  bzw. der Periodendauer
bzw. der Periodendauer  der Stromstärke
der Stromstärke  erreicht werden. Damit lässt sich auch die Änderungsrate der Stärke des Feldes und somit die Induktionsspannung erhöhen.
Ermittlung eines Wertes für diese Größe
Im konkreten Fall muss die Periodendauer um den Faktor
erreicht werden. Damit lässt sich auch die Änderungsrate der Stärke des Feldes und somit die Induktionsspannung erhöhen.
Ermittlung eines Wertes für diese Größe
Im konkreten Fall muss die Periodendauer um den Faktor  reduziert werden oder die Frequenz entsprechend erhöht herhöht.
Für die Reduzierung der Periodendauer gilt:
reduziert werden oder die Frequenz entsprechend erhöht herhöht.
Für die Reduzierung der Periodendauer gilt:
![\(\begin{array}[t]{rll}
T&=& \dfrac{3}{4}\cdot 50 \;\mu \text{s} &\quad \scriptsize \\[5pt]
&=& 37,5 \;\mu \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/15e84693716899ab7db4492e98b7e0d824d262f3a7d8eca4be6a05523833f22e_light.svg) Für die Erhöhung der Frequenz gilt:
Für die Erhöhung der Frequenz gilt:
![\(\begin{array}[t]{rll}
f&=& \dfrac{1}{T}&\quad \scriptsize \\[5pt]
&=& \dfrac{1}{37,5 \mu \text{s}} &\quad \scriptsize \\[5pt]
&=& 0.0267 \cdot \dfrac{1}{\mu \text{s}} &\quad \scriptsize \\[5pt]
&=& 0.0267 \cdot \dfrac{1}{10^{-6}\;\text{s}} &\quad \scriptsize \\[5pt]
&=& 0.0267 \cdot 10^{6}\;\text{Hz} &\quad \scriptsize \\[5pt]
&=& 26,7 \cdot 10^{3}\;\text{Hz} &\quad \scriptsize \\[5pt]
&=& 26,7 \;\text{kHz} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cbe3b1302d4ed610a370d6d42bc317c15f1438b4018f5c22d9fe740e4b0aaa81_light.svg)