HT 3
Nachweis und Eigenschaften extrem seltener Elemente
Insgesamt 10 chemische Elemente waren bereits in der Antike bekannt und bis zum Ende des 19. Jahrhunderts wurden 73 weitere chemische Elemente entdeckt. Zwar gelang in der zweiten Hälfte des 19. Jahrhunderts eine immer bessere Sortierung dieser Elemente aufgrund ihrer Atommasse und wiederkehrender ähnlicher chemischer Eigenschaften, aber es fehlte dem damals noch unvollständigen Periodensystem eine zuverlässige „Nummerierung“ dieser Elemente. Erst zu Beginn des 20. Jahrhunderts gelang es Physikerinnen und Physikern, durch die Entwicklung erklärungsstarker Atommodelle und neuer experimenteller Methoden die Reihenfolge der Elemente im Periodensystem durch ihre „Ordnungszahl
a)
- Zeichne eine beschriftete Skizze zum Aufbau einer Röntgenröhre sowie ihrer elektrischen Beschaltung.
- Erläutere die Funktionsweise einer Röntgenröhre, ohne dabei auf die atomaren Prozesse der Erzeugung der Röntgenstrahlung einzugehen.
b)
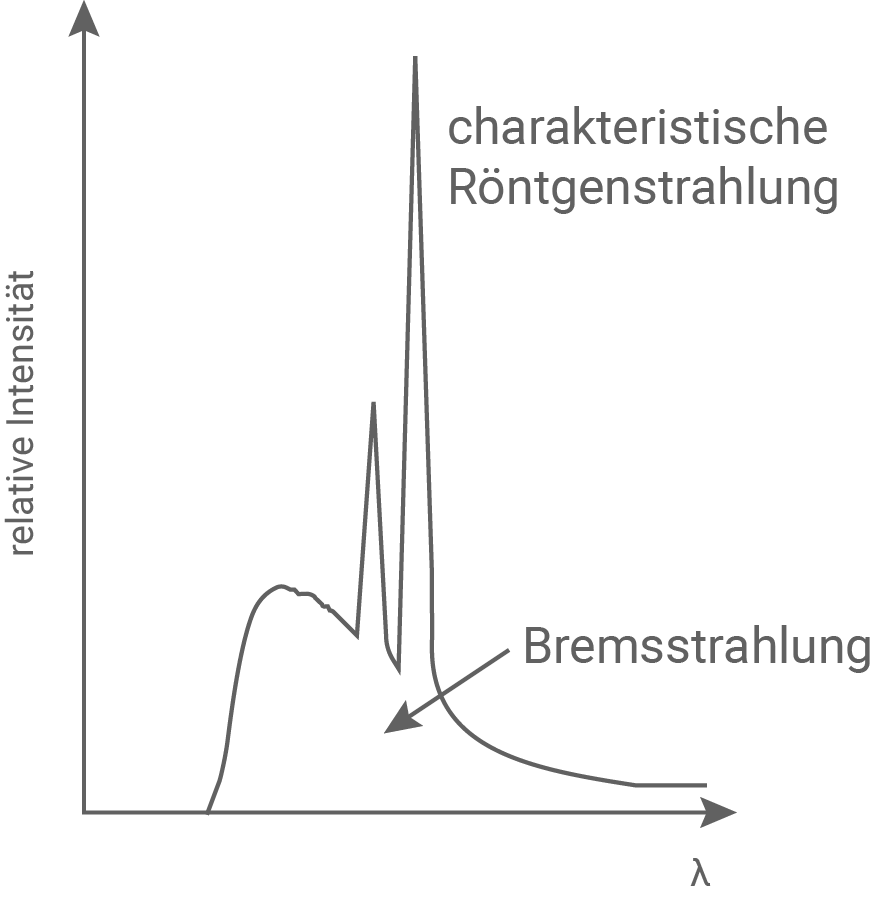
Abbildung 1 zeigt ein typisches Röntgenspektrum. Es besitzt zwei spektrale Anteile: das kontinuierliche Spektrum der Bremsstrahlung sowie die Linien der charakteristischen Röntgenstrahlung.
Erkläre die Entstehung der Bremsstrahlung sowie der charakteristischen Röntgenstrahlung anhand der zugehörigen elementaren Prozesse sowie einer geeigneten Modellvorstellung vom atomaren Aufbau des Anodenmaterials.
Erkläre die Entstehung der Bremsstrahlung sowie der charakteristischen Röntgenstrahlung anhand der zugehörigen elementaren Prozesse sowie einer geeigneten Modellvorstellung vom atomaren Aufbau des Anodenmaterials.

c)
Eine einfache Möglichkeit der Aufnahme eines Röntgenspektrums ist die Drehkristallmethode. Abbildung 2 zeigt einen typischen Aufbau zur Durchführung dieser Messmethode.
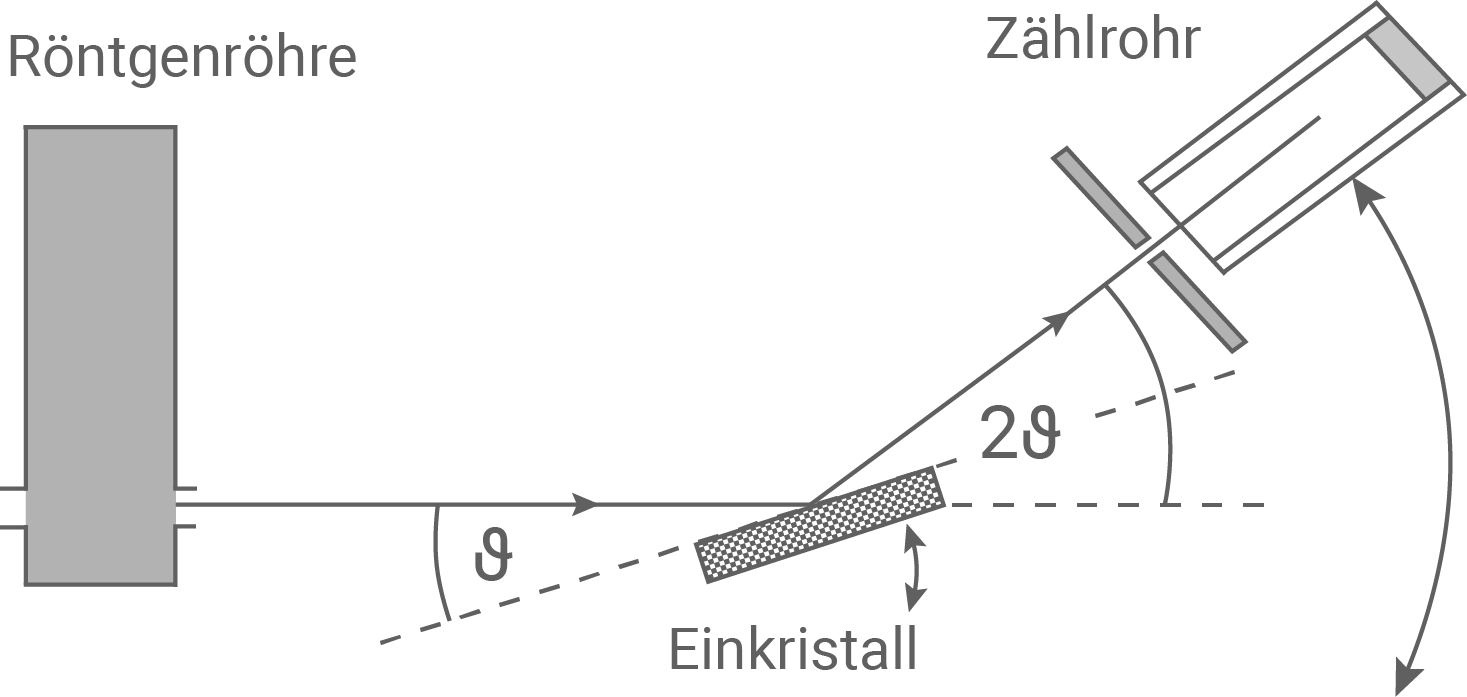 Bei der Messung des Röntgenspektrums mit dieser Methode trifft die gebündelte Strahlung unter einem Winkel
Bei der Messung des Röntgenspektrums mit dieser Methode trifft die gebündelte Strahlung unter einem Winkel  auf einen Einkristall, dessen Oberfläche parallel zu seinen Netzebenen verläuft. Unter dem Winkel
auf einen Einkristall, dessen Oberfläche parallel zu seinen Netzebenen verläuft. Unter dem Winkel  zur Einfallsrichtung der Röntgenstrahlung misst ein Zählrohr die vom Einkristall gestreute Strahlung. Für die Wellenlänge
zur Einfallsrichtung der Röntgenstrahlung misst ein Zählrohr die vom Einkristall gestreute Strahlung. Für die Wellenlänge  der dort nachgewiesenen Röntgenstrahlung gilt die sogenannte Bragg-Bedingung:
der dort nachgewiesenen Röntgenstrahlung gilt die sogenannte Bragg-Bedingung:
 mit
mit  Dabei bezeichnet
Dabei bezeichnet  den Abstand benachbarter Netzebenen des Einkristalls.
den Abstand benachbarter Netzebenen des Einkristalls.
 , beginnend bei kleinen Winkeln bis zu
, beginnend bei kleinen Winkeln bis zu  , bewegt. Das Zählrohr wird dabei entsprechend um den doppelten Drehwinkel mitgeführt. Nach jedem Drehschritt wird für eine immer gleiche Zeit
, bewegt. Das Zählrohr wird dabei entsprechend um den doppelten Drehwinkel mitgeführt. Nach jedem Drehschritt wird für eine immer gleiche Zeit  die Zahl der Strahlungsereignisse im Zählrohr gemessen und für den jeweiligen Winkel
die Zahl der Strahlungsereignisse im Zählrohr gemessen und für den jeweiligen Winkel  registriert.
registriert.
 ) beträgt die Drehschrittweite
) beträgt die Drehschrittweite  . Die Messung beginnt bei
. Die Messung beginnt bei 

Teilaufgabe 2: Sortierung des Periodensystems durch Bestimmung der Ordnungszahlen der Elemente
Nachdem sich in den 1910er-Jahren das Kern-Hülle-Atommodell etabliert hatte, gelang es, den Aufbau des Periodensystems mit der schrittweisen Auffüllung von Elektronenschalen in der Atomhülle zu verstehen. Die Ordnungszahl 
Abbildung 2: Drehkristallmethode zur Aufnahme eines Röntgenspektrums
- Leite die Bragg-Bedingung anhand einer geeigneten Skizze her.
- Erkläre, warum für die Aufnahme eines Röntgenspektrums bei jedem Messwert die Messzeit
gleich sein muss.
- Gib an, wie viele Messpunkte bei dieser Messung erfasst werden.
- Zeige, dass bei dieser Messung in erster Ordnung
der Wellenlängenbereich zwischen
und
abgedeckt wird.
- Untersuche begründet, ob das kurzwellige Ende des Röntgenspektrums unter den Bedingungen dieser Messung erfasst werden kann.
(6 + 4 + 14 Punkte)
a)
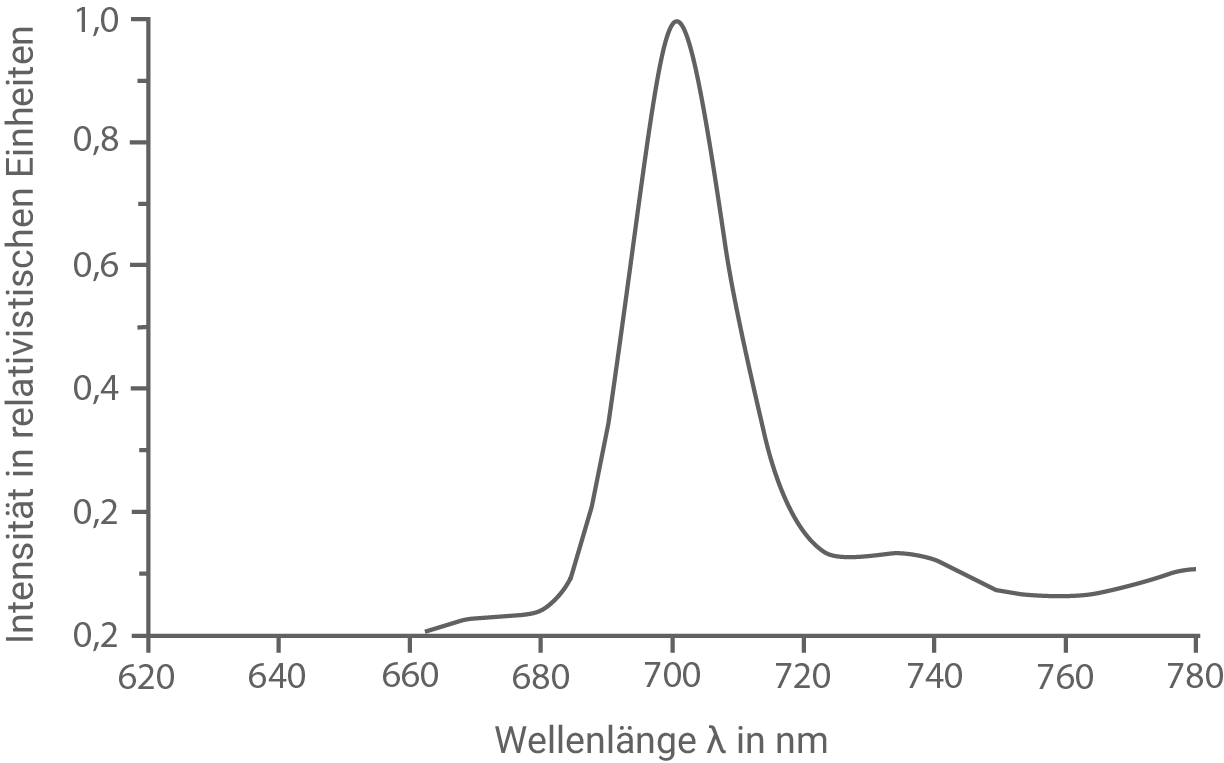
Abbildung 3 zeigt das Spektrum der Röntgenstrahlung des Kupfers. Die beiden Linien in dem Spektrum sind die  - und die
- und die  -Linie des Kupfers. Die genaue Wellenlänge der
-Linie des Kupfers. Die genaue Wellenlänge der  -Linie in diesem Spektrum beträgt
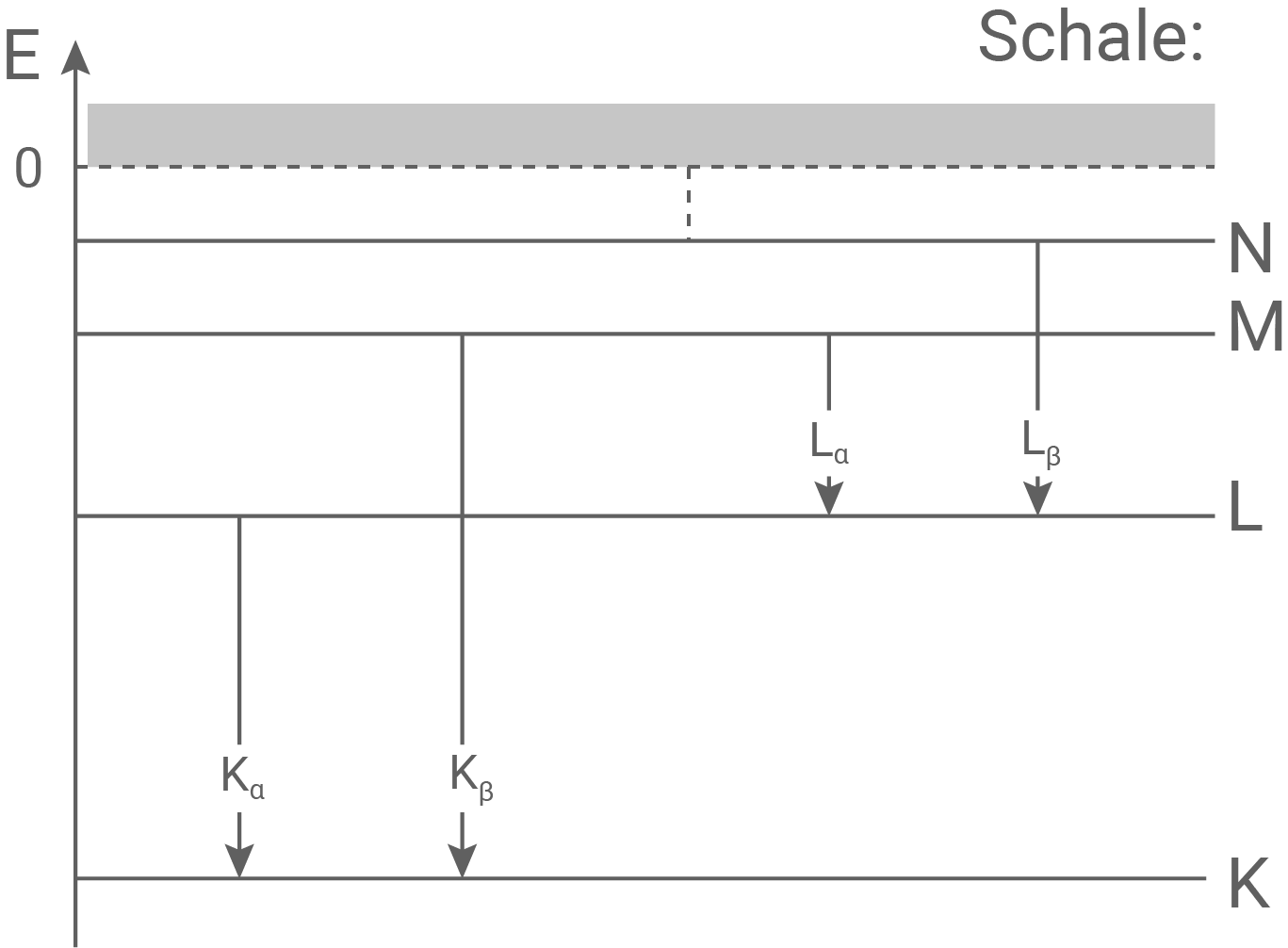
-Linie in diesem Spektrum beträgt  Abbildung 4 zeigt das vereinfachte Niveauschema eines Atoms mit den Übergängen der charakteristischen Röntgenlinien.
Abbildung 4 zeigt das vereinfachte Niveauschema eines Atoms mit den Übergängen der charakteristischen Röntgenlinien.
 Bestimme anhand von
Bestimme anhand von  aus Abbildung 3 die Energiedifferenz zwischen der L-Schale und der M-Schale im Kupferatom in der Einheit
aus Abbildung 3 die Energiedifferenz zwischen der L-Schale und der M-Schale im Kupferatom in der Einheit 

Abbildung 3

Abbildung 4: Vereinfachtes Niveauschema eines Atoms
b)
Dem britischen Physiker H. Moseley gelang es bereits 1914 empirisch, den folgenden Zusammenhang zwischen den Wellenlängen der  -Röntgenlinien der chemischen Elemente (bis zum Zirkon) und deren Ordnungszahl
-Röntgenlinien der chemischen Elemente (bis zum Zirkon) und deren Ordnungszahl  zu finden:
zu finden:
 Dabei bezeichnet
Dabei bezeichnet  eine empirisch gefundene Proportionalitätskonstante mit der Maßeinheit
eine empirisch gefundene Proportionalitätskonstante mit der Maßeinheit ![\([\sqrt{C}]=1 \dfrac{1}{\sqrt{\text m}}\)](https://www.schullv.de/resources/formulas/86ee21e0e6c640e7f4777940d7cfa9c4c1e77a715259a8a87a940f8a6bbf2e82_light.svg) .
Tabelle 1 beinhaltet die von
.
Tabelle 1 beinhaltet die von  . Moseley gemessenen Wellenlängen der
. Moseley gemessenen Wellenlängen der  -Röntgenlinien einiger Elemente.
-Röntgenlinien einiger Elemente.
Teilaufgabe 3: Extrem seltene Elemente und ihre Entstehung
Aufgrund immer besserer chemischer Analyse- und Synthesemethoden sowie einer weiter verbesserten Röntgenspektroskopie gelang es bis 1930, fast alle chemischen Elemente mit einer Ordnungszahl kleiner als der des Wismut - Zeige anhand einer grafischen Auswertung, dass die Messwerte in Tabelle 1 den oben angegebenen Zusammenhang bestätigen.
- Bestimme anhand dieser grafischen Auswertung einen Wert für die Proportiona- litätskonstante
- Bestimme anhand dieser Auswertung und der Informationen aus Teilaufgabe 2a die Ordnungszahl
von Kupfer.
(4 + 12 Punkte)
a)
Heute ist bekannt, dass das Element mit der Ordnungszahl  (Technetium
(Technetium  ) ausschließlich Isotope besitzt, welche radioaktiv zerfallen. Abbildung 5 zeigt einen Ausschnitt aus einer heutigen Nuklidkarte.
) ausschließlich Isotope besitzt, welche radioaktiv zerfallen. Abbildung 5 zeigt einen Ausschnitt aus einer heutigen Nuklidkarte.
 eine gewisse Menge an Technetium mitentstanden ist.
eine gewisse Menge an Technetium mitentstanden ist.
 Kernen) beschossen worden.
Kernen) beschossen worden.
 -Kerns. Abbildung 6 zeigt die Zerfallsgleichung dieses natürlichen Vorgangs sowie die daraus resultierende Zerfallsreihe bis zum Technetium. Die in der Zerfallsreihe angegebenen Zeiten sind die Halbwertszeiten der entsprechenden Nuklide.
-Kerns. Abbildung 6 zeigt die Zerfallsgleichung dieses natürlichen Vorgangs sowie die daraus resultierende Zerfallsreihe bis zum Technetium. Die in der Zerfallsreihe angegebenen Zeiten sind die Halbwertszeiten der entsprechenden Nuklide.
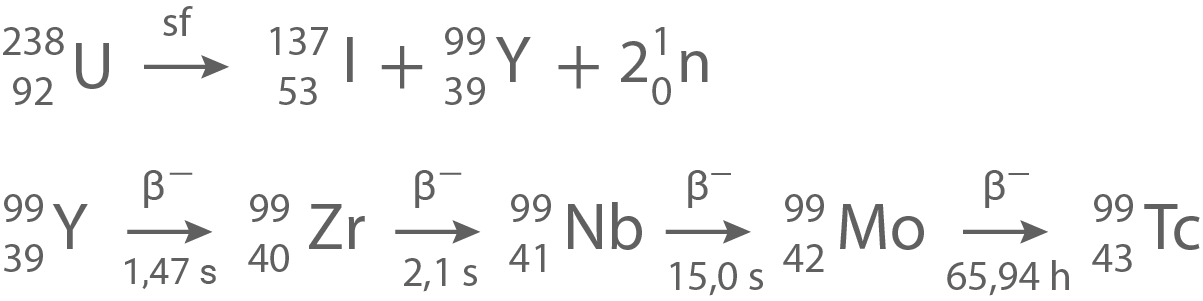 Erkläre qualitativ, warum zwar das
Erkläre qualitativ, warum zwar das  im Uranerz nachweisbar ist, die anderen Nuklide der Zerfallsreihe aus Abbildung 6 jedoch nicht.
im Uranerz nachweisbar ist, die anderen Nuklide der Zerfallsreihe aus Abbildung 6 jedoch nicht.
- Gib die Zerfallsgleichungen der beiden
-Isotope mit den längsten Halbwertszeiten an.
- Bestimme, welcher Anteil des Technetiumisotops mit der längsten Halbwertszeit nach „nur“
von der ursprünglichen Menge noch existiert hat.
- Gib die Reaktionsgleichung einer möglichen Kernreaktion an, mit der ein Technetiumisotop in der Molybdän-Folie entstanden sein kann.
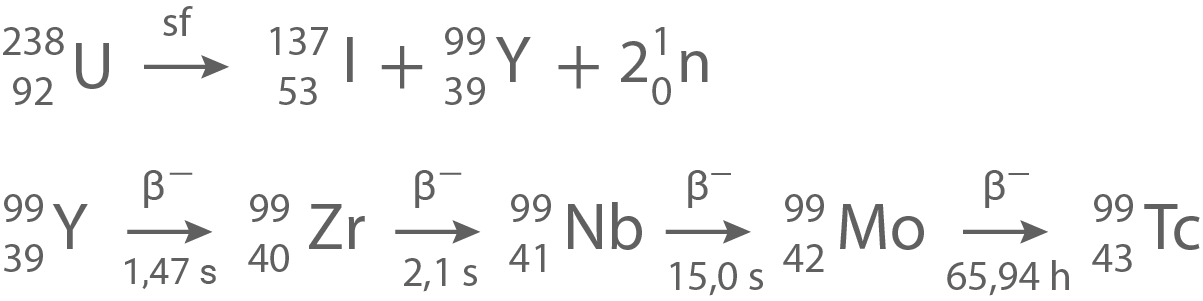
Abbildung 6: Entstehung von Technetium in der Natur
b)
Genauso wie Technetium besitzt auch das Element mit  (Promethium
(Promethium  ) keine stabilen Isotope. Die
) keine stabilen Isotope. Die  -Isotope mit den längsten Halbwertszeiten sind:
-Isotope mit den längsten Halbwertszeiten sind:
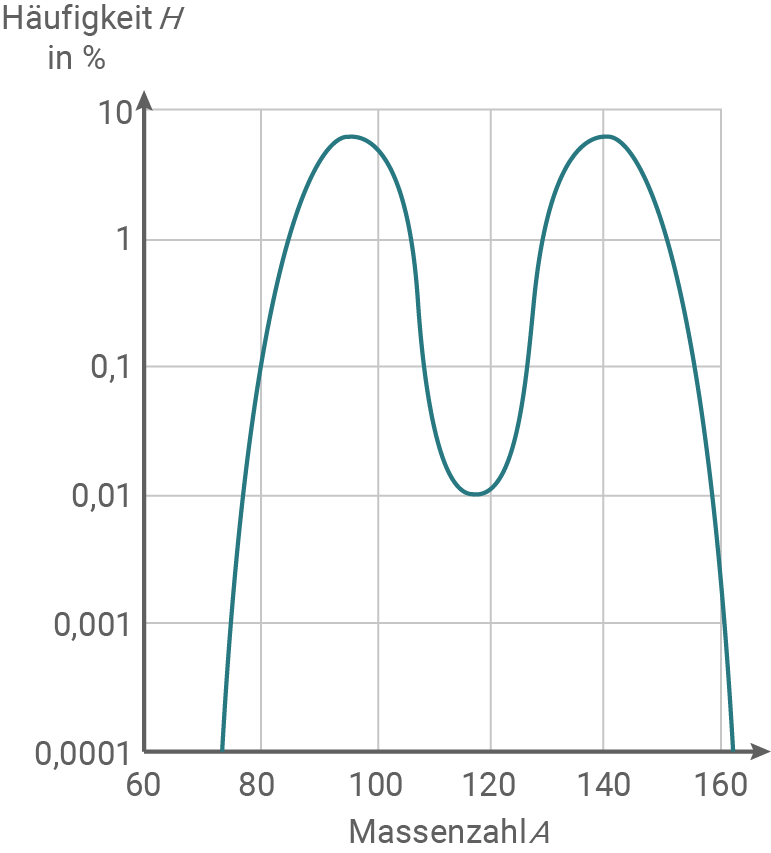
Dieses Element wurde erst 1947 im Zuge der chemischen Untersuchung der Spaltprodukte aus den ersten Kernreaktoren entdeckt. Abbildung 7 zeigt die relative Häufigkeit  der Spaltprodukte eines typischen Kernreaktors als Funktion von deren Massenzahl
der Spaltprodukte eines typischen Kernreaktors als Funktion von deren Massenzahl 
 Promethium natürlichen Ursprungs gibt. Es handelt sich dabei praktisch ausschließlich um das Isotop
Promethium natürlichen Ursprungs gibt. Es handelt sich dabei praktisch ausschließlich um das Isotop  .
.
 natürliches Promethium etwa
natürliches Promethium etwa  -Atomen entsprechen.
-Atomen entsprechen.
Teilaufgabe 4: Das extraterrestrische Vorkommen von Promethium
Heute ist bekannt, dass Promethium auf der Erde und damit wahrscheinlich auch in unserem Sonnensystem nur in verschwindend geringen Mengen natürlich vorkommt.
| Isotop: | |||
|---|---|---|---|
| Halbwertszeit |
|||
Tabelle 2:  -Isotope mit den längsten Halbwertszeiten
-Isotope mit den längsten Halbwertszeiten

Abbildung 7: Relative Häufigkeit der Spaltprodukte bei der Kernspaltung von 
- Beurteile anhand von Abbildung 7 qualitativ die relative Häufigkeit, mit der das Element Promethium in den Spaltprodukten eines Kernreaktors zu erwarten ist.
- Bestimme die Gesamtaktivität
des natürlichen Promethiums in der Erdkruste in der Einheit
(12 + 7 Punkte)
Durch Untersuchungen der optischen Absorptionsspektren einiger sehr spezieller Sterne weiß man heute aber auch, dass Promethium sowie die im Periodensystem benachbarten Elemente im Bereich der Oberfläche und der nahen Umgebung dieser Sterne in messbarer Menge vorhanden sind. Das Alter dieser seltenen speziellen Sterne ist etwa dem unserer Sonne vergleichbar (ca.
a)
Begründe qualitativ, dass der Nachweis des Promethiums in diesen Sternen nur damit erklärt werden kann, dass dieses Element dort ständig neu erzeugt wird.
Eine der Theorien, die das dortige „viel häufigere“ Vorkommen der bei uns sehr seltenen chemischen Elemente erklären soll, geht davon aus, dass im Bereich der Oberfläche dieser besonderen Sterne eine hohe Konzentration von langlebigen Uranisotopen vorhanden ist. Diese langlebigen Uranisotope existieren dort seit der Sternentstehung und werden durch die dort reichlich vorhandenen freien Neutronen aus dem Inneren des Sterns permanent gespalten. Als Spaltprodukte bleiben dabei u.a. die seltenen Elemente in messbarer Menge zurück.
b)
Erläutere qualitativ, wie es experimentell möglich wäre, diese Theorie durch Beobachtungen zu bestätigen oder zu widerlegen.
(3 +3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Teillösung 1: Physikalische Grundlagen der Röntgenspektroskopie
a)
Skizzierung des Aufbaus einer Röntgenröhre
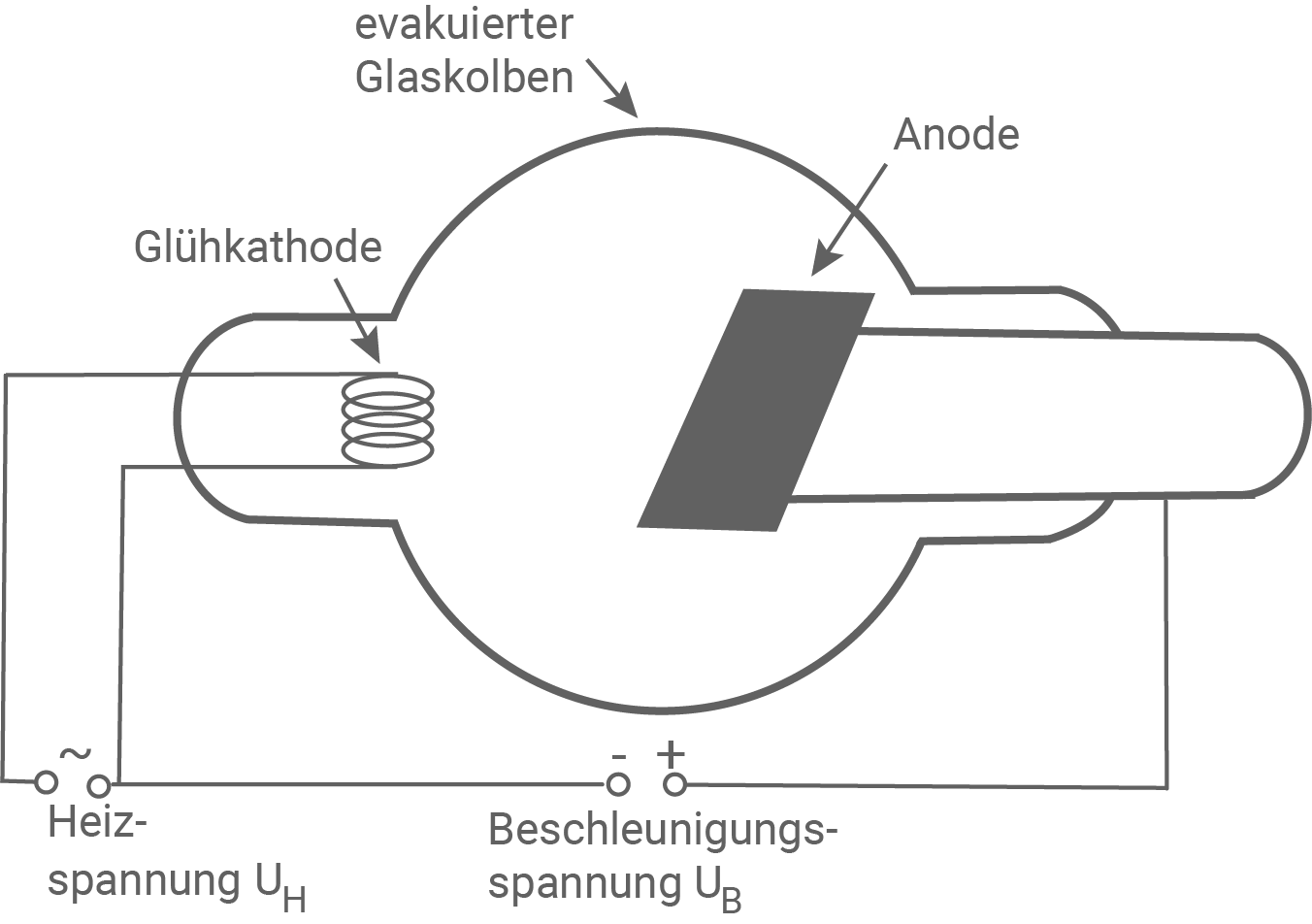 Erläuterung der Funktionsweise einer Röntgenröhre
Beim Betrieb der Röntgenröhre werden an der Glühkathode durch den glühelektrischen Effekt Elektronen ausgelöst und dann aufgrund der anliegenden Spannung
Erläuterung der Funktionsweise einer Röntgenröhre
Beim Betrieb der Röntgenröhre werden an der Glühkathode durch den glühelektrischen Effekt Elektronen ausgelöst und dann aufgrund der anliegenden Spannung  zur Anode hin beschleunigt. Beim Auftreffen dieser Elektronen auf das Anodenmaterial entsteht dann die Röntgenstrahlung, welche die Röntgenröhre verlassen kann.
zur Anode hin beschleunigt. Beim Auftreffen dieser Elektronen auf das Anodenmaterial entsteht dann die Röntgenstrahlung, welche die Röntgenröhre verlassen kann.

b)
Das Spektrum der Röntgenstrahlung setzt sich aus dem kontinuierlichen Spektrum der Bremsstrahlung und den für das Anodenmaterial charakteristischen Linien zusammen. Die Bremsstrahlung entsteht, wenn ein schnelles Elektron nach dem Eintreten ins Anodenmaterial durch die Wechselwirkung mit einem Atomkern stark abgelenkt wird und dabei einen Teil seiner kinetischen Energie in Form eines Strahlungsquants abgibt.
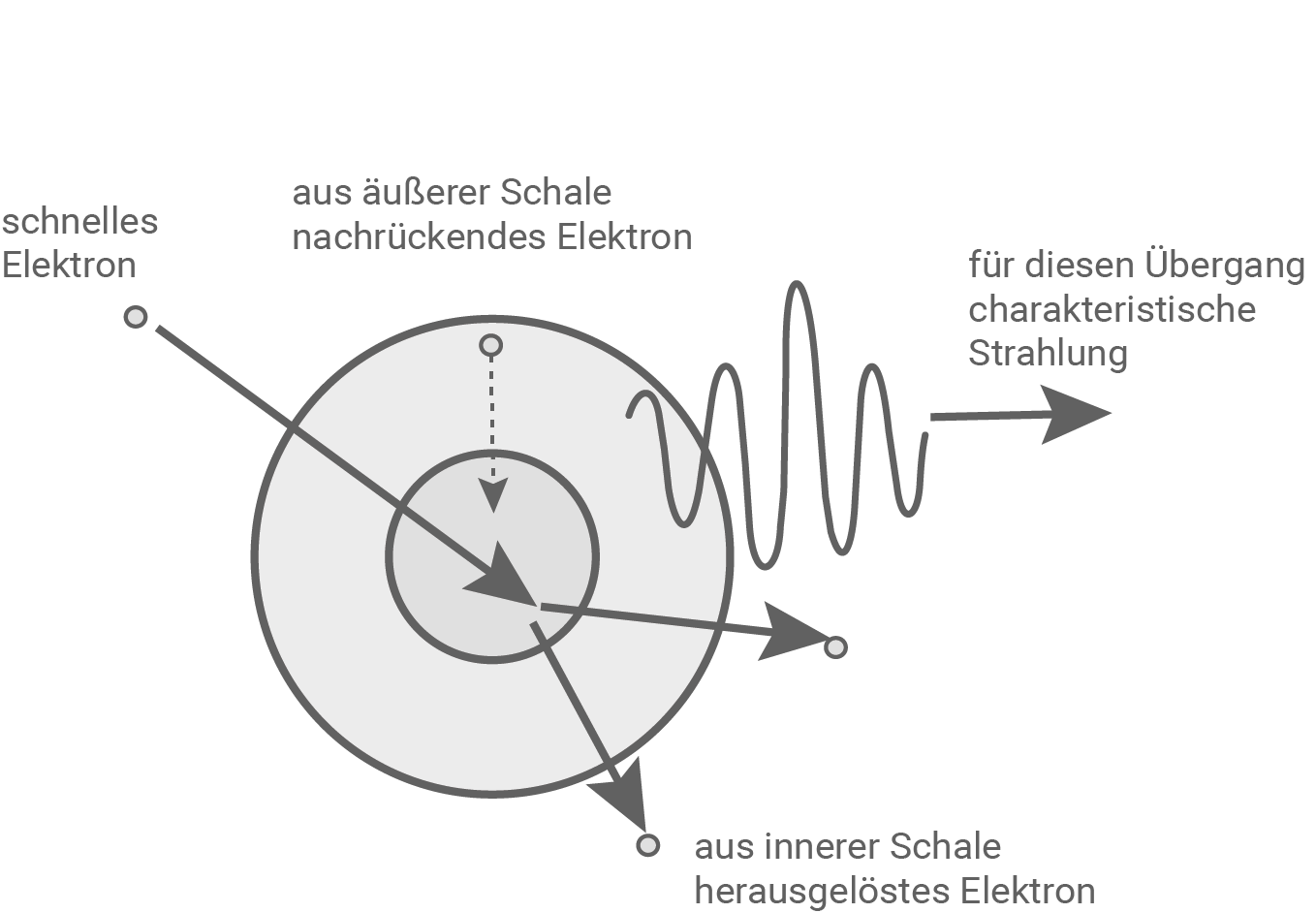
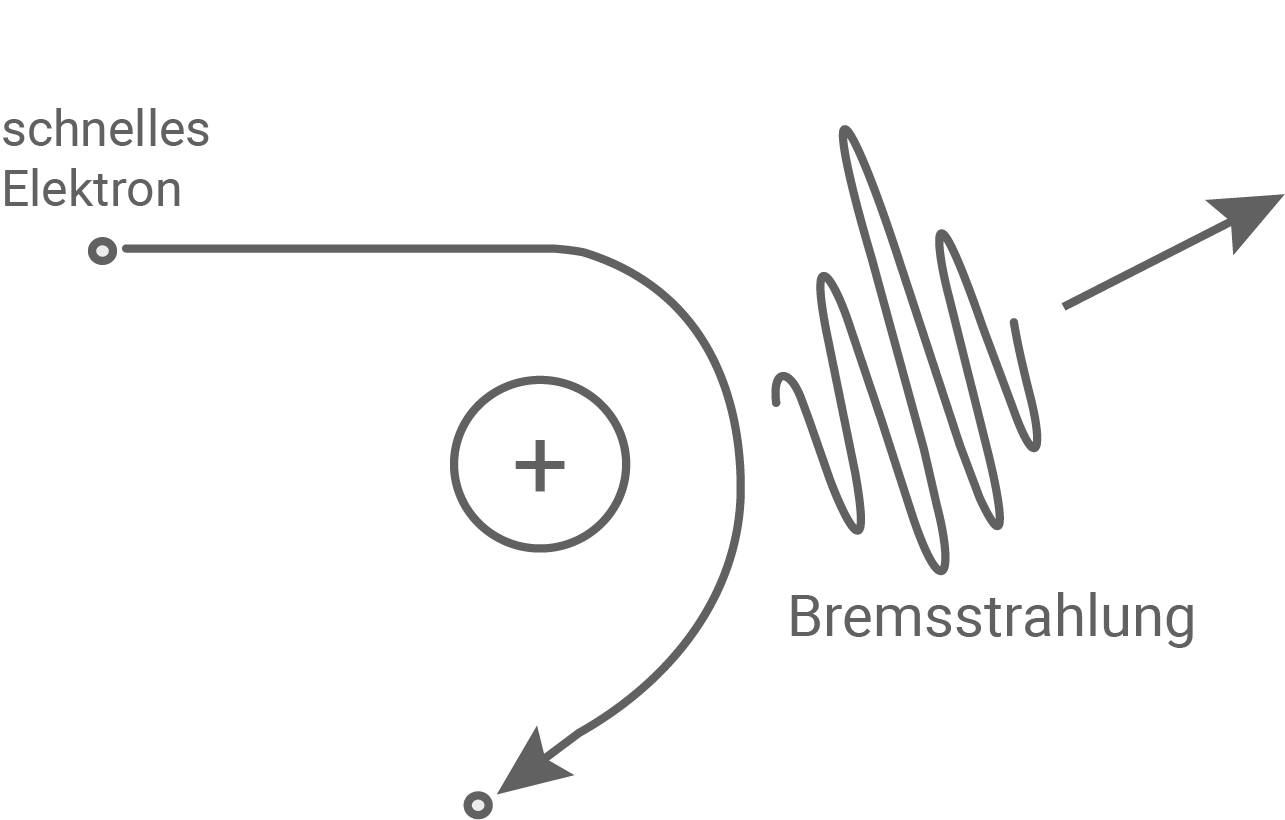 Die charakteristische Röntgenstrahlung entsteht, wenn ein schnelles Elektron nach Eintritt ins Anodenmaterial dort ein Elektron aus einer inneren Schale eines Atoms herausschlägt und dann ein anderes Elektron aus einer äußeren Schale auf diesen freien Platz übergeht. Dabei wird die für den Übergang charakteristische Energie abgestrahlt.
Die charakteristische Röntgenstrahlung entsteht, wenn ein schnelles Elektron nach Eintritt ins Anodenmaterial dort ein Elektron aus einer inneren Schale eines Atoms herausschlägt und dann ein anderes Elektron aus einer äußeren Schale auf diesen freien Platz übergeht. Dabei wird die für den Übergang charakteristische Energie abgestrahlt.


c)
Herleitung der Bragg-Bedingung anhand einer geeigneten Skizze
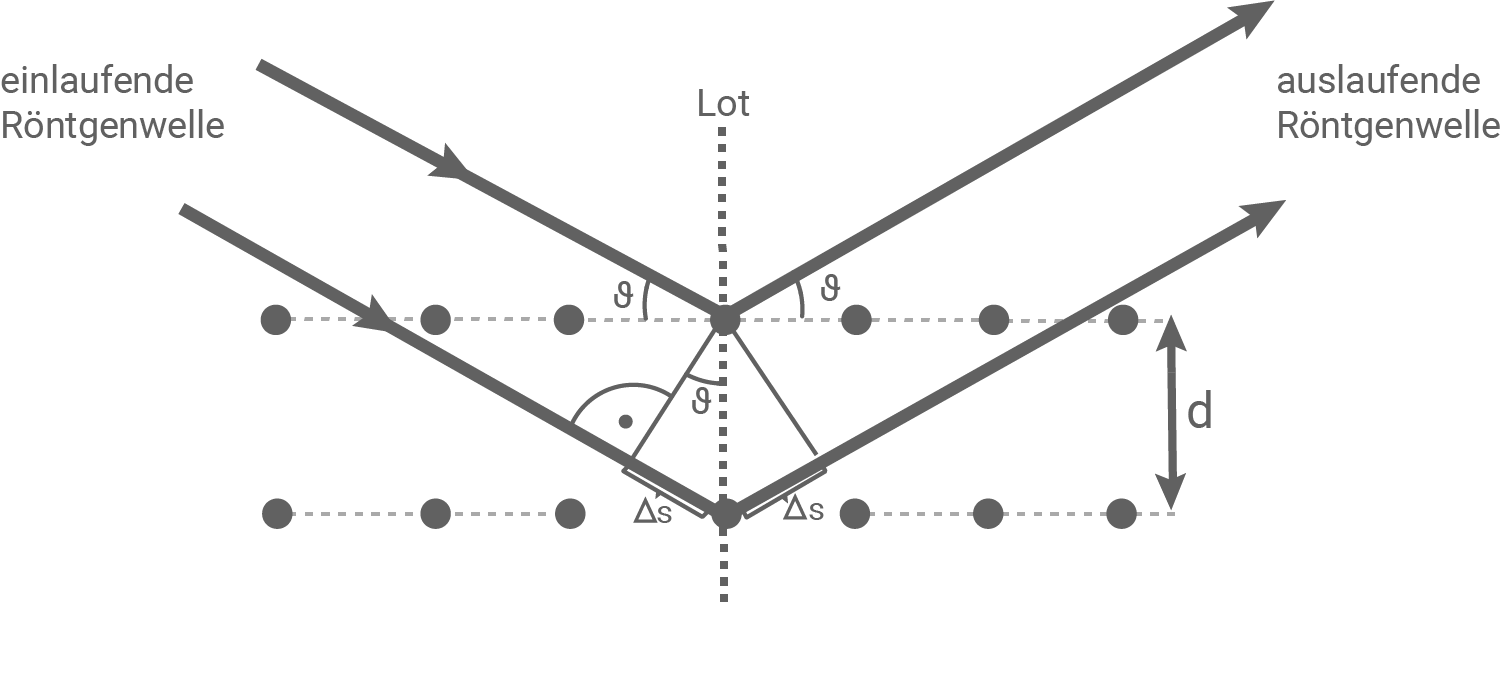 Die einlaufenden Röntgenwellen werden an den Netzebenen des Einkristalls gestreut. Der Wegunterschied, den eine einlaufende Wellenfront bis zur Streuung an der nächst tieferen Netzebene des Kristalls zurücklegen muss, ist
Die einlaufenden Röntgenwellen werden an den Netzebenen des Einkristalls gestreut. Der Wegunterschied, den eine einlaufende Wellenfront bis zur Streuung an der nächst tieferen Netzebene des Kristalls zurücklegen muss, ist  Wie aus der Skizze ersichtlich, gilt für diesen Wegunterschied der Zusammenhang
Wie aus der Skizze ersichtlich, gilt für diesen Wegunterschied der Zusammenhang  Dabei bezeichnet
Dabei bezeichnet  den Abstand benachbarter Netzebenen. Nach Streuung an der nächst tieferliegenden Netzebene muss die auslaufende Wellenfront unter Berücksichtigung der Reflexionsbedingung (Einfallswinkel
den Abstand benachbarter Netzebenen. Nach Streuung an der nächst tieferliegenden Netzebene muss die auslaufende Wellenfront unter Berücksichtigung der Reflexionsbedingung (Einfallswinkel  Ausfallswinkel
Ausfallswinkel  ) erneut den Wegunterschied
) erneut den Wegunterschied  s zusätzlich zurücklegen, sodass der Gesamtgangunterschied zwischen den an benachbarten Netzebenen reflektierten Wellenfronten
s zusätzlich zurücklegen, sodass der Gesamtgangunterschied zwischen den an benachbarten Netzebenen reflektierten Wellenfronten  beträgt. Zu einer konstruktiven Interferenz der reflektierten Wellenfronten kann es in einer solchen Situation nur kommen, wenn der Gesamtgangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist:
beträgt. Zu einer konstruktiven Interferenz der reflektierten Wellenfronten kann es in einer solchen Situation nur kommen, wenn der Gesamtgangunterschied ein ganzzahliges Vielfaches der Wellenlänge ist:  mit
mit  Erklärung, warum für die Aufnahme eines Röntgenspektrums bei jedem Messwert die Messzeit
Erklärung, warum für die Aufnahme eines Röntgenspektrums bei jedem Messwert die Messzeit  gleich sein muss
Bei der Aufnahme eines Röntgenspektrums mit der Drehkristallmethode muss die Messzeit
gleich sein muss
Bei der Aufnahme eines Röntgenspektrums mit der Drehkristallmethode muss die Messzeit  für jede Winkeleinstellung gleich sein, damit die erfasste Zahl der Strahlungsereignisse und damit die gemessene Intensität bei allen Winkeleinstellungen miteinander vergleichbar ist.
Angabe der Anzahl der Messpunkte
Bei einem erfassten Winkelbereich von
für jede Winkeleinstellung gleich sein, damit die erfasste Zahl der Strahlungsereignisse und damit die gemessene Intensität bei allen Winkeleinstellungen miteinander vergleichbar ist.
Angabe der Anzahl der Messpunkte
Bei einem erfassten Winkelbereich von  und einer Schrittweite von
und einer Schrittweite von  gilt für die Anzahl der Messerte:
gilt für die Anzahl der Messerte:
![\(\begin{array}[t]{rll}
n&=& \dfrac{\vartheta_{\text{max}}-\vartheta_{\text{min}}}{\Delta \vartheta} + 1&\quad \scriptsize \\[5pt]
n &=& \dfrac{45^{\circ}-3^{\circ}}{0,2^{\circ}}+1&\quad \scriptsize \\[5pt]
n&=& 211
\end{array}\)](https://www.schullv.de/resources/formulas/189ef77bb4edb35a91d2e4612d8659cb20c8362aab920fe3022d5e3e38de9a46_light.svg) Es werden insgesamt also 211 Messwerte aufgenommen.
Zeigen, dass bei dieser Messung in erster Ordnung
Es werden insgesamt also 211 Messwerte aufgenommen.
Zeigen, dass bei dieser Messung in erster Ordnung  der Wellenbereich zwischen
der Wellenbereich zwischen  und
und  liegt
Der LiF-Kristall hat eine Dicke von
liegt
Der LiF-Kristall hat eine Dicke von  Es gilt für diesen LiF-Kristall in erster Ordnung
Es gilt für diesen LiF-Kristall in erster Ordnung 
![\(\begin{array}[t]{rll}
\lambda_{\min .}&=& 2 \cdot d \cdot \sin\left( \vartheta_{\text{min}}\right)&\quad \scriptsize \\[5pt]
\lambda_{\max .}&=& 2 \cdot d \cdot \sin\left( \vartheta_{\text{max}}\right)&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8320055d255a7bd7f7ac0eaa9a712c99ceecf082a2a004692805df2e9b3f2827_light.svg) Einsetzen der Werte für
Einsetzen der Werte für  ,
,  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
\lambda_{\min .}&=& 2 \cdot 2,01 \cdot 10^{-10} \;\text{m} \cdot \sin\left( 3^{\circ}\right)&\quad \scriptsize \\[5pt]
&=& 2,10 \cdot 10^{-11} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/e5f8911ef82f41db5404a88d17b725445e2051079ccfdbbeef5619ab0811e761_light.svg)
![\(\begin{array}[t]{rll}
\lambda_{\max .}&=& 2 \cdot 2,01 \cdot 10^{-10} \;\text{m} \cdot \sin\left( 45^{\circ}\right)&\quad \scriptsize \\[5pt]
&=& 2,84 \cdot 10^{-10} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/0956458ed34fbe491db52dde4aa7347ffb05b0f7e647f73da7682cec2b80ba0d_light.svg) Einsetzen der Werte für
Einsetzen der Werte für  in
in  zeigt, dass die Messungen in dem Wellenbereich zwischen
zeigt, dass die Messungen in dem Wellenbereich zwischen  und
und  liegen :
liegen :
![\(\begin{array}[t]{rll}
\lambda_{\min .}&\leq& \lambda \leq \lambda_{\text {max. }}&\quad \scriptsize \\[5pt]
2,10 \cdot 10^{-11} \;\text{m}&\leq& \lambda \leq 2,84 \cdot 10^{-10} \;\text{m}&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1b5abbfd57e13995aa7bdb4cdea5bd228060de4430b2350806ad2b980727089b_light.svg) Untersuchung, ob das kurzwellige Ende des Röntgenspektrums unter den Bedingungen dieser Messung erfasst werden kann
Die Röntgenstrahlung am kurzwelligen Ende des Röntgenspektrums entsteht, wenn ein Elektron nach Durchlaufen der Beschleunigungsspannung
Untersuchung, ob das kurzwellige Ende des Röntgenspektrums unter den Bedingungen dieser Messung erfasst werden kann
Die Röntgenstrahlung am kurzwelligen Ende des Röntgenspektrums entsteht, wenn ein Elektron nach Durchlaufen der Beschleunigungsspannung  seine komplette kinetische Energie
seine komplette kinetische Energie  in einem Strahlungsquant der Grenzwellenlänge
in einem Strahlungsquant der Grenzwellenlänge  abstrahlt. Es gilt dann:
abstrahlt. Es gilt dann:
![\(\begin{array}[t]{rll}
e \cdot U_{\text{B}}&=& h \cdot f&\quad \scriptsize \mid\; f= \dfrac{c}{\lambda_{\text{Gr} .}} \\[5pt]
e \cdot U_{\text{B}}&=& h \cdot \dfrac{c}{\lambda_{\text{Gr} .}}&\quad \scriptsize \mid\; \cdot \lambda_{\text{Gr} .} \\[5pt]
e \cdot U_{\text{B}}\cdot \lambda_{\text{Gr} .}&=& h \cdot c&\quad \scriptsize \mid\; \cdot \dfrac{1}{e\cdot U_{\text{B}}} \\[5pt]
\lambda_{\text{Gr} .}&=& \dfrac{h \cdot c}{e \cdot U_{\text{B}}}
\end{array}\)](https://www.schullv.de/resources/formulas/07bf1ddd7a49d48dbf429e9959de7d40e58196ea88f68910ac0c396402ec730c_light.svg) Wenn eine Röntgenröhre mit
Wenn eine Röntgenröhre mit  betrieben wird, gilt für die Grenzwellenlänge:
Diese Grenzwellenlänge liegt innerhalb des bei der Messung erfassten Wellenlängenbereichs:
betrieben wird, gilt für die Grenzwellenlänge:
Diese Grenzwellenlänge liegt innerhalb des bei der Messung erfassten Wellenlängenbereichs: 
Teillösung 2: Sortierung des Periodensystems durch Bestimmung der Ordnungszahlen der Elemente

a)
Aus dem Röntgenspektrum des Kupfers in Abbildung 3 ergibt sich durch Ablesen die folgenden Wellenlänge der  -Linie:
-Linie:
![\(\begin{array}[t]{rll}
\lambda_{\text{K} \beta}&=& 0,140 \;\text{nm}&\quad \scriptsize \\[5pt]
&=& 1,40 \cdot 10^{-10} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/e07ac203171ffad4ff4aa1ff28e5852bed5926d60f7d8e1091c32646559c0db7_light.svg) Die Wellenlänge der
Die Wellenlänge der  -Linie beträgt:
-Linie beträgt:
![\(\begin{array}[t]{rll}
\lambda_{\text{K} \alpha}&=& 0,154 \;\text{nm}&\quad \scriptsize \\[5pt]
&=& 1,54 \cdot 10^{-10} \;\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/301c21f302008efea5b6e9a52e53c7326e68f93149f8cd2688b6c9c0075660d9_light.svg) Die Energiedifferenz
Die Energiedifferenz  zwischen der L- und M-Schale entspricht der Energiedifferenz der
zwischen der L- und M-Schale entspricht der Energiedifferenz der  - und der
- und der  -Linie. Daraus ergibt sich mit:
-Linie. Daraus ergibt sich mit:
![\(\begin{array}[t]{rll}
\Delta E_{\text{ML}}&=& E_{\text{K} \beta}-E_{\text{K} \alpha} &\quad \scriptsize \\[5pt]
&=& h\cdot f_{\text{K} \beta}- h\cdot f_{\text{K} \alpha} &\quad \scriptsize \\[5pt]
&=& h\cdot \dfrac{c}{\lambda_{\text{K} \beta}}-h\cdot \dfrac{c}{\lambda_{\text{K} \alpha}} &\quad \scriptsize \\[5pt]
&=& h \cdot\left(\dfrac{c}{\lambda_{\text{K} \beta}}-\dfrac{c}{\lambda_{\text{K} \alpha}}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/996714b68f9ecf02b22ed0498c3c2434252f3f3dc8eb6b2e5b93275ae58b6ab3_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
b)
Bestätigung der Messwerte des Zusammenhangs
Die Messwerte:
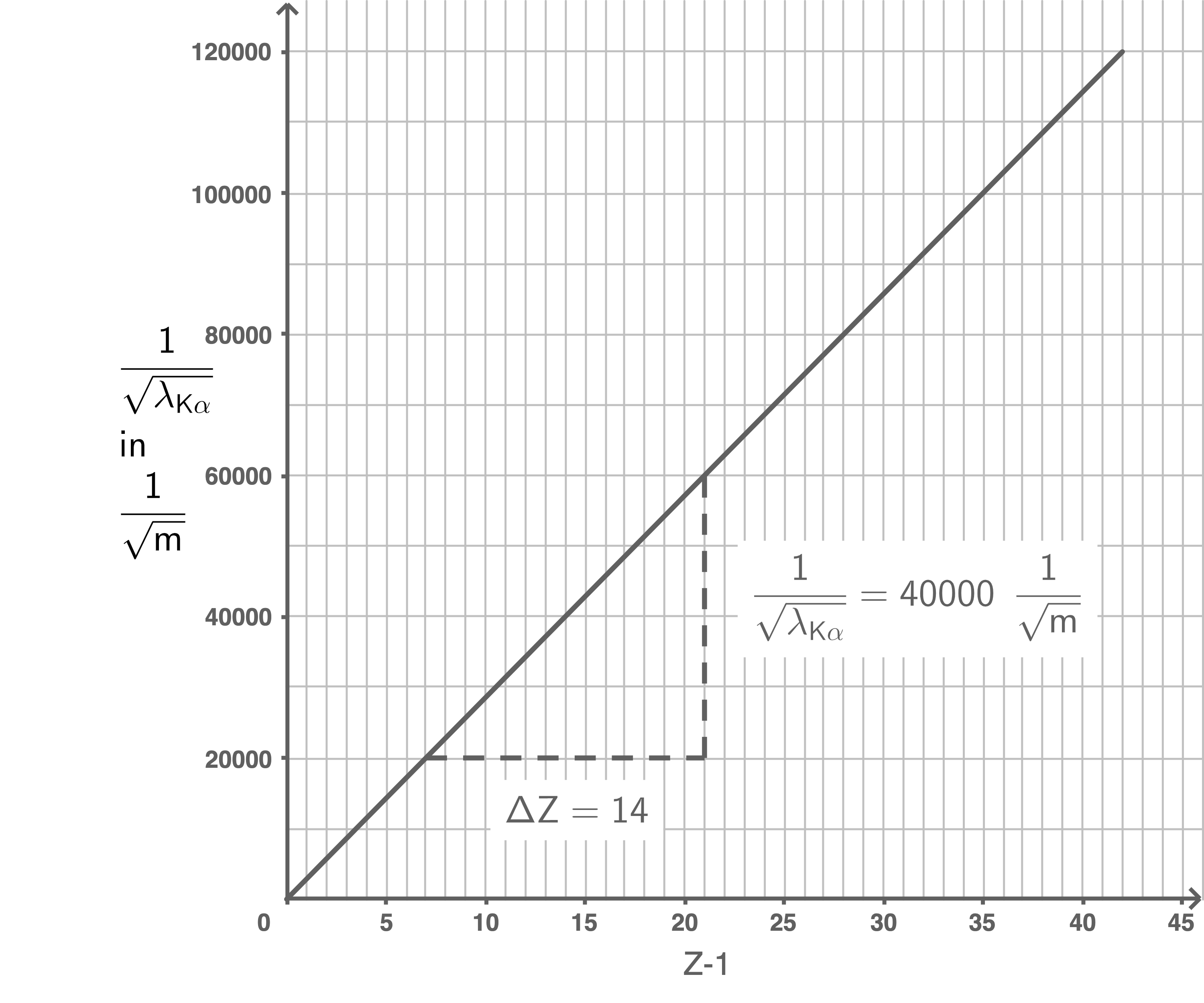
Graphische Darstellung:
 Bestimmung der Proportionalitätskonstante
Das Auftragen der gemessenen Werte von
Bestimmung der Proportionalitätskonstante
Das Auftragen der gemessenen Werte von  gegen
gegen  zeigt den proportionalen Zusammenhang dieser beiden Größen.
Aus dem Steigungsdreieck ergibt sich die Steigung:
zeigt den proportionalen Zusammenhang dieser beiden Größen.
Aus dem Steigungsdreieck ergibt sich die Steigung:
![\(\begin{array}[t]{rll}
\dfrac{\Delta \dfrac{1}{\sqrt{\lambda_{\text{K} \alpha}}}}{\Delta \text{Z}}&=& \dfrac{40000 \;\dfrac{1}{\sqrt{\text{m}}}}{14} &\quad \scriptsize \\[5pt]
&=& 2860 \;\dfrac{1}{\sqrt{\text{m}}}
\end{array}\)](https://www.schullv.de/resources/formulas/566a98cae34eb9f81c74385ec92e2b8375d4a92c3faaf419f7d337c70840cbc9_light.svg) Demnach beträgt die Proportionalitätskonstanten
Demnach beträgt die Proportionalitätskonstanten  :
:
![\(\begin{array}[t]{rll}
\sqrt{\text{C}}&=& \dfrac{\Delta \dfrac{1}{\sqrt{\lambda_{\text{K} \alpha}}}}{\Delta \text{Z}} &\quad \scriptsize \\[5pt]
&=& 2860 \; \dfrac{1}{\sqrt{\text{m}}} &
\end{array}\)](https://www.schullv.de/resources/formulas/9c6f49dd6fbb7225aba6fe94c81539e0fc3f77fd488b9ca38d795e2d23dee194_light.svg) Bestimmung der Ordnungszahl Z von Kupfer
Für Kupfer beträgt die Wellenlänge der
Bestimmung der Ordnungszahl Z von Kupfer
Für Kupfer beträgt die Wellenlänge der  -Linie:
-Linie:  Daraus ergibt sich:
Daraus ergibt sich:
![\(\begin{array}[t]{rll}
\dfrac{1}{\sqrt{\lambda_{\text{K} \alpha}}}&=& \dfrac{1}{\sqrt{1,54 \cdot 10^{-10} \text{m}}}&\quad \scriptsize \\[5pt]
&=& 8,06 \cdot 10^4 \dfrac{1}{\sqrt{\text{m}}}
\end{array}\)](https://www.schullv.de/resources/formulas/0226cb3c3c7b9a550591c132bc79db46996ce4fa62e82f306a5487c97101cb47_light.svg) Im Diagramm lässt sich damit für Kupfer ablesen:
Im Diagramm lässt sich damit für Kupfer ablesen:  Daher besitzt Kupfer die Ordnungszahl
Daher besitzt Kupfer die Ordnungszahl 
Teillösung 3: Extrem seltene Elemente und ihre Entstehung
| Z-1 | ||
|---|---|---|
| 12 | 8,36 | 3,46 |
| 19 | 3,37 | 5,45 |
| 23 | 2,30 | 6,59 |
| 26 | 1,80 | 7,45 |
| 29 | 1,45 | 8,30 |
| 39 | 0,794 | 11,2 |

a)
Angabe der Zerfallsgleichungen
Das Isotop  Tc zerfällt wie folgt zu
Tc zerfällt wie folgt zu 
 .
Das Isotop
.
Das Isotop  Tc zerfällt wie folgt zu
Tc zerfällt wie folgt zu 
 Anteil des nach
Anteil des nach  noch existierenden Technetiumisotops
Nach dem Zerfallsgesetz gilt:
noch existierenden Technetiumisotops
Nach dem Zerfallsgesetz gilt:
![\(\begin{array}[t]{rll}
N\left(t \right)&=& N_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{ T_{1 / 2}}} &\quad \scriptsize \mid\;\cdot \dfrac{1}{N_0} \\[5pt]
\dfrac{N\left(t \right)}{N_0}&=& \left(\dfrac{1}{2}\right)^{\dfrac{t}{ T_{1 / 2}}} &
\end{array}\)](https://www.schullv.de/resources/formulas/6f6eb15f110b54f777edbbafa910b5c2010700935f6dc4ac09ece03adec8daba_light.svg) Das Technetiumisotop mit der längsten Halbwertszeit
Das Technetiumisotop mit der längsten Halbwertszeit  besitzt eine Halbwertszeit von
besitzt eine Halbwertszeit von  a.Ein Zwanzigstel des Erdalters beträgt
a.Ein Zwanzigstel des Erdalters beträgt  Aus dem Zerfallsgesetz ergibt sich damit ein Anteil der noch nicht zerfallenen
Aus dem Zerfallsgesetz ergibt sich damit ein Anteil der noch nicht zerfallenen  Tc -Kerne nach dieser Zeit von:
Tc -Kerne nach dieser Zeit von:
![\(\begin{array}[t]{rll}
\dfrac{N\left(t \right)}{N_0}&=& \dfrac{N\left(\dfrac{1}{20} t_{\text{E}}\right)}{N_0} &\quad \scriptsize \\[5pt]
&=& \left(\dfrac{1}{2}\right)^{\dfrac{\dfrac{1}{20} t_{\text{E}}}{T_{1 / 2}}} &\quad \scriptsize \\[5pt]
&=& \left(\dfrac{1}{2}\right)^{\dfrac{t_{\text{E}}}{20\cdot T_{1 / 2}}}
\end{array}\)](https://www.schullv.de/resources/formulas/c4951584215ea4f32ab773795a3d69a95f845f8719e100c085eb2fe551e81b39_light.svg) Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
\dfrac{N\left(\dfrac{1}{20} t_{\text{E}}\right)}{N_0}&=& \left(\dfrac{1}{2}\right)^{\dfrac{2,5\cdot 10^8 \;\text{a}}{4,2\cdot 10^6 \;\text{a}} } &\quad \scriptsize \\[5pt]
&=& 1,2 \cdot 10^{-18}
\end{array}\)](https://www.schullv.de/resources/formulas/0a7d0da7c6400679a6874e00983fecb36eee481e839093b332b7b1818340ec77_light.svg)
 ist der Anteil des Technetiumisotops mit der längsten Halbwertszeit,der nach "nur"
ist der Anteil des Technetiumisotops mit der längsten Halbwertszeit,der nach "nur"  von der ursprünglichen Menge noch existiert hat.
Angabe der Reaktionsgleichung
Eine mögliche Kernreaktion für die Erzeugung von Technetium in diesem Experiment in der Folie wäre zum Beispiel:
von der ursprünglichen Menge noch existiert hat.
Angabe der Reaktionsgleichung
Eine mögliche Kernreaktion für die Erzeugung von Technetium in diesem Experiment in der Folie wäre zum Beispiel:
 .
Erlärung der Nachweisbarkeit von
.
Erlärung der Nachweisbarkeit von  Bei dem angegebenen natürlichen Entstehungsprozess von
Bei dem angegebenen natürlichen Entstehungsprozess von  , ausgehend von der spontanen Spaltung eines Urankerns, ist die maximale Halbwertszeit aller anderen vorkommenden Nuklide in der Zerfallsreihe ca. 65 Stunden. Das
, ausgehend von der spontanen Spaltung eines Urankerns, ist die maximale Halbwertszeit aller anderen vorkommenden Nuklide in der Zerfallsreihe ca. 65 Stunden. Das  am Ende dieser Zerfallsreihe besitzt hingegen eine Halbwertszeit von
am Ende dieser Zerfallsreihe besitzt hingegen eine Halbwertszeit von  . Im Uranerz werden alle Nuklide dieses sehr seltenen Prozesses mit kurzen Halbwertszeiten nicht auffindbar sein, da sie nur sehr kurz dort existieren, bis sie in das erheblich langlebigere
. Im Uranerz werden alle Nuklide dieses sehr seltenen Prozesses mit kurzen Halbwertszeiten nicht auffindbar sein, da sie nur sehr kurz dort existieren, bis sie in das erheblich langlebigere  Tc zerfallen sind.
Tc zerfallen sind.
b)
Beurteilung der relativen Häufigkeit
Die Massenzahlverteilung der Spaltprodukte bei einer Kernspaltung in Abbildung 7 zeigt, dass im Massenzahlbereich um 140 ein Maximum dieser Verteilung liegt. Da die langlebigsten Promethiumisotope (  bis
bis  ) Massenzahlen in diesem Bereich besitzen, treten sie relativ häufig in den Spaltprodukten eines Kernreaktors auf.
Bestimmung der Gesamtaktivität des Promethiums
In der Erdkruste gibt es insgesamt
) Massenzahlen in diesem Bereich besitzen, treten sie relativ häufig in den Spaltprodukten eines Kernreaktors auf.
Bestimmung der Gesamtaktivität des Promethiums
In der Erdkruste gibt es insgesamt  auf natürlichem Weg entstandenes
auf natürlichem Weg entstandenes  . Aus dieser Masse lässt sich die Anzahl der
. Aus dieser Masse lässt sich die Anzahl der  -Atomkerne bestimmen:
-Atomkerne bestimmen:
![\(\begin{array}[t]{rll}
N &=& 6,20\cdot 10^{23} \cdot \dfrac{0,570 \;\text{kg}}{01147 \;\text{kg}} &\quad \scriptsize \\[5pt]
&=& 2,33 \cdot 10^{24}
\end{array}\)](https://www.schullv.de/resources/formulas/ea7974d1fc7c14dffa0b4b99c2f93b8cdcd04d887141eaab97a5c7f8aaac0190_light.svg) Diese Masse entpricht folglich
Diese Masse entpricht folglich 
 -Atomkerne.
Die Halbwertszeit von
-Atomkerne.
Die Halbwertszeit von  beträgt
beträgt  Für die Aktivität
Für die Aktivität  einer radioaktiven Quelle eines einzelnen Nuklids mit Halbwertszeit
einer radioaktiven Quelle eines einzelnen Nuklids mit Halbwertszeit  und Teilchenzahl
und Teilchenzahl  gilt:
gilt:
![\(\begin{array}[t]{rll}
A_{\text{ges}}&=& \dfrac{\ln (2)}{T_{1 / 2}} \cdot N &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9f3e80a6a6513e3202cfbe8a38d0db9b4037f3bf92f3a9cb7ae7fb3f029c8bf6_light.svg) Einsetzen der Werte in die Formel ergibt:
Einsetzen der Werte in die Formel ergibt:
![\(\begin{array}[t]{rll}
A_{\text{ges}}&=& \dfrac{\ln (2)}{T_{1 / 2}} \cdot N &\quad \scriptsize \\[5pt]
&=& \dfrac{\ln (2)}{8,28 \cdot 10^7 \;\text{s}} \cdot\left(2,33 \cdot 10^{24}\right) &\quad \scriptsize \\[5pt]
&=& 1,95 \cdot 10^{16} \;\text{Bq}
\end{array}\)](https://www.schullv.de/resources/formulas/65b7613bd5f9b4c2aaef851b227e54f95086d21444740dad121245d03e97513b_light.svg)
Teillösung 4:Das extraterrestrische Vorkommen von Promethium
a)
Das in dem Stern nachgewiesene Promethium kann aufgrund seiner kurzen Halbwertszeit von nur maximal  , nicht seit der Entstehung des Sterns vor etwa
, nicht seit der Entstehung des Sterns vor etwa  , dort vorhanden sein. Es muss demnach durch einen permanenten Prozess „nachproduziert“ werden, um in nennenswerter Menge dort zu existieren.
, dort vorhanden sein. Es muss demnach durch einen permanenten Prozess „nachproduziert“ werden, um in nennenswerter Menge dort zu existieren.
b)
Wenn das nachgewiesene Element Promethium und die anderen im Periodensystem benachbarten seltenen Elemente durch die Spaltung großer Mengen langlebiger Uranisotope an der Sternoberfläche entstehen, müssten die Spektrallinien dieses Urans in den optischen Spektren des Sterns ebenfalls deutlich nachweisbar sein.