HT 2

Das Rasterelektronenmikroskop

Mit herkömmlichen Lichtmikroskopen lassen sich Strukturen im Mikrometerbereich beobachten. Noch feinere Strukturen können beispielsweise mit einem sogenannten Rasterelektronenmikroskop (REM) sichtbar gemacht werden. In einem solchen Gerät wird ein Elektronenstrahl über das zu untersuchende Objekt geführt. Dabei wird die Wechselwirkung der Elektronen mit dem Objekt zur Erzeugung eines Bildes dieses Objektes genutzt. Abbildung 1 zeigt die Aufnahme einer Ringelblumenpolle mit einem REM.

nrw physik abi lk 2023 ht 2 abbildung 1 elektronenmikroskopische aufnahme einer ringelblumenpolle

Abbildung 1: Elektronenmikroskopische Aufnahme einer Ringelblumenpolle
(Quelle: https://www.mikroskopie-forum.de/pictures005/197239_42352683.jpg)

Teilaufgabe 1: Erzeugung und Führung des Elektronenstrahls im REM

Abbildung 2 zeigt den schematischen Aufbau eines REM sowie ein Koordinatensystem.

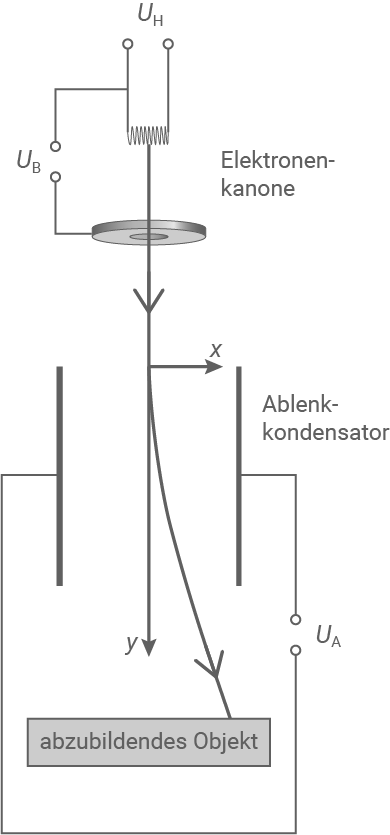
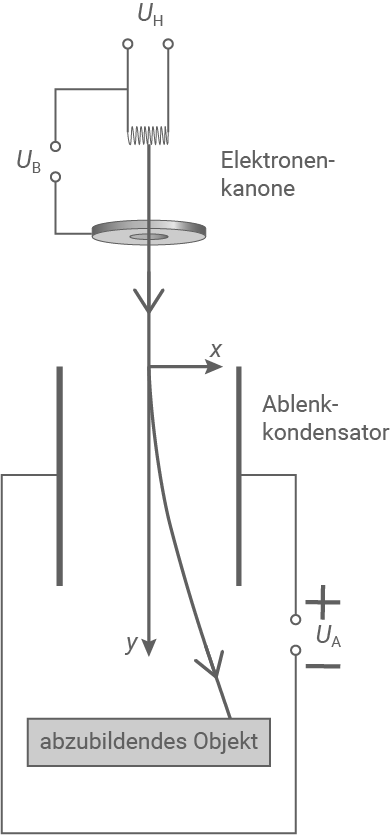
Abbildung 2: Schematischer Aufbau eines Rasterelektronenmikroskops

Um ein Objekt elektronenmikroskopisch abzubilden, werden Elektronen in einer Elektronenkanone beschleunigt und der so erzeugte Elektronenstrahl mithilfe von einem Ablenkkondensator über das abzubildende Objekt geführt.

Erläutere die Funktionsweise einer Elektronenkanone.

Während die Spannung $U_{ \text B }$ notwendigerweise eine Gleichspannung sein muss, darf die Spannung $U_{ \text H }$ als Gleich- oder Wechselspannung vorliegen.

Erkläre diesen Sachverhalt.

Die Geschwindigkeit $v$ , mit der die Elektronen die Elektronenkanone verlassen, kann mit einem klassischen Ansatz hergeleitet werden zu:

$v=\sqrt{\dfrac{2 \cdot e \cdot U_{ \text B }}{m_0}} .$

Dabei bezeichnen $m_0$ die Ruhemasse des Elektrons und $e$ die Elementarladung.

Leite den genannten Zusammenhang her.

Die Elektronenkanone in einem REM kann mit einer Beschleunigungsspannung $U_{ \text B }$ zwischen $0,10\,\text{kV}$ und $30\,\text{kV}$ betrieben werden. Betreibt man die Elektronenkanone mit einer Beschleunigungsspannung $U_{ \text B }$ , bei der der oben genannte Zusammenhang eine Geschwindigkeit $v \leq 0,10 \cdot c$ liefert, so kann das Verhalten der Elektronen ohne relativistische Korrekturen beschrieben werden.

Bestimme die maximale Beschleunigungsspannung $U_{ \text B , \max }$ , bei der das Verhalten der Elektronen ohne relativistische Korrekturen beschrieben werden kann.

Zwischen dem Verlassen der Elektronenkanone und dem Auftreffen auf dem abzubildenden Objekt legen die Elektronen im homogenen Gravitationsfeld der Erde eine vertikale Strecke von $h=50\,\text{cm}$ zurück. Dabei erfährt ein Elektron den Zuwachs $\Delta E_{\text {kin }}=m_0 \cdot g \cdot h$ an kinetischer Energie, wobei $g=9,81\,\text m / \text s ^2$ den Ortsfaktor am Betriebsort des REM bezeichnet.

Zeige, dass dieser Zuwachs der kinetischen Energie beim Betrieb des REM vernachlässigbar ist.

An dem in Abbildung 2 abgebildeten Ablenkkondensator liegt die Spannung $U_{ \text A }$ an.

Gib die Polung der Spannung $U_{ \text A }$ an, sodass sich die abgebildete Bahnkurve der Elektronen ergibt.

Bei dem verwendeten Ablenkkondensator handelt es sich um einen Plattenkondensator mit dem Plattenabstand $d.$ Das elektrische Feld zwischen den Kondensatorplatten kann dabei näherungsweise als homogen angenommen werden. Für die konstante Beschleunigung in $x$ -Richtung, die Elektronen klassisch im Inneren des Kondensators erfahren, gilt dann der folgende Zusammenhang:

$a=\dfrac{e \cdot U_{ \text A }}{m_0 \cdot d} .$

Leite diesen Zusammenhang für die Beschleunigung in $x$ -Richtung her.

Der Auftreffpunkt des Elektronenstrahls auf dem in Abbildung 2 dargestellten abzubildenden Objekt soll innerhalb einer vorgegebenen Zeitspanne vom linken Ende des Objekts zum rechten Ende des Objekts bewegt werden.

Erkläre, warum dies mit einer geeigneten zeitabhängigen Ablenkspannung $U_{ \text A }(t)$ erreicht werden kann.

(6 + 11 + 8 Punkte)

Teilaufgabe 2: Detektion der Elektronen

Während der Elektronenstrahl wie in Teilaufgabe 1 beschrieben über das abzubildende Objekt geführt wird, wechselwirken die schnellen Elektronen des Strahls mit den Hüllelektronen der Atome in der Nähe des Auftreffpunkts. Auf diese Weise entstehen freie Elektronen.

Beschreibe die Entstehung von freien Elektronen durch die Wechselwirkung von schnellen Elektronen mit Atomen.
Begründe anhand einer energetischen Betrachtung, dass die Elektronen für diese Art der Wechselwirkung mit Atomen schnell sein müssen.

Ein Teil der freien Elektronen tritt aus dem abzubildenden Objekt nach oben aus. Diese Elektronen werden mit einem Detektor registriert. Abbildung 3 zeigt schematisch einen entsprechenden Aufbau, in dem ein Wien-Filter verwendet wird.

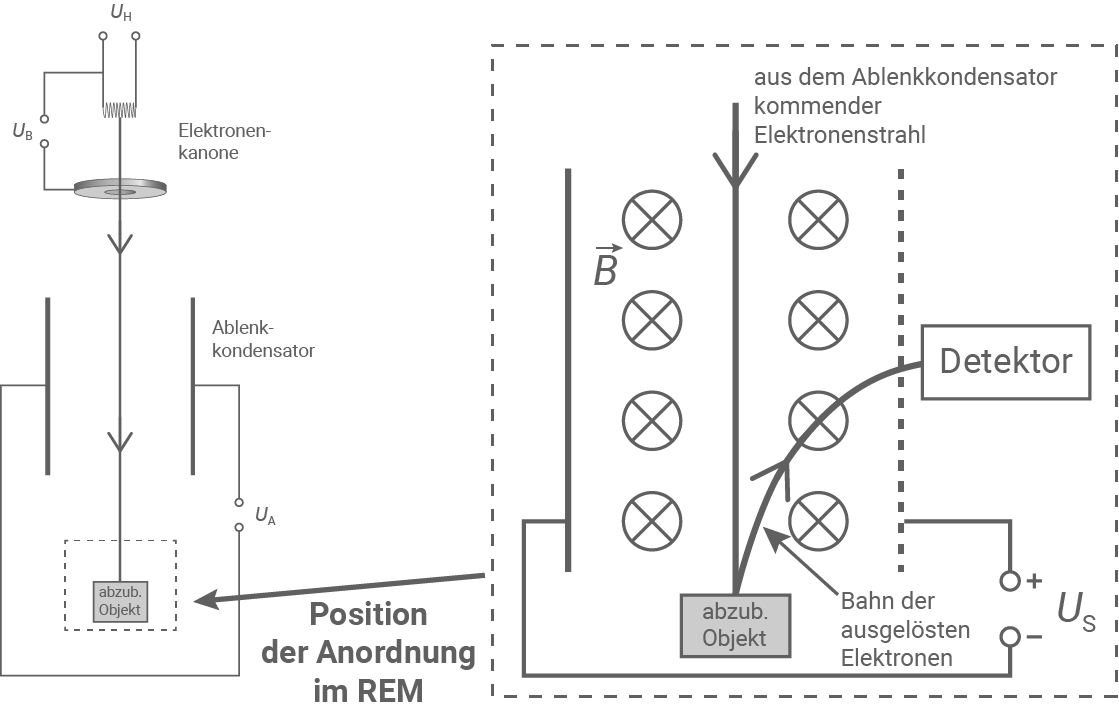
Abbildung 3: Anordnung zur Detektion der Elektronen

Zur Vereinfachung wird im Folgenden ein von oben kommender Elektronenstrahl betrachtet, der entlang der Mittelachse in den Wien-Filter eintritt, bevor er auf das abzubildende Objekt trifft. Im Bereich zwischen den Kondensatorplatten besteht ein homogenes Magnetfeld, das senkrecht zum homogenen elektrischen Feld des Plattenkondensators und senkrecht zur Bewegungsrichtung des Elektronenstrahls gerichtet ist. Hinter der rechten, durchlöcherten Kondensatorplatte befindet sich der Detektor.

Der Wien-Filter kann so eingestellt werden, dass der von oben kommende Elektronenstrahl die Anordnung geradlinig durchläuft.

Gib die Bedingung an, unter der ein von oben in den Wien-Filter eintretendes Elektron die Anordnung geradlinig durchläuft.
Zeige, dass das Elektron in Abhängigkeit von der Stärke $E$ des elektrischen Feldes und der Stärke $B$ des magnetischen Feldes die Geschwindigkeit $v=\dfrac{E}{B}$ besitzen muss, damit es geradlinig durch die Anordnung gelangt.

Bei einer Veränderung der Beschleunigungsspannung $U_{ \text B }$ an der Elektronenkanone in Abbildung 2 muss ebenfalls eine Veränderung der Spannung $U_{ \text S }$ in Abbildung 3 vorgenommen werden.

Erläutere diese Notwendigkeit unter Berücksichtigung der im Wien-Filter wirkenden Kräfte.

Vereinfachend treten die aus dem abzubildenden Objekt ausgelösten Elektronen gemäß Abbildung 3 entlang der Mittelachse von unten in den Wien-Filter ein. Dabei besitzen sie im Vergleich zu den schnellen Elektronen des auftreffenden Elektronenstrahls eine deutlich geringere Geschwindigkeit.

Begründe, dass die aus dem abzubildenden Objekt austretenden Elektronen stets in Richtung Detektor abgelenkt werden.

Den Elektronen, die auf das abzubildende Objekt treffen, kann gemäß der De-BroglieHypothese eine Wellenlänge $\lambda$ zugeordnet werden.

Erläutere die De-Broglie-Hypothese zur Analogie zwischen Licht und Materie. Für die De-Broglie-Wellenlänge gilt der Zusammenhang $\lambda=\dfrac{h}{p}$ . Dabei bezeichnen $h$ das Planck'sche Wirkungsquantum und $p$ den Impuls der Elektronen. De Broglie stellte diesen Zusammenhang zunächst für Photonen auf.
Begründe ausgehend von der für die Energie von Photonen mit der Frequenz $f$ geltenden Gleichung $E=h \cdot f$ den Zusammenhang $\lambda=\dfrac{h}{p}$ für Photonen.

Für eine bestimmte Aufnahme mit einem REM wird die Elektronenkanone mit der Beschleunigungsspannung $U_{\text B }=2,30\,\text{kV}$ betrieben.

Bestimme mit einem klassischen Ansatz die De-Broglie-Wellenlänge $\lambda,$ die den Elektronen zugeordnet werden kann.

Die mit $U_{ \text B }=2,30\,\text{kV}$ beschleunigten Elektronen treffen in einem Versuch auf ein Objekt, das aus einem regelmäßigen Atomgitter mit dem Gitterabstand $d=10^{-10} \,\text m$ besteht.

Erkläre, warum Interferenzerscheinungen bei der Streuung der Elektronen an den Atomen des Gitters möglich sind.

(4 + 9 + 3 + 12 Punkte)

Teilaufgabe 3: Fokussierung des Elektronenstrahls

Um ein möglichst hochauflösendes Bild mit einem REM zu erzeugen, muss der Elektronenstrahl fokussiert werden, bevor er auf das abzubildende Objekt trifft. Dies kann beispielsweise mithilfe von sogenannten Quadrupolmagneten erreicht werden. Diese spezielle Anordnung besteht aus zwei sich jeweils gegenüberstehenden magnetischen Nord- und Südpolen. Abbildung 4 zeigt den schematischen Aufbau eines solchen Quadrupolmagneten sowie den Querschnitt des Elektronenstrahls, der aus der Zeichenebene heraustritt.

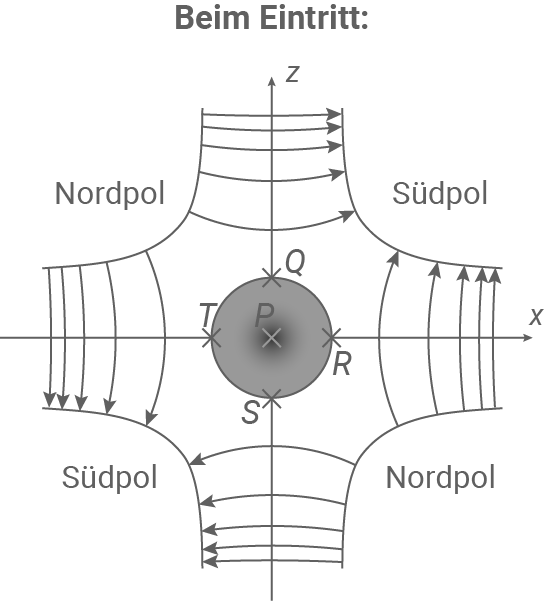
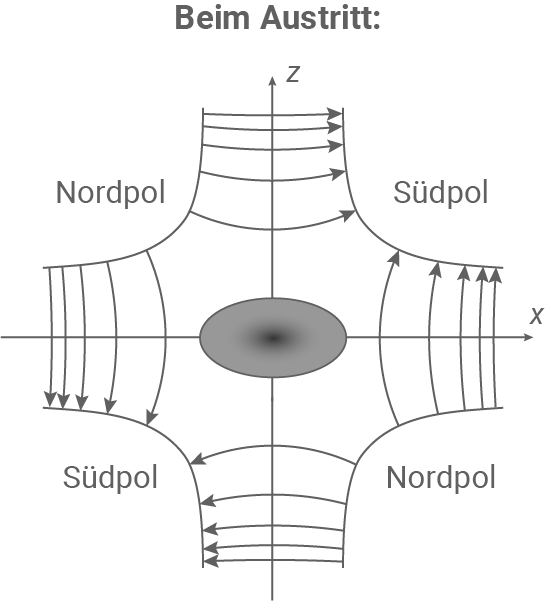
nrw physik abi lk 2023 ht 2 abbildung 4 schematische darstellung des quadrupolmagneten und des querschnitts des elektronenstrahls beim eintritt (links) und beim austritt (rechts)

Abbildung 4: Schematische Darstellung des Quadrupolmagneten und des Querschnitts des Elektronenstrahls beim Eintritt (links) und beim Austritt (rechts)

In Abbildung 4 ist ein unvollständiges Feldlinienbild des durch den Quadrupolmagneten erzeugten Magnetfeldes dargestellt. Die Dichte der Feldlinien ist dabei ein Maß für die Stärke $B$ des Magnetfeldes.

Beschreibe den Verlauf der Stärke $B$ des Magnetfeldes im dargestellten Bereich entlang der $x$ -Achse.
Erkläre, weshalb auf ein Elektron im Punkt $P$ keine Lorentzkraft $\vec{F}_{ \text L }$ wirkt.

Der Querschnitt des Elektronenstrahls ist in Abbildung 4 grau dargestellt. Die Elektronen des Elektronenstrahls bewegen sich vor dem Eintritt in das Magnetfeld parallel zur $y$ -Achse, die in Abbildung 4 aus der Zeichenebene heraus zeigt. Die vier Punkte $Q,$ $R,$ $S$ und $T$ befinden sich auf dem Rand des Elektronenstrahls.

Begründe unter Zuhilfenahme der vier Punkte $Q,$ $R,$ $S$ und $T,$ dass der Elektronenstrahl beim Austritt aus dem Quadrupolmagneten den im rechten Teil von Abbildung 4 dargestellten Querschnitt besitzt.

Nach dem Austritt aus dem Quadrupolmagneten durchquert der Elektronenstrahl einen zweiten Quadrupolmagneten, der gegenüber dem in Abbildung 4 dargestellten Quadrupolmagneten um $90^{\circ}$ um die $y$ -Achse gedreht ist.

Erläutere, dass der Elektronenstrahl beim Durchqueren des zweiten Quadrupolmagneten weiter fokussiert wird.

(5 + 3 + 4 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Teillösung 1

Elektronenkanone

Eine Elektronenkanone ist ein Gerät, das Elektronen beschleunigt und zu einem gebündelten Elektronenstrahl formt. Dieser Prozess beginnt mit der Emission von Elektronen aus einer Kathode. Diese Elektronen werden durch elektrische Felder beschleunigt, indem eine Spannung zwischen der Kathode und einer Anode angelegt wird. Anschließend werden magnetische oder elektrische Felder verwendet, um den Elektronenstrahl zu fokussieren und zu lenken. Ablenksysteme ermöglichen die präzise Steuerung und Bewegung des Strahls über das abzubildende Objekt. Die erzeugten Elektronenstrahlen finden in Elektronenmikroskopen, Röntgenröhren, Kathodenstrahlröhren und anderen Anwendungen Verwendung, um Bilder zu erstellen oder Proben zu untersuchen.

Spannungen

Die Spannung $U_{\text{B}}$ als Beschleunigungsspannung muss eine Gleichspannung sein, um eine gleichmäßige Beschleunigung der Elektronen sicherzustellen. Die gleichmäßige Beschleunigung der Elektronen erfordert eine kontinuierliche Energiezunahme. Eine konstante Gleichspannung ermöglicht, dass die Elektronen im elektrischen Feld kontinuierlich Energie gewinnen und gleichmäßig beschleunigt werden.

Die Spannung $U_{\text{H}}$ als Heizspannung für die Kathode kann sowohl als Gleich- als auch als Wechselspannung vorliegen, solange sie ausreicht, um Elektronenemission zu ermöglichen.

Die kinetische Energie $E_{\text{kin}}$ des Elektrons in einem elektrischen Feld ist gleich der geleisteten Arbeit $W$ des elektrischen Feldes an diesem Teilchen:

Rechenweg anzeigen

$v= \sqrt{\dfrac{2\cdot e\cdot U_B}{m_0}}$

Umstellen der Gleichung nach $U_B$ ergibt:

Rechenweg anzeigen

$U_{B,\text{max}}= \dfrac{ m_0\cdot 0,01\cdot c^2}{2\cdot e}$

Einsetzen der Werte für die Kontanten liefert:

Rechenweg anzeigen

$U_{B,\text{max}} =2,6\cdot 10^3\;\text V$

Die Elektronen erfahren eine zusätzliche Beschleunigung aufgrund des homogenen Gravitationsfelds der Erde. Dies führt zu einer Erhöhung ihrer kinetischen Energie, die durch die potenzielle Energie $E_{\text{pot}}=m_0 \cdot g \cdot h$ verursacht wird. Für das Verhältnis zwischen $\Delta E_{\text{kin}}$ und der kinetischen Energie $E_{\text{kin}}$ eines Elektrons gilt:

Rechenweg anzeigen

$\dfrac{E_{\text{kin}}}{\Delta E_{\text{kin}}}=...$

Die kinetische Energie der Elektronen ist somit um den Faktor $4\cdot 10^{12}$ größer. Der gravitativ bedingte Zuwachs ist somit vernachlässigbar.

Die Kraft $F$ auf ein Elektron im elektrischen Feld ist gegeben durch das Coulombsche Gesetz:

$\begin{array}[t]{rll} F&=& e\cdot E &\quad \scriptsize \mid\; F=m_0 \cdot a \\[5pt] m_0 \cdot a&=& e\cdot E &\quad \scriptsize \mid\; \cdot \dfrac{1}{m_0} \\[5pt] a&=& \dfrac{e\cdot E}{m_0} &\quad \scriptsize \mid\; E = \dfrac{U_{\text{A}}}{d} \\[5pt] a&=& \dfrac{e\cdot \dfrac{U_{\text{A}}}{d} }{m_0} &\quad \scriptsize \\[5pt] a&=& \dfrac{e\cdot U_{\text{A}}}{m_0\cdot d} \end{array}$

Durch eine zeitabhängige Ablenkspannung $U_{\text{A}}(t)$ kann der Elektronenstrahl gezielt in $x$ -Richtung abgelenkt werden. Diese Ablenkung ermöglicht es, den Auftreffpunkt auf dem abzubildenden Objekt innerhalb einer bestimmten Zeitspanne von links nach rechts zu bewegen. Die Variation von $U_{\text{A}}(t)$ beeinflusst die horizontale Ablenkung des Strahls im Ablenkkondensator, was die Bewegung des Auftreffpunkts auf dem Objekt steuert. So kann die Darstellung unterschiedlicher Bereiche des Objekts im Elektronenmikroskop erreicht werden.

Teillösung 2

Freie Elektronen entstehen durch die Wechselwirkung von schnellen Elektronen mit Atomen in einem Material. Wenn ein schnelles Elektron auf ein Atom trifft, kann es genügend Energie übertragen, um ein Elektron aus der äußersten Schale des Atoms zu entfernen. Dieses herausgelöste Elektron wird dann als freies Elektron bezeichnet.

Die hohen kinetischen Energien der Elektronen sind erforderlich, um die starken elektrostatischen Anziehungskräfte im Atom zu überwinden und Elektronen aus den äußeren Schalen zu lösen. Dies erfordert hohe Geschwindigkeiten, um die nötige kinetische Energie für die Wechselwirkung aufzubringen.

Ein Elektron, das in den Wien-Filter eintritt, bewegt sich gerade durch die Anordnung, wenn die Beträge der Lorentz-Kraft im senkrechten Magnetfeld des Filters und der elektrostatischen Kraft im Kondensatorfeld gleich sind und entgegengesetzt gerichtet sind. Die Bedingung dafür lautet:

$\begin{array}[t]{rll} e \cdot v \cdot B&=& e \cdot E &\quad \scriptsize \\[5pt] \end{array}$

Für ein geradlinig durch die Anordnung gelangendes Elektron gilt:

$\begin{array}[t]{rll} F_{\text{Lorentz}}&=& F_{\text{el}} &\quad \scriptsize \\[5pt] e \cdot v \cdot B&=& e\cdot E &\quad \scriptsize \cdot \dfrac{1}{e \cdot B }\\[5pt] v &=& \dfrac{e\cdot E}{e \cdot B } &\quad \scriptsize \\[5pt] v &=& \dfrac{ E}{ B } \end{array}$

Wenn die Beschleunigungsspannung $U_{\text{B}}$ geändert wird, ändert sich die Geschwindigkeit der Elektronen im Strahl. Die Lorentz-Kraft im Magnetfeld wirkt stärker bei höheren Geschwindigkeiten. Um sicherzustellen, dass die Elektronen weiterhin geradlinig durch den Filter laufen, muss die Spannung $U_{\text{S}}$ im Kondensatorfeld entsprechend angepasst werden. Dies gleicht die Kräfte aus und ermöglicht es den Elektronen, ihre Bahn beizubehalten, wenn sich ihre Geschwindigkeit ändert.

Die aus dem Objekt austretenden Elektronen haben niedrigere Geschwindigkeiten und erfahren daher eine geringere Lorentz-Kraft im Magnetfeld des Wien-Filters. Da die elektrostatische Ablenkung unverändert bleibt, werden diese Elektronen in Richtung Detektor abgelenkt, was ihre Detektion ermöglicht.

Die De-Broglie-Hypothese besagt, dass bewegte Teilchen wie Elektronen nicht nur Teilchen, sondern auch Wellen sind. Jedes Teilchen hat eine charakteristische Wellenlänge $\lambda$ , die mit seinem Impuls $p$ verknüpft ist: $\lambda = \dfrac{h}{p}$ . Diese Hypothese ermöglicht eine tiefere Erklärung von Phänomenen wie Elektronenbeugung, ähnlich der Beugung von Licht durch ein Gitter.

Für Teilchen mit Ruhemasse $m_0=0$ ergibt die Energie-Impuls-Beziehung:

$\begin{array}[t]{rll} p&=&\dfrac{E}{c} &\quad \scriptsize \mid\; E= h\cdot f \\[5pt] &=&\dfrac{h\cdot f}{c} &\quad \scriptsize \mid\; f=\dfrac{c}{\lambda} \\[5pt] &=& \dfrac{h\cdot \dfrac{c}{\lambda}}{c} &\quad \scriptsize \\[5pt] &=& \dfrac{h}{\lambda} \end{array}$

Für die kinetische Energie gilt:

Rechenweg anzeigen

$p= \sqrt{2\cdot E_{\text{kin} }\cdot m_0 }$

Einsetzen in den Zusammenhang für $\lambda$ ergibt:

Rechenweg anzeigen

$\lambda= \dfrac{h}{\sqrt{2\cdot e\cdot U_{B}\cdot m_0 }}$

Einsetzen der Werte liefert:

Rechenweg anzeigen

$\lambda =2,56 \cdot 10^{-11} \;\text{m}$

Interferenzerscheinungen

Es ist $\dfrac{\lambda}{ d }=\dfrac{2,56 \cdot 10^{-11} \;\text{m} }{1 \cdot 10^{-10}\;\text{m}}$ $=0,256 \approx \dfrac{1}{4}$

Für den Gangunterschied folgt:

$\Delta s =2 d \cdot \sin \vartheta \leq 2 d =2 \cdot 4 \lambda=8 \lambda$

Dadurch ergeben sich Überlagerungen und Auslöschungen der Wellen.

Teillösung 3

Am linken Rand der x-Achse erreicht die Feldstärke anfangs ihren höchsten Wert. Die Feldstärke nimmt kontinuierlich ab, bis sie schließlich im Punkt P den Wert null erreicht. Danach steigt der Betrag der Feldstärke wieder an, bis er ganz rechts auf der $x$ -Achse denselben Wert erreicht wie am linken Rand.

Im Allgemeinen sind die Punkte auf der $x$ -Achse, an denen die Beträge der Feldstärken gleich groß sind, symmetrisch bezüglich des Punktes P angeordnet.

Die Ausgangssymmetrie der Anordnung um den Koordinatenursprung P ist entscheidend. Die Dichte der Feldlinien nimmt von außen nach innen ab, und zudem ändert sich die Richtung des Feldes beim Passieren von P. Wenn beide Faktoren berücksichtigt werden, folgt, dass das Feld bei P verschwinden muss, was bedeutet, dass die Feldlinien eine Länge von null haben.

Die Lorentzkraft wirkt auf bewegte Ladungen in einem Magnetfeld. Ist die Stärke des Magnetfeldes gleich null wie hier im Punkt P, wirkt auch keine Lorentzkraft.

In Formeln:

$F_L=e \cdot v \cdot B$

Im Punkt $P$ ist $B =0$ und somit auch $F _{ L }=0$ .

Punkt Q

• Daumen in Bewegungsrichtung der Elektronen (aus Zeichenebene heraus)

• Zeigefinger in Feldrichtung (von N nach S, also von links nach rechts)

• Mittelfinger zeigt in Richtung der Lorentzkraft (in Richtung P).

Punkt S

• Daumen in Bewegungsrichtung der Elektronen (aus Zeichenebene heraus)

• Zeigefinger in Feldrichtung (von N nach S, also von rechts nach links)

• Mittelfinger zeigt in Richtung der Lorentzkraft (in Richtung P).

Punkt R

• Daumen in Bewegungsrichtung der Elektronen (aus Zeichenebene heraus)

• Zeigefinger in Feldrichtung (von N nach S, also von unten nach oben)

• Mittelfinger zeigt in Richtung der Lorentzkraft (von P weg).

Punkt T

• Daumen in Bewegungsrichtung der Elektronen (aus Zeichenebene heraus)

• Zeigefinger in Feldrichtung (von N nach S, also von oben nach unten)

• Mittelfinger zeigt in Richtung der Lorentzkraft (von P weg).

Somit wird der Elektronenstrahl in Richtung der z-Achse gebündelt und in Richtung der x-Achse aufgeweitet; es entsteht der ellipsenförmige Quer- schnitt des Elektronenstrahls beim Austritt aus dem Quadrupolmagneten.

Wenn der zweite Quadrupolmagnet um 90 Grad gegenüber dem ersten gedreht ist, führt dies dazu, dass die Kräfte in Richtung der x- und z-Achse vertauscht werden. Das bedeutet, der Elektronenstrahl wird in Richtung der x-Achse fokussiert und in Richtung der z-Achse aufgeweitet. Allerdings bedeutet dies nicht, dass die Verformungen, die beim Durchgang durch den ersten Quadrupolmagneten auftreten, beim Durchgang durch den zweiten Quadrupolmagneten wieder rückgängig gemacht werden. Der entscheidende Unterschied besteht darin, dass der Elektronenstrahl beim Eintritt in den zweiten Quadrupolmagneten nicht mehr einen kreisförmigen Querschnitt hat, sondern einen ellipsenförmigen Querschnitt, wie in Abbildung 4 dargestellt. Daraus ergibt sich: Da die Stärke des Magnetfeldes in Richtung des Punktes P abnimmt und die Punkte Q' und S' auf den Ellipsen, die den Punkten Q und S entsprechen, näher bei P liegen als die Punkte Q und S, bewirkt der zweite Durchgang, dass die Aufweitung des Elektronenstrahls in Richtung der z-Achse geringer ist als die Bündelung des Strahls in die gleiche Richtung beim ersten Durchgang. Ebenso führt die Bündelung in Richtung der x-Achse beim zweiten Durchgang zu einer stärkeren Fokussierung im Vergleich zur Aufweitung beim ersten Durchgang. Beide Effekte zusammen bewirken, dass der Elektronenstrahl beim Durchlaufen des zweiten Quadrupolmagneten weiterhin fokussiert wird.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?