HT 2

Welleneigenschaften von Farbstoffmolekülen

Teilaufgabe 1: Materialwellen

Die Abbildungen 1a und 1b zeigen Momentaufnahmen aus einer Simulation zur Ausbreitung von Wellen. In Abbildung 1a trifft eine von links einlaufende ebene Welle der Wellenlänge $\lambda$ auf einen Spalt der Breite $b \approx \lambda$ . In Abbildung 1b ist hingegen $b>\lambda.$

Abbildung 1a

Abbildung 1b

Nenne die Aussagen des Huygens'schen Prinzips.
Erläutere mithilfe des Huygens'schen Prinzips die Ausbreitung der Wellen nach dem Durchtritt durch den jeweiligen Spalt und gehen Sie dabei insbesondere auf das Phänomen der Beugung ein.

Nach de Broglie kann man jedem Objekt der Masse $m,$ das sich mit der Geschwindigkeit $v$ bewegt, die Wellenlänge $\lambda=\dfrac{h}{m \cdot v}$ zuordnen, wobei $h$ das Planck'sche Wirkungsquantum ist.

Berechne die Wellenlänge $\lambda,$ die einem $H _2$ -Molekül der Masse $m=3,32 \cdot 10^{-27} \,\text{kg}$ mit der Geschwindigkeit $v=200 \;\dfrac{\text{m} }{ \text{s} }$ zugeordnet werden kann.

Anders als bei Lichtwellen muss man bei Beugungsexperimenten mit Materiewellen materiefreie Spaltöffnungen verwenden.

Gib einen Grund dafür an, dass die Spaltöffnungen materiefrei sein müssen.
Erläutere mithilfe der Abbildungen $1 a$ und 1b, warum gemäß der De-Broglie-Beziehung die Welleneigenschaften von Materie nur bei Materieobjekten einer sehr geringen Masse $m$ deutlich in Erscheinung treten können.

De Broglie hat die Beziehung $\lambda=\dfrac{h}{m \cdot v}$ im Wesentlichen durch Übertragung der damals seit Einstein bekannten Gleichung $\lambda_{ Ph }=\dfrac{h}{m_{ Ph } \cdot c }$ für Photonen (mit $c =v_{ Ph }$ ) auf massebehaftete Objekte mit der Geschwindigkeit $v\lt c$ aufgestellt.
Leite die Einstein'sche Gleichung $\lambda_{ Ph }=\dfrac{h}{m_{ Ph } \cdot c }$ für Photonen her.

(7 + 9 + 4 Punkte)

Teilaufgabe 2: Ein Interferenzexperiment mit Farbstoffmolekülen

Im Jahr 2012 führte eine internationale Forschergruppe an der Universität Wien ein eindrucksvolles Experiment zur Untersuchung der quantenmechanischen Wellennatur von massereichen Farbstoffmolekülen durch. Abbildung 2 zeigt den prinzipiellen Aufbau der Versuchsapparatur.

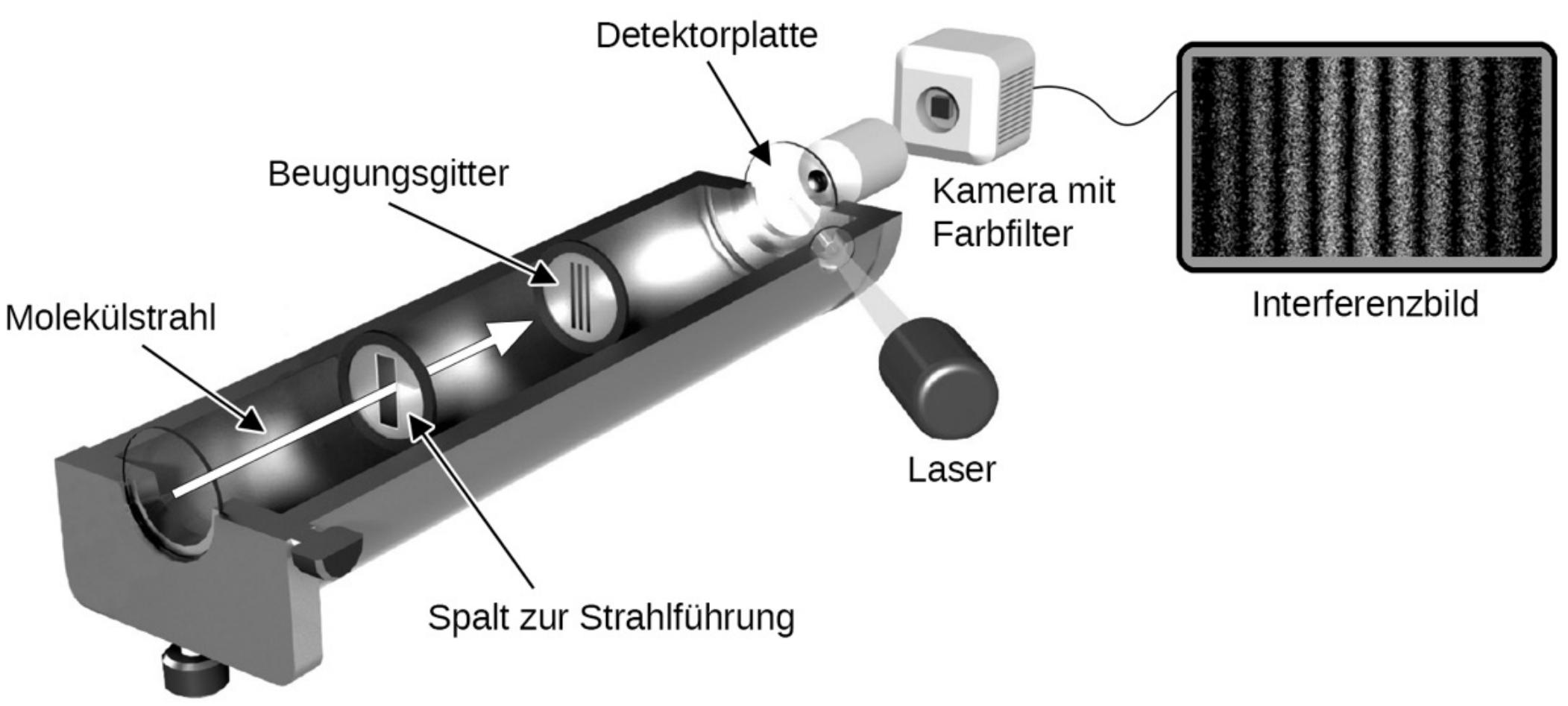
nrw abi physik lk 2022 ht 2 abbildung 2 versuchsaufbau zum interferenzexperiment mit farbstoffmolekülen

Abbildung 2: Versuchsaufbau zum Interferenzexperiment mit Farbstoffmolekülen
(Quelle: T. Juffmann et al.: „Real-time single-molecule imaging of quantum interference“, in: nature nanotechnology, Vol.7 (2012), S.298 (verändert))

Ein horizontal ausgerichteter Strahl aus Farbstoffmolekülen einheitlicher Geschwindigkeit trifft dabei im Inneren einer Vakuumkammer auf ein Beugungsgitter mit der Gitterkonstante $g=100 \,\text{nm}.$ Am Ende der Versuchsapparatur erreichen die Farbstoffmoleküle eine Detektorplatte, die sich im Abstand $a=564 \,\text{mm}$ hinter dem Beugungsgitter befindet. Mit einem Laser werden sie dort zum Leuchten angeregt. Eine Kamera, vor deren Objektiv ein Farbfilter angebracht ist, filmt das Interferenzbild auf der Detektorplatte.

Erläutere qualitativ, wie es zur Entstehung der Interferenzmaxima auf der Detektorplatte kommt.

Für den Abstand $d_{ n }$ des Maximums $n$ -ter Ordnung von dem Maximum nullter Ordnung gilt unter Berücksichtigung der Kleinwinkelnäherung $\sin (\alpha) \approx \tan (\alpha)$ der folgende Zusammenhang:

$d_{ n }=\dfrac{n \cdot \lambda \cdot a}{g} .$

Dabei bezeichnet $\lambda$ die den Farbstoffmolekülen zugeordnete Wellenlänge.
Leite den Zusammenhang mithilfe einer aussagekräftigen Skizze her.

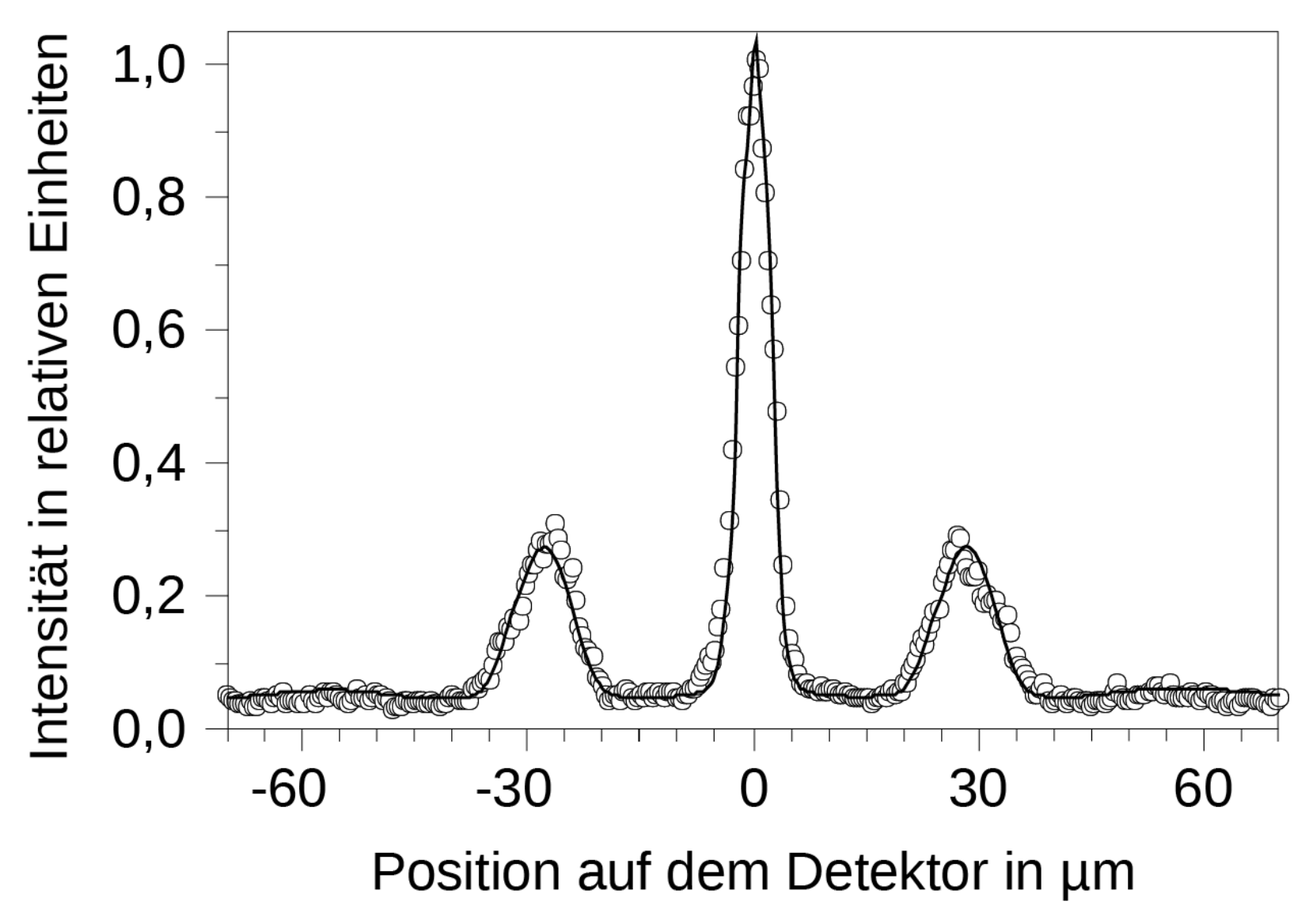
In einem ersten Versuch beträgt die Geschwindigkeit der Farbstoffmoleküle $v=150 \dfrac{ m }{ s }.$ Abbildung 3 zeigt die an der Detektorplatte registrierte Intensitätsverteilung des Interferenzmusters.

nrw abi physik lk 2022 ht 2 abbildung 3 intensitätsverteilung des interferenzmusters

Abbildung 3: Intensitätsverteilung des Interferenzmusters
(Quelle: T. Juffmann et al.: „Real-time single-molecule imaging of quantum interference“, in: nature nanotechnology, Vol.7 (2012), S.299 (verändert))

Bestimme mithilfe von Abbildung 3 sowie dem Zusammenhang aus Aufgabenteil b) und der De-Broglie-Beziehung die Masse $m$ der Farbstoffmoleküle in dem Experiment.

Die Geschwindigkeit $v$ der im Experiment verwendeten Farbstoffmoleküle weist eine geringfügige Streuung $\Delta v$ um den oben angegebenen Wert auf.

Erläutere die Veränderung der beiden Maxima erster Ordnung für den Fall, dass die Streuung $\Delta v$ verringert werden könnte.

Abbildung 4 zeigt vier Momentaufnahmen aus dem Video, das die Kamera während der Versuchsdurchführung aufgenommen hat. Zu sehen ist jeweils der gleiche Ausschnitt der Detektorplatte zu verschiedenen aufeinanderfolgenden Zeitpunkten $t_1\lt t_2\lt t_3\lt t_4.$

nrw abi physik lk 2022 ht 2 abbildung 4 interferenzmuster einzelner farbstoffmoleküle zu vier verschiedenen zeitpunkten

nrw abi physik lk 2022 ht 2 abbildung 4 interferenzmuster einzelner farbstoffmoleküle zu vier verschiedenen zeitpunkten t3

Abbildung 4: Interferenzmuster einzelner Farbstoffmoleküle zu vier verschiedenen Zeitpunkten
(Quelle: T. Juffmann et al.: „Real-time single-molecule imaging of quantum interference“, in: nature nanotechnology, Vol.7 (2012), S.299 (verändert))

nrw abi physik lk 2022 ht 2 abbildung 4 interferenzmuster einzelner farbstoffmoleküle zu vier verschiedenen zeitpunkten t2

nrw abi physik lk 2022 ht 2 abbildung 4 interferenzmuster einzelner farbstoffmoleküle zu vier verschiedenen zeitpunkten t4

Beschreiben Sie die zeitliche Entwicklung des Interferenzmusters.

In einer veränderten Version des Experiments besitzen die Farbstoffmoleküle deutlich unterschiedliche Geschwindigkeiten. In dem Strahl gibt es Farbstoffmoleküle aller Geschwindigkeiten $v$ zwischen einem Minimalwert $v_{\min }$ und einem Maximalwert $v_{\max }$ . Abbildung 5 zeigt das komplette Interferenzmuster auf der Detektorplatte. Der Pfeil veranschaulicht die Richtung der auf die Farbstoffmoleküle wirkenden Gravitationskraft $F_{ G }.$

nrw abi physik lk 2022 ht2 abbildung 5 komplettes interferenzmuster bei großer geschwindigkeitsstreuung

Abbildung 5: Komplettes Interferenzmuster bei großer Geschwindigkeitsstreuung
(Quelle: T. Juffmann et al.: „Real-time single-molecule imaging of quantum interference“, in: nature nanotechnology, Vol.7 (2012), S.299 (verändert))

Die Wissenschaftlerinnen und Wissenschaftler schreiben in der Veröffentlichung des Fotos: „Wir können [...] die Geschwindigkeit der Moleküle ableiten, da die Beugung den Molekülstrahl in horizontaler Richtung ausbreitet und die Gravitationskraft dazu führt, dass die Höhe $h$ auf der Detektorplatte von der Geschwindigkeit $v$ des Moleküls abhängt.“^[1]

Erkläre mithilfe des Zitats die nicht parallel verlaufenden Interferenzstreifen für die Maxima erster Ordnung.
Weise anhand von Abbildung 5 nach, dass die Geschwindigkeit $v_{\max }$ der schnellsten Farbstoffmoleküle etwa doppelt so groß ist wie die Geschwindigkeit $v_{\text {min }}$ der langsamsten Farbstoffmoleküle.
Beschreibe das Muster, das man bei einer Versuchsdurchführung in Schwerelosigkeit beobachten würde.

(3 + 6 + 8 + 3 + 9 Punkte)

Teilaufgabe 3: Detektion von Farbstoffmolekülen mittels eines Lasers

Der Laser, der zur Anregung der Farbstoffmoleküle verwendet wird, sendet monochromatisches Licht der Wellenlänge $\lambda_L=661 \,\text{nm}$ aus. Der Laser leuchtet die Detektorplatte homogen aus. Absorbiert ein Farbstoffmolekül auf der Detektorplatte ein Photon des Laserlichts, so nimmt es die Photonenenergie auf und gibt die aufgenommene Energie anschließend in Form eines Photons und in Form von Wärme wieder ab.

Abbildung 6 zeigt einen Ausschnitt des Emissionsspektrums der in dem Experiment verwendeten Farbstoffmoleküle.

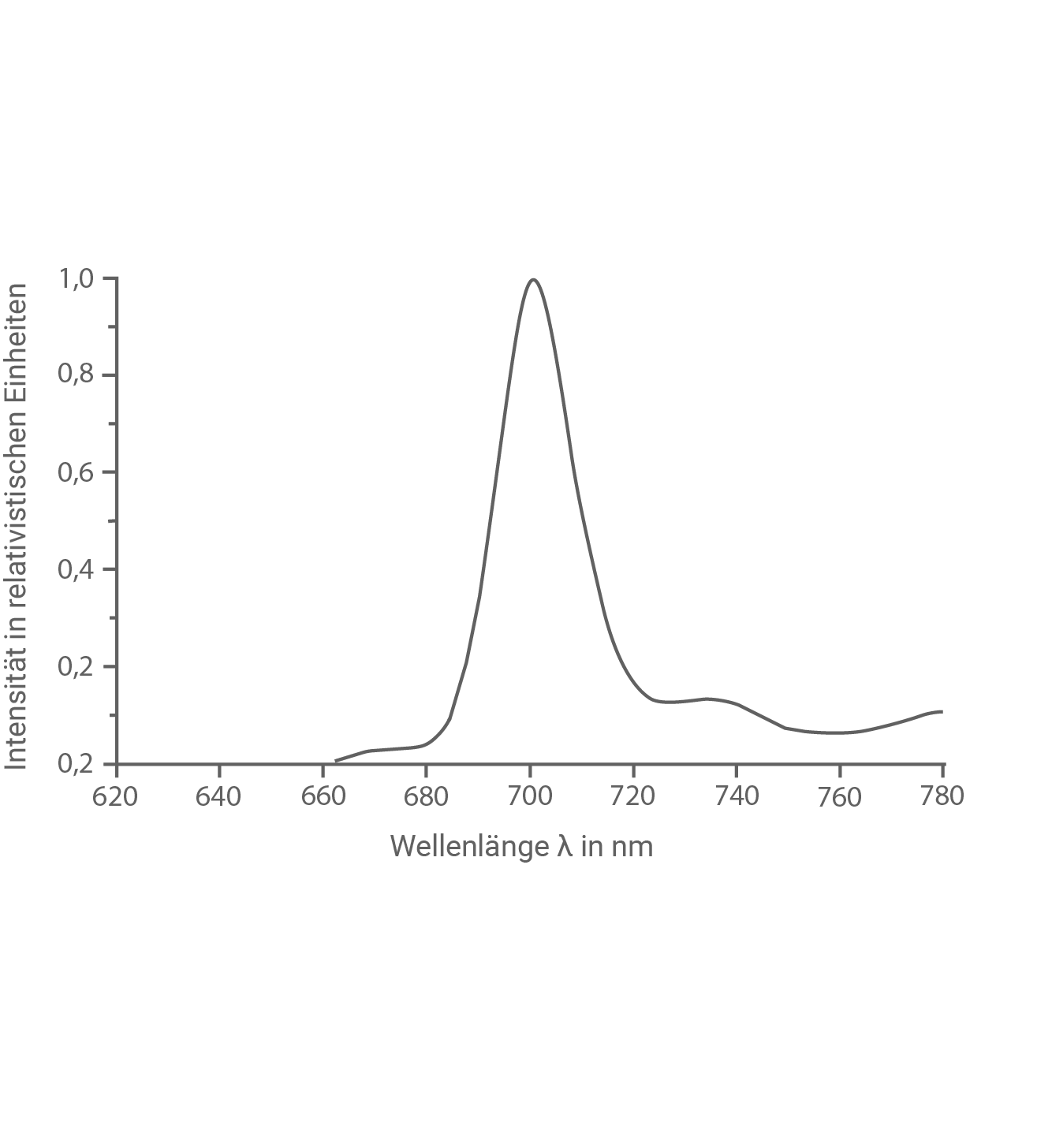Der sichtbare Teil des elektromagnetischen Spektrums entspricht dem Wellenlängenbereich $400 \,\text{nm} \leq \lambda \leq 780 \,\text{nm}.$

Gib die Farbe an, die dem in Abbildung 6 dargestellten Wellenlängenbereich zugeordnet werden kann.
Begründe, weshalb die Farbstoffmoleküle kein Licht in anderen Farben des sichtbaren Spektrums emittieren.

Für die Filmaufnahme wird ein Farbfilter vor dem Objektiv der Kamera angebracht. Dieser absorbiert das Laserlicht der Wellenlänge $\lambda_L=661\,\text{nm}$ und lässt nur Licht aus einem kleinen Wellenlängenbereich um $\lambda=700 \,\text{nm}$ passieren.

Erläutere den Zweck des Farbfilters für die Filmaufnahme.

Die Strahlungsleistung, d.h. die pro Zeiteinheit emittierte Energie des Lasers, beträgt $P_{ L }=50 \dfrac{ \text{mJ} }{ s }.$

Berechne die Anzahl der pro Sekunde vom Laser emittierten Photonen.

Das monochromatische Licht des Lasers wird zum Teil auch an der Detektorplatte reflektiert und trifft anschließend auf die Metallwand der Vakuumkammer. Durch den Photoeffekt können dort freie Elektronen erzeugt werden.

Gib an, welche Bedingung das Metall dafür erfüllen muss.

Das Licht zweier verschiedener Laser, die im Folgenden als Laser 1 und Laser 2 bezeichnet werden, trifft nacheinander auf die Metallwand. Beide Laser haben die gleiche Strahlungsleistung $P_{ L }$ , aber Laser 1 emittiert pro Sekunde weniger Photonen als Laser 2.

Entscheide begründet bei jeder der beiden Aussagen A und B, ob diese richtig bzw. falsch ist.

Aussage A: Wenn Laser 1 den Photoeffekt in der Metallwand nicht auslöst, dann löst auch Laser 2 den Photoeffekt dort nicht aus.
Aussage B: Wenn Laser 1 den Photoeffekt in der Metallwand auslöst, dann löst auch Laser 2 den Photoeffekt dort aus.

(7 + 3 + 6 Punkte)

^[1] T. Juffmann et al.: „Real-time single-molecule imaging of quantum interference“, in: nature nanotechnology, Vol. 7 (2012), S.299

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Teillösung 1: Materialwellen

Nennung der Aussagen des Huygens'schen Prinzips

Jeder Punkt einer bestehenden Wellenfront ist Ausgangspunkt einer Elementarwelle, die sich mit derselben Geschwindigkeit und Frequenz ausbreitet wie die ursprüngliche Wellenfront im betreffenden Medium. Die Einhüllende aller Elementarwellen ergibt die Wellenfront zu einem späteren Zeitpunkt.

Erläuterung der Ausbreitung der Wellen

Die Abbildungen 1a und 1b zeigen, dass sich die Welle in den geometrischen Schattenraum hinter dem Spalt ausbreitet. Dieses Phänomen wird als Beugung bezeichnet. In Abbildung 1a breitet sich die Welle hinter dem Spalt kreisförmig aus, die Beugung der Welle ist deutlich sichtbar. Der Spalt kann als Ausgangspunkt einer einzigen Elementarwelle aufgefasst werden, die sich hinter dem Spalt ausbreitet. In Abbildung 1b breitet sich die Welle in der ursprünglichen Richtung aus, an den Rändern dringt sie jedoch im Bogen in den „Schatten" ein, die Beugung der Welle ist weniger deutlich sichtbar. In dem Spalt breiten sich von mehreren Punkten Elementarwellen aus, deren Einhüllende eine ebene Wellenfront mit kreisförmigen Ausläufern bildet.

Berechnung der Wellenlänge $\lambda$

Für die Wellenlänge $\lambda$ gilt:

$\begin{array}[t]{rll} \lambda &=& \dfrac{h}{m \cdot v}&\quad \scriptsize \\[5pt] \end{array}$

Einsetzen der Werte ergibt:

$\begin{array}[t]{rll} \lambda&=& \dfrac{6,63 \cdot 10^{-34} \;\text{J} \cdot \;\text{s}}{3,32 \cdot 10^{-27} \;\text{~kg} \cdot 200 \;\dfrac{\text{m}}{\text{s}}}&\quad \scriptsize \\[5pt] &=& 9,98 \cdot 10^{-10} \;\text{m} & \quad \scriptsize \\[5pt] &\approx& 1 \;\text{nm} \end{array}$

Grund für die Notwendigkeit von materiefreien Spaltöffnungen

Teilchen können feste Materie aufgrund von Stößen mit den Gitteratomen nicht wechselwirkungsfrei durchdringen. Lediglich im Vakuum wird ein Teilchenstrahl nicht gestreut, daher müssen die Spalte materiefrei sein.

Erläuterung der Notwendigkeit von einer sehr geringen Masse für die Erscheinung der Welleneigenschaften von Materie

Gemäß den Abbildungen 1a und 1b tritt das Phänomen der Beugung nur dann deutlich in Erscheinung, wenn die Breite des verwendeten Spalts in etwa so groß wie die Wellenlänge ist. Die einem Objekt zugeordnete Wellenlänge ist antiproportional zum Produkt $m \cdot v$ . Bereits bei einem sehr massearmen (und langsamen) $\text{H}_2$ -Molekül liegt sie im unteren Nanometerbereich. Einem wesentlich massereicheren Objekt wird folglich eine wesentlich kleinere Wellenlänge zugeordnet. Dementsprechend wird auch ein wesentlich kleinerer materiefreier Spalt benötigt, der aufgrund des atomaren Aufbaus von Materie nicht realisierbar ist.

Durch Gleichsetzen der Gleichung für die Energie des Protons $E_{\text{Ph}}=h \cdot f$ mit der Energie-Masse-Äquivalenz $E= m\cdot c^2$ folgt für $\lambda_{\text{ph}}:$

$\begin{array}[t]{rll} E &=& E_{\text{Ph}}&\quad \scriptsize \\[5pt] m_{\text{ph}} \cdot c^2&=& h \cdot f &\quad \scriptsize \mid\; f=\dfrac{c}{\lambda_{\text{ph}}} \\[5pt] m_{\text{ph}} \cdot c^2&=& h \cdot \dfrac{c}{\lambda_{\text{ph}}} &\quad \scriptsize \mid\; \cdot \lambda_{\text{ph}} \\[5pt] m_{\text{ph}} \cdot c^2 \cdot \lambda_{\text{ph}}&=& h \cdot c &\quad \scriptsize \mid\; \dfrac{1}{m_{\text{ph}} \cdot c^2}\\[5pt] \lambda_{\text{ph}}&=& \dfrac{ h \cdot c }{m_{\text{ph}} \cdot c^2} &\quad \scriptsize \\[5pt] \lambda_{\text{ph}}&=& \dfrac{ h }{m_{\text{ph}} \cdot c} \end{array}$

Dabei ist $f$ die Frequenz der elektromagnetischen Strahlung und $m_{\text{ph}}$ die dem Photon zugeordnete Masse.

Teillösung 2: Ein Interferenzexperiment mit Farbstoffmolekülen

Die Spalte des Beugungsgitters sind Ausgangspunkte von Elementarwellen, die im Raumbereich hinter dem Gitter interferieren. Auf der Detektorplatte treten sehr helle Bereiche mit vielen Farbstoffmolekülen dort auf, wo konstruktive Interferenz aller Elementarwellen stattfindet. Zwischen diesen Bereichen findet weitestgehend destruktive Interferenz der Elementarwellen statt, sodass dort dunkle Bereiche ohne Farbstoffmoleküle auftreten.

Da bei einem Maximum alle Elementarwellen konstruktiv interferieren, müssen insbesondere die Elementarwellen zweier benachbarter Spalte konstruktiv interferieren.

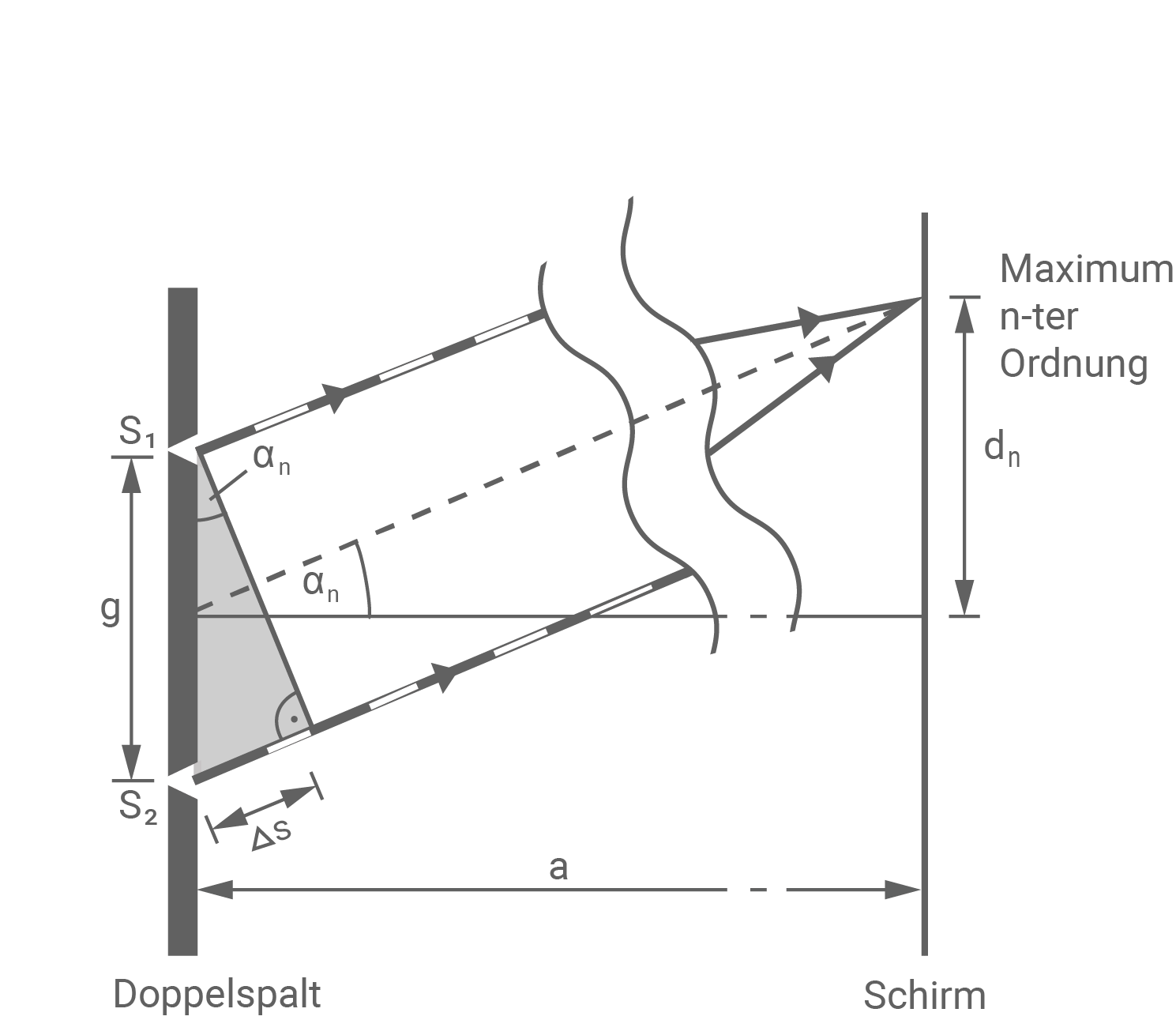Wegen $g \ll a$ sind die beiden Strecken $\overline{S_1 P}$ und $\overline{S_2 P}$ näherungsweise parallel. Der Winkel $\alpha_n$ , unter dem das Maximum $n$ -ter Ordnung beobachtet werden kann, taucht daher auch in dem grau unterlegten Dreieck auf, bei dem eine Seitenlänge dem Gangunterschied $\Delta s$ entspricht.

Mit der Kleinwinkelnäherung $\tan \left(\alpha_{\text{n}}\right)\approx \sin \left(\alpha_{\text{n}}\right)$ und der Bedingung für konstruktionve Interferenz $\Delta s=n \cdot \lambda$ mit $n=0 ; 1 ; 2 ; \ldots$ folgt:

Rechenweg anzeigen

$d_{\text{n}}=...$

Bestimmung der Masse $m$ der Farbstoffmoleküle

Einsetzen der De-Broglie-Beziehung in den Zusammenhang aus dem Aufgabenteil b) liefert:

$\begin{array}[t]{rll} d_{\text{n}}&=&\dfrac{n \cdot \lambda \cdot a}{g}&\quad \scriptsize \mid\; \lambda = \dfrac{h}{m \cdot v} \\[5pt] d_{\text{n}}&=&\dfrac{n \cdot h \cdot a}{g \cdot m \cdot v}&\quad \scriptsize \mid\; \cdot m \\[5pt] d_{\text{n}}\cdot m &=&\dfrac{n \cdot h \cdot a}{g \cdot v}&\quad \scriptsize \mid\; \cdot \dfrac{1}{d_{\text{n}}} \\[5pt] m &=&\dfrac{n \cdot h \cdot a}{g \cdot v \cdot d_{\text{n}}}& \end{array}$

Der Abstand des Maximums erster Ordnung von dem Maximum nullter Ordnung beträgt hier $d_1=28 \;\mu \text{m}.$ Durch Einsetzen der Werte erhält man die Masse der Farbstoffmoleküle

Rechenweg anzeigen

$8,9 \cdot 10^{-25} \;\text{kg}$

Erläuterung der Veränderung der beiden Maxima erster Ordnung bei Verringerung der Streuung

Die Streuung der Geschwindigkeit $\Delta v$ führt gemäß der Gleichung $d_1=\dfrac{1 \cdot h \cdot a}{g \cdot m \cdot v}$ zu einer Streuung $\Delta d_1$ bei dem Abstand des Maximums erster Ordnung von dem Maximum nullter Ordnung. Eine Verringerung von $\Delta v$ vermindert demnach $\Delta d_1$ . Dies hat zur Folge, dass die beiden Maxima erster Ordnung schmaler werden.

Zu Beginn scheinen die Farbstoffmoleküle völlig zufällig und ungeordnet auf die Detektorplatte zu treffen. Doch nach und nach wird deutlich, dass es bestimmte Bereiche auf der Detektorplatte gibt, die häufiger von Farbstoffmolekülen getroffen werden als andere. Mit der Zeit erkennt man das bekannte Interferenzmuster.

Erklärung der nicht parallel verlaufenden Interferenzstreifen für die Maxima erster Ordnung

Dem Zitat kann entnommen werden, dass in einer vorgegebenen Höhe $h$ nur Farbstoffmoleküle einer bestimmten Geschwindigkeit $v$ auftreffen. Da der Abstand $d_1$ des Maximums erster Ordnung vom Maximum nullter Ordnung von der Wellenlänge und damit von der Geschwindigkeit der Farbstoffmoleküle abhängt, ergeben sich in unterschiedlichen Höhen verschiedene Werte für $d_1$ . Damit verlaufen die zugehörigen Interferenzstreifen bei beiden Maxima erster Ordnung nicht parallel.

Nachweis der doppelt so großen Geschwindigkeit $v_{\max }$ der schnellsten Farbstoffmoleküle im Vergleich zu der Geschwindigkeit $v_{\text {min }}$ der langsamsten Farbstoffmoleküle

Die langsamsten Farbstoffmoleküle treffen am unteren Ende der Detektorplatte auf, die schnellsten hingegen am oberen Ende. Der Abstand $d_1$ ist am unteren Ende etwa doppelt so groß wie am oberen Ende. Da $d_1$ antiproportional zu $v$ ist, bedeutet das $v_{\max } \approx 2 \cdot v_{\min }$ .

Beschreibung des Musters bei einer Versuchsdurchführung in Schwerelosigkeit

Bei einer Versuchsdurchführung in Schwerelosigkeit würden alle Farbstoffmoleküle in der gleichen Höhe am oberen Rand der Detektorplatte auftreffen. Die meisten Farbstoffmoleküle würden dort in der Mitte detektiert, zu den Rändern nach links und rechts hin würde die Anzahl an detektierten Farbstoffmolekülen abnehmen.

Teillösung 3: Detektion von Farbstoffmolekülen mittels eines Lasers

Angabe der Farbe

Dem dargestellten Wellenlängenbereich kann die Farbe Rot zugeordnet werden.

Begründung, weshalb die Farbstoffmoleküle kein Licht in anderen Farben des sichtbaren Spektrums emittieren

Die Energie eines von einem Farbstoffmolekül emittieren Photons kann maximal so groß sein wie die Energie eines von ihm absorbierten Photons. Es gilt:

$\begin{array}[t]{rll} E_{\text{Ph}}&=& h \cdot f&\quad \scriptsize \mid\; f=\dfrac{c}{\lambda} \\[5pt] &=& h \cdot \dfrac{c}{\lambda} \end{array}$

Dabei ist $E_{\text{ph}}$ die Photonenenergie, $f$ die Frequenz des Lichts und c die Lichtgeschwindigkeit. Aus dem Zusammenhang für $E_{\text{Ph}}$ geht hervor, dass die Energie eines Photons antiproportional zur Wellenlänge ist. Damit können die Farbstoffmoleküle kein Licht emittieren, dessen Wellenlänge kleiner als die Wellenlänge $\lambda_L=661 \;\text{nm}$ des Lasers ist, insbesondere also kein Licht anderer Farben.

Zweck des Farbfilters für die Filmaufnahme

Sowohl der Laser als auch die Farbstoffmoleküle emittieren rotes Licht. Ein Farbfilter vor dem Objektiv der Kamera absorbiert das für die Filmaufnahme störende rote Licht des Lasers und lässt nur das von den Farbstoffmolekülen emittierte rote Licht durch.

Bei einer Strahlungsleistung von $P_{\text{L}}=50 \;\dfrac{\text{mJ}}{\text{s}}$ emittiert der Laser pro Sekunde $N$ Photonen mit der Gesamtenergie $E_{\text{ges}}=50 \cdot 10^{-3} \;\text{J}$ . Mit der Energie $E_{\text{ph}}=h \cdot \dfrac{\text{c}}{\lambda}$ eines Photons folgt:

$\begin{array}[t]{rll} N &=& \dfrac{E_{\text {ges }}}{E_{\text{ph}}} \\[5pt] N &=& \dfrac{E_{\text {ges }} \cdot \lambda}{h \cdot c}&\quad \scriptsize \\[5pt] &=& \dfrac{50 \cdot 10^{-3} \;\text{J} \cdot 661 \cdot 10^{-9} \;\text{m}}{6,63 \cdot 10^{-34} \;\text{Js} \cdot 3,00 \cdot 10^8 \;\dfrac{\text{m}}{\text{s}}}&\quad \scriptsize \\[5pt] &=& 1,7 \cdot 10^{17} \end{array}$

Angabe der Bedingung für das Metall

Die Austrittsenergie $E_{\text{A}}$ des verwendeten Metalls muss kleiner sein als die Energie eines von dem Laser emittierten Photons.

Begründete Entscheidung der Richigkeit der Aussagen A und B

Da Laser 1 bei gleicher Leistung weniger Photonen pro Sekunde als Laser 2 emittiert, ist jedes von Laser 1 emittierte Photon energiereicher. Wenn die von Laser 1 emittierten energiereicheren Photonen den Photoeffekt in der Metallwand nicht auslösen, dann lösen die von Laser 2 emittierten energieärmeren Photonen den Photoeffekt ebenfalls nicht aus. Daher ist Aussage A richtig. Wenn die von Laser 1 emittierten energiereicheren Photonen den Photoeffekt in der Metallwand auslösen, dann kann nicht darauf geschlossen werden, ob die von Laser 2 emittierten energieärmeren Photonen dazu ebenfalls in der Lage sind. Daher ist Aussage B falsch.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?