HT 1

Bestimmung des Planck'schen Wirkungsquantums auf zwei verschiedene Arten

Das sogenannte Planck'sche Wirkungsquantum $h$ ist eine wichtige Konstante in der Physik.
Im Folgenden sollen zwei Methoden zur Bestimmung von $h$ thematisiert werden.

Teilaufgabe 1: Wellen- und Teilcheneigenschaften von Licht

Ende des 19. Jahrhunderts war die Beschreibung des Lichts als elektromagnetische Welle vielfach experimentell bestätigt worden und allgemein anerkannt. Anfang des 20. Jahrhunderts führten neue experimentelle Erkenntnisse zu einer Weiterentwicklung der physikalischen Beschreibung von Licht.

Beschreibe kurz ein Experiment, mit dem man die Welleneigenschaft des Lichts zeigen kann.
Gib eine Beobachtung in Ihrem Experiment an, die sich durch die Welleneigenschaft von Licht erklären lässt.

Beschreibe kurz ein Experiment, mit dem man die Teilcheneigenschaft des Lichts zeigen kann.
Gib eine Beobachtung in Ihrem Experiment an, die sich durch die Teilcheneigenschaft von Licht erklären lässt.

(4 + 4 Punkte)

Teilaufgabe 2: $h$ -Bestimmung mit dem Fotoeffekt

Eine Möglichkeit, das Planck’sche Wirkungsquantum 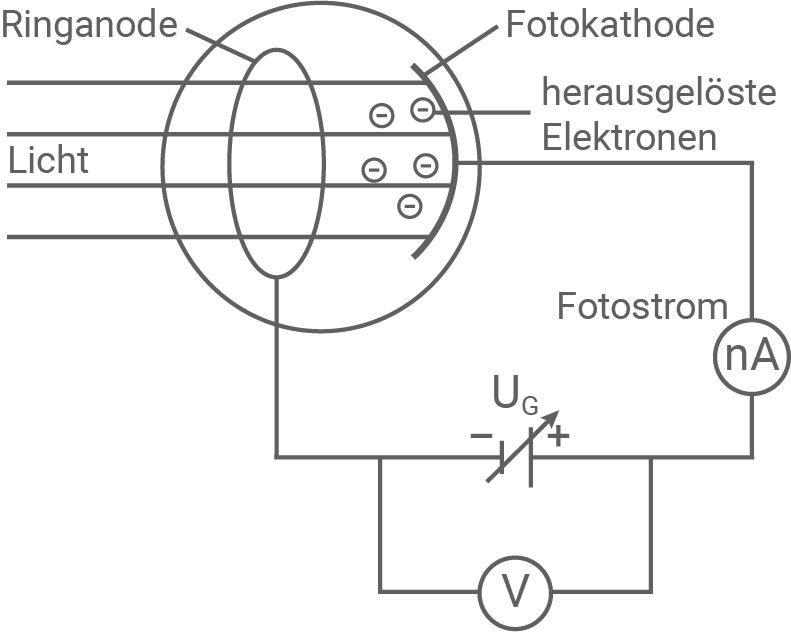$h$ zu bestimmen, ist die Gegenfeldmethode des Fotoeffekts. Abbildung 1 zeigt den schematischen Aufbau des Versuchs. In diesem Versuch bestehen die Ringanode und die Fotokathode aus demselben Material.

Abbildung 1: Schematischer Aufbau zur Gegenfeldmethode des Fotoeffekts

Beschreibe den Aufbau des Versuchs zur Gegenfeldmethode des Fotoeffekts.

Erkläre die Entstehung des Fotostroms $I_{ \text F }$ und sein Absinken bei der Erhöhung der Spannung $U_{ \text G }$ .

Die Spannung $U_{ \text G \text {,max }}$ ist die Spannung, bei der der Fotostrom $I_{ \text F }$ gerade auf null abgesunken ist.

Erläutere, dass die kinetische Energie $E_{\text{kin} }$ der schnellsten aus der Fotokathode ausgelösten Elektronen mit der Formel $E_{ \text{kin} }=e \cdot U_{ G \text {, max }}$ berechnet werden kann.
$e$ ist dabei die Elementarladung.

Bei der Durchführung des Versuchs aus Abbildung 1 werden folgende Werte aufgenommen:

$\color{#fff}{\lambda}$ in $\color{#f0f0f0}{\text{nm}}$	$\color{#fff}{f}$ in $\color{#f0f0f0}{10^{14} \,\text{Hz}}$	$\color{#f0f0f0}{U_{ \text G , \max }}$ in $\color{#f0f0f0}{\text V}$
578	5,19	0,99
546	5,49	1,13
436	6,88	1,72
405	7,41	1,90
366	8,20	2,26

Tabelle 1: Messwerte zum Versuch zur Gegenfeldmethode des Fotoeffekts

Berechne die Frequenz $f$ des eingestrahlten Lichts mit der Wellenlänge $\lambda=578\,\text{nm}.$
Zeige durch eine graphische Auswertung aller Messwerte, dass es zwischen der Frequenz $f$ des eingestrahlten Lichts und der kinetischen Energie $E_{\text {kin }}$ der schnellsten aus der Fotokathode ausgelösten Elektronen einen linearen Zusammenhang gibt.
Erläutere den Zusammenhang $e \cdot U_{ \text G , \max }=h \cdot f-W_{ \text A }$ zwischen der Spannung $U_{ \text G , \max }$ und der Frequenz $f$ des eingestrahlten Lichts.
Begründe (mit der obigen Gleichung), dass eine Intensitätsveränderung des eingestrahlten Lichts keine Änderung der Messwerte aus Tabelle 1 bewirken würde.
Bestimme unter Verwendung aller Messwerte einen Wert für das Planck'sche Wirkungsquantum $h.$
Bestimme die minimale Frequenz des eingestrahlten Lichts $f_{\min }$ , bei der in der Fotozelle des Versuchs aus Tabelle 1 gerade Elektronen aus der Fotokathode ausgelöst werden.

(4 + 6 + 19 Punkte)

Teilaufgabe 3: $h$ -Bestimmung mit einer Röntgenröhre

Die Erzeugung von Röntgenstrahlung erfolgt mit einer Röntgenröhre. Der schematische Aufbau einer Röntgenröhre ist in Abbildung 2 dargestellt.

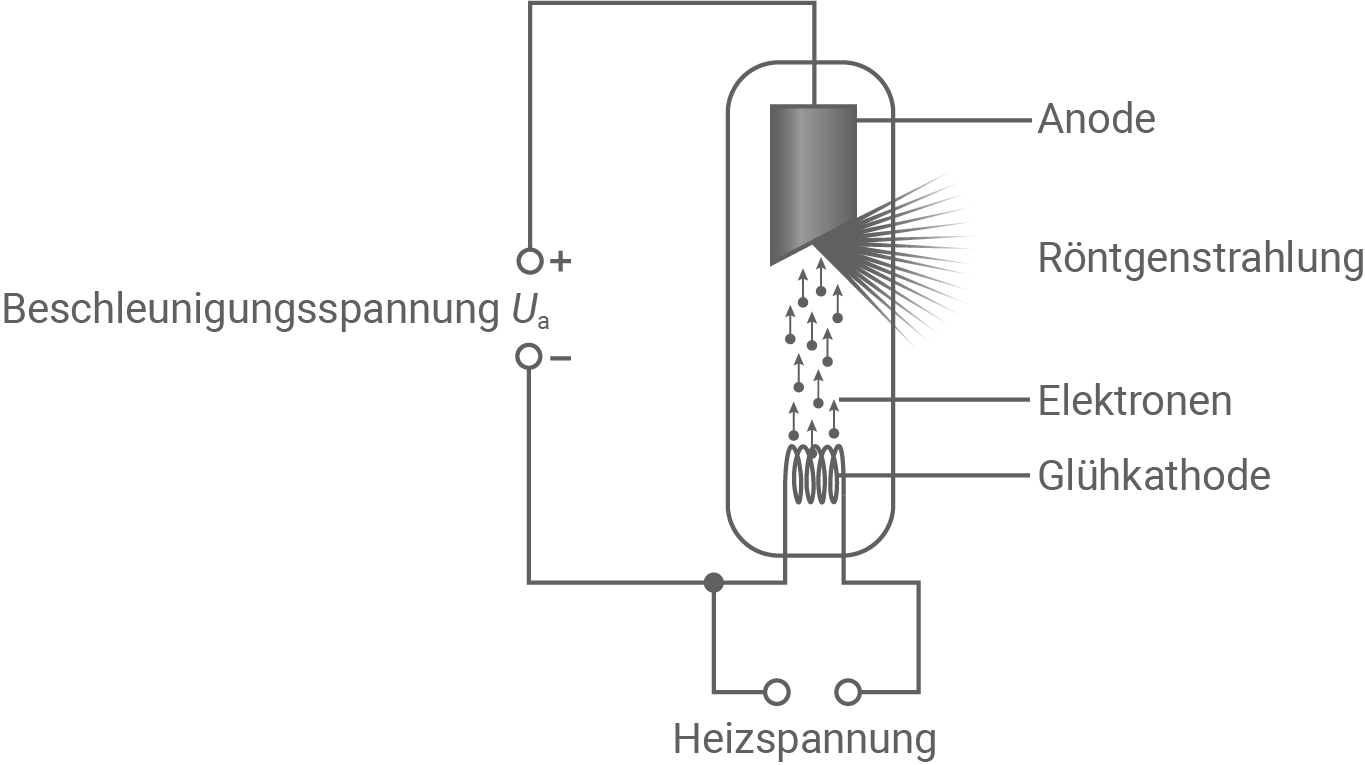
Abbildung 2: Schematischer Aufbau einer Röntgenröhre

Erläutere die Wechselwirkungsprozesse in der Anode der Röntgenröhre, die zur Emission von Röntgenbremsstrahlung und charakteristischer Röntgenstrahlung führen.

Abbildung 3 zeigt den schematischen Aufbau zur genaueren Untersuchung der Röntgenstrahlung mit dem Drehkristallverfahren nach Bragg.

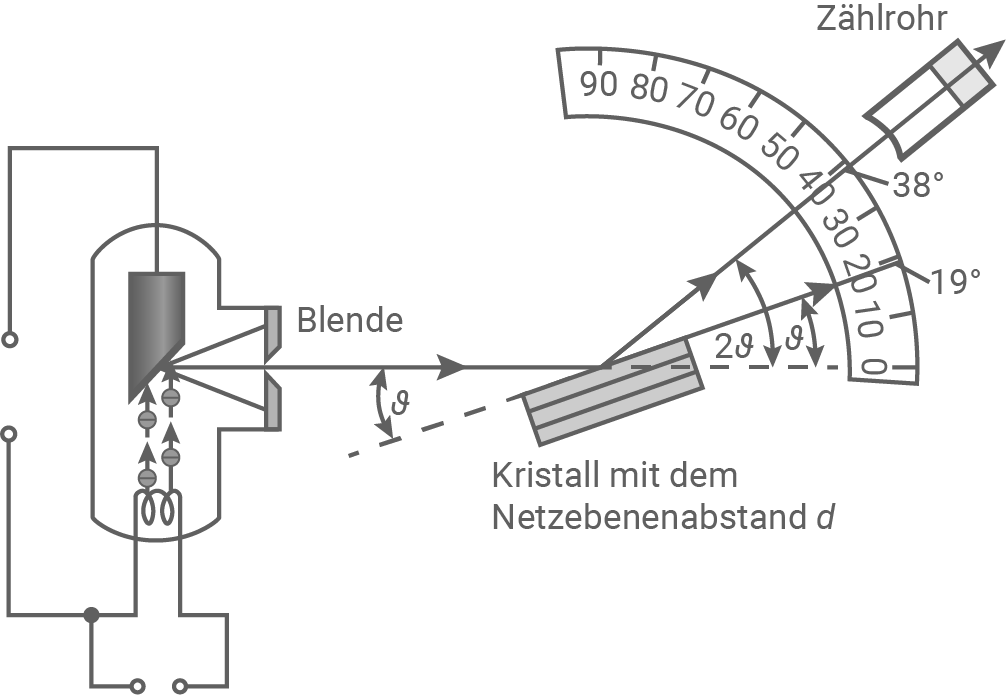
Abbildung 3: Schematischer Aufbau des Drehkristallverfahrens nach Bragg

Erläutere anhand von Abbildung 3 die Entstehung von konstruktiver Interferenz beim Drehkristallverfahren nach Bragg zur Untersuchung von Röntgenstrahlung.

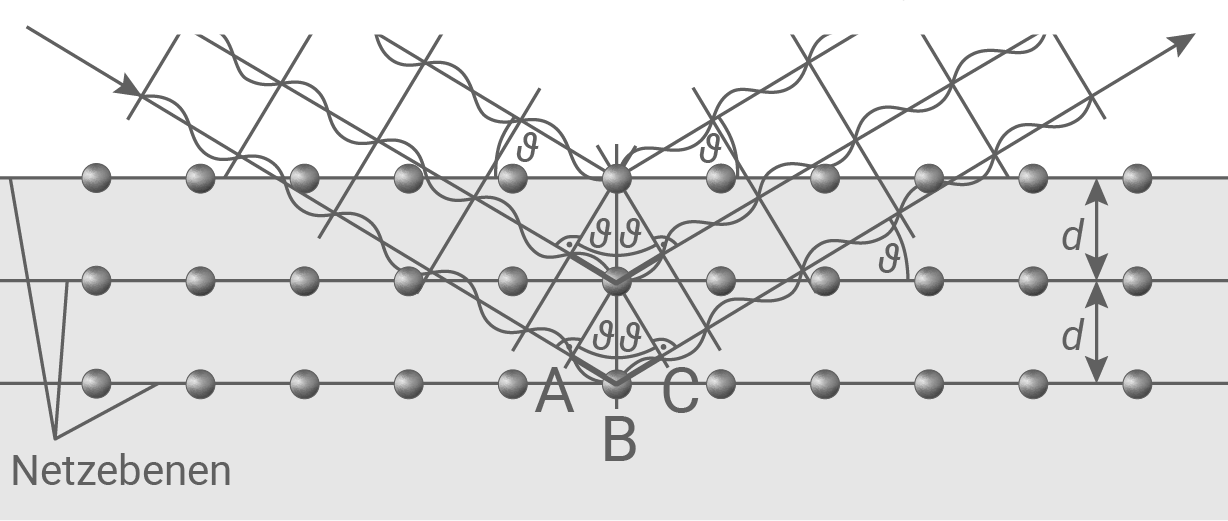
Abbildung 4

Leite mithilfe der in Abbildung 4 vorgegebenen Zeichnung die Bragg-Gleichung $2 \cdot d \cdot \sin \vartheta=n \cdot \lambda$ her.

Hierbei meint $d$ den Netzebenenabstand, $n$ die Ordnung des Maximums, $\lambda$ die Wellenlänge der Röntgenstrahlung und $\vartheta$ den sogenannten Glanzwinkel, unter dem man konstruktive Interferenz beobachten kann.

In Abbildung 5 sind kontinuierliche Bremsstrahlungsspektren für verschiedene Beschleunigungsspannungen 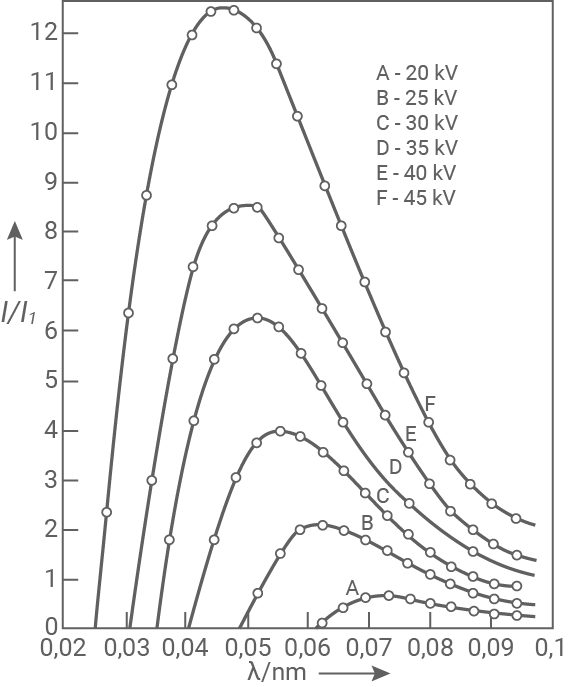$U_{ \text a }$ einer Wolfram-Anode dargestellt.

nrw physik abi lk 2023 ht 1 abbildung 5 kontinuierliches bremsstrahlungsspektrum für verschiedene beschleunigungsspannungen einer wolfram-anode; hier ist die intensität I der röntgenstrahlung in relativen einheiten gegen die wellenlänge lambda aufgetragen

Abbildung 5: Kontinuierliches Bremsstrahlungsspektrum für verschiedene Beschleunigungsspannungen einer Wolfram-Anode; hier ist die Intensität $I$ der Röntgenstrahlung in relativen Einheiten gegen die Wellenlänge $\lambda$ aufgetragen

Erläutere die Entstehung der kurzwelligen Grenze der Röntgenbremsstrahlung $\lambda_{\text {min. }}.$

Bestimme für die verschiedenen Beschleunigungsspannungen $U_{ \text a }$ die kurzwelligen Grenzen der Röntgenbremsstrahlung $\lambda_{\min }$ aus Abbildung 5.
Zeige mithilfe der abgelesenen Werte für $\lambda_{\min }$ aus Abbildung 5, dass die maximale Energie der Röntgenstrahlung $E_{ \text R }$ proportional zum Kehrwert der kurzwelligen Grenze der Röntgenbremsstrahlung $\lambda_{\min }$ ist: $E_{ \text R } \sim \dfrac{1}{\lambda_{\min }}$ .
Bestimme mithilfe Ihrer Messwerte aus Abbildung 5 einen Wert für das Planck'sche Wirkungsquantum $h.$

(6 + 3 + 5 + 2 + 12 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Teillösung 1

Sämtliche Experimente, die Interferenz aufzeigen, eignen sich.

So beispielsweise auch das Doppelspaltexperiment.

Laserlicht beleutet einen Doppelspalt. Zu beobachten ist ein Streifenmuster aus abwechselnd hellen und dunklen Bereichen. Dies lässt sich durch die Interferenz von Wellen erklären.

Gegenfeldmethode zum Nachweis des Fotoeffektes:

Wenn Licht passender Frequenz auf eine Metalloberfläche trifft, werden Elektronen aus dem festen Metallverbund gelöst und Lichtquanten emittiert.

Licht lässt sich als Strom von Photonen deuten. Ein Photon überträgt seine gesamte Energie auf das Elektron um es aus dem Metallverbund zu lösen.

Die Teilcheneigenschaft des Lichts erklärt den Fotoeffekt: Energie elektromagnetischer Strahlung wird quantisiert.

Teillösung 2

An eine Vakuumfotozelle - bestehend aus einer Ringanode, einer Fotokathode und einer mit Gas gefüllten Röhre - wird eine Gleichspannung $U_G$ angelegt. Der Minuspol der Spannungsquelle wird mit der Ringanode verbunden.

Messgeräte: Ein Voltmeter zeigt die Spannung in Volt an und ein Amperemeter misst den Fotostrom in Nanoampere.

Entstehung des Fotostroms

Licht geeigneter Frequenz löst Elektronen aus dem Metallverbund, welche sich in Richtung der Anode bewegen. Dadurch wird der Stromkreis geschlossen und der Fotostrom $I_{\text{F}}$ ist messbar.

Erklärung des Absinkens des Fotostroms bei Erhöhung der Spannung

Durch die Spannung $U_{\text{G}}$ entsteht ein elektrisches Feld zwischen Fotokathode und Anode. Dieses bremst die Bewegung der Elektronen ab. Um also die Anode zu erreichen, muss die kinetische Energie eines Elektrons groß genug sein um die elektrische Feldenergie zu überwinden.

In Formeln:

$\begin{array}[t]{rll} E_{\text{kin}}&\geq& E_{\text{el}} \\[5pt] &\geq& U_G \cdot e \end{array}$

Wird die Spannung $U_{\text{G}}$ erhöht, erhöht sich die elektrische Feldenergie. Ist die elektrische Feldenergie ebenso groß wie die kinetische Energie der Elektronen, schaffen es nur die schnellsten Elektronen zur Anode zu gelangen. Ist die elektrische Feldenergie größer als die kinetische Energie der Elektronen, können die Elektronen die Anode nicht mehr erreichen. Dadurch sinkt der Fotostrom auf null ab.

Maximale kinetische Energie der Elektronen

$\begin{array}[t]{rll} E_{\text{kin}}&=& E_{\text{el}} \\[5pt] &=& U_G \cdot e \end{array}$

Frequenz $\boldsymbol{f}$ berechnen

Gegeben: $\lambda = 578 \;\text{nm} =578\cdot 10^{-8}\;\text{m}$

Gesucht: $f$

Lösung: Es ist $c=3\cdot 10^8 \;\frac{\text{m}}{\text{s}}.$ Die Frequenz $f$ ergibt sich durch Einsetzen der Werte:

$\begin{array}[t]{rll} f&=&\dfrac{c}{\lambda} &\quad \scriptsize \\[5pt] &=&\dfrac{3\cdot 10^8 \;\frac{\text{m}}{\text{s}}}{578 \;\text{nm}} &\quad \scriptsize \\[5pt] &=&\dfrac{3\cdot 10^8 \;\frac{\text{m}}{\text{s}}}{578\cdot 10^{-9} \;\text{m}} &\quad \scriptsize \\[5pt] &=& 5,19\cdot 10^{14} \text{Hz} \end{array}$

Linearer Zusammenhang zwischen $\boldsymbol{E_{\text{kin}}}$ und $\boldsymbol{f}$

Gegeben: Werte in Tabelle und $e= 1\;\text{eV}= 1,6\cdot 10^{-19}\;\text{J}$

Gesucht: $E_{\text{kin}}$

Lösung: Es ist $E_{\text{kin}}= e \cdot U_{G,\text{max}}.$ Damit kann die Tabelle wie folgt ergänzt werden:

$\color{#fff}{f}$ in $\color{#fff}{10^{14}\;\text{Hz}}$	$\color{#fff}{U_{G,\text{max}}}$ in $\color{#fff}{\text{V}}$	$\color{#fff}{E_{\text{kin}}}$ in $\color{#fff}{10^{-19}\;\text{J}}$
5,19	0,99	1,58
5,49	1,13	1,81
6,88	1,72	2,75
7,41	1,90	3,04
8,2	2,26	3,62

Die Werte aus der Tabelle werden im $f$ - $E_{\text{kin}}$ -Diagramm eingezeichnet.

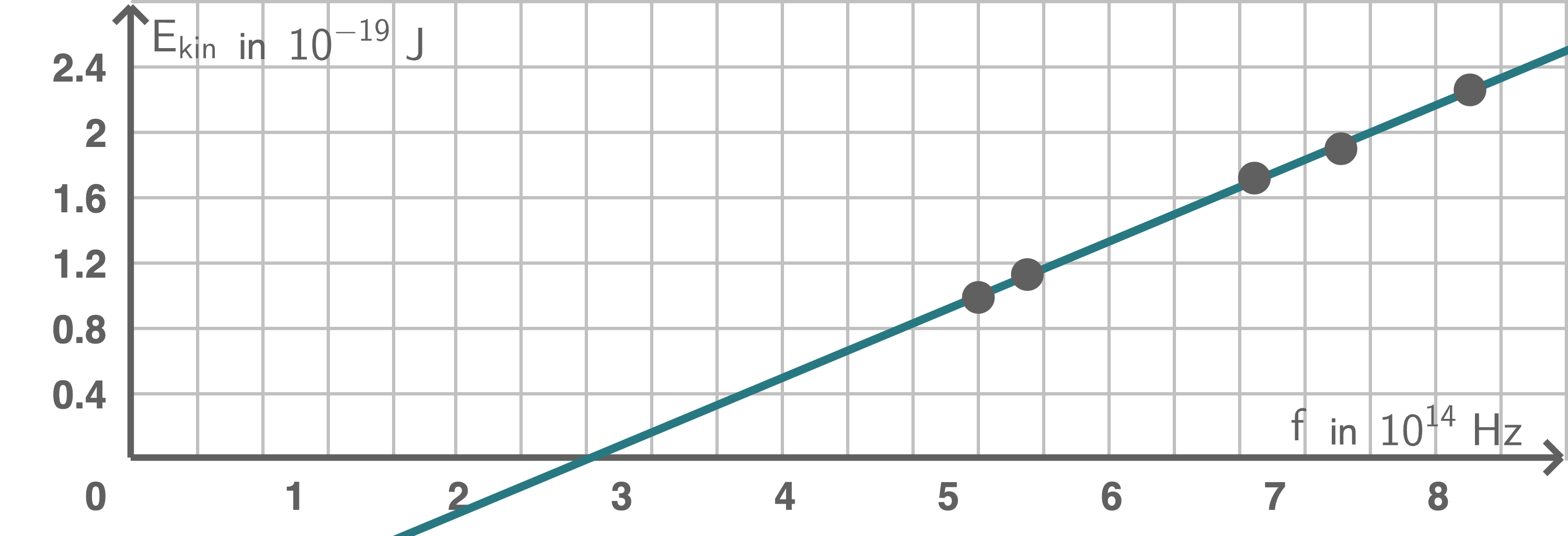Im Diagramm wird eine Ausgleichsgerade gezogen. Von dieser Ausgleichsgeraden weichen die Punkte nur minimal ab. Dies zeigt den linearen Zusammenhang.

Zusammenhang $\boldsymbol{U_{\text{G, max}}}$ und $\boldsymbol{f}:$

Um ein Elektron aus dem Metallverbund lösen zu können, überträgt ein Lichtquant seine gesamte Energie $E_{\text{Ph}}= h\cdot f$ auf das Elektron.

Das Elektron nutzt die vom Photon übertragene Energie, um sich (mittels Austrittsarbeit $W_{\text{A}}$ ) aus dem Metallverbund zu lösen und sich zur Anode (mittels kinetischer Energie $E_{\text{kin}}$ )zu bewegen.

Es gilt also:

$\begin{array}[t]{rll} E_{\text{Ph}}&=& E_{\text{kin}}+W_{\text{A}} \\[5pt] h \cdot f&=& e\cdot U_{\text{G, max}}+W_{\text{A}} &\quad \scriptsize \mid\;- W_{\text{A}} \\[5pt] h \cdot f-W_{\text{A}}&=& e\cdot U_{\text{G, max}} &\quad \scriptsize \\[5pt] e\cdot U_{\text{G, max}}&=& h \cdot f - W_{\text{A}} &\quad \scriptsize \\[5pt] \end{array}$

Intensitätsveränderung

$\begin{array}[t]{rll} e\cdot U_{\text{G, max}}&=& h \cdot f - W_{\text{A}} \\[5pt] E_{\text{kin}}&=& E_{\text{Ph}} -W_{\text{A}} \end{array}$

Um ein Elektron aus dem Metallverbund lösen zu können, überträgt ein Lichtquant seine gesamte Energie $E_{\text{Ph}}= h\cdot f$ auf das Elektron. Dabei hängt die Energie des Photons nur von der Frequenz $f$ ab. Da $f= \dfrac{c}{\lambda}$ gilt, hängt die Energie des Photons auch von der Wellenlänge $\lambda$ des eingestrahlten Lichtes ab.

Die Energie des Photons ist unabhängig von der Lichtintensität.

Die Elementarladung $e$ und die Austrittsarbeit $W_A$ sind konstant. Dadurch hängt die Spannung $U_{\text{G, max}}$ ebenfalls nur von der Frequenz $f$ und der Wellenlänge des eingestrahlten Lichtes $\lambda$ ab.

Wenn die Intensität des eingestrahlten Lichts verändert wird, betrifft dies die Anzahl der eintreffenden Photonen pro Zeiteinheit, nicht jedoch ihre Energie. Das bedeutet, dass bei einer Änderung der Intensität zwar mehr oder weniger Elektronen ausgelöst werden können, die Energie jedes einzelnen Elektrons jedoch unverändert bleibt.

Eine Intensitätsänderung nimmt keinen Einfluss auf die Messwerte.

Planck'sches Wirkungsquantum $\boldsymbol{h}$ bestimmen

Die Ausgleichsgerade wird durch die Geradengleichung $E_{\text{kin}}= h\cdot f-W_A$ beschrieben.

Das Planck'sche Wirkungsquantum $h$ entspricht der Steigung der Geraden. Dazu kann ein Steigungsdreieck in die Abbildung eingezeichnet werden, bzw. ein Wertepaar aus der Tabelle genutzt werden:

$h= \dfrac{2,75\cdot 10^{-19}\;\text{J}-1,81\cdot 10^{-19}\;\text{J}}{6,88\cdot 10^{14}\;\text{Hz}-5,49\cdot 10^{14}\;\text{Hz}}$ $= \dfrac{0,94\cdot 10^{-19}\;\text{J}}{1,39\cdot 10^{14}\;\text{Hz}}$ $\approx 6,76 \cdot 10^{-34} \;\text{Js}$

Alternativ kann auch mit dem Taschenrechner der Graph der Ausgleichsgeraden dargestellt werden und die Gleichung bestimmt werden.

Minimale Frequenz bestimmen

$\begin{array}[t]{rll} 0&=&h\cdot f_{\text{min}}- 1,17\;\text{eV} &\quad \scriptsize \\[5pt] \dfrac{1,17\;\text{eV}}{h}&=& f_{\text{min}}&\quad \scriptsize \\[5pt] 2,79 \cdot 10^{14} \,\text{Hz}&=& f_{\text{min}} \end{array}$

Alternativ kann die minimale Frequenz auch aus dem Diagramm als Nullstelle der Ausgleichsgeraden abgelesen werden.

Teillösung 3

Die aus der Glühkathode emittierten Elektronen werden in der Röntgenröhre beschleunigt und treffen auf die Anode. Hier treffen sie auf die Atome der Anode.

Röntgenbremsstrahlung

Der positive Anodentomkern zieht die Elektronen an und lenkt (bremst) sie ab. Die verlorene kinetische Energie wird in Form von Röntgenstrahlung abgestrahlt.

Charakteristische Röntgenstrahlung

Trifft das Elektron auf ein Hüllenelektron des Anodenatoms, kann es dieses bei genügend großer Energie aus der K-Schale stoßen. Es kommt zur Rekombination aus der L-, M-... Schale (Das Elektron überträgt beim Stoßprozess seine Energie auf kernnahem Hüllelektronen, welche in eine höhere Schale springen können. Dadurch entsteht eine Lücke einer innerliegenden Schale. Diese wird durch ein Elektron einer äußerliegenden Schale gefüllt.)
Durch diesen Prozess wird Energie in Form von Licht frei.

Ein schmales Röntgenlichtbündel trifft auf den Kristall und wird von diesem reflektiert. Um dies zu verstehen, können werden die Atomrümpfe im Gitter als Ursprungspunkte von Elementarwellen betrachten, die miteinander interferieren.

Konstruktive Interferenz tritt auf, wenn sich Wellenzüge überlagern (also Wellenberge und -täler addieren). Somit ist der Gangunterschied ein Vielfaches der Wellenlänge $\lambda$ ist.

Ein Gangunterschied entsteht, weil sich die Wellen, an unterschiedlichen Gitterebenen reflektieren, dadurch unterschiedlich lange Wege zurücklegen und schließlich überlagern.

Dies passiert nur für bestimmte Winkel $\theta.$

Das Dreieck A,B mit dem Winkel $\theta$ ist rechtwinklig. Es gilt:

$\begin{array}[t]{rll} \sin(\theta)&=&\dfrac{\overline{AB} }{d} &\quad \scriptsize \mid\;\cdot d \\[5pt] d\cdot \sin(\theta) &=& \overline{AB} \end{array}$

Für den Gangunterschied $\Delta s$ der an den beiden Netzebenen reflektieten Wellen gilt:

Rechenweg anzeigen

$n\cdot \lambda= 2\cdot d\cdot \sin(\theta)$

Die kurzwellige Grenze $\lambda_{\min}$ der Röntgenbremsstrahlung entsteht, wenn hochenergetische Elektronen auf die Anode treffen und durch die Anziehung der Atomkerne abgebremst werden. Diese Grenze markiert die kürzeste Wellenlänge im Röntgenspektrum, was bedeutet, dass die erzeugten Photonen die größtmögliche Energie haben. Dies geschieht, wenn die gesamte kinetische Energie der Elektronen vollständig in Röntgenstrahlungsenergie umgewandelt wird, gemäß der Gleichung $E = h \cdot f$ .

Beschleunigungsspannung	$\color{#fff}{\lambda}$ in nm
A	0,062
B	0,048
C	0,041
D	0,035
E	0,031
F	0,025

Diese maximale kinetische Energie ist direkt proportional zur Beschleunigungsspannung: $E_{R}=e\cdot U_{a}$

Durch die erkennbare Gerade ist die Proportionalität $E_R \sim \dfrac{1}{\lambda_{\text{min}}}$ nachgewiesen.

Die Gleichung für die Regressionsgerade lautet:

Rechenweg anzeigen

$E_{R} =h \cdot f- 0,96\;\text{kV}$

Alternativ kann die regressionsgerade auch mit dem Taschenrechner bestimmt werden. Die Steigung kann dann ausgegeben und passend umgerechnet werden, woraus sich $h$ ergibt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

HT 1

Bestimmung des Planck'schen Wirkungsquantums auf zwei verschiedene Arten

Teilaufgabe 1: Wellen- und Teilcheneigenschaften von Licht

Teilaufgabe 2: -Bestimmung mit dem Fotoeffekt

Teilaufgabe 3: -Bestimmung mit einer Röntgenröhre

Weiter lernen mit SchulLV-PLUS!

Teillösung 1

Teillösung 2

Teillösung 3

Weiter lernen mit SchulLV-PLUS!

Teilaufgabe 2: $h$ -Bestimmung mit dem Fotoeffekt

Teilaufgabe 3: $h$ -Bestimmung mit einer Röntgenröhre