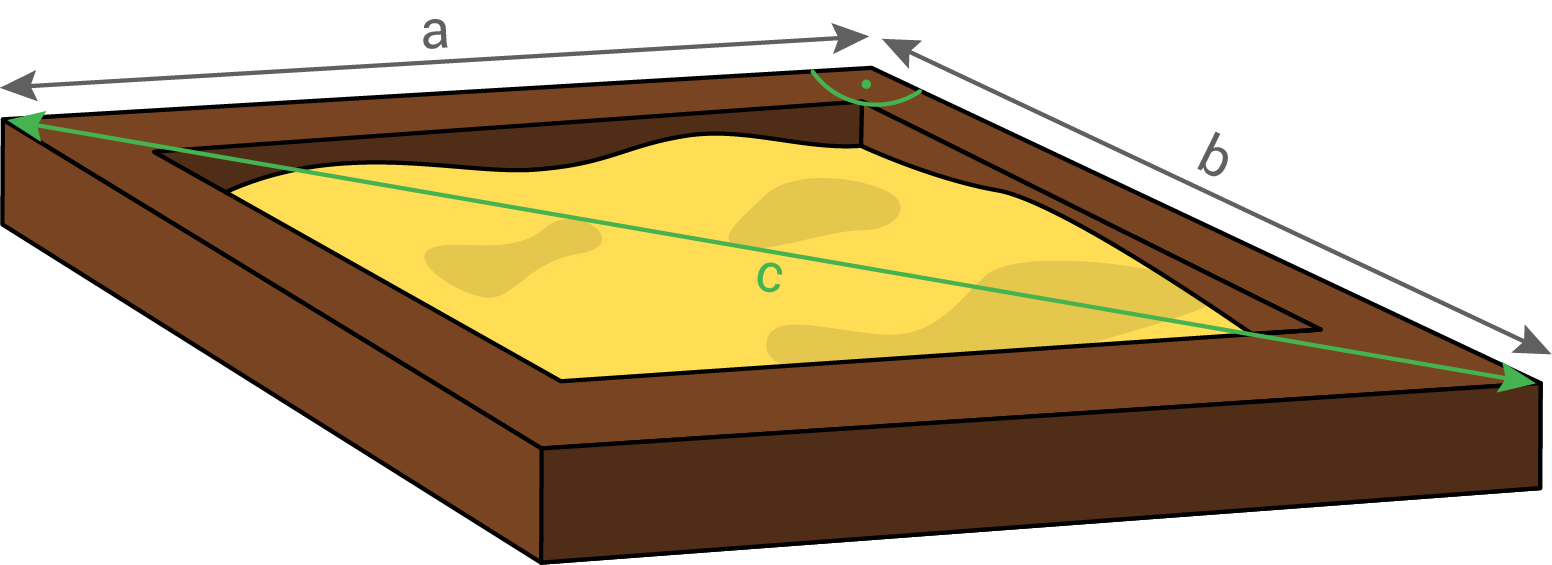
Satz des Pythagoras in der Ebene
Um Streckenlängen in ebenen Figuren zu berechnen, hilft es, Figuren so zu zerlegen, dass rechtwinklige Dreiecke entstehen.
Dann kann der Satz des Pythagoras verwendet werden.
Dann kann der Satz des Pythagoras verwendet werden.
Diagonale im Rechteck
Gegeben ist das nebenstehende Rechteck mit den Seitenlängen 
und 
und der Diagonale 
Die Diagonale bildet mit und ein rechtwinkliges Dreieck.
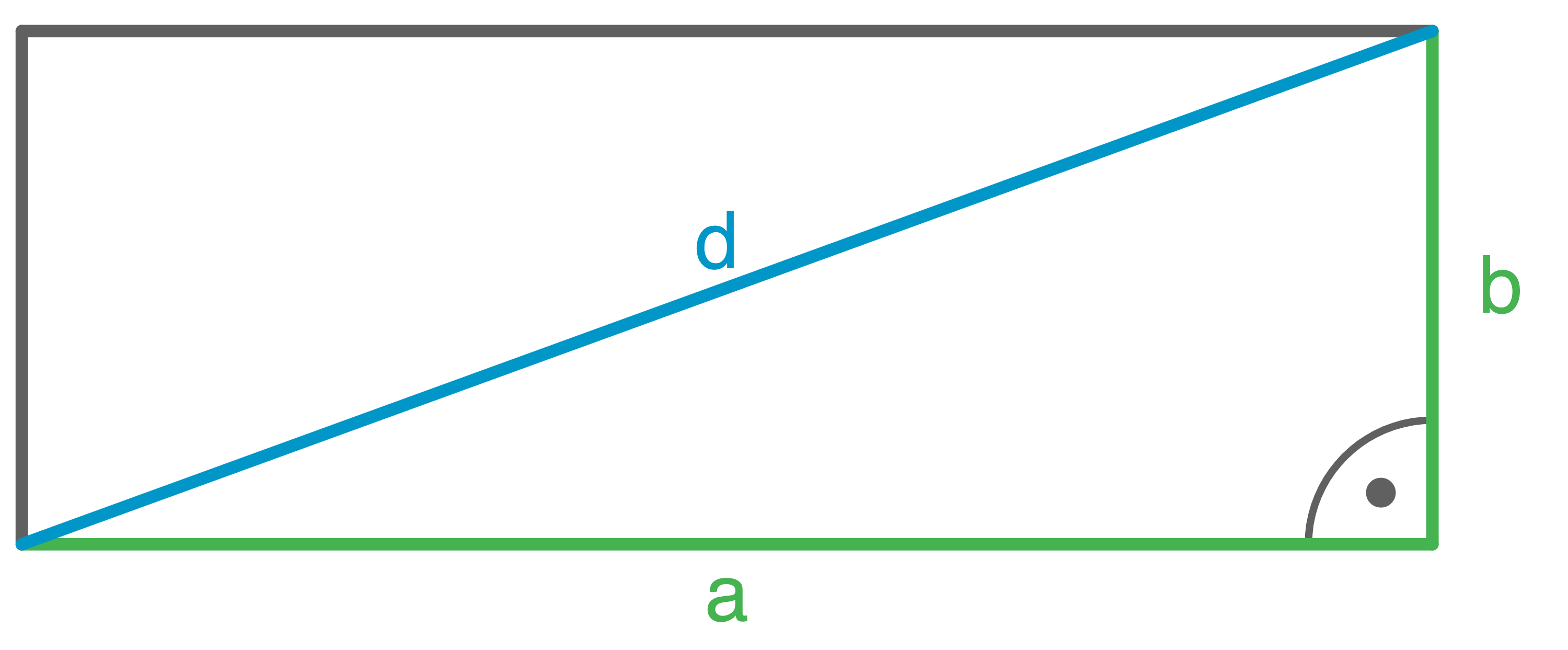Es gilt 
Damit erhält man die Formel, um die Länge der Diagonale zu berechnen: 
Formel: Diagonale
Diagonale im Quadrat
Gegeben ist das untenstehende Quadrat mit der Seitenlänge und der Diagonale Die Diagonale bildet mit den beiden anliegenden Seiten ein rechtwinkliges Dreieck.
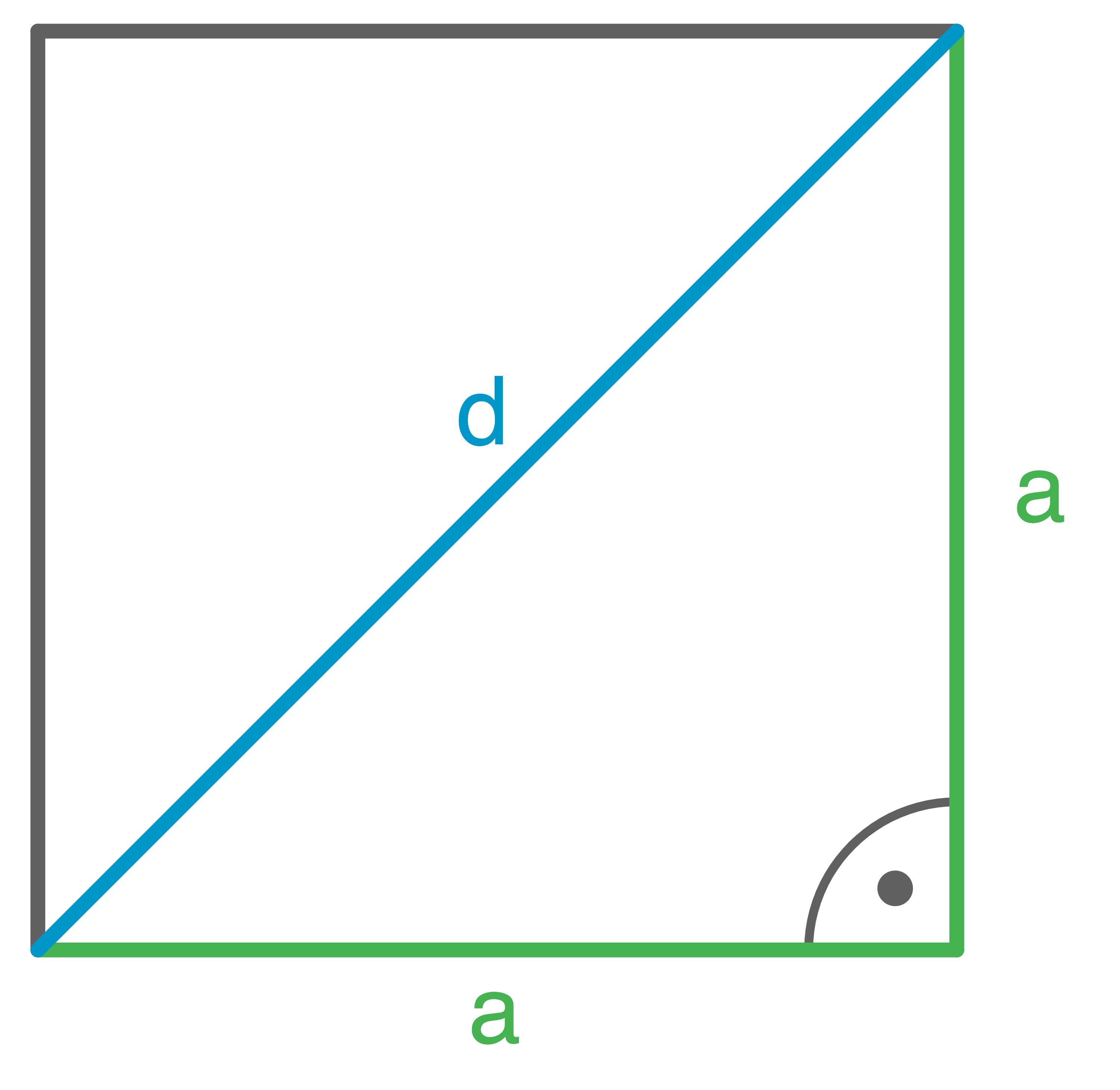Auch hier wird die Formel des Satz des Pythagoras umgestellt, um die Länge der Diagonale zu berechnen:
![\(\begin{array}[t]{rll}
d^2&=& a^2+a^2 &\\[5pt]
d^2&=& 2a^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
d&=&\sqrt{2a^2} \\[5pt]
d&=& a\cdot \sqrt{2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/da2e645d10bb766895bba633d216881687ebc3787f4310bef79588cbcd3a0ef4?color=5a5a5a)
Formel: Diagonale
Höhe eines gleichseitigen Dreiecks
Gegeben ist ein gleichseitiges Dreieck der Seitenlänge 
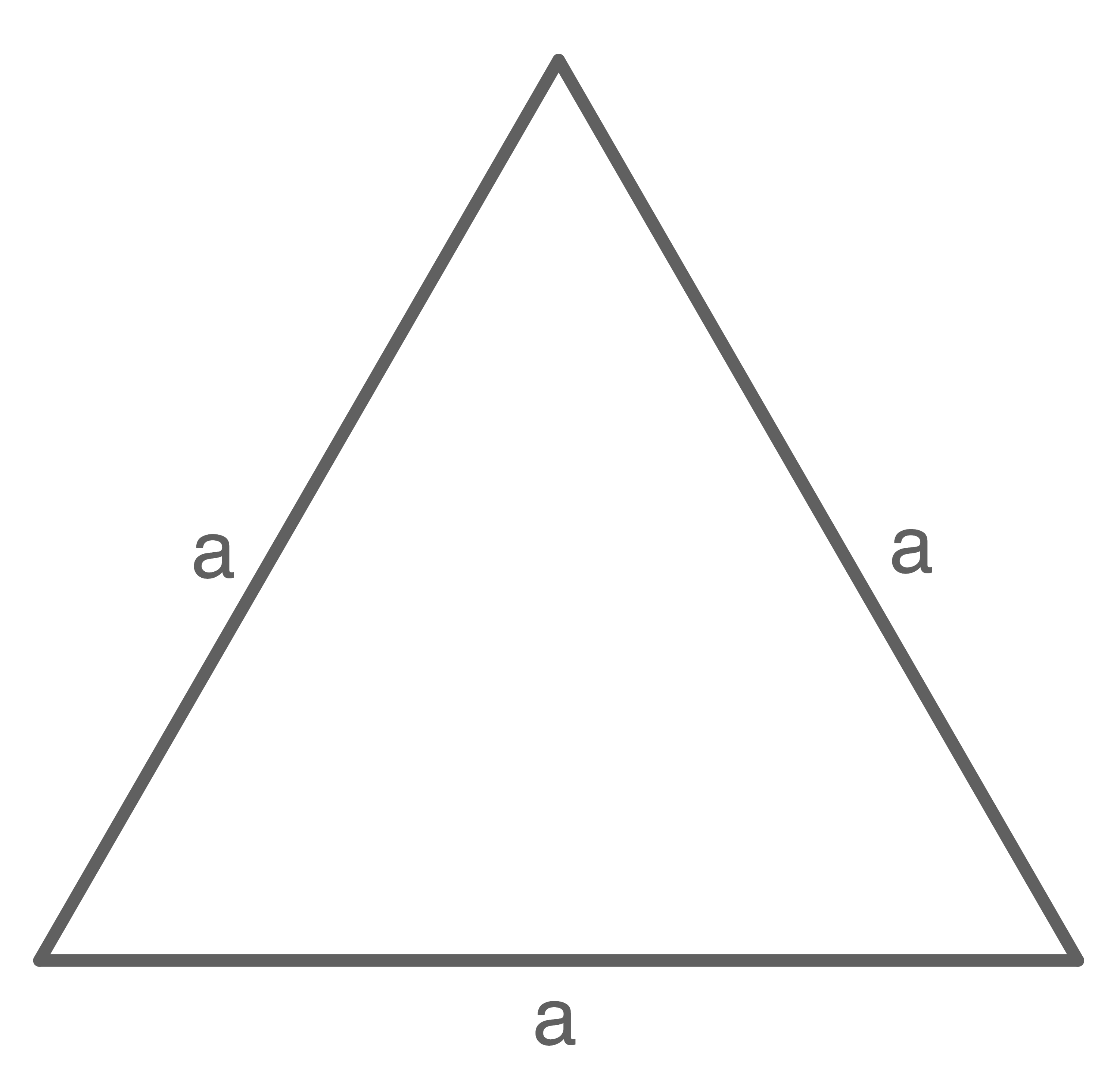Durch Einzeichnen der Höhe ergibt sich ein rechtwinkliges Dreieck mit 
und 
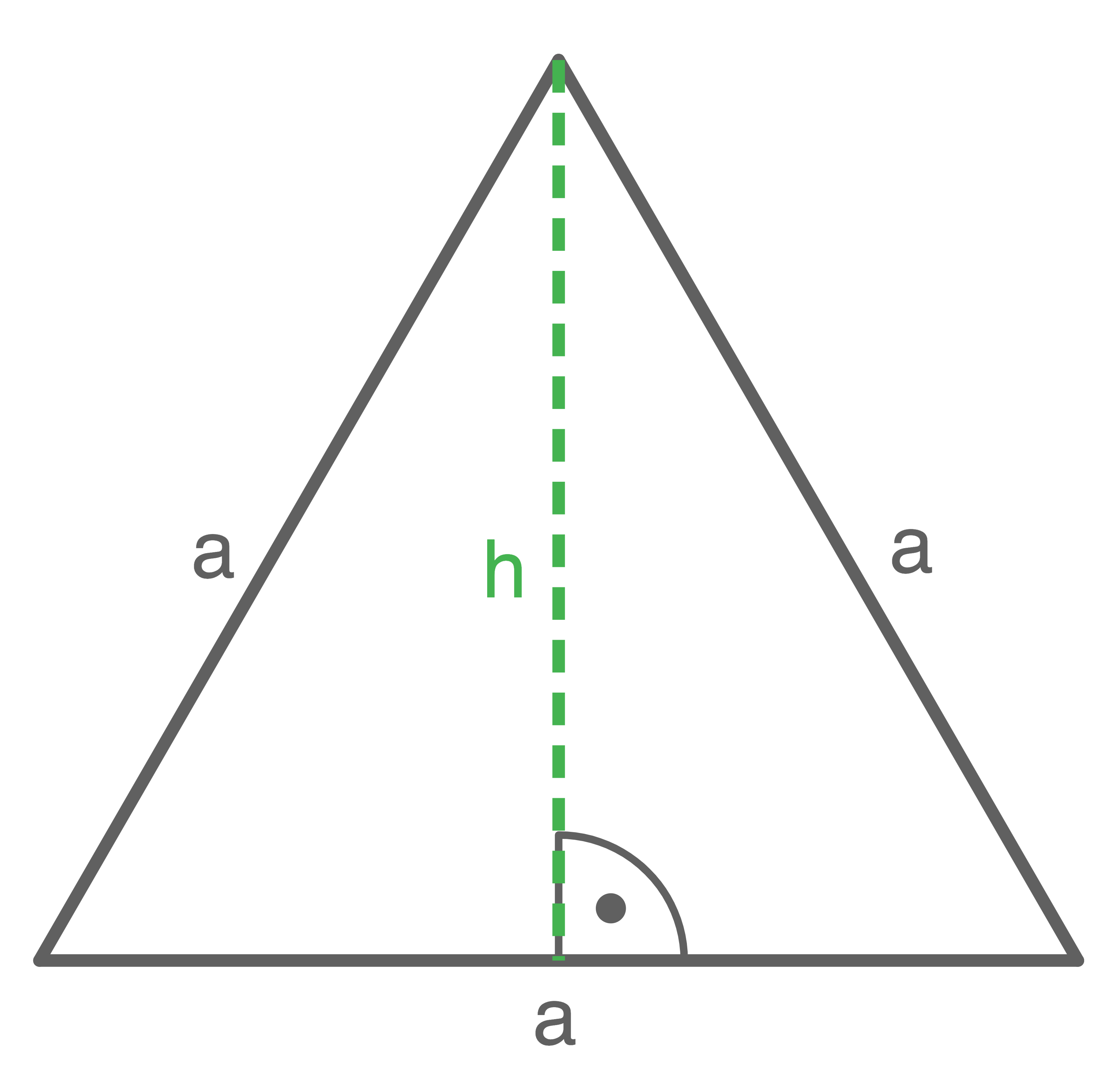
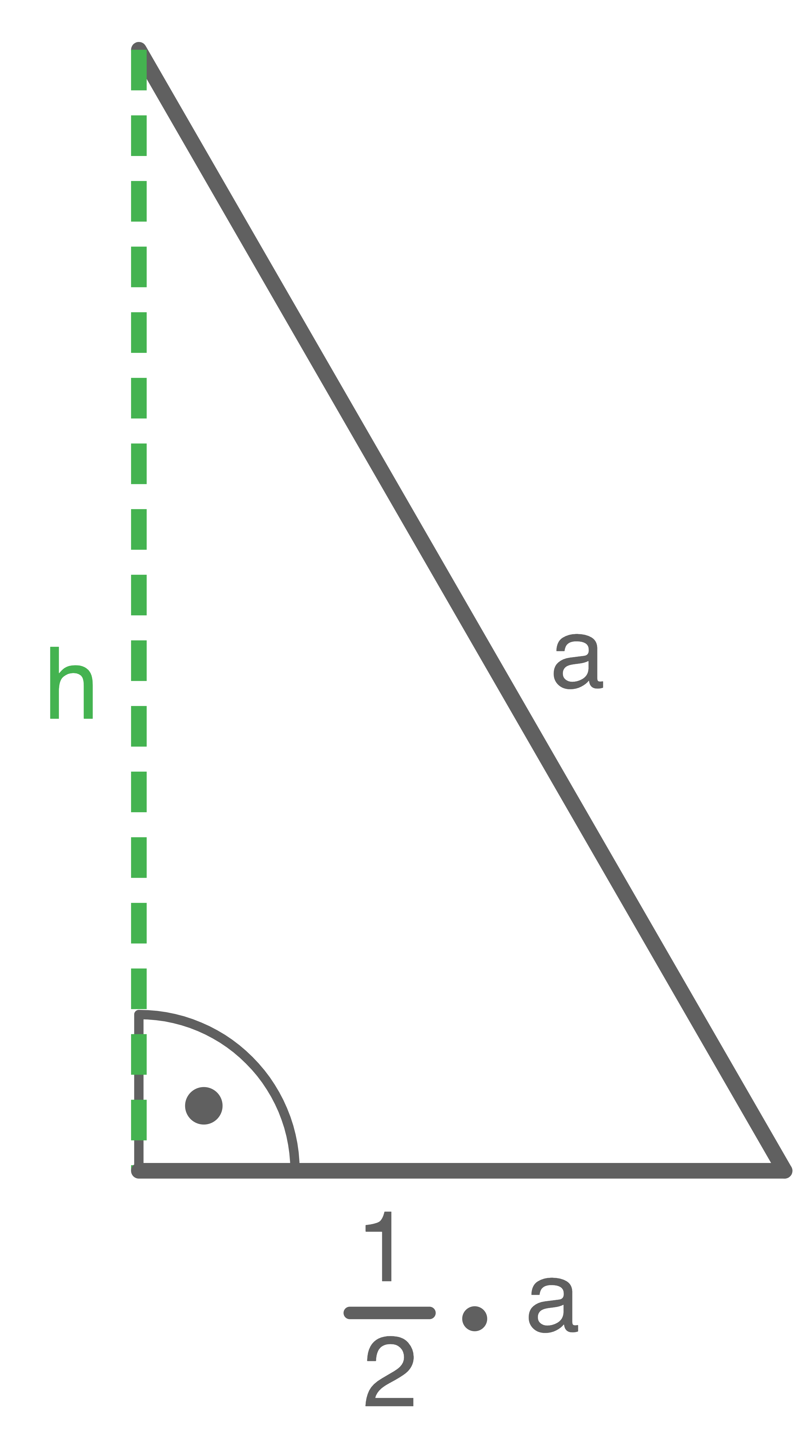Damit lässt sich nun die Formel des Satz des Pythagoras so umstellen, dass die Höhe berechnet werden kann:
![\(\begin{array}[t]{rll}
h^2&=& a^2-\left(\dfrac{1}{2}\cdot a\right)^2&\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
h&=& \sqrt{a^2-\left(\dfrac{1}{2}\cdot a\right)^2} \\[5pt]
h&=& \sqrt{\dfrac{3}{4}\cdot a^2} \\[5pt]
h&=& \dfrac{1}{2}\cdot \sqrt{3}\cdot a \\[5pt]
\end{array}\)](https://mathjax.schullv.de/81ed1d1339284c8ed0b3d6c6cef818a3e6d663639b6b634f37c30ecb85e65ca5?color=5a5a5a)
Formel: Höhe
1
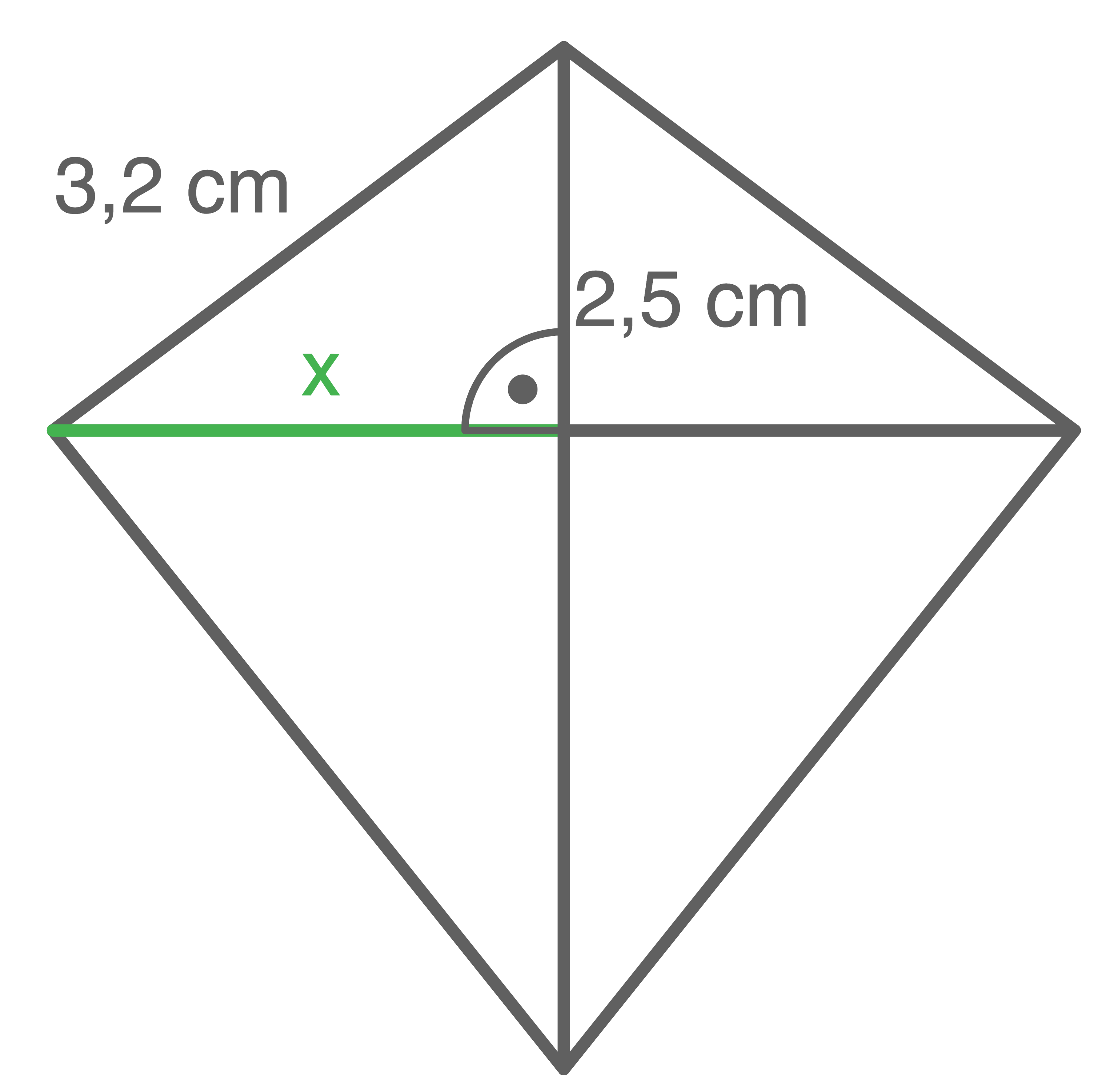
Berechne die Länge der Seite 
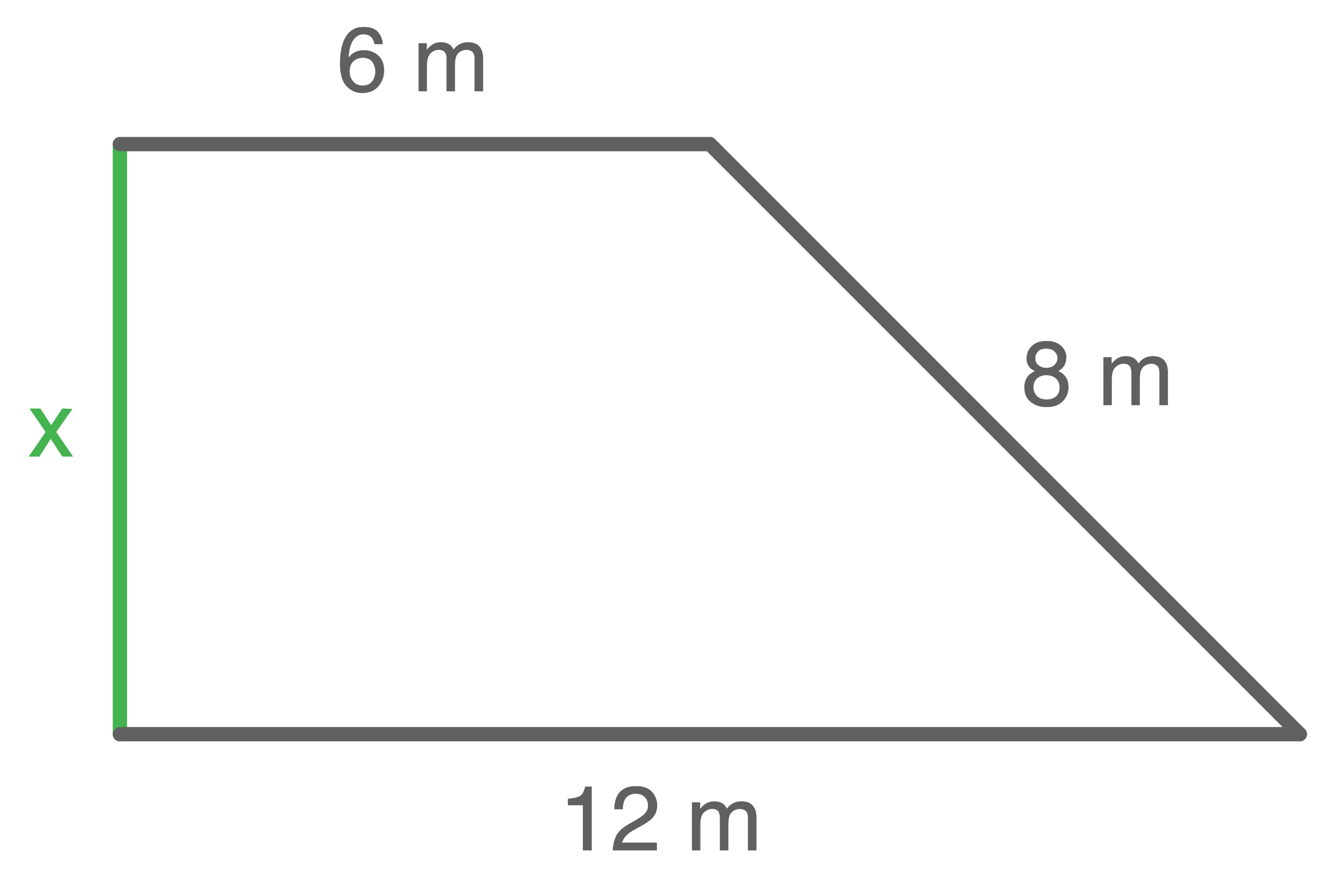
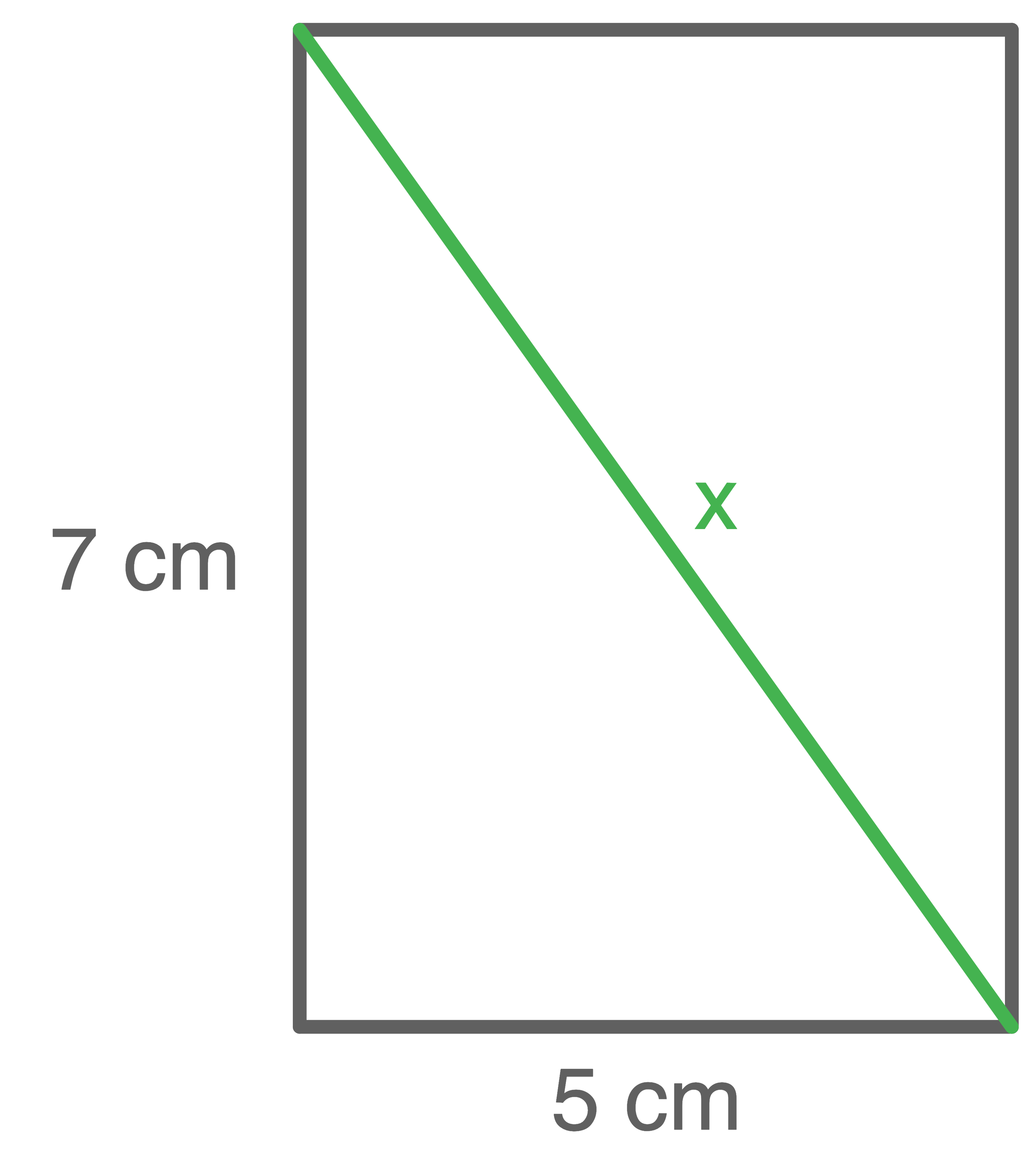
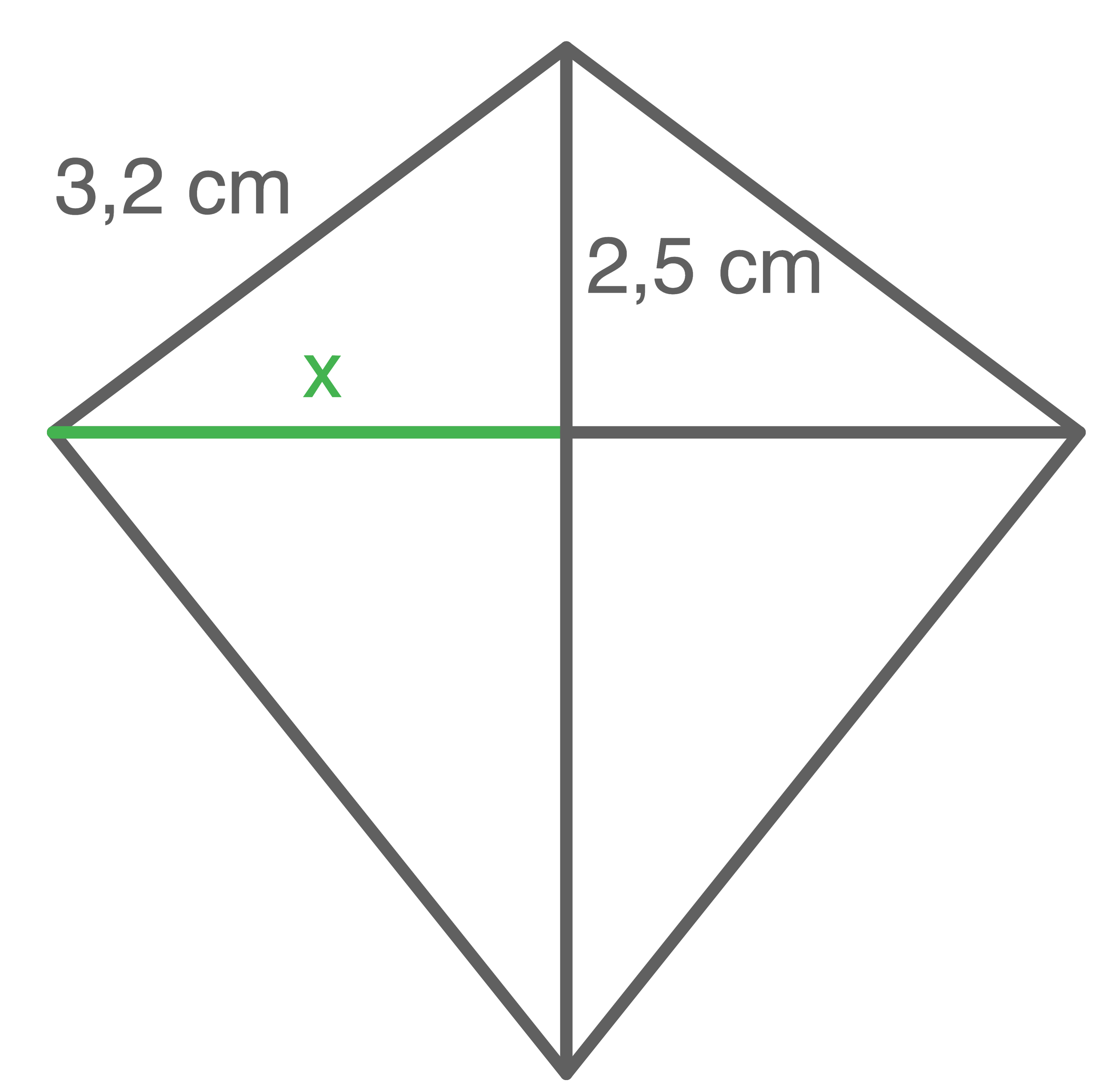
a)
b)
c)
2
Sonjas Eltern haben sich einen Pool in den Garten einbauen lassen. Der Pool hat eine Breite von 
und eine Länge von 
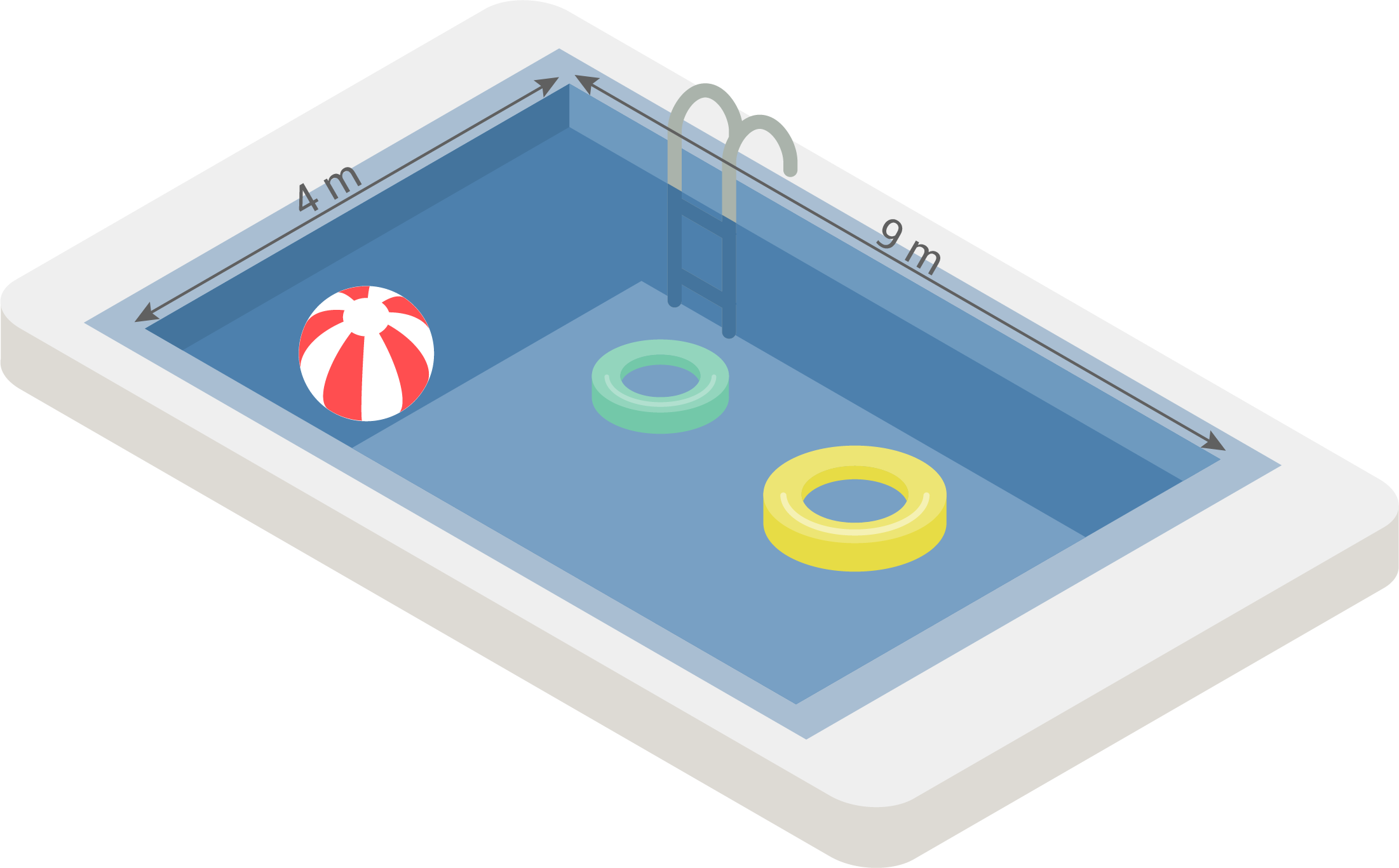
a)
Sonja möchte wissen, wie lang die längste Bahn des Pools ist, die sie schwimmen kann.
b)
Sonjas Großeltern entscheiden sich auch dazu, einen Pool im Garten einbauen zu lassen.
Sie wählen folgende Maße:
Sie wählen folgende Maße:
- Breite:
- Länge:
3
Die Eingangstür einer Altbauwohnung soll renoviert werden. Der Handwerker kennt die folgenden Maße:
- Diagonale:
- Höhe:
4
Maurice möchte seiner kleinen Schwester einen Sandkasten bauen.
Der Sandkasten soll quadratisch sein und eine Diagonale von 
haben.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
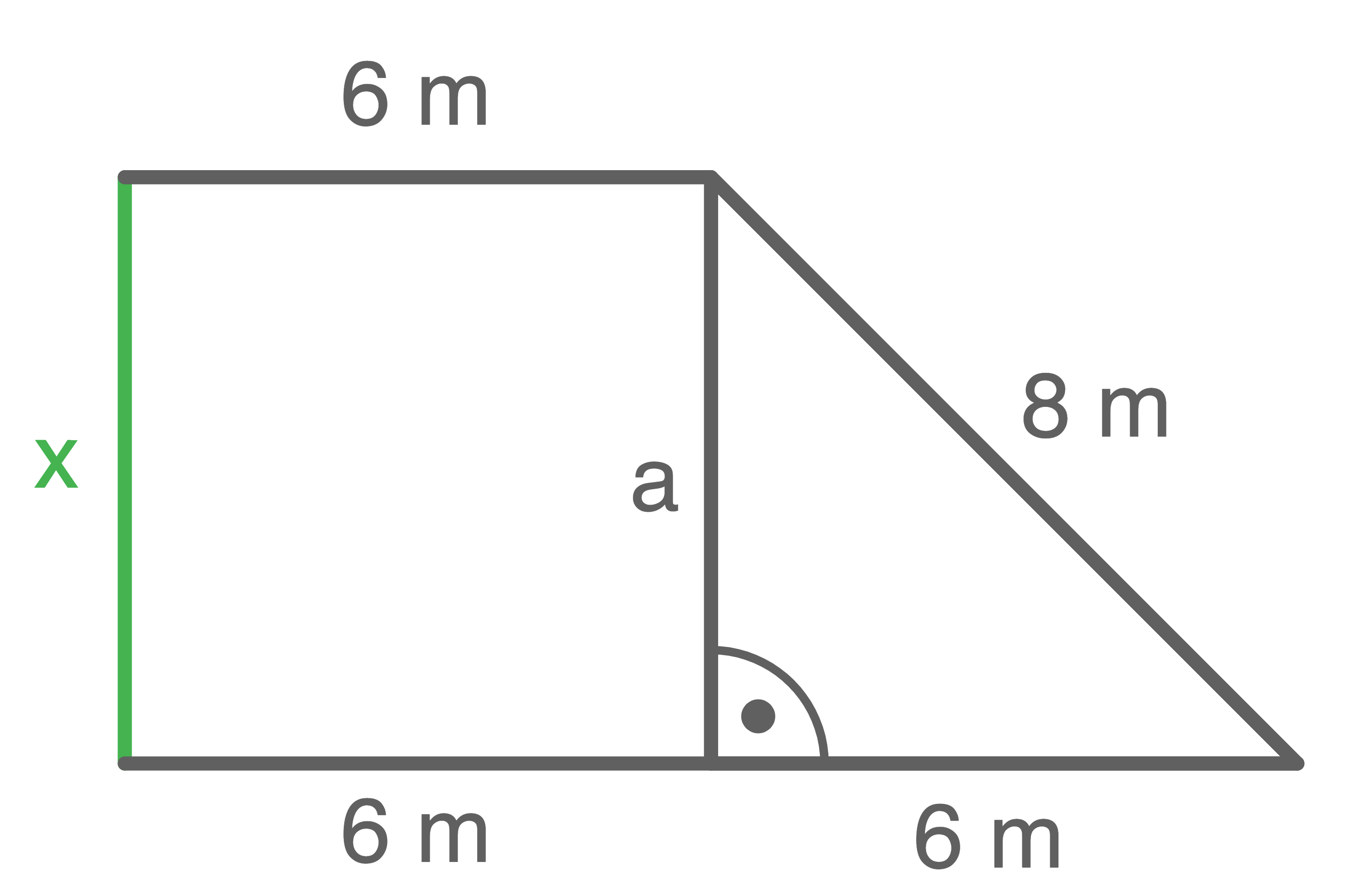
b)
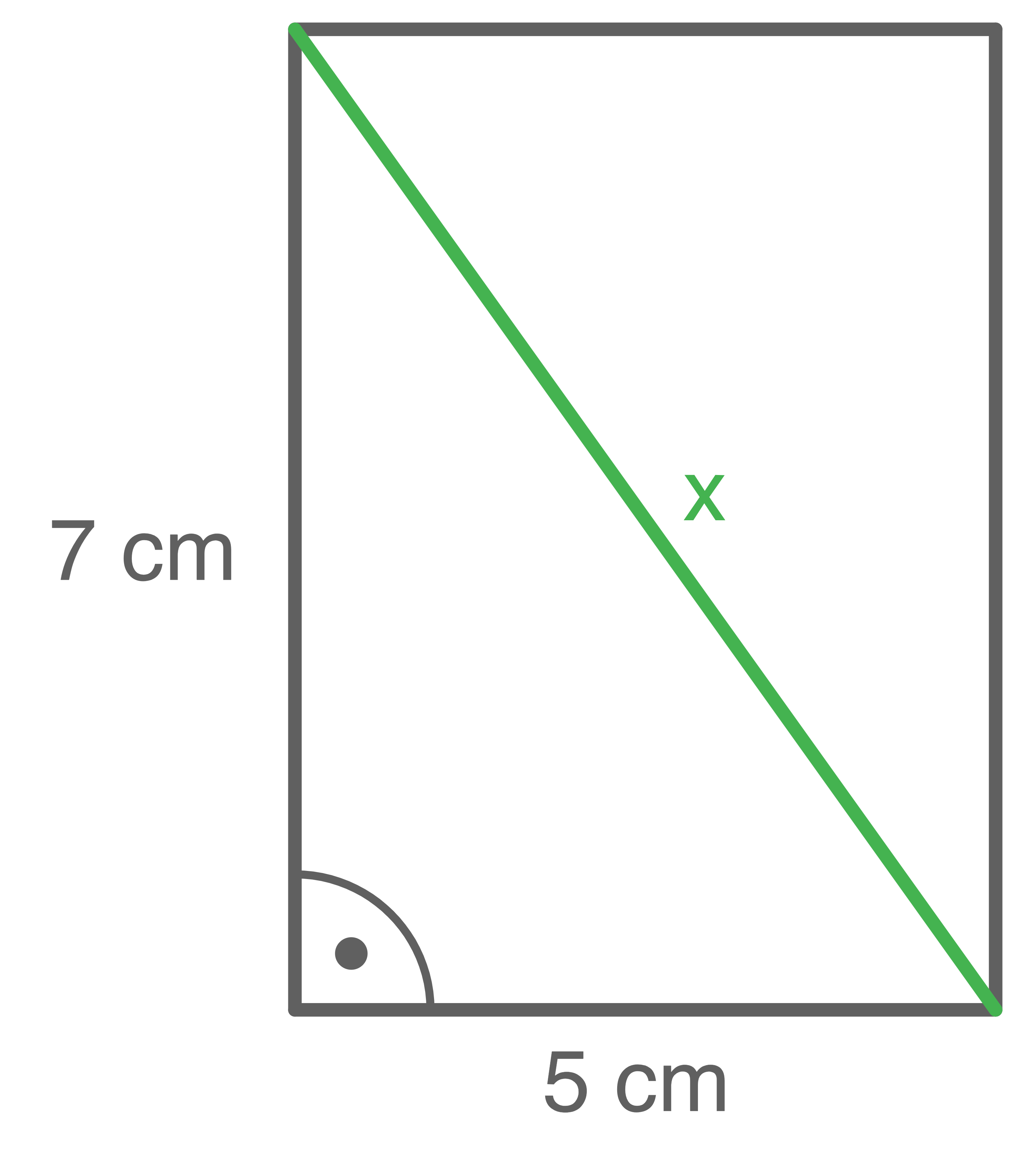
c)
2
a)
Die längste Bahn des Pools entspricht der Hypotenuse 
(siehe Skizze).
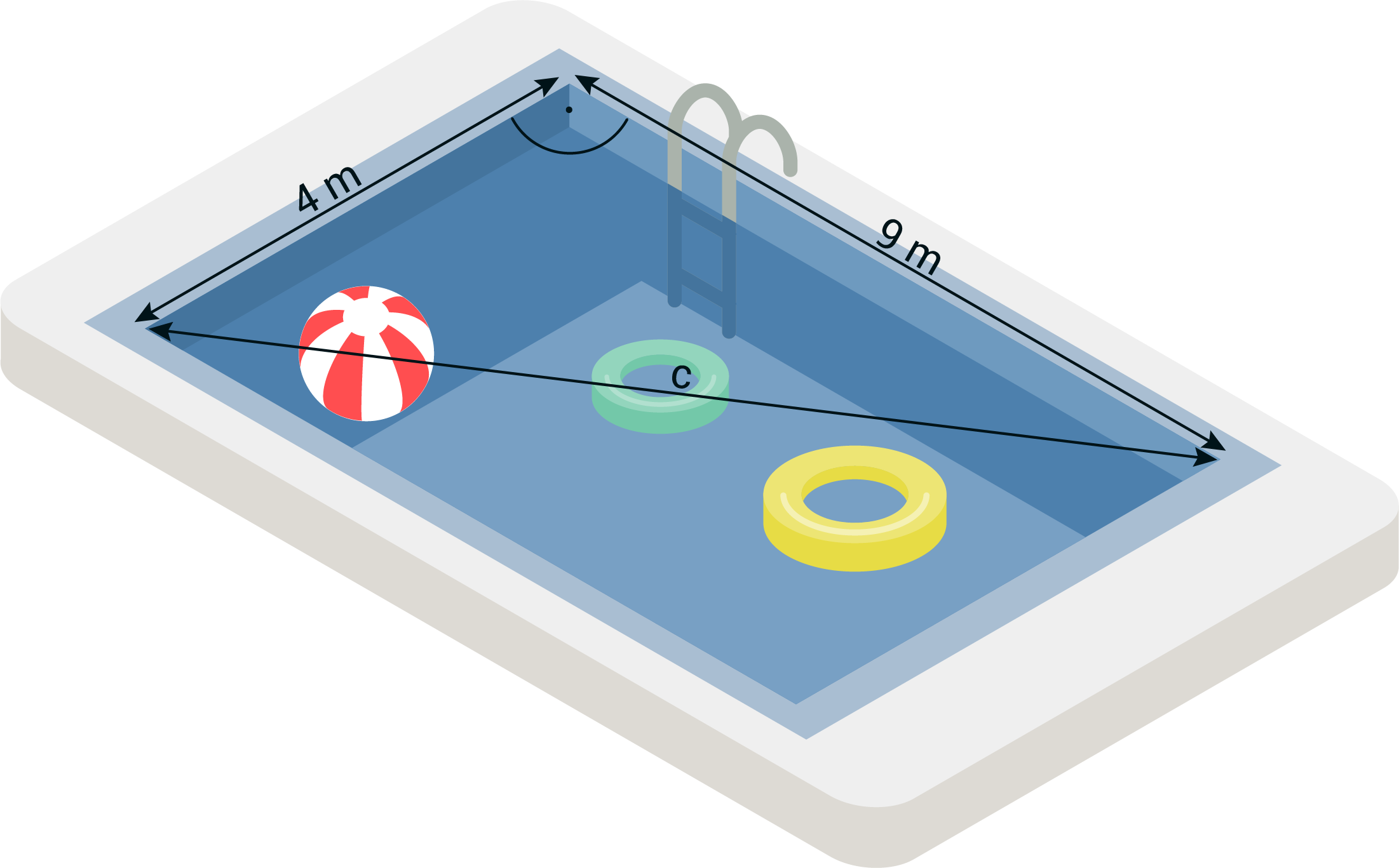
![\(\begin{array}[t]{rll}
c^2&=&(4\,\text{m})^2+(9\,\text{m})^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
c&=&\sqrt{(4\,\text{m})^2+(9\,\text{m})^2 } \\[5pt]
c&=&\sqrt{16\,\text{m}^2+81\,\text{m}^2 } \\[5pt]
c&\approx&9,8\,\text{m}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/2bc7d67b2fb588aeea4424133f48c6beef5433c5b2a0224589e0b70a4f3359bc?color=5a5a5a)
Die längste Bahn, die Sonja im Pool schwimmen kann, ist
b)
3
Es gilt:
– die Länge der zweiten Kathete – berechnet werden:
![\(\begin{array}[t]{rll}
a^2+b^2&=& c^2 &\quad \scriptsize \mid\; -a^2 \\[5pt]
b^2&=& c^2-a^2 \\[5pt]
b^2&=& (3,2\,\text{m})^2-(2,5\,\text{m})^2 &\quad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
b&=&\sqrt{(3,2\,\text{m})^2-(2,5\,\text{m})^2} \\[5pt]
b&\approx& 2,0\,\text{m} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cf6841c7818826cc5a4bdd667822e27021d3485482fa982f0b12d2ec4ee0fbda?color=5a5a5a)
Die Tür ist 
breit.
- Die Diagonale ist die Hypotenuse:
- Die Höhe ist eine der beiden Katheten:
4
Bei dieser Aufgabe haben die zwei Katheten und die gleiche Länge.
Somit gilt:
Somit gilt:
