Funktionen, Terme und Gleichungen
Aufgabe 1
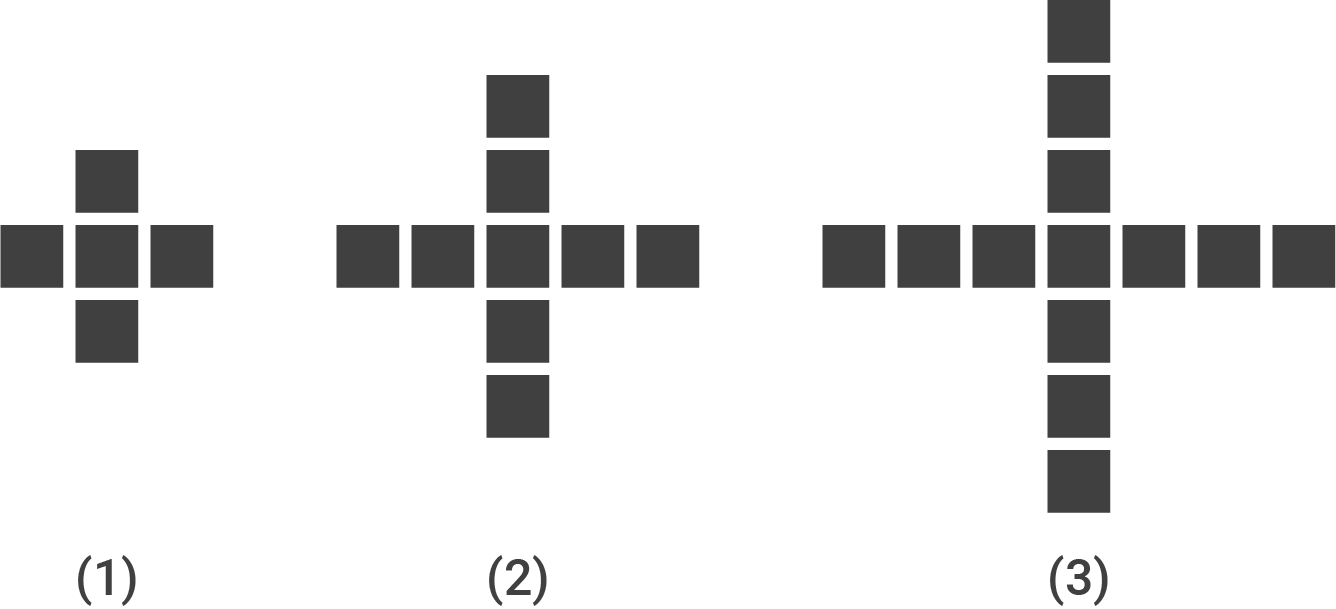
Eva hat drei Muster aus Holzstäbchen gelegt.
Dabei liegt keines der Holzstäbchen über einem anderen.
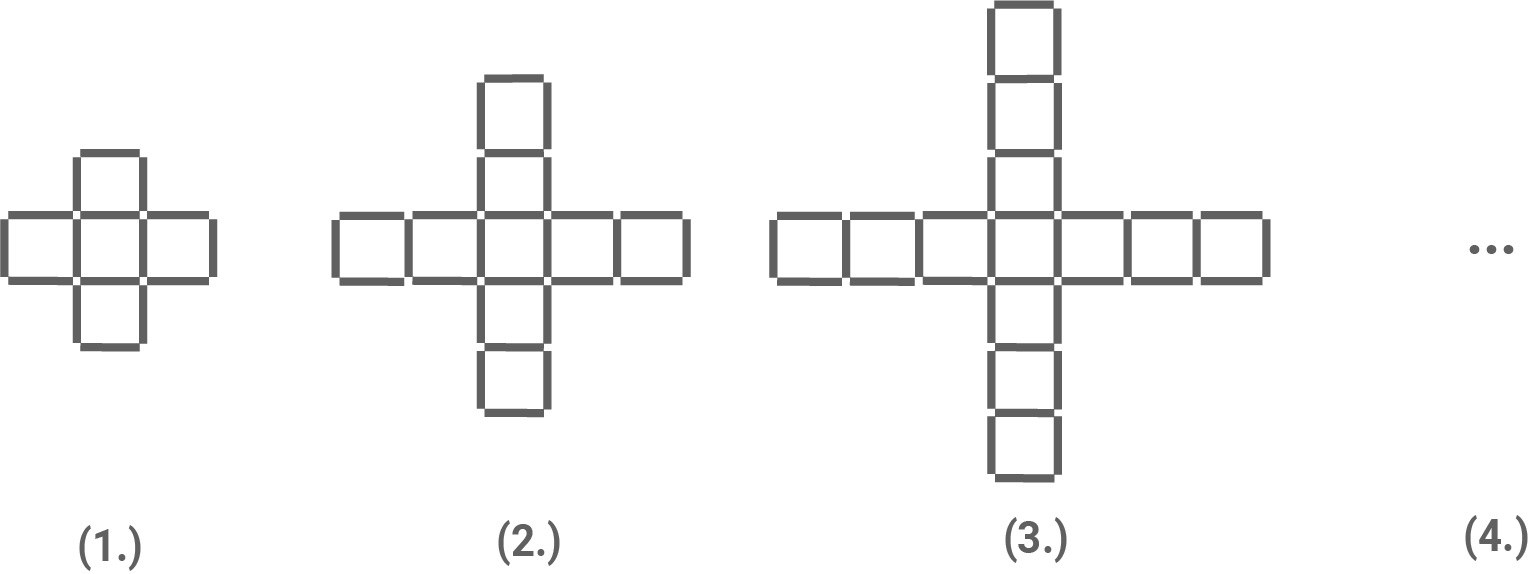
Eva möchte die Anzahl der Holzstäbchen bei jedem Muster berechnen.
Sie überlegt:
„Das erste Muster besteht aus vier Holzstäbchen in der Mitte und zwölf Holzstäbchen außen herum. Beim zweiten Muster kommen zwölf Holzstäbchen dazu."
Welche der beiden Formeln
oder
kann nicht für die Berechnung der Anzahl der
Holzstäbchen verwendet werden?
Begründe deine Entscheidung.
Aufgabe 2
Setze das richtige Zeichen ein.
Aufgabe 3
Löse die Gleichung.
Aufgabe 4
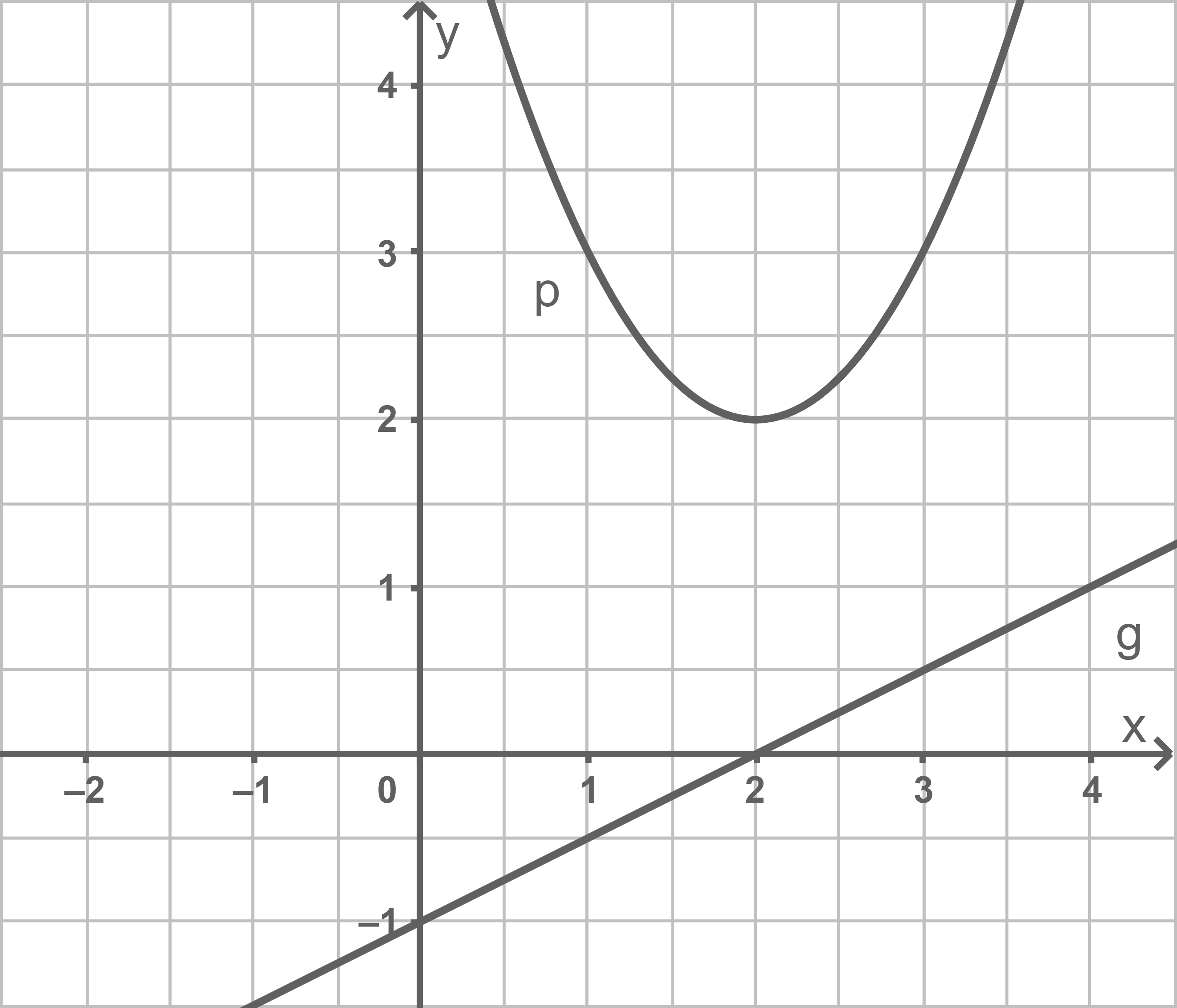
Benjamin hat die verschobene Normalparabel mit der Funktionsgleichung
und die Gerade
mit der Funktionsgleichung
falsch gezeichnet.
Welche Fehler hat Benjamin gemacht? Beschreibe die Fehler.
Aufgabe 5
Gib diesen ohne Zehnerpotenzschreibweise an.
Aufgabe 6
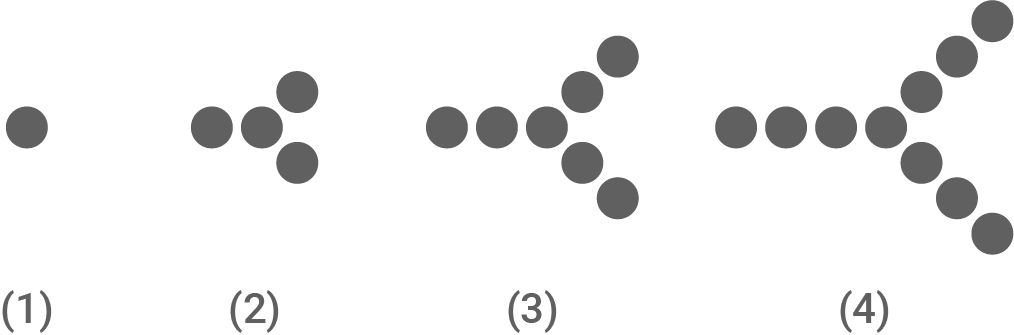
Luana hat die ersten drei Muster aus Kärtchen gelegt.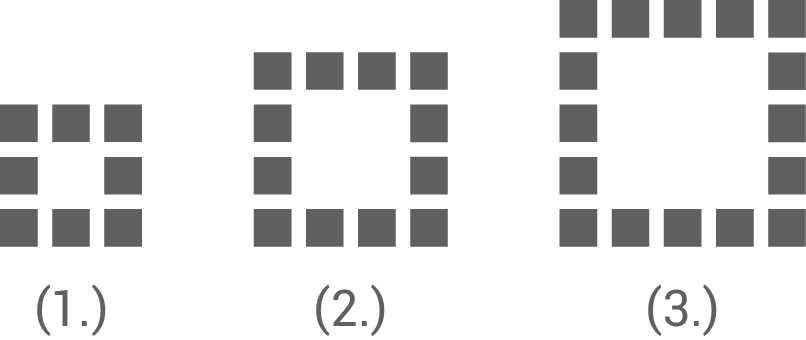
Begründe deine Antwort.
Sie hat vier Formeln zur Auswahl. Welche beiden Formeln sollte sie auswählen?
Kreuze jeweils richtig oder falsch an.
| richtig | falsch | |
Aufgabe 7
Welcher Sinuswert ist positiv, welcher negativ? Kreuze an.| positiv | negativ | |
Aufgabe 8
Begründe deine Entscheidung.
Aufgabe 9
Aufgabe 10
Kreuze jeweils richtig oder falsch an.
| richtig | falsch | |
Aufgabe 11
| 1 Million | |
| 10 Millionen | |
| 1 Milliarde |
Aufgabe 12
Die ersten drei Muster hat sie bereits gelegt.
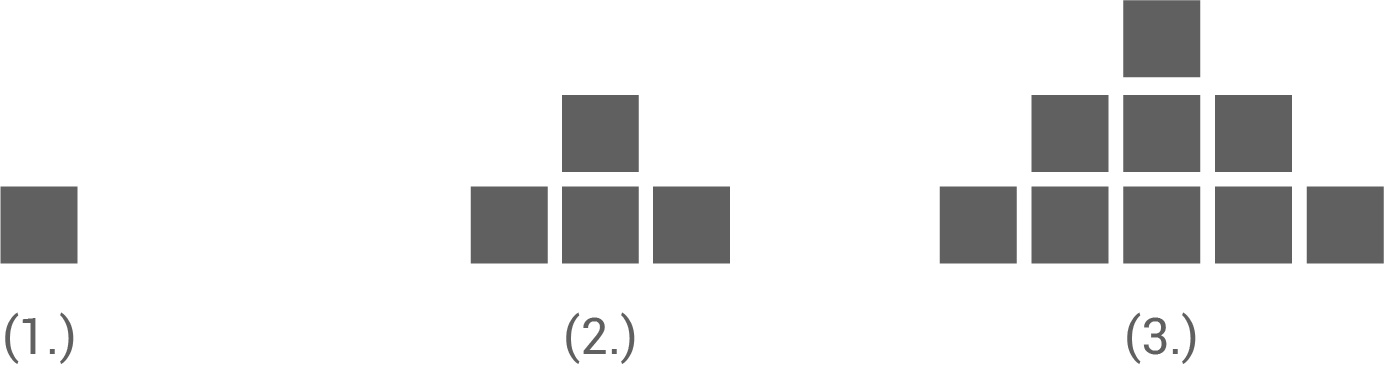
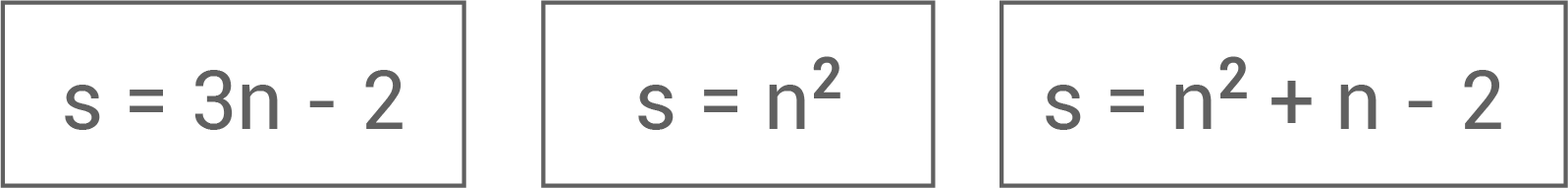
- n gibt die Stelle des jeweiligen Musters an.
- s ist die Summe der einzelnen Kärtchen.
Aufgabe 13
Aufgabe 14
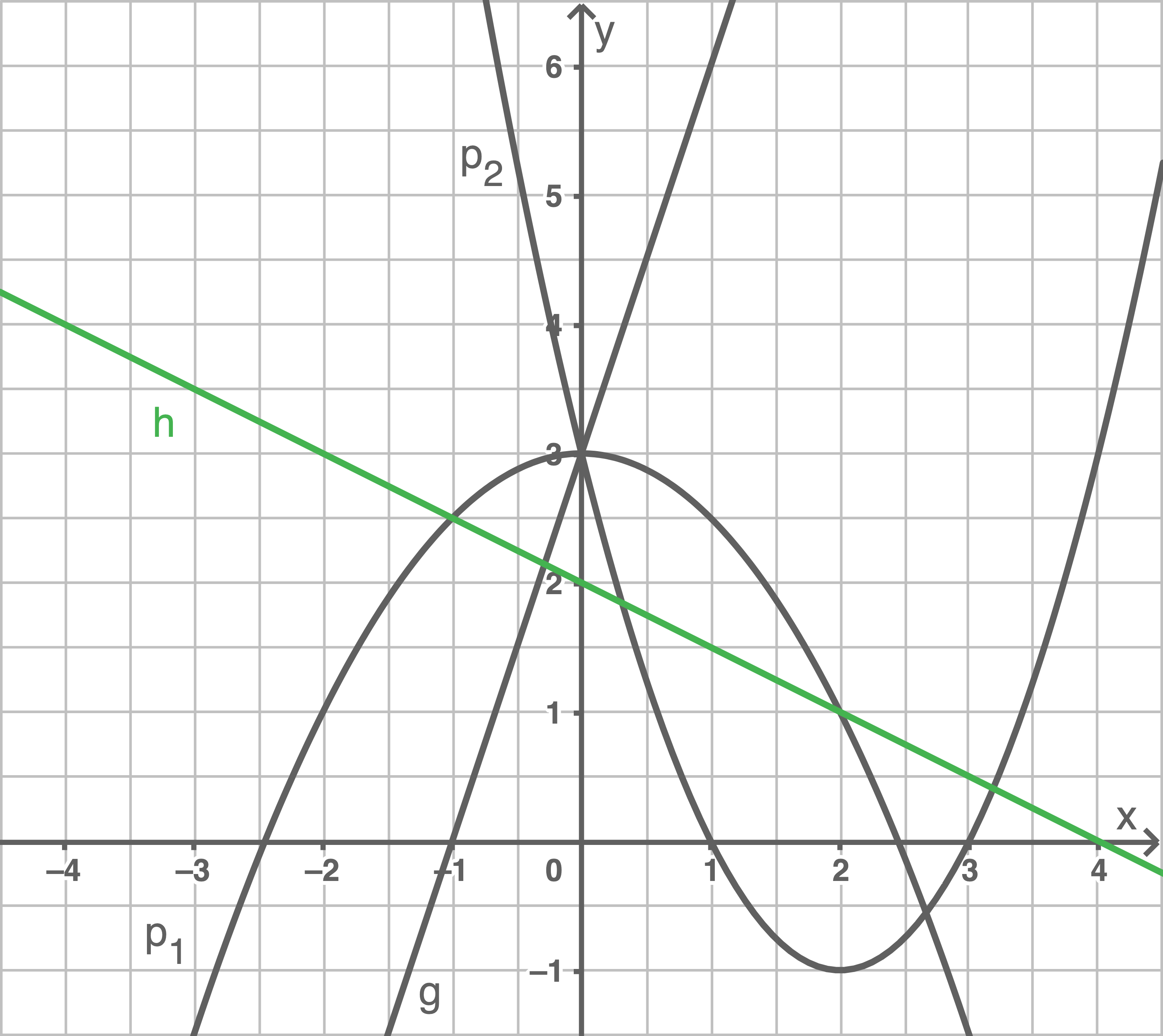
Welche Funktionsgleichung gehört zu welchem Graphen? (1)
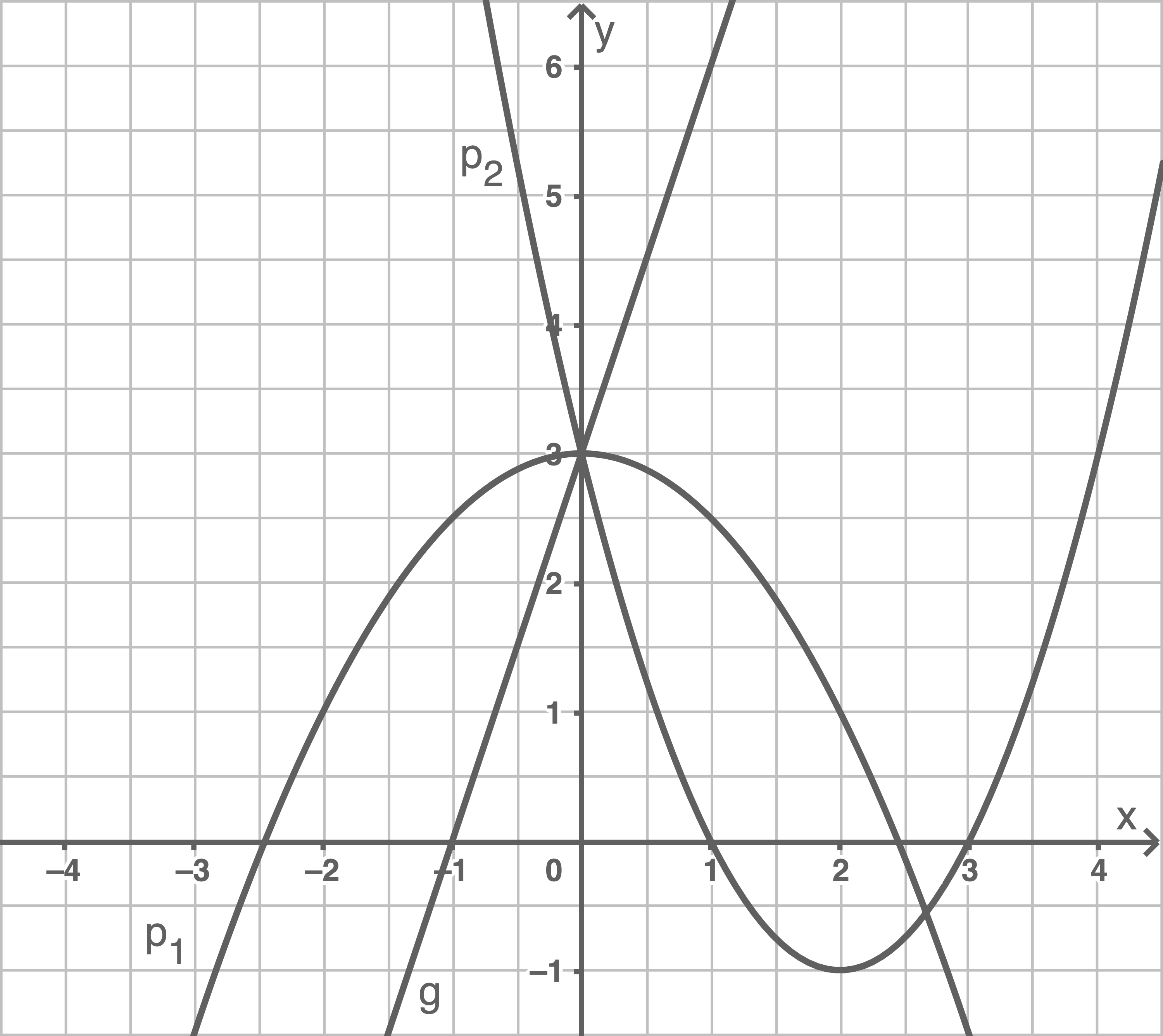
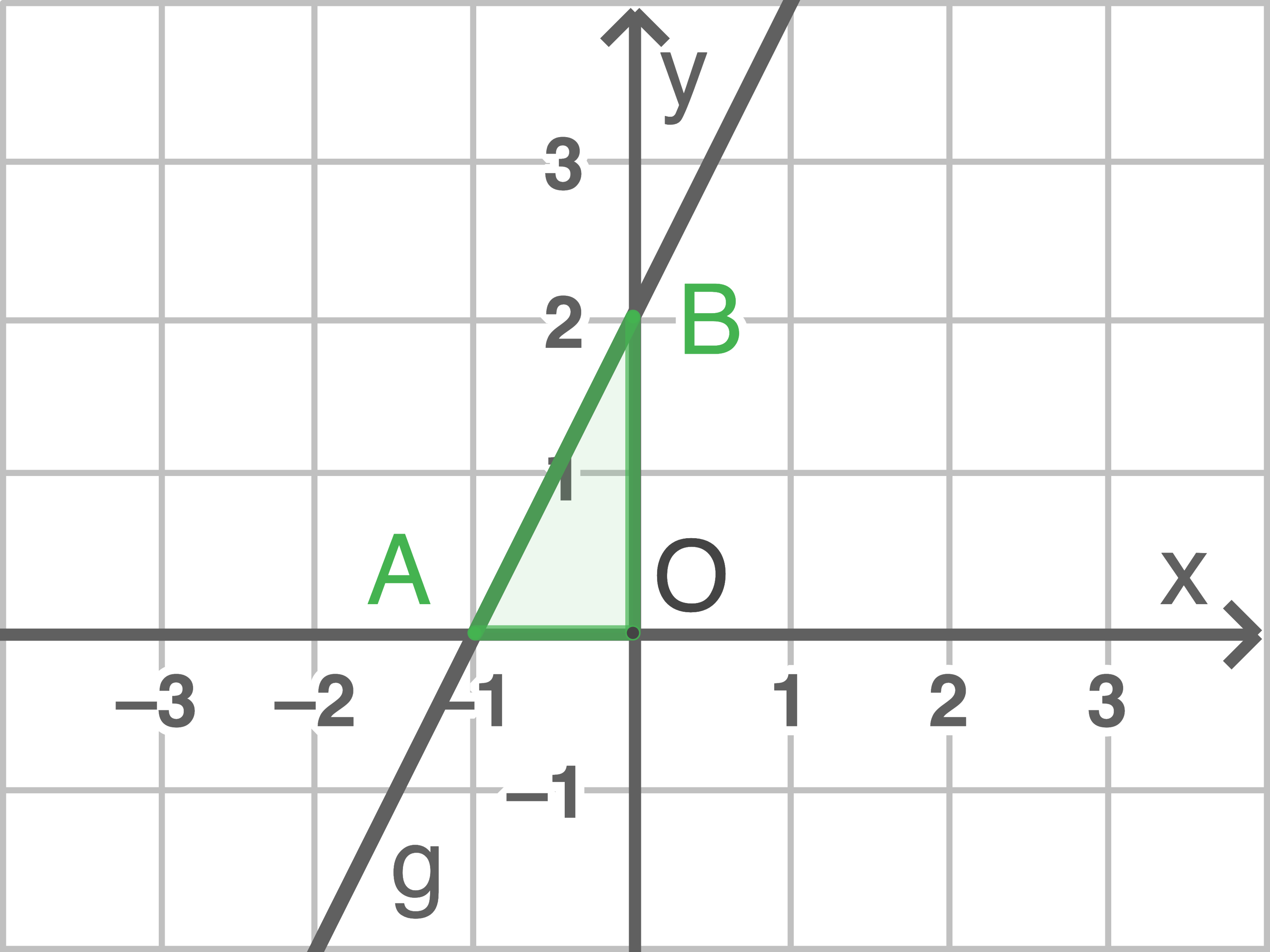
Zeichne die Gerade
Aufgabe 15
Aufgabe 16
Hat Ben recht? Begründe deine Aussage.
Aufgabe 17
Aufgabe 18
Aufgabe 19
Aufgabe 20
Berechne den Scheitelpunkt
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
Die Formel kann nicht verwendet werden.
Rechnerische Begründung (Für das 2. Muster):
Argumentative Begründung:
Bei dieser Formel kämen immer nur anstatt
Stäbchen hinzu.
Lösung 2
Lösung 3
Lösung 4
Abschlussprüfung 2025Lösung 5
Lösung 6
| richtig | falsch | |
Lösung 7
| positiv | negativ | |
Lösung 8
Mögliche Begründung: Die Parabel
Lösung 9
Lösung 10
| richtig | falsch | |
Zwei oder drei richtige Antworten: 0,5 P
Lösung 11
| 1 Million | |
| 10 Millionen | |
| 1 Milliarde |
Lösung 12
Lösung 13
Abschlussprüfung 2021Lösung 14
Denn
ist der
-Achsenabschnitt
ist die Steigung
- Die dazugehörige Funktionsgleichung hat die Form
Denn
- Nach unten geöffnet
- Die dazugehörige Funktionsgleichung ist eine quadratische Gleichung der Form
Denn
- Nach oben geöffnet
- Nach rechts verschoben
- Scheitelpunkt
- Die dazugehörige Funktionsgleichung ist eine quadratische Gleichung der Form
Lösung 15
Lösung 16
Der Term
Lösung 17
Lösung 18
Koordinaten des Punktes- Für die
-Koordinate gilt:
- Für die
-Koordinate gilt:
- Für die
-Koordinate gilt:
- Für die
-Koordinate gilt: