Lösung 1
Punkte in die Standardform einer verschobenen Normalparabel  einsetzen:
einsetzen:
Punkt  einsetzen:
einsetzen:
![\(\begin{array}[t]{rlll}
-5&=&(-2)^{2}-2b+c \\[5pt]
-5&=&4-2b+c &\mid\;-4+2b \\[5pt]
c&=&-9+2b \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a056de8422178b285d086b560c8e1e389459a09423d31a667a084c6b335e9447_light.svg)
Punkt  einsetzen:
einsetzen:
 einsetzen:
einsetzen:
![\(\begin{array}[t]{rlll}
c&=&-9+2\cdot 8 \\[5pt]
c&=&-9+16 \\[5pt]
c&=&7
\end{array}\)](https://www.schullv.de/resources/formulas/be3d6cbd4f86eeb3ae71c192765e7508a5cfa3068c75fb7d5637f992559f625e_light.svg)
 und
und  in die Standardform einsetzen:
in die Standardform einsetzen:


Parabelgleichung gleich null setzen und mit Hilfe der Mitternachtsformel die  -Koordinate des Nullpunktes berechnen:
-Koordinate des Nullpunktes berechnen:
 einsetzen um die
einsetzen um die  -Koordinate zu erhalten:
-Koordinate zu erhalten:

So erhält man folgenden Punkt:

 und
und  in die Gleichung
in die Gleichung  einsetzen, um die Steigung
einsetzen, um die Steigung  zu erhalten:
zu erhalten:
![\(\begin{array}[t]{rlll}
m&=&\dfrac{0-(-9)}{(-7)-(-4)} \\[5pt]
&=& \dfrac{9}{-3}\\[5pt]
&=& -3
\end{array}\)](https://www.schullv.de/resources/formulas/dd35b0b079b98aef5cc9437c46db10df974ceec3f5566ad6e0fc93e051f8b33f_light.svg)
 und
und  in die Geradengleichung
in die Geradengleichung  einsetzen und nach
einsetzen und nach  auflösen:
auflösen:
![\(\begin{array}[t]{rlll}
y&=&mx+b \\[5pt]
-9&=&(-3)\cdot (-4)+b \\[5pt]
-9&=&12+b \\[5pt]
b&=&-21
\end{array}\)](https://www.schullv.de/resources/formulas/7c8f44ac45c436ff3d0e4ae7da61bf4240418126483989b022a59f8ef74da27b_light.svg)
So ergibt sich folgende Gleichung für die Gerade  :
:

Abschlussprüfung 2025
Lösung 2
Graphen zu Funktionsgleichungen zuordnen

Der Graph der Funktion ist nach unten geöffnet.

Der Graph der Funktion ist um drei Einheiten nach rechts und um vier nach unten verschoben. Für

lässt sich der Scheitelpunkt direkt aus der Scheitelpunktform ablesen.

![\(\begin{array}[t]{rll}
y&=& x^2+4x+5 \\[5pt]
&=& x^2+4x+4-4+5 \\[5pt]
&=& (x+2)^2+1
\end{array}\)](https://www.schullv.de/resources/formulas/1edb9e00462d5662446f9f1d84a8e9ba489404c66c414986a7bee39400e44957_light.svg)
Es lässt sich der zur Parabel

passende Scheitelpunkt

ablesen.
Wert  bestimmen
bestimmen
Die Parabel ist um vier Einheiten nach unten verschoben. Daher gilt
 Funktionsgleichung der Geraden bestimmen
Funktionsgleichung der Geraden bestimmen

Steigung

berechnen:

Aus den Koordinaten des Punktes

lässt sich direkt der

-Achsenabschnitt

ablesen.
Damit ergibt sich insgesamt:
 Abschlussprüfung 2024
Abschlussprüfung 2024
Lösung 3
Mit der pq-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-9}{2}\pm\sqrt{\left(\dfrac{-9}{2}\right)^2-18} \\[5pt]
&=& 4,5\pm 1,5
\end{array}\)](https://www.schullv.de/resources/formulas/6cd0e6abb1adb349a72fc3b927b34f1d5b8f22d7d282eb3cb191f15c985a4d78_light.svg)
 Abschlussprüfung 2024
Abschlussprüfung 2024
Lösung 4
Einsetzungsverfahren

Einsetzen von (2'') in (1):
![\(\begin{array}[t]{rll}
3\cdot (6y+5-y)&=&y+8 \\[5pt]
15y+15&=&y+8 &\quad \scriptsize \mid\;-y-15\\[5pt]
14y&=&-7&\quad \scriptsize \mid\;:14\\[5pt]
y&=&\underline{\underline{-\dfrac{1}{2}}}
\end{array}\)](https://www.schullv.de/resources/formulas/6db39aaf671d1f64813f7d76eb8f3d4fe9e8e58e9ae9dee40c2e4d3323e60f2c_light.svg)
Einsetzen von \(y=-\dfrac{1}{2}\) in (2''):


Lösung 5
Funktionsgleichung bestimmen
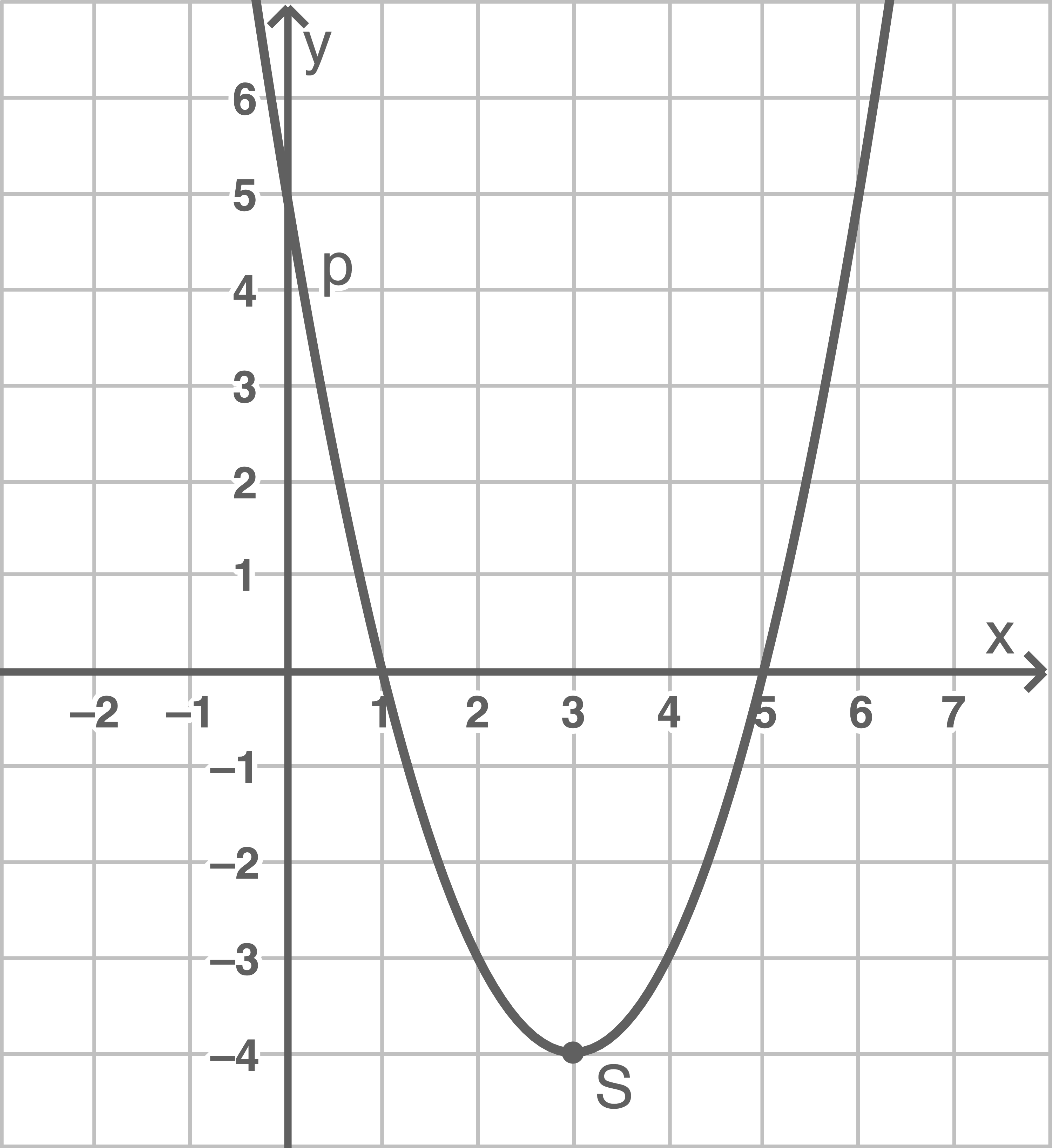
Aus der Zeichnung lassen sich die Schnittpunkte von

mit der

-Achse ablesen:


Daraus folgt für den Scheitelpunkt:
Die

-Koordinate des Scheitelpunkts liegt bei

Die

-Koordinate des Scheitelpunkts liegt bei

 Koordinaten berechnen
Koordinaten berechnen
Geradengleichung aufstellen:


in


also


Gleichsetzen:
![\(\begin{array}[t]{rll}
(x-4)^2-9&=&-2x+2\\[5pt]
x^2-8x+16-9&=&-2x+2 \quad \scriptsize \mid\;+2x-2 \\[5pt]
x^2-6x+5&=&0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8464f91488f3e7040fa8f4d947ed6ba071b15a74be238b875d61ac220dbf5959_light.svg)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-6}{2} \pm \sqrt{\left(\dfrac{-6}{2}\right)^2-5} \\[5pt]
x_{1,2}&=& 3 \pm 2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fe66a689c90fd583e2da09023e854cfe3959ec4ad5481e1e6e6f6fef2d2d1190_light.svg)



in



in




Abschlussprüfung 2023
Lösung 6
Abschlussprüfung 2022
Lösung 7
Funktionsgleichung von  bestimmen
Graphische Lösung mit der Symmetrieachse
bestimmen
Graphische Lösung mit der Symmetrieachse
- Durch Abzählen ergeben sich
 bis zur Symmetrieachse
bis zur Symmetrieachse
- Somit gilt:
 bis zum Scheitelpunkt
bis zum Scheitelpunkt
Für den Scheitelpunkt gilt also:

Daraus folgt:

in Scheitelpunktform
Rechnerische Lösung mit einem LGS
1. Schritt: Funktionsgleichung der Parabel aufstellen
Allgemeine Funktionsgleichung der Normalparabel:

2. Schritt: LGS mit

und

aufstellen

3. Schritt:

in (1) einsetzen
![\(\begin{array}[t]{rll}
0&=& 1+(-8)\cdot 1+c \\[5pt]
0&=&-7+c&\quad \mid\;+7 \\[5pt]
c&=&7 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/55929c2dccba37516afd01ae235251092808de6042ff35ac8f8a7094a742041a_light.svg)
Daraus folgt:

in Normalform
Fehlende  -Werte in der Wertetabelle ergänzen
1. Rechnung:
-Werte in der Wertetabelle ergänzen
1. Rechnung:  in
in  einsetzen
einsetzen
 2. Rechnung:
2. Rechnung:  in
in  einsetzen
einsetzen
 3. Rechnung:
3. Rechnung:  in
in  einsetzen
einsetzen
 4. Rechnung:
4. Rechnung:  in
in  einsetzen
einsetzen

 |
-3 |
-2 |
-1 |
0 |
 |
40 |
27 |
16 |
7 |
Koordinaten der Schnittpunkte berechnen
1. Schritt:

-Koordinaten berechnen
![\(\begin{array}[t]{rll}
(x-4)^2-9&=&-2x+2 \\[5pt]
x^2-8x+16-9&=&-2x+2 \\[5pt]
x^2-6x+5&=&0&
\end{array}\)](https://www.schullv.de/resources/formulas/b7fead04284396b82f7b455961674062c75a19db886008d0bf5e8b9211f7dc52_light.svg)
![\(\begin{array}[t]{rll}
x_{1,2}&=&-\dfrac{-6}{2}\pm\sqrt{\left(\dfrac{-6}{2}\right)^2-5}& \\[5pt]
x_{1,2}&=&3\pm\sqrt{4}& \\[5pt]
x_1&=&3+2=5& \\[5pt]
x_2&=&3-2=1& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/58298bbfab75bd6f0db3dc64f177d794c2da852387b2d101c30fe02a2d81fb66_light.svg)
2. Schritt:

-Koordinaten berechnen
![\(\begin{array}[t]{rll}
y_1&=&-2\cdot 5+2 \\[5pt]
y_1&=&-8
\end{array}\)](https://www.schullv.de/resources/formulas/4414be929b2c637db70874efa818600211ca92e77e005bd49487f295228536c3_light.svg)

![\(\begin{array}[t]{rll}
y_2&=&-2\cdot 1+2 \\[5pt]
y_2&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/0a714d76f41c6c8c187349a68004cd95e07c1928725e0f485bc74c953462e487_light.svg)

Abschlussprüfung 2022
Lösung 8
Koordinaten des zweiten Schnittpunkts  der Parabel
der Parabel  mit der Geraden
mit der Geraden  berechnen.
1. Schritt: Scheitelpunkt mit der quadratischen Ergänzung bestimmen
berechnen.
1. Schritt: Scheitelpunkt mit der quadratischen Ergänzung bestimmen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10 \\[5pt]
&=& x^2-2\cdot 3x+10 \\[5pt]
&=& x^2-2\cdot 3x+3^2-3^2+10 \\[5pt]
&=& (x-3)^2-9+10\\[5pt]
&=& (x-3)^2+1
\end{array}\)](https://www.schullv.de/resources/formulas/bc481073c09d34d48f4d5b6b2564d652cdcf27083e2b13fe112869c5f7dd5233_light.svg)
Der Scheitelpunkt lässt sich ablesen mit
 2. Schritt: Geradengleichung von
2. Schritt: Geradengleichung von  aufstellen
aufstellen


in

einsetzen:
![\(\begin{array}[t]{rll}
1&=& -2\cdot 3+c &\quad \scriptsize \\[5pt]
1&=& -6+c \quad \scriptsize \mid\; +6\\[5pt]
7&=& c \\
c&=& 7
\end{array}\)](https://www.schullv.de/resources/formulas/fbb72b2b008e034cc7ba43eda075ea192c1abb28cc98b8f6bf810632e81b6c7d_light.svg)
Daraus folgt:
 3. Schritt: Schnittpunkte berechnen
3. Schritt: Schnittpunkte berechnen
![\(\begin{array}[t]{rll}
-2x+7&=&x^2-6x+10 \quad \scriptsize \mid\;+2x-7 \\[5pt]
0&=&x^2-4x+3 \\[5pt]
x_{1/2}&=&-\dfrac{(-4)}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-3} \\[5pt]
x_{1/2}&=& 2 \pm \sqrt{(-2)^2-3} \\[5pt]
x_{1/2}&=& 2 \pm \sqrt{4-3} \\[5pt]
x_{1/2}&=& 2\pm 1 \\[5pt]
x_1&=& 2+1=3 \\[5pt]
x_2&=& 2-1=1
\end{array}\)](https://www.schullv.de/resources/formulas/c0bee6473dcc4e79ae5343b9be13eb01480130e7115063d6d56ff7f60c339dd5_light.svg)

in

ergibt:
![\(\begin{array}[t]{rll}
y&=& -2\cdot 1+7 &\quad \scriptsize \\[5pt]
&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/75f9ebc762c9f5c5190b0a692a72facf796a18d747bb850ce70770b80e25c964_light.svg)
Somit folgt für den zweiten Schnittpunkt:
 Funktionsgleichung der Geraden
Funktionsgleichung der Geraden  berechnen
1. Schritt: Steigung
berechnen
1. Schritt: Steigung  der Geraden
der Geraden  bestimmen
bestimmen
 2. Schritt: Geradengleichung aufstellen
2. Schritt: Geradengleichung aufstellen


in

einsetzen:
![\(\begin{array}[t]{rll}
5&=& \dfrac{1}{2}\cdot 1+c \quad \scriptsize \\[5pt]
5&=& 0,5+c \quad \scriptsize \mid\; -0,5\\[5pt]
4,5&=& c\\
c&=& 4,5
\end{array}\)](https://www.schullv.de/resources/formulas/58df357247fdc17b7fd23f0f03345114a288a0a8b062c3116f85c782daa704d2_light.svg)
Somit lautet die Funktionsgleichung

Abschlussprüfung 2021
Lösung 9
Scheitelpunkt mit der quadratischen Ergänzung bestimmen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+5 &\quad \scriptsize \\[5pt]
y&=& x^2-2\cdot 3x+3^2-3^2+5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2-4
\end{array}\)](https://www.schullv.de/resources/formulas/3ce45064696ab14c622311d8fe8a83bb464f4d95e4b3494894286b6045d5391f_light.svg)
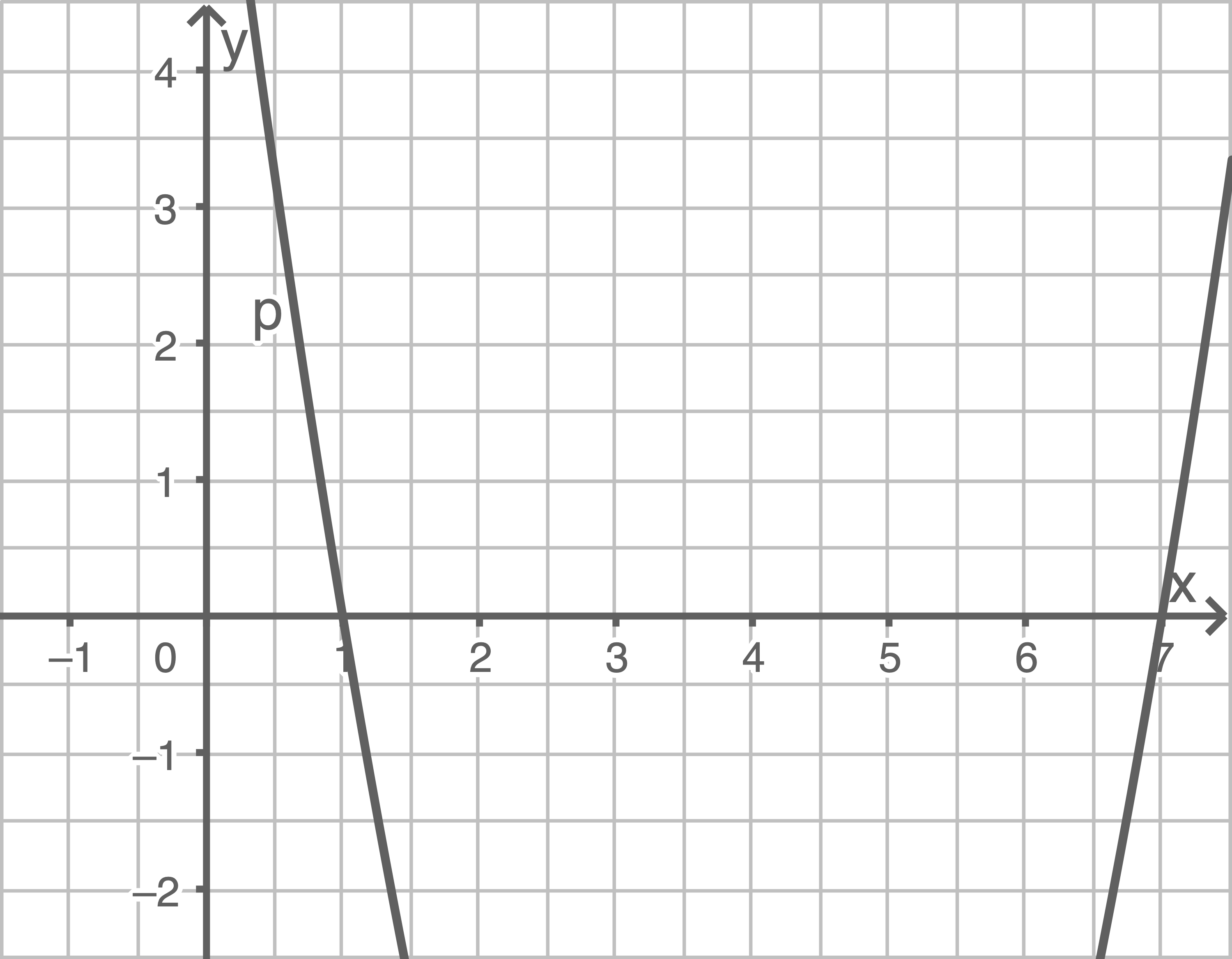
 Parabel zeichnen
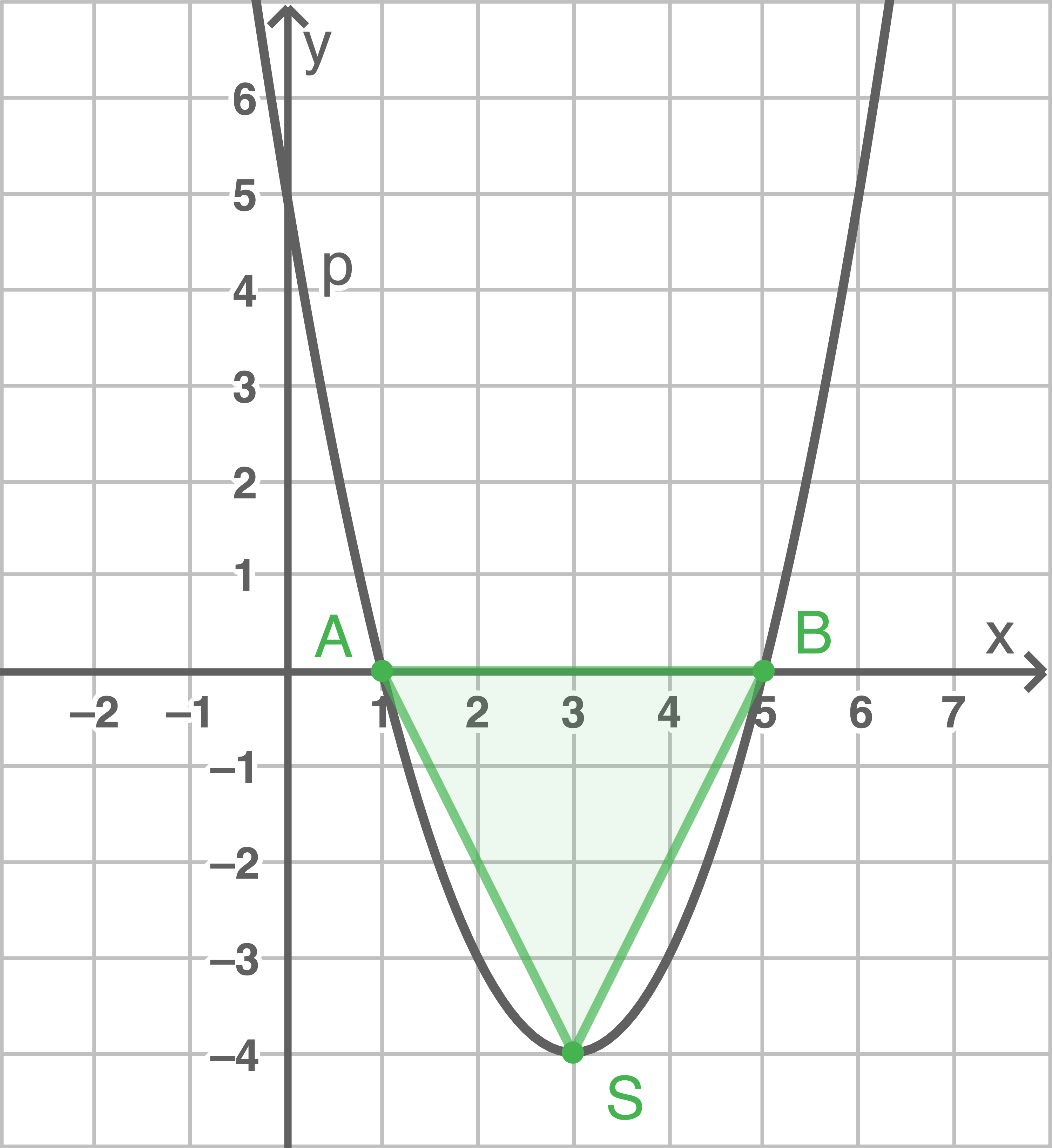
Umfang des Dreiecks berechnen
Schnittpunkte von
Parabel zeichnen
Umfang des Dreiecks berechnen
Schnittpunkte von  mit der
mit der  -Achse berechnen
-Achse berechnen

![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{-6}{2}\pm\sqrt{\left(\dfrac{-6}{2}\right)^2-5} \\[5pt]
x_{1,2}&=& 3\pm 2 \\[5pt]
x_1&=& 1 \Rightarrow A(1\mid 0)\\[5pt]
x_2&=& 5 \Rightarrow B(5\mid 0)
\end{array}\)](https://www.schullv.de/resources/formulas/2e0f68df15e5f7bc2d39d3817382ffb181a162335598180008d7756d41886cfb_light.svg) Länge der Strecke
Länge der Strecke  mit dem Satz des Pythagoras berechnen
mit dem Satz des Pythagoras berechnen
![\(\begin{array}[t]{rll}
\overline{AS}^2&=& (2\,\text{LE})^2+(4\,\text{LE})^2 &\quad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
\overline{AS}&=& \sqrt{(4\,\text{LE})^2+(2\,\text{LE})^2}&\quad \scriptsize \\[5pt]
\overline{AS}&=& 4,47\,\text{LE}
\end{array}\)](https://www.schullv.de/resources/formulas/0b8a1626e92dc00ad74aebd79eee624b72e3892bdb0c7a6d8afb35011d801089_light.svg) Umfang des Dreiecks berechnen
Umfang des Dreiecks berechnen
![\(\begin{array}[t]{rll}
u&=& 4\,\text{cm}+2\cdot 4,47\,\text{cm} &\quad \scriptsize \\[5pt]
u&=& \underline{\underline{ 12,94\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/14d27c8e5ab2cbbf098c4236054ef02d9570c8d14b811ba9d1747bf61c849a1f_light.svg) Musterprüfung 1
Musterprüfung 1
Lösung 10
1. Schritt: Scheitelpunkt über die Scheitelpunktform ermitteln
![\(\begin{array}[t]{rll}
y&=&x^2-8x+4& \\[5pt]
y&=&x^2-8\cdot x+4\quad \scriptsize \mid\ \,\text{quadr. Ergänzung} \\[5pt]
y&=&x^2-8\cdot x+16-16+4 \\[5pt]
y&=&(x-4)^2-16+4 \\[5pt]
y&=&(x-4)^2-12 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c2e03eeef03db76b9b11b23fa80f47d699674c2e3de50c2f4016d021b76d1277_light.svg)
 2. Schritt: Fehlende
2. Schritt: Fehlende  -Koordinate von Punkt
-Koordinate von Punkt  berechnen
berechnen

in

einsetzen:
![\(\begin{array}[t]{rll}
y&=&2^2-8\cdot 2+4 \\[5pt]
y&=&4-16+4 \\[5pt]
y&=&-8 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7aaa085d0d7d7e09093ce2334272daa1729dddb0748394a517fbb1cd9bee905d_light.svg)
 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen

und

![\(\begin{array}[t]{rll}
{\overline{AS}}&=&\sqrt{(x-x_p)^2+(y-y_p)^2} & \\[5pt]
&=&\sqrt{(4-2)^2+(-12-(-8))^2} \\[5pt]
&=&\sqrt{2^2+(-4)^2} \\[5pt]
&=&\sqrt{4+16} \\[5pt]
&=&\sqrt{20} \\[5pt]
{\overline{AS}}&=&\underline{\underline{ 4,5}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1300e365929df1c9f460284e4efc38349e2badb0c6789605561db39f8d2530bb_light.svg)
Der Abstand beträgt

Musterprüfung 2
Lösung 11

![\(\begin{array}[t]{rll}
(2x+1)^2-3(x+4)&=&(x-1) (2x+1)+2 \quad \scriptsize \,\text{ausmultiplizieren} \\[5pt]
4x^2+2\cdot 2x+1^2-3x-12&=& 2x^2+x-2x-1+2 \\[5pt]
4x^2+4x+1-3x-12&=& 2x^2-x+1\\[5pt]
4x^2+x-11&=&2x^2-x+1\quad \scriptsize \mid\;-2x^2+x-1 \\[5pt]
2x^2+2x-12&=&0 \quad \scriptsize \mid\;:2 \\[5pt]
x^2+x-6&=&0 \quad \scriptsize \mid\; p,q-\,\text{Formel}\\[5pt]
x_{1/2}&=&-\frac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2+6} \\[5pt]
x_{1/2}&=&-\frac{1}{2}\pm\sqrt{\frac{25}{4}} \\[5pt]
x_1&=&-\frac{1}{2}-\frac{5}{2}=-\frac{6}{2} =-3\\[5pt]
x_2&=&-\frac{1}{2}+\frac{5}{2}=\frac{4}{2} =2
\end{array}\)](https://www.schullv.de/resources/formulas/61c33b4e3e20d7781b811e982aa413f1e75b3913fbd4dd78df6afe0c11ae9178_light.svg)
\underline{\underline{

}}
Abschlussprüfung 2020
Lösung 12
Graphen zuordnen
(1)


kein passender Graph
Die Funktionsgleichung beschreibt eine Gerade mit positiver Steigung

und dem

-Achsenabschnitt

Da es keine steigende Gerade gibt, kann die Funktionsgleichung keinem Graphen zugeordnet werden. Der Graph muss neu eingezeichnet werden.
(2)


kein passender Graph
Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2+4x+3 \\[5pt]
y&=&x^2+2\cdot 2x+3 \\[5pt]
y &=&x^2+2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x+2)^2-1
\end{array}\)](https://www.schullv.de/resources/formulas/44fea7027af27698b625d482825718af3584b26ff40a8a2ad930c4426addf2c6_light.svg)
Der zugehörige Graph besitzt den Scheitelpunkt

Da es keinen Graphen mit diesem Scheitelpunkt gibt, muss der Graph dieser Funktion neu eingezeichnet werden.
(3)



Die Funktionsgleichung beschreibt eine Parabel, die durch ihren

-Achsenabschnitt um

Einheiten nach oben verschoben ist, mit dem Faktor

gestaucht wurde und den Scheitelpunkt

besitzt.
Diese Eigenschaften treffen auf den Graphen

zu.
(4)



Umformung mit quadratischer Ergänzung:
![\(\begin{array}[t]{rll}
y&=&x^2-4x+3 \\[5pt]
y &=&x^2-2\cdot 2x+3 \\[5pt]
y &=&x^2-2\cdot 2x+2^2-2^2+3 \\[5pt]
y &=&(x-2)^2-1
\end{array}\)](https://www.schullv.de/resources/formulas/3474b22a98df445d59f0f5671f2e98bbd618a919d4acb9ac9956a06b2e871548_light.svg)
Der Graph besitzt den Scheitelpunkt

.
Deshalb kann die Funktionsgleichung dem Graphen

zugeordnet werden.
(5)



Die Funktionsgleichung beschreibt eine Gerade mit negativer Steigung

und mit dem

-Achsenabschnitt

.
Dies trifft auf den Graphen

zu.
Fehlende Graphen einzeichnen
Abschlussprüfung 2020
Lösung 13
1. Schritt:  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\dfrac{x+2}{4}-y&=& 6 &\quad \scriptsize \mid\;\cdot\,4 \\[5pt]
x+2-4y&=& 24 &\quad \scriptsize \mid\; -2 \mid\; +4y \\[5pt]
x&=& 22 + 4y
\end{array}\)](https://www.schullv.de/resources/formulas/edb1f9155e0da20a00a0666e8cd83493f5d1f771aee750be8c49e44fad4ffe81_light.svg) 2. Schritt:
2. Schritt:  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
7-(x-2y)&=& y \\[5pt]
7-x+2y&=& y &\quad \scriptsize \mid\; -2y \\[5pt]
7-x&=& -y&\quad \scriptsize \mid\; \cdot\,(-1)\\[5pt]
y&=& -7+x
\end{array}\)](https://www.schullv.de/resources/formulas/494c132cb585c808b1bdc104a3761f308278557ad631c61b4c72caf693f0d04e_light.svg) 3. Schritt:
3. Schritt:  in
in  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=& -7+(22+4y) \\[5pt]
y&=& 15 + 4y &\quad \scriptsize \mid\;\, -4y \\[5pt]
-3y&=&15 &\quad \scriptsize \mid\; \,\cdot\,(-1)\\[5pt]
3y&=&-15 &\quad \scriptsize \mid\;:3 \\[5pt]
y&=& -5
\end{array}\)](https://www.schullv.de/resources/formulas/8f1b01665a58ad65d0215306d7c90e83263834de146367572a7327847595838f_light.svg) 4. Schritt:
4. Schritt:  in
in  einsetzen und
einsetzen und  berechnen
berechnen
![\(\begin{array}[t]{rll}
-5&=& -7+x&\quad \scriptsize \mid\;+7 \\[5pt]
x&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/e18ffe684fa496350d60aefdc172e7e38d45e13c7ccabfd8e1b0858b0e9451af_light.svg)
 Abschlussprüfung 2019
Abschlussprüfung 2019
Lösung 14
Wertetabelle, Graph und Funktionsgleichung zuordnen
In der Wertetabelle ist das Wertepaar

angegeben. Der Punkt

liegt auf dem Graphen

Also gehört die Wertetabelle zum Graphen

Punkt

in die drei Gleichungen einsetzen:
![\(\begin{array}[t]{rrl}
(A)& 0 &=& 1^2-6\cdot 1+5 \\[5pt]
& 0 &=& 1-6+5 \\[5pt]
&0&=& 0 \\[5pt]
(B)&0&=& 1^2-2\cdot 1+5 \\[5pt]
&0&=& 1-2+5 \\[5pt]
&0&\neq& 4 \\[5pt]
(C)& 0 &=& 1^2+4\cdot 1+5 \\[5pt]
& 0 &=& 1+4+5 \\[5pt]
&0&\neq& 10 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/96a3cd25a50c5ea12ea8389e1164519dcf6e25c7e06aa6771966157b7897c748_light.svg)
Die Funktionsgleichung

gehört somit zur Wertetabelle und zu
 Fehlenden Graph
Fehlenden Graph  einzeichnen
einzeichnen
Gehört Funktionsgleichung

oder Funktionsgleichung

zu

?

mit quadratischer Ergänzung überprüfen:
![\(\begin{array}[t]{rll}
y&=& x^2 -2x + 5 \\[5pt]
&=& x^2-2x+\left(\dfrac{2}{2}\right)^2-\left(\dfrac{2}{2}\right)^2+5 \\[5pt]
&=& x^2-2x+1^2-1^2+5 \\[5pt]
y&=& (x-1)^2+4\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/388037564b86d3de833a31388de7c8bfb8650ecc96b3385598d2fac721febeb3_light.svg)

mit Scheitelpunkt

passt also nicht zu

mit Scheitelpunkt

Also gilt:
Die Funktionsgleichung

gehört zum fehlenden Graphen

Infos zum Einzeichnen von Graph


- Verschobene Normalparabel
- Nach oben geöffnet
- Scheitelpunkt

Abschlussprüfung 2019
Lösung 15
Definitionsmenge bestimmen
Einschränkung: Der Nenner eines Bruchs darf nicht Null sein.
Für

und

wird mindestens einer der Nenner gleich Null.
Daraus folgt also
 Lösungsmenge bestimmen
Lösungsmenge bestimmen
Gemeinsamen Hauptnenner für alle Brüche bestimmen:
Es gilt

Ein möglicher Hauptnenner ist also

Multiplikation mit dem Hauptnenner:
Da

aus der Definitionsmenge ausgeschlossen ist, ist dieser Wert kein Teil der Lösungsmenge.
 Abschlussprüfung 2018
Abschlussprüfung 2018
Lösung 16
Funktionsgleichung  ermitteln
ermitteln
 -Koordinate des Scheitelpunkts bestimmen
-Koordinate des Scheitelpunkts bestimmen
Funktionsform für eine nach oben geöffnete Normalparabel:

Dabei sind

die Koordinaten des Scheitelpunkts.
Da eine Normalparabel achsensymmetrisch ist, kann man mit den Werten

und

die den gleichen Funktionswert besitzen, die

-Koordinate des Scheitelpunktes berechnen. Dieser muss genau in der Mitte der beiden Werte liegen.
Es ist also


 -Koordinate des Scheitelpunkts berechnen
-Koordinate des Scheitelpunkts berechnen

einsetzen:
![\(\begin{array}[t]{rll}
y &=& (x-3)^2 + y_S \\[5pt]
5&=& (0-3)^2 + y_S \\[5pt]
5&=& 9+y_S \quad \scriptsize \mid\;-9 \\[5pt]
-4&=& y_S
\end{array}\)](https://www.schullv.de/resources/formulas/f966fa274279ba02e3e7f1778dcc1f92f6e5250193d7e4f9c2e6938e81ebae7f_light.svg)
Die Funktionsgleichung der Parabel

lautet also:
 Tabelle ergänzen
Tabelle ergänzen
Durch Einsetzen der gegebenen

-Werte in die Funktionsgleichung und durch Nutzung der Achsensymmetrie ergibt sich:
Steigung der Geraden berechnen
Die Parabel

hat an der Stelle

den Funktionswert

Sie schneidet die

-Achse also im Punkt

Die Koordinaten des Scheitelpunkts sind

![\(\begin{array}[t]{rll}
m &=& \dfrac{y_S -y_P}{x_S-x_P} \\[5pt]
&=& \dfrac{-4-5}{3-0} \\[5pt]
&=& \dfrac{-9}{3} \\[5pt]
m&=& -3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0d506161a9c686e4984f343526f69ae1f6dc5e74100bbb4214a87559df9bcbca_light.svg)
Die Steigung der Geraden

beträgt
 Abschlussprüfung 2018
Abschlussprüfung 2018
Lösung 17
1. Schritt: Scheitelpunktform der verschobenen Normalparabel  bestimmen
bestimmen
Scheitelpunktform:

Die

-Koordinate des gesuchten Scheitelpunkts lässt sich ablesen, da sie in der Mitte der Punkte

und

liegt.
Somit ist

Koordinaten des Punktes

in die vorläufige Scheitelpunktform einsetzen:
![\(\begin{array}[t]{rll}
0&=&(-3+1)^2+b \\[5pt]
0&=&4+b &\quad \scriptsize \mid\; -4\\[5pt]
b&=&-4 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/064666640f6dcee7d477bc8051e7137f8a3f892841907c804f978cdf5ef2de04_light.svg)
Damit folgt:
- Scheitelpunktform:

- Koordinaten des Scheitelpunkts:

2. Schritt: Geradengleichung  aufstellen
aufstellen
Scheitelpunkt in die Geradengleichung

einsetzen:
![\(\begin{array}[t]{rll}
-4&=& 3\cdot (-1)+b \\[5pt]
-4&=& -3+b &\quad \scriptsize \mid\; +3 \\[5pt]
b&=&-1
\end{array}\)](https://www.schullv.de/resources/formulas/c7b4d4c485211969761d96866459fdc1d53ed5a31fe705e6afc006a5792a8fa0_light.svg)

3. Schritt: Koordinaten des Schnittpunktes berechnen
Die

-Koordinate

gehört zum Scheitelpunkt

Somit ist

die

-Koordinate des zweiten Schnittpunkts


in die Geradengleichung

einsetzen:
![\(\begin{array}[t]{rll}
y&=&3\cdot2-1 \\[5pt]
y&=&5
\end{array}\)](https://www.schullv.de/resources/formulas/2553303b0694e48ea557cd38765cc48a8a7330b3d0228867fef41a9584fdb3ba_light.svg)
Die Koordinaten des zweiten Schnittpunkts sind

.
Abschlussprüfung 2017
Lösung 18
 Abschlussprüfung 2017
Abschlussprüfung 2017
Lösung 19
1. Hauptnenner bestimmen
 2. Schritt: Definitionsmenge angeben
2. Schritt: Definitionsmenge angeben

 3. Schritt: Lösungsmenge angeben
3. Schritt: Lösungsmenge angeben
Weiter mit der

-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\left(\dfrac{3}{2}\right)^2-(-18)} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{9}{4}+18} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm\sqrt{\dfrac{81}{4}} \\[5pt]
x_{1/2}&=&-\dfrac{3}{2}\pm \dfrac{9}{2} \\[5pt]
x_1&=&-\dfrac{3}{2}+ \dfrac{9}{2}= \dfrac{6}{2}=3\\[5pt]
x_2&=&-\dfrac{3}{2}- \dfrac{9}{2}= -\dfrac{12}{2}=-6 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/973caaf0cf870f6fc2e6515e36e47d10d8c7c3b92a8df61b9ba61a2c02433121_light.svg)


zählt nicht in die Lösungsmenge, da dies in der Definitionsmenge ausgeschlossen wurde.
Abschlussprüfung 2016
Lösung 20
1. Schritt: Koordinaten des Scheitelpunkts der Parabel  berechnen
berechnen
![\(\begin{array}[t]{rll}
y&=& x^2-6x+10,5 \\[5pt]
y&=& x^2-2\cdot 3x+10,5 &\quad \scriptsize \\[5pt]
y&=& x^2-2\cdot 3x+3^2-3^2+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2-9+10,5 &\quad \scriptsize \\[5pt]
y&=& (x-3)^2+1,5
\end{array}\)](https://www.schullv.de/resources/formulas/5f72e07eaab66399d7fdfd800fe0836f0eb219715f6bdc1933676fedfe856688_light.svg)
Daraus folgt:
 2. Schritt: Geradengleichung von
2. Schritt: Geradengleichung von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
y&=&mx+c \quad \scriptsize \mid\;-mx \\[5pt]
c&=& y-mx \quad \scriptsize \mid\;S(3\mid 1,5), m=2 \\[5pt]
c&=&1,5-2\cdot 3& \\[5pt]
c&=&-4,5
\end{array}\)](https://www.schullv.de/resources/formulas/9e715a9eb4c9f3bd3f010883d8015d59f53713d88f2c7a07a0d1efea716ff3fc_light.svg)
Es gilt also
 3. Schritt: Koordinaten des Schnittpunkts
3. Schritt: Koordinaten des Schnittpunkts  berechnen
berechnen
![\(\begin{array}[t]{rll}
p&=&g \\[5pt]
x^2-6x+10,5&=& 2x-4,5 \quad \scriptsize \mid\;-\, 2x\, +4,5 \\[5pt]
x^2-8x+15&=& 0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c67eac57a41507ab8c65e25fba315f7e5872b0a7de1c3ec2c3e94501360db7a3_light.svg)
Weiter mit der

-Formel:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{(-8)}{2}\pm \sqrt{\left(\dfrac{-8}{2}\right)^2-15} \\[5pt]
x_{1/2} &=&4\pm \sqrt{16-15} \\[5pt]
x_{1/2} &=&4\pm 1 \\[5pt]
x_1&=&5 \\[5pt]
x_2&=&3
\end{array}\)](https://www.schullv.de/resources/formulas/ca229b9eb6fb745b34bf6553baebaba954a2f42e41c93d5ccddeb5e599eba5f5_light.svg)

ist die

-Koordinate des bekannten Schnittpunkts

Deswegen wird

in

eingesetzt:

in

einsetzen:
![\(\begin{array}[t]{rll}
y&=& 2\cdot 5 - 4,5 \\[5pt]
y&=& 10-4,5 \\[5pt]
y&=& 5,5 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2a80286a5ee0281db1e9554124fd82cf44efaa9dfea08550311f1f6d1434a2e3_light.svg)
Somit gilt:

Abschlussprüfung 2016
Lösung 21
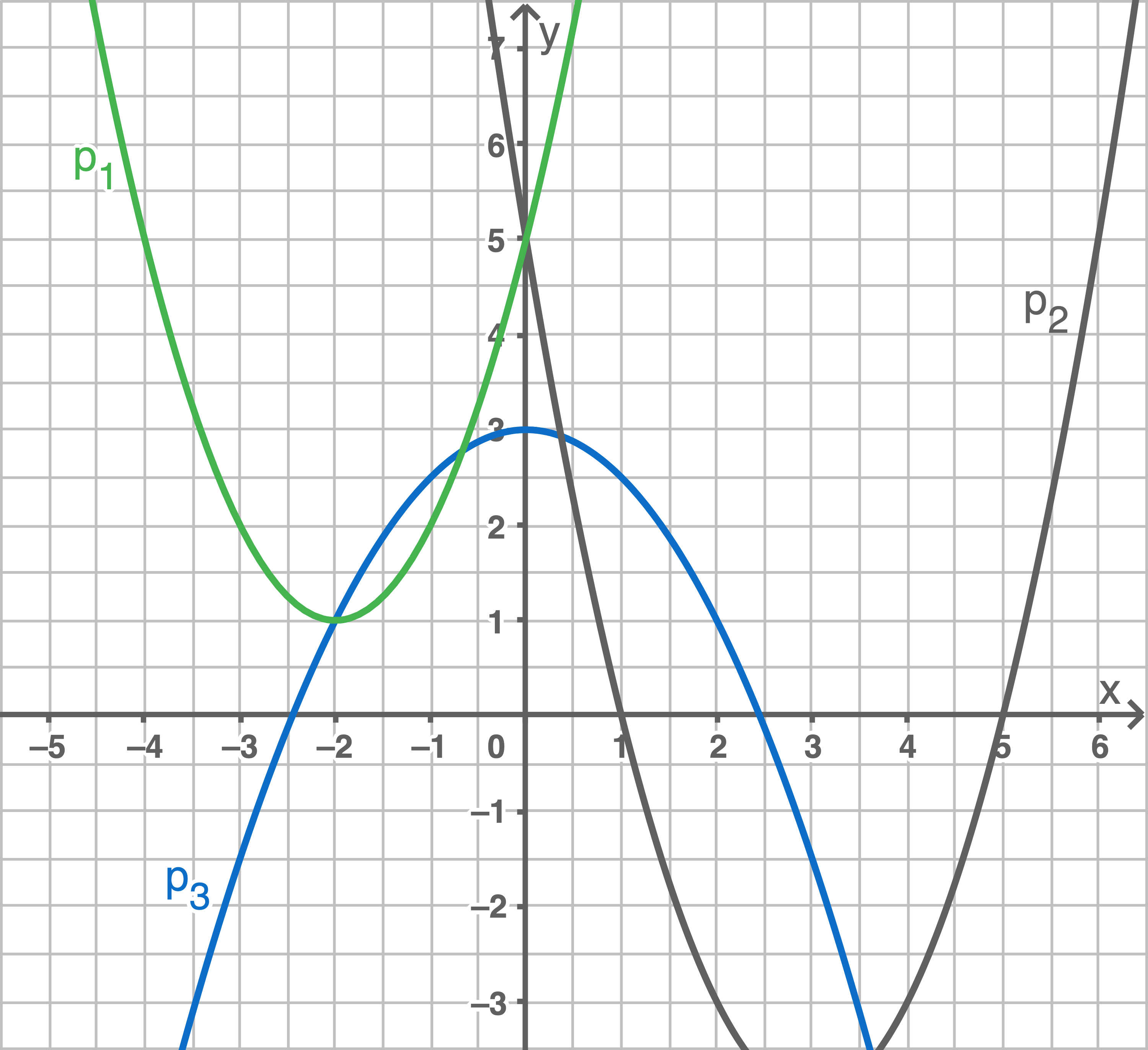
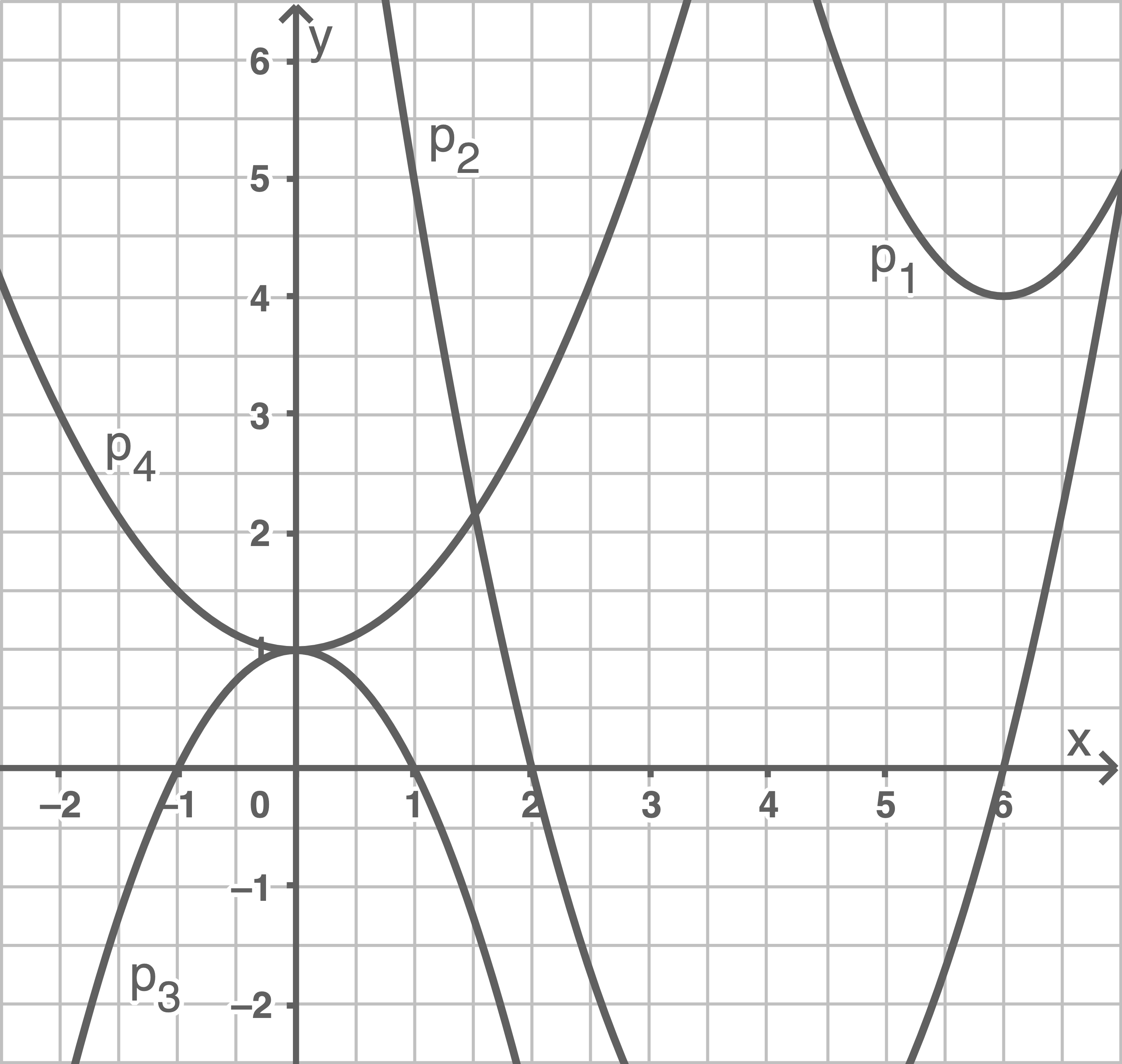
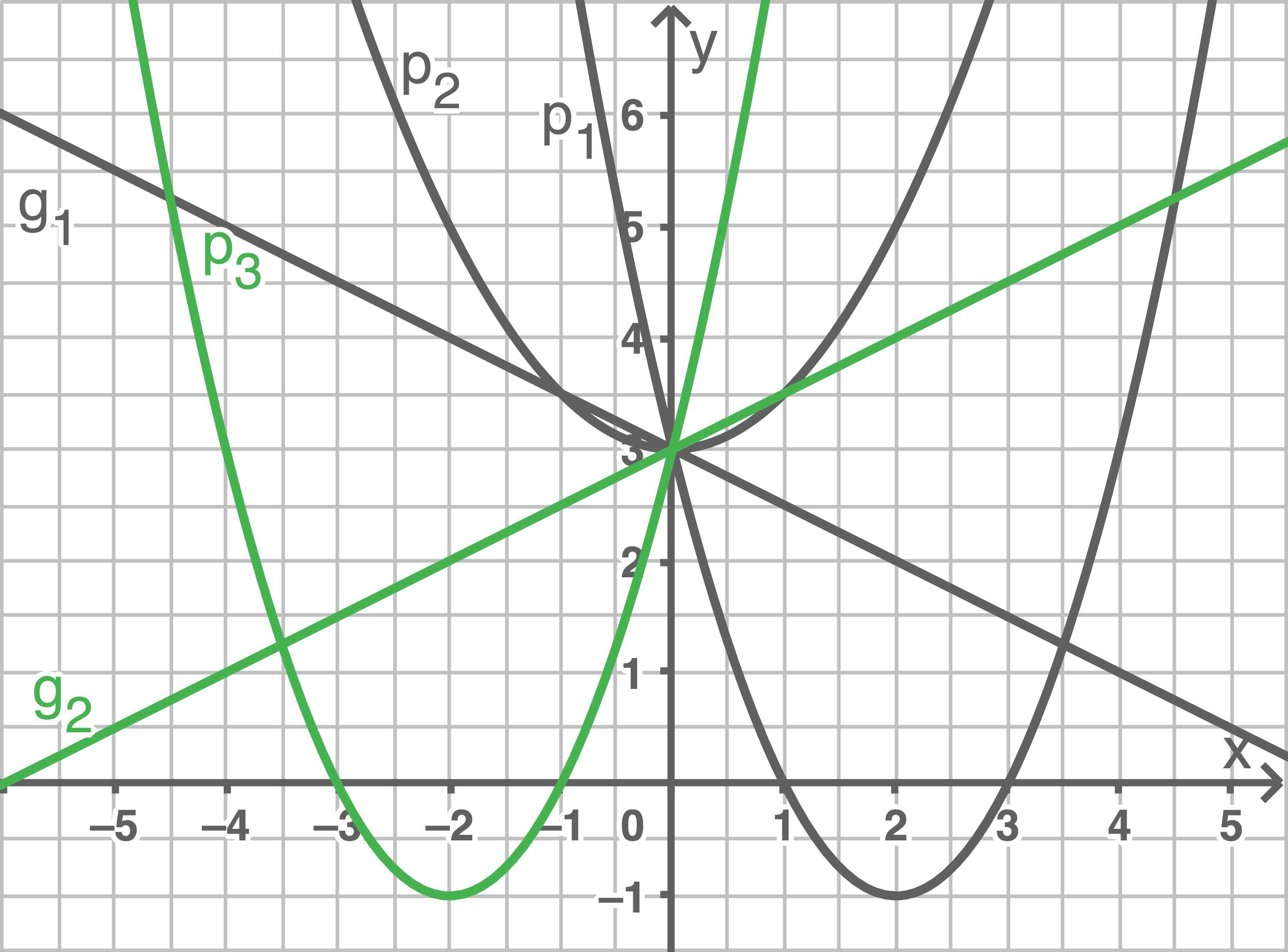
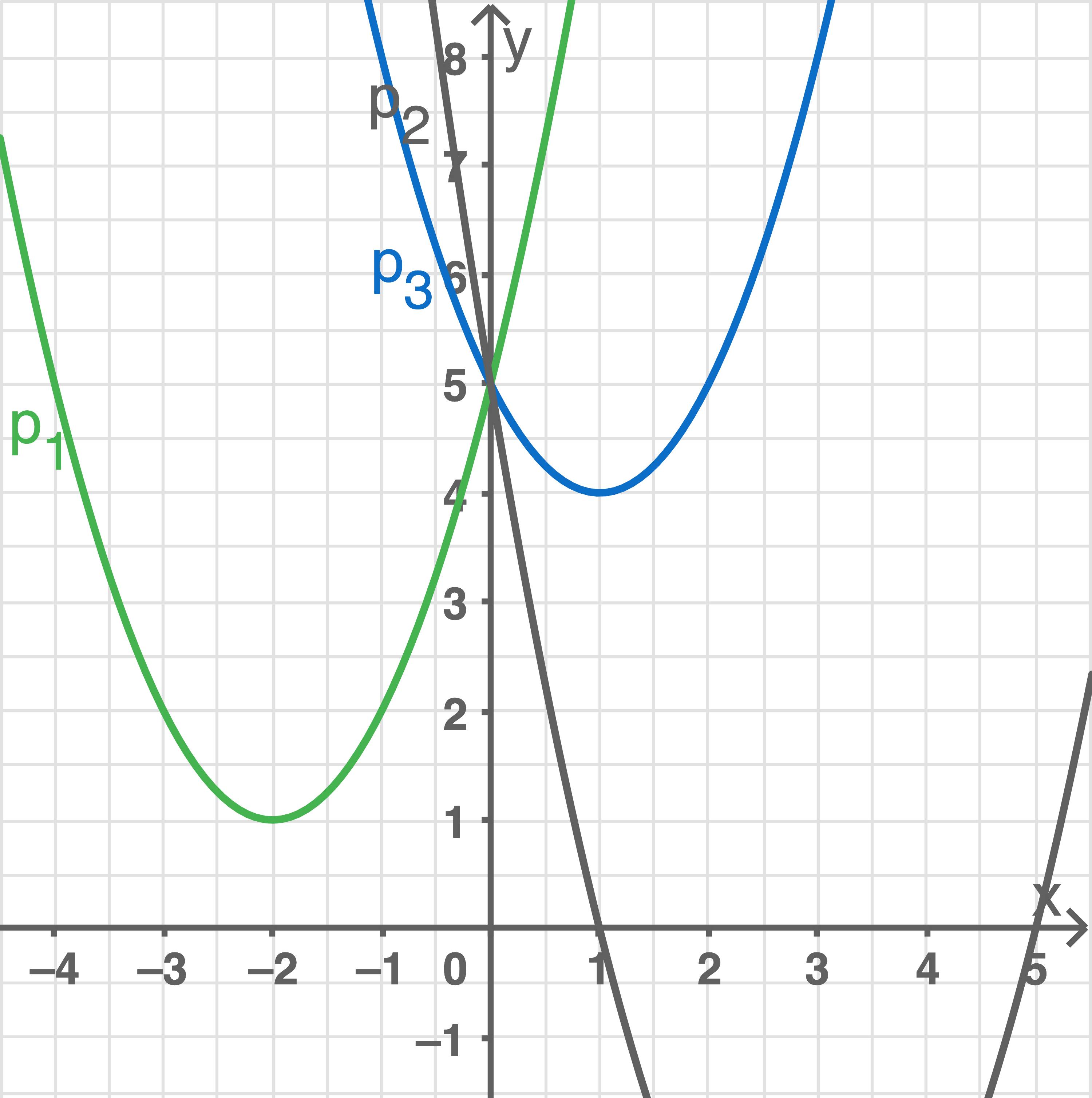
Welcher Graph gehört zur angegebenen Wertetabelle?
Durch die Punktprobe können die verschiedenen Werte geprüft werden:
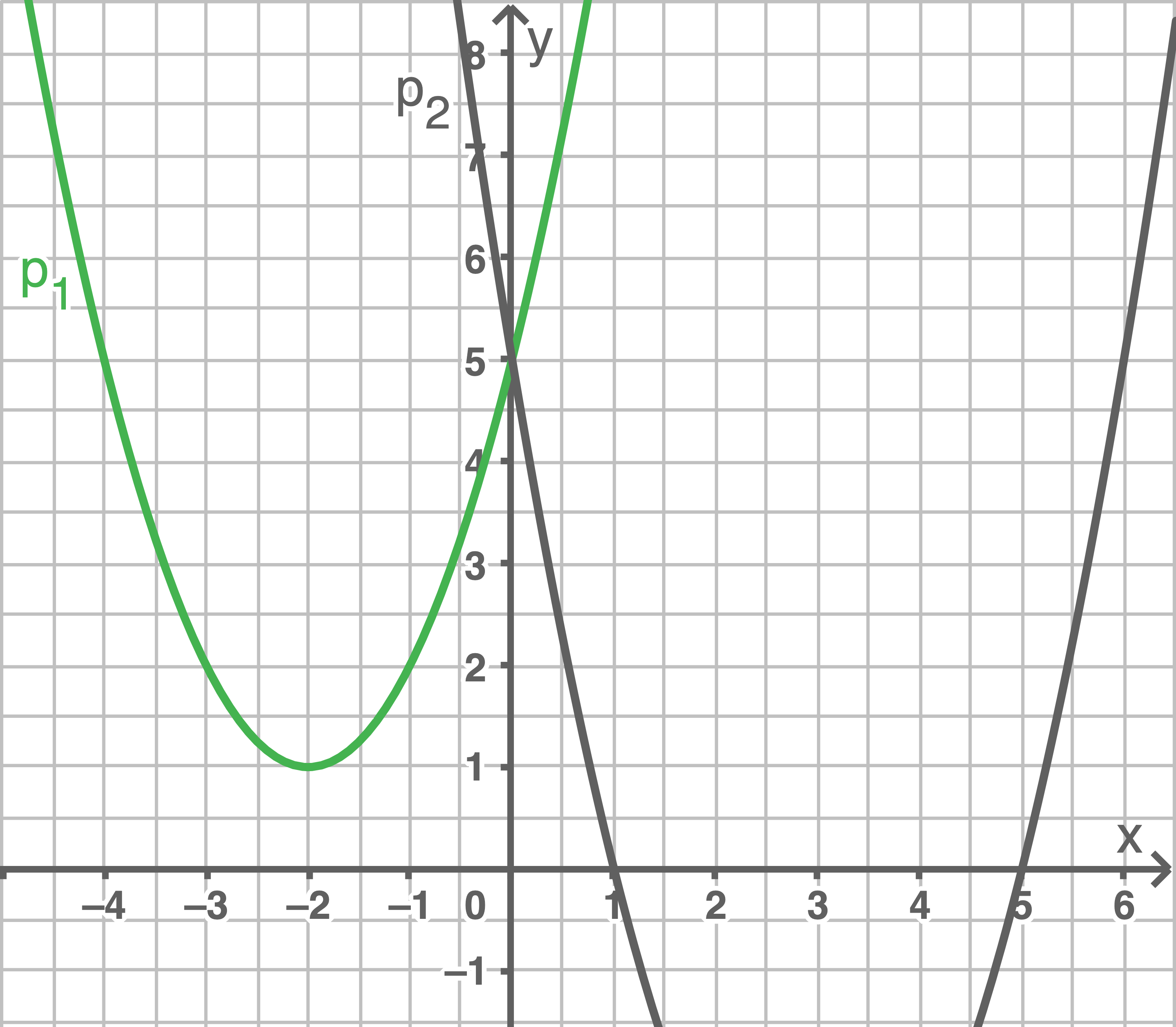
Koordinaten des Schnittpunkts  berechnen
1. Schritt: Scheitelpunktform von
berechnen
1. Schritt: Scheitelpunktform von  erstellen
erstellen
Der Scheitelpunkt

kann direkt von der Abbildung abgelesen werden. Da es sich um eine Normalparabel handelt, kann die Scheitelpunktform erstellt werden:
 2. Schritt: Scheitelpunktform von
2. Schritt: Scheitelpunktform von  erstellen
erstellen
Der Scheitelpunkt kann nicht abgelesen werde, jedoch sind die Nullstellen

und

bekannt. Die

- Koordinate des Scheitelpunkts von

muss also bei

liegen.
Es gilt also:

Mit der Punktprobe des Punkts

kann die Unbekannte

ermittelt werden:
![\(\begin{array}[t]{rll}
y&=& (x-4)^2+c &\quad \scriptsize \mid\; (2\mid 0)\\[5pt]
0&=&(2-4)^2+c &\quad \scriptsize \mid\; -(2-4)^2\\[5pt]
c&=& -(2-4)^2&\quad \scriptsize \\[5pt]
c&=& -4
\end{array}\)](https://www.schullv.de/resources/formulas/b3e8248fb7fff0a0b727fee2a87494b9f8bbf000d7d585174f50bdb610904f88_light.svg)
Es gilt also:
 3. Schritt: Parabelgleichungen gleichsetzen
4. Schritt:
3. Schritt: Parabelgleichungen gleichsetzen
4. Schritt:  in
in  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=&(7-6)^2+4 &\quad \scriptsize \\[5pt]
y&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/3910fc4034b9064f7db935067c6555ab1e4c2e5300ddd8b19e59cc7a36856ca8_light.svg)
Der Schnittpunkt

hat also die Koordinaten
 Wie heißt die Gleichung der Parabel
Wie heißt die Gleichung der Parabel 
Die Gleichung

kann über die Scheitelpunktform mit dem Scheitelpunkt

aufgestellt werden. Da es sich aber um keine Normalparabel handelt, hat sie einen Streckungsfaktor

und die Form

1. Schritt: Streckungsfaktor

berechnen
Punktprobe mit Punkt

![\(\begin{array}[t]{rll}
1,5&=& a\cdot 1^2+1 &\quad \scriptsize \mid\; -1 \\[5pt]
a&=& 0,5
\end{array}\)](https://www.schullv.de/resources/formulas/6bad5c44969dd8f91366e4723edbdc85e27df0ae7bf5a48de8ab95a96ebddfb7_light.svg)
Somit entsteht folgende Gleichung für

 Abschlussprüfung 2015
Abschlussprüfung 2015
Lösung 22
1. Schritt: Gleichung (1) nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\dfrac{x-4y}{3}&=&4 \quad \scriptsize \mid\;\cdot 3 \\[5pt]
x-4y&=&12 \quad \scriptsize \mid\;+4y \\[5pt]
x&=&12+4y
\end{array}\)](https://www.schullv.de/resources/formulas/97fd1a862cb37fb10722c6b663b3bed833616fe4b59f945c26efdb4d5e1c160b_light.svg) 2. Schritt:
2. Schritt:  in Gleichung (2) einsetzen und
in Gleichung (2) einsetzen und  berechnen
3. Schritt:
berechnen
3. Schritt:  in Gleichung (1) einsetzen und
in Gleichung (1) einsetzen und  berechnen
berechnen
![\(\begin{array}[t]{rll}
x&=& 12+4y \quad \scriptsize y=-2 \\[5pt]
x&=& 12+4\cdot(-2) \quad \scriptsize \\[5pt]
x&=& 4
\end{array}\)](https://www.schullv.de/resources/formulas/ced234becf39bdbd0ff5bff2e195102524f060e88049ed8d4cdf7f4af7265d97_light.svg)
Die Lösung des linearen Gleichungssystems lautet:
 Abschlussprüfung 2015
Abschlussprüfung 2015
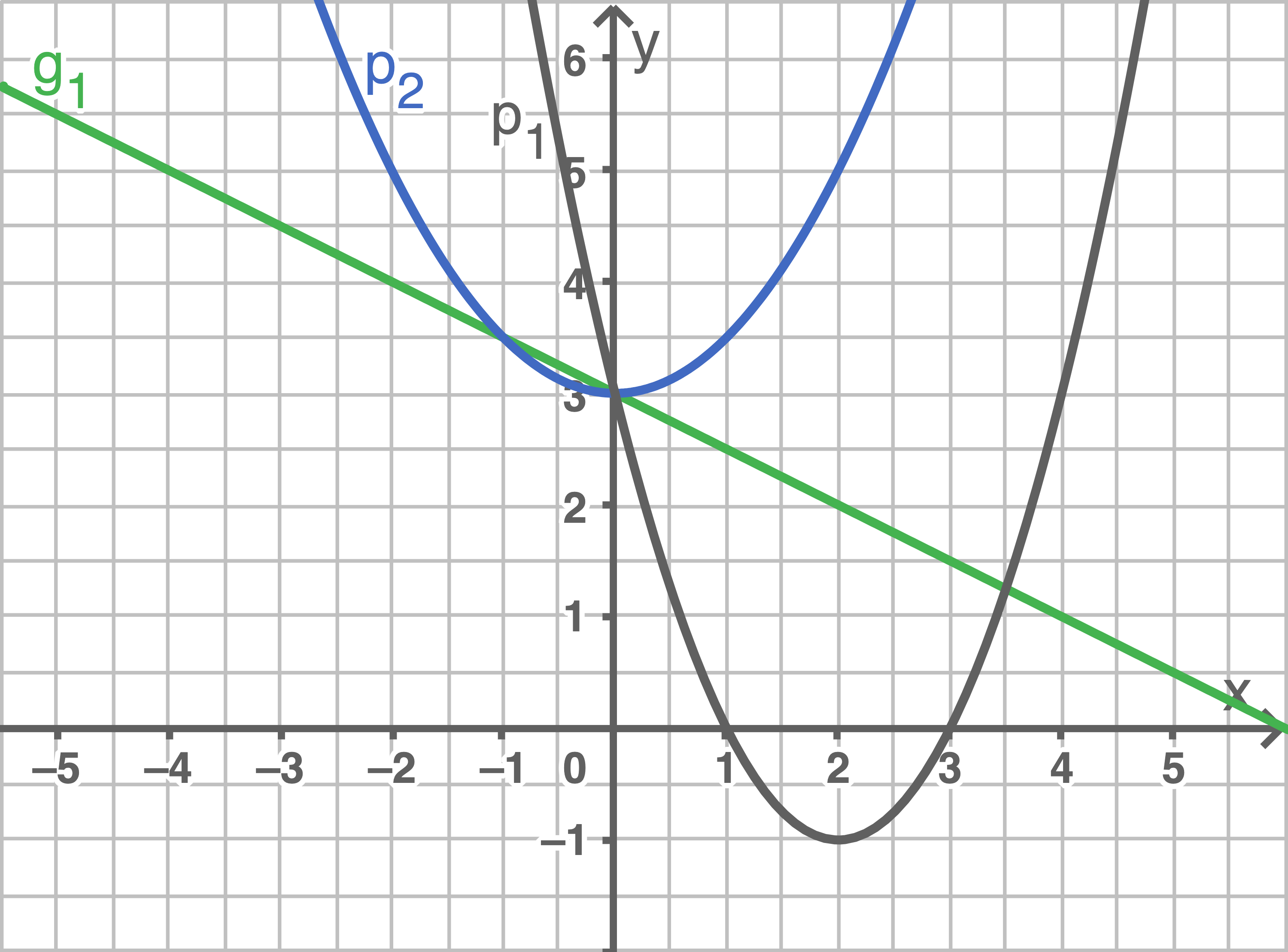
und
liegen auf
besitzt mit der
-Achse die beiden Schnittpunkte
und
geht durch den Scheitelpunkt
der Parabel
und durch
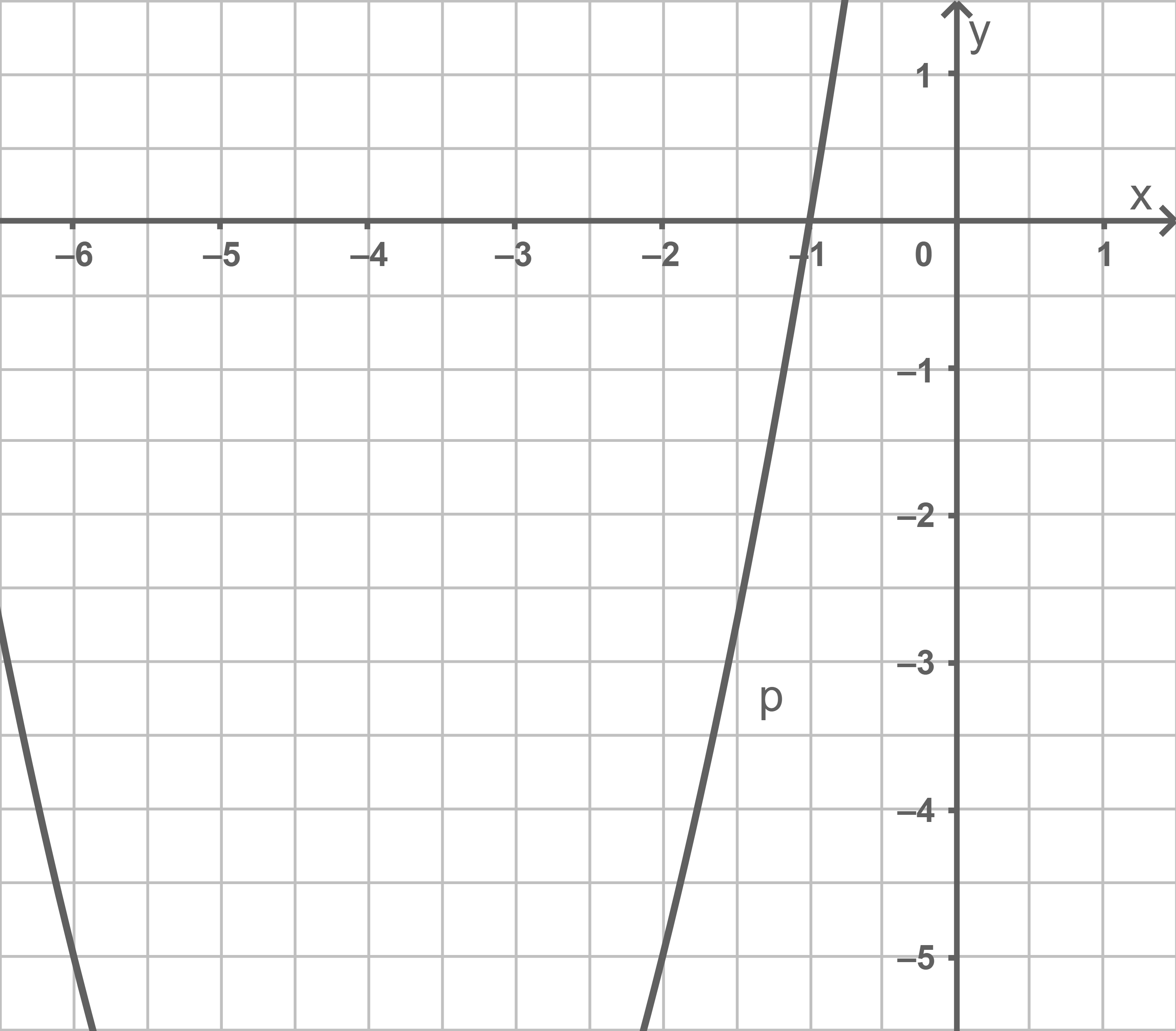
mithilfe des Schaubildes.
Entnimm dazu geeignete Werte aus der Zeichnung.
und
der Parabel und der Geraden.
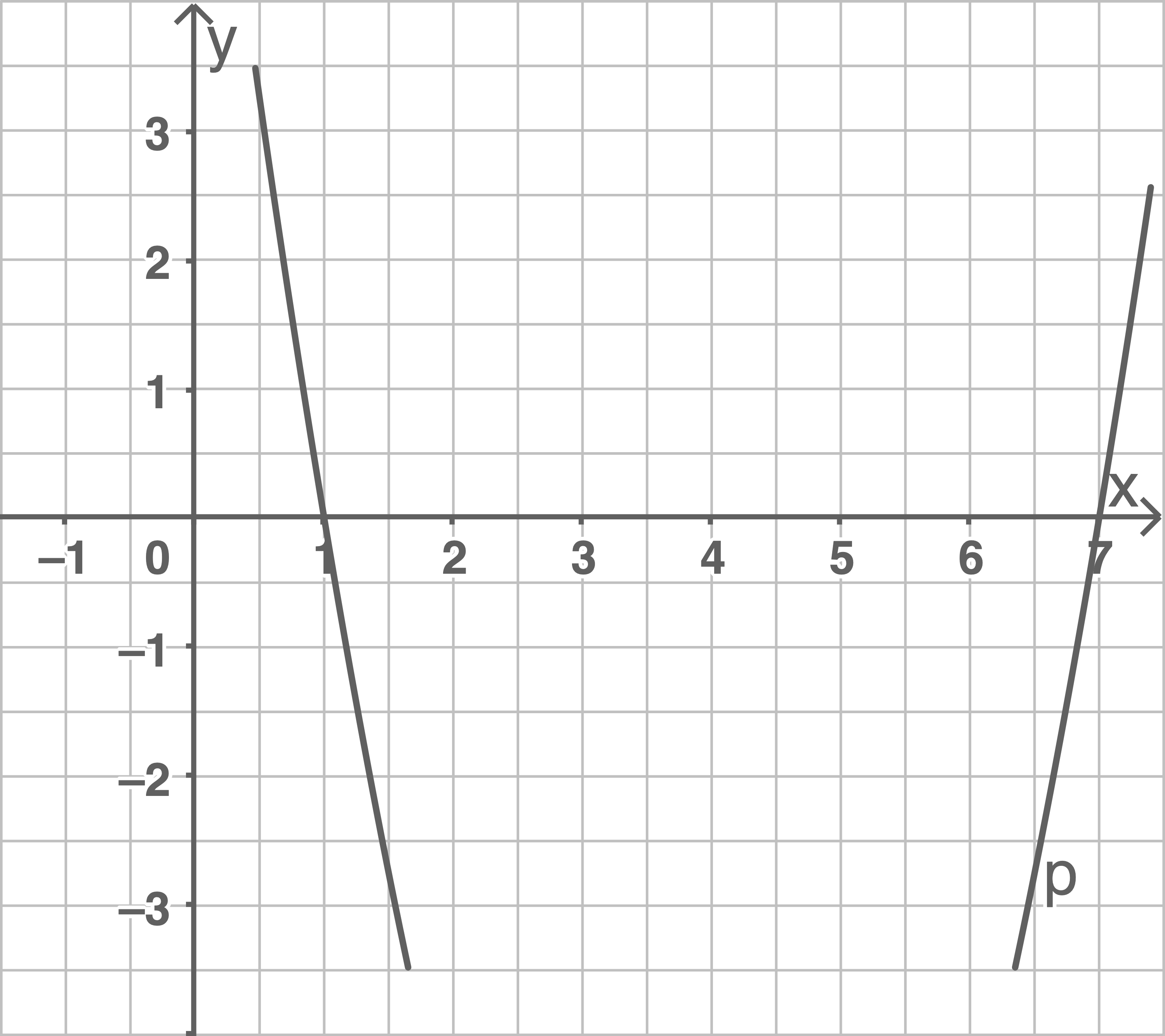
-Werte in der Wertetabelle.
und
der Parabel
mit der Geraden
einsetzen:
einsetzen:
einsetzen:
einsetzen:
und
in die Standardform einsetzen:
-Koordinate des Nullpunktes berechnen:
einsetzen um die
-Koordinate zu erhalten:
und
in die Gleichung
einsetzen, um die Steigung
zu erhalten:
und
in die Geradengleichung
einsetzen und nach
auflösen:
:
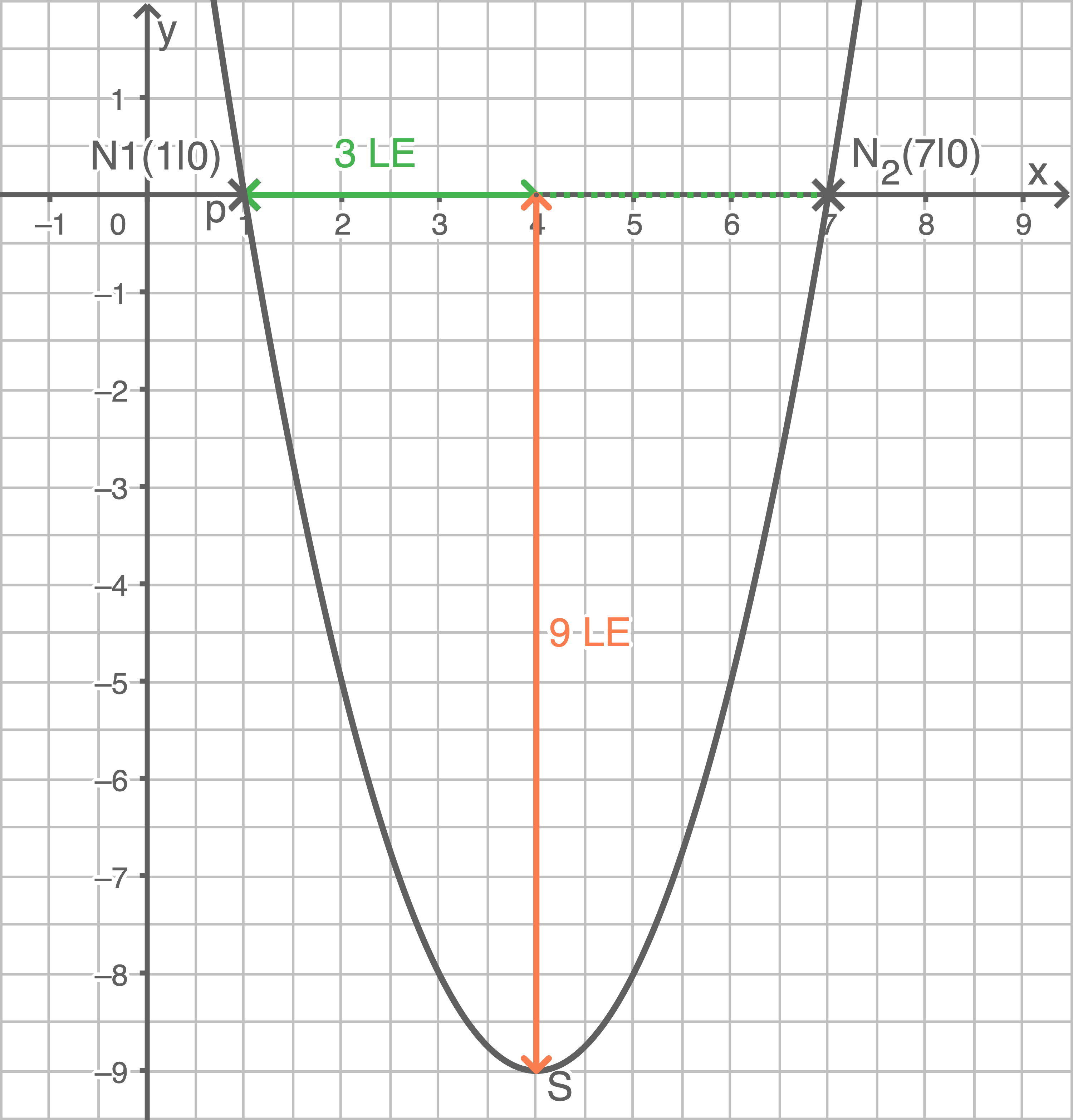
bis zur Symmetrieachse
bis zum Scheitelpunkt
ist für
gleich Null
ist für
gleich Null
Daraus folgt:
und
![[ALT-TAG]](https://www.schullv.de/resources/images/mathe/desktop/bw_rs2017_p5_lsg.png)
: Da nur die Parabeln
und
durch diesen Punkt verlaufen, können die anderen beiden Parabeln ausgeschlossen werden.
: Nur Parabel
verläuft durch diesen Punkt. Die gegebene Wertetabelle gehört also zur Parabel
.