Lösung 1
a)
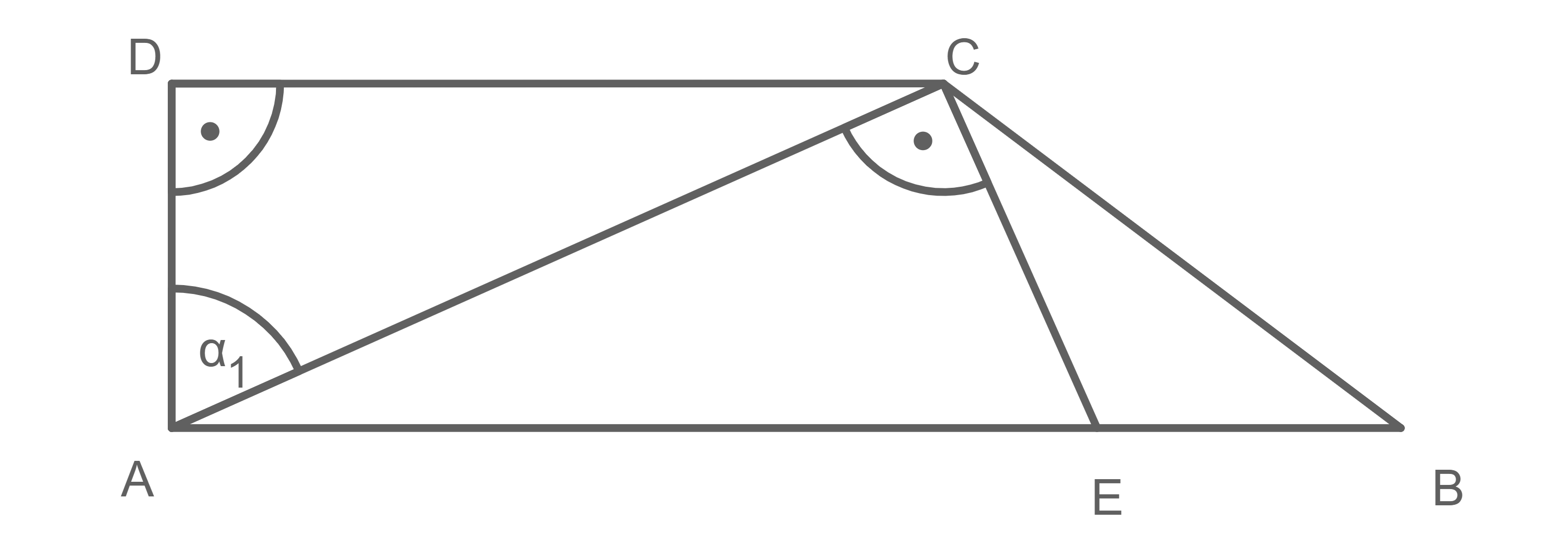
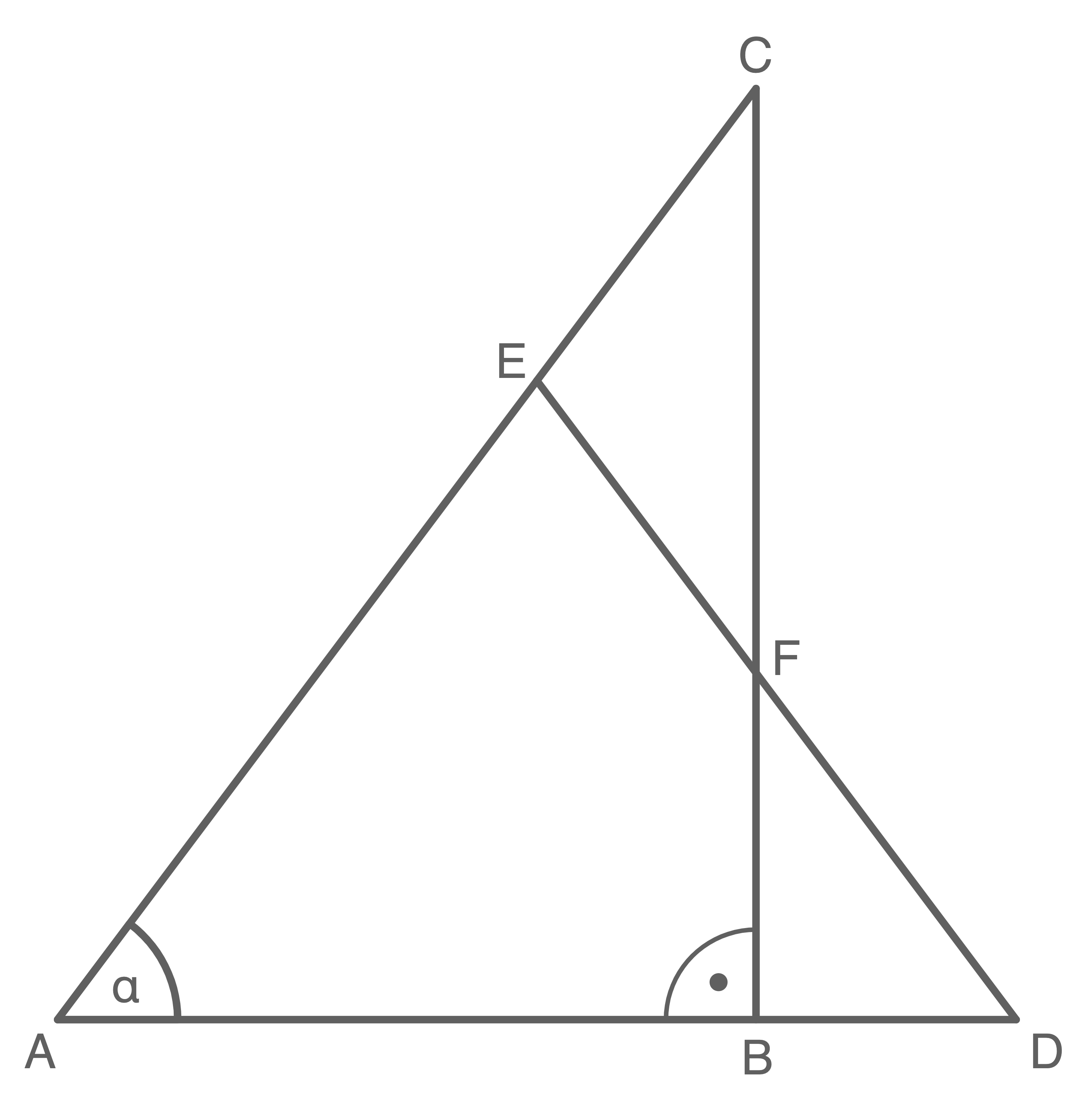
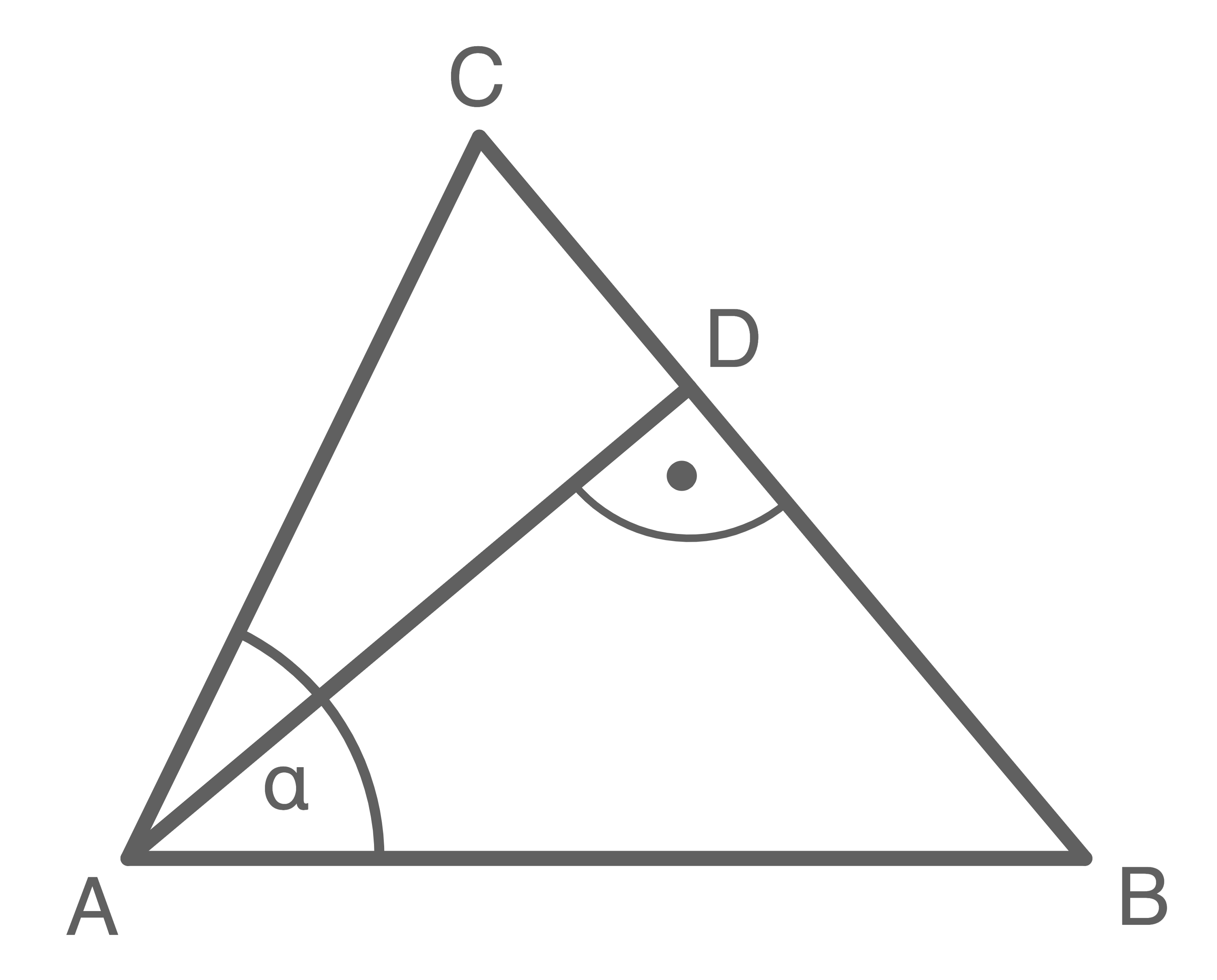
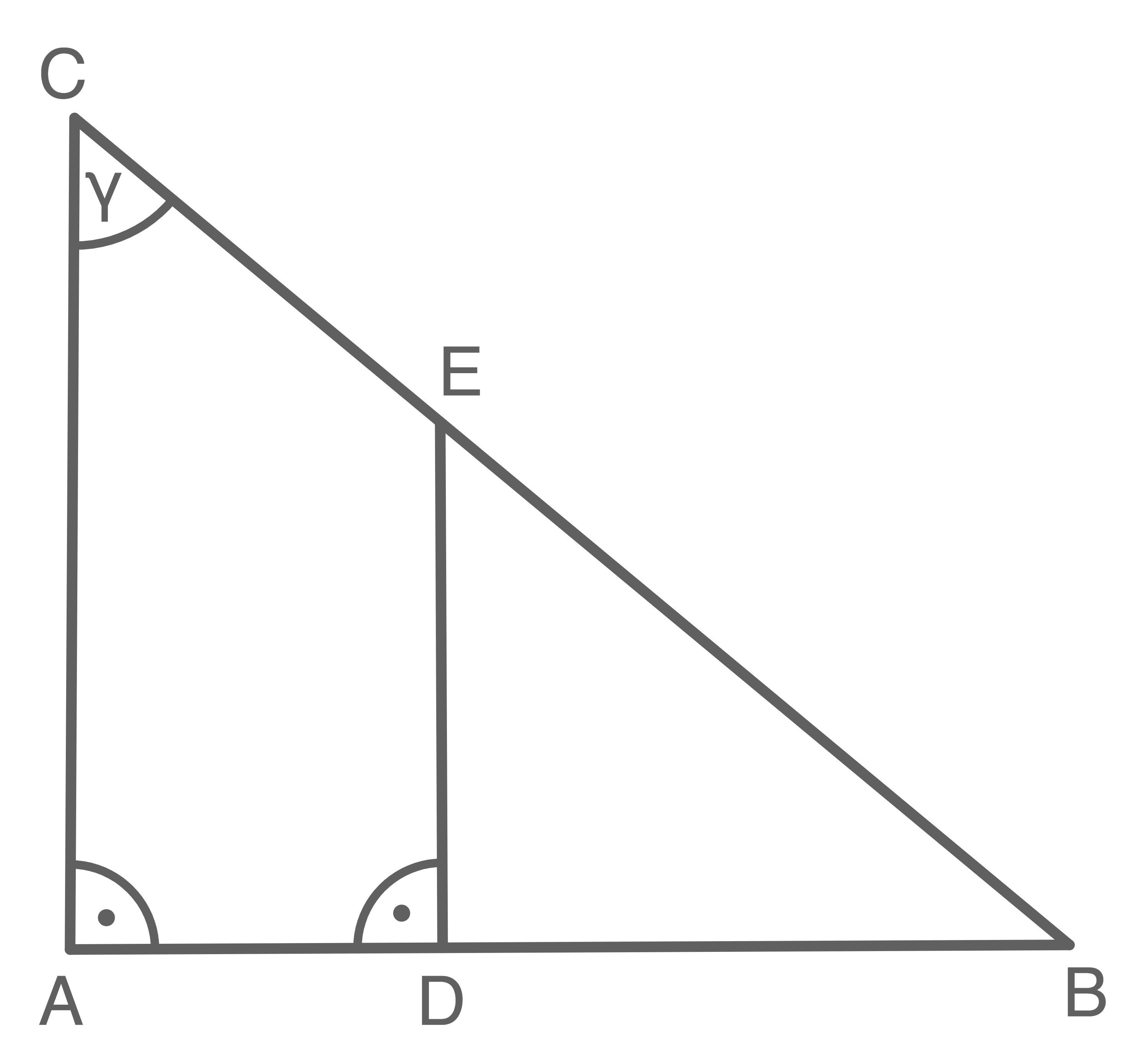
Beim Punkt  bilden die Winkel
bilden die Winkel  und
und  zusammen einen rechten Winkeln. Da
zusammen einen rechten Winkeln. Da  bekannt ist:
bekannt ist:
![\(\begin{array}[t]{rlll}
90^\circ-\sphericalangle \text{DAC}&=& \sphericalangle \text{CAE} \\[5pt]
90^\circ-65^\circ&=&25^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/dec2f916575de952a8e4c9b9c7fab5a0a354bee0ed5bb5ba0f908addb7e168d9_light.svg)
Nun kann die Länge  durch Längenbeziehungen innerhalb eines rechtwinkligen Dreiecks errechnet werden:
durch Längenbeziehungen innerhalb eines rechtwinkligen Dreiecks errechnet werden:
Das Gleiche Verfahren kann nun für die Strecken  und
und  verwendet werden.
verwendet werden.

![\(\begin{array}[t]{rlll}
\tan(\alpha_1)&=&\dfrac{Gegenkathete}{Ankathete} \\[5pt]
\tan(65^\circ)&=&\dfrac{\overline{DC}}{\overline{AD}} \\[5pt]
\tan(65^\circ)&=&\dfrac{\overline{DC}}{3,8\;\text{cm}} &\mid\; \cdot 3,8\;\text{cm} \\[5pt]
\overline{DC}&=&\tan(65^\circ)\cdot 3,8\;\text{cm} \\[5pt]
\overline{DC}&=&8,15\;\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/f30d77aefebe2798a7ead6b2b9d29f6d94d29b28de2fb7804ecfb0925a8a87ce_light.svg)


Daraus folgt dann:
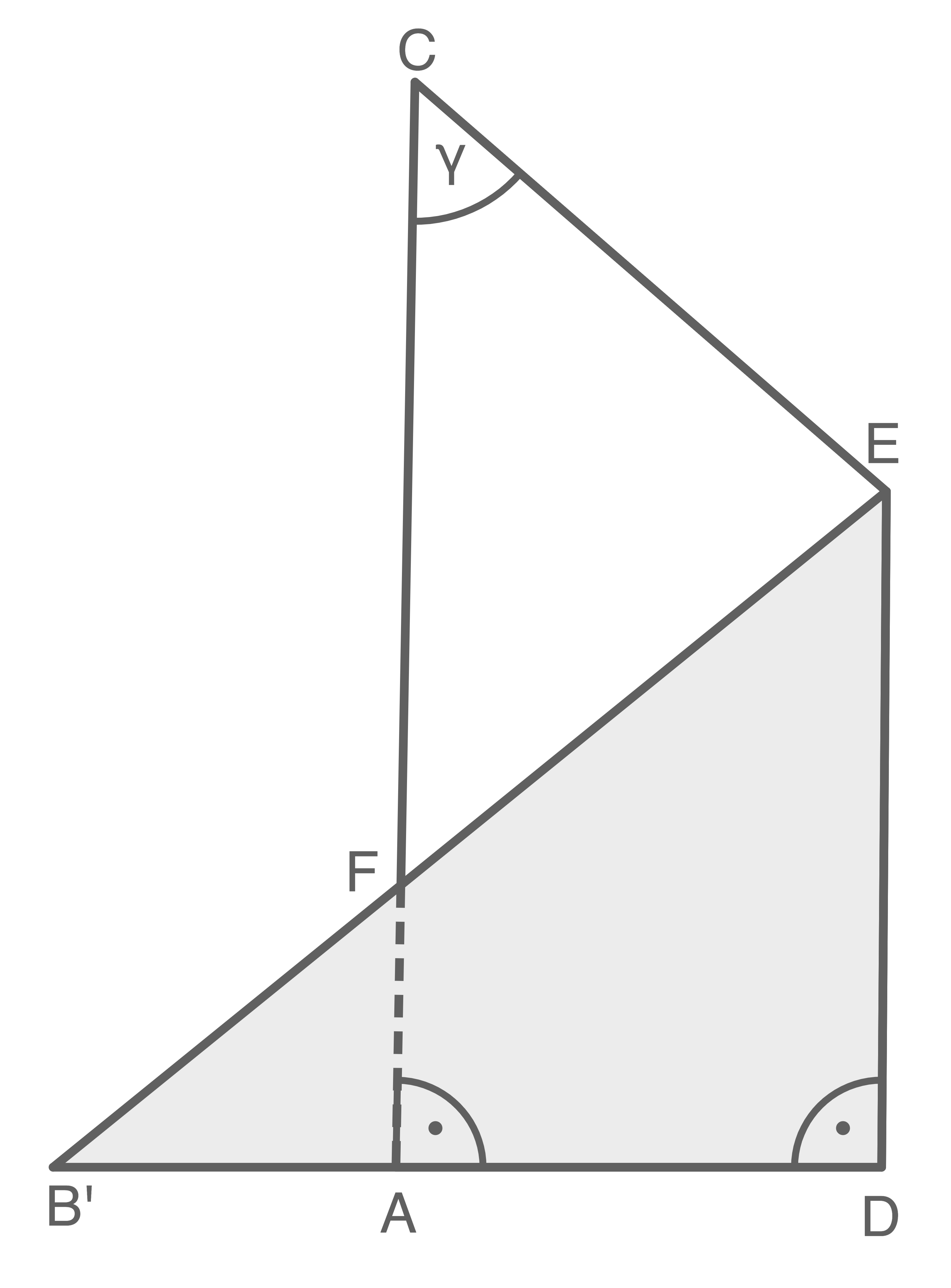
Um den Umfang des Dreiecks  bestimmen zu können, muss die Strecke
bestimmen zu können, muss die Strecke  ermittelt werden.
ermittelt werden.
Senkrechte durch  errichten:
errichten:
Durch Punkt  verläuft die Senkrechte
verläuft die Senkrechte  Sie ist ebenso lang wie die Höhe
Sie ist ebenso lang wie die Höhe 
Hilfsstrecke bestimmen:

Rechtwinkliges Dreieck  betrachten:
betrachten:
Mit Hilfe des Satz des Pythagoras  bestimmen:
bestimmen:

Zahlenwerte einsetzen:
![\(\begin{array}[t]{rlll}
\overline{BC}^{2}&=&4,75^{2}+3,8^{2} &\mid\; \sqrt{\;} \\[5pt]
\overline{BC}&=&\sqrt{4,75^{2}+3,8^{2}} \\[5pt]
\overline{BC}&=&6,08\;\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/25ea88eab55d8284e6cb6a2360fb5ba025815f9ca3ececaa4c7b31634f60883d_light.svg)
Der Umfang  ergibt sich aus:
ergibt sich aus:
Der Umfang des Dreiecks  beträgt
beträgt 
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2025
Lösung 2
a)
Winkel  berechnen
berechnen
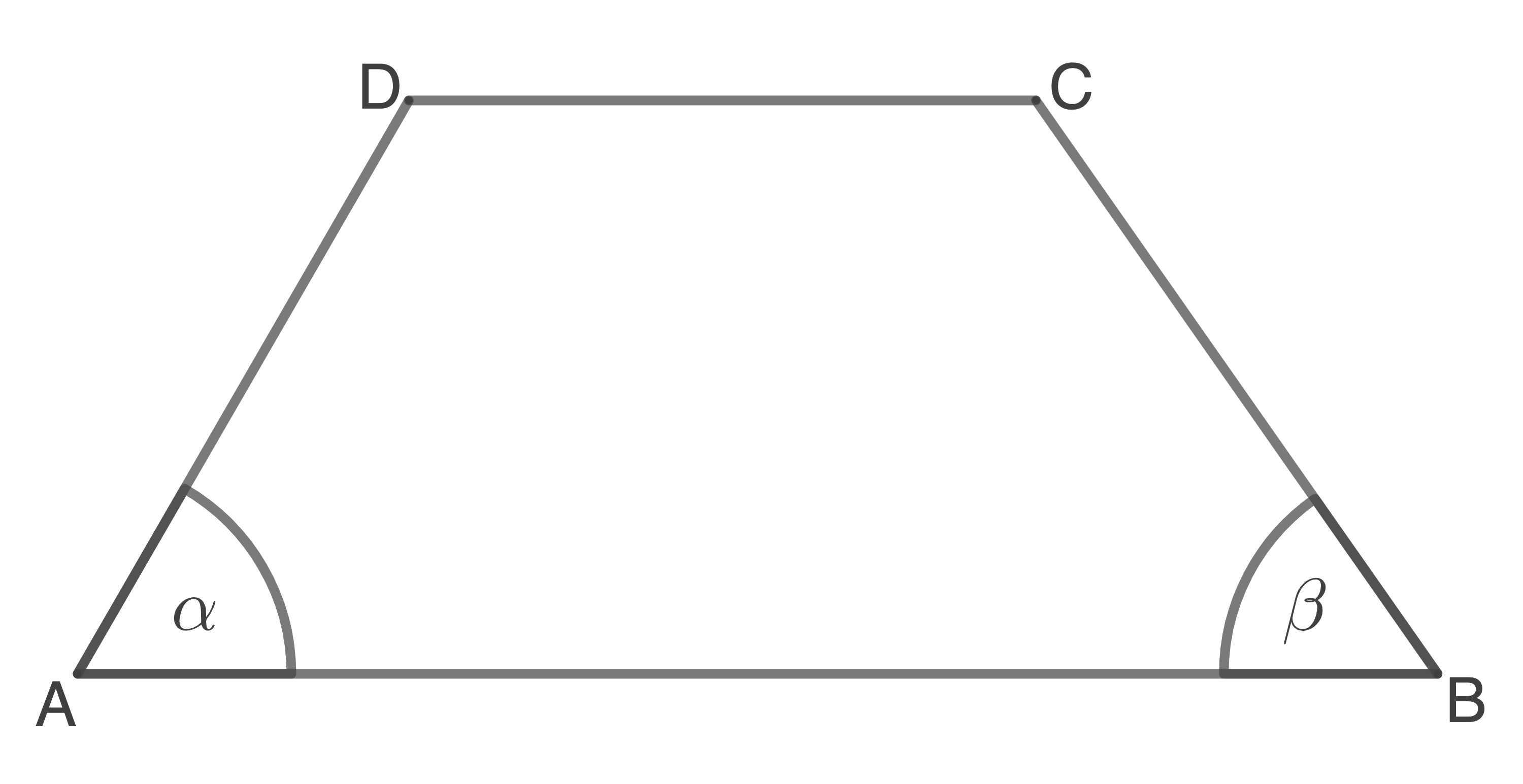
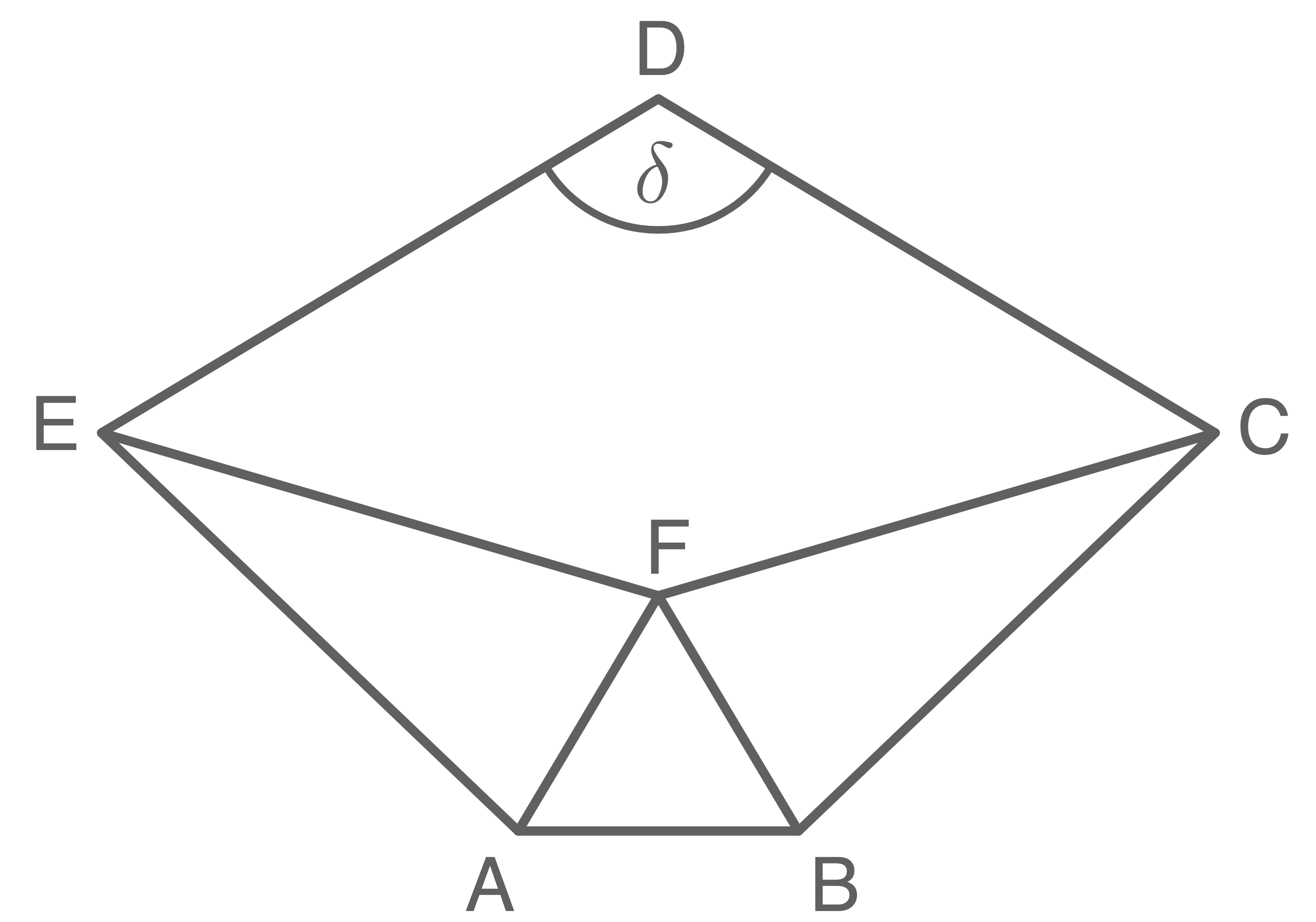
Aufgrund des Symmetrie des Drachenvierecks hat der Winkel

die gleiche Größe wie der Winkel

Daher gilt:

 Umfang des Vierecks
Umfang des Vierecks  berechnen
1. Schritt:
berechnen
1. Schritt:  bestimmen
bestimmen
Aufgrund der Symmetrie des Drachenvierecks gilt
 2. Schritt:
2. Schritt:  berechnen
berechnen

 3. Schritt:
3. Schritt:  berechnen
berechnen
Aufgrund der Symmetrie des Drachenvierecks gilt

Damit folgt:
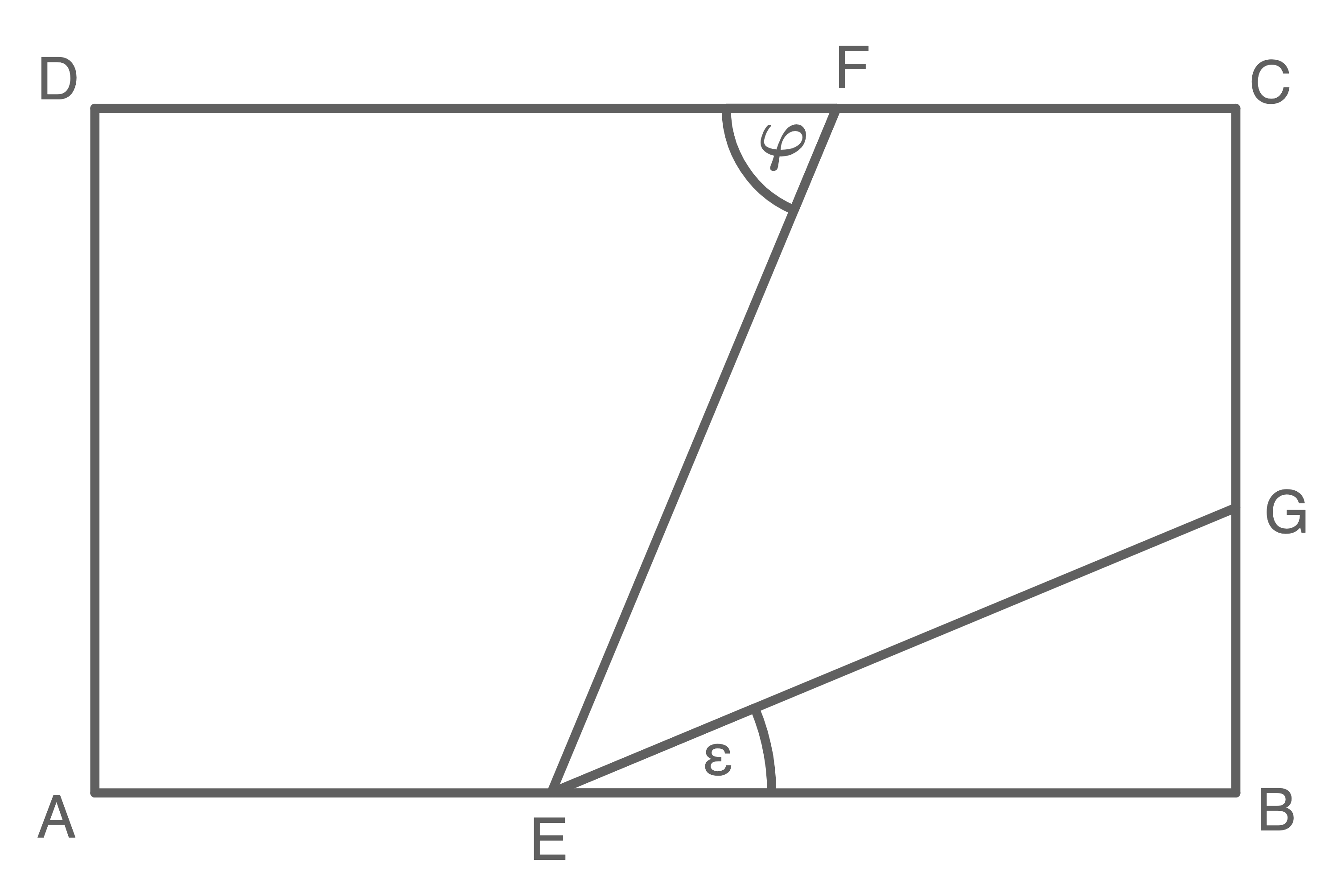
![\(\begin{array}[t]{rll}
\cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EG}} \\[5pt]
\cos \varepsilon&=& \dfrac{\overline{BE}}{\overline{EF}} \\[5pt]
\cos 20,0°&=& \dfrac{5,6\,\text{cm}}{\overline{EF}} \quad \scriptsize \mid\;\cdot \overline{EF} \\[5pt]
\cos 20,0°\cdot \overline{EF}&=& 5,6\,\text{cm} \quad \scriptsize \mid\; :\cos 20,0°\\[5pt]
\overline{EF}&=& \dfrac{5,6\,\text{cm}}{\cos 20,0°} \\[5pt]
\overline{EF}&=& \underline{5,96\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/75eb9ed924378bc1792b1c1507f2436b34ff38e9e9540393c96ee244c70620dc_light.svg) 4. Schritt:
4. Schritt:  berechnen
berechnen
Zunächst muss die Länge der Strecke

berechnet werden:
Damit folgt für die Länge der Strecke

![\(\begin{array}[t]{rll}
\overline{CF}&=& \overline{CG} \\[5pt]
&=& \overline{AD}-\overline{BG} \\[5pt]
&=& 5,6\,\text{cm}-2,04\,\text{cm} \\[5pt]
&=& 3,56\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/a9c412125f4629abaad1d1f1bb9539cd9015eeb45ae08469566e80f54b7812cc_light.svg)
Insgesamt gilt dann für die Strecke

![\(\begin{array}[t]{rll}
\overline{DF}&=& \overline{AB}-\overline{CF} \\[5pt]
&=& 9,4\,\text{cm}-3,56\,\text{cm} \\[5pt]
&=& \underline{5,84\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/de52816477fd78dcda7a852f8864a5a288b3480375577a1a6de01b6bb76c1d9a_light.svg) 5. Schritt: Umfang berechnen
5. Schritt: Umfang berechnen
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2024
Lösung 3
a)
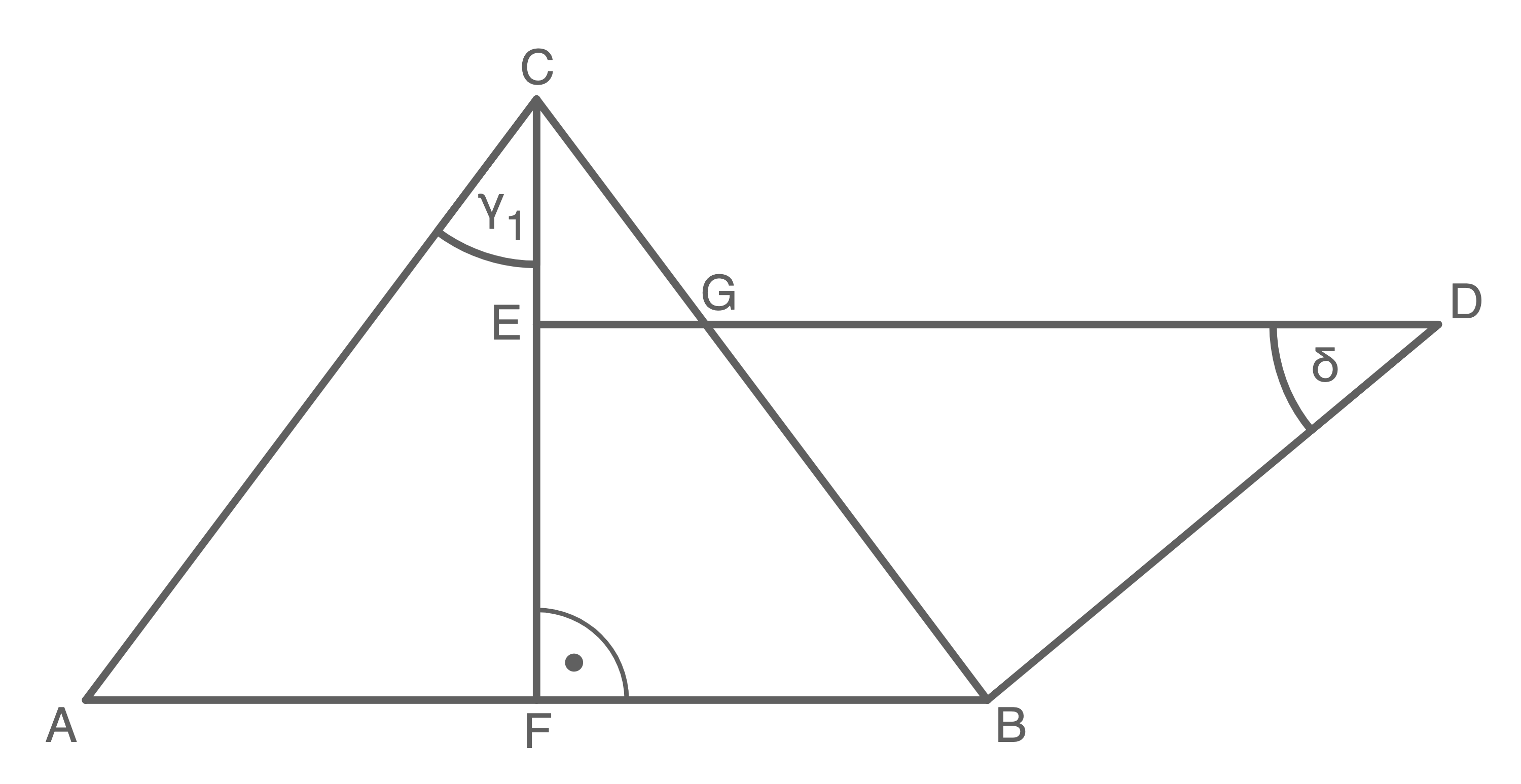
Hilfsskizze:
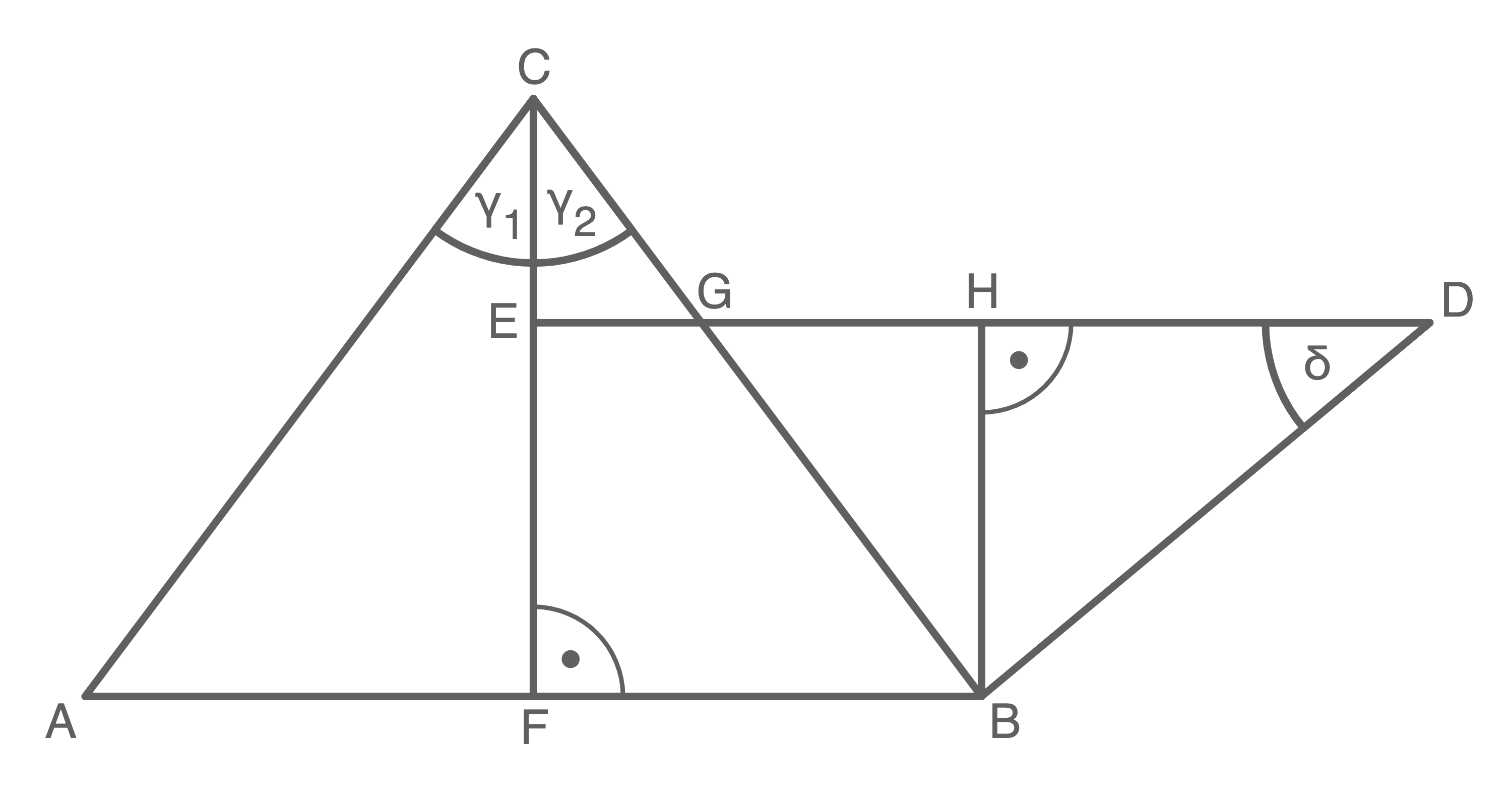
1. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\gamma_1&=&\dfrac{\overline{AF}}{\overline{AC}} \quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\sin\gamma_1\cdot \overline{AC}&=&\overline{AF}\\[5pt]
\overline{AF}&=&\sin\gamma_1\cdot \overline{AC}\\[5pt]
&=&\sin 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{AF}&=&\underline{6,96\,\text{cm}}=\overline{BF}
\end{array}\)](https://www.schullv.de/resources/formulas/f117be89cd18c2721247be3d6cdd8dce5a70e9d1ea60ba536fac5e109adcbee0_light.svg) 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin\delta&=&\dfrac{\overline{BH}}{\overline{BD}} \quad \scriptsize \mid\;\cdot \overline{BD} \\[5pt]
\sin\delta\cdot \overline{BD}&=&\overline{BH}\\[5pt]
\overline{BH}&=&\sin\delta\cdot \overline{BD}\\[5pt]
&=&\sin 39,2^\circ\cdot 8,2\,\text{cm}\\[5pt]
\overline{BH}&=&\underline{5,18\,\text{cm}}=\overline{EF}
\end{array}\)](https://www.schullv.de/resources/formulas/6d7867800c748f34a8a9f65c9b427166812029b8d1d338d1df3425c6ad7a6546_light.svg) 3. Schritt: Länge von
3. Schritt: Länge von  berechnen
3.1. Schritt: Länge von
berechnen
3.1. Schritt: Länge von  berechnen
berechnen
Es gilt:

und

![\(\begin{array}[t]{rll}
\cos\gamma_2&=&\dfrac{\overline{CF}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt]
\cos\gamma_2\cdot \overline{BC}&=&\overline{CF}\\[5pt]
\overline{CF}&=&\cos\gamma_2\cdot \overline{BC}\\[5pt]
&=&\cos 37,6^\circ\cdot 11,4\,\text{cm}\\[5pt]
\overline{CF}&=&9,03\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/3fc464ca0829003058de304a618f444b89d070eb7b9159ab34b56c58c6893fb6_light.svg) 3.2. Schritt: Länge von
3.2. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CE}&=&\overline{CF}-\overline{EF}\\[5pt]
\overline{CE}&=&9,03\,\text{cm}-5,18\,\text{cm}\\[5pt]
\overline{CE}&=&3,85\,\text{cm}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/15b7496483fda77f5fa342a59f42c6a589d4d504f6c80e6060728ee707bcf45e_light.svg) 3.3. Schritt: Länge von
3.3. Schritt: Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\gamma_2&=&\dfrac{\overline{EG}}{\overline{CE}} \quad \scriptsize \mid\;\cdot \overline{CE} \\[5pt]
\tan\gamma_2\cdot \overline{CE}&=&\overline{EG}\\[5pt]
\overline{EG}&=&\tan\gamma_2\cdot \overline{CE}\\[5pt]
&=&\tan37,6^\circ\cdot 3,85\,\text{cm}\\[5pt]
\overline{EG}&=&\underline{2,96\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/86cae91396842a03524c0c0133d1a192286cfc3f09a61359f628b013386f9088_light.svg) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{\overline{BF}+\overline{EG}}{2}\cdot\overline{EF}\\[5pt]
&=&\dfrac{6,96\,\text{cm}+2,96\,\text{cm}}{2}\cdot 5,18\,\text{cm}\\[5pt]
A&=&\underline{\underline{25,7\,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/75a4c3dd27ebbf0262b34bc2fe3863175364bb8414cd13408aae10d7feeaee9c_light.svg)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2023
Lösung 4
a)
Flächeninhalt des Dreiecks berechnen
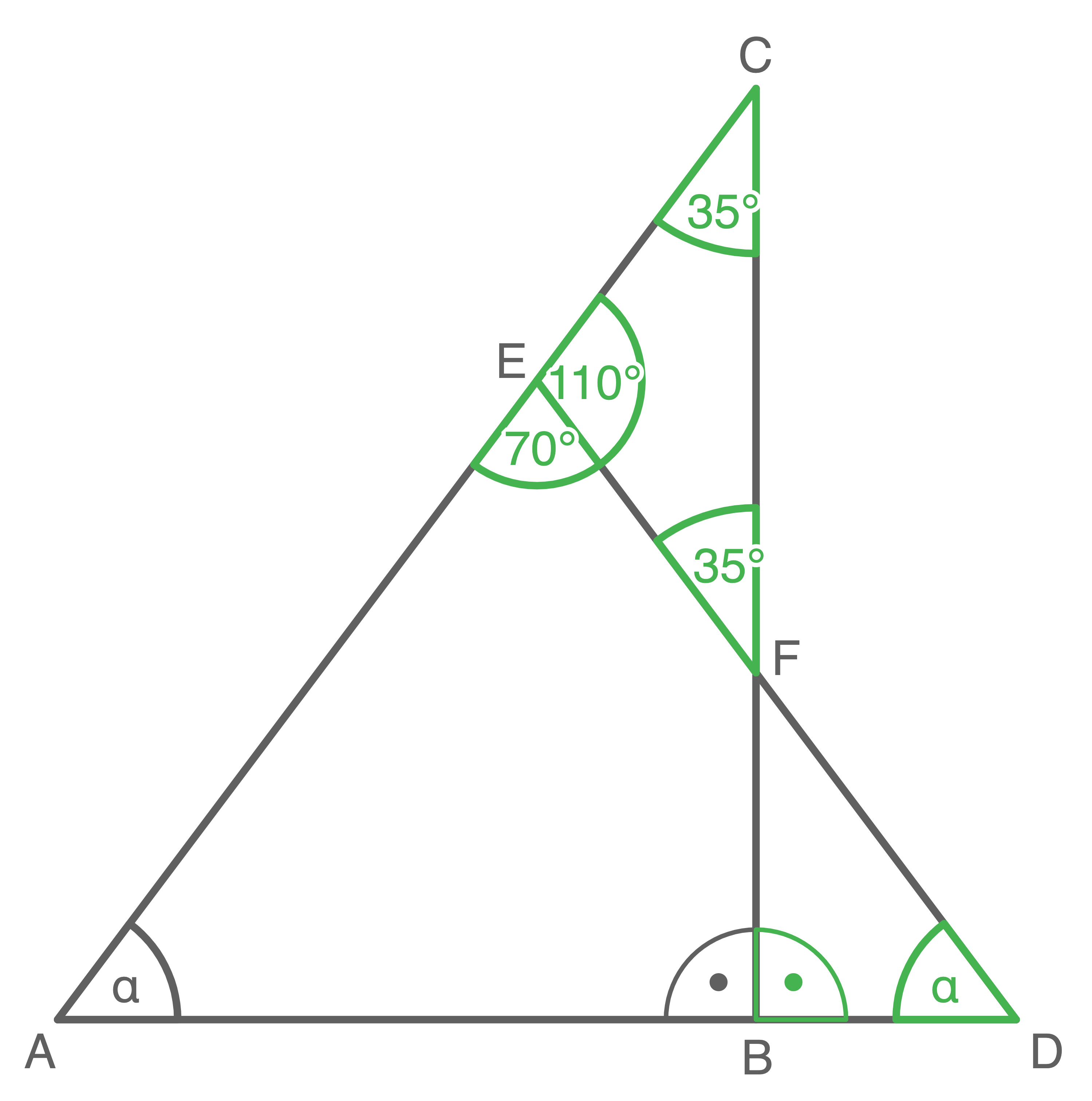
1. Schritt: Länge von  berechnen
berechnen
 2. Schritt: Länge von
2. Schritt: Länge von  berechnen
berechnen











 3. Schritt: Flächeninhalt berechnen
3. Schritt: Flächeninhalt berechnen



 Größe des Winkels
Größe des Winkels  berechnen
1. Schritt: Größe des Winkels
berechnen
1. Schritt: Größe des Winkels  berechnen
berechnen


 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
berechnen


 3. Schritt: Größe des Winkels
3. Schritt: Größe des Winkels  berechnen
berechnen



b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2022
Lösung 5
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
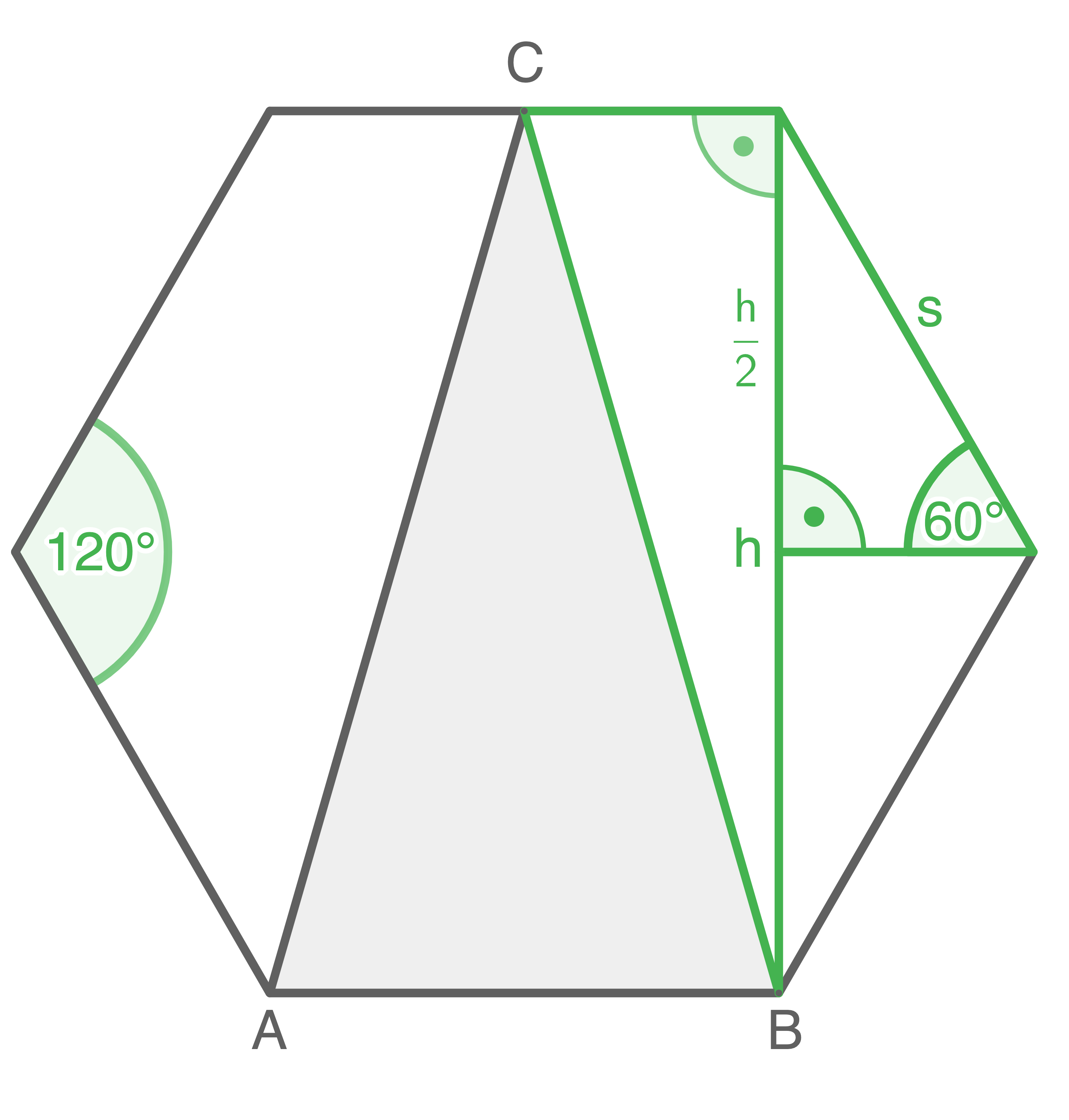
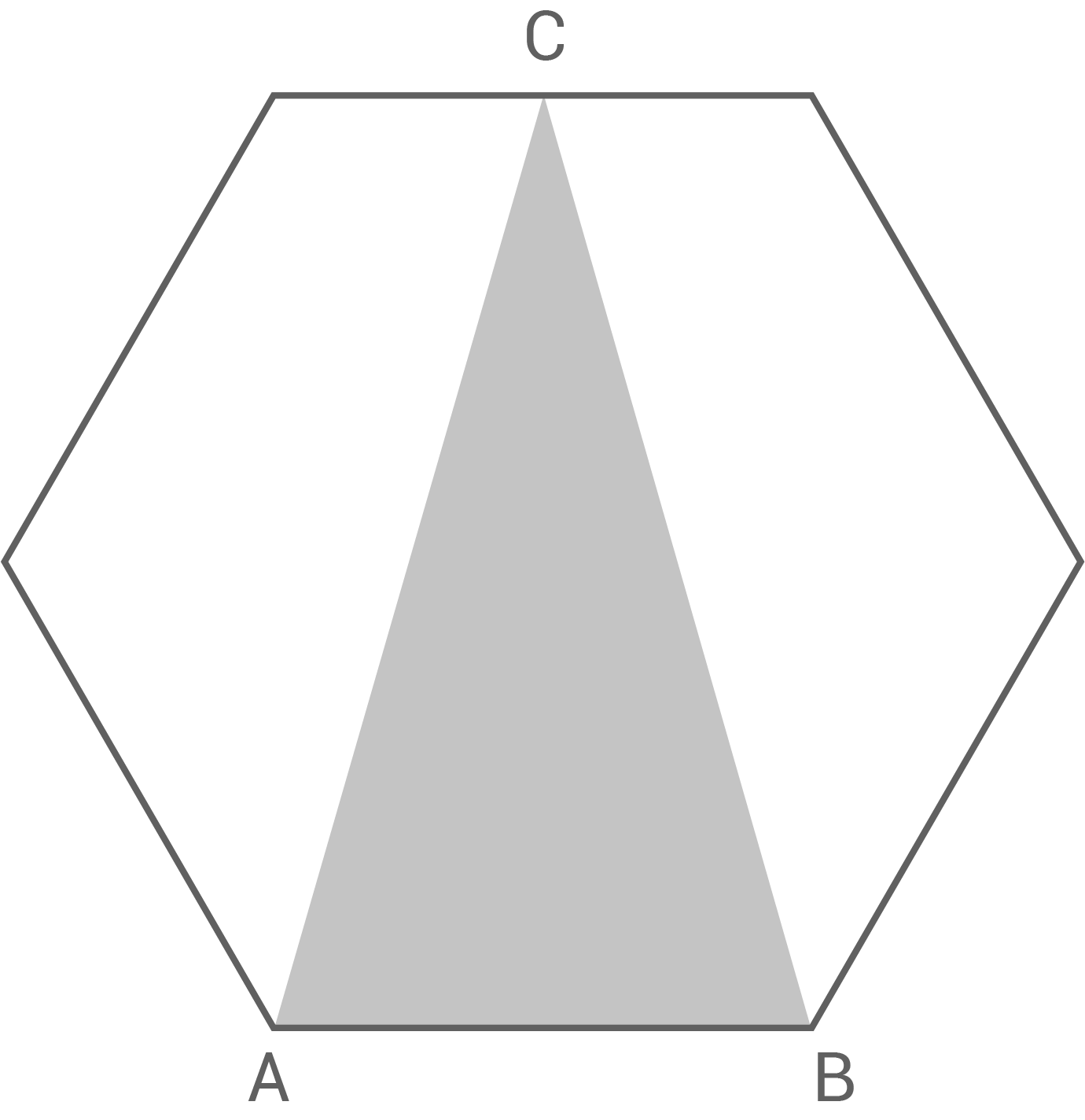
Umfang des Dreiecks berechnen
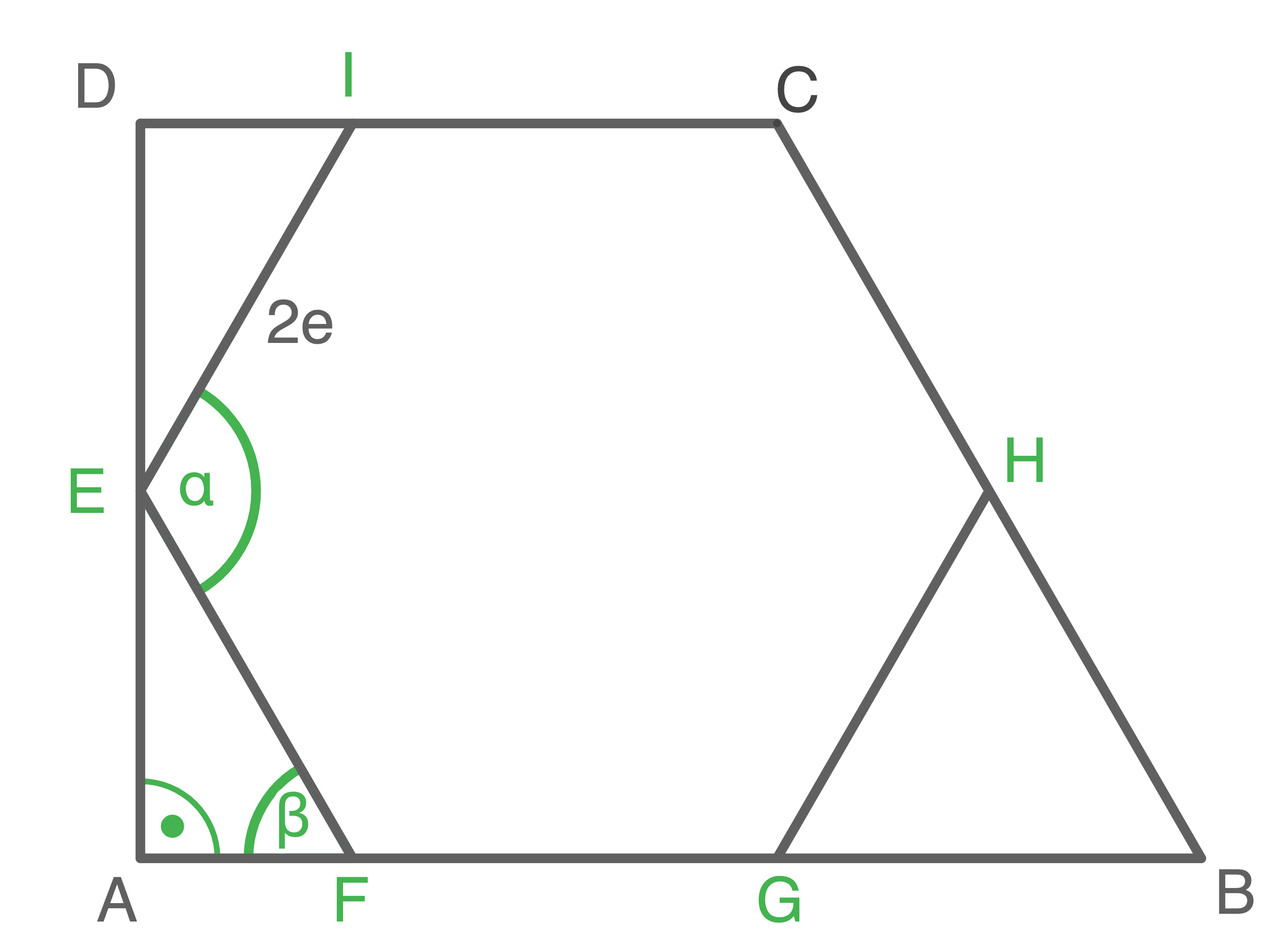
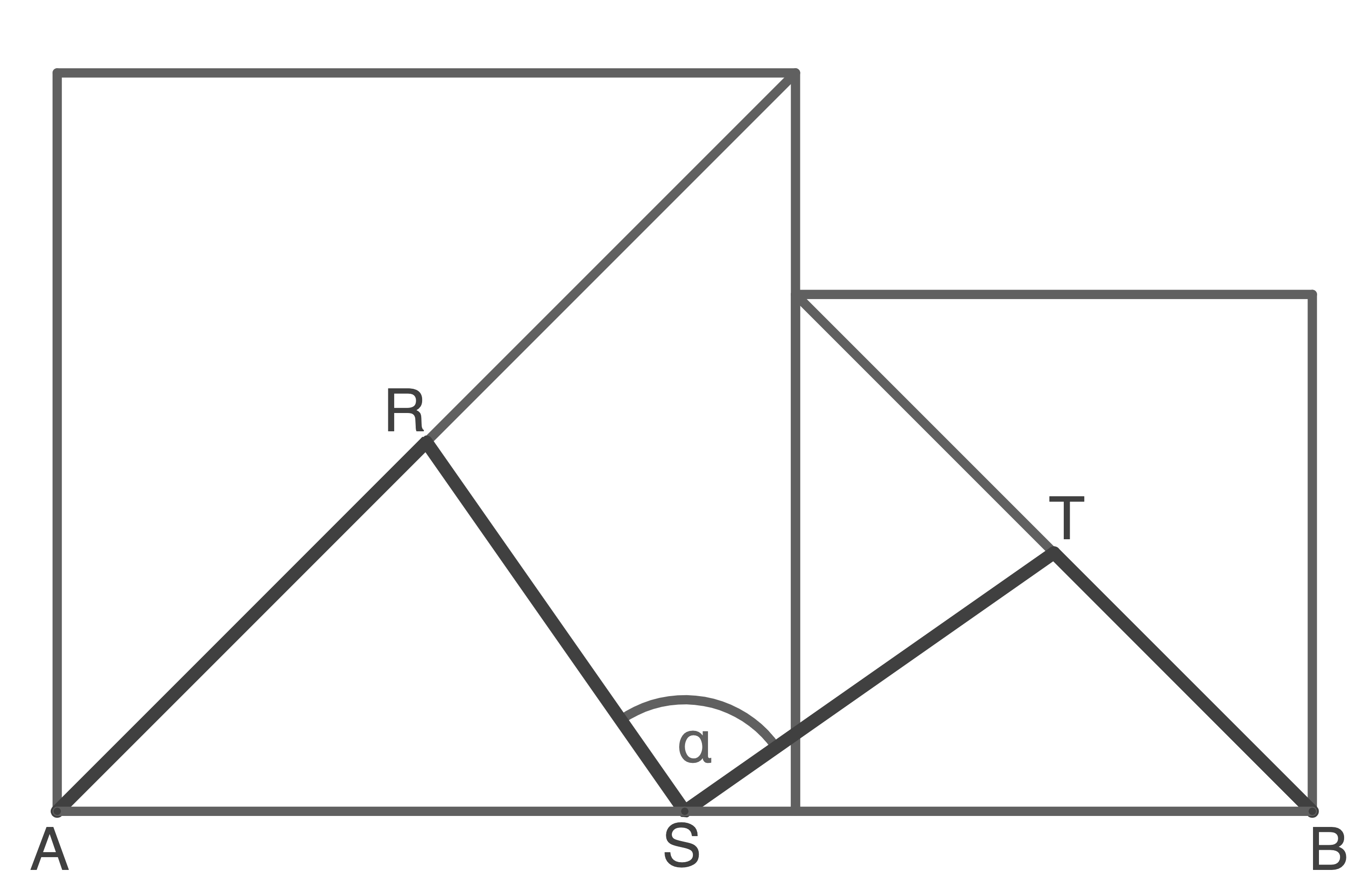
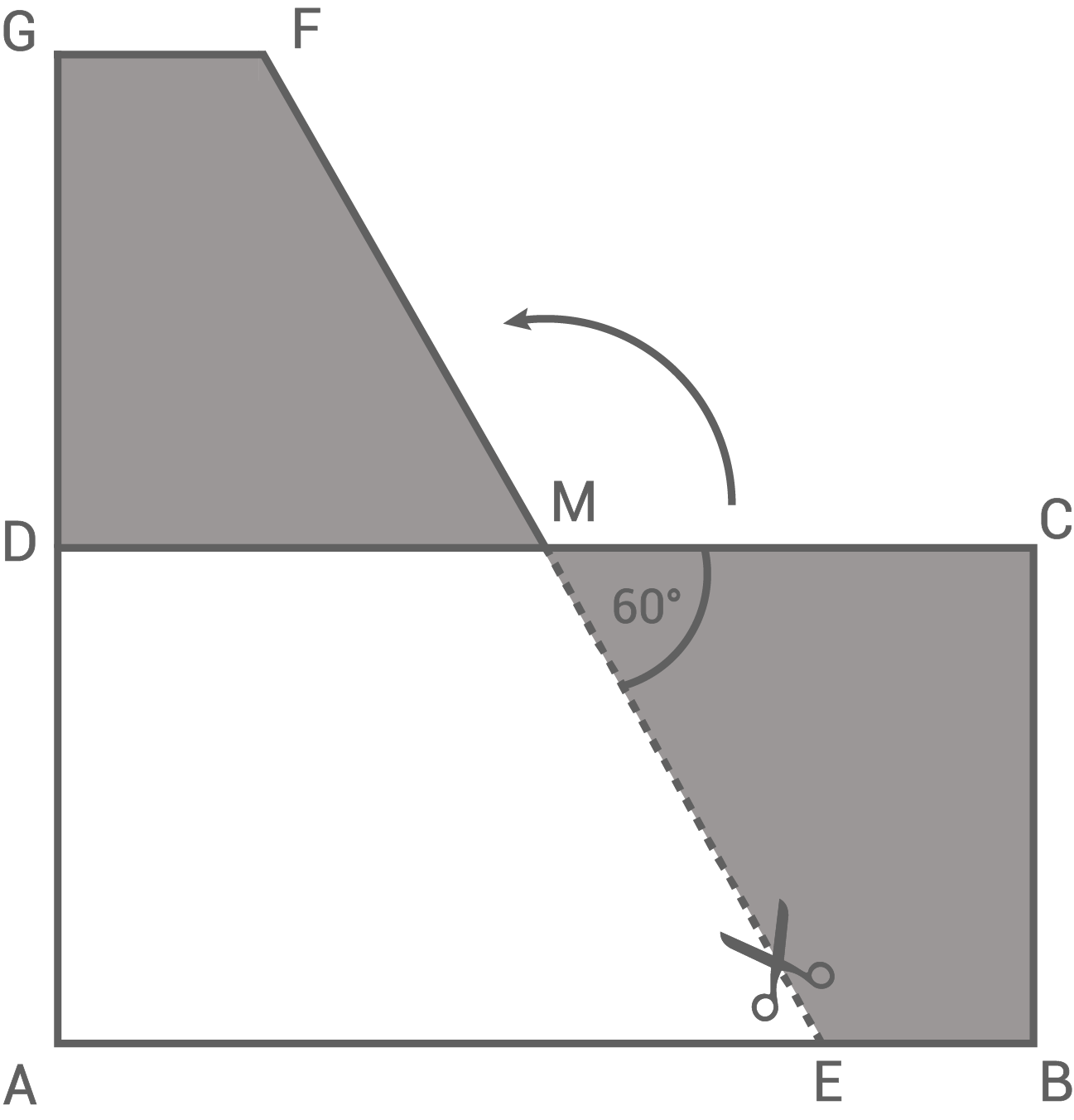
Die Innenwinkel eines Sechsecks sind 120° groß. Daher beträgt der Winkel im Dreiecks rechts 60°.
Die Länge der Strecke

entspricht der Länge der Strecke

Damit kann die halbe Höhe

von

berechnet werden, mit der dann die Seitenlänge

berechnet werden kann.
1. Schritt:  berechnen
berechnen




 2. Schritt:
2. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BC}^2&=&\left(\frac{1}{2}\overline{AB}\right)^2+h^2 \quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\overline{BC}&=&\sqrt{\left(\frac{1}{2}\overline{AB}\right)^2+h^2}
\\[5pt]
&=&\sqrt{\left(6,2\,\text{cm}\right)^2+(21,48\,\text{cm})^2}\\[5pt]
\overline{BC}&=&\underline{ 22,36\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/1802a7ad265c6902459ae8e88d33490d5ce2ab7ca281f1ae52d243997d56c164_light.svg) 3. Schritt: Umfang berechnen
3. Schritt: Umfang berechnen


 Beurteilen, ob Tom Recht hat und begründen
Argumentativ:
Beurteilen, ob Tom Recht hat und begründen
Argumentativ:
Das regelmäßige Sechseck besteht aus sechs gleichseitigen Dreiecken mit der Grundseite

und der Höhe

. Das Dreieck

hat ebenfalls die Grundseite

und die Höhe

.
Dadurch ist der Flächeninhalt des Dreiecks

doppelt so groß wie der eines der sechs gleichseitigen Dreiecke.
Damit ist der Flächeninhalt des Sechsecks dreimal so groß wie der Flächeninhalt des Dreiecks

.
Rechnerisch:



was dem Dreifachen entspricht.
Weitere mögliche Lösung:



Abschlussprüfung 2022
Lösung 6
a)
Länge der Strecke  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
Dazu wird zunächst die Länge der Strecke

berechnet:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overline{AB}}{\overline{AC}} \quad \scriptsize \mid\;\cdot\overline{AC}\;\\[5pt]
\cos(\alpha)\cdot \overline{AC}&=&\overline{AB} \quad \scriptsize \mid\; :\cos(\alpha) \\[5pt]
\overline{AC}&=&\dfrac{\overline{AB}}{\cos(\alpha)}\\[5pt]
\overline{AC} &=&\dfrac{13,2\,\text{cm}}{\cos(55^\circ)}\\[5pt]
\overline{AC} &=& 23,01\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/c3d5204d2ec558c4dcc216970b07a6a102b170f63aede46b10f96486cd75b543_light.svg)
Damit kann nun die Länge der Strecke

berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AC}-\overline{CE} \\[5pt]
&=& 23,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& \underline{ 15,01\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/23e52ccdfce04b53322bfcdd6d292c12543a8b6a4fbbb6c7cb3f56cf4dc220d3_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
Das Dreieck

ist gleichschenklig.
Begründung:
1.


2.

3.

4.

Daraus folgt:

Da das Dreieck

gleichschenklig ist, gilt:

Damit kann nun die Länge der Strecke

berechnet werden:
![\(\begin{array}[t]{rll}
\overline{DF}&=& \overline{DE}-\overline{EF} \\[5pt]
&=& \overline{AE}-\overline{EF} \\[5pt]
&=& 15,01\,\text{cm}-8,0\,\text{cm} \\[5pt]
&=& 7,01\,\text{cm}\\[5pt]
&=& \underline{\underline{ 7\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/f442d6c586f7ceed40a2c62e2ed229ff65b9eb637998beee9d8e69756df7832e_light.svg) Umfang des Vierecks
Umfang des Vierecks  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BF}}{\overline{DF}}\quad \scriptsize \mid\;\cdot \overline{DF} \\[5pt]
\sin(\alpha)\cdot\overline{DF} &=& \overline{BF}\\[5pt]
\sin(55^\circ)\cdot 7\,\text{cm} &=& \overline{BF}\\[5pt]
5,73\,\text{cm} &\approx& \overline{BF}\\
\overline{BF} &\approx&\underline{ 5,73\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/e7d829a371a9c767d08542e54dec5a8eb3d0bffd0da533cdb1bb9df15e6770b5_light.svg) 2. Schritt: Umfang berechnen
2. Schritt: Umfang berechnen
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Abschlussprüfung 2021
Lösung 7
a)
Die Teilaufgabe a) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
b)
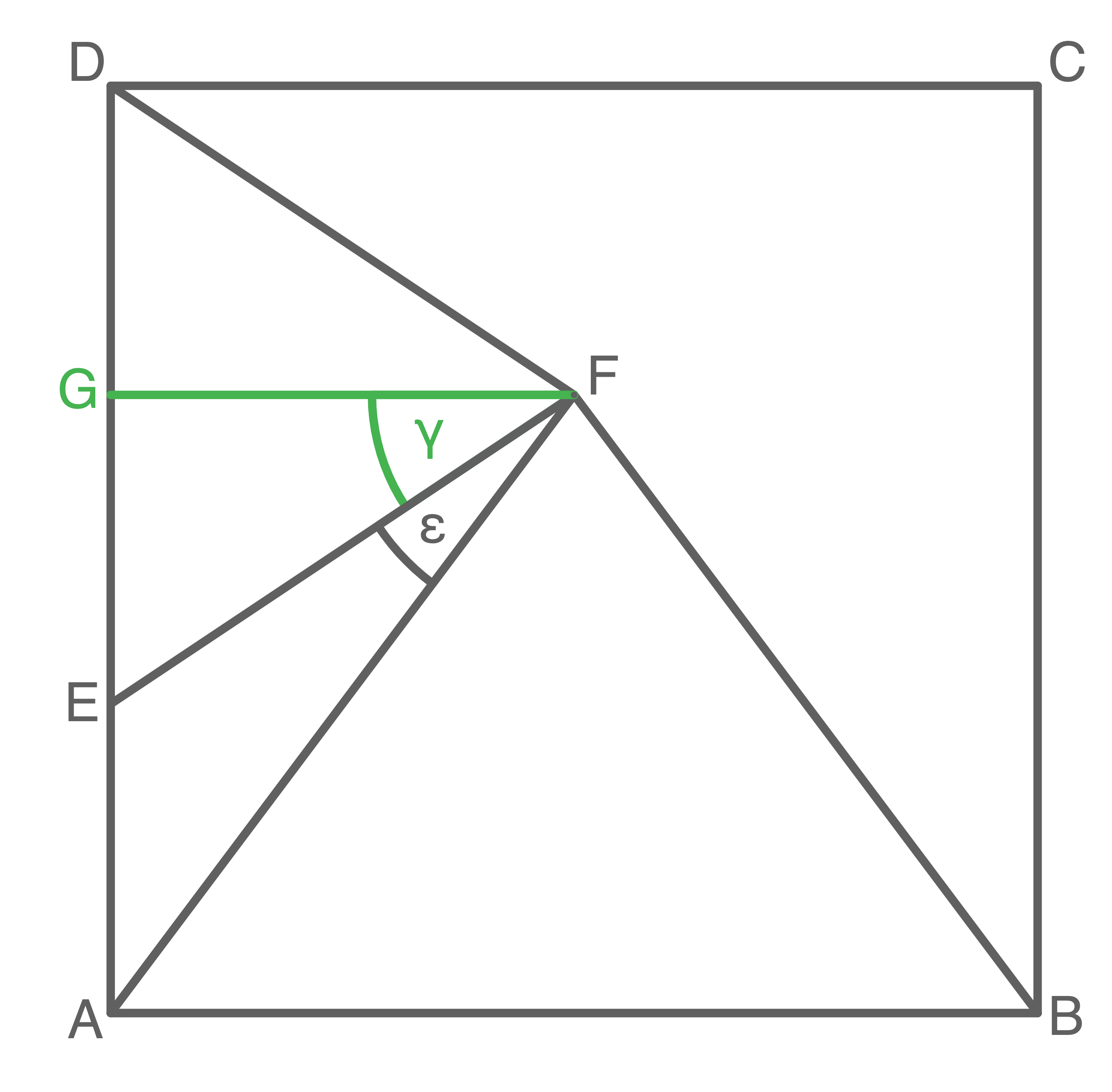
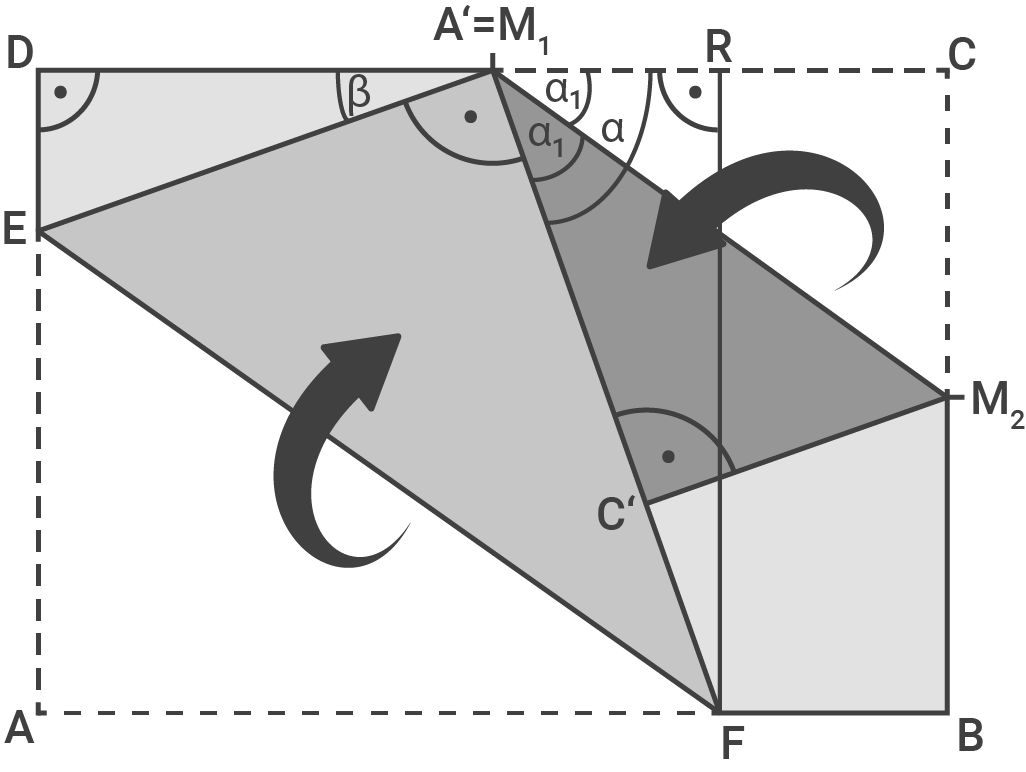
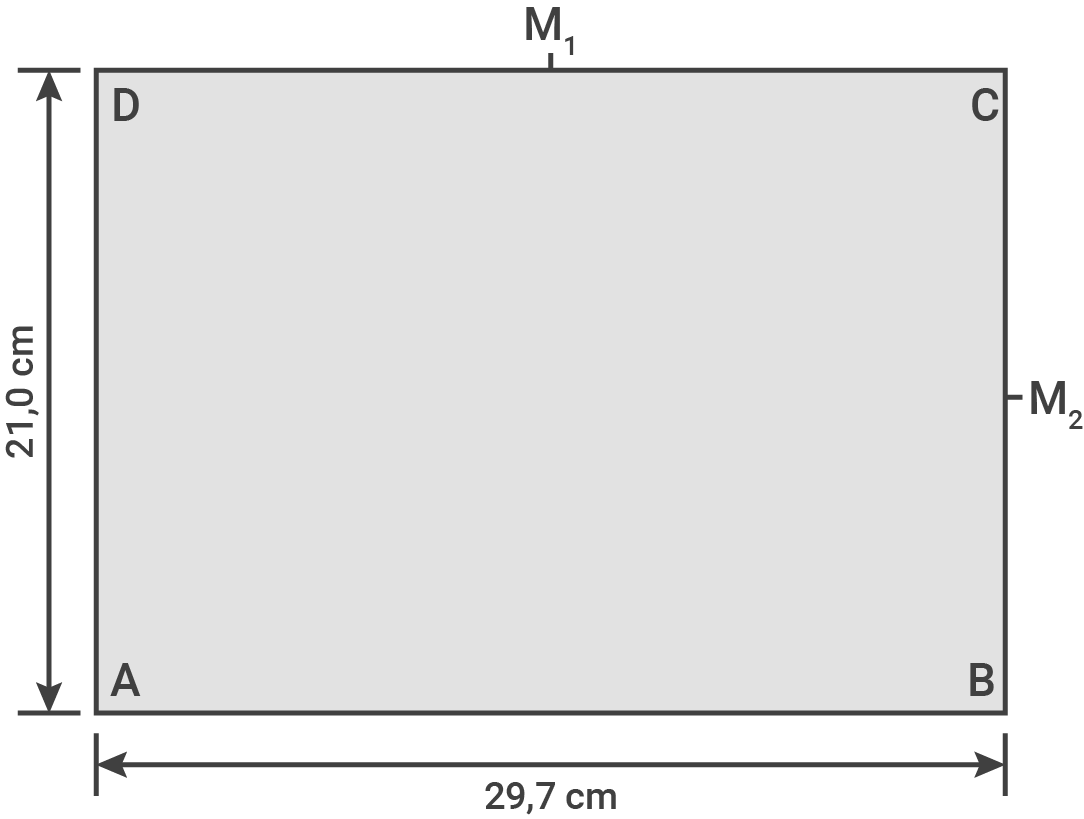
Flächeninhalt des Dreicks  berechnen
berechnen
Formel zur Berechnung des Flächeninhalts:
 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
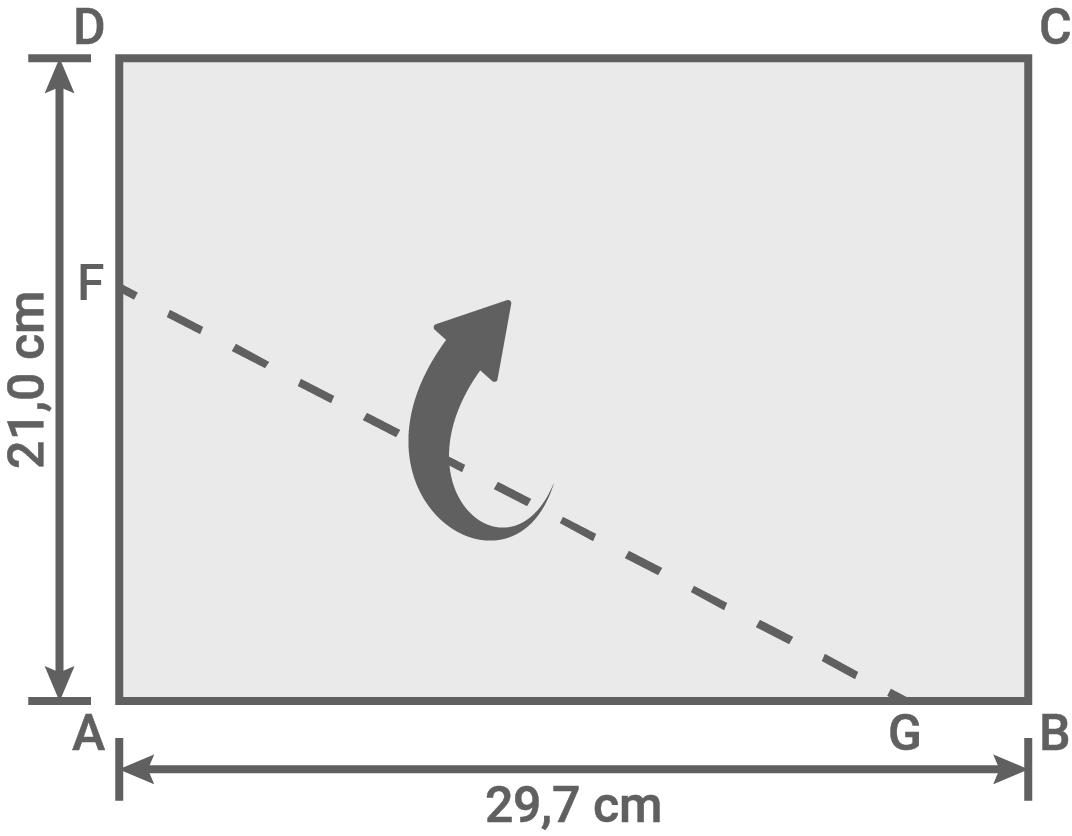
![\(\begin{array}[t]{rll}
\overline{M_1D}&=&\dfrac{1}{2}\cdot \overline{CD} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 29,7\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 14,85\,\text{cm} }
\end{array}\)](https://www.schullv.de/resources/formulas/e9d4ece7e27455a9444a5c015172586a4bfb47e29caee49ae3128785716d7013_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
Länge der Strecke

berechnen:
![\(\begin{array}[t]{rll}
\overline{M_2C}&=&\dfrac{1}{2}\cdot \overline{BC} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 21\,\text{cm} \\[5pt]
&=& 10,5\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/d04f309714c430572e655507f40ca0f01735f1f07e7b492cb055c95fb1f5f41f_light.svg)
Länge der Strecke

berechnen:
![\(\begin{array}[t]{rll}
\overline{CM_1}&=& \overline{M_1D}\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/ee7970f59d0829619da6a01bff18d34e70855c5515ae3b55951dd6849700d28b_light.svg)
Größe des Winkels

berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha_1)&=& \dfrac{\overline{M_2C}}{\overline{CM_1}} \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{\overline{M_2C}}{\overline{CM_1}}\right)&\quad \scriptsize \\[5pt]
\alpha_1&=& \tan^{-1}\left(\dfrac{10,5}{14,85}\right) &\quad \scriptsize \\[5pt]
\alpha_1&=& 35,26^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/af7fffc5616f491f0f500bef3ce5c3312b48bd32cc097d6eb8c6a8bcc718a87a_light.svg)
Größe des Winkels

berechnen:
![\(\begin{array}[t]{rll}
\alpha&=& 2\cdot \alpha_1 &\quad \scriptsize \\[5pt]
&=& 2\cdot 35,26^{\circ} &\quad \scriptsize \\[5pt]
&=& 70,52^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/2b2ec0b2d012e556731e707974db4e68d713a2a2bf3e68d0d7959b7d741bd2db_light.svg)
Größe des Winkels

berechnen:
![\(\begin{array}[t]{rll}
\beta&=& 180^{\circ}-90^{\circ}-\alpha &\quad \scriptsize \\[5pt]
&=& 180^{\circ}-90^{\circ}- 70,52^{\circ} &\quad \scriptsize \\[5pt]
&=& 19,48^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/1a8717e0557daf10dba456795cc590c662c34a83b3e1dc04ad22eed8def5eaed_light.svg)
Länge der Strecke

berechnen:
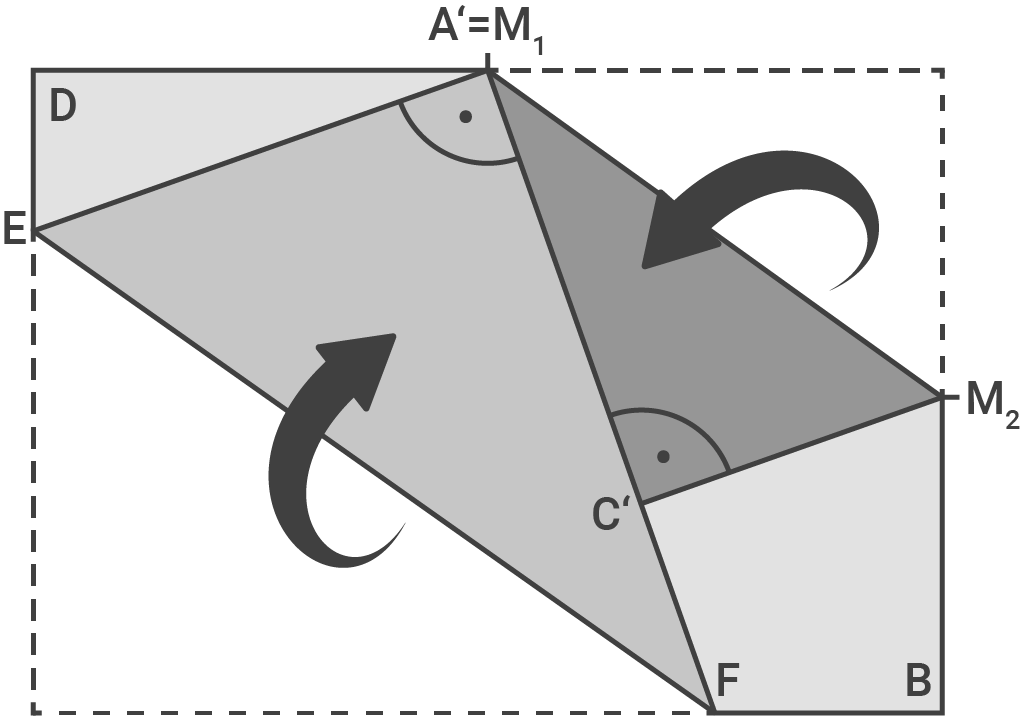
3. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A_{EM_1D}&=&\dfrac{1}{2}\cdot \overline{M_1D}\cdot \overline{DE} \\[5pt]
&=&\dfrac{1}{2}\cdot 14,85\,\text{cm} \cdot 5,25\,\text{cm} \\[5pt]
&=& 38,98\,\text{cm} ^2
\\[5pt]
&=& \underline{\underline{ 39\,\text{cm} ^2 }}
\end{array}\)](https://www.schullv.de/resources/formulas/328894f12375f29894e45cadd5b67aaad932b783464ae443e2a19873ef6d3d56_light.svg) Flächeninhalt des Vierecks
Flächeninhalt des Vierecks  berechnen
berechnen
Formel zur Berechnung des Flächeninhalts:
 1. Schritt: Flächeninhalt des Dreiecks
1. Schritt: Flächeninhalt des Dreiecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{M_1M_2C}&=&\dfrac{1}{2}\cdot \overline{M_2C}\cdot \overline{CM_1} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 10,5\,\text{cm} \cdot 14,85\,\text{cm} &\quad \scriptsize \\[5pt]
&= & \underline{ 77,96 \,\text{cm}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/d57533c299534bf11b564966c2cb537f253f2ee57d8b00dd69dee2f30ccae0d4_light.svg) 2. Schritt: Flächeninhalt des Trapezes
2. Schritt: Flächeninhalt des Trapezes  berechnen
berechnen
Formel zur Berechnung des Flächeninhalts:

Länge der Strecke

berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha) &=&\dfrac{\overline{FR}}{\overline{RM_1}} \quad \scriptsize \mid\; \cdot \overline{RM_1} \\[5pt]
\tan(\alpha)\cdot \overline{RM_1} &=& \overline{FR} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{RM_1} &=& \dfrac{\overline{FR} }{\tan(\alpha)} \quad \scriptsize \\[5pt]
\overline{RM_1} &=& \dfrac{21\,\text{cm} }{\tan(70,52^{\circ} )} \quad \scriptsize \\[5pt]
\overline{RM_1}&=& 7,43\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/2ef0d1956fce75632e57ffb41699572a434364cd88937a182b95fc582752c114_light.svg)
![\(\begin{array}[t]{rll}
\overline{CR}&=&\overline{CM_1}-\overline{RM_1} &\quad \scriptsize \\[5pt]
&=& 14,85\,\text{cm} - 7,43\,\text{cm} &\quad \scriptsize \\[5pt]
&=& 7,42\,\text{cm} = \overline{BF}
\end{array}\)](https://www.schullv.de/resources/formulas/8f51288e66b6bd3f069f48523f68332770343ee5b9c3c494e7f18c6ee3359129_light.svg)
Es gilt also:
3. Schritt: Flächeninhalt des Vierecks  berechnen
berechnen
Abschlussprüfung 2021
Lösung 8
a)
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{BF}}{\overline{BC}} \quad \scriptsize \mid\; \cdot\overline{BC}\\[5pt]
\cos(\beta)\cdot\overline{BC}&=&\overline{BF}\\[5pt]
\overline{BF}&=&\cos(60^\circ)\cdot 4,8\,\text{cm}\\[5pt]
\overline{BF}&=&\underline{ 2,4\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/3a05be29573d42c967eb294545a16fc6569f223204d55e75b22c9ee8c6b8785c_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CF}^2+\overline{BF}^2&=&\overline{BC}^2 \quad\quad\quad\quad \quad \quad \quad \scriptsize \mid\;
-\overline{BF}^2\\[5pt]
\overline{CF}^2&=&\overline{BC}^2-\overline{BF}^2 \quad \quad \quad \quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
\overline{CF}&=&\sqrt{\overline{BC}^2-\overline{BF}^2} \\[5pt]
&=&\sqrt{(4,8\,\text{cm})^2-(2,4\,\text{cm})^2} \\[5pt]
\overline{CF}&=&\underline{ 4,16\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/4434674e68c931b52ab28236e991006d26dba0ee8527b650341a629aa824c376_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{\overline{DE}}{\overline{AE}} \quad \scriptsize \mid\; \cdot\overline{AE}\quad \scriptsize
\mid\; :\tan(\alpha)\\[5pt]
\overline{AE}&=&\dfrac{\overline{DE}}{\tan(\alpha)}\\[5pt]
\overline{AE} &=&\dfrac{4,16\,\text{cm}}{\tan(70^\circ)}\\[5pt]
\overline{AE}&=&\underline{ 1,51\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/027e7becd7be30033bdac40fbee6de6f36c34720dac3e1a6ed986d19e87606dd_light.svg) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD}&=&\overline{AB}-\overline{BF}-\overline{AE}&\quad \scriptsize \\[5pt]
&=& 6,0\,\text{cm}-2,4\,\text{cm}-1,51\,\text{cm} &\quad \scriptsize \\[5pt]
&=& \underline{\underline{ 2,09\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/f2ef4b7a5cacef2a80ac67bfdaaf3f85f91689a6797d7d1d197e4911982f444b_light.svg)
b)
Die Teilaufgabe b) wurde in das Thema "Funktionen und Gleichungen" eingeordnet.
Musterprüfung 1
Lösung 9
a)
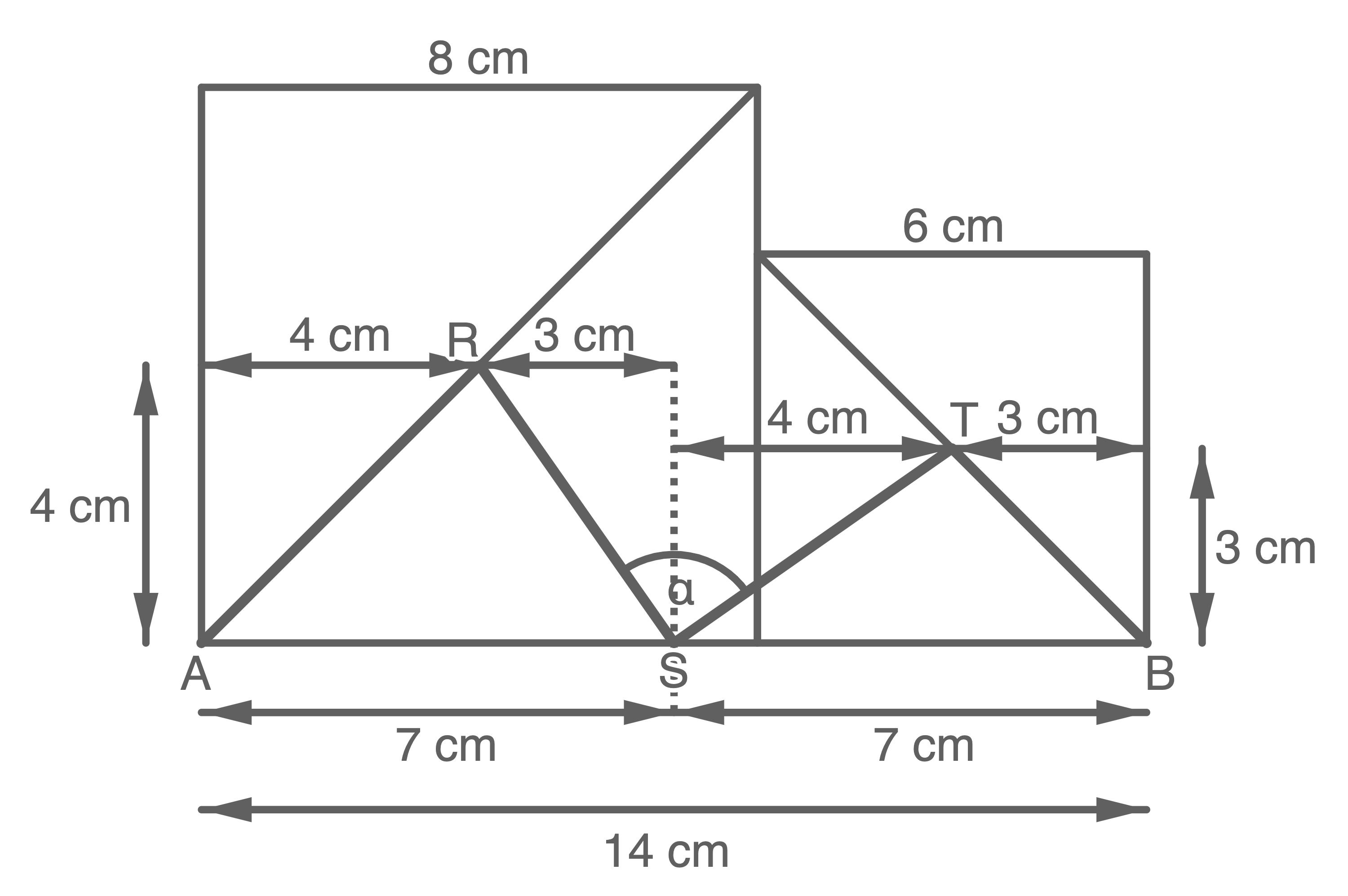
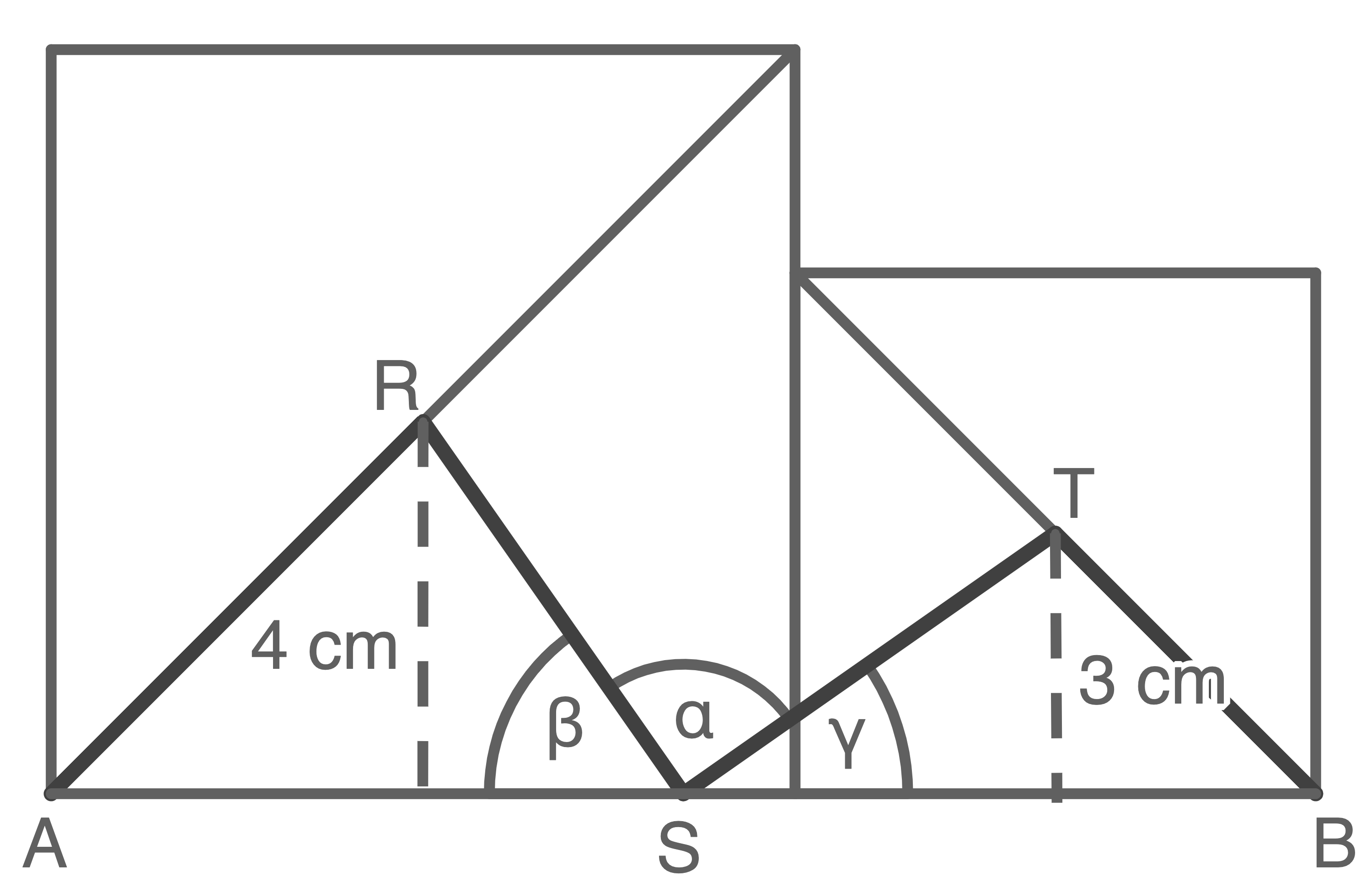
Länge des Streckenzugs  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AR}^2&=& (4 \,\text{cm})^2 + (4 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{AR}&=& \sqrt{(4 \,\text{cm})^2 + (4 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5,66 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/f9ad5ac534a05e6d4ff294fdc92d9267d7f96c82610e97ac30177b2ef95a3fdf_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{RS}^2&=& (4 \,\text{cm})^2 + (3 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{RS}&=& \sqrt{(4 \,\text{cm})^2 + (3 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/7050c29b7c6b9217cf22ff15aca12056e6c0c6bd4cdc633e43c4acb1f35c59fb_light.svg) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{ST}^2&=& (3 \,\text{cm})^2 + (4 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{ST}&=& \sqrt{(3 \,\text{cm})^2 + (4 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 5 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/a87ac3fc1815f17348789ff2e83cfe320c021ffbaa29e11fb2ee8b6ee7f00695_light.svg) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{TB}^2&=& (3 \,\text{cm})^2 + (3 \,\text{cm})^2 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
\overline{TB}&=& \sqrt{(3 \,\text{cm})^2 + (3 \,\text{cm})^2 } \\[5pt]
&=& \underline{ 4,24 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/81de60fa3b1a6093edc433686041f61df47a45ad28a79a9e8c1795a4ccb18d15_light.svg) 6. Schritt: Gesamten Streckenzug
6. Schritt: Gesamten Streckenzug  berechnen
Größe des Winkels
berechnen
Größe des Winkels  berechnen
1. Schritt: Größe des Winkels
berechnen
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma)&=& \dfrac{3\,\text{cm}}{5\,\text{cm}}\\[5pt]
\gamma&=& \underline{ 36,9^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/79908b405a3920cc9cbf187d6f61791ebc797d6f3d64af6ba457e590d8f8eed5_light.svg) 2. Schritt: Größe des Winkels
2. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{4\,\text{cm}}{5\,\text{cm}}\\[5pt]
\beta&=& \underline{ 53,1^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/0424f537bb82a1f05ff97832c5572ec6432f7d073ff53a4c66ee9ff2a73febd8_light.svg) 3. Schritt: Größe des Winkels
3. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\alpha&=& 180^{\circ} -\gamma - \beta &\quad \scriptsize \\[5pt]
\alpha&=& 180^{\circ} -36,9^{\circ} - 53,1^{\circ} &\quad \scriptsize \\[5pt]
&=& \underline{\underline{ 90^{\circ}}}
\end{array}\)](https://www.schullv.de/resources/formulas/ae9c1fa8af94f4229bbc65b1ca8964c437d128be989406ee2771855a244b940a_light.svg)
b)
Die Teilaufgabe b) wurde in das Thema "Anwendungsaufgaben" eingeordnet.
Musterprüfung 2
Lösung 10
a)
Formel zur Berechnung des Flächeninhalts:
 Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
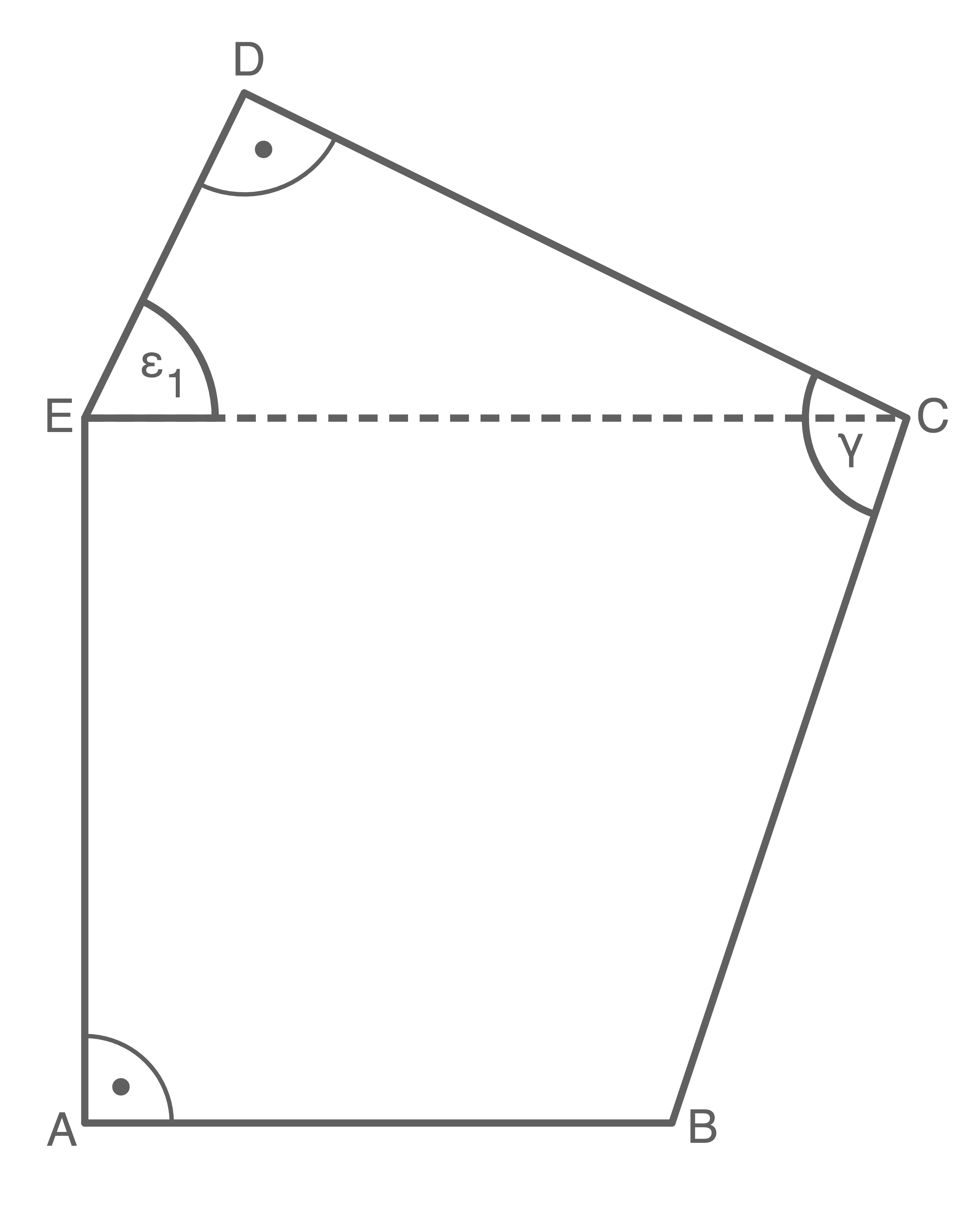
\sin(\varepsilon_1 )&=&\dfrac{\overline{CD}}{\overline{EC}} &\quad \scriptsize \\[5pt]
\sin(64^{\circ} )&=&\dfrac{9,5\,\text{cm}}{\overline{EC}} &\quad \scriptsize \mid\; \cdot \overline{EC} \\[5pt]
\sin(64^{\circ} )\cdot \overline{EC} &=& 9,5\,\text{cm} &\quad \scriptsize \mid\; : \sin(64^{\circ} ) \\[5pt]
\overline{EC}&=&\dfrac{9,5\,\text{cm}}{\sin(64^{\circ})} \\[5pt]
\overline{EC}&= &\underline{ 10,57\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/21d327c8ef5f391b877bbe963403454b0f35ef406d1c3e838670aff27447999b_light.svg) Länge der Strecke
Länge der Strecke  berechnen
1. Schritt: Größe des Winkels
berechnen
1. Schritt: Größe des Winkels  berechnen
berechnen
 2. Schritt: Länge der Seite
2. Schritt: Länge der Seite  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma_1)&=&\dfrac{\overline{FD}}{\overline{CD}} \quad \scriptsize
\\[5pt]
\sin(26 ^{\circ} )&=&\dfrac{\overline{FD}}{9,5\,\text{cm}} \quad \scriptsize \mid\; \cdot 9,5\,\text{cm} \\[5pt]
\sin(26 ^{\circ} )\cdot 9,5\,\text{cm} &=& \overline{FD} & \\[5pt]
\overline{FD} &=& \sin(26 ^{\circ} )\cdot 9,5\,\text{cm} & \\[5pt]
\overline{FD} &= &\underline{ 4,16\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/6fb9c79a8f7ac80201dc811f29cab58abb83774455652709ad27684271da2fe2_light.svg)
3. Schritt: Länge der Strecke

berechnen
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{HD}-\overline{FD} \\
&=& 12,9\,\text{cm}-4,16\,\text{cm} \\[5pt]
&=& \underline{ 8,74\,\text{cm} }
\end{array}\)](https://www.schullv.de/resources/formulas/432009508e251492ca921e092b7599c448cacb17977fdcfc48ba1f85799017a5_light.svg) Länge der Strecke
Länge der Strecke  berechnen
1. Schritt: Größe des Winkels
berechnen
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma_2&=& \gamma-\gamma_1 \\[5pt]
&=& 95^{\circ}-26^{\circ} \\[5pt]
&=& \underline{ 69^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/4ef11eb799682b4d4748d3af087ecbc9db6b28016f768bf6d9db466c65781ba3_light.svg) 2. Schritt: Länge der Seite
2. Schritt: Länge der Seite  berechnen
berechnen

![\(\begin{array}[t]{rll}
\tan(\gamma_2)&=&\dfrac{\overline{BG}}{\overline{CG}} \\[5pt]
\tan(69^{\circ} )&=&\dfrac{8,74\,\text{cm}}{\overline{CG}} &\quad \scriptsize \mid\; \cdot \overline{CG} \\[5pt]
\tan(69^{\circ} ) \cdot \overline{CG} &=&8,74 \,\text{cm} &\quad \scriptsize \mid\; : \tan(69^{\circ} ) \\[5pt]
\overline{CG}&=&\dfrac{8,74\,\text{cm}}{\tan(69^{\circ})} \\[5pt]
\overline{CG}&= &\underline{ 3,35\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/94d5c9aeb0e2f9fadc55e6ac159cb536fd09b8ea759c93b859d2267f63132ba0_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AB}&=& \overline{EC}-\overline{CG}&\quad \scriptsize \\[5pt]
&=& 10,57\,\text{cm}-3,35\,\text{cm}&\quad \scriptsize \\[5pt]
&=& \underline{ 7,22\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/1d1feb42cf7ab370247d7cf348626658efeeb15a5f3d4c3faf06bc9aceae542d_light.svg) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot (\overline{AB}+\overline{EC})\cdot \overline{AE}\\[5pt]
&=&\dfrac{1}{2}\cdot (7,22\,\text{cm}+10,57\,\text{cm}) \cdot 8,74\,\text{cm} \\[5pt]
&=& 77,74\,\text{cm}^2
\\[5pt]
A&=&\underline{\underline{ 77,7\,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/97dc776be09ae896b647dfe8d9ba773b5e6e71621dfeb951ba71f29a5f69ac40_light.svg)
b)
Formel zur Berechnung des Flächeninhalts:

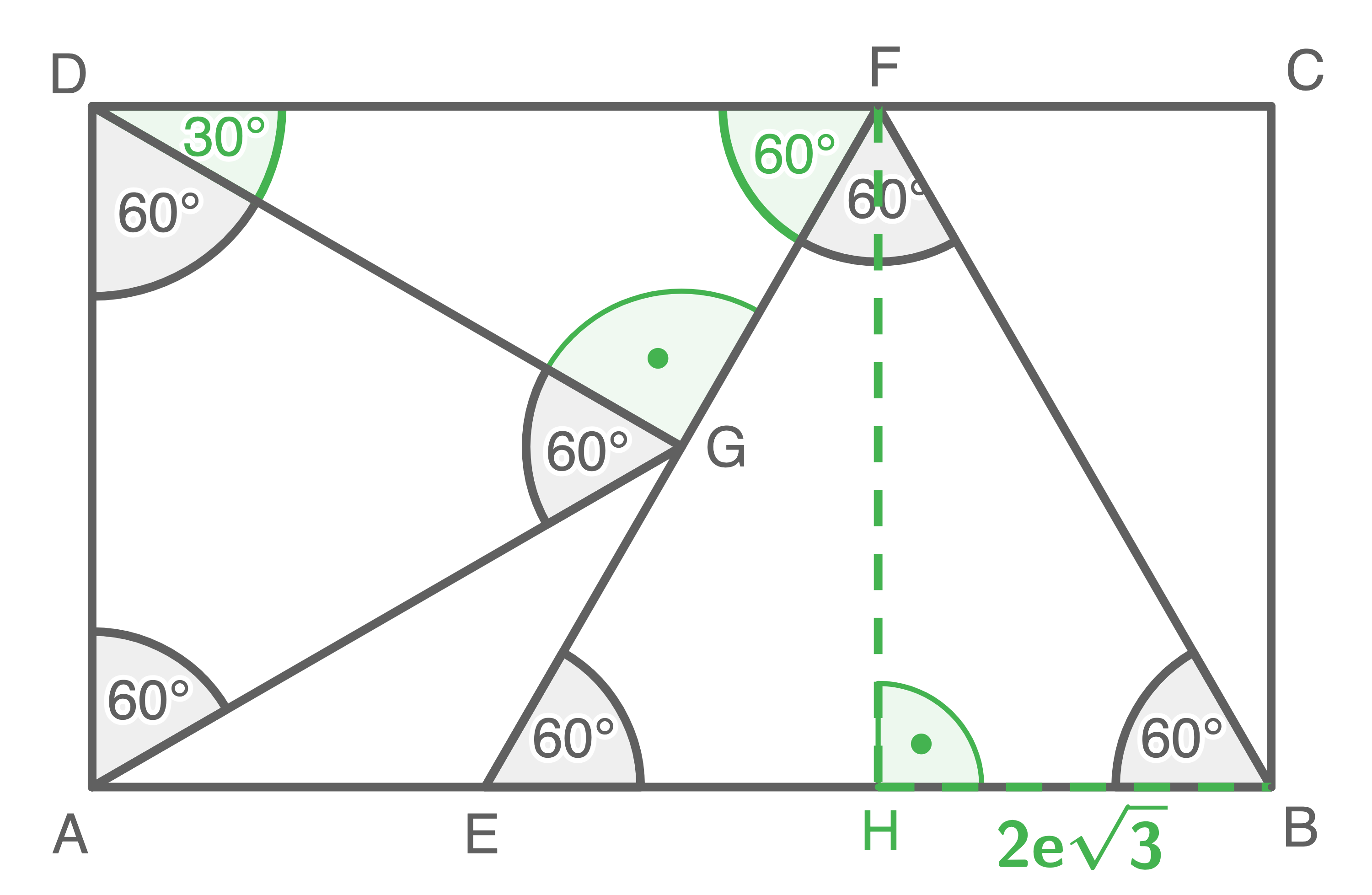
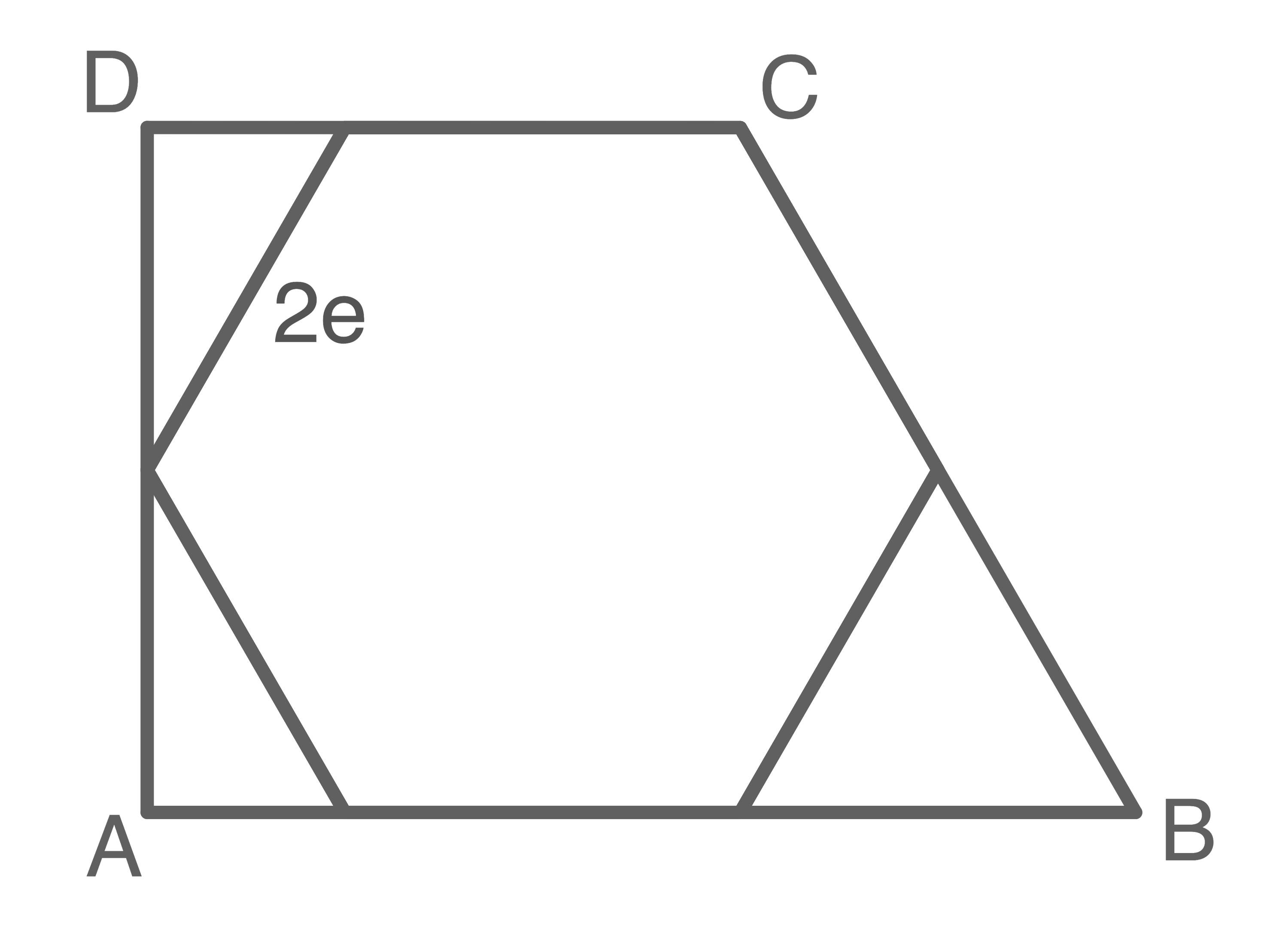
In einem gleichseitigen Dreieck sind alle Winkel

groß:
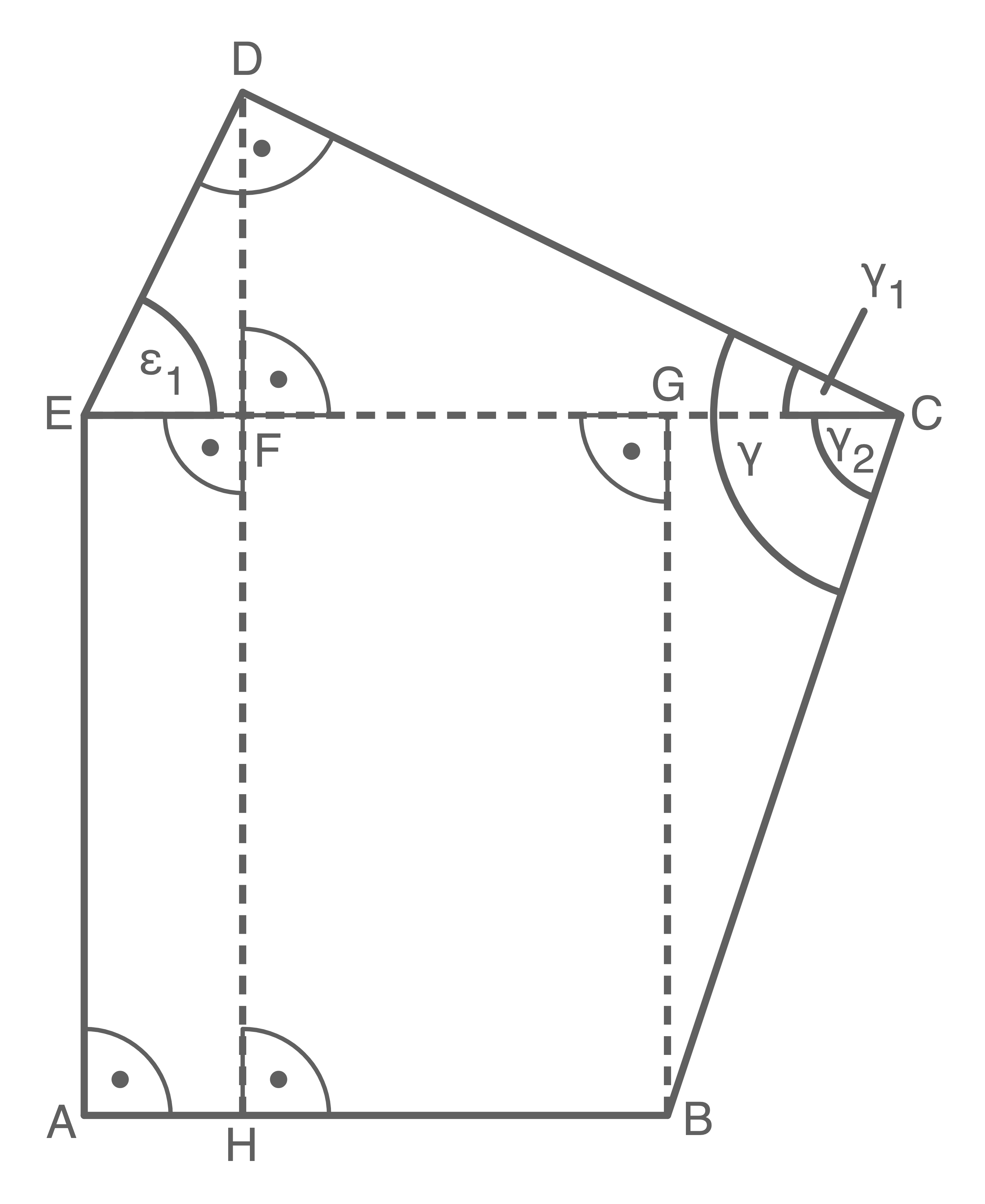
1. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\tan(60^{\circ})&=&\dfrac{\overline{HF}}{2\mathrm{e}\sqrt{3}} \quad \scriptsize \mid\; \cdot 2 \mathrm{e}\sqrt{3}
\\[5pt]
\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3} &=& \overline{HF}\\[5pt]
\overline{HF} &=&\tan(60^{\circ}) \cdot 2 \mathrm{e}\sqrt{3}\\[5pt]
\overline{HF}&=&\underline{ 6\mathrm{e}} \quad = \overline{AD} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b3240df0881a1e23d75721ce5c157bb5fd89e7fc72b5d158f5fca43dac2b89d3_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
Da in einem gleichseitigen Dreieck alle Seiten gleich lang sind, gilt

![\(\begin{array}[t]{rll}
\cos(30^{\circ}) &=& \dfrac{\overline{DG}}{\overline{DF}} \\[5pt]
\cos(30^{\circ}) &=& \dfrac{6\mathrm{e}}{\overline{DF}}\quad \scriptsize \mid\; \cdot \overline{DF}\\[5pt]
\cos(30^{\circ}) \cdot \overline{DF} &=& 6\mathrm{e} \quad \scriptsize \mid\; :\cos(30^{\circ}) \\[5pt]
\overline{DF} &=& \dfrac{6\mathrm{e}}{\cos(30^{\circ})} \\[5pt]
\overline{DF} &=& \underline{ 4 \mathrm{e}\sqrt{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/55cb1b844e283fafe8b9a711d28431f86e4f09b6b632ffa2eb2a5210848c5055_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen

![\(\begin{array}[t]{rll}
\overline{DC}&=& \overline{DF} + \overline{FC}\\[5pt]
&=& 4 \mathrm{e}\sqrt{3} + 2 \mathrm{e}\sqrt{3}\\[5pt]
&=& \underline{ 6\mathrm{e}\sqrt{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/11562293c7100cef302115bd5f35553c93623463a60b4911390ee9250e07b738_light.svg) 4. Schritt: Flächeninhalt berechnen
4. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& \overline{AD} \cdot \overline{DC} \\[5pt]
&=& 6\mathrm{e} \cdot 6\mathrm{e}\sqrt{3} \\[5pt]
&=& \underline{\underline{ 36\mathrm{e}^2\sqrt{3}}}
\end{array}\)](https://www.schullv.de/resources/formulas/ecff40f0f903c480e387d5f3f2b9833c731639c50af2a768776d904803f80a21_light.svg)
Damit ist die Aussage bewiesen.
Lösung 11
a)
1. Schritt: Länge der Strecke  berechnen
berechnen
Satz des Pythagoras anwenden
![\(\begin{array}[t]{rll}
\overline{AF}^2&=& \overline{AG}^2+\overline{FG}^2\quad \scriptsize \mid\;-\overline{AG}^2 \\[5pt]
\overline{FG}^2&=&\overline{AF}^2-\overline{AG}^2\\[5pt]
\overline{FG}^2&=&(3,4\,\text{cm})^2-(1,7\,\text{cm})^2\quad \scriptsize \mid\; \sqrt{\,\,\,} \\[5pt]
\overline{FG}&=& \sqrt{(3,4\,\text{cm})^2-(1,7\,\text{cm})^2}\\[5pt]
\overline{FG}&=& \underline{ 2,94\,\text{cm} }
\end{array}\)](https://www.schullv.de/resources/formulas/47c200cf3f30cf6086e2fa21d9012ee60085c5b41d5f81b7c61017dfb94cbb14_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Größe des Winkels
berechnen
Größe des Winkels  berechnen
berechnen
Da das Dreieck

gleichschenklig ist, gilt

![\(\begin{array}[t]{rll}
\cos(\beta)&=&\dfrac{\overline{FI}}{\overline{CF}} &\quad \\[5pt]
\cos(\beta)&=&\dfrac{1,7\,\text{cm} }{7,0\,\text{cm} } \\[5pt]
\beta&=&\underline{ 75,94^{\circ}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f47829dc4bc7131cff114d726532cc7a3d55f2ba86cbe66f98e54209d381000e_light.svg) Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=&180^{\circ}-\beta-\dfrac{\alpha}{2} \\[5pt]
\gamma&=&180^{\circ}-75,94^{\circ}-\dfrac{60^{\circ}}{2} \\[5pt]
\gamma&=&\underline{ 74,06^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/72ff6465ef5ece0b0a912047d3a488cfcf4a9e5390fa17154e7dca784c1f09ce_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\gamma)&=&\dfrac{\overline{HF}}{\overline{CF}} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{HF}&=&\overline{CF}\cdot \cos(\gamma) \\[5pt]
\overline{HF}&=&7,0\,\text{cm}\cdot \cos(74,06^{\circ}) \\[5pt]
\overline{HF}&=&\underline{ 1,92\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/8db02f0d87cd45c689719dc60f3a8be45e4b6870b6d44bece549ea30b24d0b8d_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\gamma)&=&\dfrac{\overline{CH}}{CF} &\quad \scriptsize \mid\;\cdot\overline{CF} \\[5pt]
\overline{CH}&=&\overline{CF}\cdot \sin(\gamma) \\[5pt]
\overline{CH}&=&7,0\,\text{cm}\cdot \sin(74,06^{\circ}) \\[5pt]
\overline{CH}&=&\underline{ 6,73\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7b9a3cddf7b716c276bb1781c596c67b2ec89b456ba6bfe64a1e87792f354721_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan\left(\dfrac{\delta}{2}\right)&=&\dfrac{\overline{CH}}{\overline{DH}} &\quad \scriptsize \mid\;\cdot
\overline{DH} \\[5pt]
\overline{DH}\cdot \tan\left(\dfrac{\delta}{2}\right) &=& \overline{CH}&\quad\scriptsize
\mid\;:\tan\left(\dfrac{\delta}{2}\right) \\[5pt]
\overline{DH}&=&\dfrac{\overline{CH}}{\tan\left(\dfrac{\delta}{2}\right)} \\[5pt]
\overline{DH}&=&\dfrac{6,73\,\text{cm}}{\tan(59^{\circ})} \\[5pt]
\overline{DH}&=&\underline{ 4,04\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/5394a66daf68c0e9247f976c3ecbaeb15022a3b334a2596795e99f8679e03b4f_light.svg) 3. Schritt: Abstand des Punktes
3. Schritt: Abstand des Punktes  zur Strecke
zur Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DG}&=&\overline{DH}+\overline{HF}+\overline{FG} & \\[5pt]
\overline{DG}&=&4,04\,\text{cm}+1,92\,\text{cm}+2,94\,\text{cm} \\[5pt]
\overline{DG}&=&\underline{\underline{ 8,9\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/249199456a9a8cc30ec1111d7ee985dccd0a5037a45caef03fe4f3392c347bca_light.svg)
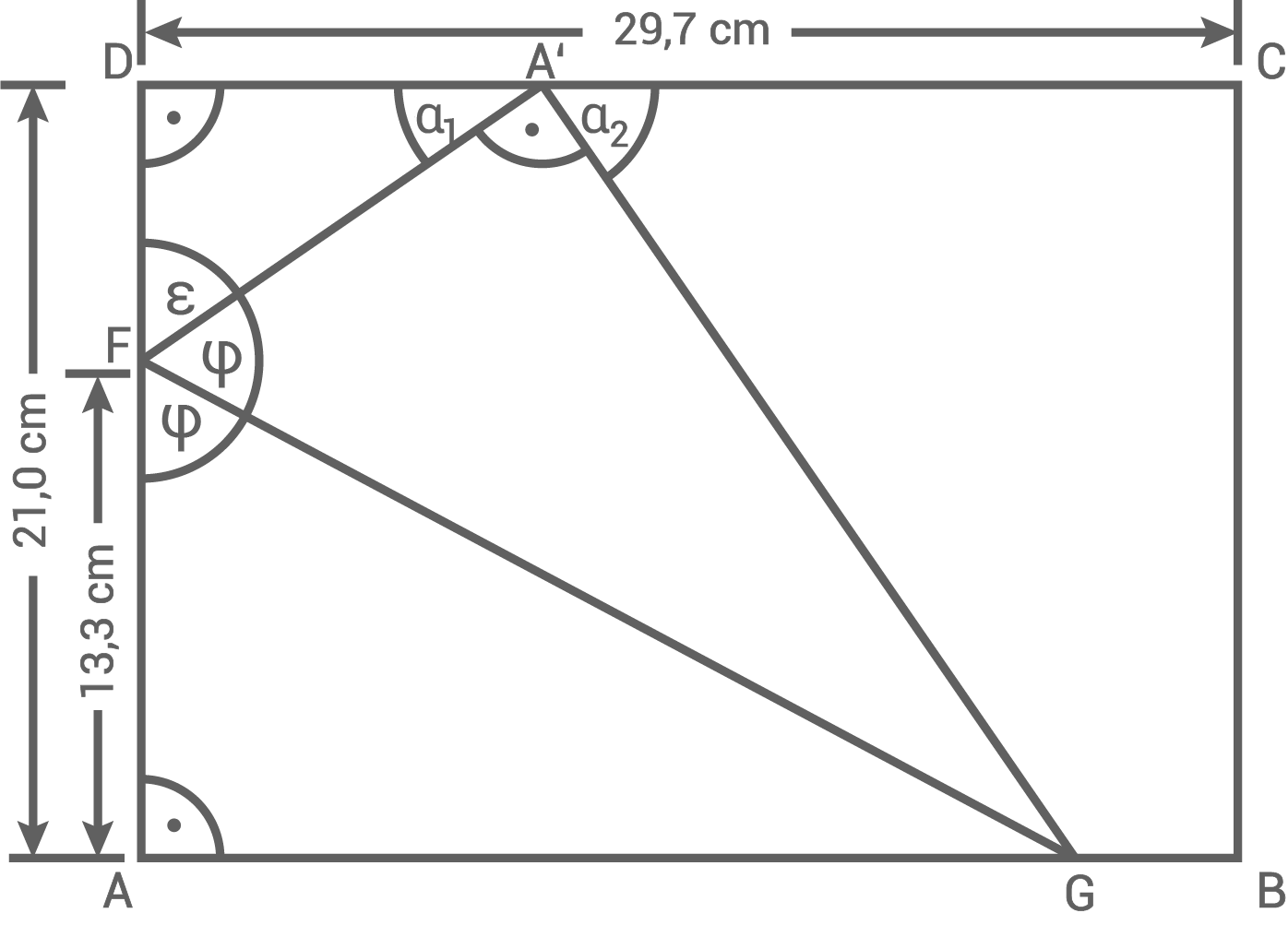
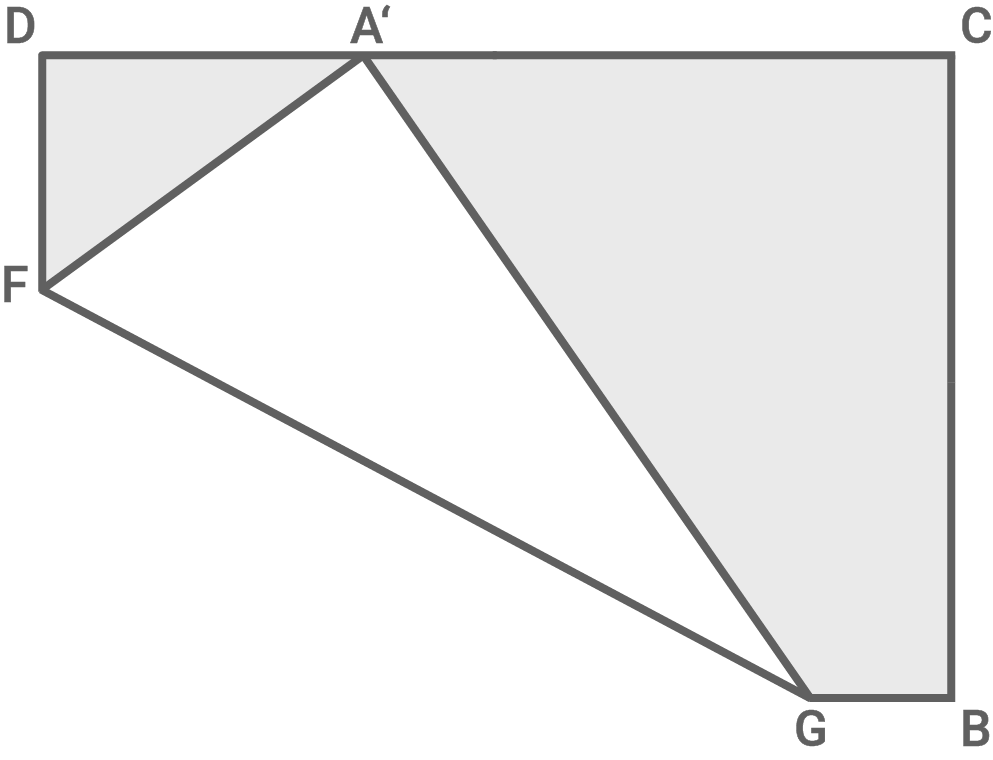
b)
1. Schritt: Länge der Strecke  berechnen
Länge der Strecke
berechnen
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DF}&=&\overline{DA}-\overline{AF} & \\[5pt]
\overline{DF}&=&21,0\,\text{cm}-13,3\,\text{cm} \\[5pt]
\overline{DF}&=&\underline{ 7,70\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/129a7793847a2743ebf1a395a75cf6874379ca5d7671a1ceb1fa6281e2e1aafb_light.svg) Länge der Srecke
Länge der Srecke  mit dem Satz des Pythagoras berechnen
mit dem Satz des Pythagoras berechnen
![\(\begin{array}[t]{rll}
\overline{A](https://www.schullv.de/resources/formulas/df950dfe69650dd3d39a541694d35689323330fe9a1843dfc93dcddc50278979_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CA](https://www.schullv.de/resources/formulas/ba28a459984ea378c17ecc1fa44cf8905cc41ac10829a9c95d9f92aa6097192b_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Größe des Winkels
berechnen
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\epsilon)&=&\dfrac{\overline{A](https://www.schullv.de/resources/formulas/c667875bd025cc090648161fb8e1afd79b3db80efb91373d2e01ee0dad1a8475_light.svg) Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
180^{\circ}&=&2\cdot \varphi+\epsilon &\quad \scriptsize \mid\;-\epsilon \\[5pt]
2\cdot \varphi&=&180^{\circ}-\epsilon &\quad \scriptsize \mid\; :2 \\[5pt]
\varphi&=&(180^{\circ}-\epsilon):2 \\[5pt]
\varphi&=&(180^{\circ}-54,61^{\circ}):2 \\[5pt]
\varphi&=&\underline{ 62,70^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/6c51ef5bc2315aeb7a70c9c772c0ae4ff55b4e1a7d3216c3aec562728be1ece1_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\varphi)&=&\dfrac{\overline{AG}}{\overline{AF}} &\quad \scriptsize \mid\;\cdot \overline{AF} \\[5pt]
\overline{AG}&=&\overline{AF}\cdot \tan(\varphi) \\[5pt]
\overline{AG}&=&13,3\,\text{cm}\cdot \tan(62,70^{\circ}) \\[5pt]
\overline{AG}&=&\underline{ 25,77\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ec93cfb1ba331a91a71ee9ea2d9e0b00292866fb63f17828b4f86afeba743dc7_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{GB}&=&\overline{AB}-\overline{AG} & \\[5pt]
\overline{GB}&=&29,7\,\text{cm}-25,77\,\text{cm} \\[5pt]
\overline{GB}&=&\underline{ 3,93\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e5f51b8061a67f0141152540fe5796aa3d9ce01b1e8614c85f3cca49e1805ffa_light.svg) 3. Schritt: Flächeninhalt des Vierecks berechnen
3. Schritt: Flächeninhalt des Vierecks berechnen
![\(\begin{array}[t]{rll}
A&=&\frac{1}{2}\cdot (\overline{GB}+\overline{CA](https://www.schullv.de/resources/formulas/f36d9905383800b50b19d220ceb2bdca48897a4e314faf0f6bd5db139643fb14_light.svg)
Abschlussprüfung 2019
Lösung 12
a)
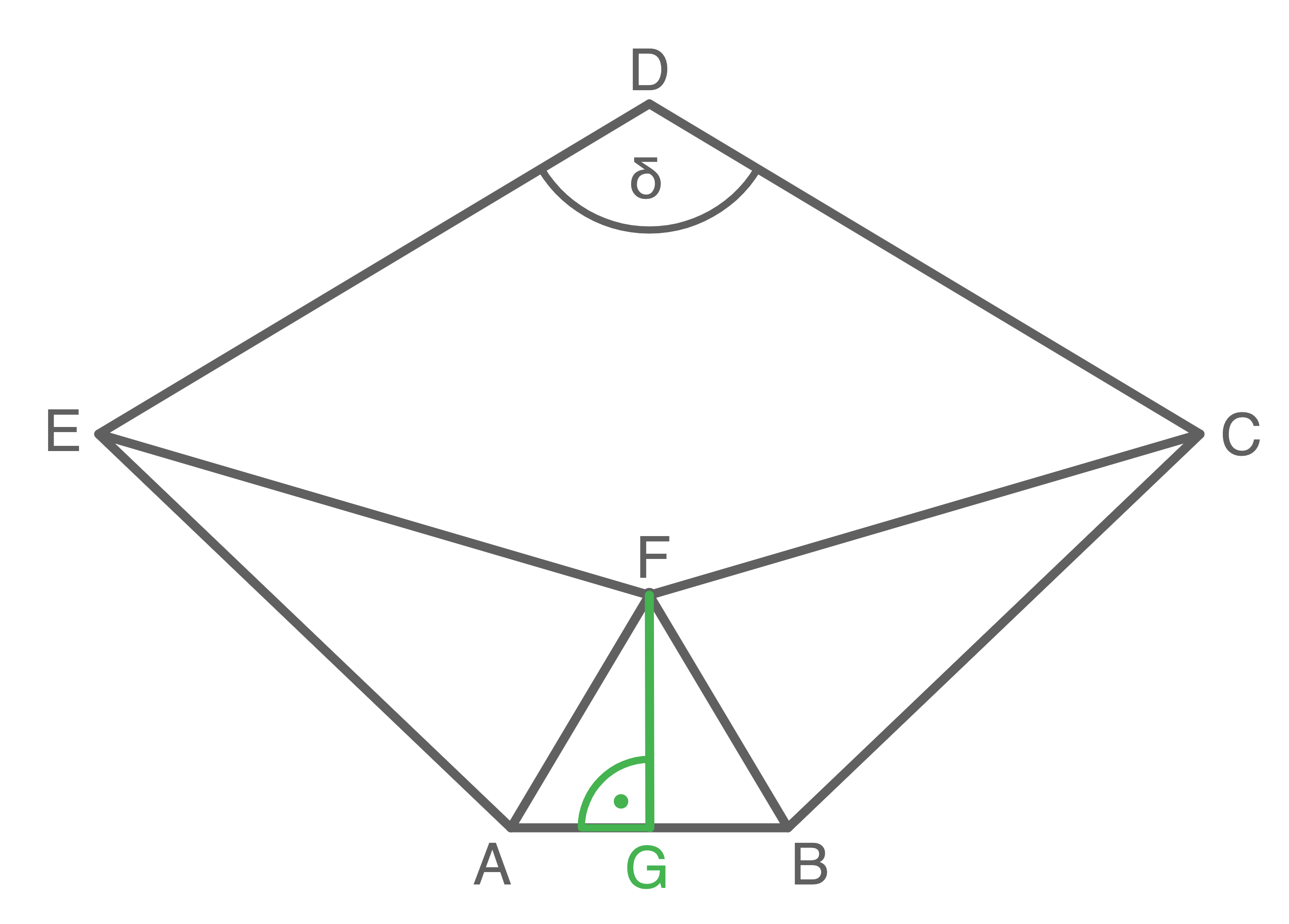
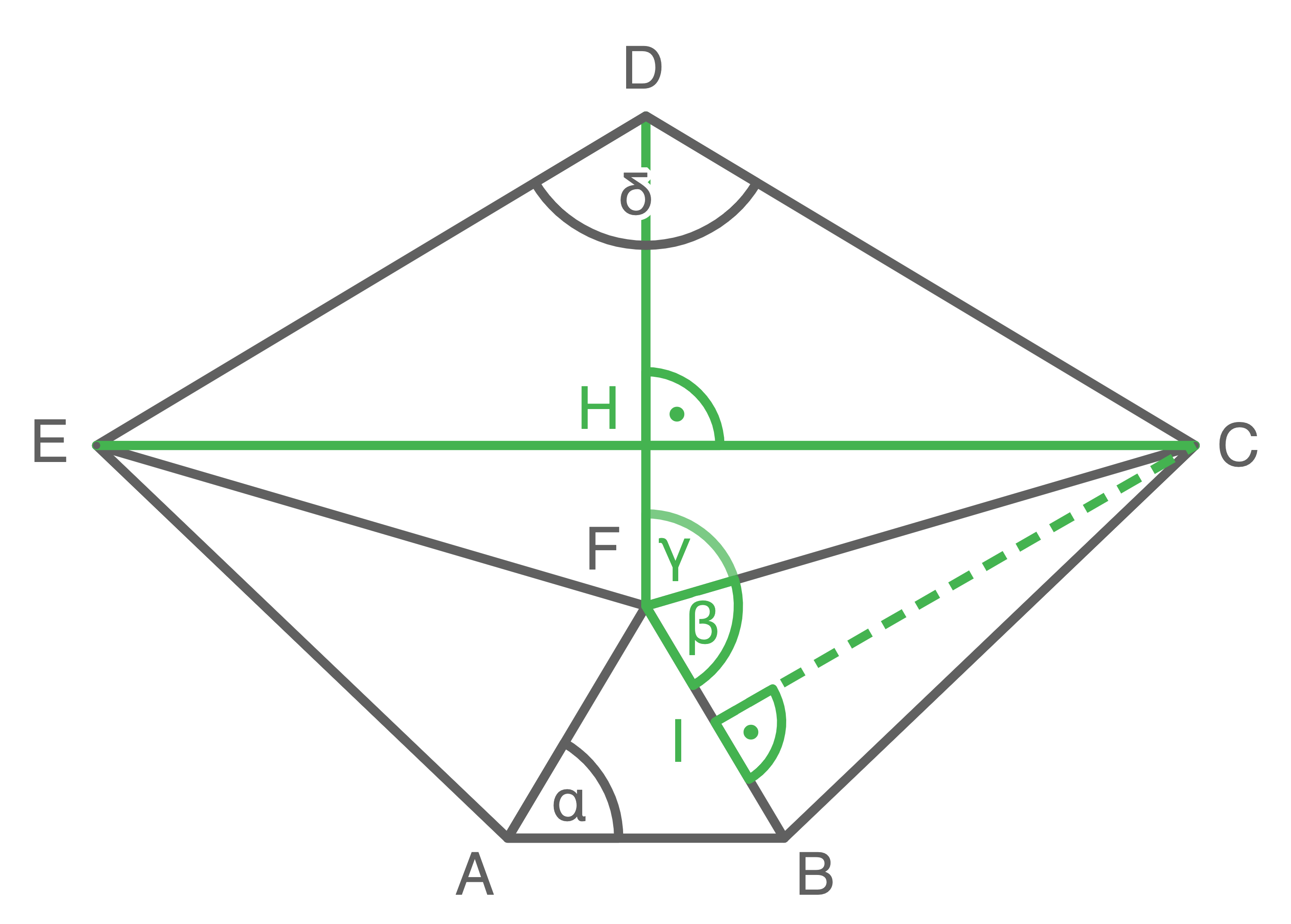
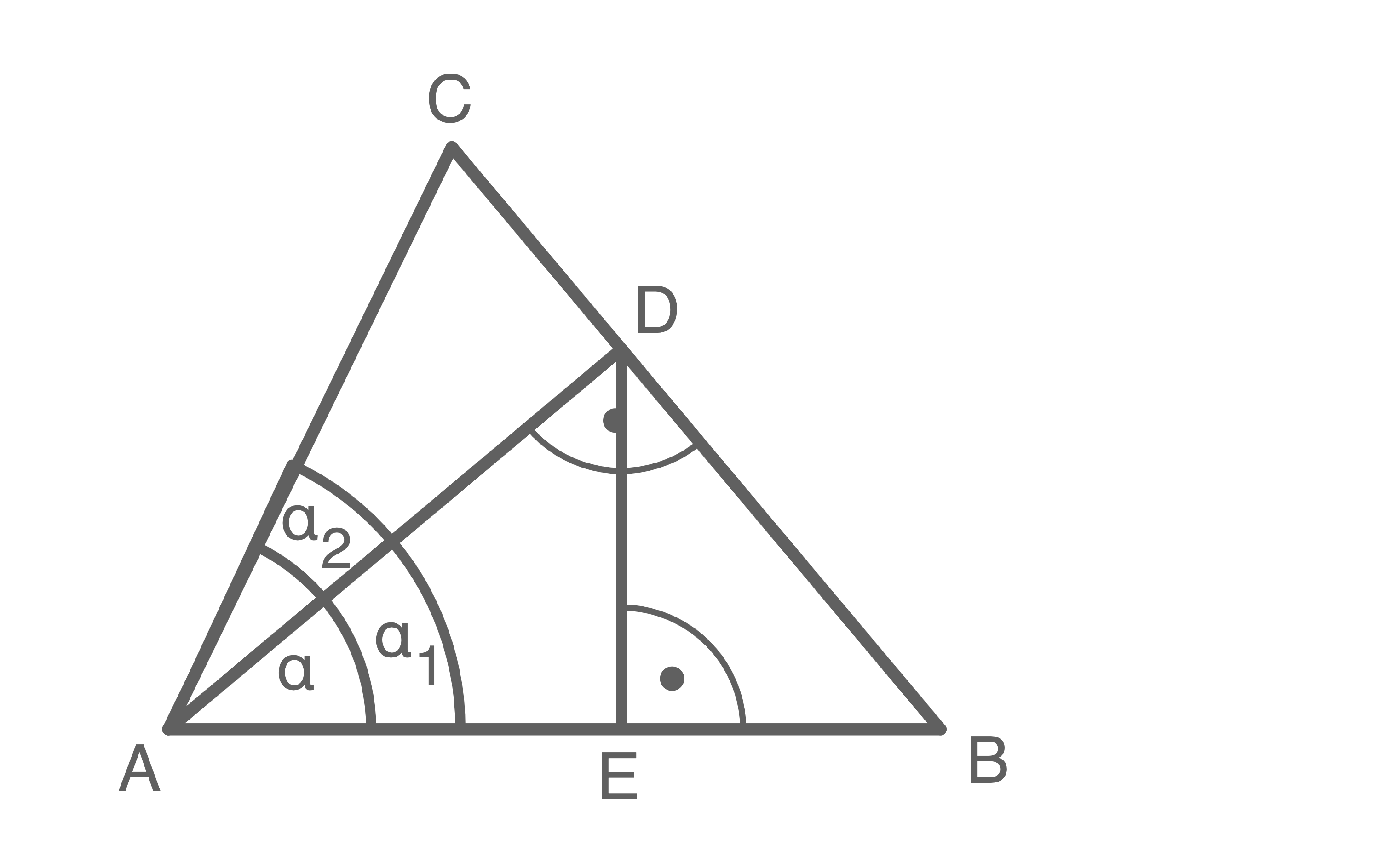
Hilfsskizze
Winkel  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
Die Strecke

ist die Höhe des Dreiecks

zur Grundseite

![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2} \cdot g \cdot h \\[5pt]
A_{ABC}&=& \dfrac{1}{2} \cdot \overline{BC} \cdot \overline{AD}\\[5pt]
54\,\text{cm}^2 &=& \dfrac{1}{2} \cdot 11,6\,\text{cm} \cdot \overline{AD} \\[5pt]
54\,\text{cm}^2 &=& 5,8\,\text{cm} \cdot \overline{AD} \quad\scriptsize \mid\; :5,8\,\text{cm} \\[5pt]
\overline{AD} &=& \underline{ 9,31 \,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/44aa4385ee1b0cf84b4cd6b7213128df627295167aa2b46bd2b062f02d9c9cf3_light.svg) 2. Schritt: Winkel
2. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha_1)&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} &\quad \scriptsize \\[5pt]
\cos(\alpha_1) &=& \dfrac{\overline{AD}}{\overline{AB}} &\quad \scriptsize \\[5pt]
\cos(\alpha_1) &=& \dfrac{9,31\,\text{cm}}{12,0\,\text{cm}} \quad \scriptsize \mid\;\cos^{-1} \\[5pt]
\alpha_1&=& \underline{ 39,12^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/bfd85f3ddf45460d6cb525dcbc9807f3a0617853c22b31f0f4421af0ae98f368_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
4. Schritt: Länge der Strecke
berechnen
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{CD} &=& \overline{BC} - \overline{BD} &\quad \scriptsize \\[5pt]
&=& 11,6 \,\text{cm} - 7,57 \,\text{cm} &\quad \scriptsize \\[5pt]
\overline{CD} &=& \underline{ 4,03 \,\text{cm}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1abf4b7d12ab945378b510ab89ef87e6b8852e4f08ef23e7385d4f20bb09551e_light.svg) 5. Schritt: Winkel
5. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha_2)&=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} &\quad \scriptsize \\[5pt]
\tan(\alpha_2) &=& \dfrac{\overline{CD}}{\overline{AD}} &\quad \scriptsize \\[5pt]
\tan(\alpha_2) &=& \dfrac{4,03\,\text{cm}}{9,31\,\text{cm}} \quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\alpha_2&=& \underline{ 23,41^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/c18002303fbf07c784f58ed3b56a3af2194a108a1414c12102bbdc3dc81326ae_light.svg) 6. Schritt: Winkel
6. Schritt: Winkel  berechnen
berechnen
![\(\begin{array}[t]{rll}
\alpha &=& \alpha_1 + \alpha_2 &\quad \scriptsize \\[5pt]
&=& 39,12^{\circ} + 23,41^{\circ} &\quad \scriptsize \\[5pt]
&=& 62,53^{\circ} \\[5pt]
\alpha&=&\underline{\underline{ 62,5^{\circ}}}
\end{array}\)](https://www.schullv.de/resources/formulas/3e84023eee33a74411e0b0af0f39ea05e44d21dc329f8561f48b1fb26f939422_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} &=& \sin(\alpha_1)&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9b90173eaaf7cf48022ec7f5e1c5a6c665b75f99168ae73edf5bb63a7ae6e2e4_light.svg)
![\(\begin{array}[t]{rll}
\dfrac{\overline{DE}}{\overline{AD}} &=& \sin(\alpha_1)\quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt]
\overline{DE} &=& \sin(\alpha_1)\cdot \overline{AD} &\quad \scriptsize\\[5pt]
&=& \sin(39,12^{\circ}) \cdot 9,31\,\text{cm} &\quad \scriptsize \\[5pt]
&=& 5,87\,\text{cm} \\[5pt]
\overline{DE} &=& \underline{\underline{ 5,9\,\text{cm}}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ce682426264a8a382be338094066401832d5de12bc97833363090ed479fd761a_light.svg)
b)
Nachweis, dass die Dreiecke flächengleich sind
1. Schritt: Flächeninhalt des Dreiecks  berechnen
Länge von
berechnen
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{AC}}{\overline{BC}} \quad \scriptsize \mid\;\cdot\overline{BC}\\[5pt]
\tan(\beta)\cdot \overline{BC}&=&\overline{AC}\quad \scriptsize \mid\;:\tan(\beta)\\[5pt]
\overline{BC}&=&\dfrac{\overline{AC}}{\tan(\beta)}\quad \scriptsize \mid\;:\tan(\beta)
\end{array}\)](https://www.schullv.de/resources/formulas/c9e0702db9731170fe7bcf713757aeaabe5cd3fb44fa970a128b6890fc344548_light.svg)
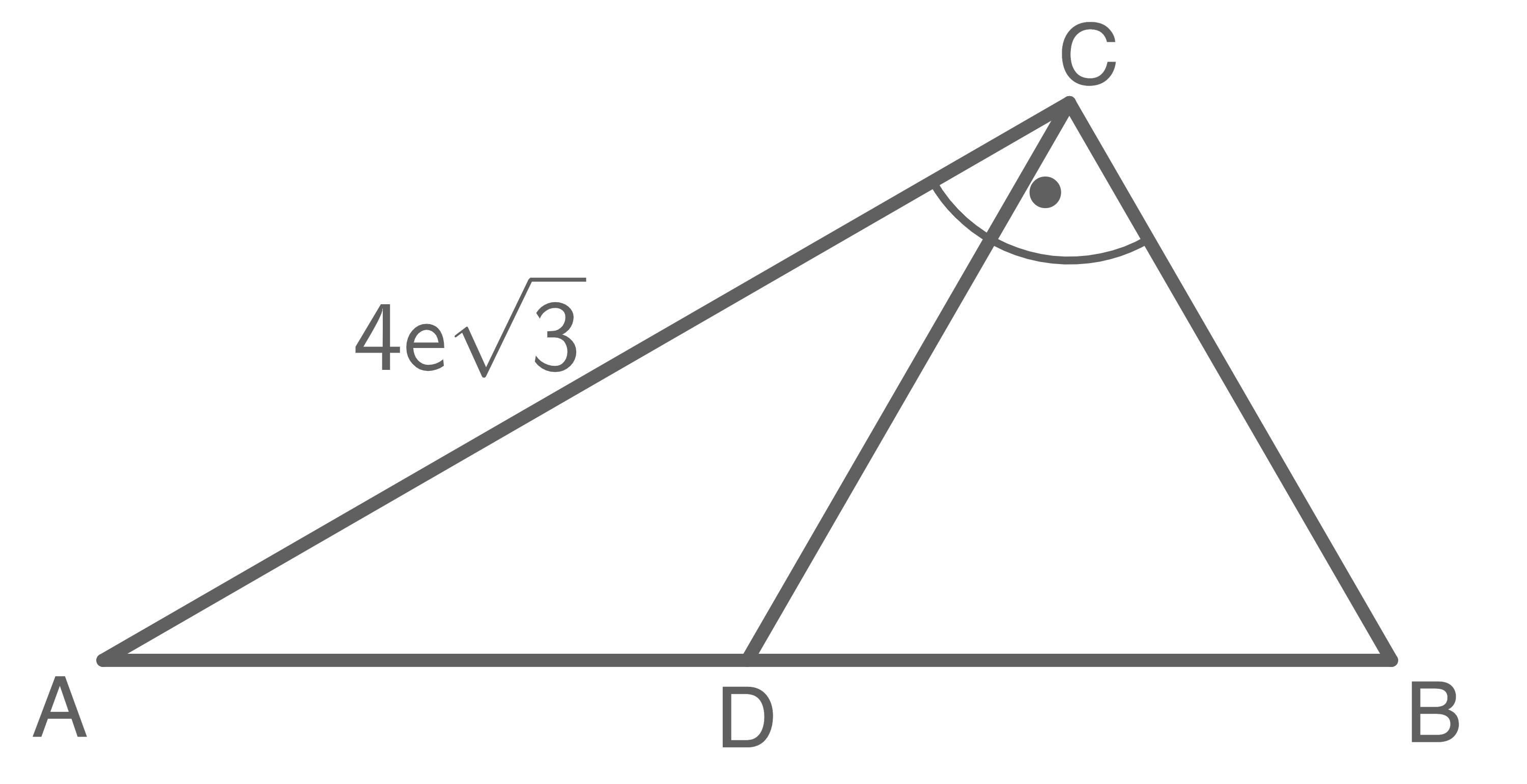
Da das Dreieck

gleichseitig ist, gilt:


 Flächeninhalt
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{DBC}&=&\dfrac{\overline{BC}^2}{4}\sqrt{3}\\[5pt]
&=&\dfrac{(4e)^2}{4}\sqrt{3}\\[5pt]
&=&\dfrac{16e^2}{4}\sqrt{3}\\[5pt]
A_{DBC}&=&\underline{ 4e^2\sqrt{3}}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/21db4228ec8f1f6f60fc93775ad45d36c7e63426eca22aaa0c291cd7057b3608_light.svg) 2. Schritt: Flächeninhalt des Dreiecks
2. Schritt: Flächeninhalt des Dreiecks  berechnen
Flächeninhalt
berechnen
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{ABC}&=&\dfrac{1}{2}\cdot\overline{BC}\cdot \overline{AC}\\[5pt]
&=&\dfrac{1}{2}\cdot4e\cdot 4e\sqrt{3}\\[5pt]
A_{ABC}&=&8e^2\sqrt{3}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6d2af57c670997cb703f04c167d926b0c1ceccaa619d60d8575a69471526bd1f_light.svg) Flächeninhalt
Flächeninhalt  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{ADC}&=&A_{ABC}-A_{DBC}\\[5pt]
&=&8e^2\sqrt{3}-4e^2\sqrt{3}\\[5pt]
A_{ADC}&=&\underline{ 4e^2\sqrt{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/d441d231c5ac86101c5ebf31651d2dc8461772163c926b06c1d59f6df27b7483_light.svg)
Damit ist gezeigt, dass beide Dreiecke flächengleich sind.
Wert von  berechnen
berechnen
Der Flächeninhalt des Dreiecks

lautet (s.o.)

![\(\begin{array}[t]{rll}
A_{ABC}&=& 200 \\[5pt]
8e^2\sqrt{3}&=& 200 \quad \scriptsize \mid\;:(8\sqrt{3}) \\[5pt]
e^2&=&\dfrac{25}{\sqrt{3}}\\[5pt]
&=&\dfrac{25\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}}\\[5pt]
e^2&=&\dfrac{25\cdot \sqrt{3}}{3}\\[5pt]
e_1&=&5\sqrt{\dfrac{\sqrt{3}}{3}}
\\[5pt]
e_2&=&-5\sqrt{\dfrac{\sqrt{3}}{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/9cc9a156c90157bd6048039b9576282d1f0fe01f2f8e9fc6afd00d4ee0f6a8b8_light.svg)

ist negativ und scheidet somit als Ergebnis aus.
Für

beträgt der Flächeninhalt

Abschlussprüfung 2018
Lösung 13
a)
Abstand von  zu
zu  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{BD}}{\overline{AD}} \\[5pt]
\sin(42,0^{\circ})&=& \dfrac{7,2 \,\text{cm}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD}\\[5pt]
\sin(42,0^{\circ})\cdot \overline{AD}&=& 7,2 \,\text{cm} \quad \scriptsize \mid\; : \sin(42,0^{\circ}) \\[5pt]
\overline{AD}&=& \dfrac{7,2 \,\text{cm}}{\sin(42,0^{\circ})} \\[5pt]
\overline{AD}&=& \underline{10, 76 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/48e31b07d7554a9560d9a9d6822a6e5d188ec4cc71ba0a05160a8816138e73fc_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\overline{AE}&=& \overline{AD}-\overline{DE} \\[5pt]
&=& 10,76 \,\text{cm} - 3,0 \,\text{cm} \\[5pt]
&=& \underline{7,76 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/9d25c2675ddaf6bda0d1b0ddf2ec19def2ef52e85f3f4ce618923289e5b17337_light.svg) 3. Schritt: Abstand bestimmen
Größe des Winkels
3. Schritt: Abstand bestimmen
Größe des Winkels  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{\overline{BD}}{\overline{AB}} \\[5pt]
\tan(42,0^{\circ})&=& \dfrac{7,2\,\text{cm}}{\overline{AB}} \quad \scriptsize \mid\; \cdot \overline{AB} \\[5pt]
\tan(42,0^{\circ})\cdot \overline{AB} &=& 7,2\,\text{cm} \quad \scriptsize \mid\; : \tan(\alpha) \\[5pt]
\overline{AB}&=& \dfrac{7,2 \,\text{cm}}{\tan(42,0^{\circ})} \\[5pt]
\overline{AB}&=& 8,00 \,\text{cm} \\[5pt]
\overline{AB}&=& \underline{8\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/290c165c9d47e588e4e19b9655c727a90bbac7a6c2faf7d35da4958f6dff33c3_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  bestimmen
3. Schritt: Länge der Strecke
bestimmen
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BS}&=& \overline{AB} - \overline{AS} \\[5pt]
&=& 8 \,\text{cm} - 5,77 \,\text{cm} \\[5pt]
&=& \underline{2,23 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/d5b351aff2815f26b297353b725af0c828da674f5a530b53160679cabcac8a6a_light.svg) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan (\beta)&=&\dfrac{\overline{ES}}{\overline{BS}} \\[5pt]
\tan (\beta)&=&\dfrac{5,19\text{ cm}}{2,23 \,\text{cm} } &\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\beta&=& \underline{66,75^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/8d3fa08a5b7a68213960f2756ffe16afcbb4f3b10d7f87998424472a1db4b2ba_light.svg) 5. Schritt: Größe des Winkels
5. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\gamma&=& 180^{\circ}-2\cdot \beta \\[5pt]
&=& 180^{\circ}-2\cdot 66,75^{\circ} \\[5pt]
&=& \underline{\underline{ 46,5^{\circ}}}
\end{array}\)](https://www.schullv.de/resources/formulas/5c2cb8e02eebe1ead9b561d8cef36348a09f9266065da608338c902833945696_light.svg)
b)
1. Schritt: Innenwinkel des Sechsecks berechnen
Winkelsumme in einem Sechseck:

In einem regelmäßigen Vieleck sind alle Innenwinkel gleich groß.
 2. Schritt: Höhe des Trapezes berechnen
2. Schritt: Höhe des Trapezes berechnen


![\(\begin{array}[t]{rll}
\sin(\beta) &=& \dfrac{\overline{AE}}{\overline{EF}} \\[5pt]
\sin (60^{\circ})&=& \dfrac{\overline{AE}}{2e} &\quad \scriptsize \mid\; \cdot 2e \\[5pt]
\sin (60^{\circ}) \cdot 2e &=& \overline{AE}\\[5pt]
\overline{AE}&=& \sin (60^{\circ}) \cdot 2e\\[5pt]
\overline{AE}&=& \sqrt{3}e \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/dc70271460724d70193e3fae58c813ee37662c7f1c10e81ff64a38ca9985d955_light.svg)
 3. Schritt: Strecke
3. Schritt: Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}^2+\overline{AF}^2&=&\overline{EF}^2 \\[5pt]
\left(\sqrt{3}e\right)^2+\overline{AF}^2 &=& (2e)^2\\[5pt]
3e^2+\overline{AF}^2 &=& 4e^2 &\quad \scriptsize \mid \; -3e^2\\[5pt]
\overline{AF}^2 &=& e^2&\quad\scriptsize\mid \;\sqrt{\;}\\[5pt]
\overline{AF} &=& \underline{ e}
\end{array}\)](https://www.schullv.de/resources/formulas/1e77480bed83f02b243d1917bd6236e282b91abf378b59a152ab160aee765d07_light.svg) 4. Schritt: Strecke
4. Schritt: Strecke  bestimmen
bestimmen
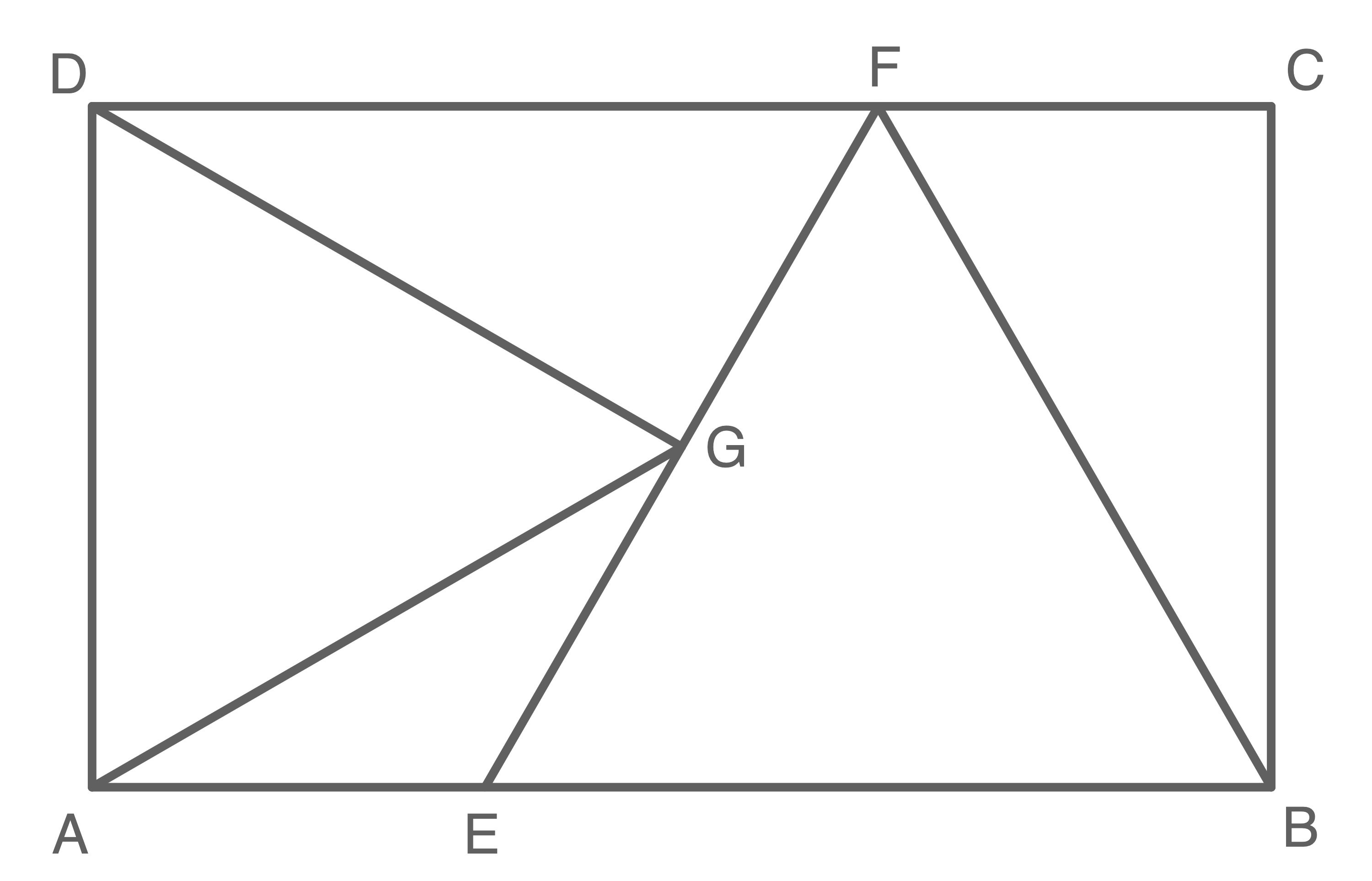
Im Dreieck

sind zwei der Innenwinkel Nebenwinkel zu jeweils einem der Innenwinkel des Sechsecks und somit genau wie


groß.
Somit sind alle Innenwinkel von

gleich groß und es handelt sich um ein gleichseitiges Dreieck mit der Seitenlänge

 5. Schritt: Flächeninhalt berechnen
5. Schritt: Flächeninhalt berechnen

![\(\begin{array}[t]{rll}
\overline{DC}&=&\overline{DI} + \overline{IC} \\[5pt]
&=& e + 2e \\[5pt]
&=& \underline{ 3e}
\end{array}\)](https://www.schullv.de/resources/formulas/b1c30ef471465bf18f3ffe2816f875d12f53e5b9afafa7bae8f02ae89f4482ab_light.svg)
![\(\begin{array}[t]{rll}
\overline{AB}&=& \overline{AF} + \overline{FG}+ \overline{GB} \\[5pt]
&=& e + 2e + 2e \\[5pt]
&=& \underline{ 5e}
\end{array}\)](https://www.schullv.de/resources/formulas/37aefe956bceec1709ae04fcaf5b0854b2928e85bc4332a843dbd5ff0a11006c_light.svg)
![\(\begin{array}[t]{rll}
A_{ABCD}&=&\frac{1}{2}\cdot \left(\overline{AB} + \overline{DC} \right) \cdot \overline{AD} \\[5pt]
&=& \frac{1}{2}\cdot \left(5e + 3e \right) \cdot 2\cdot \sqrt{3}e \\[5pt]
&=& \underline{\underline{ 8 e^2\sqrt{3}}}
\end{array}\)](https://www.schullv.de/resources/formulas/a59c343d2fc0dc841874d1c36acf5c3a258c746fed1e49f208d1a78ad3c150fc_light.svg) Länge der Diagonale
Länge der Diagonale  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2 &=& \overline{AD}^2 +\overline{DC}^2 \\[5pt]
\overline{AC}^2&=& \left( 2\cdot \sqrt{3}e\right)^2 + \left( 3e\right)^2\\[5pt]
\overline{AC}^2 &=& 21e^2 \quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
\overline{AC} &=& \underline{\underline{ \sqrt{21}e}}
\end{array}\)](https://www.schullv.de/resources/formulas/1c8c4b2f5d8bba7a7557eef43162106b2b6927fcbc5f502118bb61947930c52a_light.svg)
Abschlussprüfung 2017
Lösung 14
a)
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\text{sin}(\beta)&=&\dfrac{CE}{BC} \quad \scriptsize \mid\;\cdot \, \overline{BC}\;\mid\; : \text{sin}(\beta)\\[5pt]
\overline{BC}&=&\dfrac{\overline{CE}}{\sin(\beta)} \\[5pt]
\overline{BC}&=&\dfrac{9,0\,\text{cm}}{\sin(70^{\circ})} \\[5pt]
\overline{BC} &=& \underline{ 9,58\text{ cm}}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ee6e5f7609ea37b9f86397b06e0bb9496a8966809db8c5273c9e76ad8d30650d_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
Größe des Winkels
berechnen
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
180^{\circ}&=&\alpha+\beta+\gamma \quad \scriptsize \mid\;-\,\beta\, -\,\gamma \\[5pt]
\alpha&=&180^{\circ}-\beta-\gamma \\[5pt]
\alpha&=&180^{\circ}-70^{\circ}-70^{\circ} \\[5pt]
\alpha&=&\underline{ 40^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/5cc919066cb7d0383170a5be601df31b462b051ae6768213be378f54796ceffe_light.svg) Länge der Strecke
Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{\overline{CE}}{AC} \quad \scriptsize \mid\;\cdot\,\overline{AC}\; \mid\;:\,\sin(\alpha)
\\[5pt]
\overline{AC}&=&\dfrac{\overline{CE}}{\sin(\alpha)} \\[5pt]
\overline{AC}&=&\dfrac{9,0\,\text{cm}}{\sin(40^{\circ})} \\[5pt]
\overline{AC}&=&\underline{ 14,00\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/ca5ac11a4ca388660fc53d91e2d89cf41e193fecb9426cb2fbc1fd1a6cf49ef1_light.svg)
Es gilt:

 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{FD}^2+\overline{AF}^2&=&\overline{AD}^2 \quad\scriptsize \mid\;-\,\overline{FD}^2 \\[5pt]
\overline{AF}^2&=&\overline{AD}^2-\overline{FD}^2 \;\quad\scriptsize \mid\;\,\sqrt{\,\,\,}\\[5pt]
\overline{AF}&=&\sqrt{\overline{AD}^2-\overline{FD}^2} \\[5pt]
\overline{AF}&=&\sqrt{(10,4\,\text{cm})^2-(9\,\text{cm})^2} \\[5pt]
\overline{AF}&=&\underline{ 5,21\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/572089fec6f995c7cadf64b7d2b22dba74b40bdec95740eecb7519851b061bc3_light.svg) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=& \dfrac{\overline{CE}}{\overline{BE}} \quad \scriptsize \mid\; \cdot\,\overline{BE}\, \mid\;
:\tan(\beta) \\[5pt]
\overline{BE} &=& \dfrac{\overline{CE}}{\tan(\beta)} \\[5pt]
\overline{BE} &=& \dfrac{9,0\,\text{cm}}{\tan(70^{\circ})} \\[5pt]
\overline{BE} &=& \underline{ 3,28\text{ cm}}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/034c07716357cccc8c62481ddc0eb6e2cf3bbd621ea7a28624b6820639c6e077_light.svg) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  ermitteln
ermitteln
![\(\begin{array}[t]{rll}
\overline{FE}&=& \overline{AB} - \overline{AF} - \overline{BE} \\[5pt]
&=& 14,00\,\text{cm} - 5,21\,\text{cm} - 3,28\,\text{cm}\\[5pt]
\overline{FE}&=& \underline{ 5,51\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2f1eb8db8198de92fa19b990c63bba2c1bd5a5da725dfadb32b211a59816e0eb_light.svg)
Es gilt:

 6. Schritt: Umfang des Trapezes berechnen
6. Schritt: Umfang des Trapezes berechnen
![\(\begin{array}[t]{rll}
u&=&\overline{AB}+\overline{BC}+\overline{CD}+\overline{AD} \\[5pt]
&=&14\,\text{cm}+9,58\,\text{cm}+5,51\,\text{cm}+10,4\,\text{cm} \\[5pt]
u&=&\underline{\underline{ 39,5\,\text{cm}}}
\end{array}\)](https://www.schullv.de/resources/formulas/370f6e1ffb9f28bfdb5f00a874af592cec3c1ae88e5aefcb01db3d3a1d7df194_light.svg)
b)
1. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\beta&=&180^{\circ}-90^{\circ}-\gamma \\[5pt]
&=&180^{\circ}-90^{\circ}-50^{\circ} \\[5pt]
\beta&=&\underline{ 40^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/b6b44a5e9792822a54c41969aef4e9864563dd670a6b9459d9bfe23b5ef0eddf_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\gamma)&=&\dfrac{\overline{AB}}{\overline{AC}} \quad \scriptsize \mid\;\cdot \overline{AC} \\[5pt]
\overline{AB}&=& \tan(\gamma) \cdot \overline{AC} \\[5pt]
\overline{AB}&=& \tan(50^{\circ}) \cdot 11,4\,\text{cm} \\[5pt]
\overline{AB}&=& \underline{ 13,59\,\text{cm}} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7728bb7298b777a348b7558a6ae85f3494135db402f10eecc7d854d614abd3dd_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DB}&=& \overline{AB}-\overline{AD}& \\[5pt]
&=& 13,59\,\text{cm}-5,0\,\text{cm}& \\[5pt]
\overline{DB}&=& \underline{ 8,59\,\text{cm}}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3c3a996ca464ff84fc7d0dd0872b51f35937129d4f9c79d1df79e6aaf59a81da_light.svg)
Es gilt:
 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{DE}}{\overline{DB}} \quad \scriptsize \mid\;\cdot \overline{DB} \\[5pt]
\overline{DE}&=& \tan(\beta)\cdot \overline{DB} \\[5pt]
\overline{DE}&=& \tan(40^{\circ})\cdot 8,59\,\text{cm} \\[5pt]
\overline{DE}&=& \underline{ 7,21\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/dd85a607649ecc1e160a5a25cb9fb23cec5b4a2a64e17db211c818c0992f1f1a_light.svg) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AB](https://www.schullv.de/resources/formulas/751a3642adafc79fbb51241bd9167acaffe16dd4cbe5fd9a1ea1ecbcd59d5dd4_light.svg) 6. Schritt: Länge der Strecke
6. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta](https://www.schullv.de/resources/formulas/aeeecb284f6869c85f97e22fc9b5f2baf76bcc8195cac87e6b6301c4f54b31ec_light.svg) 7. Schritt: Flächeninhalt berechnen
7. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot (\overline{DE}+\overline{AF})\cdot \overline{AD} & \\[5pt]
A&=&\dfrac{1}{2}\cdot (7,21\,\text{cm}+3,01\,\text{cm})\cdot 5,0\,\text{cm} & \\[5pt]
A&=&\underline{\underline{ 25,6\,\text{cm}^2}} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a8156298c69a96fa0d8af8dd0db06fde0615b70f22563140a34894fd7018269b_light.svg)
Abschlussprüfung 2016
Lösung 15
a)
Größe des Winkels  berechnen
1. Schritt: Länge der Strecke
berechnen
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{\overline{DR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt]
\overline{DR} &=& \sin(\alpha)\cdot \overline{AD} &\quad \scriptsize \\[5pt]
\overline{DR} &=& \sin(50^{\circ}) \cdot 8,4 \,\text{cm} &\quad \scriptsize \\[5pt]
\overline{DR} &=& \underline{ 6,43 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/1987b228e97235c3568be38bc01eaf1b06f3cf82e6fea408ec469e77f65dd7a9_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overline{AR}}{\overline{AD}} \quad \scriptsize \mid\; \cdot \overline{AD} \\[5pt]
\overline{AR} &=& \cos(\alpha) \cdot \overline{AD} &\quad \scriptsize \\[5pt]
\overline{AR} &=& \cos(50^{\circ}) \cdot 8,4\,\text{cm} &\quad \scriptsize \\[5pt]
\overline{AR} &= & \underline{ 5,40\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/e4919c57b8807028c393e440d6b6bdfeb94679d03bd777b3b4c23c476345ef09_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{ER}&=&\overline{AE}-\overline{AR} &\quad \scriptsize \\[5pt]
\overline{ER}&=& 7,8\,\text{cm}- 5,40\,\text{cm} &\quad \scriptsize \\[5pt]
\overline{ER}&=& \underline{ 2,40 \,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/3b45589ae0d2ca6288cc60602ccc12881d530686c913887478de909dc1507166_light.svg) 4. Schritt: Größe des Winkels
4. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\beta)&=&\dfrac{2,4\,\text{cm}}{6,43\,\text{cm} } \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\beta&=& \underline{ 20,5^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/2f8bb38486a0b3dd314f5c0a3cd31fc8e56f7dff1b8149e0aa9f06e71a0c9487_light.svg) 5. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=& \dfrac{\overline{ER}}{\overline{DE}}\quad \scriptsize \mid\; \cdot \overline{DE} \\[5pt]
\sin(\beta)\cdot \overline{DE}&=& \overline{ER}\quad \scriptsize \mid\; : \sin(\beta) \\[5pt]
\overline{DE}&=&\dfrac{\overline{ER}}{\sin(\beta)} &\quad \scriptsize \\[5pt]
\overline{DE}&=&\dfrac{2,4\,\text{cm}}{\sin(20,5^{\circ} )} &\quad \scriptsize \\[5pt]
\overline{DE}&=& \underline{ 6,85\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/a1fbc9840d79e61f0aad612dae437b3007610fa48749dbf9969bdb4e754d0300_light.svg) 6. Schritt: Größe des Winkels
6. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\delta_2)&=&\dfrac{\overline{BR}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\delta_2)&=&\dfrac{\overline{BE}+\overline{ER}}{\overline{DR}} &\quad \scriptsize \\[5pt]
\tan(\delta_2)&=& \dfrac{6,85\,\text{cm}+2,4\,\text{cm}}{6,43\,\text{cm}}\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\delta_2&=& \underline{ 55,2^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/2fe23ba1ba509d1e46adea26775a538991a18a6c2480fbb06f3d46e3c153c981_light.svg) 7. Schritt: Größe des Winkels
7. Schritt: Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\delta_1&=&90^{\circ}-\delta_2 &\quad \scriptsize \\[5pt]
&=&90^{\circ}- 55,2^{\circ} &\quad \scriptsize \\[5pt]
\delta_1 &=& \underline{\underline{ 34,8^{\circ}}}
\end{array}\)](https://www.schullv.de/resources/formulas/02c91e46bf8e6a1d122db870cedff0b0ccc2ab9f065eea3af49ada667d74d7dc_light.svg) Flächeninhalt des Dreiecks
Flächeninhalt des Dreiecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
A_{\,\text{EBD}}&=&\dfrac{1}{2}\cdot g\cdot h &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot \overline{EB}\cdot \overline{DR} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{2}\cdot 6,86 \,\text{cm}\cdot 6,43 \,\text{cm} &\quad \scriptsize \\[5pt]
A_{EBD}&=& \underline{\underline{ 22,1 \,\text{cm}^2}}
\end{array}\)](https://www.schullv.de/resources/formulas/867cfdfdea74ed4ec0bf41dcfee30ee404dfe96e9c888bd7c8cf72671316849b_light.svg)
b)
Beas Aussage prüfen
![\(\begin{array}[t]{rll}
u_{\,\text{Rechteck}}&=& 2\cdot 6e+2\cdot 3e &\quad \scriptsize \\[5pt]
u_{\,\text{Rechteck}}&=& 18e
\end{array}\)](https://www.schullv.de/resources/formulas/ed736c0083a450677b5fbd11e4209ed03638a21278bb103580c5d46e2c26831c_light.svg)
 1. Schritt: Länge der Strecke
1. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AG}&=& 2\cdot \overline{BC}&\quad \scriptsize \\[5pt]
&=& 2\cdot 3e &\quad \scriptsize \\[5pt]
\overline{AG}&=& \underline{ 6e}
\end{array}\)](https://www.schullv.de/resources/formulas/0bdf4536cc0727fa9526103c135eec9069f5f50736286a8459b9e044ec9640c3_light.svg) 2. Schritt: Länge der Strecke
2. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BE}&=&\dfrac{\overline{CM}}{2} &\quad \scriptsize \\[5pt]
&=&\dfrac{3e}{2} &\quad \scriptsize \\[5pt]
\overline{BE}&=& \underline{ 1,5e }=\overline{FG}
\end{array}\)](https://www.schullv.de/resources/formulas/50c468a26dee9e5460fdedcb0ae250a6764859ed7fea9bc085d0da4337312a93_light.svg) 3. Schritt: Länge der Strecke
3. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AE}&=&\overline{AB}-\overline{BE} &\quad \scriptsize \\[5pt]
&=& 6e-1,5e &\quad \scriptsize \\[5pt]
\overline{AE}&=&\underline{ 4,5e}
\end{array}\)](https://www.schullv.de/resources/formulas/b08f965fcaba5069261bba816bd75130a640247aa4367222a9a378e0097b5cfd_light.svg) 4. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(30^{\circ})&=&\dfrac{\overline{MR}}{\overline{EM}} \quad \scriptsize \mid\; \cdot \overline{EM} \\[5pt]
\cos(30^{\circ}) \cdot \overline{EM}&=& \overline{MR}\quad \scriptsize \mid\; :\cos(30^{\circ})\\[5pt]
\overline{EM}&=&\dfrac{\overline{MR}}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt]
\overline{EM}&=&\dfrac{3e}{\cos(30^{\circ})} &\quad \scriptsize \\[5pt]
\overline{EM}&=& 2\cdot \sqrt{3}e
\end{array}\)](https://www.schullv.de/resources/formulas/4f335d2edc1a2ff5445c94b73531128c00174427587e4e864e86b1c7a0cf2736_light.svg)
![\(\begin{array}[t]{rll}
\overline{EF}&=& 2 \cdot \overline{EM} &\quad \scriptsize \\[5pt]
&=& 2 \cdot 2\cdot \sqrt{3}e &\quad \scriptsize \\[5pt]
\overline{EF}&=& \underline{ 4\sqrt{3}e}
\end{array}\)](https://www.schullv.de/resources/formulas/34fecb05e03372d9805faca69cddbccd1473dc584575580faabf77311e1dc238_light.svg) 5. Schritt: Umfang des Vierecks
5. Schritt: Umfang des Vierecks  berechnen
berechnen
![\(\begin{array}[t]{rll}
u_{AEFG}&=& \overline{AG}+\overline{FG}+\overline{AE}+\overline{EF} \quad \scriptsize \\[5pt]
&=& 6e+1,5e+4,5e+4\cdot \sqrt{3}e \\[5pt]
u_{AEFG}&=& \underline{ 18,93e}
\end{array}\)](https://www.schullv.de/resources/formulas/8add193e45da3ec668d212f13fe372d3e147e02ece5460313afd0e901797484d_light.svg)
Beas Aussage ist
nicht richtig, da

gilt.
Abschlussprüfung 2015
liegt das rechtwinklige Dreieck
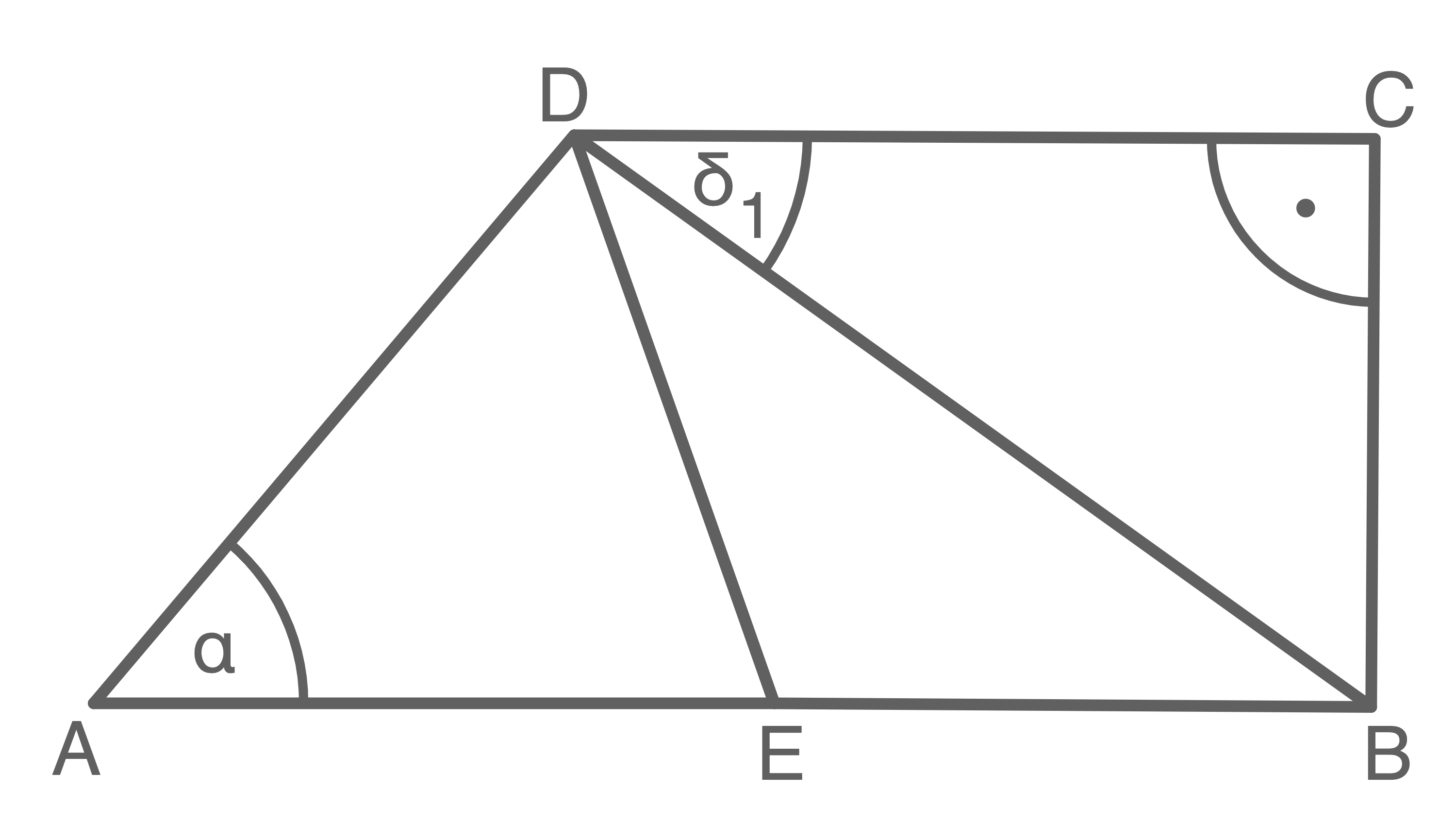
bilden die Winkel
und
zusammen einen rechten Winkeln. Da
bekannt ist:
durch Längenbeziehungen innerhalb eines rechtwinkligen Dreiecks errechnet werden:
und
verwendet werden.
bestimmen zu können, muss die Strecke
ermittelt werden.
errichten:
verläuft die Senkrechte
Sie ist ebenso lang wie die Höhe
betrachten:
bestimmen:
ergibt sich aus:
beträgt