Geometrie in der Ebene
Aufgabe 1
Das abgebildete Zirkuszelt ist ein zusammengesetzter Körper.
Dieser besteht annähernd aus einem Zylinder mit aufgesetztem Kegel.
Der Hersteller gibt folgende Maße an:
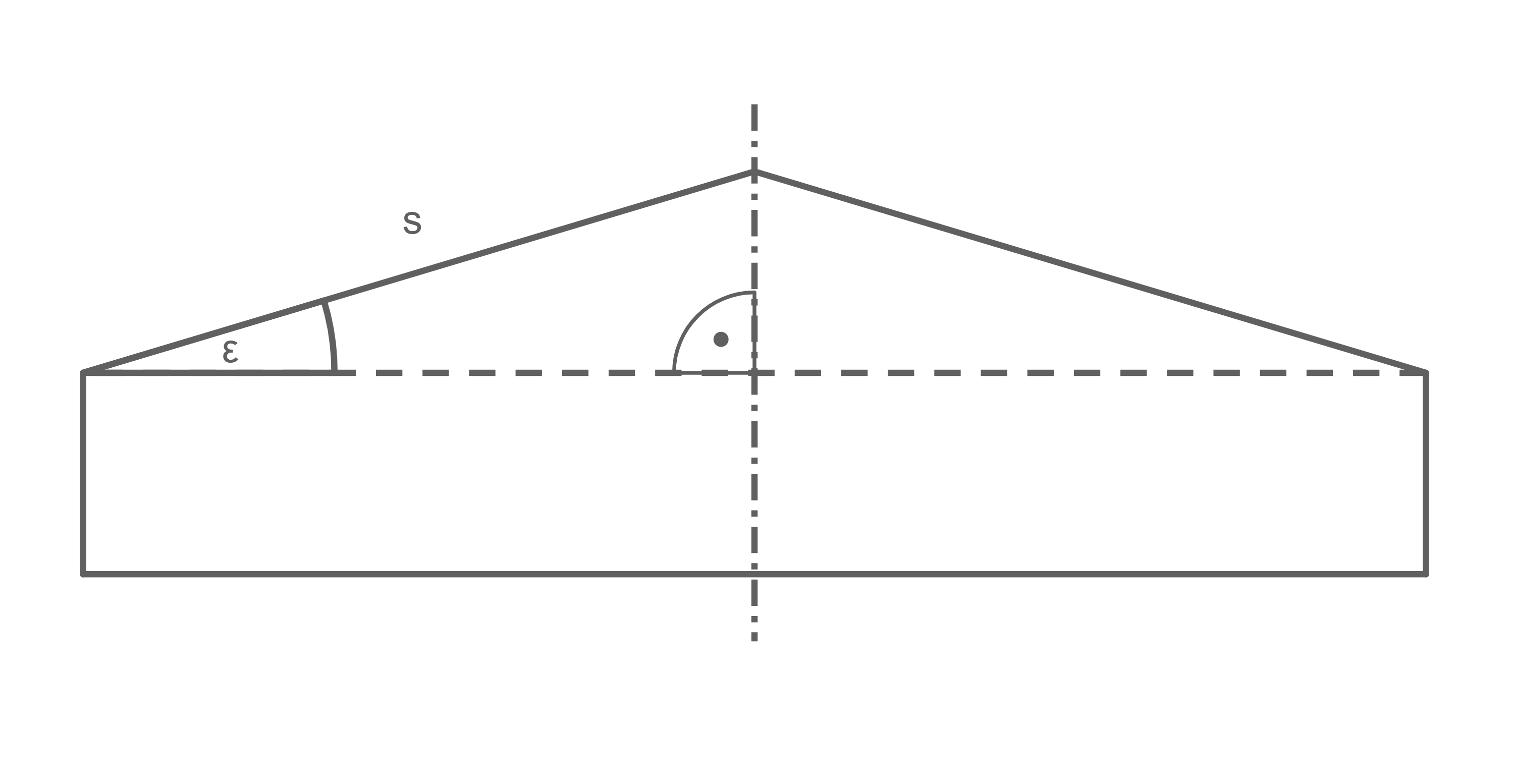

Das Dach und die Seitenwand des Zirkuszeltes bestehen aus einer Kunststoffplane.
Wie viele Kunststoffplane werden benötigt? Berechne.
Aufgabe 2
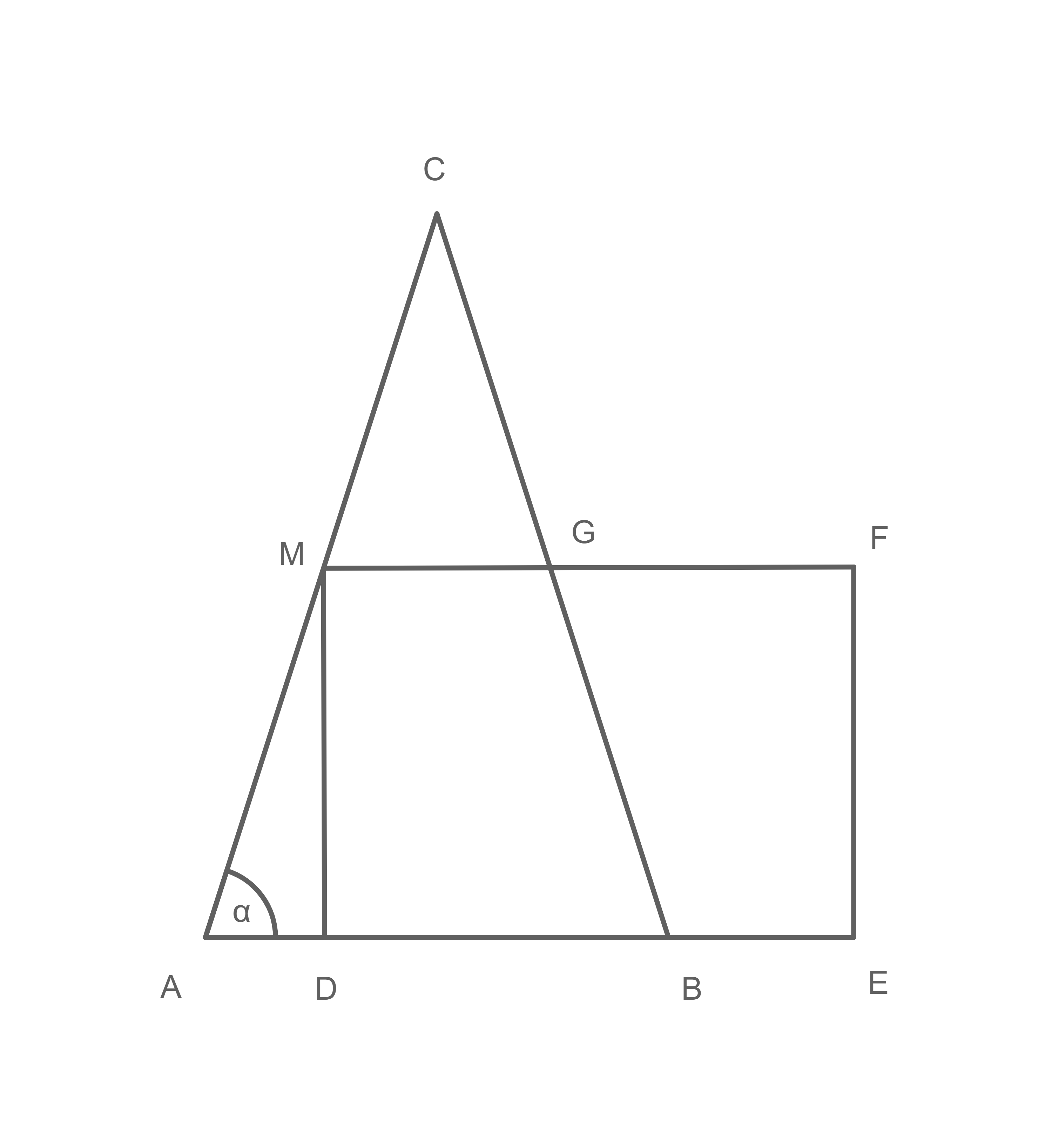
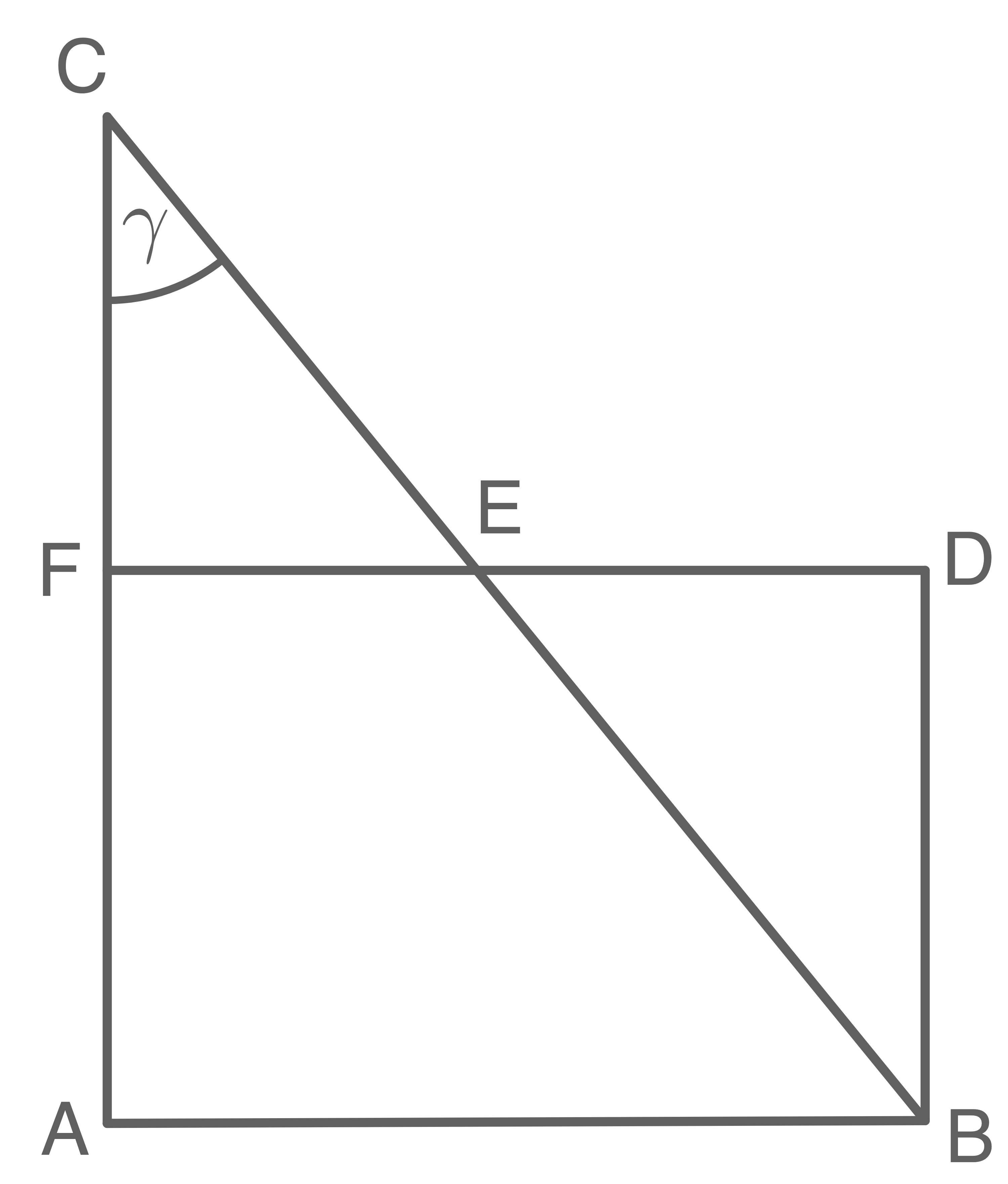
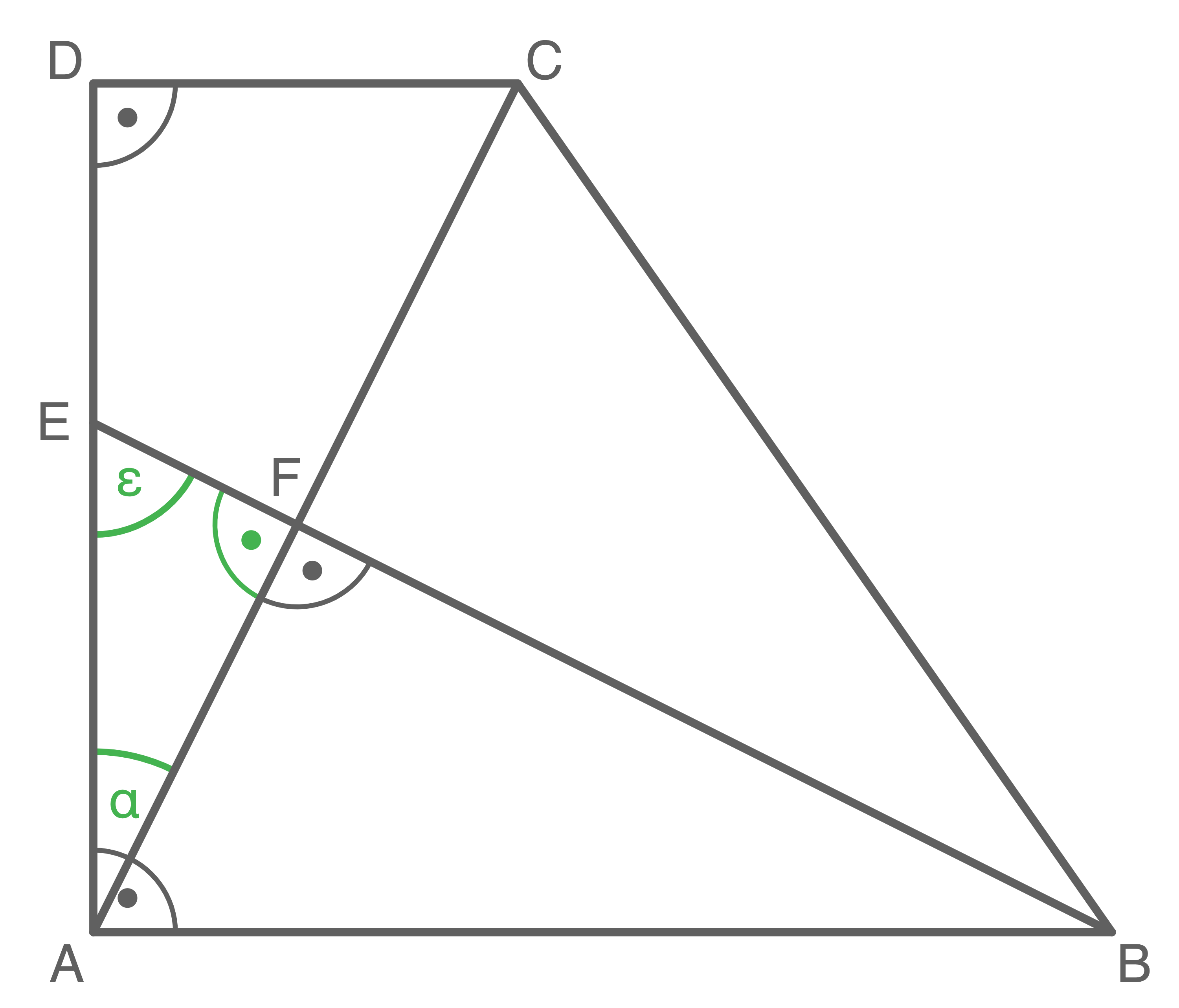
Das Dreieck und das Rechteck
haben die Punkte
und
gemeinsam.
Es gilt:
halbiert die Strecke
Berechne den Flächeninhalt des Vierecks
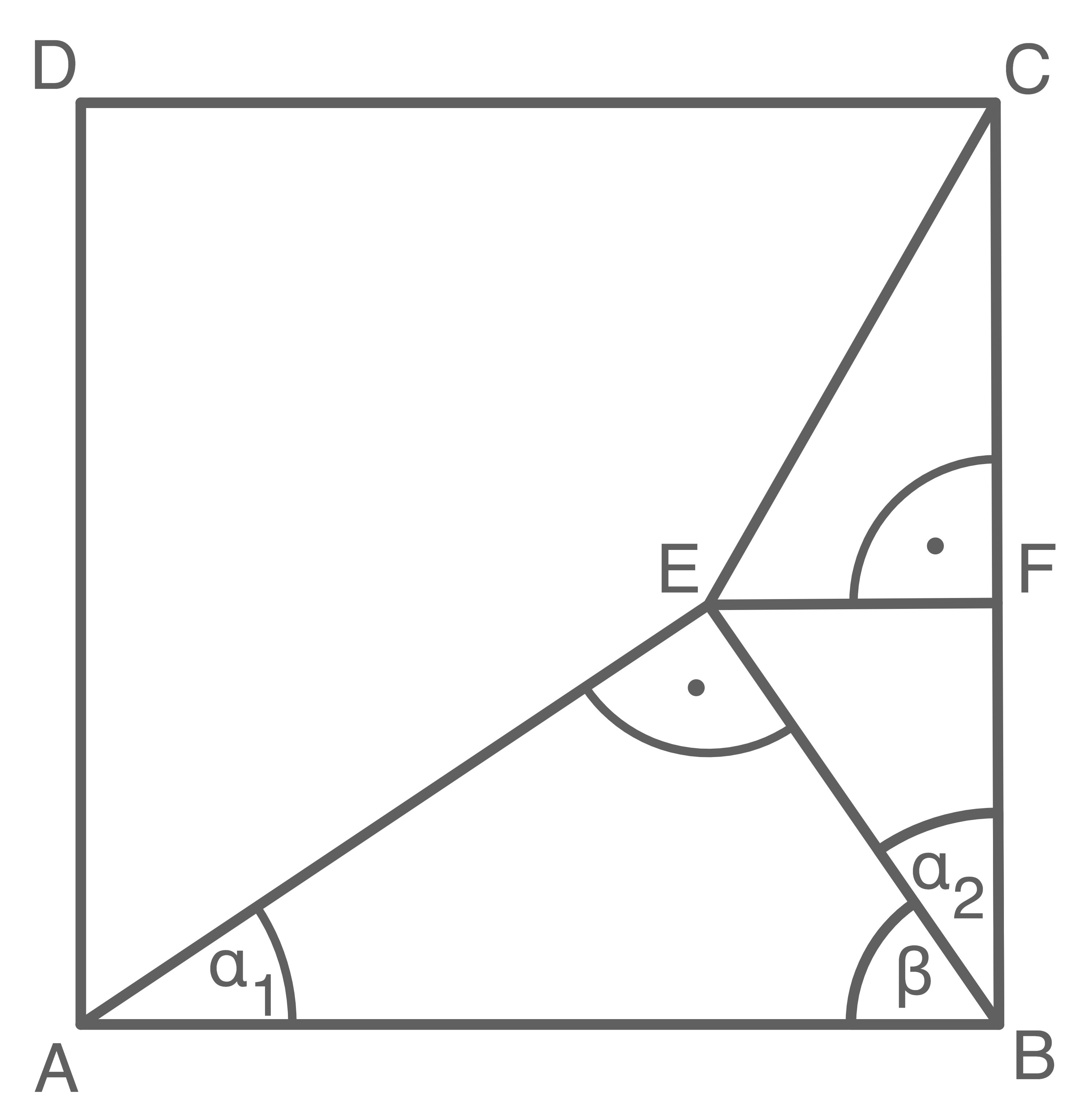
Aufgabe 3
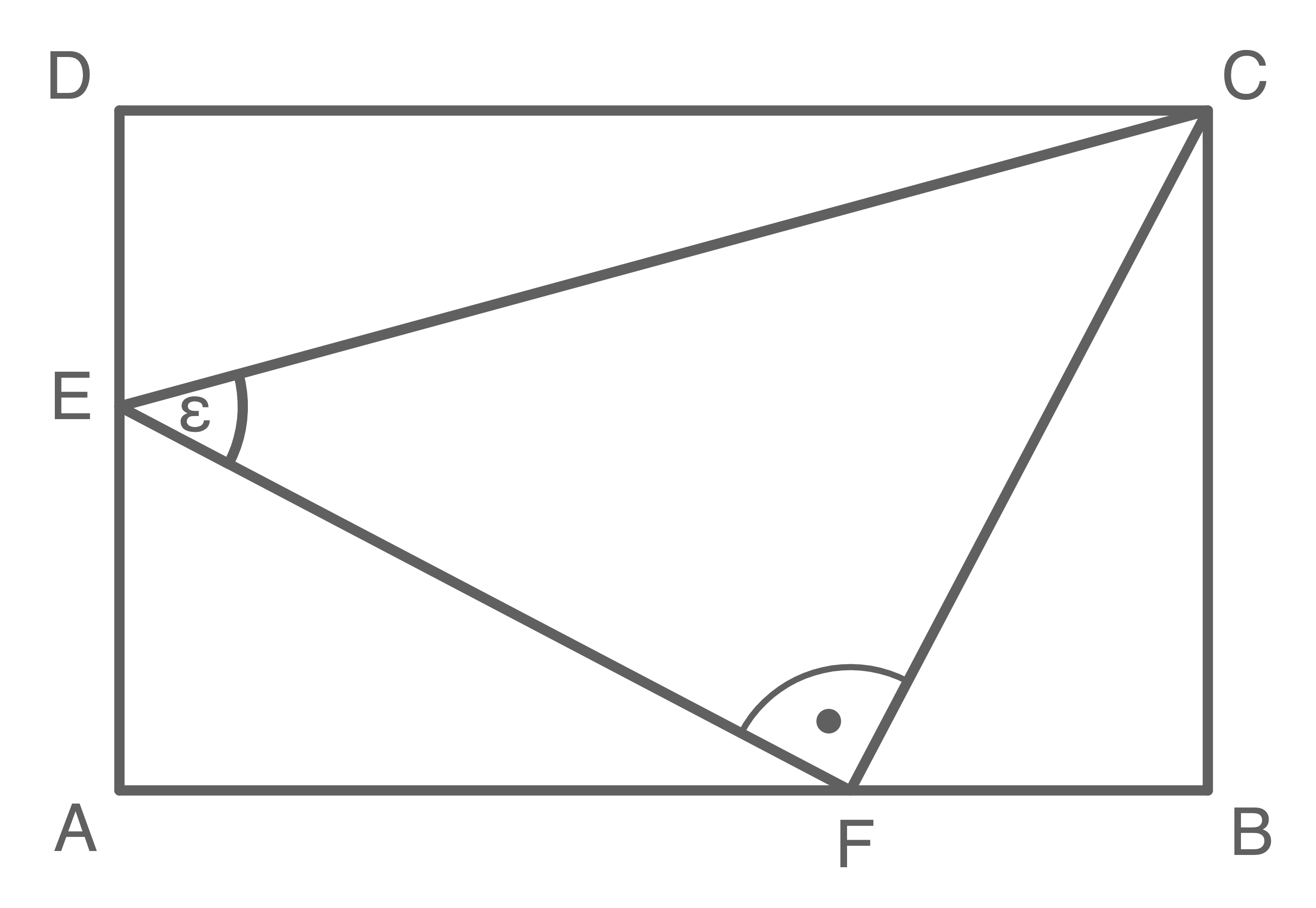
Aufgabe 4
- Berechne den Umfang des Dreiecks
- Berechne den Flächeninhalt des Dreiecks
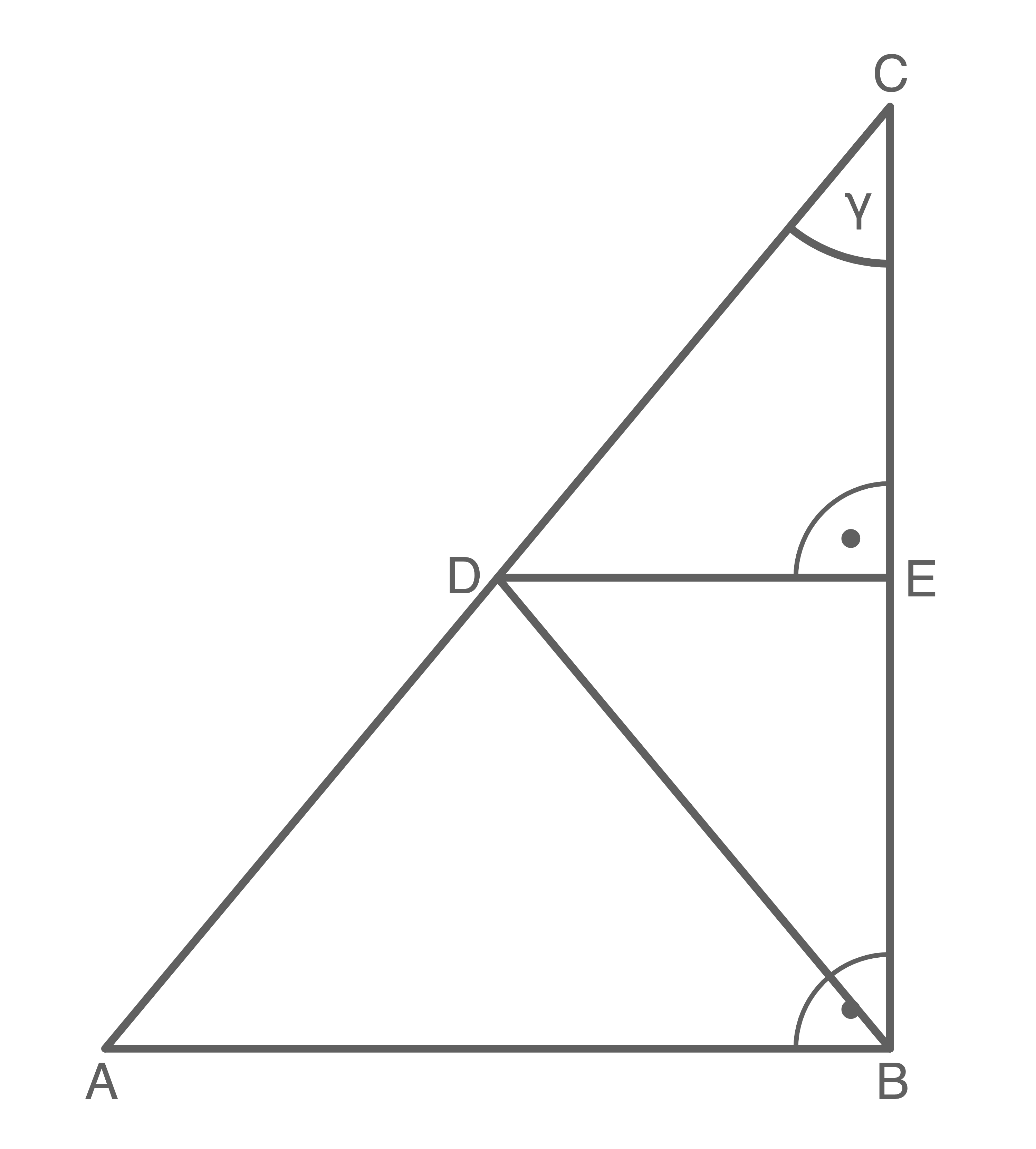
Aufgabe 5
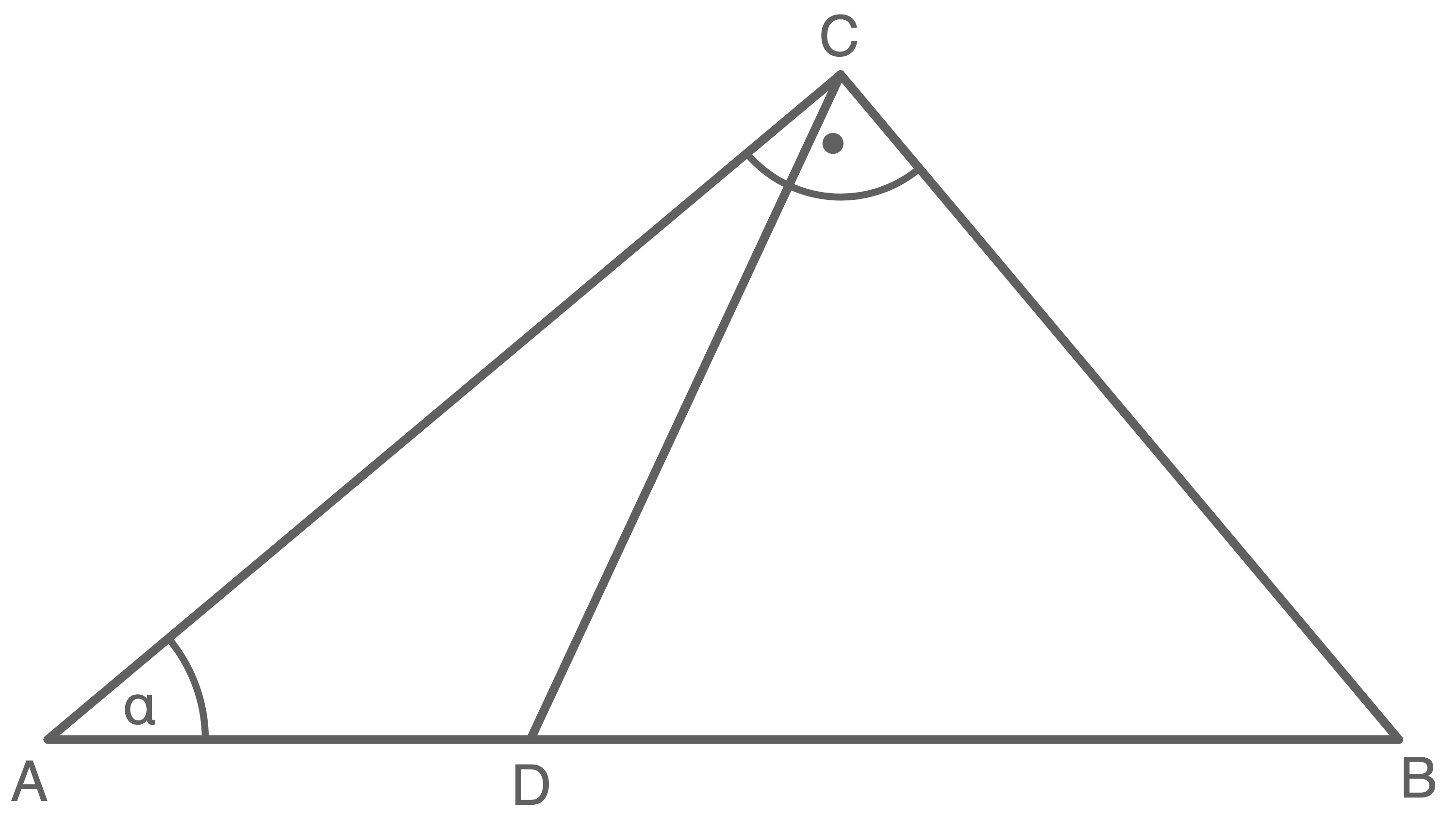
Aufgabe 6
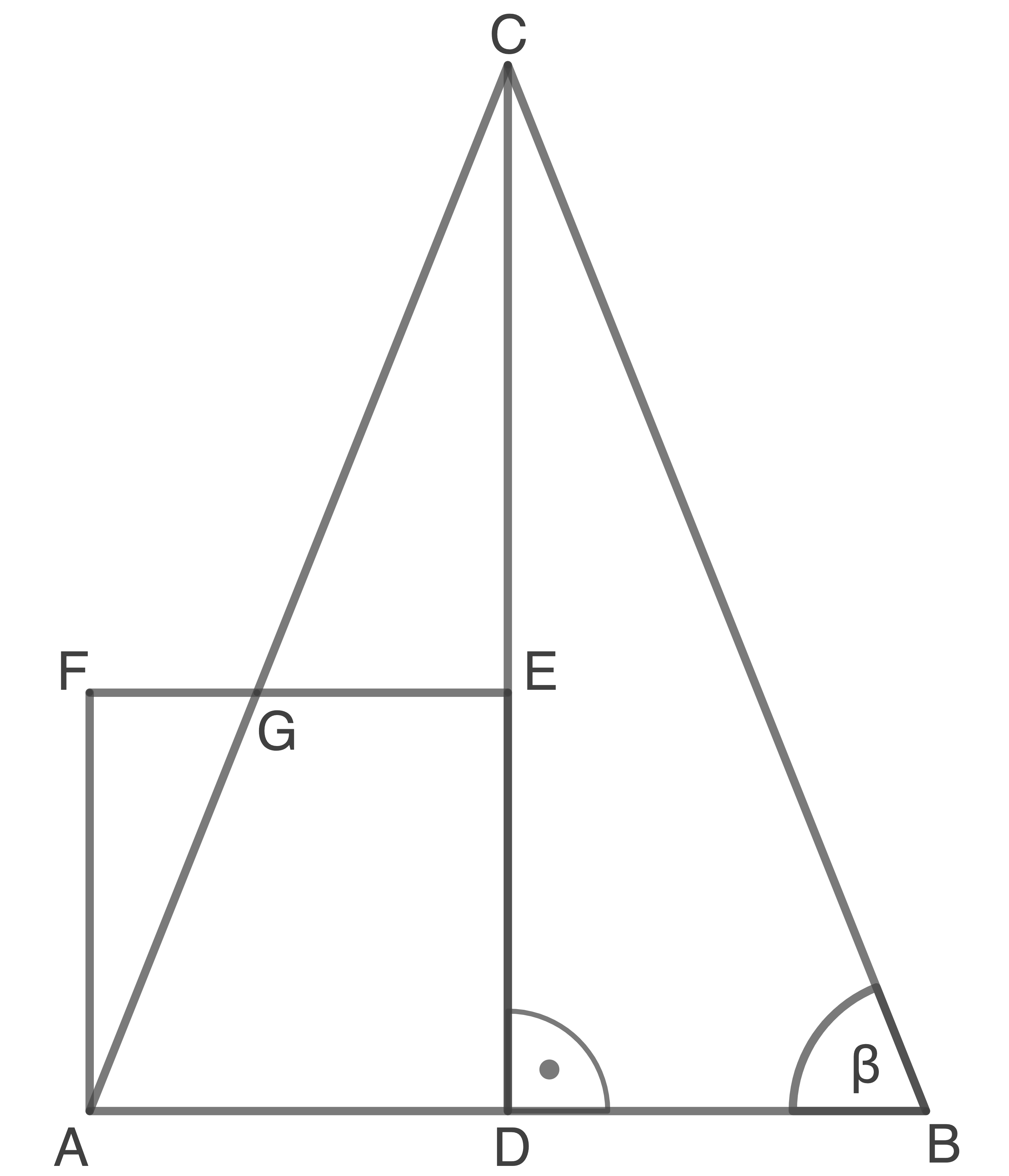
Aufgabe 7
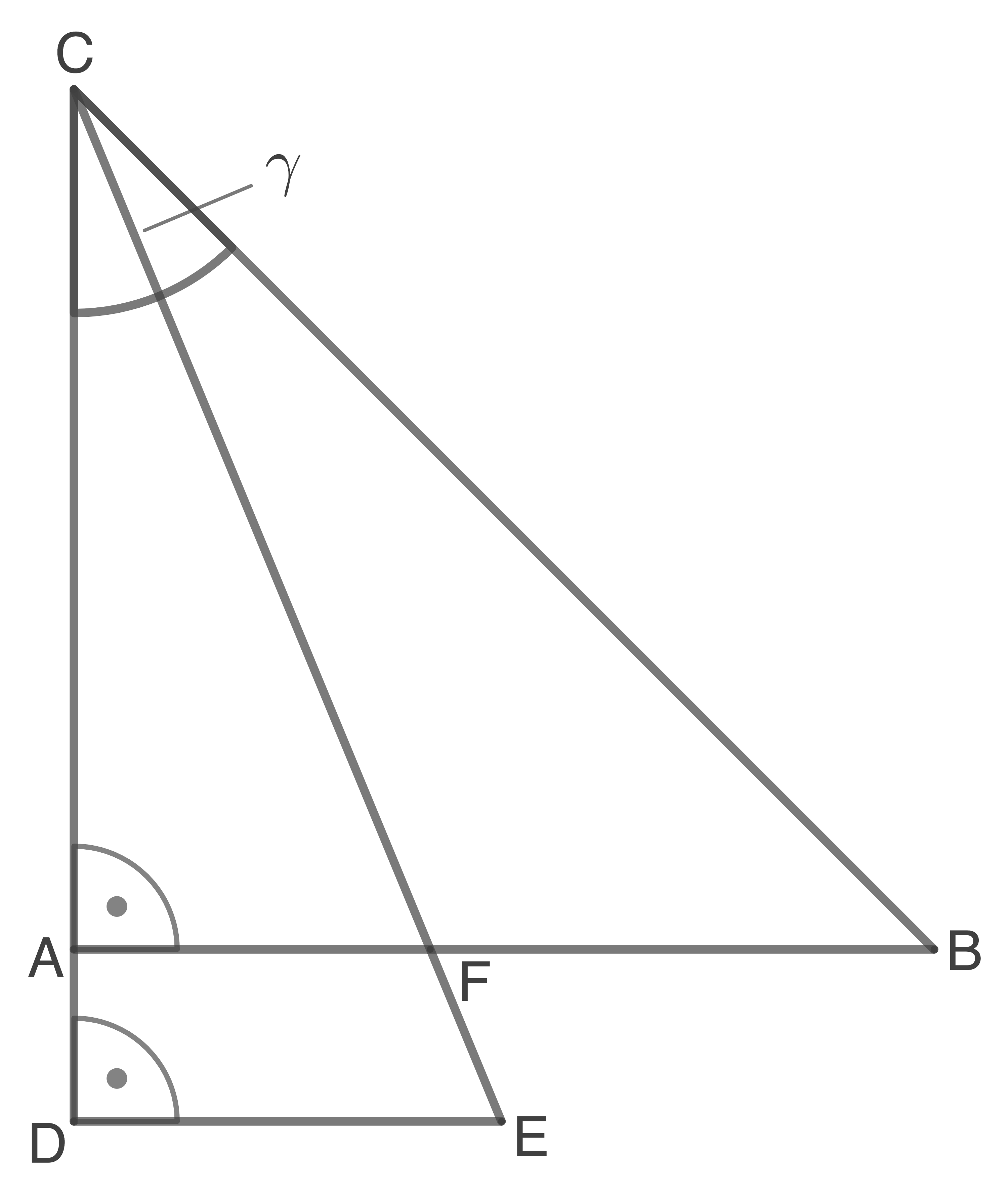 (Skizze nicht maßstäblich)
(Skizze nicht maßstäblich)
Aufgabe 8
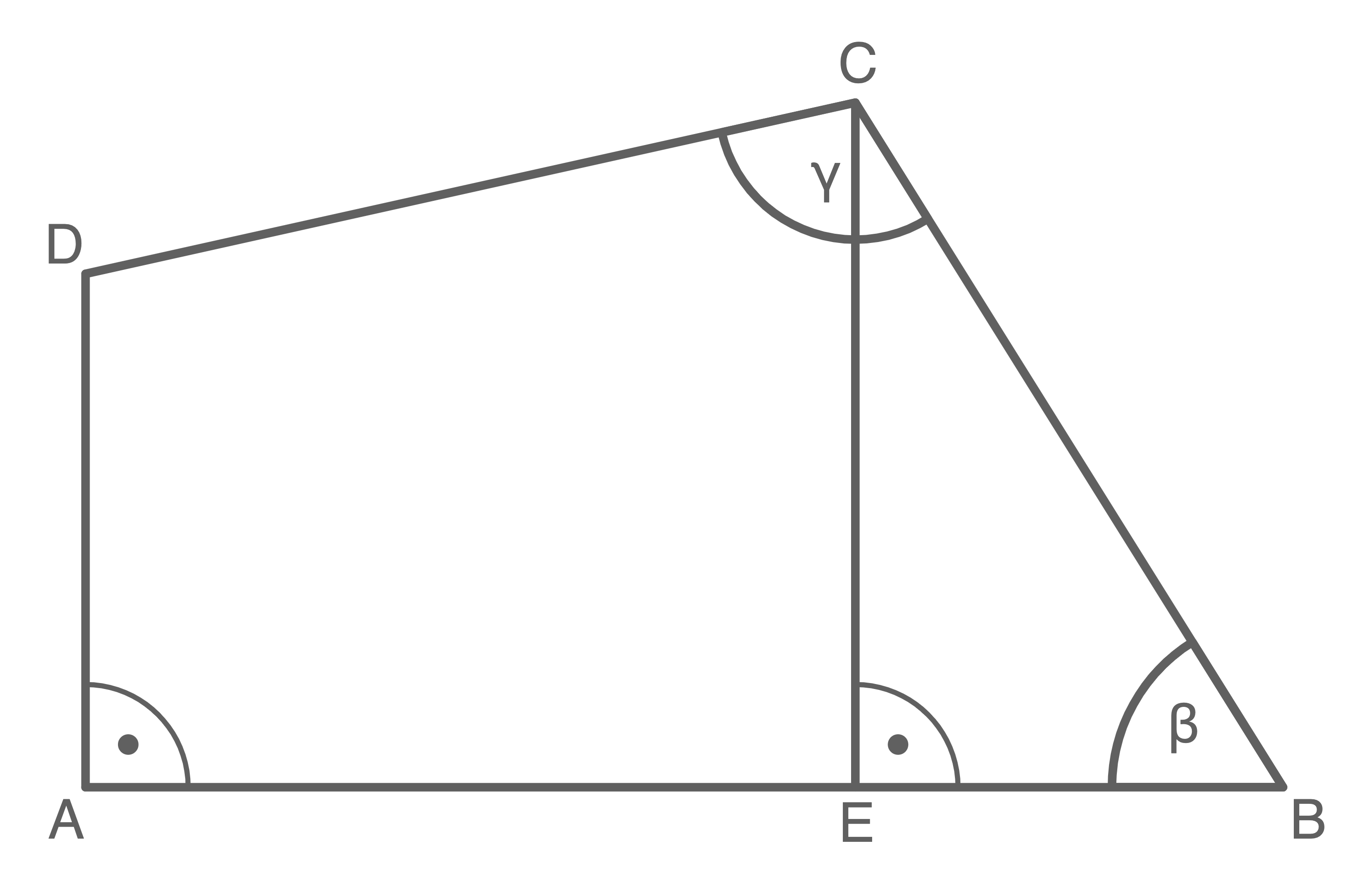
Aufgabe 9
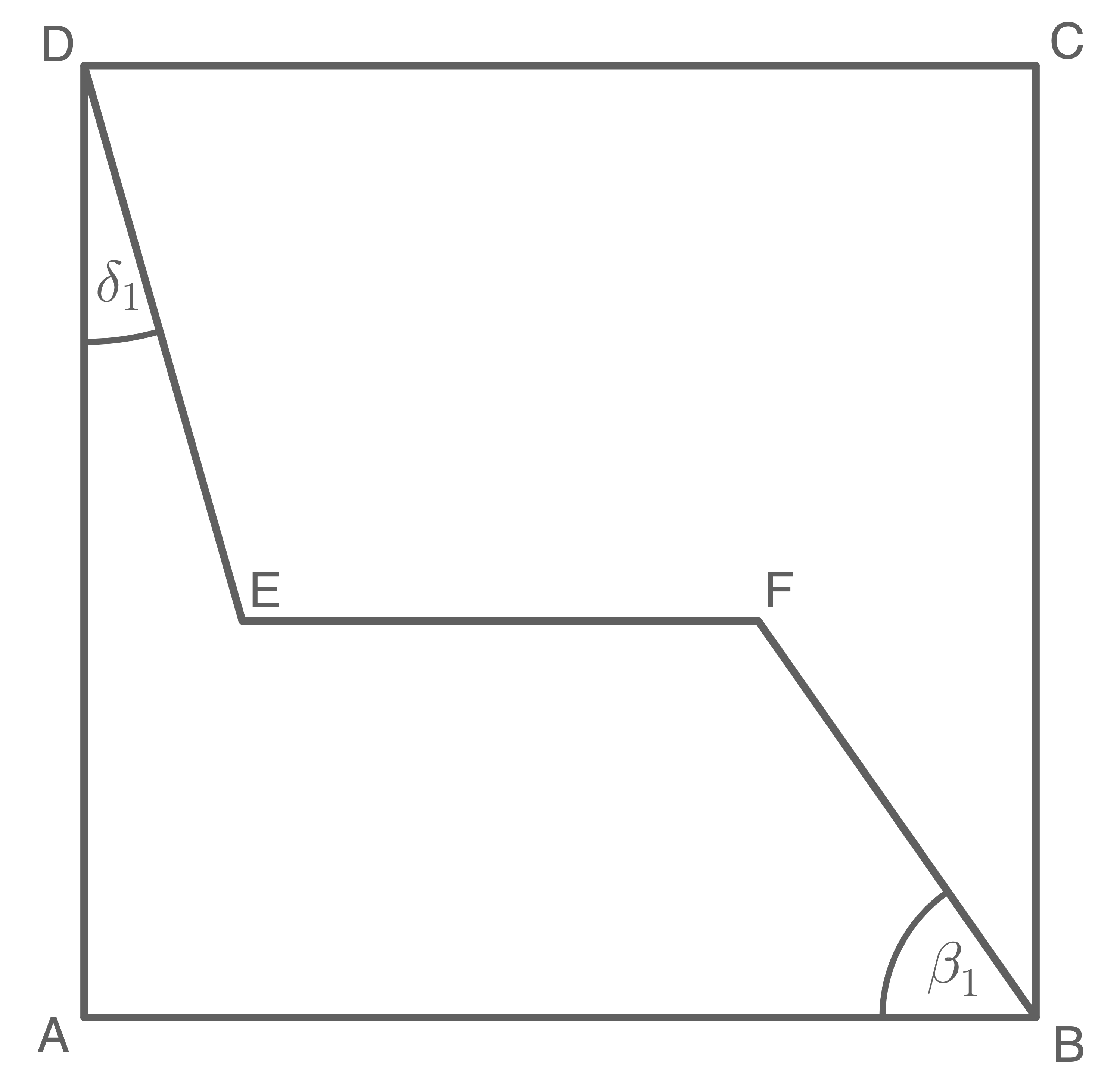
Aufgabe 10
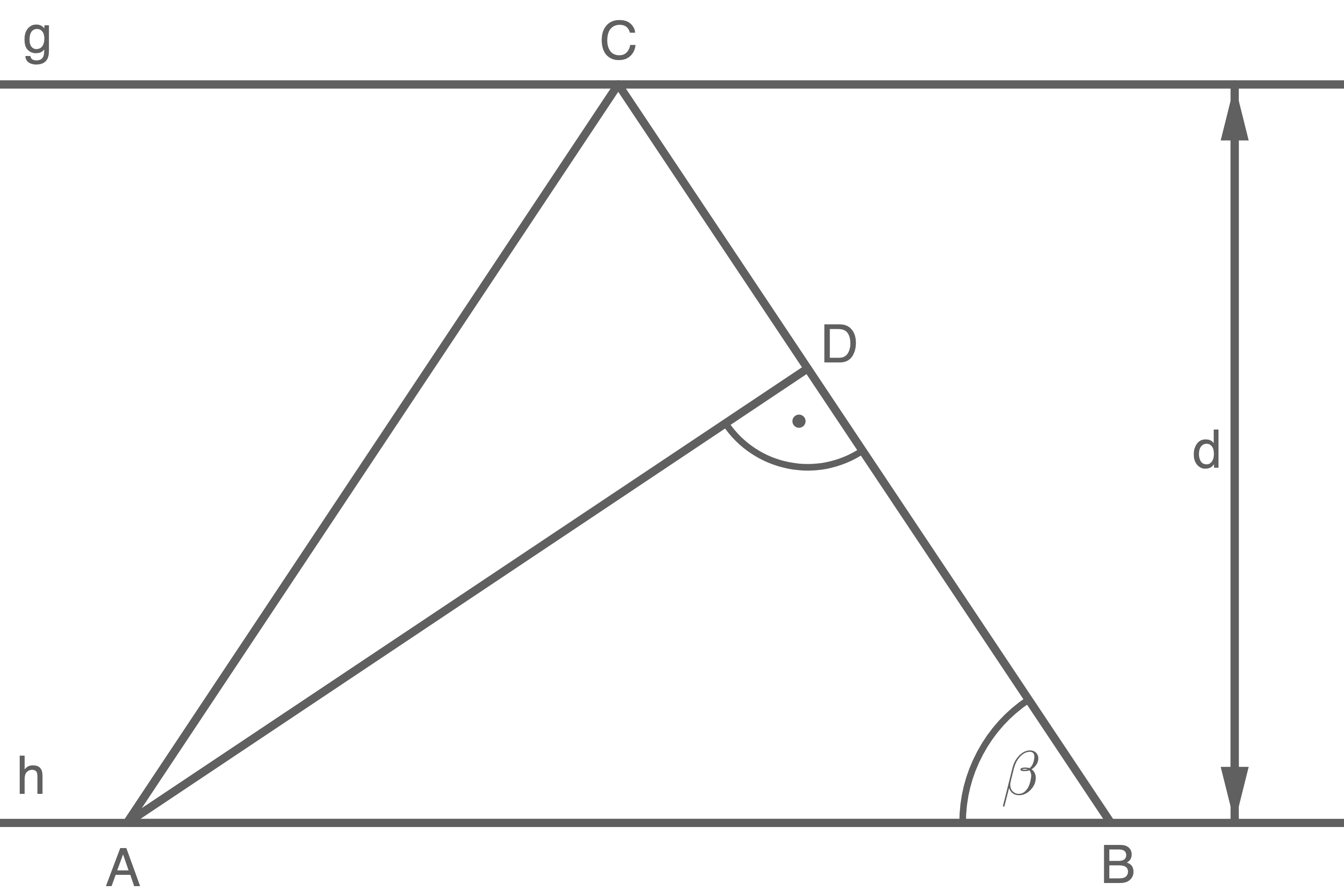
Aufgabe 11
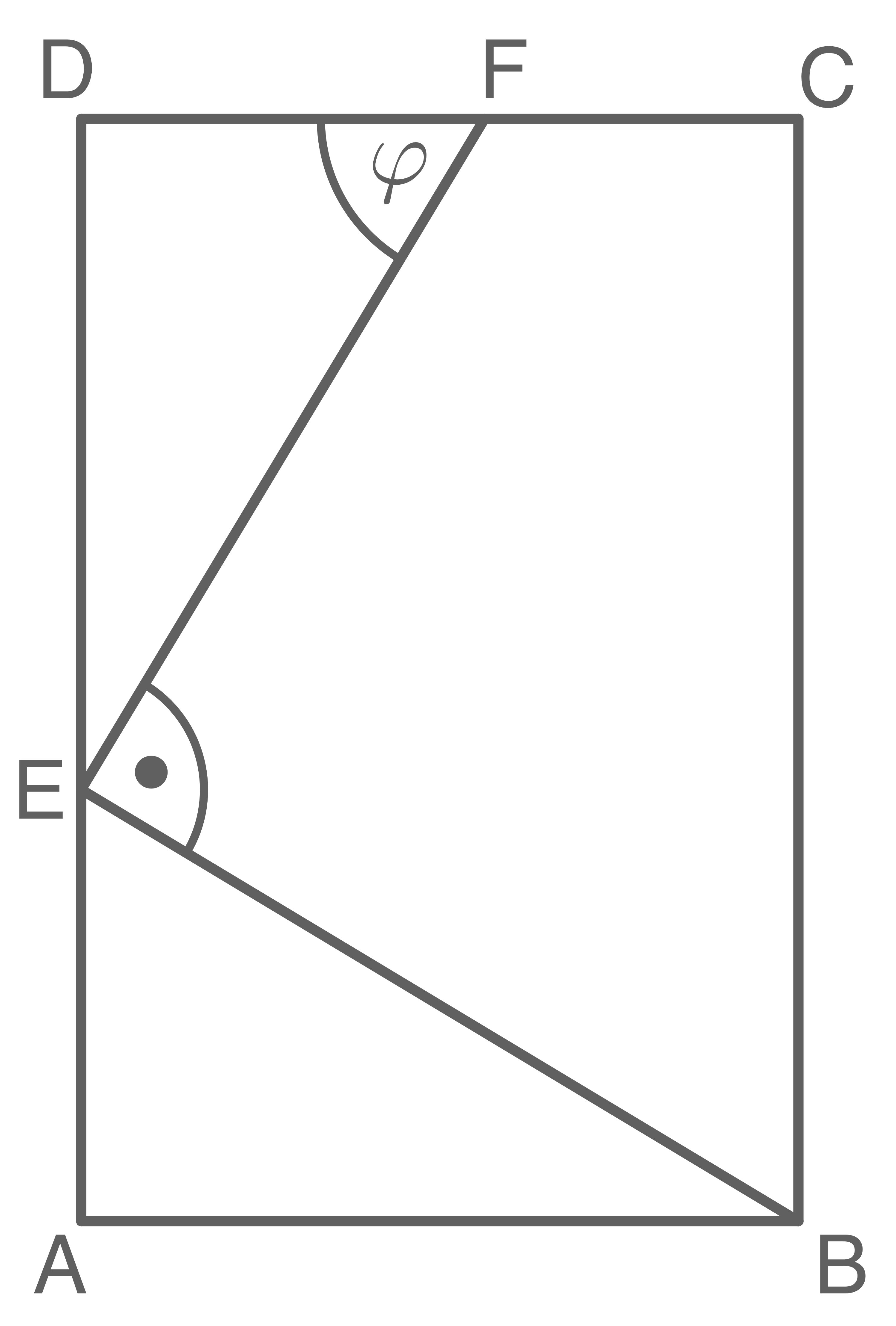
Aufgabe 12
Aufgabe 13
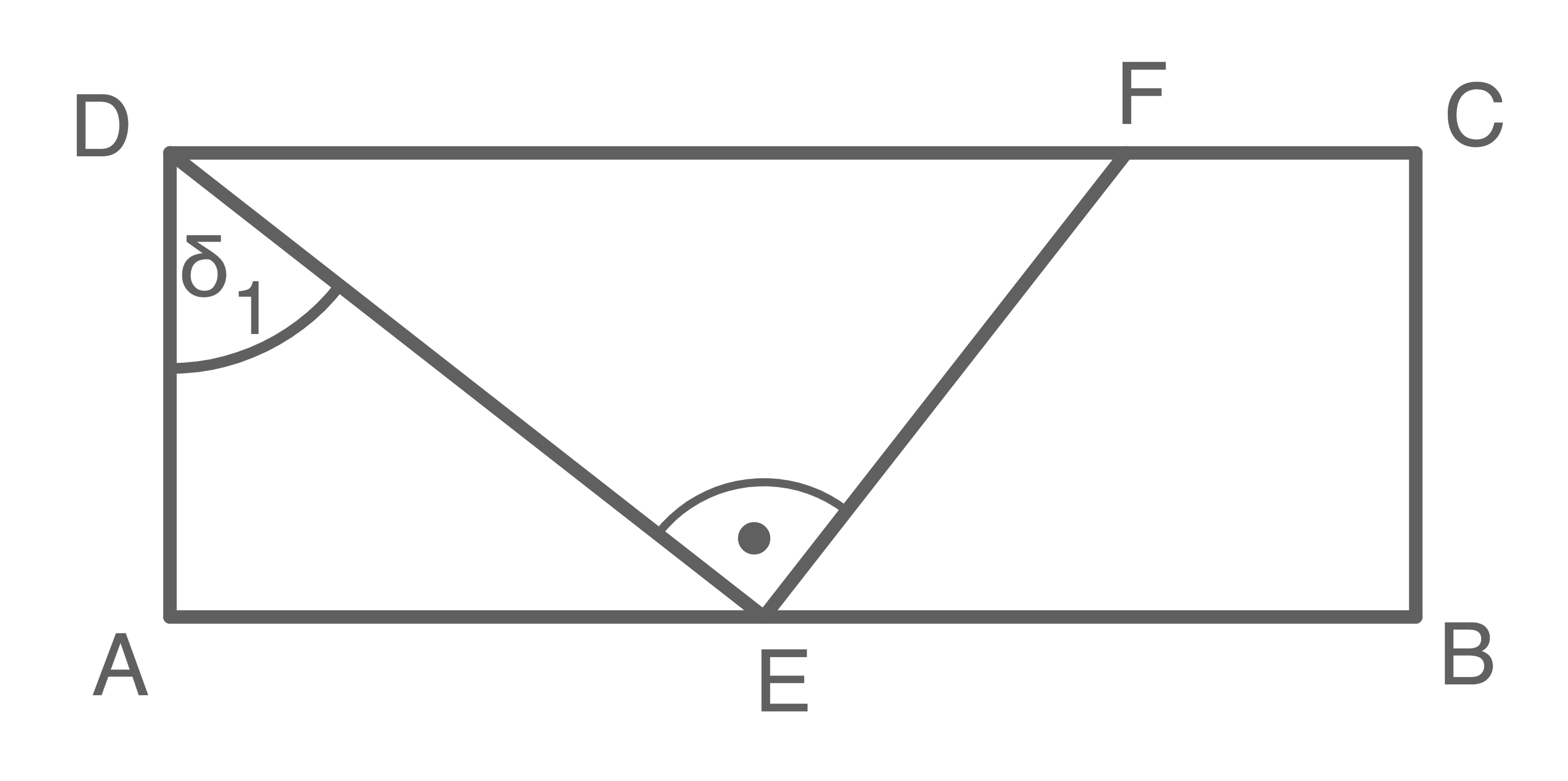
Aufgabe 14
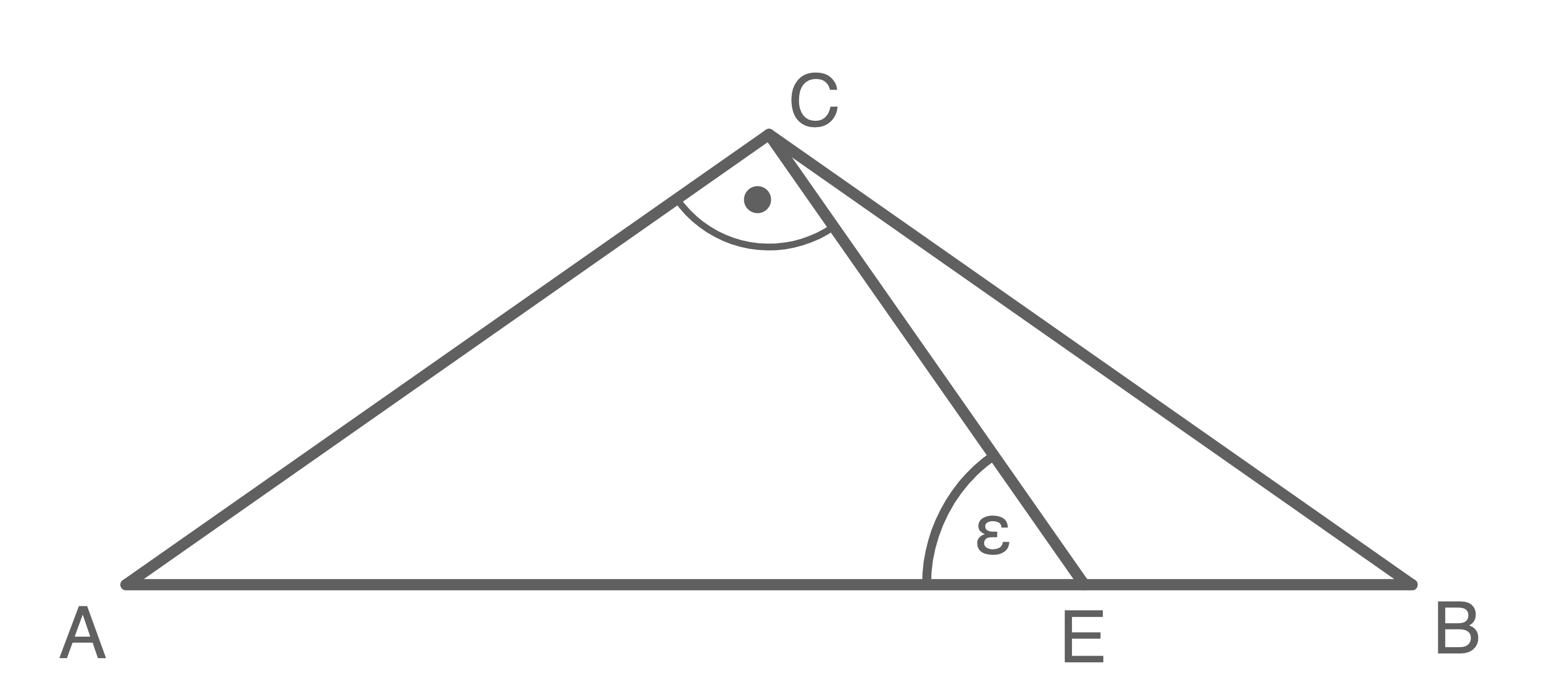
Es gilt:
Aufgabe 15
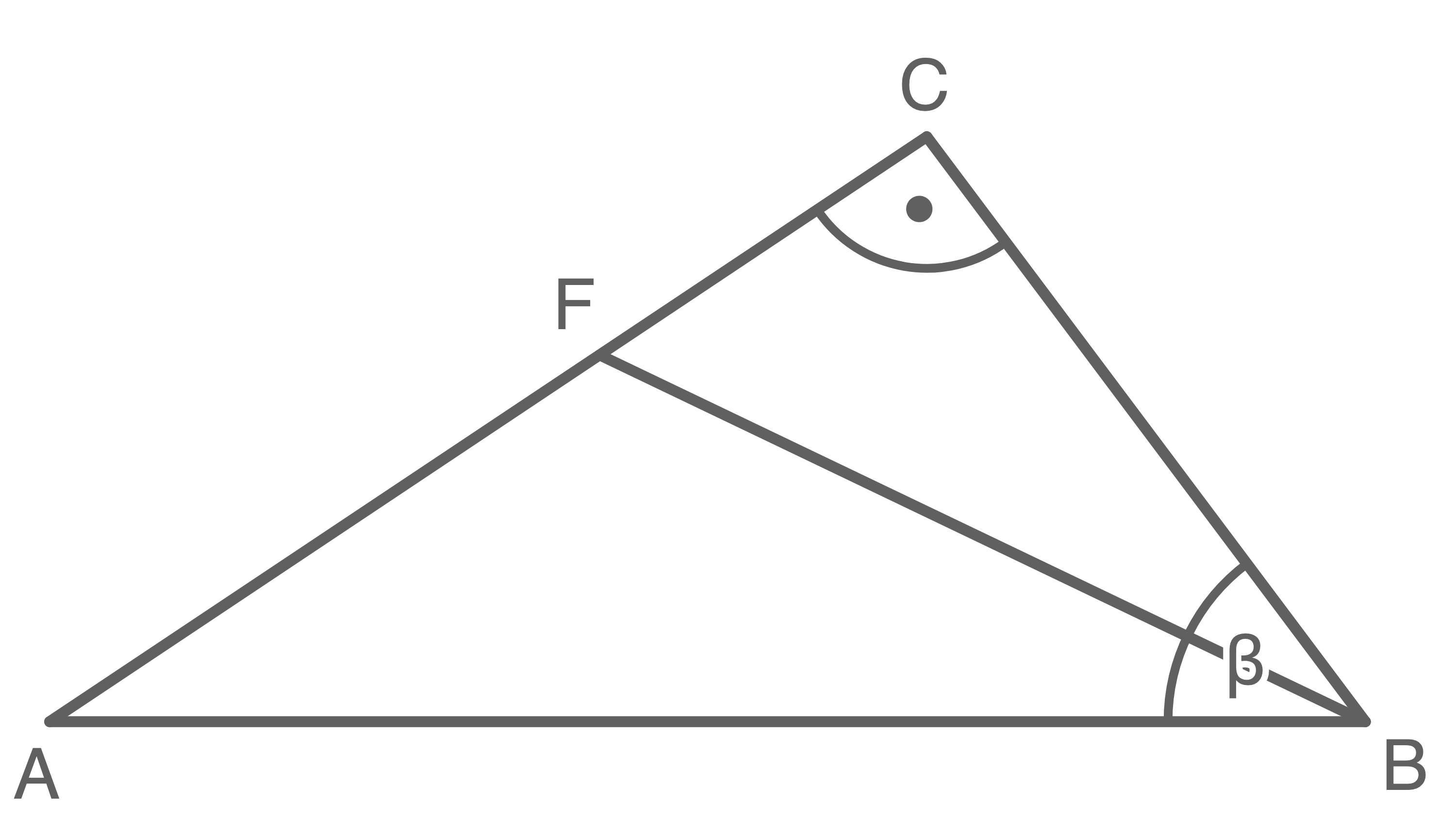
Aufgabe 16
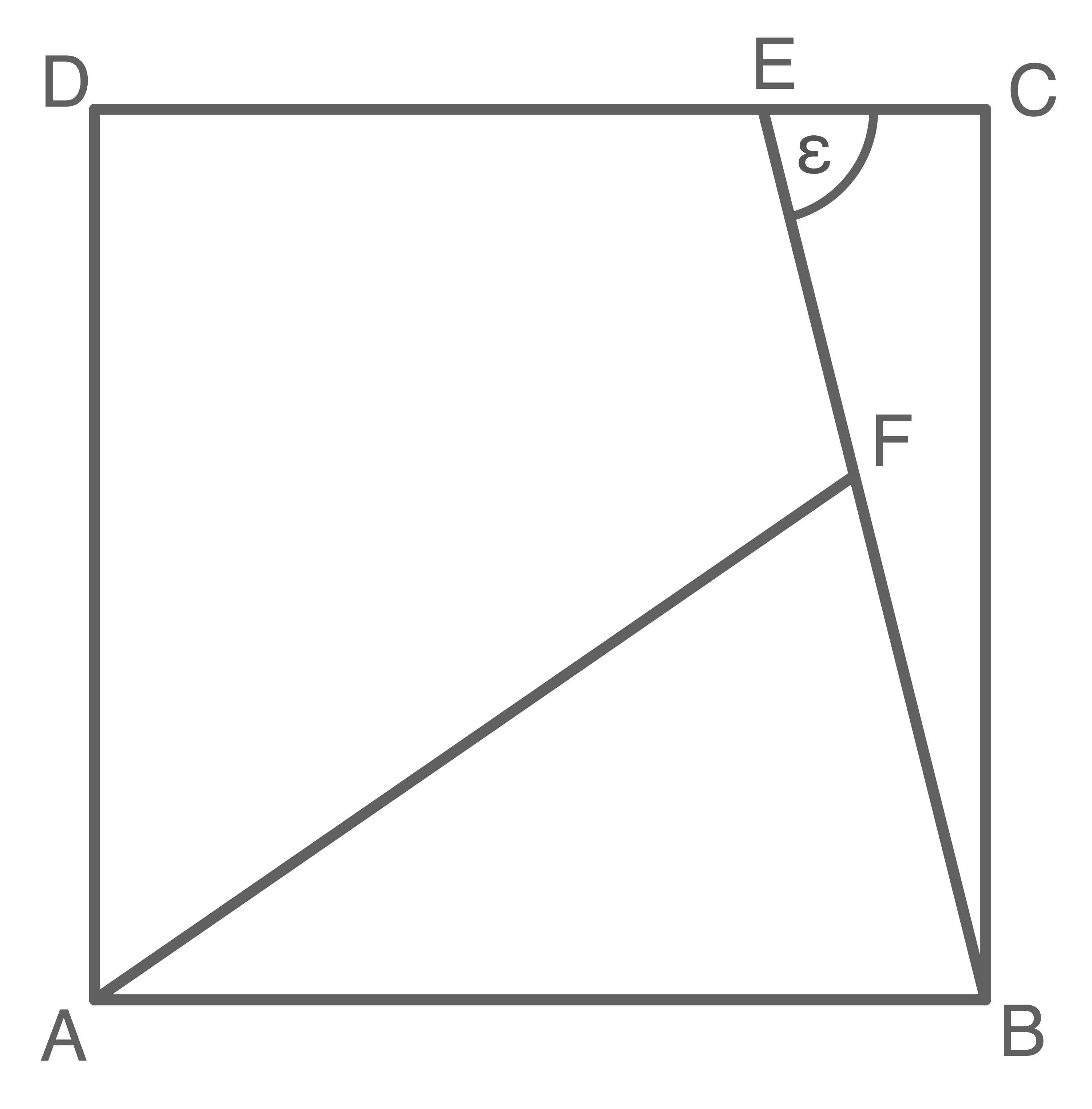
Aufgabe 17
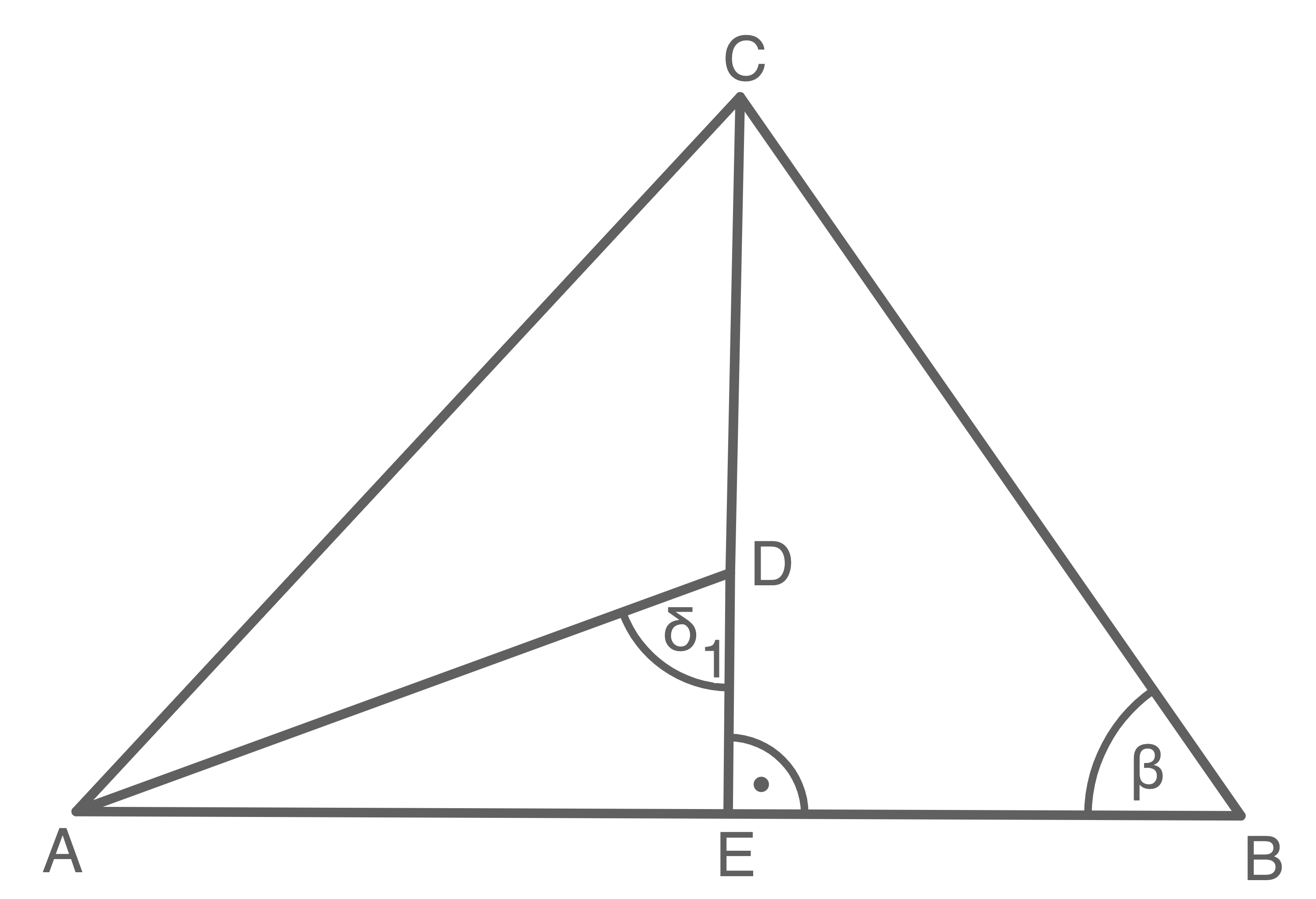
Aufgabe 18
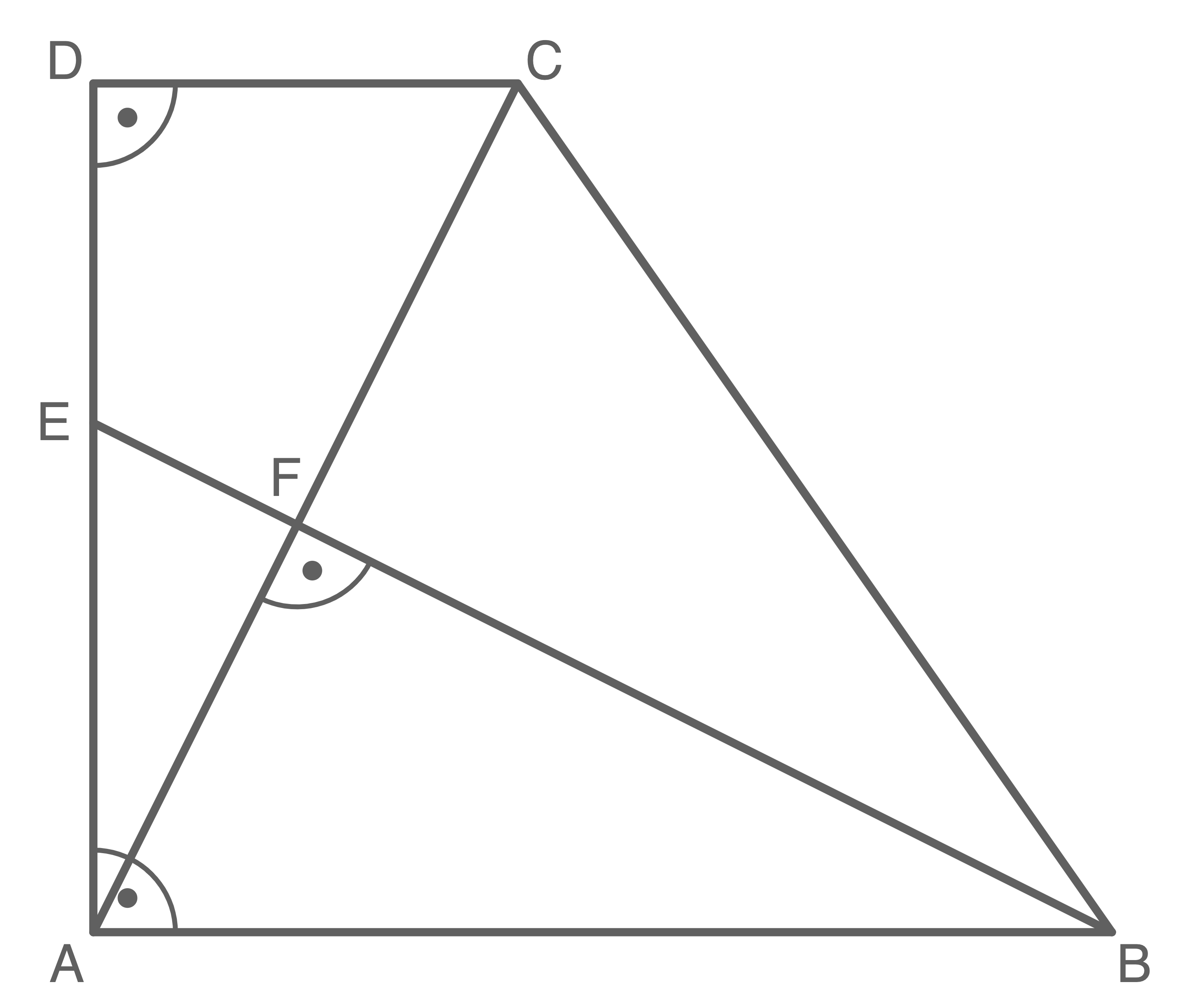
Aufgabe 19
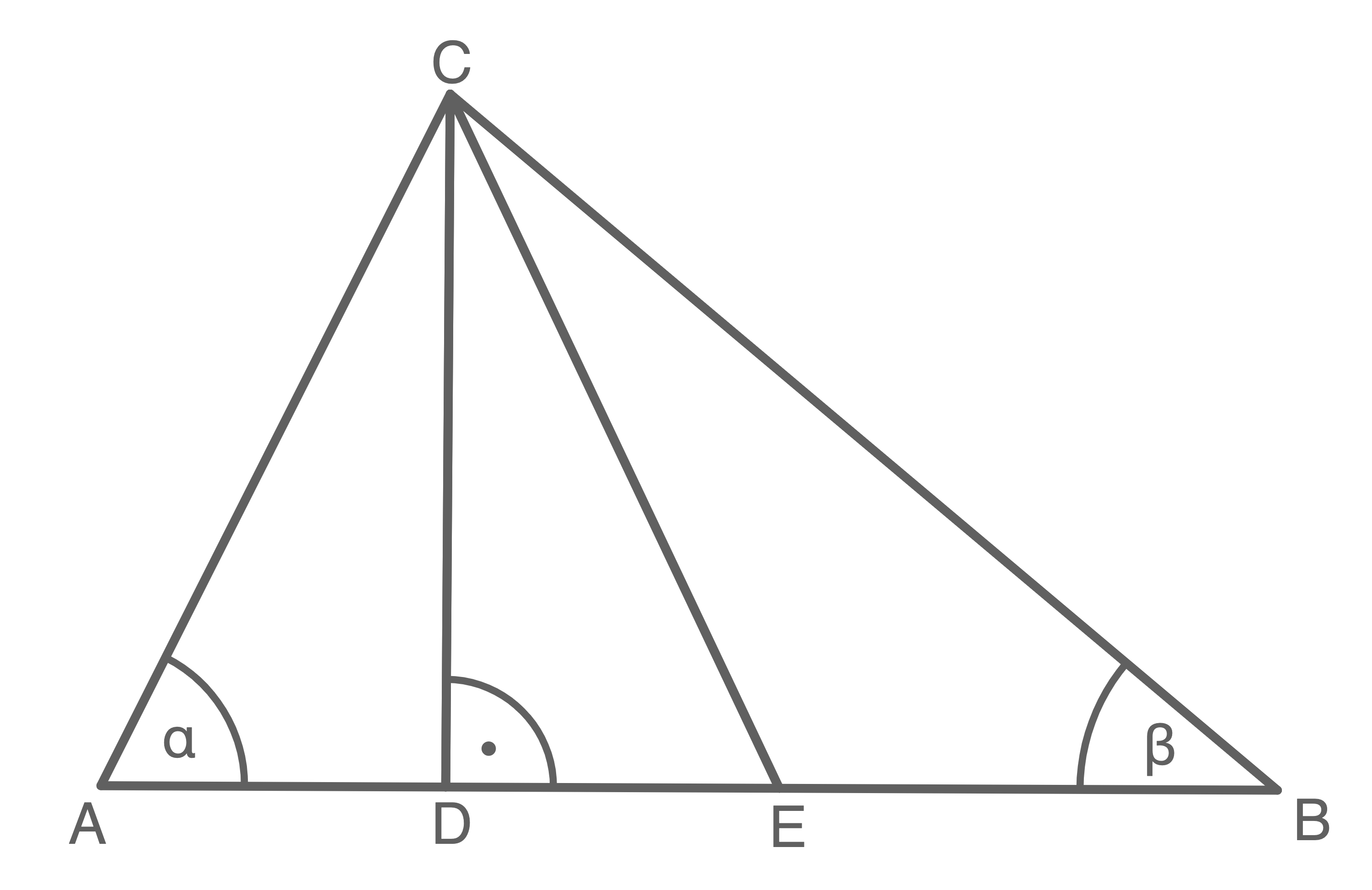
Berechne den Umfang des Dreiecks
Aufgabe 20
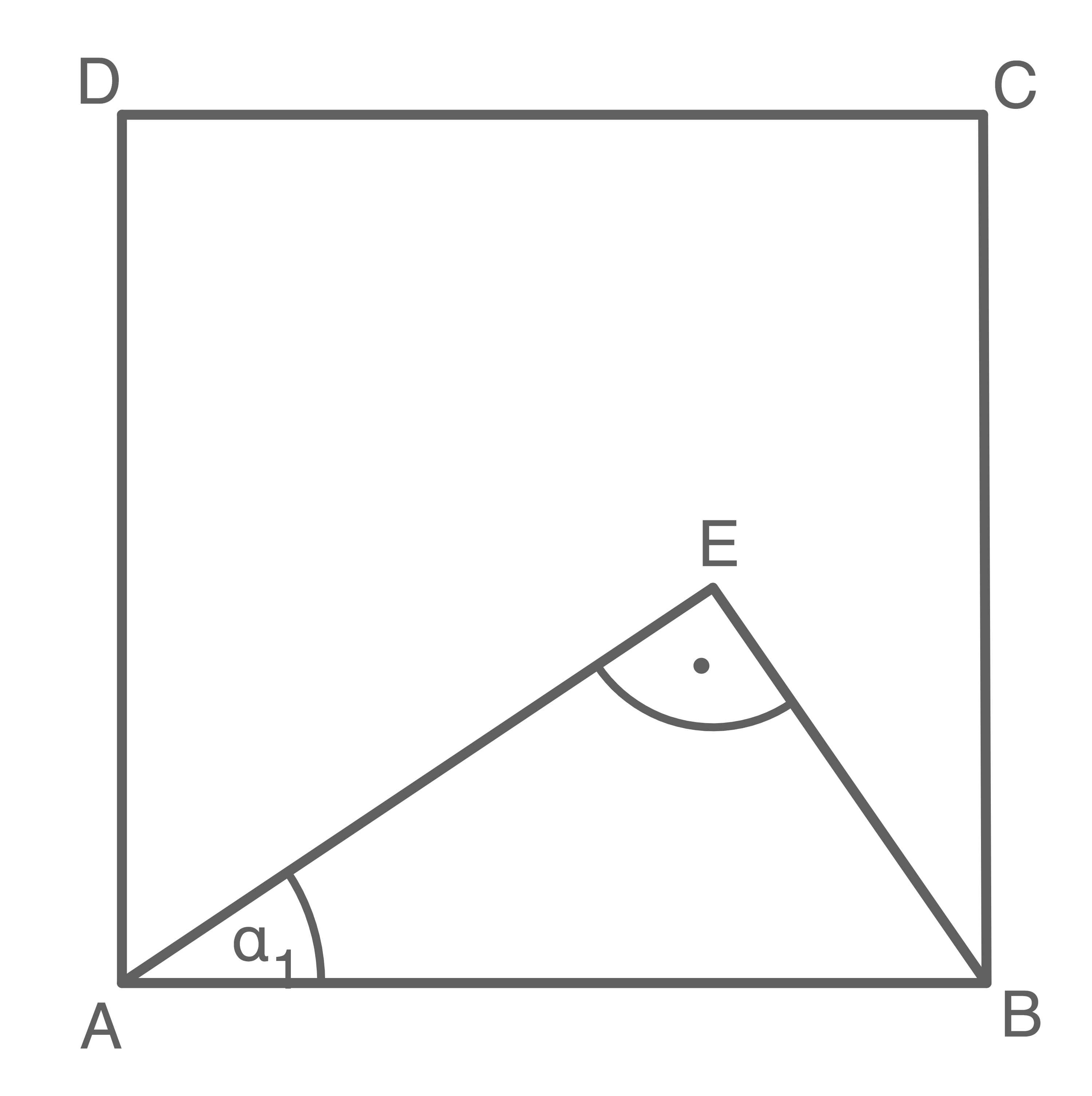
Berechne die Länge von
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
Da der Kegel im Querschnitt ein rechtwinkliges Dreieck mit der Hypotenuse bildet und der Winkel
gegeben ist, können der Radius und die Höhe des Kegels wie folgt berechnet werden:
Zylinderhöhe durch das gegebene Gesamtvolumen berechnen:
Planenfläche berechnen:
Mantel Zylinder:
Mantel Kegel:
Es werden etwa Kunststoffplane für Seitenwand und Dach benötigt.
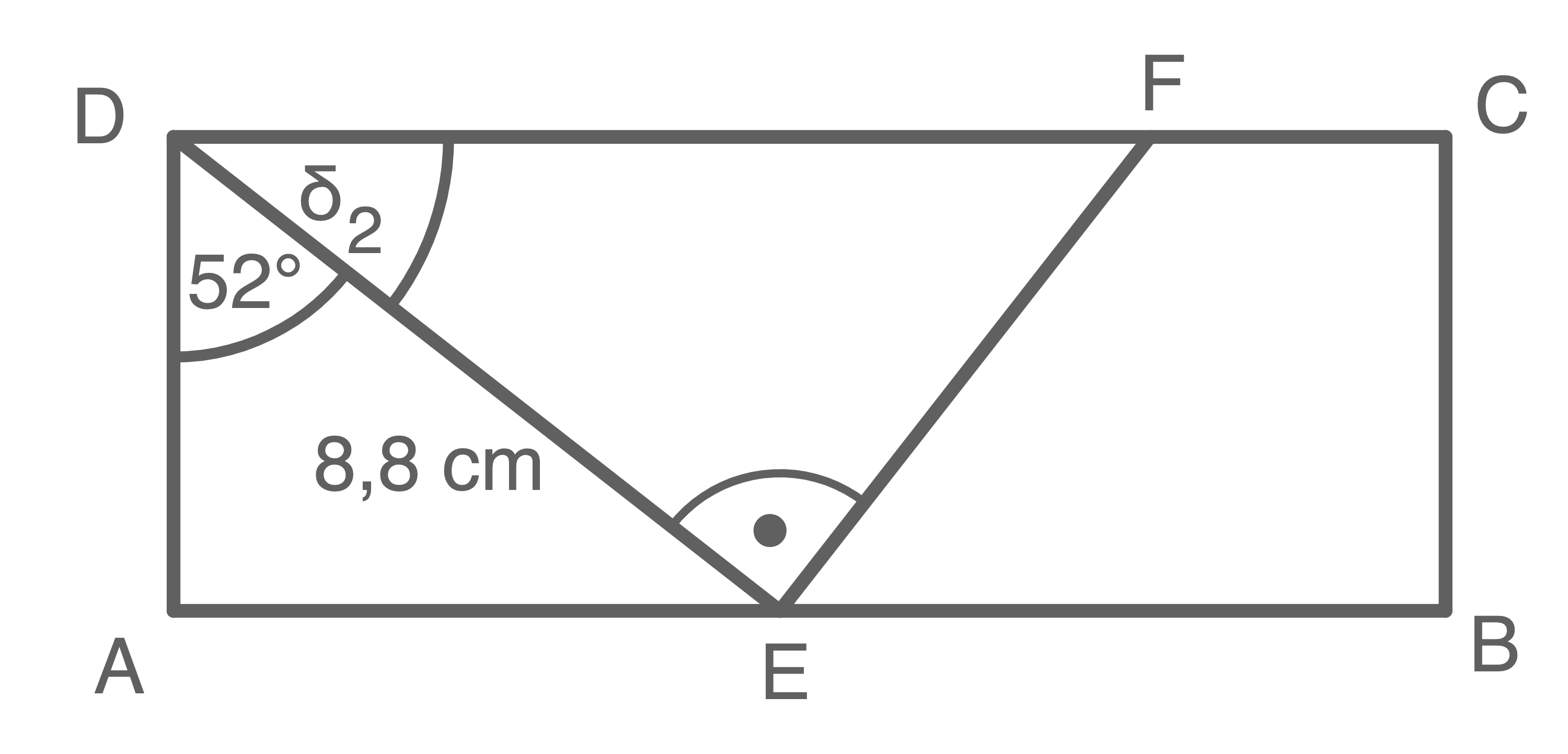
Lösung 2
Für kann gleich vorgegangen werden:
Da ein gleichschenkliges Dreieck ist, folgt:
einsetzen ergibt:
Weitere benötigte Strecken:
Flächeninhalt Rechteck:
Flächeninhalt Trapez:
Gesuchte Fläche des Vierecks
Lösung 3
1. Schritt: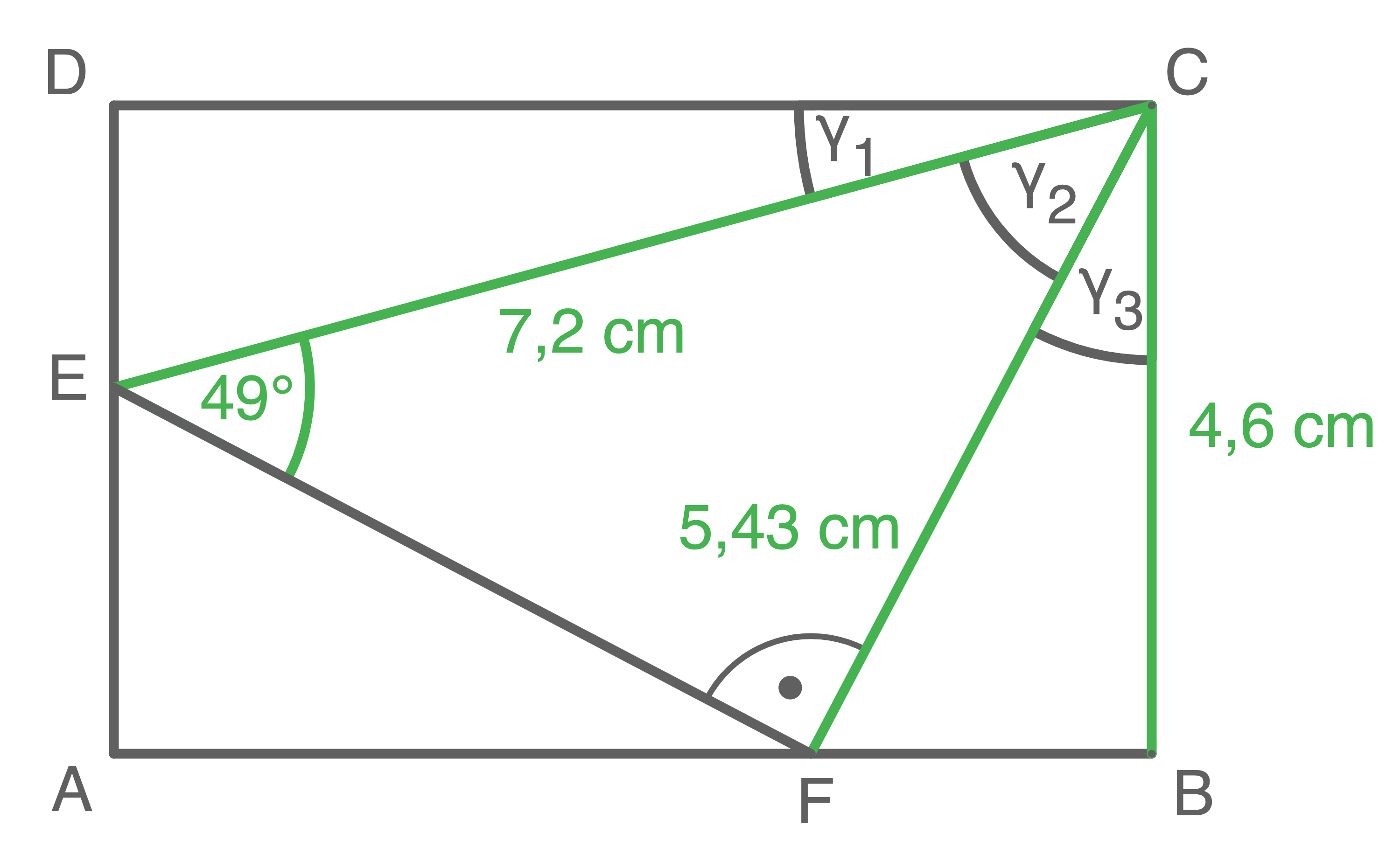
Lösung 4
Lösung 5
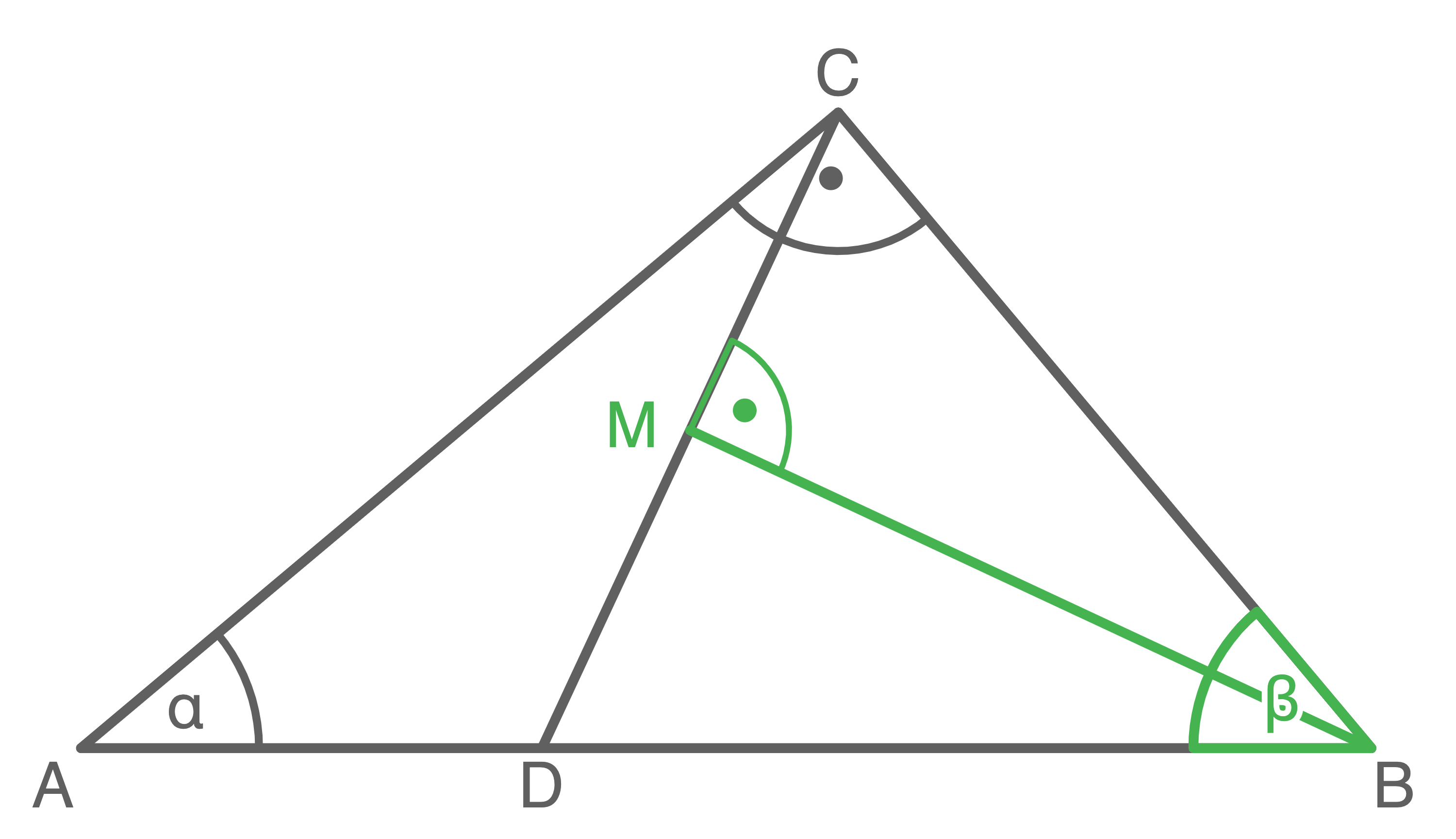
Lösung 6
Lösung 7
1. Schritt: Länge der StreckeLösung 8
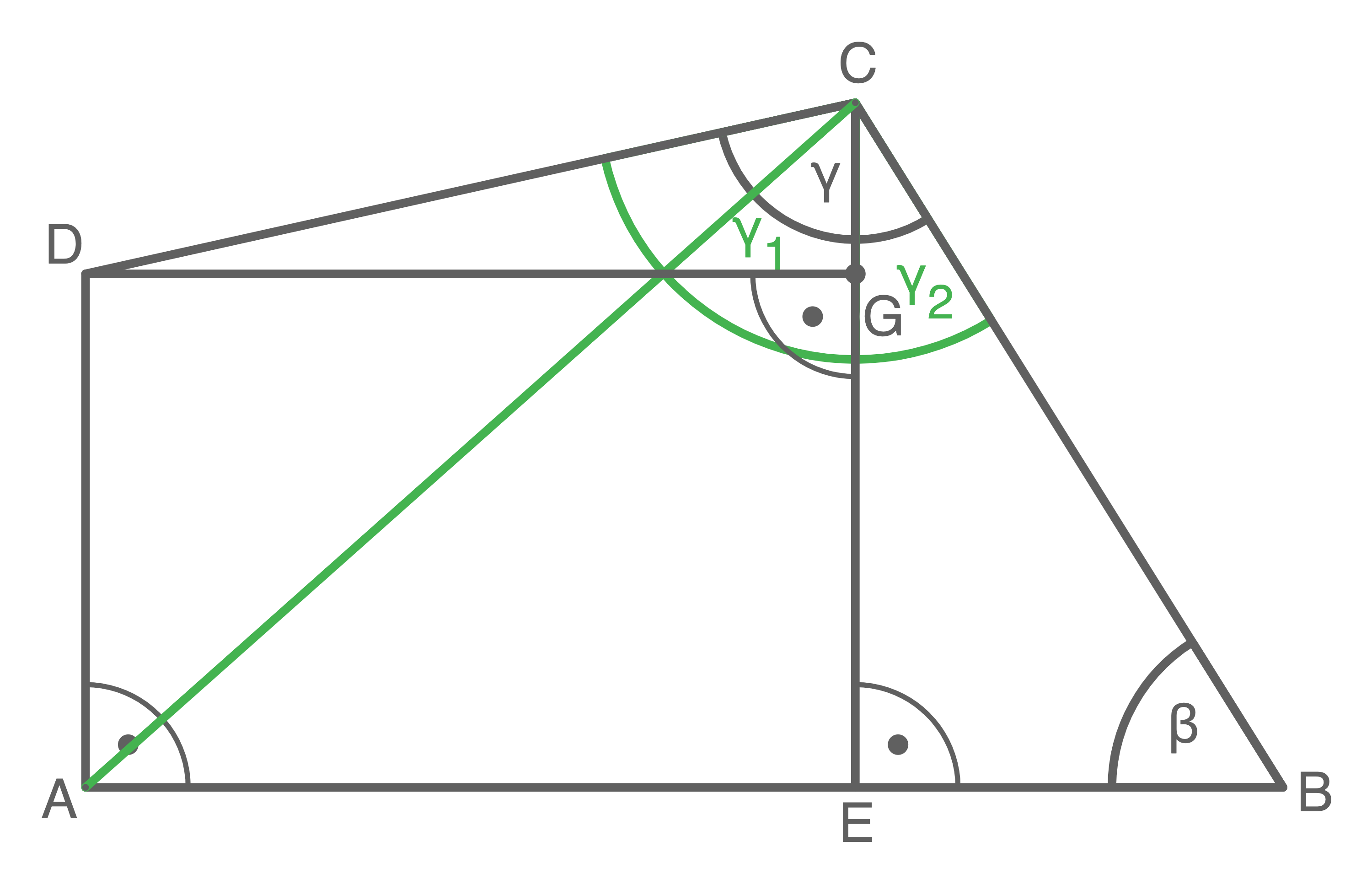
2. Schritt: Winkel
3. Schritt: Länge der Strecke
4. Schritt: Länge der Strecke
5. Schritt: Länge der Strecke
Flächeninhalt des Dreiecks
Lösung 9
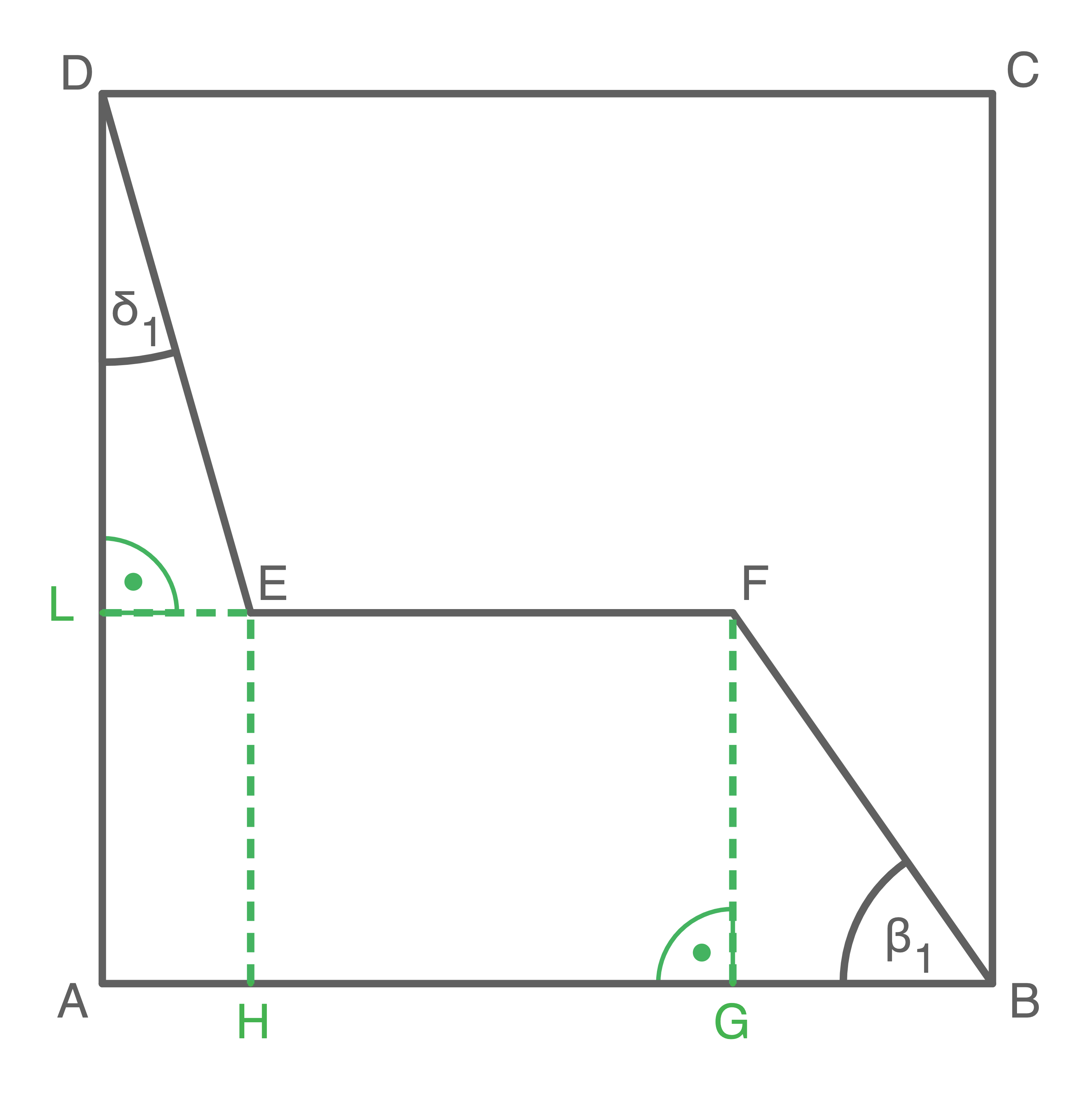
Lösung 10
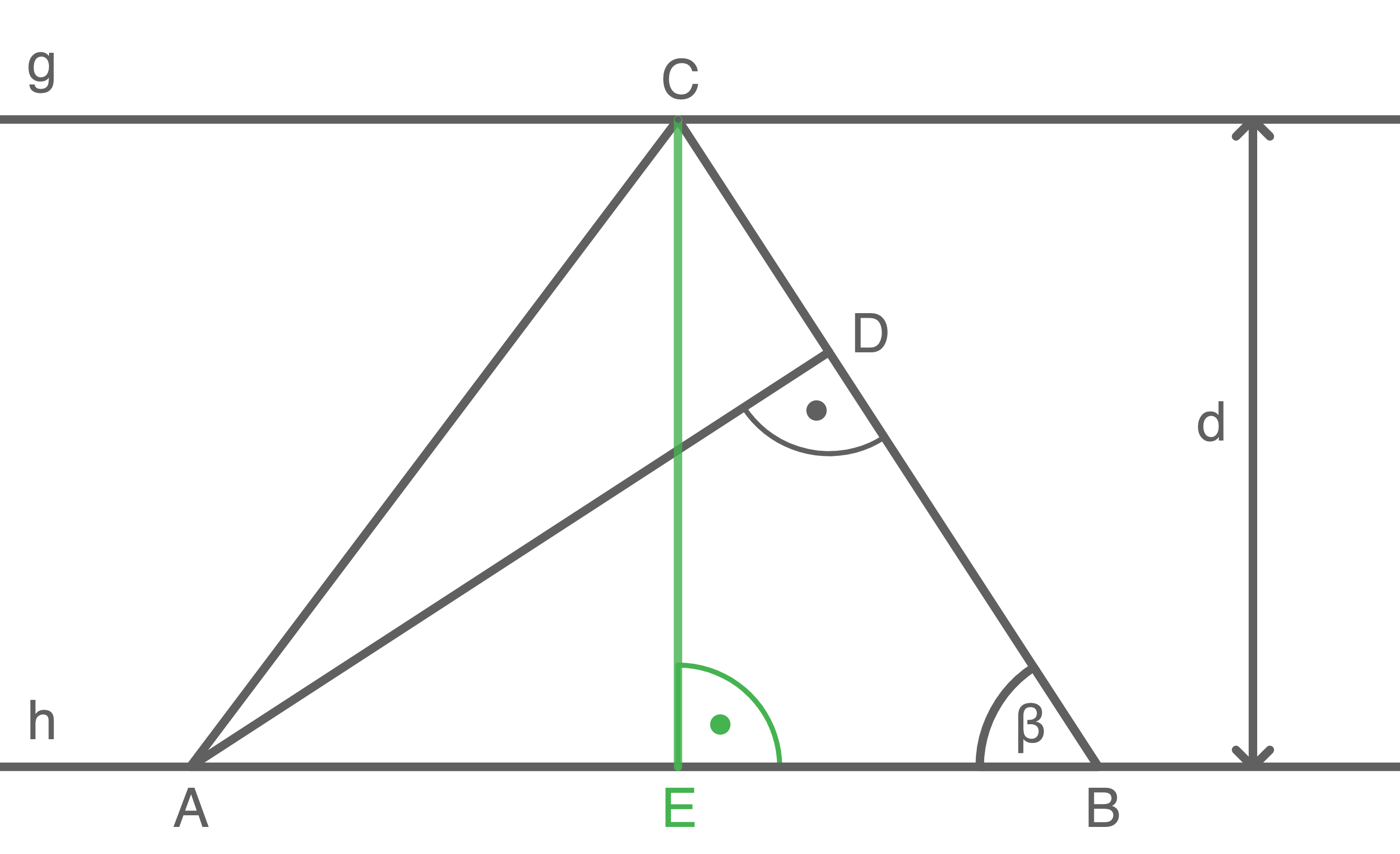
Lösung 11
1. Schritt: Länge der Strecke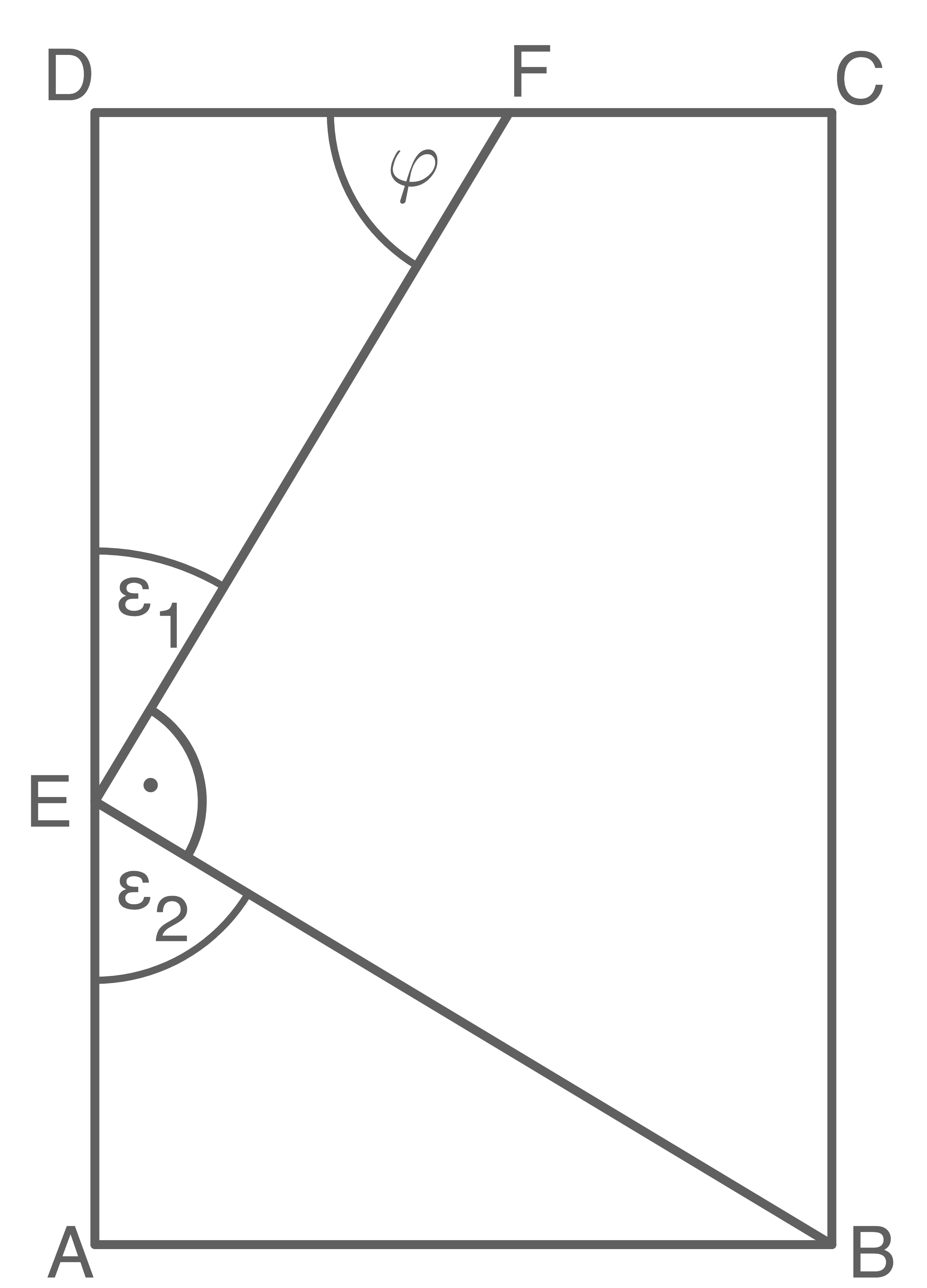
Lösung 12
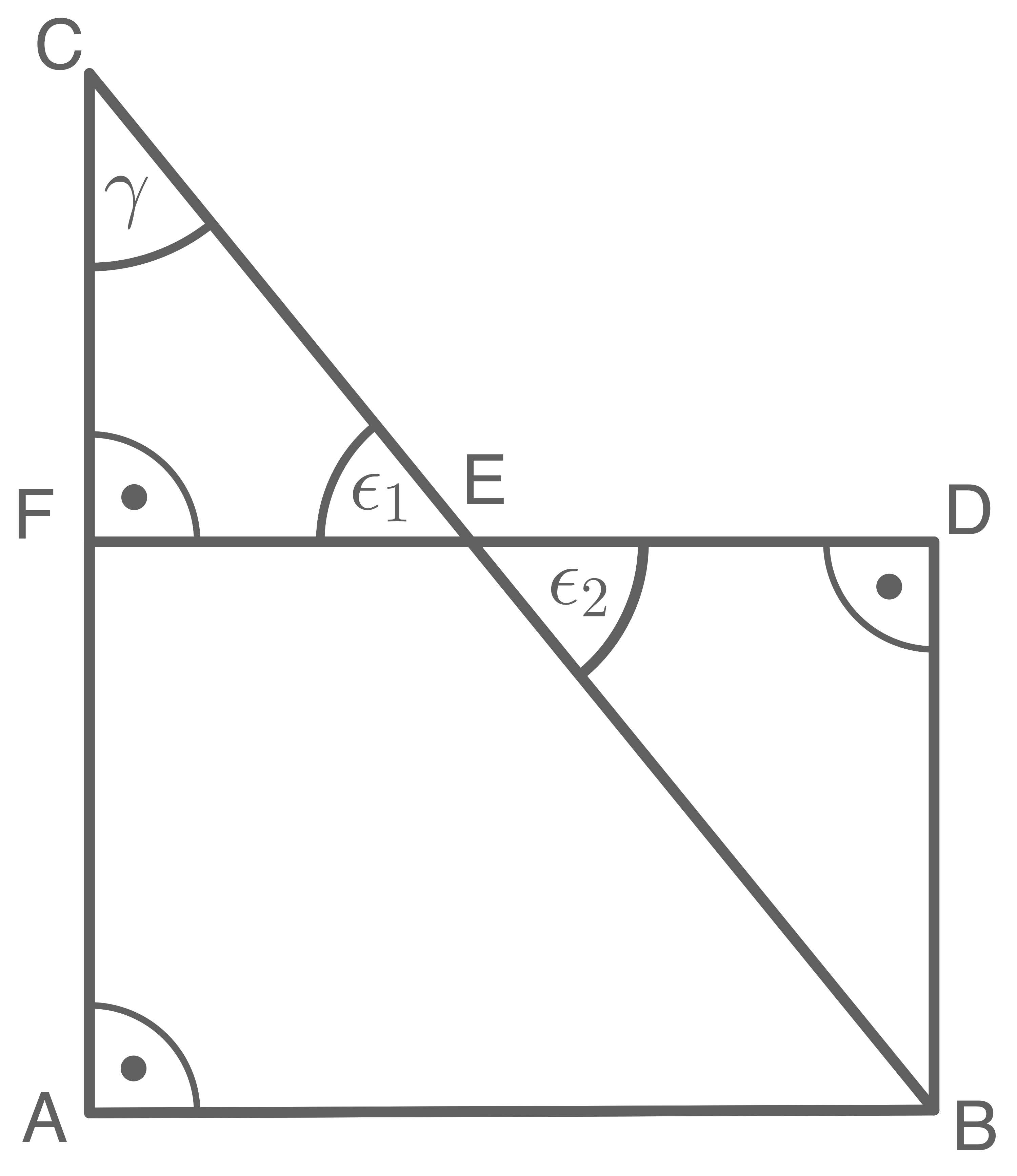
Lösung 13
Lösung 14
1. Schritt: Länge der Strecke
Lösung 15
Lösung 16
Lösung 17
Lösung 16
Lösung 18
1. Schritt: Länge der StreckeLösung 18