Funktionen und Gleichungen
Aufgabe 1
Die Teilaufgabe a) wurde in das Thema "Geometrie in der Ebene" eingeordnet.
Die Parabel mit der Funktionsgleichung
geht durch den Punkt
- Berechne die Funktionsgleichung von
Die Parabel ist eine verschobene, nach oben geöffnete Normalparabel mit den beiden Punkten
und
Sie hat den Scheitelpunkt
- Berechne die Funktionsgleichung von
Die Parabel mit dem Scheitelpunkt
hat die Funktionsgleichung
Die Punkte ,
und
bilden das Dreieck
- Berechne den Flächeninhalt des Dreiecks
Der Punkt bewegt sich auf der Parabel
Dadurch entsteht der Punkt und somit das Dreieck
- Für welchen Punkt
hat das Dreieck
den kleinsten Flächeninhalt?
Gib die Koordinaten vonan. Begründe.
Aufgabe 2
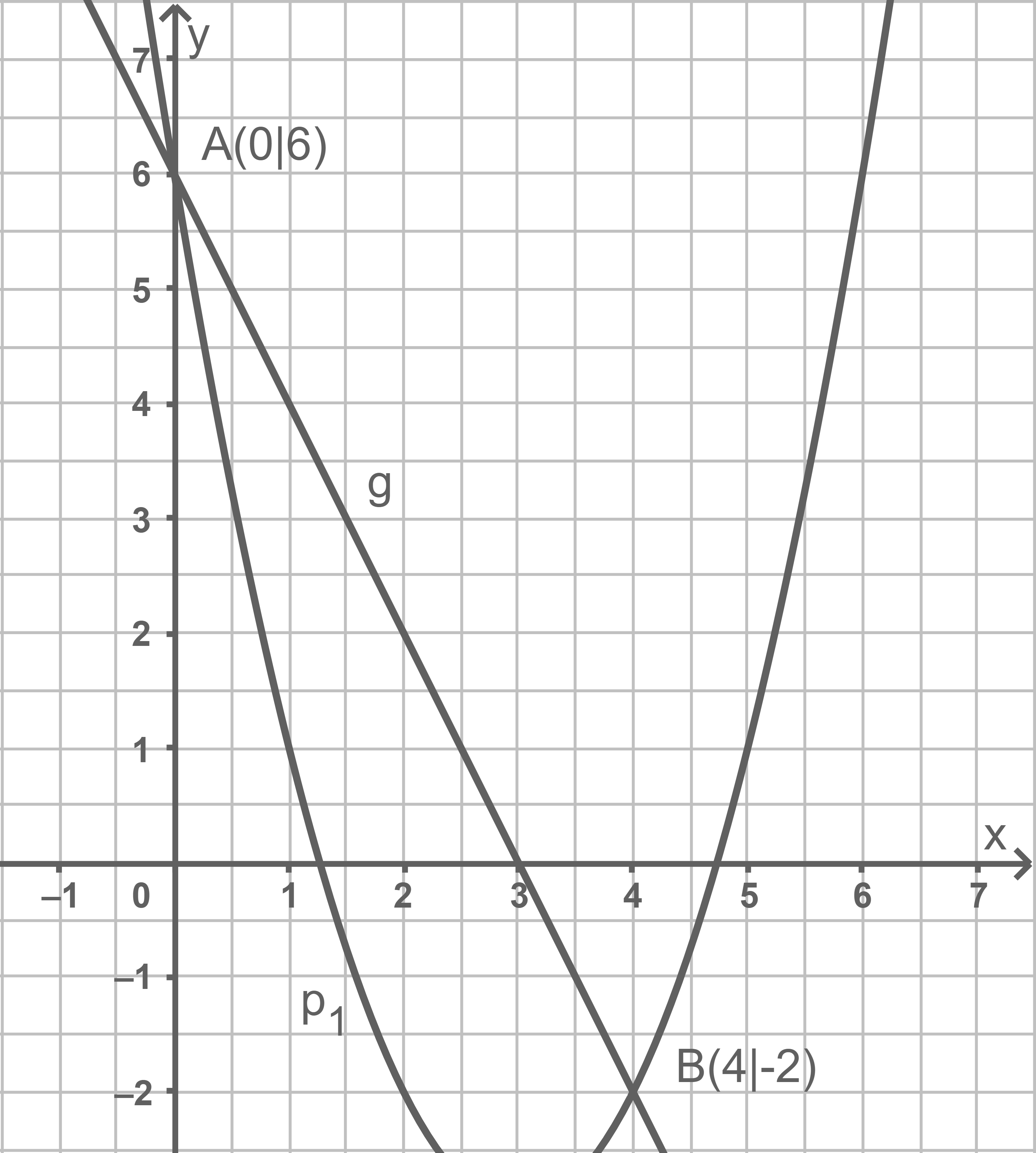
Die Abbildung zeigt die verschobene Normalparabel und die Gerade
Die Gerade schneidet die Parabel
in den Punkten
und
- Bestimme die Funktionsgleichungen von
und
Entnimm geeignete Werte aus dem Schaubild.
Die Parabel hat die Funktionsgleichung
und geht durch den Punkt
- Berechne die Koordinaten des Scheitelpunkts
von
Die Gerade ist senkrecht zu
und geht durch den Scheitelpunkt
von
- Berechne die Funktionsgleichung der Geraden
Die Gerade schneidet die Gerade
im Punkt
- Berechne die Entfernung von
zu
Die Teilaufgabe b) wurde in das Thema "Geometrie im Raum" eingeordnet.
Aufgabe 3
Die Parabel
Die Parabel
- Bestimme die Funktionsgleichungen von
und
.
- Berechne die Funktionsgleichung von
- Berechne die Entfernung zwischen
und
- Überprüfe diese Behauptung. Begründe deine Antwort rechnerisch.
Aufgabe 4
Sie schneidet die
- Bestimme die Koordinaten der Punkte
und
.
- Berechne die Funktionsgleichung der Parabel
und die Koordinaten ihres Scheitelpunktes
Sie bilden zusammen mit dem Scheitelpunkt
- Berechne den Flächeninhalt des Dreiecks
Aufgabe 5
- Berechne die Funktionsgleichung der Parabel
Sie schneidet die
- Bestimme die Koordinaten der Punkte
und
- Berechne den Flächeninhalt des Dreiecks
- Gib die Funktionsgleichung von
an.
- Überprüfe diese Aussage und begründe deine Antwort durch Rechnung oder Argumentation.
Aufgabe 6
- Bestimme die Funktionsgleichung von
- Vervollständige die Wertetabelle.
- Berechne die Funktionsgleichung von
- Zeige rechnerisch, dass
keinen Schnittpunkt mit
hat.
- Gib die Funktionsgleichung einer verschobenen nach oben geöffneten Normalparabel
an, die keinen Schnittpunkt mit
und
hat.
Aufgabe 7
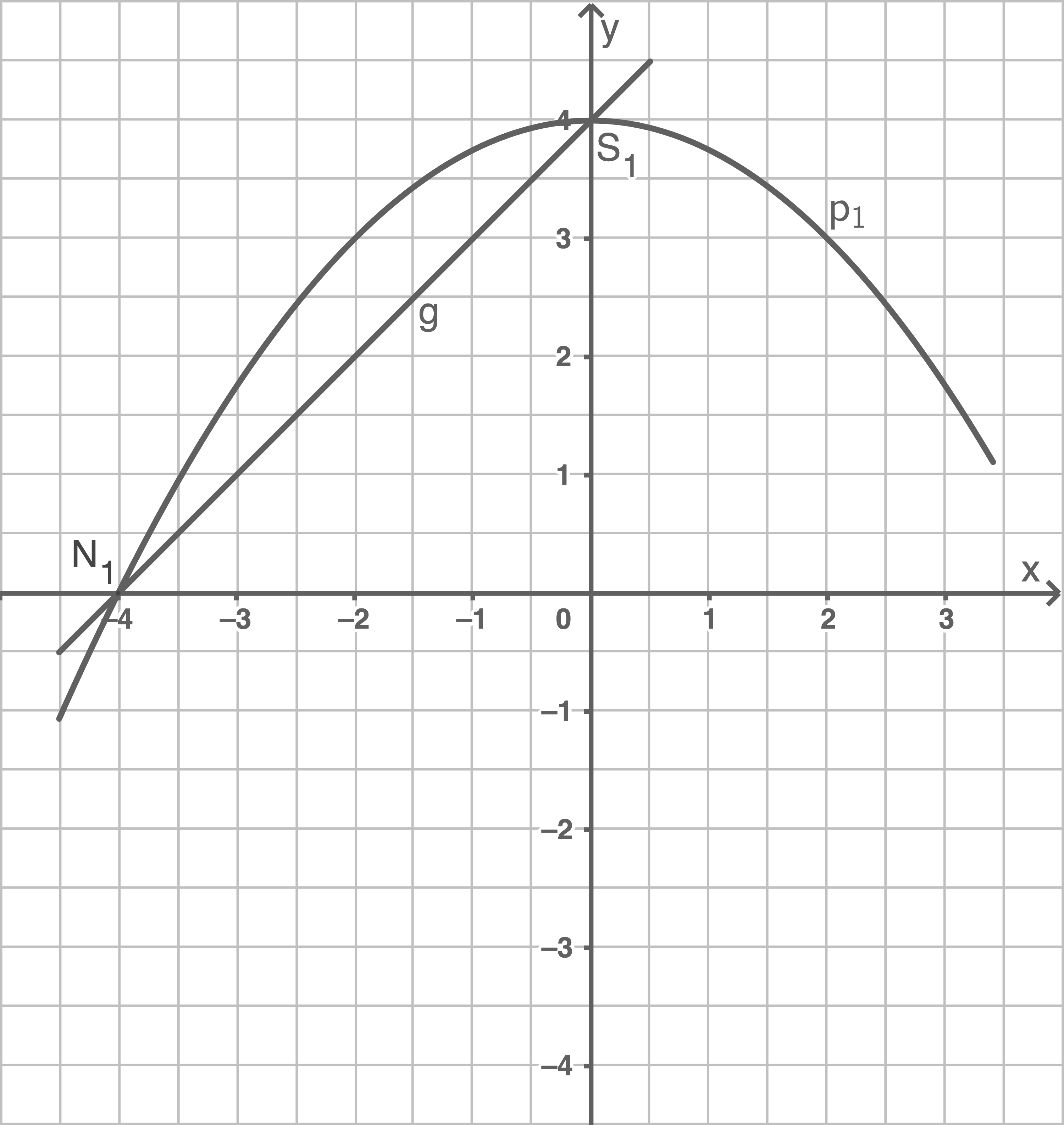
- Bestimme die Funktionsgleichungen von
und
.
Entnimm dazu geeignete Werte aus dem Schaubild.
- Gib die Koordinaten von
an.
- Berechne die Koordinaten des Scheitelpunktes
von
- Um wie viele Flächeneinheiten (FE) unterscheiden sich die Flächeninhalte dieser beiden Dreiecke?
Aufgabe 8
Die Parabel
Die Parabel
- Berechne die Koordinaten der Schnittpunkte
und
- Berechne die Koordinaten des Scheitelpunkts
von
- Hat Robin Recht? Begründe deine Antwort rechnerisch.
Aufgabe 9
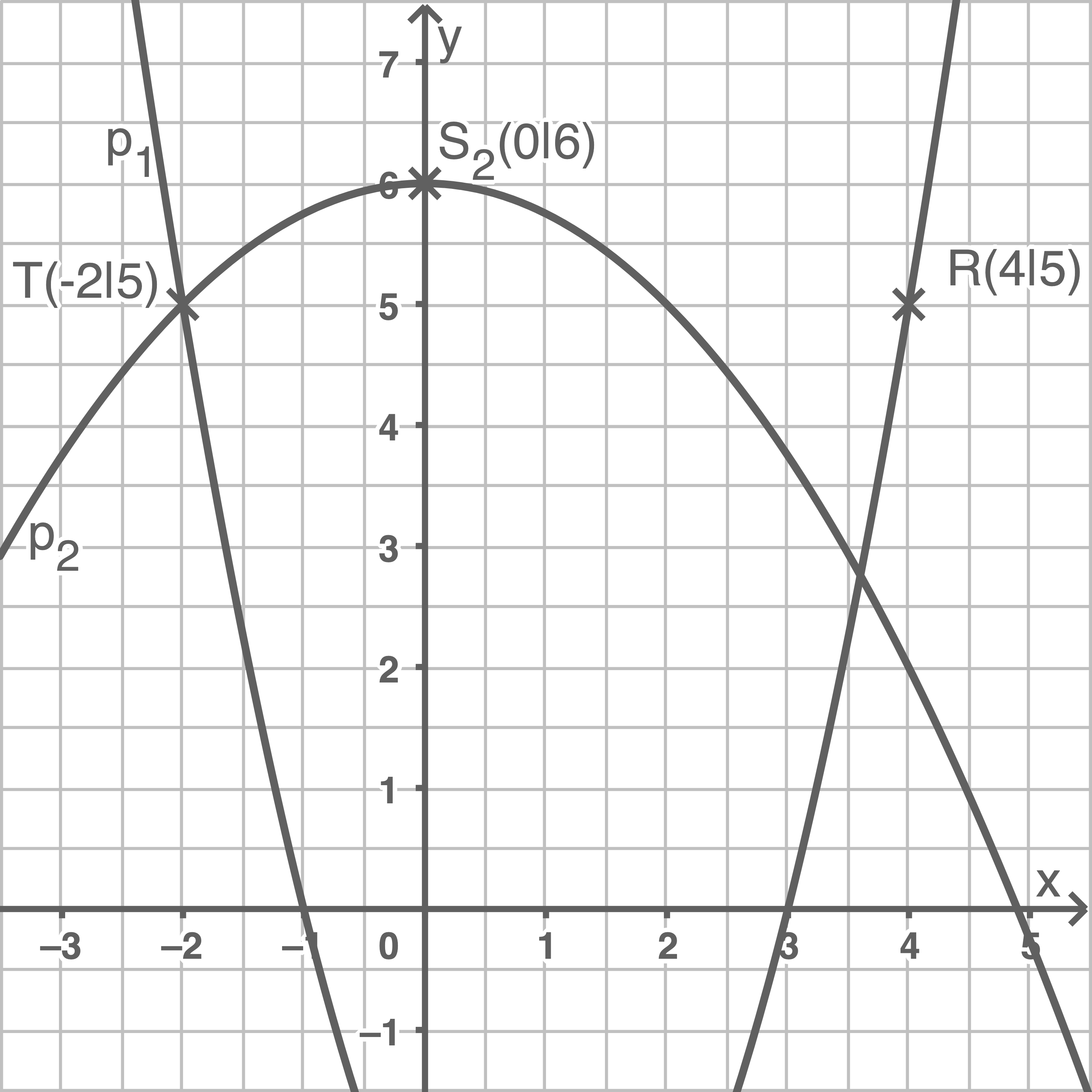
- Bestimme die Funktionsgleichungen der beiden Parabeln. Entnimm dazu geeignete Werte aus dem Schaubild.
- Berechne die Funktionsgleichung von
.
- Berechne die Funktionsgleichung von
- Gib die Funktionsgleichung einer weiteren verschobenen nach oben geöffneten Normalparabel
an, die keine Punkte mit
und
gemeinsam hat.
Aufgabe 10
Die verschobene nach oben geöffnete Normalparabel
- Berechne die Koordinaten des Schnittpunkts
der beiden Parabeln
und
- Berechne die Koordinaten von
und
- Berechne den Flächeninhalt des Dreiecks
- Für welche Lage von
wird der Flächeninhalt des Dreiecks am größten?
- Berechne diesen maximalen Flächeninhalt.
Aufgabe 11
- Gib die Funktionsgleichung der Parabel
in der Normalform
an.
- Berechne den Flächeninhalt dieses Vierecks.
Sie schneiden sich im Punkt
- Berechne die Koordinaten des Schnittpunktes
Aufgabe 12
- Berechne die Funktionsgleichungen der Parabel
und der Geraden
- Gib die Funktionsgleichung von
in der Form
an.
- Berechne die Funktionsgleichung der Parabel
Aufgabe 13
Der Punkt
Die Gerade
Die Gerade
Aufgabe 14
- Bestimme die Gleichung dieser Geraden
.
- Bestimme die Gleichung der zur Geraden
senkrechten Gerade
durch den Punkt
und gib deren Schnittpunkt mit der
-Achse an.
Aufgabe 15
Eine zweite Gerade
- Gib die Gleichung der Parabel
in Scheitelpunktform an.
- Berechne die Koordinaten des Schnittpunkts der Geraden
mit der
-Achse.
Aufgabe 16
- Durch den Schnittpunkt
der Parabeln verläuft eine zur
-Achse parallele Gerade
Gib deren Gleichung an. - Berechne den Abstand von
zum Scheitelpunkt
der Parabel
Aufgabe 17
- Berechne die Koordinaten der gemeinsamen Punkte
und
der Geraden und der Parabel.
- Der Punkt
liegt auf der Parabel
und bildet zusammen mit den Punkten
und
ein Dreieck. Berechne den Flächeninhalt des Dreiecks.
Aufgabe 18
Berechne die Funktionsgleichung der Geraden
Die Gerade
Unter welchen Winkeln schneiden sich die Geraden
Begründe deine Antwort durch Rechnung oder Argumentation.
Die Gerade
Berechne den Flächeninhalt des Dreiecks
Hat Peter Recht? Begründe rechnerisch.
Aufgabe 19
Berechne die Koordinaten des gemeinsamen Punktes
Berechne die Gleichung von
Berechne die Winkel, unter denen sich die Gerade
Eine zweite Parabel
Der Punkt
Aufgabe 20
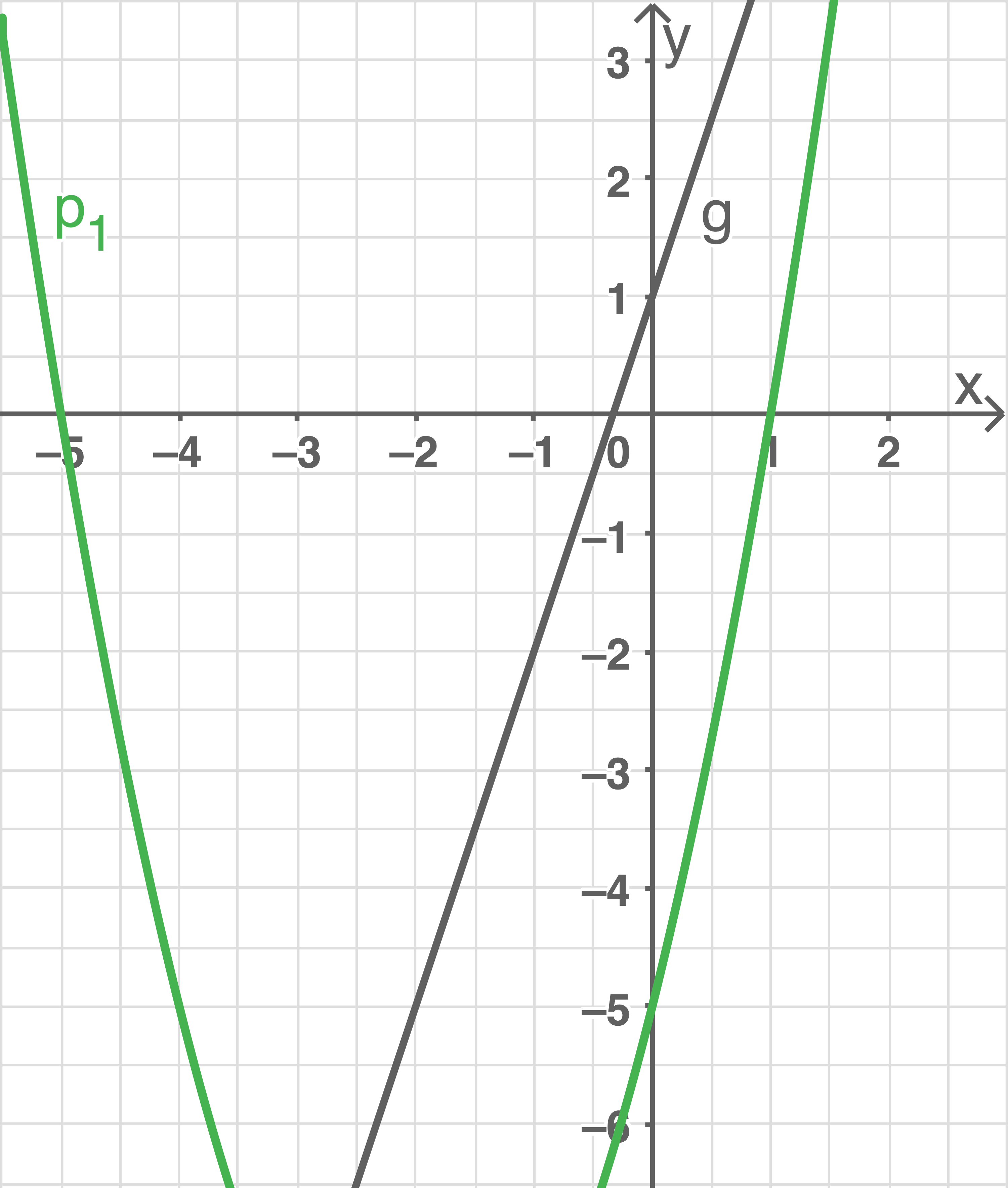
Bestimme die Funktionsgleichungen der Parabel
Die verschobene, nach oben geöffnete Normalparabel
Prüfe rechnerisch, ob der Schnittpunkt
Die Gerade
Berechne die Funktionsgleichung der Geraden
Die Gerade
Die Punkte
Die Seiten des Rechtecks verlaufen parallel zur
Berechne den Flächeninhalt des Rechtecks.
Aufgabe 21
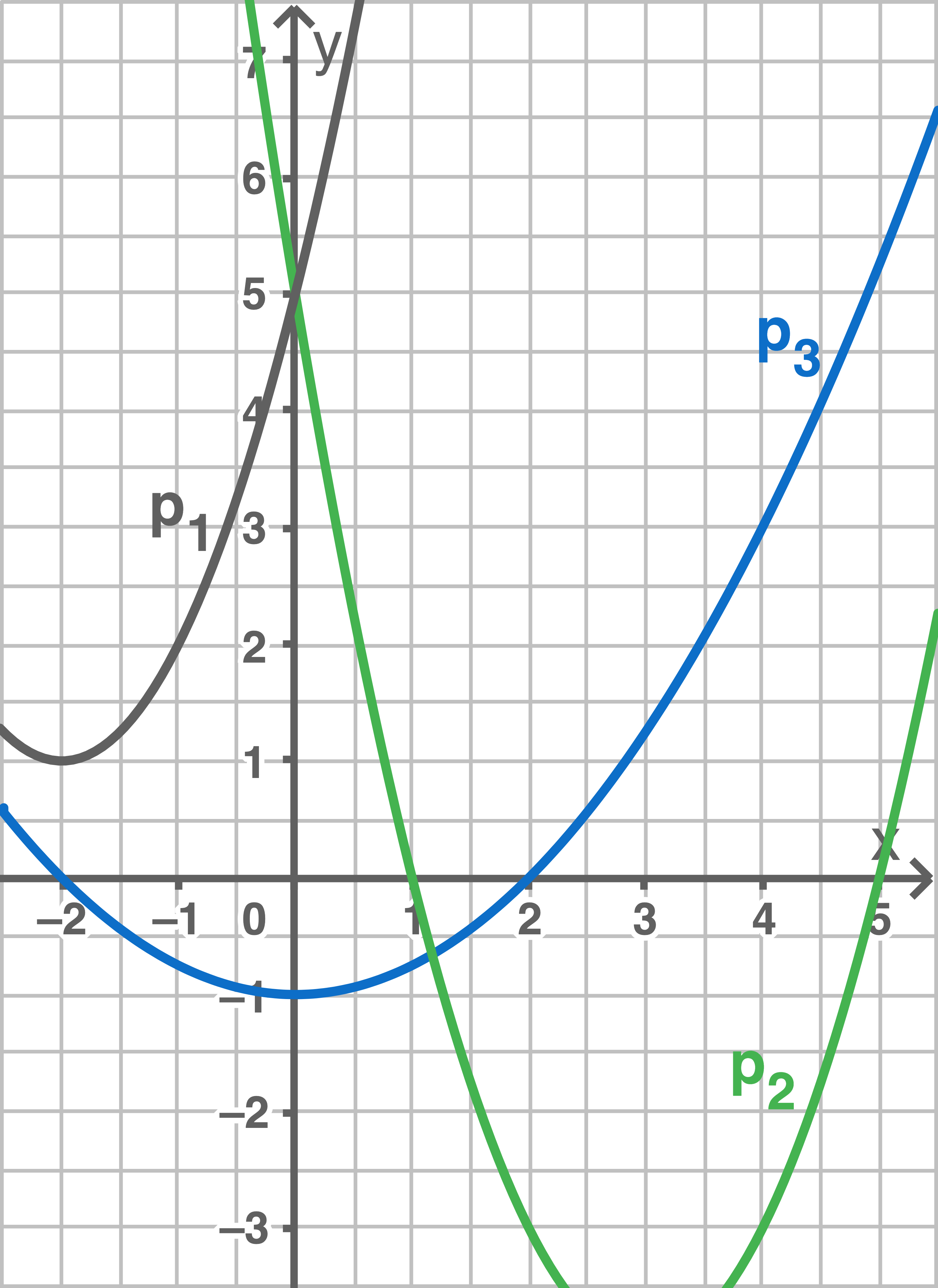
Begründe deine Entscheidung. Vervollständige die Funktionsgleichungen von
Berechne die Funktionsgleichung von
Die Gerade
Bestimme die Funktionsgleichung der Geraden
Bestimme den Flächeninhalt dieses Dreiecks. Bastian behauptet:
„Die Gerade
Hat Bastian recht?
Begründe deine Antwort durch Rechnung oder Argumentation.
Aufgabe 22
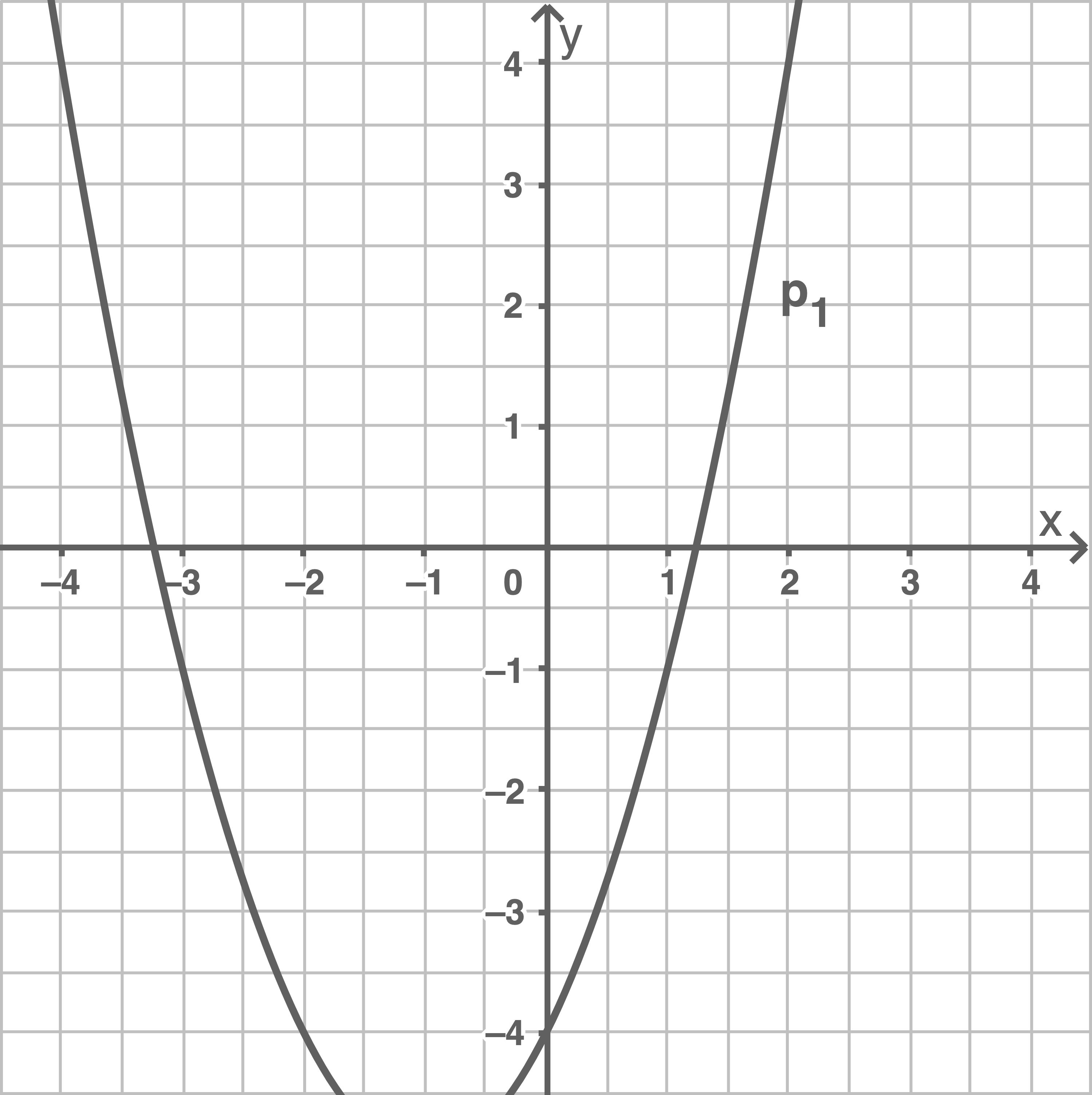
Bestimme die Gleichung der Parabel
Aufgabe 23
|
|
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
|
|
11 | 6 | 3 |
Vervollständige die Wertetabelle.
Eine Gerade
Weise rechnerisch nach, dass
Eine Gerade
Berechne die Koordinaten des Schnittpunktes
Eine nach oben geöffnete Normalparabel
Die beiden Parabeln haben einen gemeinsamen Punkt
Berechne die Koordinaten von
Die Punkte
Berechne den Flächeninhalt des Dreiecks
Der Punkt
Für welche Lage von
Begründe deine Aussage rechnerisch oder durch Argumentation.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
Die Teilaufgabe a) wurde in das Thema "Geometrie in der Ebene" eingeordnet.
Punkt in
einsetzen und nach
auflösen:
Somit lautet die Funktionsgleichung der Parabel
Zur Berechnung von wird die Scheitelpunktform
benötigt. Dabei ist
der Scheitelpunkt.
und
einsetzen.
Punkt einsetzen:
Gleichung :
Punkt einsetzen:
Gleichung
Gleichung in
einsetzen:
Vereinfachen mit Binomischer Formel :
in Gleichung
einsetzen um
zu erhalten:
Damit lautet die Parabel bzw.
mit dem Scheitelpunkt
Aus ergibt sich der Scheitelpunkt
Damit liegen ,
und
vor.
Die Strecke liegt waagerecht, da beide
-Koordinaten gleich sind.
Länge der Strecke:
Diese Strecke nehmen wir als Grundseite an.
Die Höhe ergibt sich als senkrechter Abstand des Punktes zur Grundseite.
Da unsere Grundseite bei liegt und der Punkt
den Wert
hat, lässt sich die Höhe wie folgt bestimmen:
Flächeninhalt eines Dreiecks:
Grundseite und Höhe einsetzen:
Die Grundseite bleibt gleich. Die dazugehörige Höhe nimmt für
den kleinsten Wert an.
Mögliche Begründung:
Nur der Punkt liegt auf
Die Grundseite bleibt dieselbe, waagerecht auf
mit der Länge
.
Da nach oben geöffnet und über der Grundseite liegt, tritt das Minimum im Scheitelpunkt auf.
Also muss der Scheitelpunkt bestimmt werden, indem die Funktionsgleichung in Scheitelpunktform gebracht wird:
Hieraus folgt:
Somit ist der Flächeninhalt von am kleinsten wenn
der Scheitelpunkt von
ist.
Lösung 2
Eine veschobene Normalparabel hat die Form
Punkt einsetzen:
Punkt einsetzen:
einsetzen:
einsetzen, um
zu erhalten:
bzw.
Gerade durch
und
aufstellen.
Steigung berechnen:
oder
in Punktsteigungsformel einsetzen. (Hier wurde der Punkt
gewählt.)
Somit ergibt sich folgende Funktionsgleichung für
Koordinaten des Scheitelpunkts von berechnen.
Punkt einsetzen:
Die Funktionsgleichung liegt in quadtratischer Form () vor, dementsprechend können die Koordinaten des Scheitelpunkts wie folgt errechnet werden:
und
einsetzen:
Als nächstes soll die Funktionsgleichung einer Gerade gefunden werden, die senkrecht zu
verläuft und durch
geht.
Für senkrechte Geraden gilt:
und
in die Punktsteigungsform
mit
einsetzen:
Daraus folgt:
Entfernung zwischen den Punkten und
bestimmen. Da
der Schnittpunkt von
und
ist, wird er durch Gleichsetzen der beiden Geradengleichungen berechnet.
-Koordinate in
oder
einsetzen um die
-Koordinate zu erhalten.
Daraus folgt:
Abstand zwischen zwei Punkten:
Zahlenwerte einsetzen:
Die Entfernung zwischen dem Punkt und
beträgt ca.
Die Teilaufgabe b) wurde in das Thema "Geometrie im Raum" eingeordnet.
Lösung 3
Lösung 4
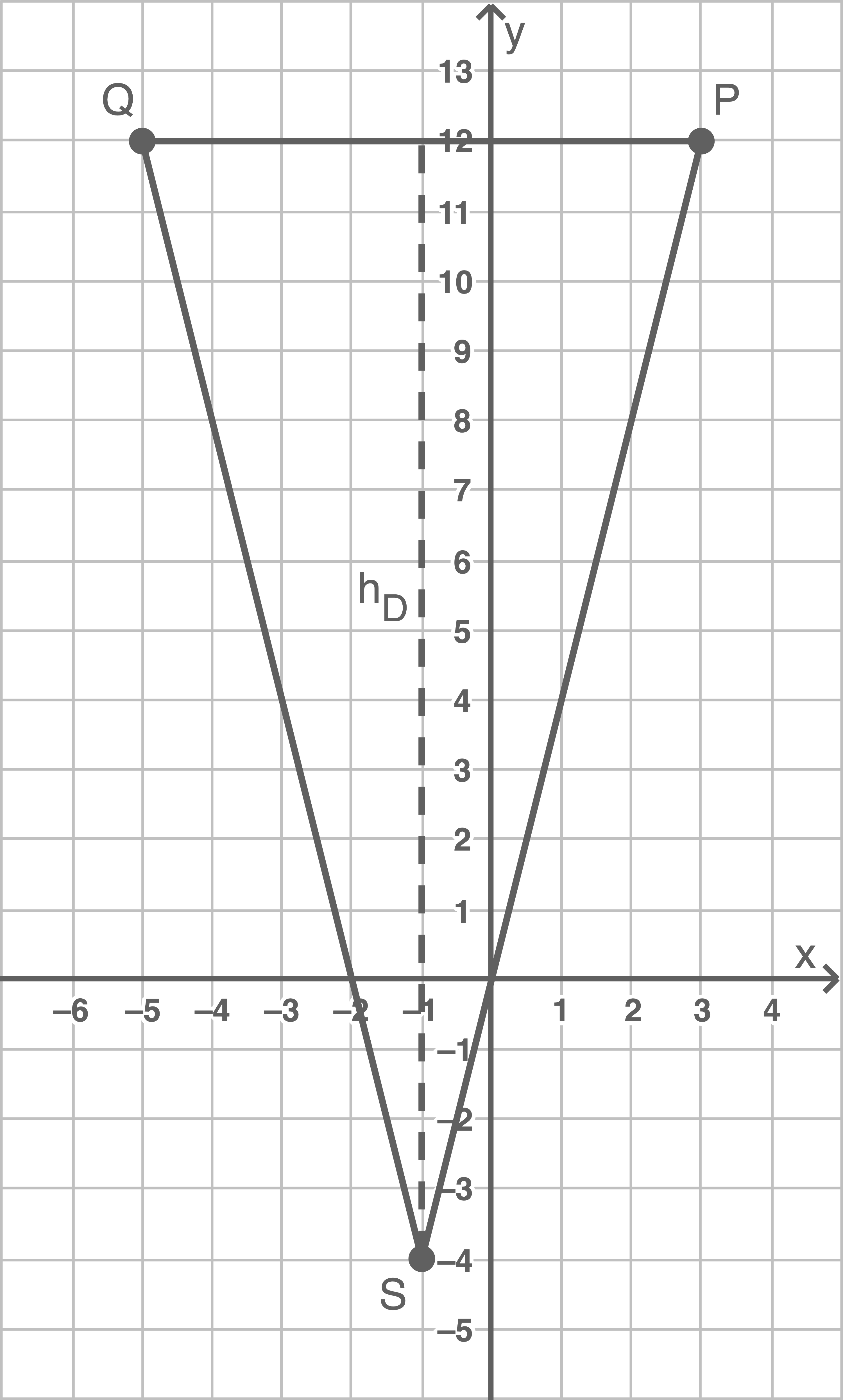
Lösung 5
Lösung 6
Lösung 7
Lösung 8
Lösung 9
Lösung 10
Lösung 11
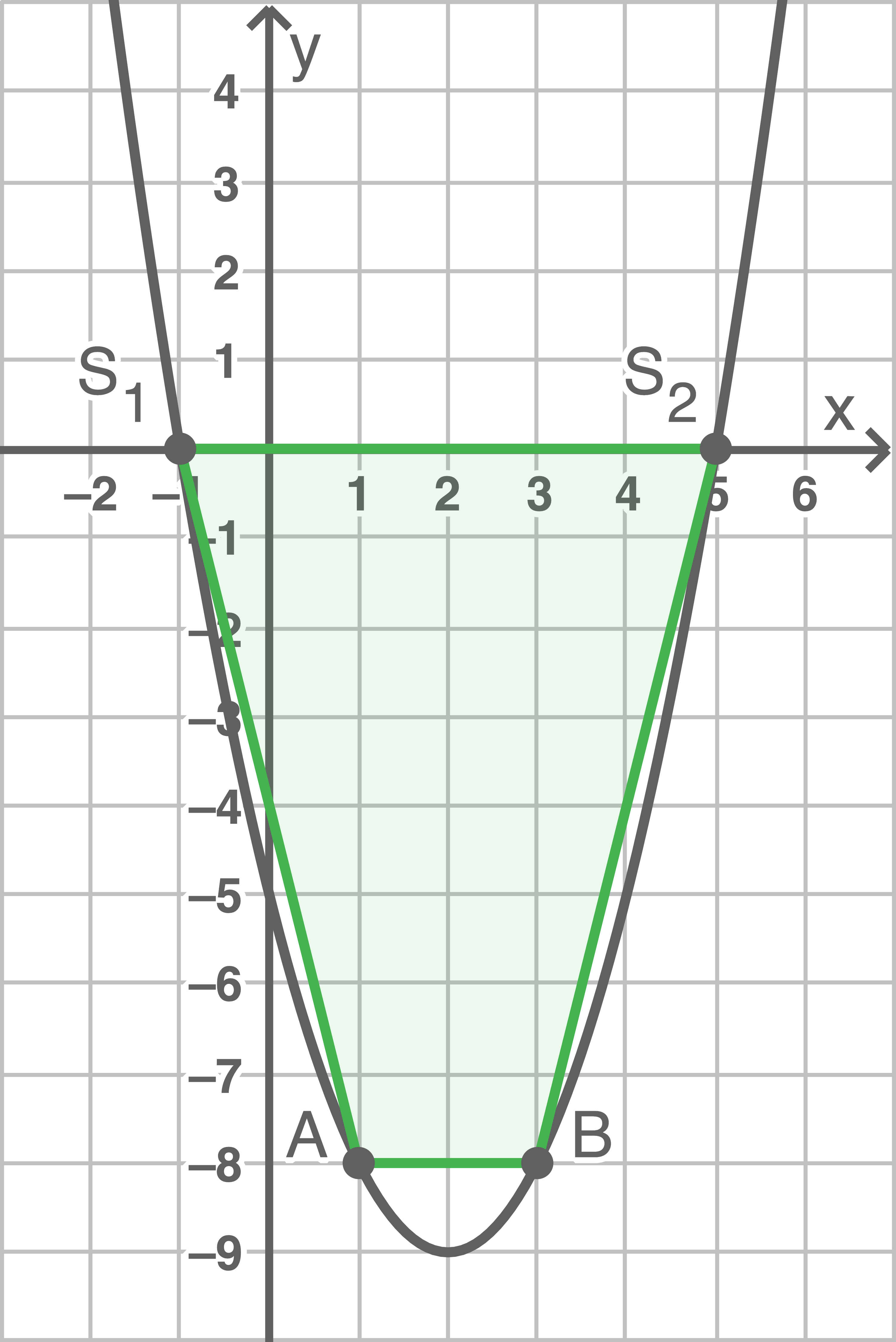
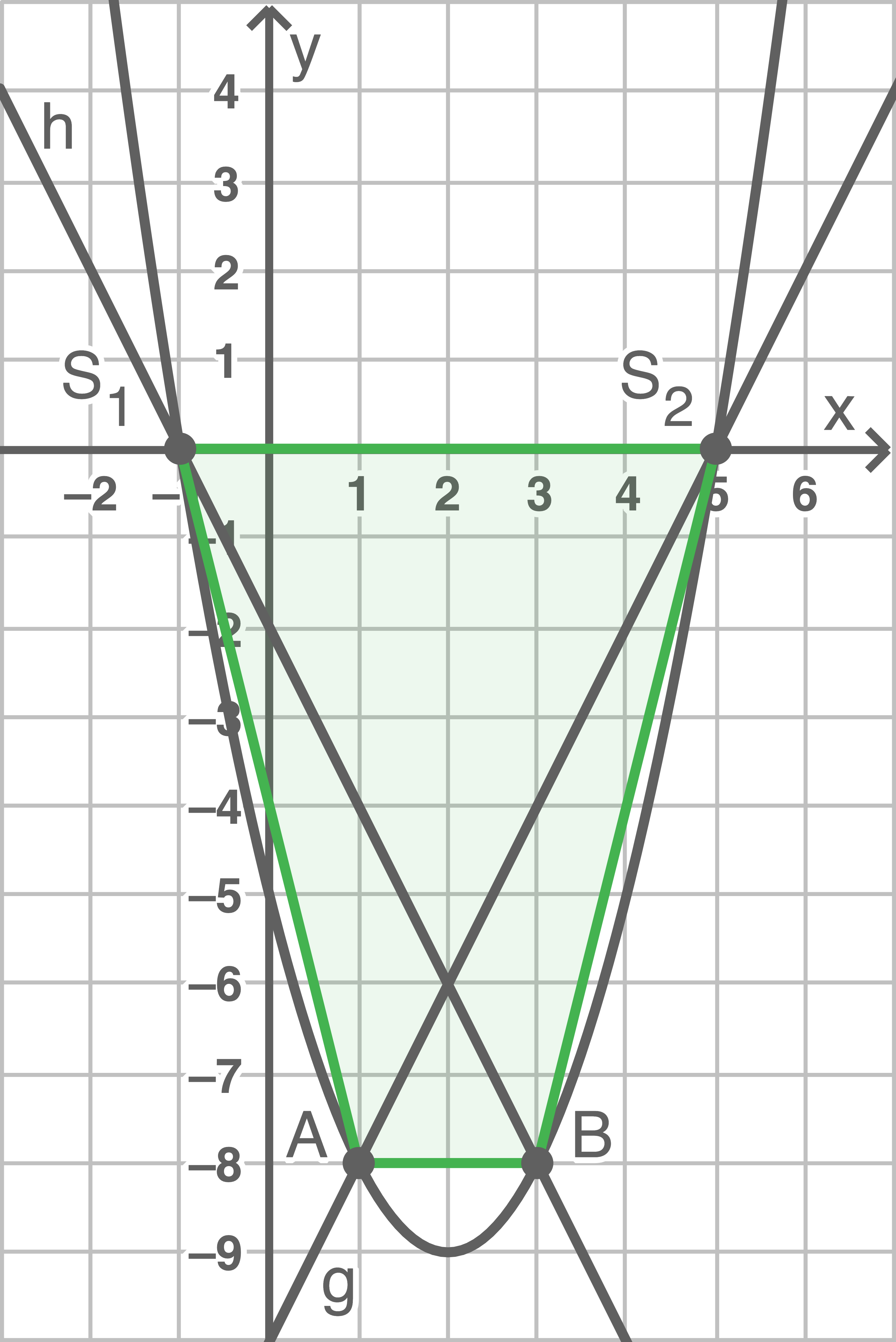
Lösung 12
Lösung 13
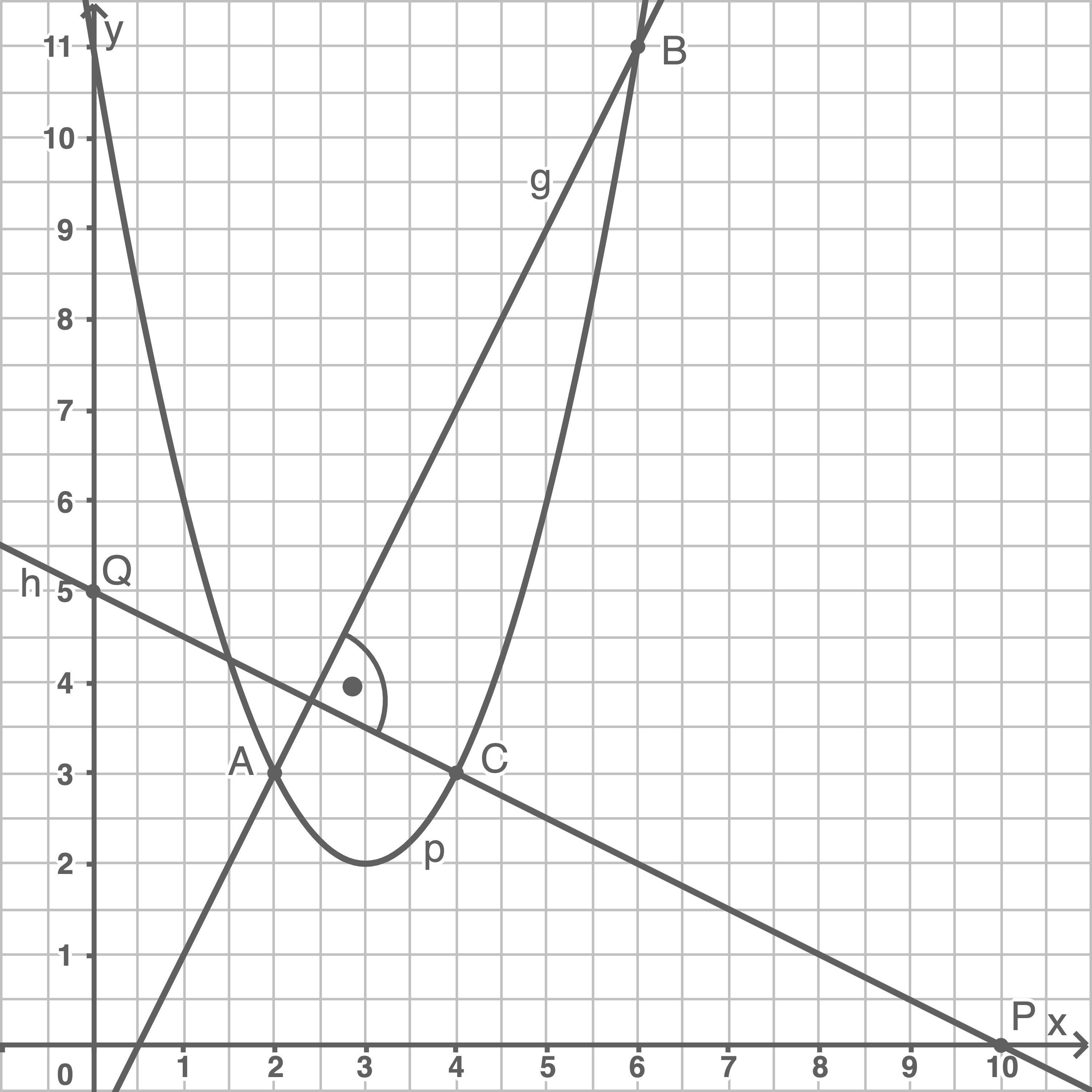
Lösung 14
Lösung 15
- Allgemeine Geradengleichung:
- Da die Geraden
und
parallel sind, gilt für den Steigungsfaktor:
- Also gilt für
Lösung 16
Lösung 17
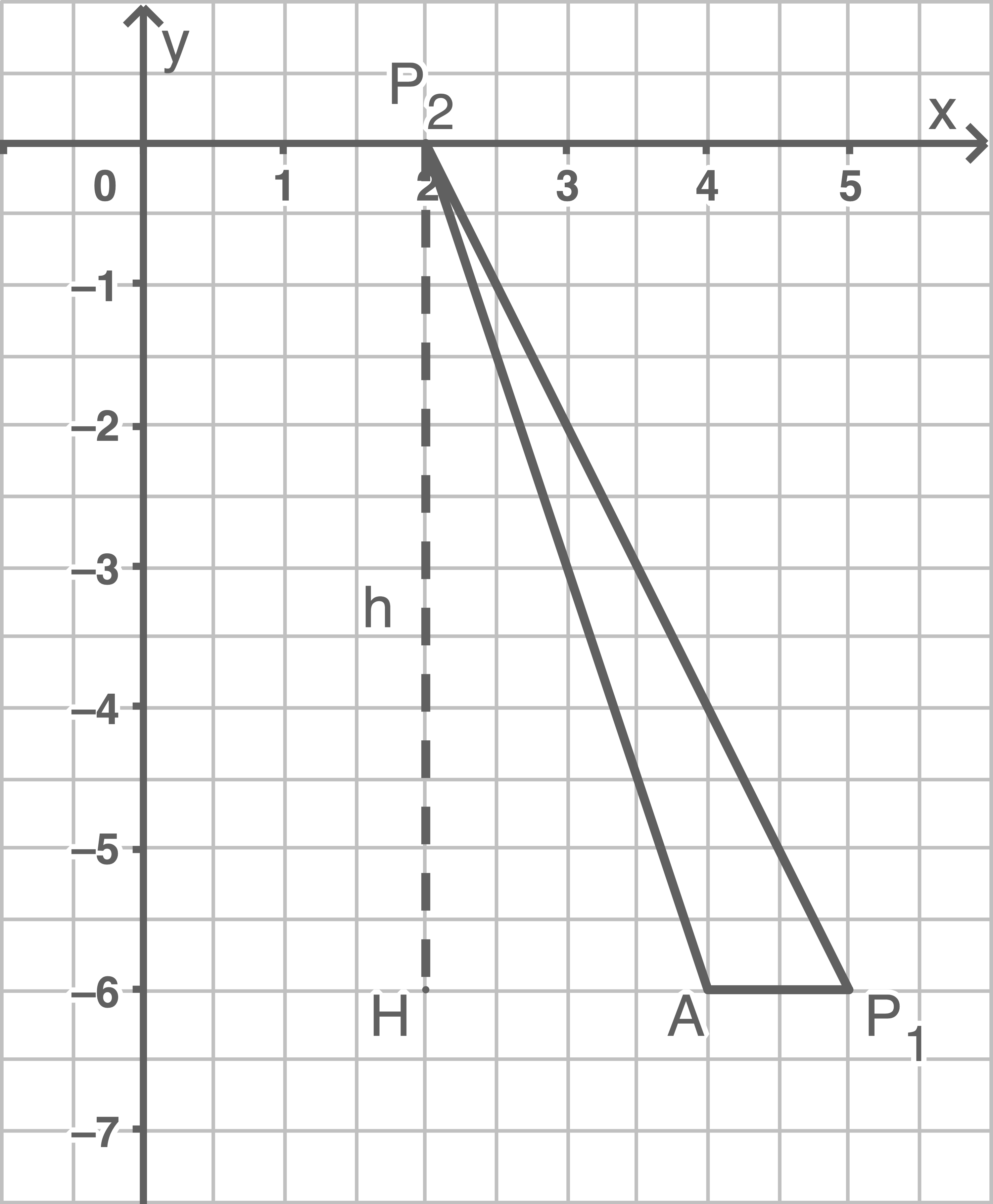
Höhe
Lösung 18
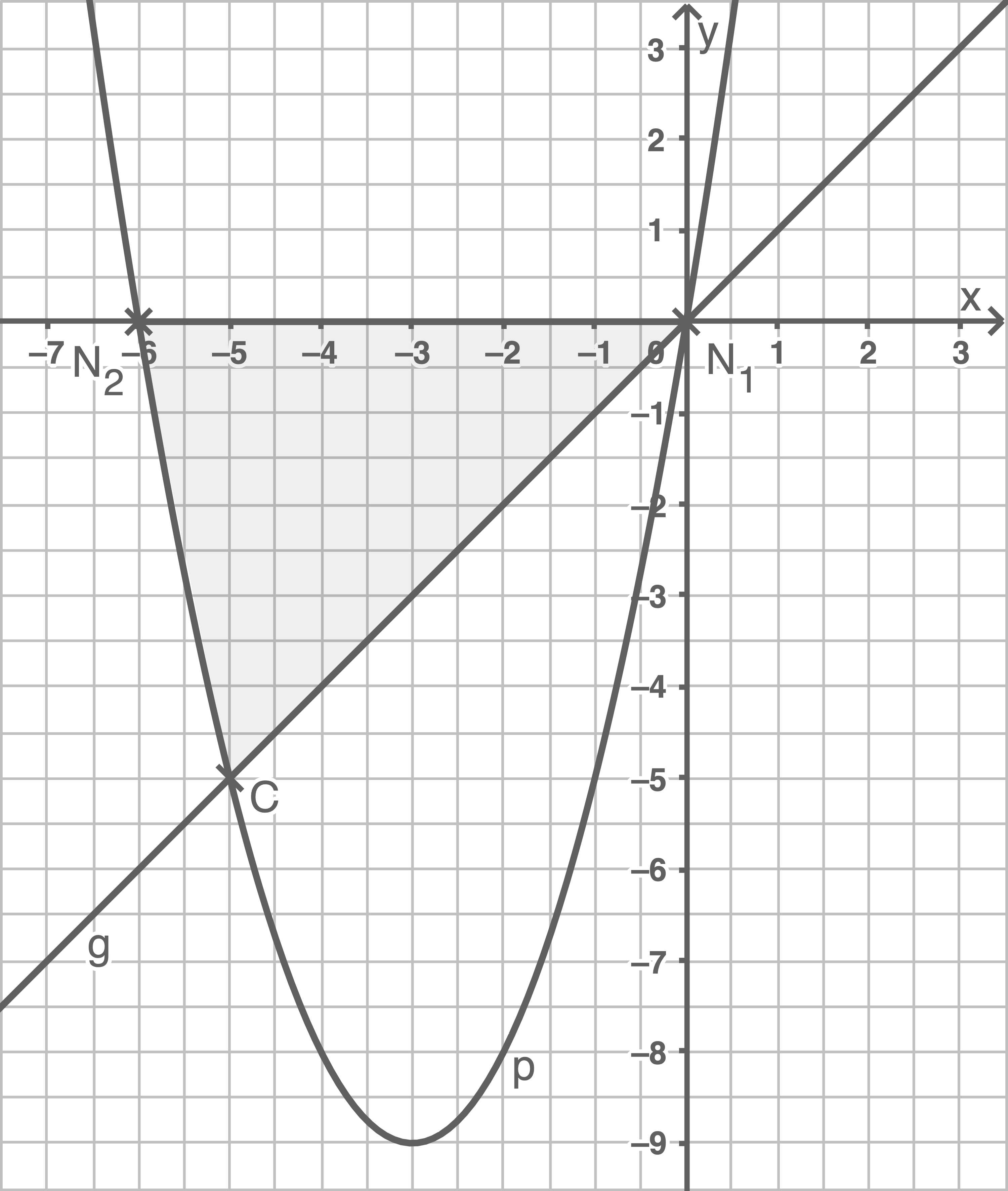
Die Länge der Grundseite ergibt sich deshalb aus den
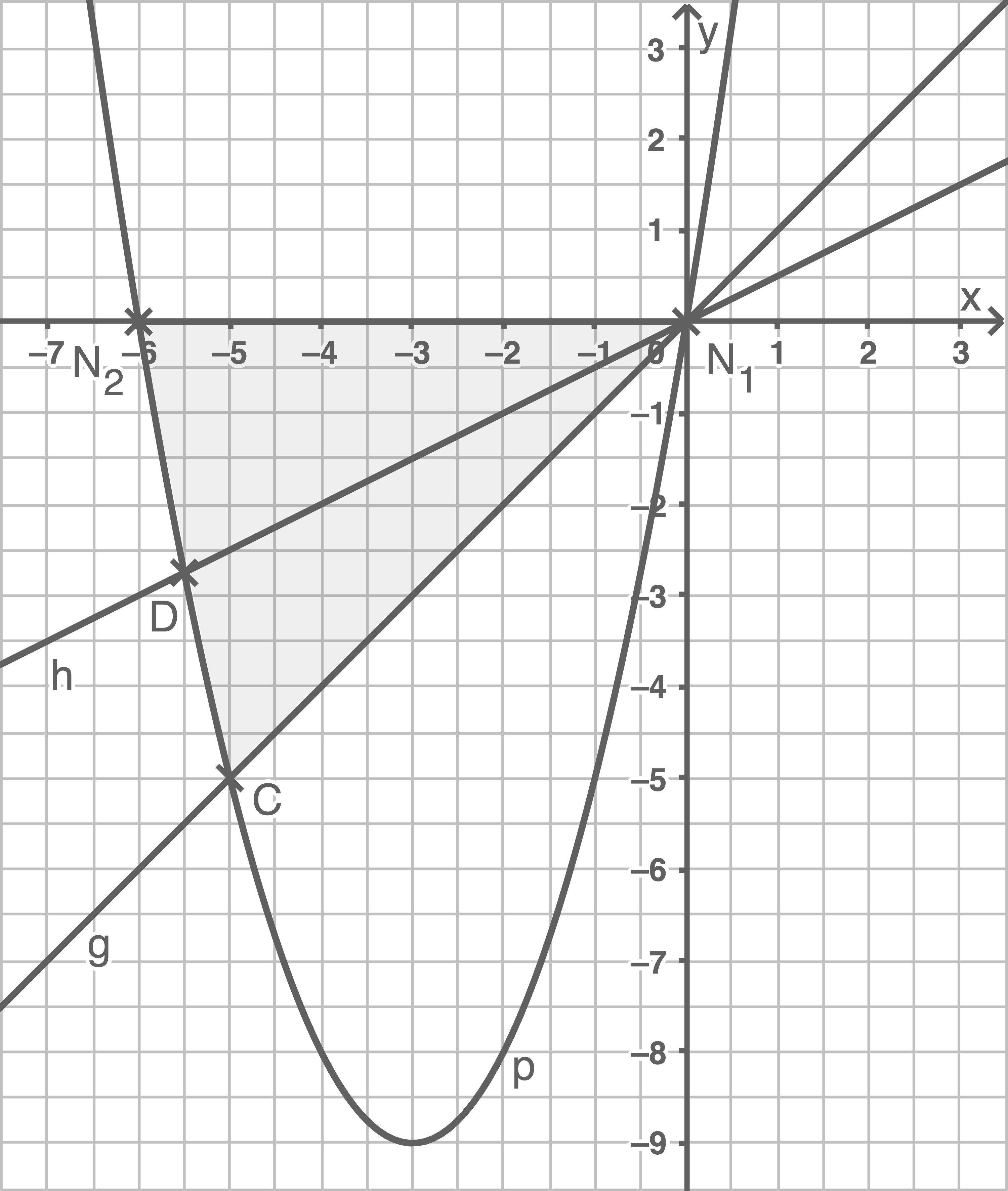
Peter hat also nicht recht.
Lösung 19
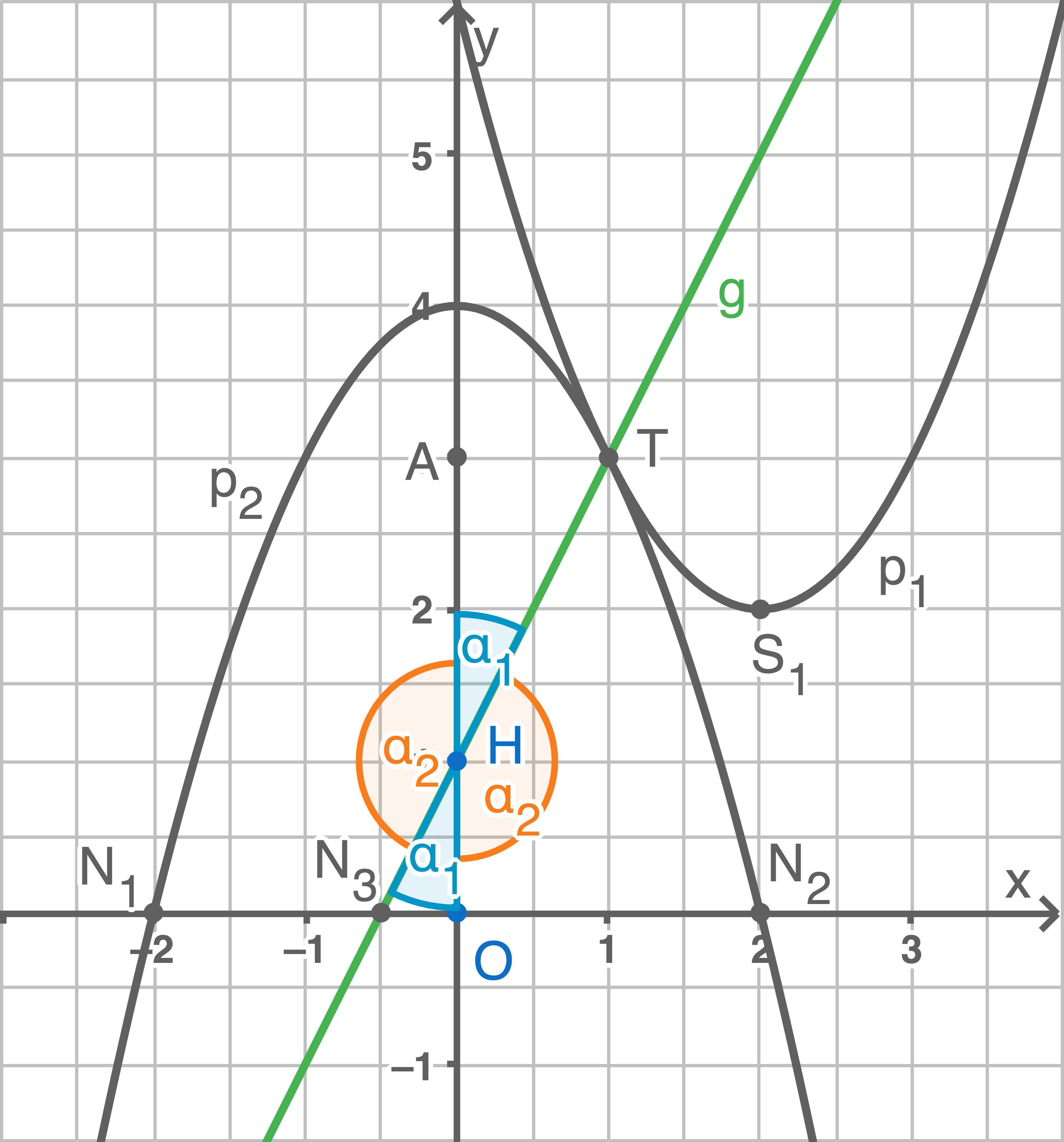
| Scheitelwinkel zu
| Scheitelwinkel zu
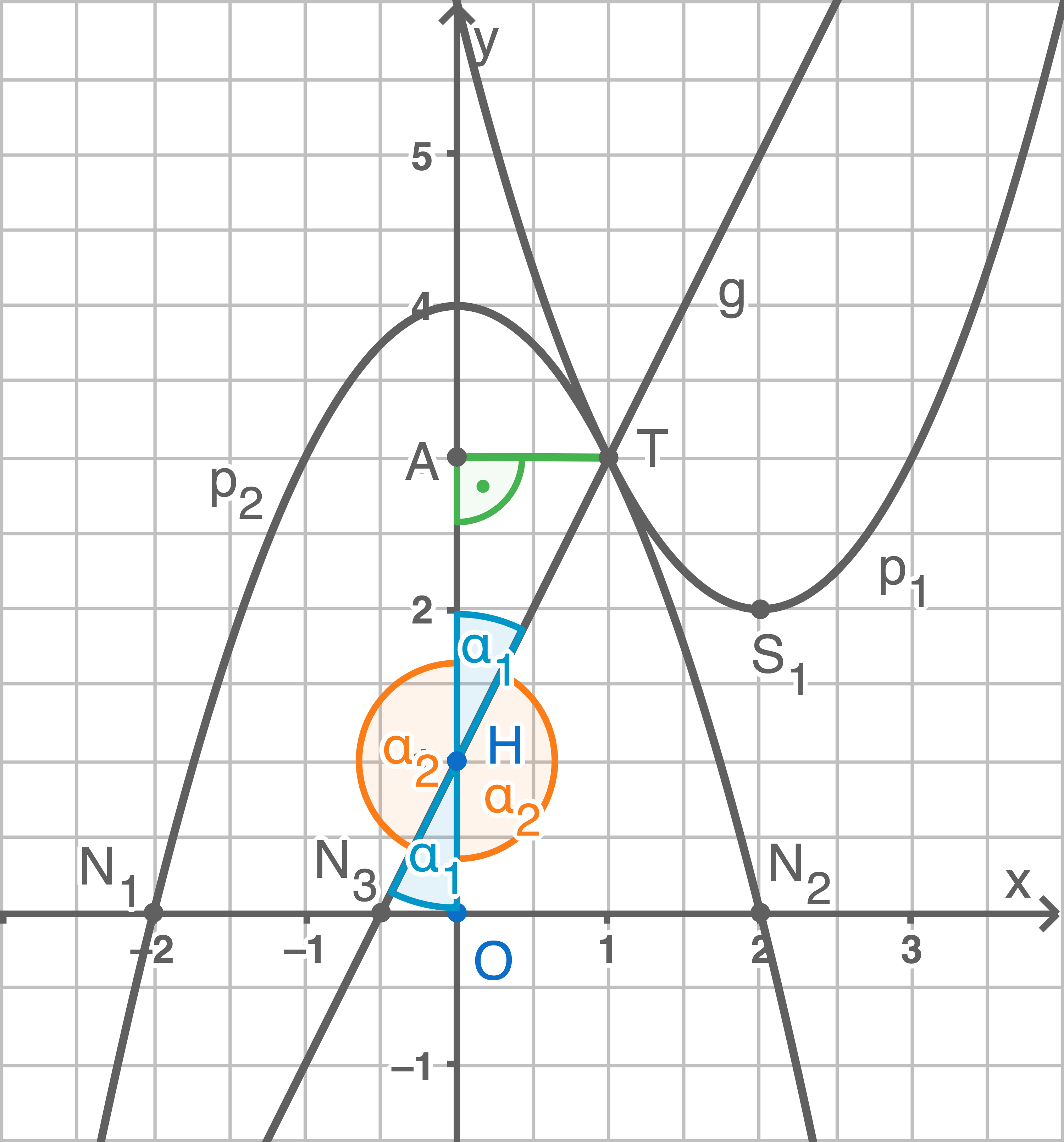
- Liegt unterhalb von
auf der
-Achse
- Scheitelpunkt
mit
- Form der Gleichung:
- Nach unten geöffnet
- Also gilt:
- Gleich gestreckt oder gestreckter als
- Also gilt:
- Aus
und
folgt:
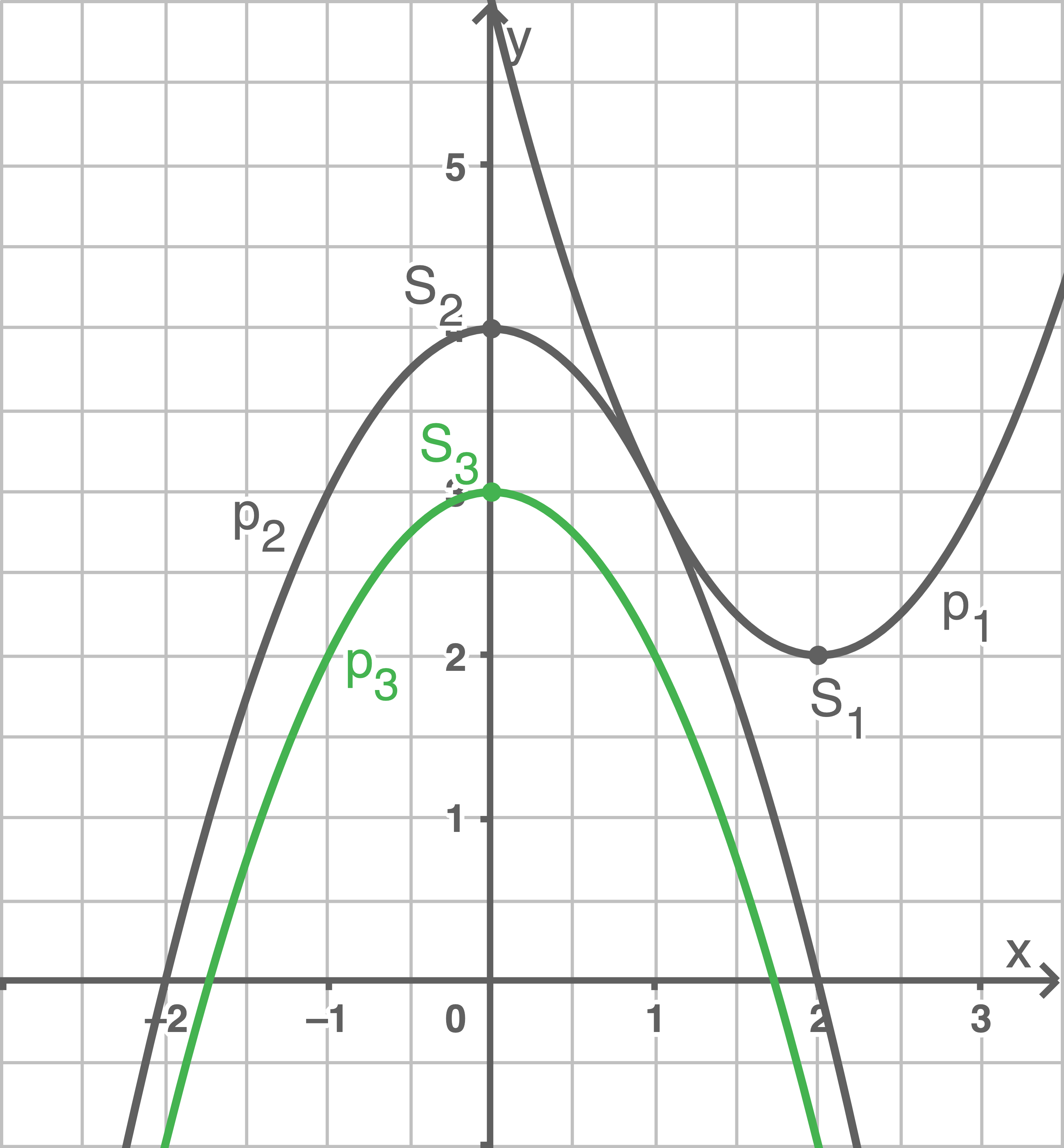
- Scheitelpunkt
- Allgemeine Geradengleichung:
- Für den Steigungsfaktor
gilt:
- Also gilt für
Lösung 19
Die Abbildung zeigt, dass
Wegen der Symmetrie, muss die
Daher lautet die Geradengleichung:
Einsetzen in eine der beiden Funktionsgleichungen, z.B. in
Lösung 20
Da der Graph
Gleichung mit quadratischer Ergänzung in die Scheitelpunktform bringen:
Da
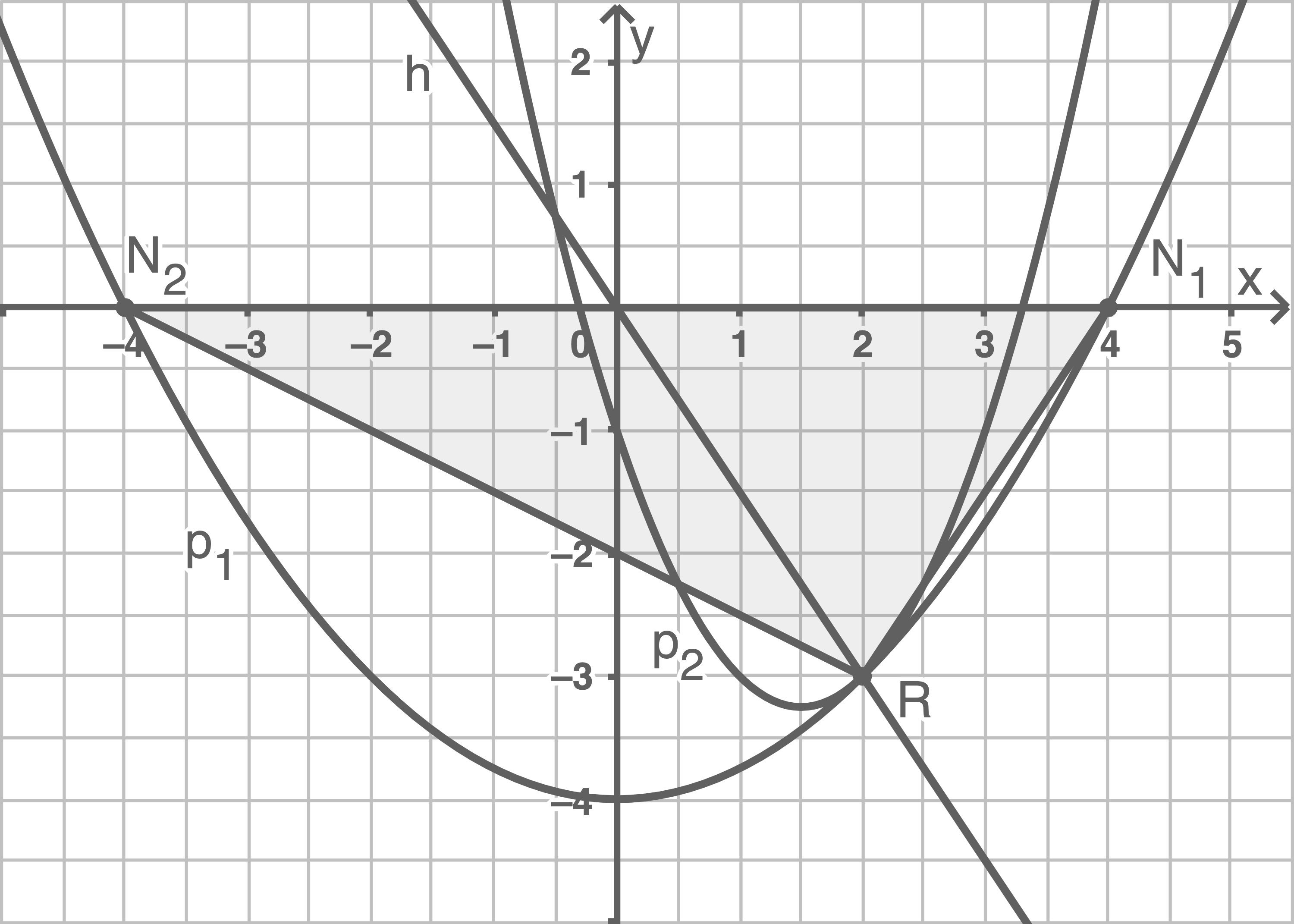
Da
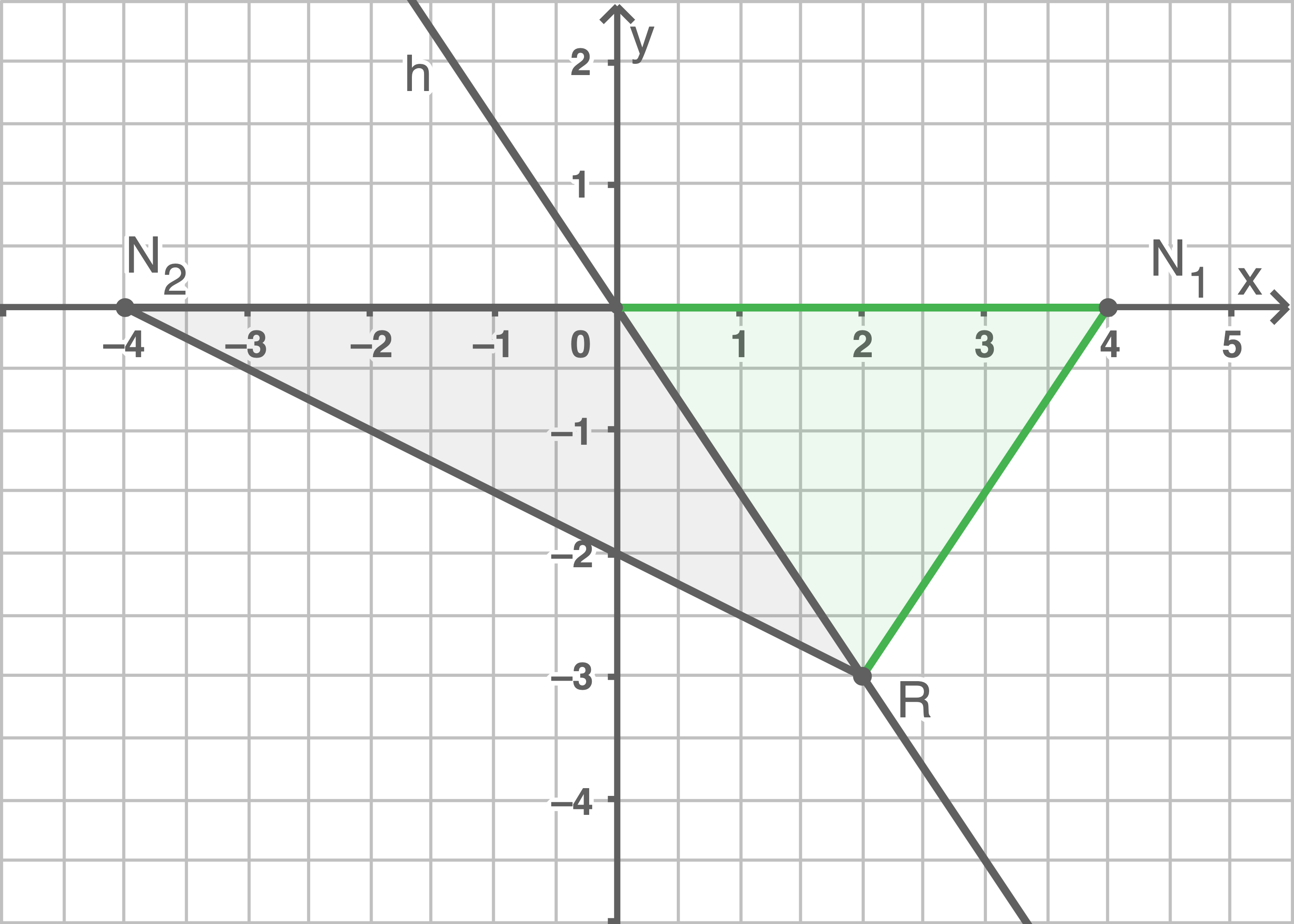
Somit gilt für die Grundseite des Teildreiecks
Somit ist Bastians Behauptung richtig. Argumentative Begründung Die Höhe beider Teildreiecke entspricht weiterhin dem Abstand von
Die Gerade
Dadurch, dass die Höhe gleich bleibt und die Grundseite halbiert wird, wird insgesamt auch der Flächeninhalt halbiert.
Bastian hat also recht.
Lösung 21
- Allgemeine Geradengleichung:
- Für den Steigungsfaktor
gilt:
- Da
durch
verläuft und
auf der
-Achse liegt, gilt:
- Da
eine nach unten geöffnete Normalparabel ist und ihr Scheitelpunkt
auf der
-Achse liegt, gilt:
- Da der Scheitelpunkt
auf der
-Achse liegt, gilt auch:
- Allgemeine Geradengleichung:
- Da
und
parallel verlaufen, gilt für den Steigungsfaktor:
- Daraus folgt für
- Allgemeine Geradengleichung:
- Da
und
parallel verlaufen, gilt für den Steigungsfaktor:
- Daraus folgt für
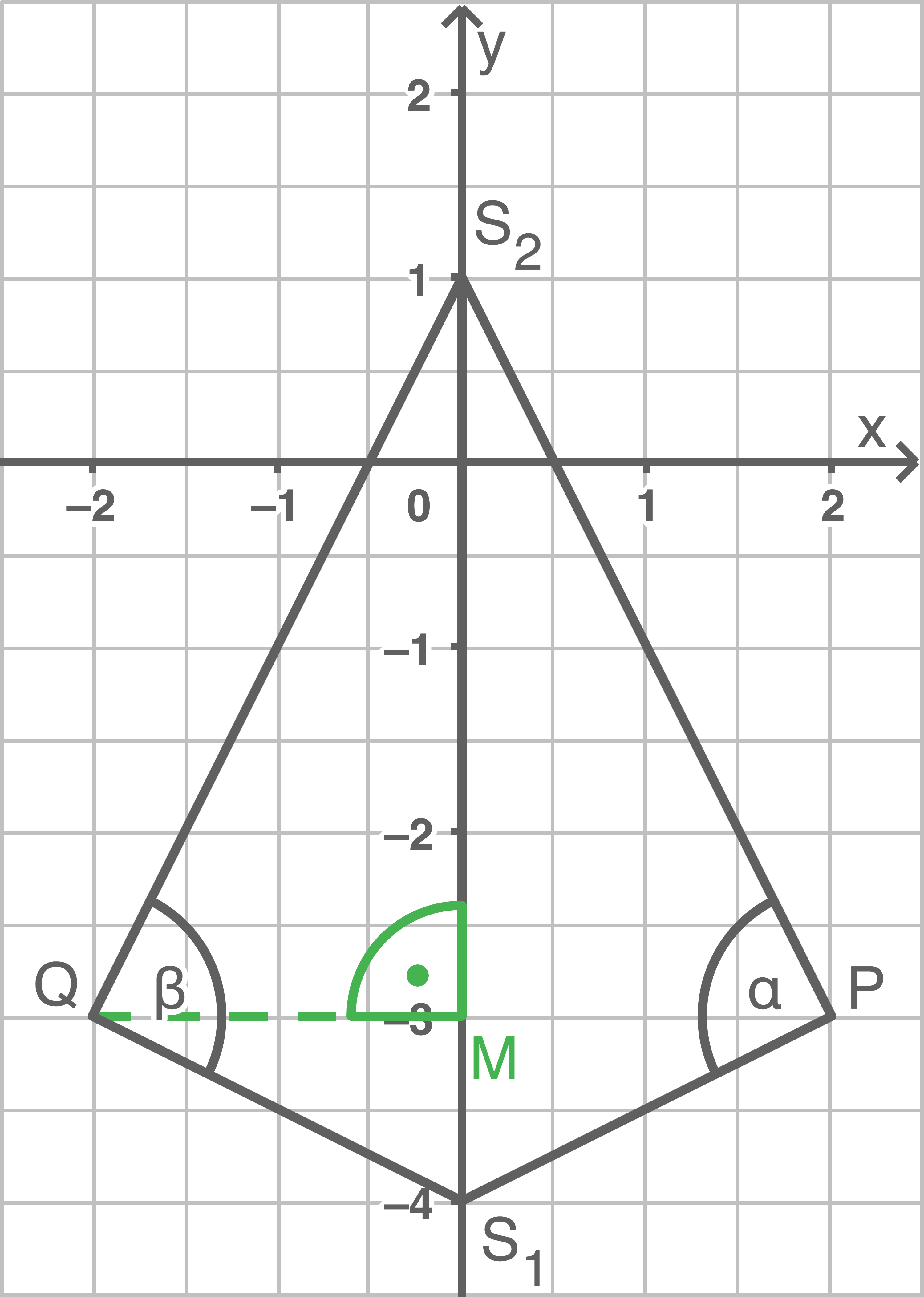
- Falls ja
Winkel
ist ein rechter Winkel
- Falls nein
Winkel
ist kein rechter Winkel
Lösung 22
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 11 | 6 | 3 | 2 | 3 | 6 |
