Hilfsmittelfreier Teil
1.1 Analysis
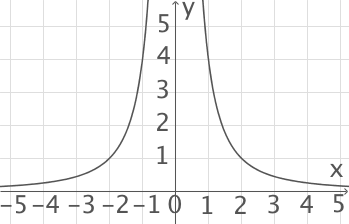
Die Abbildung zeigt den Graphen
a)
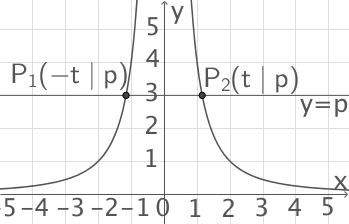
Die Gerade, die parallel zur  -Achse durch den Punkt
-Achse durch den Punkt  verläuft, schneidet
verläuft, schneidet  in zwei Punkten. Der Abstand dieser beiden Schnittpunkte hat die Länge 1.
in zwei Punkten. Der Abstand dieser beiden Schnittpunkte hat die Länge 1.
Berechne den Wert von .
.
Berechne den Wert von
(2 BE)
b)
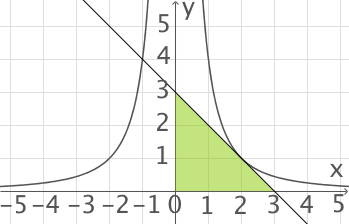
Die Koordinatenachsen schließen mit der Tangente an  in einem Punkt
in einem Punkt  mit
mit  ein gleichschenkliges Dreieck ein.
ein gleichschenkliges Dreieck ein.
Berechne die Koordinaten von .
.
Berechne die Koordinaten von
(3 BE)
1.2 Analytische Geometrie
Der Punkt
a)
Begründe, dass das Quadrat in der  -Ebene liegt.
-Ebene liegt.
(2 BE)
b)
Der Schnittpunkt der beiden Diagonalen des Quadrates liegt auf der Geraden  der punkt
der punkt  in der
in der  -Ebene. Zeige, dass
-Ebene. Zeige, dass  einer der beiden Eckpunkte des Quadrates ist, die dem Eckpunkt
einer der beiden Eckpunkte des Quadrates ist, die dem Eckpunkt  benachbart sind.
benachbart sind.
(3 BE)
1.3 Stochastik
Ein Landwirt möchte zu seinem Hoffest ein Glücksrad mit blauen, gelben und roten 6°-Sektoren anbieten. Für einen Preis von einem Euro darf man einmal drehen.Dreht man gelb, erhält man einen Gutschein für eine Packung Bio-Eier, bei blau gibt es als Hauptgewinn einen Ökokorb mit landwirtschaftlichen Produkten und bei rot geht man leer aus.
Eine Packung Bio-Eier kostet den Landwirt
a)
Ermittle, wie viele blaue, gelbe und rote 6°-Sektoren das Glücksrad haben muss.
(2 BE)
b)
Bestimme, welche Kosten dem Landwirt pro Dreh "auf lange Sicht" entstehen.
(3 BE)
(15 BE)
Lösung zu 1.1 Analysis
a)
b)
Die Steigung wird gegeben durch die erste Ableitung, d.h.:
Lösung zu 1.2 Analytische Geometrie
a)
Die Gerade
Damit muss die Ebene, in der das Quadrat liegt, parallel zur
Das Quadrat liegt also in der
b)
- Die Vektoren
und
stehen senkrecht aufeinander.
- Die Seiten
und
sind gleich lang.
Damit muss
Lösung zu 1.3 Stochastik
a)
b)