Teil B2
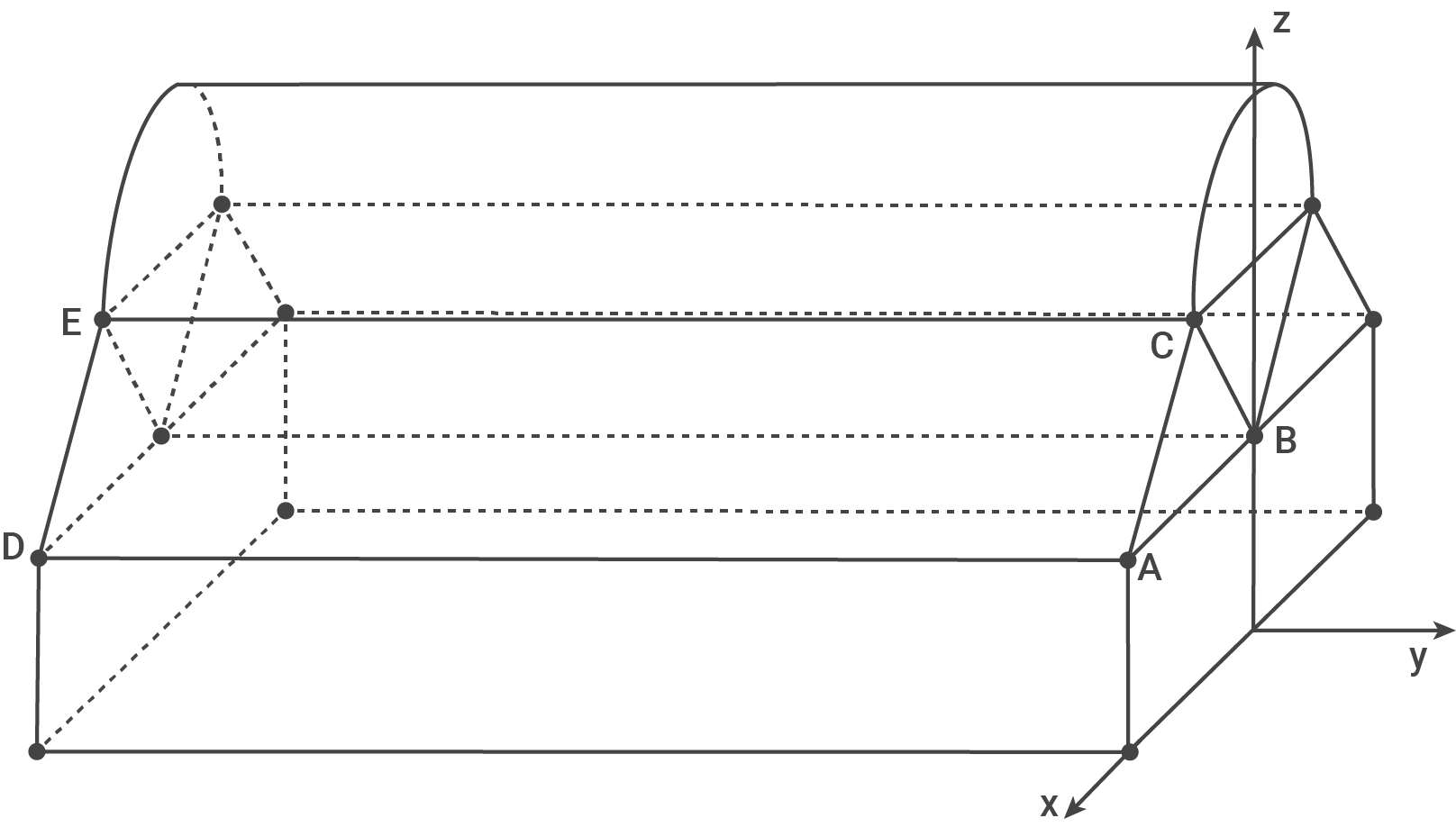
Die Abbildung zeigt das Gebäude eines Flughafens, in das ein kartesisches Koordinatensystem (1 Längeneinheit entspricht 1 Meter) gelegt ist.
 Die
Die  Meter lange Dachkonstruktion ist aus einem halben geraden Kreiszylinder und drei geraden Prismen zusammengesetzt. Die dreieckigen Grundflächen dieser Prismen sind kongruent zueinander.
Meter lange Dachkonstruktion ist aus einem halben geraden Kreiszylinder und drei geraden Prismen zusammengesetzt. Die dreieckigen Grundflächen dieser Prismen sind kongruent zueinander.
Die Seitenkanten der Prismen verlaufen parallel zur -Achse. Die Punkte
-Achse. Die Punkte 
 und
und  sowie
sowie  und
und  sind Eckpunkte eines der Prismen.
sind Eckpunkte eines der Prismen.
Der Boden des Gebäudes sowie die Startbahnen des Flughafens liegen in der -
- -Ebene.
-Ebene.
 Die Dachfläche
Die Dachfläche  ist eine Seitenfläche eines der dreiseitigen Prismen und liegt in der Ebene
ist eine Seitenfläche eines der dreiseitigen Prismen und liegt in der Ebene 
Für die Sitzplätze eines Flugzeugs lässt eine Fluggesellschaft deshalb mehr als
Sitzplätze eines Flugzeugs lässt eine Fluggesellschaft deshalb mehr als  Buchungen zu. Erscheinen mehr als
Buchungen zu. Erscheinen mehr als  Personen mit Buchung zu diesem Flug, so können nur
Personen mit Buchung zu diesem Flug, so können nur  von ihnen am Flug teilnehmen. Die übrigen Personen müssen abgewiesen werden.
von ihnen am Flug teilnehmen. Die übrigen Personen müssen abgewiesen werden.
Vereinfachend wird angenommen, dass die Anzahl der Personen mit Buchung, die am Flug auch teilnehmen, binomialverteilt ist.

Abbildung (nicht maßstäblich)
Die Seitenkanten der Prismen verlaufen parallel zur
Der Boden des Gebäudes sowie die Startbahnen des Flughafens liegen in der
2.1
Weise nach, dass das Dreieck  gleichschenklig und im Punkt
gleichschenklig und im Punkt  rechtwinklig ist.
rechtwinklig ist.
Erreichbare BE-Anzahl: 03
2.2
Bestimme das Volumen der gesamten Dachkonstruktion.
Das Gebäude des Flughafens wird fotografiert. Die Position der Kamera dafür ist der Punkt
Erreichbare BE-Anzahl: 03
2.3
Zeige, dass  durch die Gleichung
durch die Gleichung  dargestellt werden kann.
dargestellt werden kann.
Erreichbare BE-Anzahl: 02
2.4
Eine Sichtlinie verläuft von der Position der Kamera aus geradlinig zum Mittelpunkt der Dachfläche 
Berechne die Größe des Winkels, den diese Sichtlinie mit der Dachfläche einschließt.
einschließt.
Berechne die Größe des Winkels, den diese Sichtlinie mit der Dachfläche
Erreichbare BE-Anzahl: 04
2.5
Hinter dem Gebäude startet ein Flugzeug. Ab einer bestimmten Höhe über der Startbahn ist die Flugzeugspitze von der Position der Kamera aus oberhalb des Gebäudes sichtbar. Im Folgenden soll diese Höhe ermittelt werden.
Begründe, dass diejenigen Punkte der Dachkonstruktion, die am höchsten über dem Boden des Gebäudes liegen, für die Ermittlung der gesuchten Höhe keine Rolle spielen.
Von der Position der Kamera aus wird die Flugzeugspitze unmittelbar oberhalb derjenigen Punkte der Dachkonstruktion sichtbar, die auf der Gerade mit der Gleichung  liegen. Die Spitze des startenden Flugzeugs bewegt sich entlang der Gerade mit der Gleichung
liegen. Die Spitze des startenden Flugzeugs bewegt sich entlang der Gerade mit der Gleichung 
 Ermittle die gesuchte Höhe.
Ermittle die gesuchte Höhe.
Möchte eine Person an einem Flug teilnehmen, muss dafür im Voraus eine Buchung vorgenommen werden. Erfahrungsgemäß gibt es Personen mit Buchung, die nicht am Flug teilnehmen.
Erreichbare BE-Anzahl: 03
Für die
Vereinfachend wird angenommen, dass die Anzahl der Personen mit Buchung, die am Flug auch teilnehmen, binomialverteilt ist.
2.6
Gib einen Grund dafür an, dass es sich bei dieser Annahme im Sachzusammenhang um eine Vereinfachung handelt.
Erreichbare BE-Anzahl: 01
2.7
Es liegen  Buchungen für die
Buchungen für die  Sitzplätze für einen Flug mit diesem Flugzeug vor. Erfahrungsgemäß nehmen
Sitzplätze für einen Flug mit diesem Flugzeug vor. Erfahrungsgemäß nehmen  aller Personen mit Buchung an diesem Flug teil.
aller Personen mit Buchung an diesem Flug teil.
Gib an, wie viele Personen zu erwarten sind, die mit Buchung an diesem Flug teilnehmen. Berechne die Wahrscheinlichkeit der folgenden Ereignisse:
Ereignis A: Genau Personen mit Buchung nehmen an diesem Flug teil.
Personen mit Buchung nehmen an diesem Flug teil.
Ereignis B: Es muss mindestens eine Person mit Buchung abgewiesen werden.
Gib an, wie viele Personen zu erwarten sind, die mit Buchung an diesem Flug teilnehmen. Berechne die Wahrscheinlichkeit der folgenden Ereignisse:
Ereignis A: Genau
Ereignis B: Es muss mindestens eine Person mit Buchung abgewiesen werden.
Ereichbare BE-Anzahl: 05
2.1
Gleichschenkligkeit zeigen
Da das Dreieck  im Punkt
im Punkt  rechtwinklig sein soll, müssen die beiden Seiten
rechtwinklig sein soll, müssen die beiden Seiten  und
und  gleich lang sein.
gleich lang sein.
![\(\begin{array}[t]{rll}
\overline{AC} &=& \left|\overrightarrow{AC} \right| \\[5pt]
&=& \left|\pmatrix{-3,5 \\ 0 \\ 3,5 } \right| \\[5pt]
&=& \sqrt{(-3,5)^2 + 0^2 +3,5^2 } \\[5pt]
&=& \sqrt{24,5} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/7728af7738831417b77ee0c780516f0906252e4ce71594f6c6b396b00bb1db18?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overline{BC} &=& \left|\overrightarrow{BC} \right| \\[5pt]
&=& \left|\pmatrix{3,5 \\ 0 \\ 3,5 } \right| \\[5pt]
&=& \sqrt{3,5^2 + 0^2 +3,5^2 } \\[5pt]
&=& \sqrt{24,5} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/4d146e262f92ea490d7aabb4424e838413aea8c4b34cbfe32d82f02f52c8ea66?color=5a5a5a) Beide Seiten
Beide Seiten  und
und  sind also gleich lang und das Dreieck
sind also gleich lang und das Dreieck  damit gleichschenklig.
Rechtwinkligkeit zeigen
Das Dreieck
damit gleichschenklig.
Rechtwinkligkeit zeigen
Das Dreieck  besitzt bei
besitzt bei  einen rechten Winkel, wenn die Seiten
einen rechten Winkel, wenn die Seiten  und
und  orthogonal zueinander sind, also ihr Skalarprodukt gleich Null ist.
Das Dreieck
orthogonal zueinander sind, also ihr Skalarprodukt gleich Null ist.
Das Dreieck  ist im Punkt
ist im Punkt  also rechtwinklig.
also rechtwinklig.
2.2
Die Dachkonstruktion besteht insgesamt aus vier Teilen:
 Der Durchmesser der Grundfläche des Kreiszylinders entspricht daher der Streckenlänge
Der Durchmesser der Grundfläche des Kreiszylinders entspricht daher der Streckenlänge 
![\(\begin{array}[t]{rll}
d_K &=& \overline{AB} \\[5pt]
&=& \left|\overrightarrow{AB} \right| \\[5pt]
&=& \left|\pmatrix{-7\\0\\0} \right| \\[5pt]
&=& 7\,[\text{m}]
\end{array}\)](https://mathjax.schullv.de/0b25be13ed128ab27d231c97aa20da5db07747ecdeb59a1ba2502478d1bb0284?color=5a5a5a) Die Höhe des halben Kreiszylinders ist
Die Höhe des halben Kreiszylinders ist  Mit der entsprechenden Formel folgt:
Mit der entsprechenden Formel folgt:
![\(\begin{array}[t]{rll}
V_K &=& \dfrac{1}{2} \cdot \pi \cdot \left(\dfrac{7\,\text{m}}{2} \right)^2 \cdot 140,0\,\text{m} \\[5pt]
&\approx& 2.693,92\,\text{m}^3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7d6bd1f5990dbf027716fefe2029150f6474c56c6cb03689e44dcd74462e3865?color=5a5a5a) 2. Schritt: Volumen eines Prismas berechnen
Mithilfe der Berechnungen aus 2.1 ergib sich für den Flächeninhalt der Grundfläche
2. Schritt: Volumen eines Prismas berechnen
Mithilfe der Berechnungen aus 2.1 ergib sich für den Flächeninhalt der Grundfläche 
![\(\begin{array}[t]{rll}
G_{ABC} &=& \dfrac{1}{2}\cdot \overline{AC}\cdot \overline{BC} \\[5pt]
&=& \dfrac{1}{2}\cdot \sqrt{24,5} \cdot \sqrt{24,5} \\[5pt]
&=& 12,25 \,[\text{m}^2] \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eeec83783093bbf58b96303e212f6bb038be0d90d2aed1d5ec86e15e3560c44c?color=5a5a5a) Die Höhe des Prismas beträgt ebenfalls
Die Höhe des Prismas beträgt ebenfalls  Für das Volumen folgt:
Für das Volumen folgt:
![\(\begin{array}[t]{rll}
V_P &=& G_{ABC} \cdot h \\[5pt]
&=& 12,25 \,\text{m}^2\cdot 140,0\,\text{m} \\[5pt]
&=& 1.715\,\text{m}^3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eb50b3288bb465c611ecf301dad713091afb3271830d8d81c45d4f17a21bfc7d?color=5a5a5a) 3. Schritt: Gesamtvolumen berechnen
3. Schritt: Gesamtvolumen berechnen
![\(\begin{array}[t]{rll}
V &=& V_K + 3\cdot V_P \\[5pt]
&\approx& 2.693,92\,\text{m}^3 + 3\cdot 1.715\,\text{m}^3 & \\[5pt]
&=& 7.838,92\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/4a3c0552569c834f98ba51d7939dbd1c3a9694c7d20bc55b9a05818a3f26aa9d?color=5a5a5a) Das gesamte Volumen der Dachkonstruktion beträgt also ca.
Das gesamte Volumen der Dachkonstruktion beträgt also ca. 
- Ein halber Kreiszylinder mit dem Volumen
- Drei identische Prismen jeweils mit dem Volumen
2.3
Da die Strecke  parallel zur
parallel zur  -Achse verläuft, lässt sich die Ebene
-Achse verläuft, lässt sich die Ebene  in Parameterform wie folgt darstellen:
Das Kreuzprodukt der beiden Spannvektoren lässt sich wie folgt berechnen:
Multipliziert mit
in Parameterform wie folgt darstellen:
Das Kreuzprodukt der beiden Spannvektoren lässt sich wie folgt berechnen:
Multipliziert mit  liefert dies den Normalenvektor
liefert dies den Normalenvektor  Folglich gilt
Folglich gilt  Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert schließlich die Behauptung:
liefert schließlich die Behauptung:

2.4
1. Schritt: Koordinaten des Mittelpunkts bestimmen
Da das Prisma gerade ist, handelt es sich bei  um ein Rechteck. Der Mittelpunkt dieses Rechtecks ist daher der Mittelpunkt der Diagonale
um ein Rechteck. Der Mittelpunkt dieses Rechtecks ist daher der Mittelpunkt der Diagonale 
![\(\begin{array}[t]{rll}
\overrightarrow{OM} &=& \dfrac{1}{2}\cdot \left(\overrightarrow{OA}+ \overrightarrow{OE} \right) \\[5pt]
&=& \dfrac{1}{2}\cdot \left(\pmatrix{7\\0\\4}+ \pmatrix{3,5 \\-140,0 \\7,5} \right) \\[5pt]
&=& \pmatrix{5,25 \\ -70,0 \\ 5,75} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1431466d2fe4380c42ec00410ddac2379876a218ccea4e7161182d370c461673?color=5a5a5a) 2. Schritt: Geradengleichung aufstellen
Die Sichtlinie liegt auf der Geraden
2. Schritt: Geradengleichung aufstellen
Die Sichtlinie liegt auf der Geraden  durch die beiden Punkte
durch die beiden Punkte  und
und  Diese Gerade kann mit folgender Gleichung beschrieben werden:
Diese Gerade kann mit folgender Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
s: \, \overrightarrow{x} &=& \overrightarrow{OK} + r\cdot \overrightarrow{KM} \\[5pt]
&=& \pmatrix{30\\20\\1,5} + r\cdot \pmatrix{-24,75 \\ -90 \\ 4,25} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eb62ebd315076fc91627e1109eb0ba30fc50c866b2d0948997b984f3a8ed7ef2?color=5a5a5a) 3. Schritt: Größe des Schnittwinkels berechnen
Der gesuchte Winkel entspricht dem Schnittwinkel
3. Schritt: Größe des Schnittwinkels berechnen
Der gesuchte Winkel entspricht dem Schnittwinkel  der Geraden
der Geraden  und der Ebene
und der Ebene  Mithilfe der zugehörigen Formel folgt:
Die Sichtlinie schließt mit der Dachfläche
Mithilfe der zugehörigen Formel folgt:
Die Sichtlinie schließt mit der Dachfläche  einen Winkel mit einer Größe von ca.
einen Winkel mit einer Größe von ca.  ein.
ein.
2.5
Begründen, dass Höhe keine Rolle spielt
Die Sichtlinie der Kamera in dem Moment, in dem sie die Flugzeugspitze erfassen kann, verläuft entlang einer Geraden. Diese Gerade berührt die Dachkonstruktion in einem Punkt tangential.
Um die halbzylinderförmige Dachkonstruktion in ihrem höchsten Punkt zu berühren, müsste die Gerade waagerecht verlaufen. Da die Position der Kamera aber die -Koordinate
-Koordinate  besitzt, liegt sie deutlich unter der höchsten Stelle des Dachs, wodurch diese Gerade nicht waagerecht verlaufen kann.
besitzt, liegt sie deutlich unter der höchsten Stelle des Dachs, wodurch diese Gerade nicht waagerecht verlaufen kann.
Der Punkt, in dem die Sichtlinie die Dachkonstruktion tangiert, ist also keiner der Punkte, die am höchsten über dem Boden des Gebäudes liegen, sondern ein anderer Punkt der Dachkonstruktion. Daher spielt die Höhe der höchsten Punkte keine Rolle bei der Ermittlung der gesuchten Höhe. Gesuchte Höhe ermitteln Zunächst wird die Gleichung der Ebene bestimmt, in der die Gerade
bestimmt, in der die Gerade  und der Punkt
und der Punkt  liegen.
liegen.
 beschreibt dabei den Verbindungsvektor zwischen dem Punkt
beschreibt dabei den Verbindungsvektor zwischen dem Punkt  und dem Stützvektor der Geraden
und dem Stützvektor der Geraden  Die
Die  -Koordinate des Schnittpunkts von
-Koordinate des Schnittpunkts von  mit der Geraden
mit der Geraden  liefert dann die gesuchte Höhe.
Der Taschenrechner liefert
liefert dann die gesuchte Höhe.
Der Taschenrechner liefert  Die gesuchte Höhe beträgt also ungefähr
Die gesuchte Höhe beträgt also ungefähr 
Um die halbzylinderförmige Dachkonstruktion in ihrem höchsten Punkt zu berühren, müsste die Gerade waagerecht verlaufen. Da die Position der Kamera aber die
Der Punkt, in dem die Sichtlinie die Dachkonstruktion tangiert, ist also keiner der Punkte, die am höchsten über dem Boden des Gebäudes liegen, sondern ein anderer Punkt der Dachkonstruktion. Daher spielt die Höhe der höchsten Punkte keine Rolle bei der Ermittlung der gesuchten Höhe. Gesuchte Höhe ermitteln Zunächst wird die Gleichung der Ebene
2.6
Geht man vereinfachend von einer Binomialverteilung aus, so geht man davon aus, dass jede Person mit einer Buchung unabhängig von den übrigen Personen mit Buchung am Flug teilnimmt. Die Entscheidung, am Flug teilzunehmen, fällt aber in der Realität nicht unbedingt unabhängig von anderen Personen (z.B. Familien oder Freundesgruppen).
2.7
Die Zufallsgröße  beschreibt die zufällige Anzahl der Personen mit Buchung, die tatsächlich am Flug teilnehmen.
beschreibt die zufällige Anzahl der Personen mit Buchung, die tatsächlich am Flug teilnehmen.  ist
ist  -verteilt.
Erwartete Anzahl der teilnehmenden Personen angeben
Der Erwartungswert lässt sich wie folgt berechnen:
-verteilt.
Erwartete Anzahl der teilnehmenden Personen angeben
Der Erwartungswert lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
E(X) &=& n\cdot p \\[5pt]
&=& 220 \cdot 0,9 \\[5pt]
&=& 198 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9e0f434a4abd3ff8d8d94eea48f2aa94f9f3d8ebcc284f6beccc7331a4e961ca?color=5a5a5a) Es sind
Es sind  Personen mit Buchung zu erwarten, die tatsächlich am Flug teilnehmen.
Wahrscheinlichkeiten berechnen
Mithilfe der Formel für die Binomialverteilung folgt für Ereignis
Personen mit Buchung zu erwarten, die tatsächlich am Flug teilnehmen.
Wahrscheinlichkeiten berechnen
Mithilfe der Formel für die Binomialverteilung folgt für Ereignis 
![\(\begin{array}[t]{rll}
P(A) &=& P(X= 200) \\[5pt]
&=& \pmatrix{220\\200}\cdot 0,9^{200} \cdot 0,1^{20} \\[5pt]
&\approx& 0,084 \\[5pt]
&=& 8,40\,\%\\[5pt]
\end{array}\)](https://mathjax.schullv.de/53f261162ae2399e6381b3bf4d771b0b7d8e460170d3ca18725a3818f06ad10b?color=5a5a5a) Für Ereignis
Für Ereignis  kann der GTR verwendet werden:
kann der GTR verwendet werden:
![\(\begin{array}[t]{rll}
P(B) &=& P(X\geq 211) &\quad \scriptsize \mid\; CAS \\[5pt]
&\approx& 0,0010 \\[5pt]
&=& 0,1\,\%
\end{array}\)](https://mathjax.schullv.de/6cfbeebfe9624f5b5b50e5858f23e4eef5c449d1c5bdbb0866accc0cc64696cb?color=5a5a5a)
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Casio fx-CG
2nd  vars (distr)
vars (distr)  B: binomcdf
B: binomcdf
Statistik: F5: DIST  F5: BINOM
F5: BINOM  F2: Bcd
F2: Bcd