Teil A

1 In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1 Welchen Anstieg besitzt der Graph der Funktion $f$ mit $f(x)=\mathrm{e}^{-\frac{1}{4}\cdot x+2}\quad(x\in\mathbb{R})$ an der Stelle $x=0$ ?

▢	▢	▢	▢	▢
$-\mathrm{e}^2$	$-\dfrac{1}{4}\cdot\mathrm{e}^2$	$-\dfrac{1}{4}\cdot\mathrm{e}^{-\frac{1}{4}}$	$\dfrac{1}{4}\cdot\mathrm{e}^2$	$\mathrm{e}^2$

1.2 Welches der folgenden bestimmten Integrale hat den Wert $0$ ?

▢	▢	▢	▢	▢
$\mathop{\displaystyle\int}\limits_{0}^{\pi}\sin(x)\;\mathrm dx$	$\mathop{\displaystyle\int}\limits_{0}^{1}\mathrm{e}^x\;\mathrm dx$	$\mathop{\displaystyle\int}\limits_{-1}^{1}x^2\;\mathrm dx$	$\mathop{\displaystyle\int}\limits_{-2}^{1}(2\cdot x)\;\mathrm dx$	$\mathop{\displaystyle\int}\limits_{-1}^{1}x\;\mathrm dx$

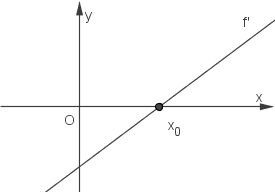
1.3 In der Abbildung ist der Graph der ersten Ableitungsfunktion $f‘$ einer Funktion $f$ in einem Intervall ihres Definitionsbereichs dargestellt. Die Nullstelle von $f‘$ ist $x_0$ .

Welche der folgenden Aussagen ist für die Funktion $f$ im dargestellten Intervall wahr?

▢	Die Funktion $f$ ist streng monoton fallend.
▢	Die Funktion $f$ ist streng monoton wachsend.
▢	Die Funktion $f$ ist für $x\lt x_0$ streng monoton wachsend.
▢	Die Funktion $f$ ist für $x\gt x_0$ streng monoton wachsend.
▢	Die Funktion $f$ besitzt keine Extremstelle.

Diagramm mit einem Koordinatensystem und einer Funktion f' in einem grafischen Format.

1.4 Eine parameterfreie Gleichung der Geraden $g$ mit $g:\vec{x}=\begin{pmatrix}0\\2\end{pmatrix}+t\cdot\begin{pmatrix}2\\1\end{pmatrix}\quad(t\in\mathbb{R})$ ist:

▢	▢	▢	▢	▢
$y=\dfrac{1}{2}\cdot x+\dfrac{1}{2}$	$y=\dfrac{1}{2}\cdot x+2$	$y=2\cdot x+\dfrac{1}{2}$	$y=2\cdot x+2$	$y=\dfrac{1}{2}\cdot x$

1.5 Ein Glücksrad ist in zehn zueinander kongruente Sektoren eingeteilt. Fünf der Sektoren sind weiß, vier blau und einer gelb angestrichen.
Durch Drehen des Glücksrades wird genau ein Sektor zufällig ausgewählt.

Das Glücksrad wird zweimal gedreht.
Die Wahrscheinlichkeit für das Ereignis „Es werden zwei Sektoren der gleichen Farbe ausgewählt.“ beträgt:

▢	▢	▢	▢	▢
$0,10$	$0,41$	$0,42$	$0,50$	$0,51$

(5P)

2 Gegeben ist die Funktion $f$ mit $f(x)=3\cdot x\cdot(x-2)\quad (x\in\mathbb{R})$ .

2.1 Der Graph der Funktion $f$ begrenzt mit der $x$ -Achse eine Fläche vollständig.
Berechne den Inhalt dieser Fläche.

(3P)

2.2 Gib die Koordinaten des lokalen Extrempunktes des Graphen der Funktion $f$ an.

(1P)

3 Gegeben sind der Punkt $A(2\mid1\mid-3)$ und eine Ebene $E$ mit $E:2\cdot x-y-z=0$ .
Der Punkt $A$ wird an der Ebene $E$ gespiegelt. Der Bildpunkt ist $B$ .
Berechne die Koordinaten des Bildpunktes $B$ .

(3P)

4 In einer Schachtel befinden sich neun Chips im Wert von je $2\,€$ , fünf Chips im Wert von je $1\,€$ und sechs Chips im Wert von je $50$ Cent.

Der Schachtel wird ein Chip zufällig entnommen.
Die Zufallsgröße $X$ beschreibt den Wert des gezogenen Chips.
Ermittle den Erfahrungswert der Zufallsgröße $X$ .

(3P)

1.1

$\blacktriangleright$ Anstieg berechnen

Hier sollst du den Anstieg des Graphen der Funktion $f$ an der Stelle $x=0$ bestimmen. Der Anstieg des Graphen an der Stelle $x=0$ ist gerade der Funktionswert der ersten Ableitung $f‘$ an der Stelle $x=0$ . Berechne also zuerst die Ableitung $f‘$ , damit kannst du dann den Anstieg des Graphen berechnen, indem du $x=0$ in die Funktionsgleichung der Ableitung $f‘(x)$ einsetzt.

1. Schritt: Ableitung bestimmen

Leite die Funktion $f$ ab. Beachte dabei die Kettenregel zu benutzen:

$\begin{array}{rll} f(x)&=& \mathrm{e} ^{- \frac{1}{4} \cdot x +2}& \\[10pt] f‘(x)&=& \left(-\dfrac{1}{4}\right) \cdot \mathrm{e} ^{- \frac{1}{4} \cdot x +2} \end{array}$

2. Schritt: $\boldsymbol{f‘(0)}$ berechnen

Setze dazu $x=0$ in den Funktionsterm $f‘(x)$ ein:

$f‘(0)=\left(-\dfrac{1}{4}\right) \cdot \mathrm{e} ^{- \frac{1}{4} \cdot 0 +2} = \left(-\dfrac{1}{4}\right) \cdot \mathrm{e}^{2}$

Damit ist $\left(-\dfrac{1}{4}\right) \cdot \mathrm{e}^{2}$ , also die zweite Antwortmöglichkeit, die korrekte Antwort.

1.2

$\blacktriangleright$ Integral bestimmen

Berechne hier jeweils die einzelnen Integrale und überprüfe das Ergebnis. Um die Integrale zu berechnen, bestimmst du zuerst eine Stammfunktion, dann kannst du die Integrale mit dem Hauptsatz der Integralrechnung bestimmen.

1. Schritt: $\boldsymbol{\displaystyle\int_{0}^{\pi}\sin(x)\;\mathrm dx}$ bestimmen

Stammfunktion bestimmen:

$\displaystyle\int_{}^{}\sin(x)\;\mathrm dx=-\cos(x)$

Integral berechnen:

$\begin{array}[t]{rll} \displaystyle\int_{0}^{\pi}\sin(x)\;\mathrm dx&=& \left[-\cos(x)\right]^\pi_0 \\[5pt] &=& (-\cos(\pi))-(-\cos(0))\\[5pt] &=& \cos(0)-\cos(\pi)\\[5pt] &=& 1-(-1)\\[5pt] &=&2 \end{array}$

Das Integral hat nicht den Wert 0.

2. Schritt: $\boldsymbol{\displaystyle\int_{0}^{1}\mathrm e^x \;\mathrm dx}$ bestimmen

Stammfunktion bestimmen:

$\displaystyle\int_{}^{}\mathrm e^x\;\mathrm dx=\mathrm e^x$

Integral berechnen:

$\displaystyle\int_{0}^{1}\mathrm e^x\;\mathrm dx= \left[\mathrm e^x\right]^1_0=\mathrm e^1-\mathrm e^0=\mathrm e-1 \neq 0$

Das Integral hat nicht den Wert 0.

3. Schritt: $\boldsymbol{\displaystyle\int_{-1}^{1}x^2\;\mathrm dx}$ bestimmen

Stammfunktion bestimmen:

$\displaystyle\int_{}^{} x^2\;\mathrm dx=\dfrac{1}{3} \cdot x^3$

Integral berechnen:

$\displaystyle\int_{-1}^{1}x^2 \;\mathrm dx= \left[\dfrac{1}{3} \cdot x^3\right]^1_{-1} = \left(\dfrac{1}{3} \cdot 1^3\right)-\left(\dfrac{1}{3} \cdot (-1)^3\right)=\dfrac{1}{3} + \dfrac{1}{3} = \dfrac{2}{3}$

Das Integral hat nicht den Wert 0.

4. Schritt: $\boldsymbol{\displaystyle\int_{-2}^{1}\left(2 \cdot x\right)\;\mathrm dx}$ bestimmen

Stammfunktion bestimmen:

$\displaystyle\int_{}^{} \left(2 \cdot x\right)\;\mathrm dx=x^2$

Integral berechnen:

$\displaystyle\int_{-2}^{1}\left( 2 \cdot x\right) \;\mathrm dx= \left[ x^2 \right]^1_{-2} = \left(1^2\right)-\left( (-2)^2 \right)=1 -4 = -3$

Das Integral hat nicht den Wert 0.

5. Schritt: $\boldsymbol{\displaystyle\int_{-1}^{1}x\;\mathrm dx}$ bestimmen

Stammfunktion bestimmen:

$\displaystyle\int_{}^{} x \;\mathrm dx=\dfrac{1}{2}\cdot x^2$

Integral berechnen:

$\displaystyle\int_{-1}^{1} x \;\mathrm dx= \left[ \dfrac{1}{2}\cdot x^2 \right]^1_{-1} = \left(\dfrac{1}{2} \cdot 1^2\right)-\left( \dfrac{1}{2}\cdot (-1)^2 \right)=\dfrac{1}{2} -\dfrac{1}{2} = 0$

Das Integral hat den Wert 0.

Somit ist $\displaystyle\int_{-1}^{1}x\;\mathrm dx$ die korrekte Antwort.

1.3

$\blacktriangleright$ Funktion $\boldsymbol{f}$ untersuchen

Hier hast du den Graphen der ersten Ableitungsfunktion $f‘$ einer Funktion $f$ in einem Intervall ihres Definitionsbereichs dargestellt. Anhand dieser Abbildung kannst du die Eigenschaften der Ableitungsfunktion bestimmen und die fünf Antwortmöglichkeiten überprüfen. Dabei hilft dir folgende Eigenschaft:

Eine Funktion $f$ ist genau dann streng monoton wachsend für $x \in \left[a,b\right]$ (bzw. fallend), falls $f‘(x) \gt 0$ (bzw. $f‘(x) \lt 0$ ) für $x \in \left[a,b\right]$ gilt.

Nach Aufgabenstellung ist dir die Nullstelle $x_0$ von $f‘$ gegeben. Du erkennst , dass $f‘(x) \lt 0$ für $x \lt x_0$ und $f‘(x) \gt 0$ für $x \gt x_0$ ist. Damit findet an der Nullstelle ein Vorzeichenwechsel statt.

$x_0$ erfüllt damit die notwendige Bedingung, also $f‘(x_0)=0$ , und die hinreichende Bedingung, also graphisch ein Vorzeichenwechsel, für eine Extremstelle. $x_0$ ist somit eine Extremstelle der Funktion $f$ . Also ist die fünfte Aussage falsch.

Die Eigenschaft $f‘(x) \lt 0$ für $x \lt x_0$ besagt, dass die Funktion $f$ für $x \lt x_0$ streng monoton fallend ist. Somit sind die zweite und dritte Aussage falsch.

Die Eigenschaft $f‘(x) \gt 0$ für $x \gt x_0$ besagt, dass die Funktion $f$ für $x \gt x_0$ streng monoton wachsend ist. Dies ist genau die vierte Aussage, die somit wahr ist. Außerdem erkennst du damit, dass die erste Aussage falsch ist.

1.4

$\blacktriangleright$ Parameterfreie Gleichung bestimmen

Hier ist deine Aufgabe eine korrekte parameterfreie Gleichung zur Geraden $g$ mit

$g:\, \overrightarrow{x}=\begin{pmatrix}0\\ 2\end{pmatrix} + t \cdot \begin{pmatrix}2\\1\end{pmatrix};\quad t \in \mathbb{R}$

aus den Antwortmöglichkeiten auszuwählen. Dafür hast du zwei Möglichkeiten. Zum einen kannst du eine parameterfreie Gleichung direkt bestimmen, zum anderen kannst du durch Punktproben mit dem Ausschlussverfahren die richtige Antwort bestimmen.

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Parameterfreie Gleichung direkt bestimmen

Betrachtest du die Vektorengleichung für $\overrightarrow{x}=\begin{pmatrix}x\\ y\end{pmatrix}$ komponentenweiße, so erhältst du ein lineares Gleichungssystem. Mit dem Einsetzungsverfahren kannst du dann eine parameterfreie Gleichung der Form $y=a \cdot x + b$ bestimmen. Das LGS lautet:

$\begin{array}{} \text{I}\quad&x&=&0&+&t \cdot 2 \\ \text{II}\quad&y&=&2&+&t \cdot 1\\ \end{array}$

Löse dazu $\left(\text{I}\right)$ nach $t$ auf:

$x=0+2\cdot t \quad \Rightarrow t=\dfrac{1}{2}x$

Setze nun $t=\dfrac{1}{2}x$ in $\left(\text{II}\right)$ ein:

$y=2 +\left( \dfrac{1}{2}x \right)\cdot 1 = 2+ \dfrac{1}{2}x$

Damit ist $y= \dfrac{1}{2}x + 2$ eine parameterfreie Gleichung der Geraden $g$ . Da es nur genau eine korrekte Antwort gibt, ist die zweite Antwortmöglichkeit die korrekte Antwort.

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Ausschlussverfahren durch Punktprobe

Setze hier dir bekannte Punkte in die verschiedenen parameterfreien Gleichungen ein und überprüfe die Ergebnisse. Damit kannst du mit dem Ausschlussverfahren die richtige Antwort bestimmen.

Setzt du $t=1$ in die Geradengleichung ein, so erhältst du den Vektor $\begin{pmatrix}2\\ 3\end{pmatrix}$ . Also liegt der Punkt $P(2 \mid 3)$ auf der Geraden. Setze also $x=2$ in die Gleichungen ein. Erhältst du nicht $y=3$ als Ergebnis, so kannst du die Antwort ausschließen.

$y=\dfrac{1}{2} \cdot 2 + \dfrac{1}{2}=1+0,5=1,5 \neq 3$
$\quad \Rightarrow$ Antwort 1 ist falsch

$y=\dfrac{1}{2} \cdot 2 + 2=1+2=3$
$\quad \Rightarrow$ Antwort 2 ist mögliche Antwort

$y=2 \cdot 2 + \dfrac{1}{2}= 4 + 0,5=4,5 \neq 3$
$\quad \Rightarrow$ Antwort 3 ist falsch

$y=2 \cdot 2 + 2= 4 + 2 = 6 \neq 3$
$\quad \Rightarrow$ Antwort 4 ist falsch

$y=\dfrac{1}{2} \cdot 2 =1 \neq 3$
$\quad \Rightarrow$ Antwort 5 ist falsch

Damit ist Antwort 2 die einzig verbleibende mögliche Antwort und $y= \dfrac{1}{2}x + 2$ somit die richtige Antwort.

1.5

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

Hier sollst du die korrekte Wahrscheinlichkeit für das Ereignis

$C=$ „Es werden zwei Sektoren der gleichen Farbe ausgewählt“ (bei zweimaligem Drehen)

bestimmen. Bestimme zuerst die Wahrscheinlichkeit eines Sektors bei einmaligem Drehen, dann kannst du die gesuchte Wahrscheinlichkeit $P(C)$ mit der Pfadmultiplikationsregel berechnen, da die erste und zweite Drehung des Glücksrads unabhängig voneinander sind.

Es gibt drei Möglichkeiten, dass zwei Sektoren der gleichen Farbe gewählt werden:

$\left(„Weiß“,„Weiß“\right)$ , $\left(„Blau“,„Blau“\right)$ und $\left(„Gelb“,„Gelb“\right)$ .

Die Wahrscheinlichkeit nach einmaligem Drehen kannst du nach Laplace bestimmen:

$P\left(„Weiß“\right)=\dfrac{5}{10}; \quad P\left(„Blau“\right)=\dfrac{4}{10}; \quad P\left(„Gelb“\right)=\dfrac{1}{10}$ .

Berechne nun die Wahrscheinlichkeiten nach zweimaligem Drehen mit den Pfadregeln:

$P\left(„Weiß“,„Weiß“\right)=P\left(„Weiß“\right) \cdot P\left(„Weiß“\right)= \dfrac{5}{10} \cdot \dfrac{5}{10} = 0,25$

$P\left(„Blau“,„Blau“\right)=P\left(„Blau“\right) \cdot P\left(„Blau“\right)= \dfrac{4}{10} \cdot \dfrac{4}{10} = 0,16$

$P\left(„Gelb“,„Gelb“\right)=P\left(„Gelb“\right) \cdot P\left(„Gelb“\right)= \dfrac{1}{10} \cdot \dfrac{1}{10} = 0,01$

Somit gilt für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rll} P(C)&=&P\left(„Weiß“,„Weiß“\right) + P\left(„Blau“,„Blau“\right) + P\left(„Gelb“,„Gelb“\right) \\[5pt] &=& 0,25 + 0,16 +0,01 = 0,42 \end{array}$

Also ist $0,42=42\,\%$ die gesuchte Wahrscheinlichkeit und die dritte Antwort ist korrekt.

2.1

$\blacktriangleright$ Inhalt der Fläche berechnen

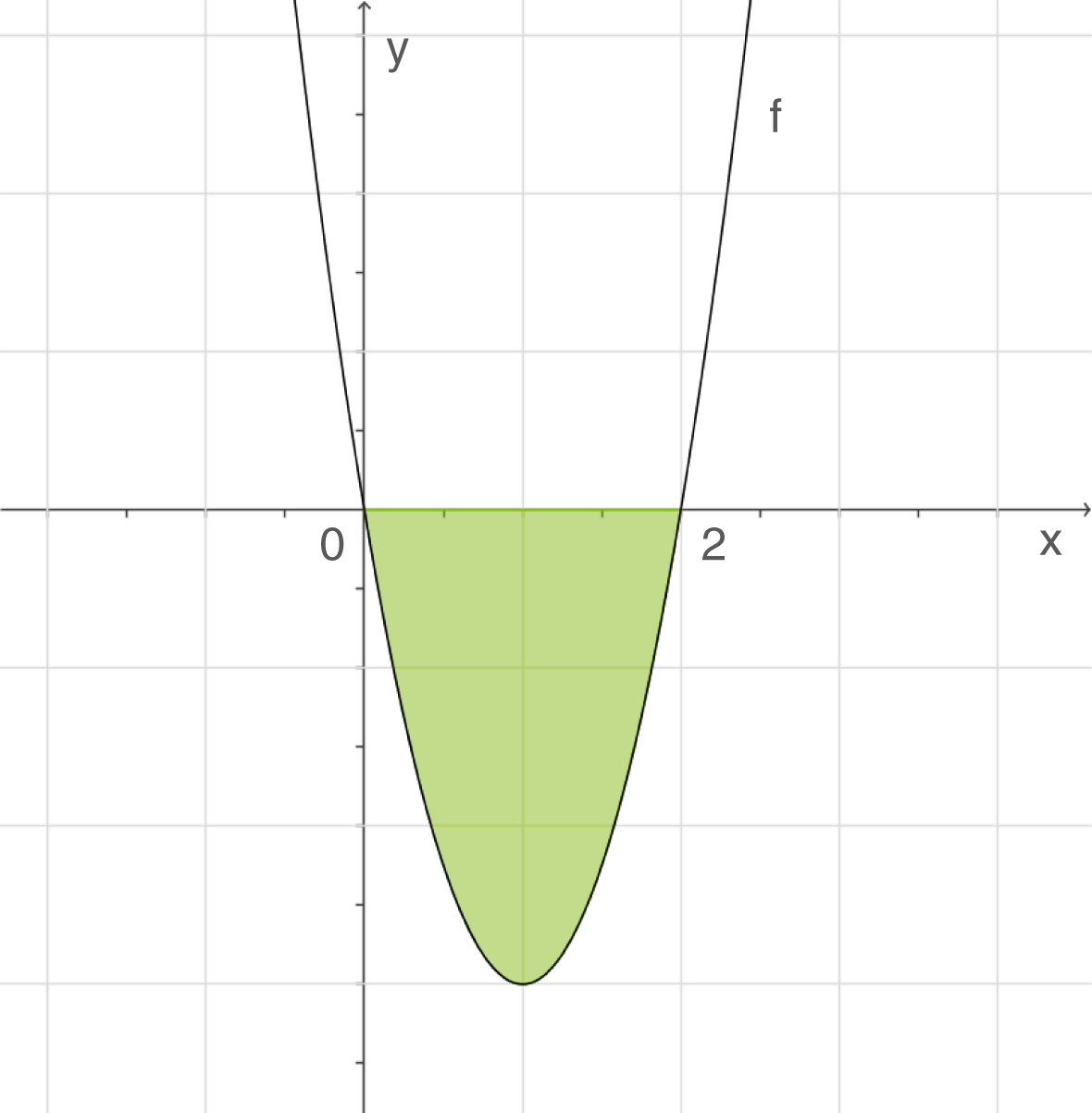Grafik einer grünen Parabel auf einem Koordinatensystem mit Achsen und Gitterlinien.

Die Funktion $f$ begrenzt mit der $x$ -Achse eine Fläche vollständig. Deine Aufgabe ist es nun den Inhalt dieser Fläche zu berechnen. Berechne dazu zuerst Nullstellen der Funktion $f$ , die die Fläche begrenzen. Berechne den Betrag des Integrals über die Funktion $f$ mit den Nullstellen als Grenzen, um den Inhalt der Fläche zu erhalten. Dies kannst du auf der nebenstehenden Skizze erkennen.

1. Schritt: Nullstellen berechnen

Setze den Funktionsterm der Funktion $f$ gleich Null und bestimme die Nullstellen:

$f(x)= 3 \cdot x \cdot \left(x-2\right)=0$

Nach dem Satz über das Nullprodukt ist ein Produkt genau dann Null, wenn einer der Faktoren gleich Null ist. Dies bedeutet hier das entweder $x=0$ oder $x-2=0$ gelten muss. Somit sind $x_1=0$ und $x_2=2$ Nullstellen der Funktion $f$ .

2. Schritt: Flächeninhalt berechnen

Berechne nun den Betrag des Integral über $f$ im Intervall $\left[0;2\right]$ . Bestimme dazu eine Stammfunktion $F$ von $f$ und wende dann den Hauptsatz der Integralrechnung an.

$\begin{array}[t]{rll} \left|\displaystyle\int_{0}^{2}f(x)\;\mathrm dx\right|&=&\left|\displaystyle\int_{0}^{2}\left(3 \cdot x \cdot \left(x-2\right)\right)\;\mathrm dx\right| &\quad \scriptsize \\[5pt] &=&\left|\displaystyle\int_{0}^{2}\left(3 x^2 - 6x\right)\;\mathrm dx\right| \\[5pt] &=& \left|\left[x^3-3x^2\right]^2_0\right| \\[5pt] &=& \left|\left(2^3 - 3 \cdot 2^2\right) - 0\right| \\[5pt] &=& \left|8 - 12\right| \\[5pt] &=& \left|-4\right| \\[5pt] &=& 4 \\[5pt] \end{array}$

Damit ist der Inhalt der Fläche 4 FE.

2.2

$\blacktriangleright$ Koordinaten des lokalen Extrempunkts angeben

Berechne hier den lokalen Extrempunkt mit dem notwendigen und hinreichenden Kriterium. Gehe also folgendermaßen vor:

Bestimme die erste und zweite Ableitung von $f$ .

Wende das notwendige Kriterium an.
Das notwendige Kriterium für eine Extremstelle $x_E$ lautet $f‘(x_E)=0$ .

Überprüfe das hinreichende Kriterium.
Das hinreichende Kriterium für eine Extremstelle $x_E$ lautet $f‘‘(x_E)\lt 0$ für ein Maximum sowie $f‘‘(x_E)\gt 0$ für ein Minimum.

Berechne noch den zugehörigen Extremwert.

1. Schritt: Erste und zweite Ableitung bestimmen

Leite die Funktion $f$ zweimal ab:

$\begin{array}[t]{rll} f(x)&=&3 \cdot x \cdot \left(x-2\right) \\[5pt] &=&3 x^2 - 6x \\[10pt] f‘(x)&=&6x - 6 \\[10pt] f‘‘(x)&=&6 \end{array}$

2. Schritt: Notwendiges Kriterium anwenden

Setze die erste Ableitung gleich Null und bestimme die potenzielle Extremstelle:

$\begin{array}[t]{rll} f‘(x)&=&0 \\[5pt] 6x-6&=&0 \quad \scriptsize \mid\; +6\\[5pt] 6x&=&6 \quad \scriptsize \mid\; :6\\[5pt] x&=&1 \end{array}$

Also ist $x=1$ eine potenzielle Extremstelle.

3. Schritt: Hinreichendes Kriterium überprüfen

Für alle $x \in \mathbb{R}$ gilt, also auch für $x=1$ :

$f‘‘(x)=6 \gt 0$

Also ist die hinreichende Bedingung erfüllt und es handelt sich hierbei um eine Minimalstelle.

4. Schritt: Extremwert berechnen

Berechne nun noch den Extremwert der Extremstelle indem du $x=1$ in die Funktionsgleichung $f(x)$ einsetzt:

$f(1)=3 \cdot 1 \cdot \left( 1- 2\right)=3 \cdot \left(-1\right)=-3$ .

Somit lauten die Koordinaten des lokalen Extrempunkts $(1 \mid -3)$ .

$\blacktriangleright$ Punkt $\boldsymbol{A}$ an der Ebene $\boldsymbol{E}$ spiegeln

Deine Aufgabe ist es den Punkt $A$ an der Ebene $E$ zu spiegeln. Gehe dazu folgendermaßen vor:

Bilde einen Normalenvektor $\overrightarrow{n}$ der Ebene $E$ .

Stelle die Gerade $g$ durch $A$ mit Richtungsvektor $\overrightarrow{n}$ auf.

Berechne den Schnittpunkt $S$ der Geraden $g$ mit der Ebene $E$ .

Berechne den Verbindungsvektor $\overrightarrow{AS}$ .

Bestimme die Koordinaten von $B$ durch $\overrightarrow{OB}=\overrightarrow{OS} + \overrightarrow{AS}$ .

1. Schritt: Normalenvektor $\boldsymbol{\overrightarrow{n}}$ bilden

Den Normalenvektor einer Ebene kannst du direkt aus einer Ebenengleichung in Koordinatenform ablesen. Da $E$ in Koordinatenform gegeben ist, kannst du einen Normalenvektor direkt ablesen:

$\overrightarrow{n}=\begin{pmatrix}2\\ -1\\ -1\end{pmatrix}$

2. Schritt: Gerade $\boldsymbol{g}$ aufstellen

Hast du einen Punkt $P$ und einen Richtungsvektor $\overrightarrow{u}$ gegeben und willst damit eine Gerade $h$ aufstellen, so ist die dazugehörige Geradengleichung gegeben durch:

$h:\; \overrightarrow{x}= \overrightarrow{OP} + t \cdot \overrightarrow{u}$

Mit Punkt $A$ und dem Normalenvektor $\overrightarrow{n}$ erhältst du folgende Geradengleichung für $g$ :

$g:\; \overrightarrow{x}= \overrightarrow{OA} + t \cdot \overrightarrow{n} = \begin{pmatrix}2\\ 1\\ -3\end{pmatrix} + t \cdot \begin{pmatrix}2\\ -1\\ -1\end{pmatrix}=\begin{pmatrix}2+ t \cdot 2\\ 1 - t \\ -3 - t\end{pmatrix}$

3. Schritt: Schnittpunkt $\boldsymbol{S}$ der Geraden $\boldsymbol{g}$ mit der Ebene $\boldsymbol{E}$ berechnen

Du hast eine Geradengleichung in Parameterform und eine Ebenengleichung in Koordinatenform gegeben und sollst den Schnittpunkt der Geraden mit der Ebene berechnen. Dies kannst du mit dem Einsetzungsverfahren. Setze dazu den allgemeinen Punkt der Gerade $g$ in die Gleichung in Koordinatenform der Ebene ein und löse nach dem Parameter $t$ auf:

$\begin{array}[t]{rll} 2 \cdot x - y- z &=& 0 &\quad \scriptsize \mid\; \text{Allgemeinen Punkt der Gerade $g$ einsetzen}\\[5pt] 2 \cdot \left( 2+ 2t \right) - \left( 1 - t \right) - \left( -3 - t \right)&=&0 \\[5pt] 4+ 4t -1 + t +3 +t &=& 0\\[5pt] 6t + 6 &=& 0 &\quad \scriptsize \mid\; -6\\[5pt] 6t &=& -6 &\quad \scriptsize \mid\; :6\\[5pt] t &=& -1\\[5pt] \end{array}$

Berechne nun den Ortsvektor des Schnittpunkts $S$ , indem du $t=-1$ in die Gleichung der Geraden $g$ einsetzt:

$\overrightarrow{OS} = \begin{pmatrix}2\\ 1\\ -3\end{pmatrix} + \left(-1\right) \cdot \begin{pmatrix}2\\ -1\\ -1\end{pmatrix} = \begin{pmatrix}2\\ 1\\ -3\end{pmatrix} + \begin{pmatrix}-2\\ 1\\ 1\end{pmatrix}= \begin{pmatrix}0\\ 2\\ -2\end{pmatrix}$

4. Schritt: Verbindungsvektor $\boldsymbol{\overrightarrow{AS}}$ berechnen

Berechne nun den Verbindungsvektor der Punkte $A$ und $S$ :

$\overrightarrow{AS} = \overrightarrow{OS} - \overrightarrow{OA} = \begin{pmatrix}0\\ 2\\ -2\end{pmatrix} - \begin{pmatrix}2\\ 1\\ -3\end{pmatrix} = \begin{pmatrix}-2\\ 1\\ 1\end{pmatrix}$

5. Schritt: Koordinaten des Bildpunkts $\boldsymbol{B}$ berechnen

Berechne jetzt den Ortsvektor des Bildpunktes $B$ mit der Gleichung $\overrightarrow{OB} = \overrightarrow{OS} + \overrightarrow{AS}$ :

$\overrightarrow{OB} = \overrightarrow{OS} + \overrightarrow{AS} = \begin{pmatrix}0\\ 2\\ -2\end{pmatrix} + \begin{pmatrix}-2\\ 1\\ 1\end{pmatrix} = \begin{pmatrix}-2\\ 3\\ -1\end{pmatrix}$

Die Koordinaten des Bildpunktes $B$ kannst du vom Ortsvektor $\overrightarrow{OB}$ ablesen. Der Bildpunkt ist $B\left( -2 \mid 3 \mid -1\right)$ .

$\blacktriangleright$ Erwartungswert der Zufallsgröße $\boldsymbol{X}$ ermitteln

Hier ist deine Aufgabe den Erwartungswert der Zufallsgröße $X$ zu ermitteln. Ermittle dazu zuerst die Werte die $X$ annehmen kann und deren Wahrscheinlichkeiten. Für den Ergebnisraum $\Omega=\left\{x_1,x_2,...,x_n\right\}$ von $X$ lässt sich der Erwartungswert mit folgender Formel berechnen:

$E\left(X\right)=\displaystyle\sum\limits_{i=1}^{n}x_i \cdot P\left(X=x_i\right)$

1. Schritt: Mögliche Werte von $\boldsymbol{X}$ und Wahrscheinlichkeiten bestimmen

Die Zufallsgröße $X$ beschreibt den Wert eines zufällig gezogenen Chips. Du kannst Chips im Wert von $2 \,€$ , $1\,€$ oder $0,5 \,€$ ziehen, also $\Omega=\left\{0,5;1;2\right\}$ .

Der Chip wird der Schachtel zufällig entnommen, dementsprechend handelt es sich hierbei um ein Laplace-Experiment. In der Schachtel befinden sich insgesamt $9 + 5+ 6 = 20$ Chips. Damit kannst du die Wahrscheinlichkeiten der verschiedenen Ereignisse berechnen:

$P(X=0,5)=\dfrac{6}{20}$ , $P(X=1)=\dfrac{5}{20}$ und $P(X=2)=\dfrac{9}{20}$ .

2. Schritt: Erwartungswert von $\boldsymbol{X}$ bestimmen

Den Erwartungswert kannst du nun mit der obigen Formel und den Werten aus dem 1. Schritt berechnen:

$\begin{array}[t]{rll} E(X) &=& 0,5 \cdot P(X=0,5) + 1 \cdot P(X=1) + 2 \cdot P(X=2)\\[5pt] &=& 0,5 \cdot \dfrac{6}{20} + \dfrac{5}{20} + 2 \cdot \dfrac{9}{20}\\[5pt] &=& \dfrac{3}{20} + \dfrac{5}{20} + \dfrac{18}{20} \\[5pt] &=& \dfrac{26}{20} \\[5pt] &=& 1,3 \\[5pt] \end{array}$

Der Erwartungswert der Zufallsgröße $X$ ist $1,30\, €$ .