Teil A
1
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1.1
Gegeben ist die Funktion  mit
mit  Eine Gleichung der ersten Ableitungsfunktion
Eine Gleichung der ersten Ableitungsfunktion  von
von  lautet:
lautet:
1.2
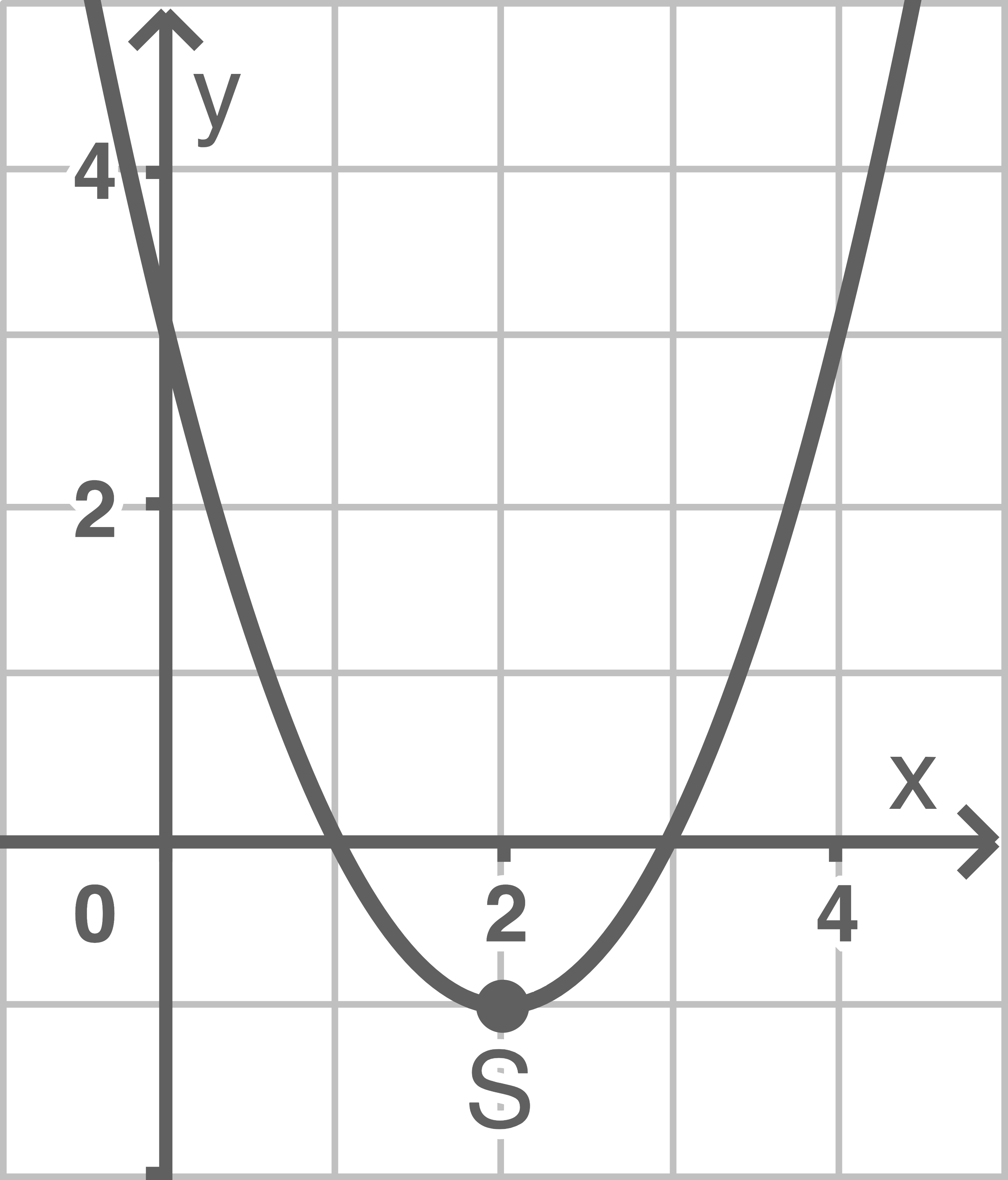
Die Abbildung zeigt den Graphen einer ganzrationalen Funktion  zweiten Grades mit dem Scheitelpunkt
zweiten Grades mit dem Scheitelpunkt  Welche Gleichung beschreibt die erste Ableitungsfunktion
Welche Gleichung beschreibt die erste Ableitungsfunktion  von
von 
1.3
Der Graph der Funktion  mit
mit 
| verläuft durch den Koordinatenursprung. | |
| schneidet die |
|
| besitzt keine Asymptote. | |
| hat eine waagerechte und eine senkrechte Asymptote. | |
| hat zwei waagerechte Asymptoten. |
1.4
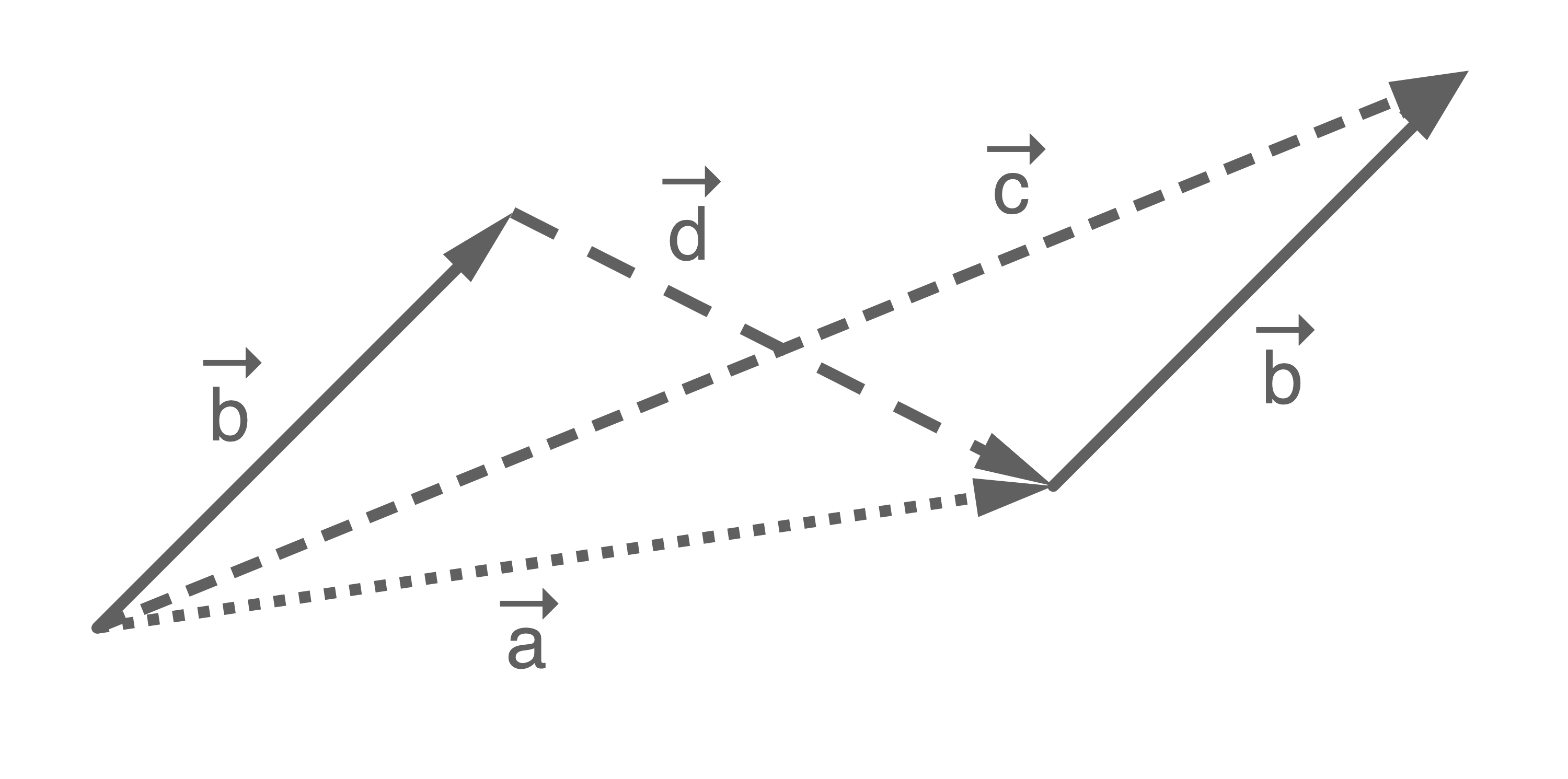
Betrachtet werden die in der Abbildung dargestellten Vektoren.
Welche der folgenden Gleichungen ist falsch?
1.5
Die Ebene 
| verläuft durch den Koordinatenursprung. | |
| verläuft parallel zur |
|
| schneidet alle drei Koordinatenachsen. | |
| kann auch durch die Gleichung |
|
| verläuft parallel zur |
(5 BE)
2
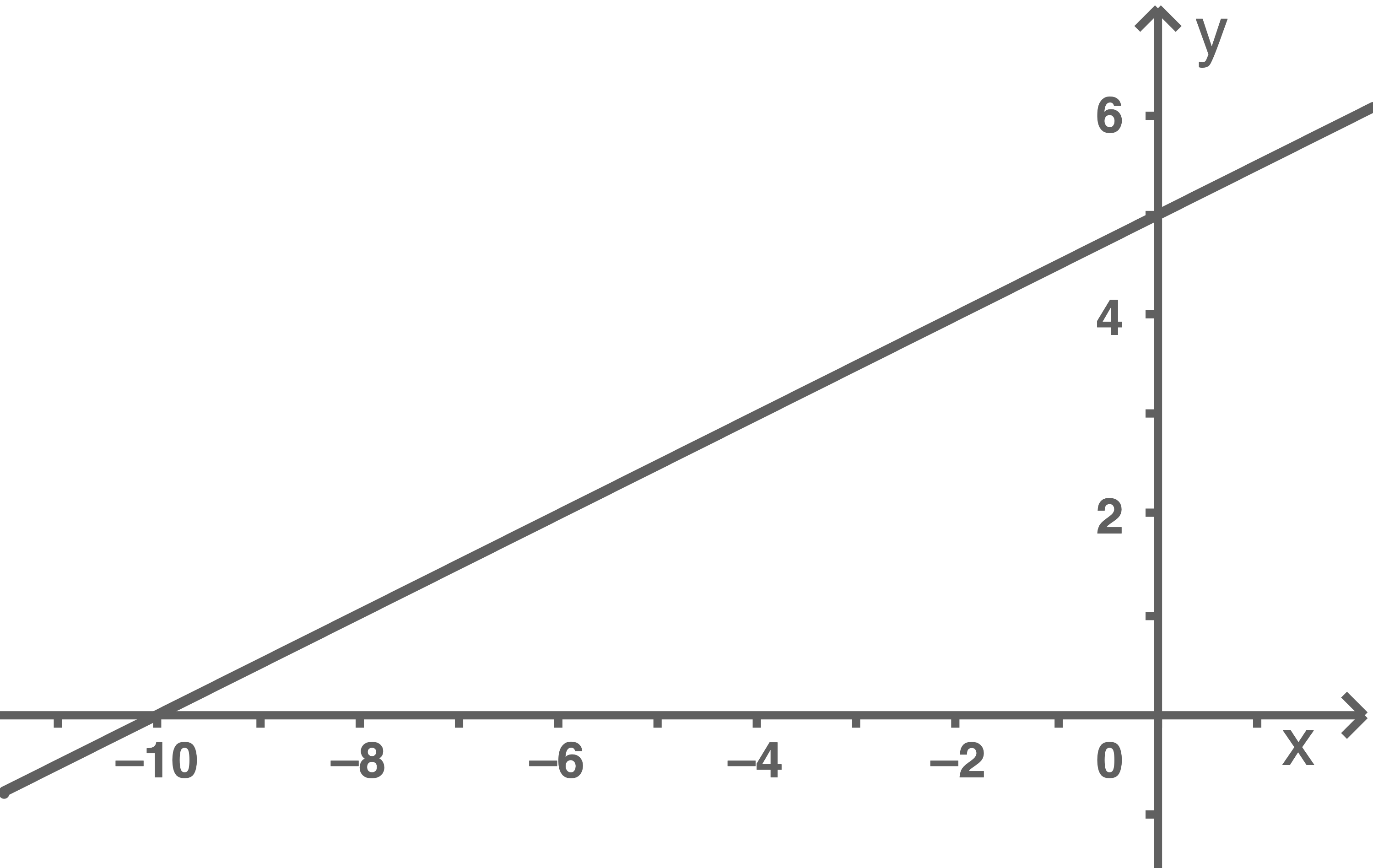
Die Abbildung zeigt den Graphen der in  definierten linearen Funktion
definierten linearen Funktion 
2.1
Begründe, dass  gilt.
gilt.
(1 BE)
2.2
Berechne den Abstand des Koordinatenursprungs zum Graphen.
(4 BE)
3
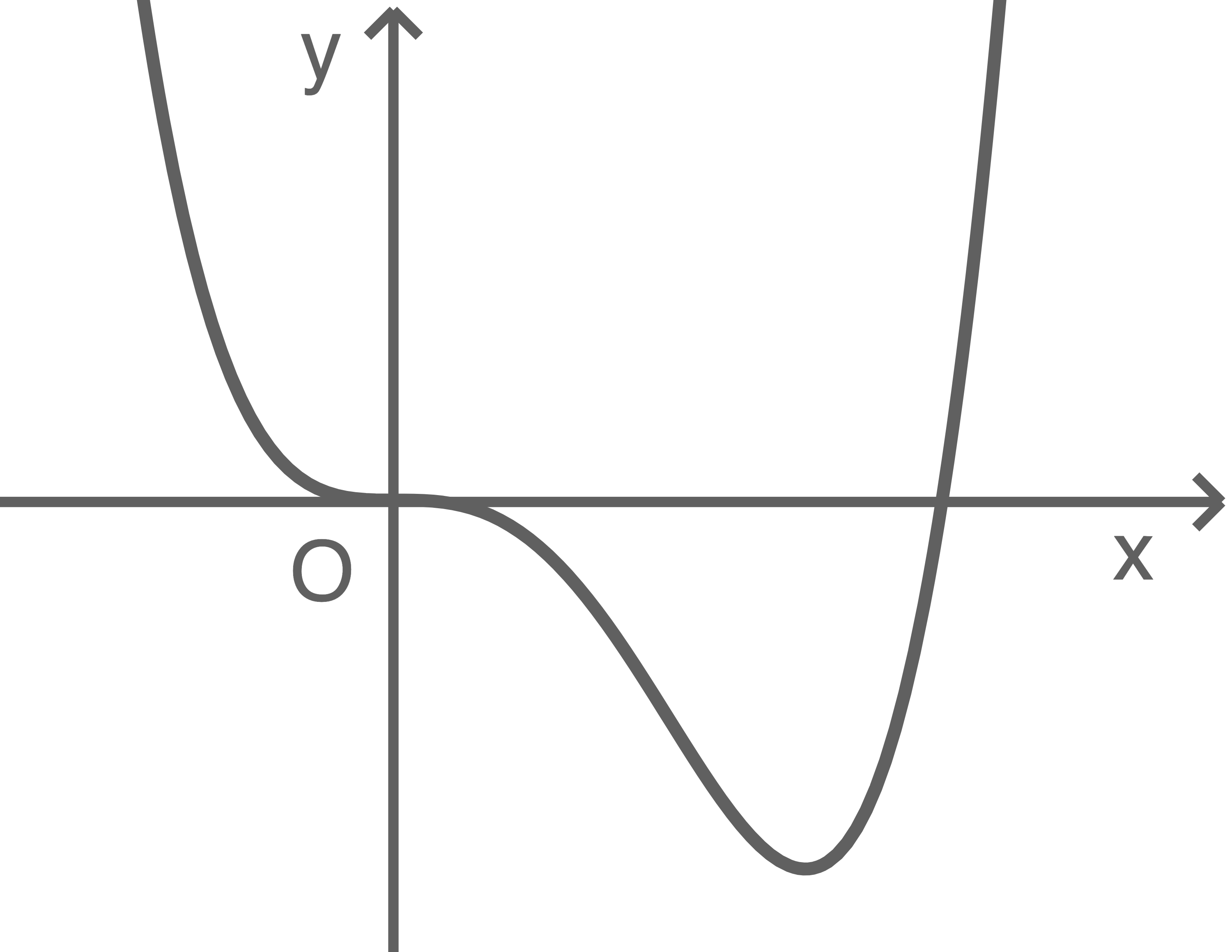
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion  mit
mit 
3.1
Berechne den Wert des Integrals 
(2 BE)
3.2
Beurteile, ob die folgende Aussage richtig ist:
Für die Abbildung wurde eine Längeneinheit auf der  -Achse ebenso groß gewählt wie auf der
-Achse ebenso groß gewählt wie auf der  -Achse.
-Achse.
(3 BE)
4
Gegeben sind die Gerade  mit
mit  sowie die Gerade
sowie die Gerade  durch die Punkte
durch die Punkte  und
und  mit einer reellen Zahl
mit einer reellen Zahl 
4.1
Begründe, dass  nicht auf
nicht auf  liegt.
liegt.
(1 BE)
4.2
Die Geraden  und
und  haben einen gemeinsamen Punkt.
Ermittle den Wert von
haben einen gemeinsamen Punkt.
Ermittle den Wert von 
(4 BE)
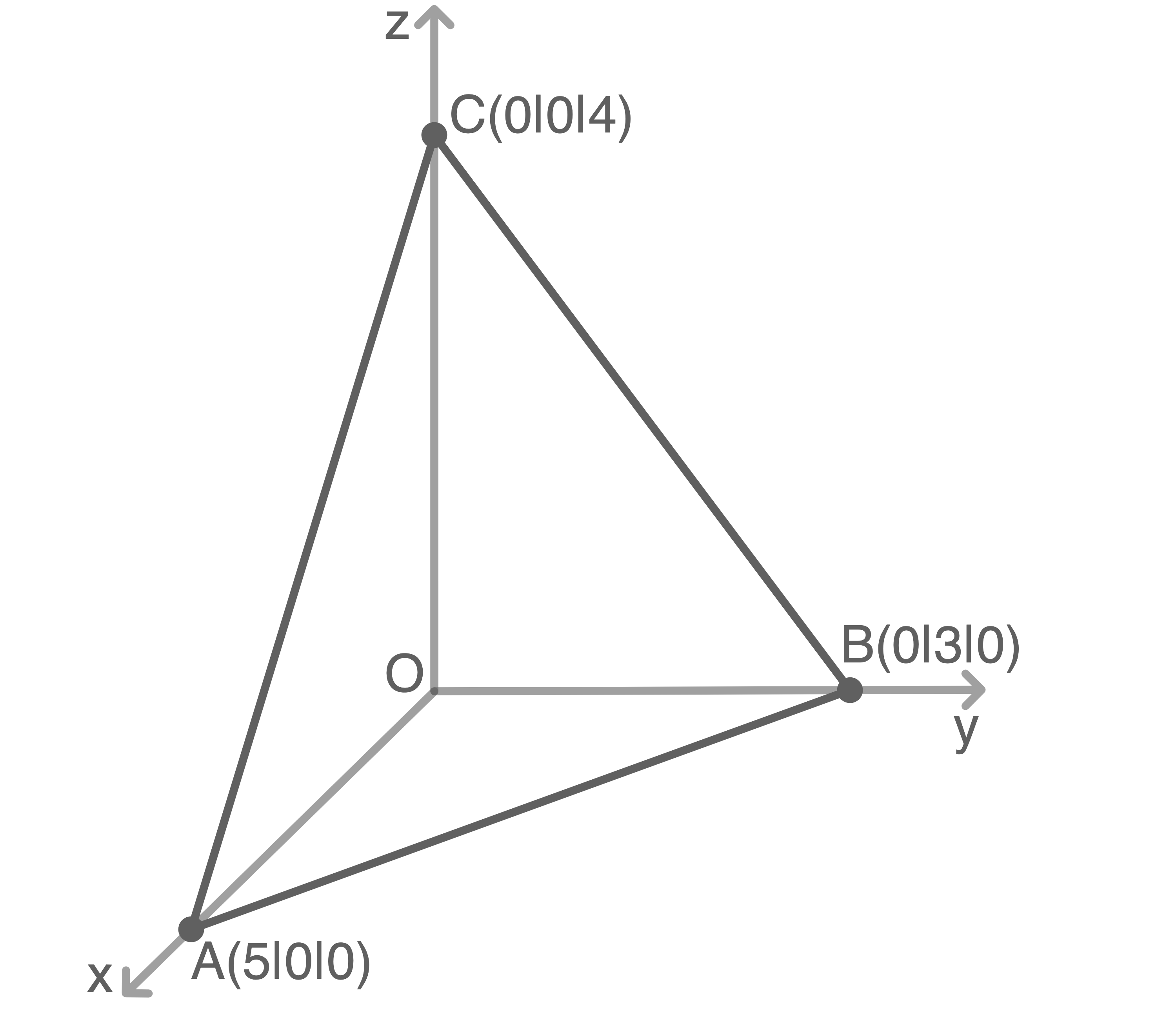
5
Die Abbildung zeigt das Dreieck  Der Koordinatenursprung wird mit
Der Koordinatenursprung wird mit  bezeichnet.
bezeichnet.
5.1
Die Ebene, in der das Dreieck  liegt, kann durch eine Gleichung der Form
liegt, kann durch eine Gleichung der Form  dargestellt werden.
Bestimme den Wert von
dargestellt werden.
Bestimme den Wert von  .
.
(1 BE)
5.2
Für jeden Wert von  mit
mit  wird die Pyramide
wird die Pyramide  mit
mit  und
und  betrachtet.
Bestimme denjenigen Wert von
betrachtet.
Bestimme denjenigen Wert von  für den die Pyramide das größte Volumen hat.
für den die Pyramide das größte Volumen hat.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Rechnung
Mit der Kettenregel ergibt sich:

1.2
Lösungsweg
Aus der Verschiebung der Normalparabel um 2 Längeneinheiten in positive  -Richtung und um eine Längeneinheit in negative
-Richtung und um eine Längeneinheit in negative  -Richtung ergibt sich die Gleichung von
-Richtung ergibt sich die Gleichung von  mit:
mit:
![\(\begin{array}[t]{rll}
f(x)&=& (x-2)^2-1& \\[5pt]
&=& (x^2-4x-4)-1& \\[5pt]
&=& x^2-4x-5
\end{array}\)](https://www.schullv.de/resources/formulas/2888ed4c849500b7c28a38312cd2c1c7742c81d707558ef9bfe4944791738e0c_light.svg) Die Gleichung der ersten Ableitungsfunktion folgt also durch:
Die Gleichung der ersten Ableitungsfunktion folgt also durch:

1.3
| verläuft durch den Koordinatenursprung. | |
| schneidet die |
|
| besitzt keine Asymptote. | |
| hat eine waagerechte und eine senkrechte Asymptote. | |
| hat zwei waagerechte Asymptoten. |
Lösungsweg
Die senkrechte Asymptote des Graphen der Funktion  ist
ist  Da der Funktionsterm nur einen negativen, geraden Exponenten besitzt und keinen Summanden, welcher für eine Verschiebung in positive oder negative
Da der Funktionsterm nur einen negativen, geraden Exponenten besitzt und keinen Summanden, welcher für eine Verschiebung in positive oder negative  -Richtung sorgt, hat der Graph von
-Richtung sorgt, hat der Graph von  eine waagerechte Asymptote, welche der
eine waagerechte Asymptote, welche der  -Achse entspricht.
Der Graph der Funktion
-Achse entspricht.
Der Graph der Funktion  hat folglich eine waagrechte und eine senkrechte Asymptote.
hat folglich eine waagrechte und eine senkrechte Asymptote.
1.4
1.5
| verläuft durch den Koordinatenursprung. | |
| verläuft parallel zur |
|
| schneidet alle drei Koordinatenachsen. | |
| kann auch durch die Gleichung |
|
| verläuft parallel zur |
2.1
Aus der Abbildung können der  -Achsenabschnitt
-Achsenabschnitt  sowie die Steigung
sowie die Steigung  abgelesen werden.
Einsetzen in die Geradengleichung liefert
abgelesen werden.
Einsetzen in die Geradengleichung liefert 
2.2
1. Schritt: Gleichung des Lots vom Koordinatenursprung auf den Graphen
 2. Schritt: Koordinaten des Schnittpunkts bestimmen
Gleichsetzen liefert:
2. Schritt: Koordinaten des Schnittpunkts bestimmen
Gleichsetzen liefert:
![\(\begin{array}[t]{rll}
\dfrac{1}{2}\cdot x+5&=& -2\cdot x&\quad \scriptsize \mid\; -\dfrac{1}{2}\cdot x\\[5pt]
5&=& -2,5\cdot x&\quad \scriptsize \mid\; :-2,5\\[5pt]
-2&=& x
\end{array}\)](https://www.schullv.de/resources/formulas/baacaa653b9155b81be9bad84cf29532730f076f0aa32cc599ba3e7987c374b5_light.svg)
 -Koordinate des Lots bestimmen:
-Koordinate des Lots bestimmen:
 3. Schritt: Abstand berechnen
3. Schritt: Abstand berechnen

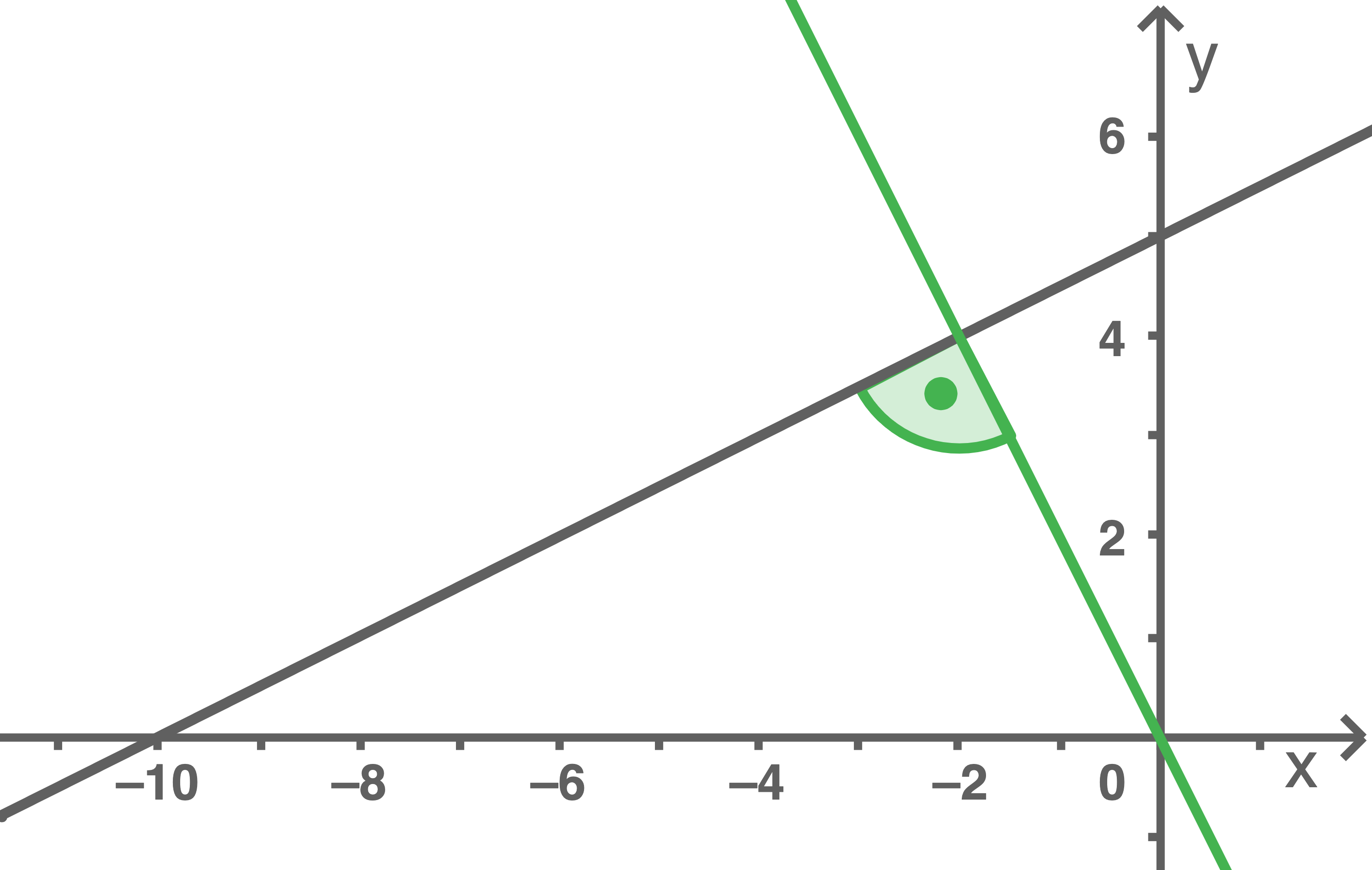
Hilfsskizze
3.1
3.2
4.1
4.2
Geradengleichung von  aufstellen:
aufstellen:
 Gleichsetzen der beiden Geraden liefert:
Aus der zweiten Zeile folgt
Gleichsetzen der beiden Geraden liefert:
Aus der zweiten Zeile folgt  Einsetzen in die erste Zeile ergibt:
Einsetzen in die erste Zeile ergibt:
![\(\begin{array}[t]{rll}
2+s&=& 4+3&\quad \scriptsize \mid\; -2\\[5pt]
s&=& 5&
\end{array}\)](https://www.schullv.de/resources/formulas/20871d7e275f01fc1a0890d054397b84683cefe45e600f3d774218824c5f97b8_light.svg) Aus der dritten Zeile folgt nun:
Aus der dritten Zeile folgt nun:
![\(\begin{array}[t]{rll}
-7+5\cdot 5&=& r\cdot b& \\[5pt]
18&=& 3\cdot b &\quad \scriptsize \mid\; :3\\[5pt]
6 &=& b
\end{array}\)](https://www.schullv.de/resources/formulas/d1745ed00033c19f3297baa034f24a520ec15974b40e58ec7f6cc5e7012de3ef_light.svg)
5.1
Da der Punkt  in der Ebene liegt, gilt:
in der Ebene liegt, gilt:
![\(\begin{array}[t]{rll}
12\cdot 0+20\cdot 0+t\cdot 4&=& 60 &\quad \scriptsize \mid\; :4 \\[5pt]
t&=& 15
\end{array}\)](https://www.schullv.de/resources/formulas/005c5343fa37301b0e22a4973831f67082de3635f652a394e8af36569278558a_light.svg)
5.2
Das Volumen der Pyramide  kann mit folgender Formel berechnet werden:
kann mit folgender Formel berechnet werden:
![\(\begin{array}[t]{rll}
V&=& \dfrac{1}{3}\cdot G\cdot h& \\[5pt]
&=& \dfrac{1}{3}\cdot \left(\dfrac{1}{2}\cdot (5-k)\cdot (3+k)\right)\cdot 4& \\[5pt]
&=& \dfrac{2}{3}\cdot (5-k)\cdot (3+k) & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/77262e1cfdf61ff176b3a65b66489ee5ed9afbd38b418333543e9d49b63953e3_light.svg) Die graphische Darstellung des Terms in Abhängigkeit von
Die graphische Darstellung des Terms in Abhängigkeit von  entspricht einer Parabel mit den Nullstellen
entspricht einer Parabel mit den Nullstellen  und
und  Aufgrund der Symmetrie folgt der Hochpunkt an der Stelle
Aufgrund der Symmetrie folgt der Hochpunkt an der Stelle  Für diesen Wert hat die Pyramide somit das größte Volumen.
Für diesen Wert hat die Pyramide somit das größte Volumen.