Aufgabe B1
Gegeben ist die in 
definierte Funktion 
mit 
1.1
Gib die Koordinaten des lokalen Tiefpunkts des Graphen von an.
Gib das Verhalten von für 
an.
an.
Gib das Verhalten von
für an.
(3 BE)
1.2
Es gilt: 
und 
und 
Beschreibe die Bedeutung dieser Aussage für den Graphen von
Es gibt Paare von Tangenten an den Graphen von und und
Beschreibe die Bedeutung dieser Aussage für den Graphen von
(3 BE)
die parallel zueinander verlaufen.
Sie berühren den Graphen von
an den Stellen 
bzw. 
1.3
Betrachtet werden die beiden Tangenten eines solchen Paares mit dem Anstieg 
Zeige, dass für diesen Fall die Stellen und 
den gleichen Abstand zu 
haben.
Zeige, dass für diesen Fall die Stellen
und den gleichen Abstand zu haben.
(2 BE)
1.4
Begründe mithilfe der ersten Ableitungsfunktion von dass für alle derartigen Paare von Tangenten gilt: 
Betrachtet wird die in dass für alle derartigen Paare von Tangenten gilt:
(3 BE)
definierte Funktion 
mit 
1.5
Es gilt: 
Beschreibe, wie der Graph von aus dem Graphen von hevorgeht.
Beschreibe, wie der Graph von
aus dem Graphen von hevorgeht.
(2 BE)
Die Abbildung zeigt modellhaft drei Wegabschnitte einer Parkanlage in einem Koordinatensystem mit dem Koordinatenursprung 
Die Punkte, in denen die drei Abschnitte ineinander übergehen, werden im Modell durch
und 
beschrieben.
Der Wegabschnitt I von
nach 
wird mithilfe von beschrieben.
Der Wegabschnitt II von nach 
wird mithilfe eines Kreises mit den Mittelpunkt 
beschrieben.
Der Wegabschnitt III von nach wird durch die Funktion beschrieben, deren Graph bei Spiegelung des Graphen von mit 
an der Geraden 
entsteht.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
Die Punkte, in denen die drei Abschnitte ineinander übergehen, werden im Modell durch
und beschrieben.
Der Wegabschnitt I von
nach wird mithilfe von beschrieben.
Der Wegabschnitt II von
nach wird mithilfe eines Kreises mit den Mittelpunkt beschrieben.
Der Wegabschnitt III von
nach wird durch die Funktion beschrieben, deren Graph bei Spiegelung des Graphen von mit an der Geraden entsteht.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
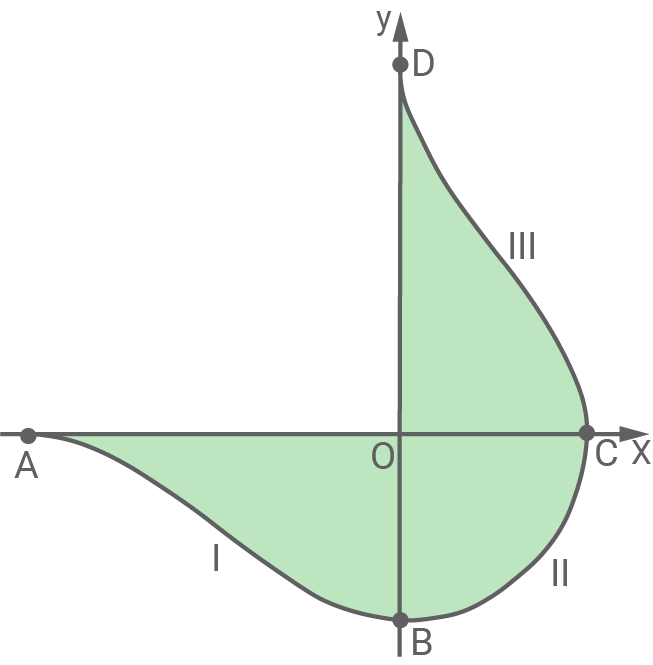
Abbildung (nicht maßstäblich)
1.6
Zeige, dass die durch und beschriebenen Punkte in der Realität 
voneinander entfernt sind.
Bestimme die Länge des Wegabschnitts II.
und beschriebenen Punkte in der Realität voneinander entfernt sind.
Bestimme die Länge des Wegabschnitts II.
(4 BE)
1.7
In einem Punkt des Wegabschnitts I und in einem Punkt des Wegabschnitts III wechselt jeweils der Weg von einer Rechts- in eine Linkskurve bzw. umgekehrt.
Bestimme die Koordinaten des Punkts des Wegabschnitts I.
Gib die Koordinaten des Punkts des Wegabschnitts III an.
Bestimme die Koordinaten des Punkts des Wegabschnitts I.
Gib die Koordinaten des Punkts des Wegabschnitts III an.
(4 BE)
1.8
Die in der Abbildung grün dargestellte Fläche soll bepflanzt werden. Dafür wird auf die gesamte Fläche Mutterboden mit einer Höhe von 
aufgebracht.
Bestimme das Volumen des Mutterbodens, der aufgebracht wird.
aufgebracht.
Bestimme das Volumen des Mutterbodens, der aufgebracht wird.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Mit der graphischen Darstellung des MMS folgt, dass die Koordinaten des lokalen Tiefpunkts 
betragen und 
gilt.
betragen und gilt.
1.2
Bei 
hat der Graph von einen lokalen Hochpunkt.
hat der Graph von einen lokalen Hochpunkt.
1.3
Mit dem MMS folgt für die erste Ableitung von 
Die Gleichung 
liefert mit dem solve-Befehl des MMS:
![\(\begin{array}[t]{rlll}
x_1&=&-1,5 \\[5pt]
x_2&=&-0,5
\end{array}\)](https://www.schullv.de/resources/formulas/b4868e0ee7daae26494dc5e1a0007402a87a7c83ae3c391c2f3bf2919b250ec6_light.svg)
Der Abstand zu ist somit in beiden Fällen 
Die Gleichung liefert mit dem solve-Befehl des MMS:
Der Abstand zu ist somit in beiden Fällen
1.4
Die graphische Darstellung des MMS zeigt, dass der Graph der ersten Ableitungsfunktion eine Parabel mit der Symmetrieachse ist. Da 
gilt, ist somit das arithmetische Mittel von und und es gilt 
ist. Da gilt, ist somit das arithmetische Mittel von und und es gilt
1.5
Der Graph von geht aus dem Graphen von durch Streckung in 
-Richtung um den Faktor 
und Streckung in 
-Richtung um den Faktor 
hervor.
geht aus dem Graphen von durch Streckung in -Richtung um den Faktor und Streckung in -Richtung um den Faktor hervor.
1.6
Abstand von 
und 
zeigen
Mit dem MMS folgt, dass der Achsenabschnitt von bei 
liegt. Da die Nullstelle der Funktion, die den Wegabschnitt III beschreibt, den Betrag dieses Werts besitzt, gilt 
Für den Abstand von und ergibt sich damit 
Länge bestimmen
Die Länge 
des Wegabschnitts II ist durch ein Viertel des Umfangs eines Kreises mit Radius gegeben. Somit folgt:
und zeigen
Mit dem MMS folgt, dass der Achsenabschnitt von bei liegt. Da die Nullstelle der Funktion, die den Wegabschnitt III beschreibt, den Betrag dieses Werts besitzt, gilt Für den Abstand von und ergibt sich damit
Länge bestimmen
Die Länge des Wegabschnitts II ist durch ein Viertel des Umfangs eines Kreises mit Radius gegeben. Somit folgt:
1.7
Der gesuchte Punkt im Wegabschnitt I ist durch den Wendepunkt von gegeben. Mit dem MMS folgt, dass dieser die Koordinaten 
besitzt. Aus der Definition des Wegabschnitts III folgt somit, dass der zweite gesuchte Punkt die Koordinaten 
besitzt.
gegeben. Mit dem MMS folgt, dass dieser die Koordinaten besitzt. Aus der Definition des Wegabschnitts III folgt somit, dass der zweite gesuchte Punkt die Koordinaten besitzt.
1.8
Die von den Wegabschnitten I und III mit den Achsen eingeschlossenen Flächeninhalte sind aufgrund der Symmetrie gleich groß und jeweils durch den folgenden Term gegeben:
Der Flächeninhalt der Fläche, die durch den Wegabschnitt II begrenzt ist, ist ein Viertel des Flächeninhalts eines Kreises mit Radius 
also 
Es gilt 
Somit ergibt sich für das gesuchte Volumen 
insgesamt:
![\(\begin{array}[t]{rlll}
V&=&\left(\left\vert\displaystyle\int_{-200}^{0}g(x)\;\mathrm dx\right\vert+2500\pi\right)\cdot0,2 \\[5pt]
&\approx&5570,8\;[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/648fffd91e64d4a05364fc37e4d814159d1c8d139400f36f633321a23509844d_light.svg)
Der Flächeninhalt der Fläche, die durch den Wegabschnitt II begrenzt ist, ist ein Viertel des Flächeninhalts eines Kreises mit Radius also
Es gilt Somit ergibt sich für das gesuchte Volumen insgesamt: