Teil B2
Ein Anbau eines Gebäudes wird modellhaft durch das abgebildete Prisma mit den Eckpunkten 
und 
beschrieben.
Das Viereck 
stellt das Glasdach dar, das Viereck 
eine geschlossene Wand; die anderen Seiten des Anbaus bestehen vollständig aus Glas.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Die
-Ebene beschreibt den Untergrund, auf dem der Anbau steht.
und beschrieben.
Das Viereck stellt das Glasdach dar, das Viereck eine geschlossene Wand; die anderen Seiten des Anbaus bestehen vollständig aus Glas.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Die
-Ebene beschreibt den Untergrund, auf dem der Anbau steht.
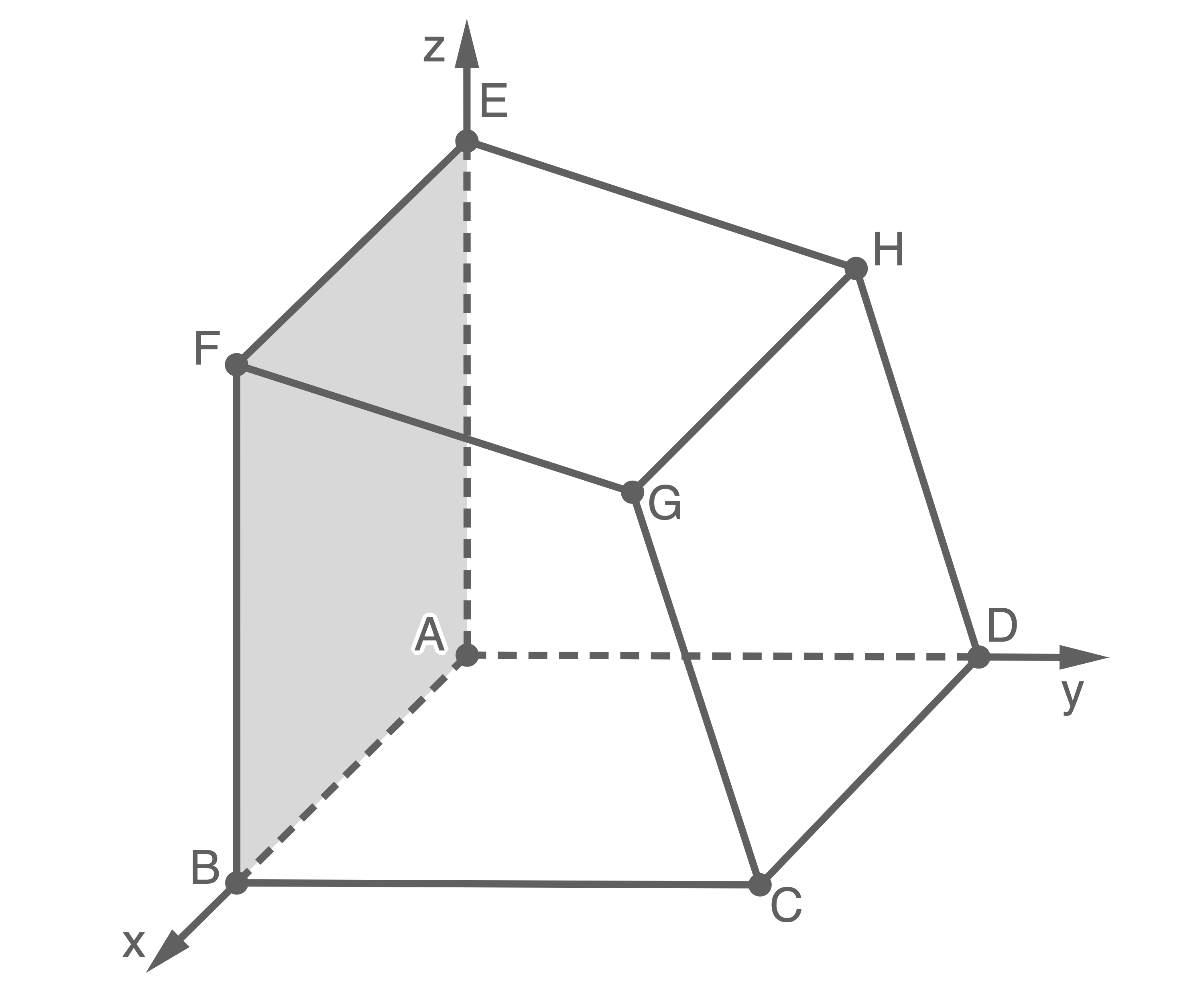
(nicht maßstäblich)
2.1
Begründe, dass das Viereck 
ein Drachenviereck ist.
Ermittle das Verhältnis der Längen der beiden Diagonalen im Viereck 
Die Winkel 
und 
sind Innenwinkel des Drachenvierecks. Die Seiten 
und 
schließen den Winkel , die Seiten 
und den Winkel ein.
Begründe, ohne die Größen von und zu berechnen, dass gilt: 
.
ein Drachenviereck ist.
Ermittle das Verhältnis der Längen der beiden Diagonalen im Viereck
Die Winkel und sind Innenwinkel des Drachenvierecks. Die Seiten und schließen den Winkel , die Seiten und den Winkel ein.
Begründe, ohne die Größen von und zu berechnen, dass gilt: .
(8 BE)
2.2
Die Ebene 
in der die Punkte 
und 
liegen, kann durch eine Gleichung der Form 
dargestellt werden.
Bestimme passende Werte für 
und 
Begründe, dass die Ebene 
eine Symmetrieebene des Körpers 
ist.
in der die Punkte und liegen, kann durch eine Gleichung der Form dargestellt werden.
Bestimme passende Werte für und
Begründe, dass die Ebene eine Symmetrieebene des Körpers ist.
(6 BE)
2.3
Die Seiten des Anbaus, die aus Glas bestehen und senkrecht zum Untergrund verlaufen, sollen gereinigt werden. Die Kosten betragen 
pro Quadratmeter zu reinigender Fläche.
Berechne die Kosten für die beidseitige Reinigung dieser Seiten.
Auf dem Glasdach kann ein Rollo herabgelassen werden. Dabei bewegt sich die Unterkante des Rollos innerhalb einer Minute gleichförmig von der oberen Kante des Daches, die durch pro Quadratmeter zu reinigender Fläche.
Berechne die Kosten für die beidseitige Reinigung dieser Seiten.
(4 BE)
dargestellt wird, bis zur unteren Kante des Daches.
2.4
Während des Herablassens liegt die Unterkante des Rollos im Modell zu jedem Zeitpunkt auf einer Gerade.
Ermittle eine Gleichung dieser Gerade 20 Sekunden nach Beginn der Bewegung.
Zu einem bestimmten Zeitpunkt kann das auf den Anbau treffende Sonnenlicht durch parallele Geraden mit dem Richtungsvektor
(4 BE)
beschrieben werden.
2.5
Berechne die Größe des Winkels, unter dem das Sonnenlicht auf den Untergrund trifft.
(3 BE)
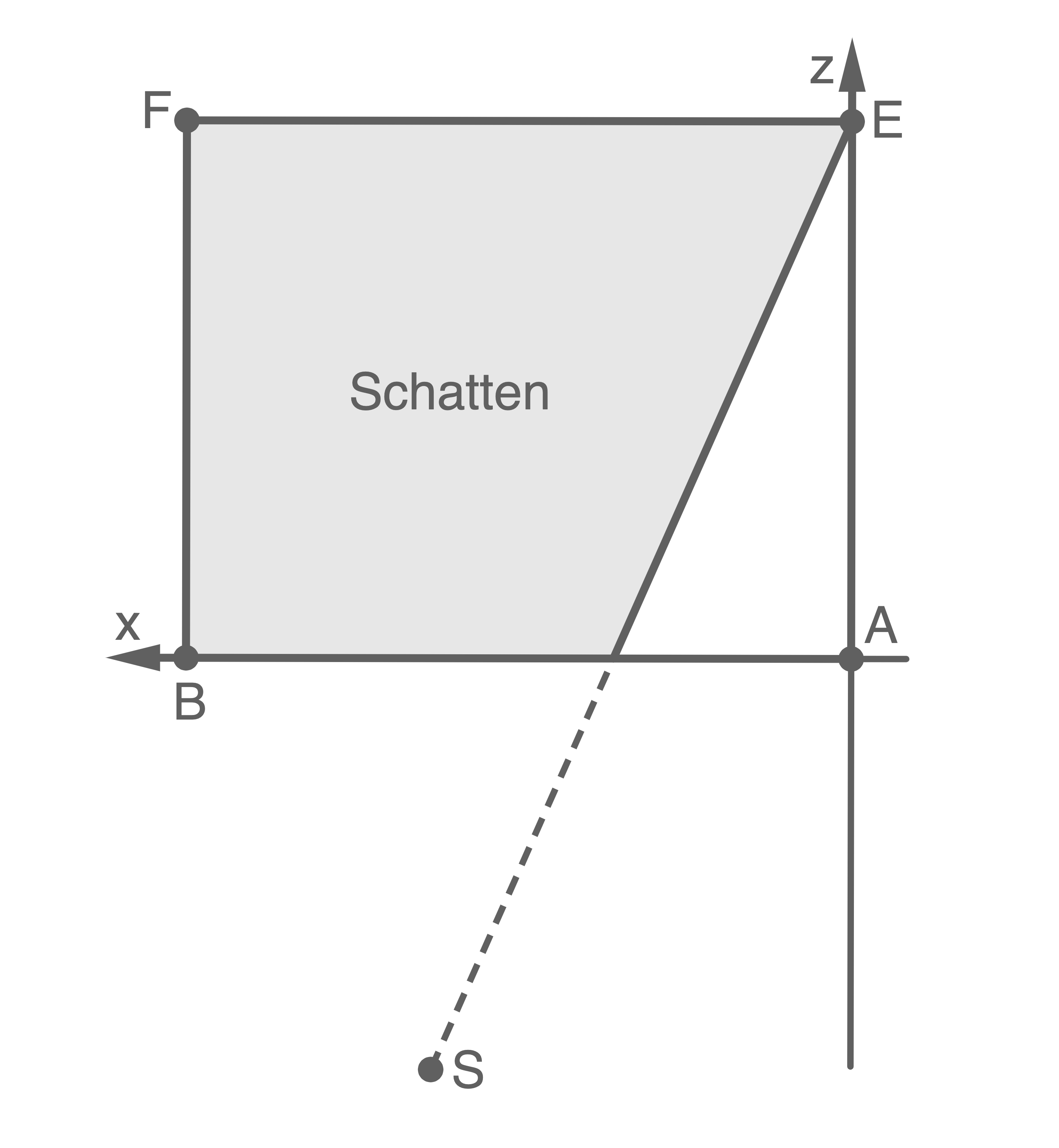
2.6
Die geschlossene Wand sowie der Schatten, den das vollständig herabgelassene Rollo auf dieser Wand erzeugt, sollen - in Form einer gesonderten zweidimensionalen Zeichnung - in der 
-Ebene graphisch dargestellt werden.
Die folgende Rechnung stellt einen wesentlichen Schritt zur Lösung dieser Aufgabe dar:
liefert 
und damit 
Beschreibe die Bedeutung dieses Lösungsschritts und fertige die angestrebte Zeichnung an.
-Ebene graphisch dargestellt werden.
Die folgende Rechnung stellt einen wesentlichen Schritt zur Lösung dieser Aufgabe dar:
liefert und damit
Beschreibe die Bedeutung dieses Lösungsschritts und fertige die angestrebte Zeichnung an.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
Drachenviereck nachweisen
Da 
und 
gilt, ist das Viereck somit ein Drachenviereck.
Verhältnis ermitteln
![\(\begin{array}[t]{rll}
\mid\overline{BG}\mid&=& \left| \pmatrix{0\\3\\3} \right|& \\[5pt]
&=& \sqrt{18}& \\[5pt]
&=& 3\cdot \sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/a8cb58d9bf5fc0087638357810918777883ac1e1e6527fa1a78ecd8873b2789f_light.svg)
![\(\begin{array}[t]{rll}
\mid\overline{CF}\mid&=& \left| \pmatrix{0\\-4\\4} \right|&\\[5pt]
&=& \sqrt{32}&\\[5pt]
&=& 4 \cdot \sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/81ce80bad6b5f62165bc431e9b100352d759e884586f93f3f61264fa9701ad89_light.svg)
Das Verhältnis der Längen der beiden Diagonalen folgt also mit 
Formel begründen
und gilt, ist das Viereck somit ein Drachenviereck.
Verhältnis ermitteln
Formel begründen
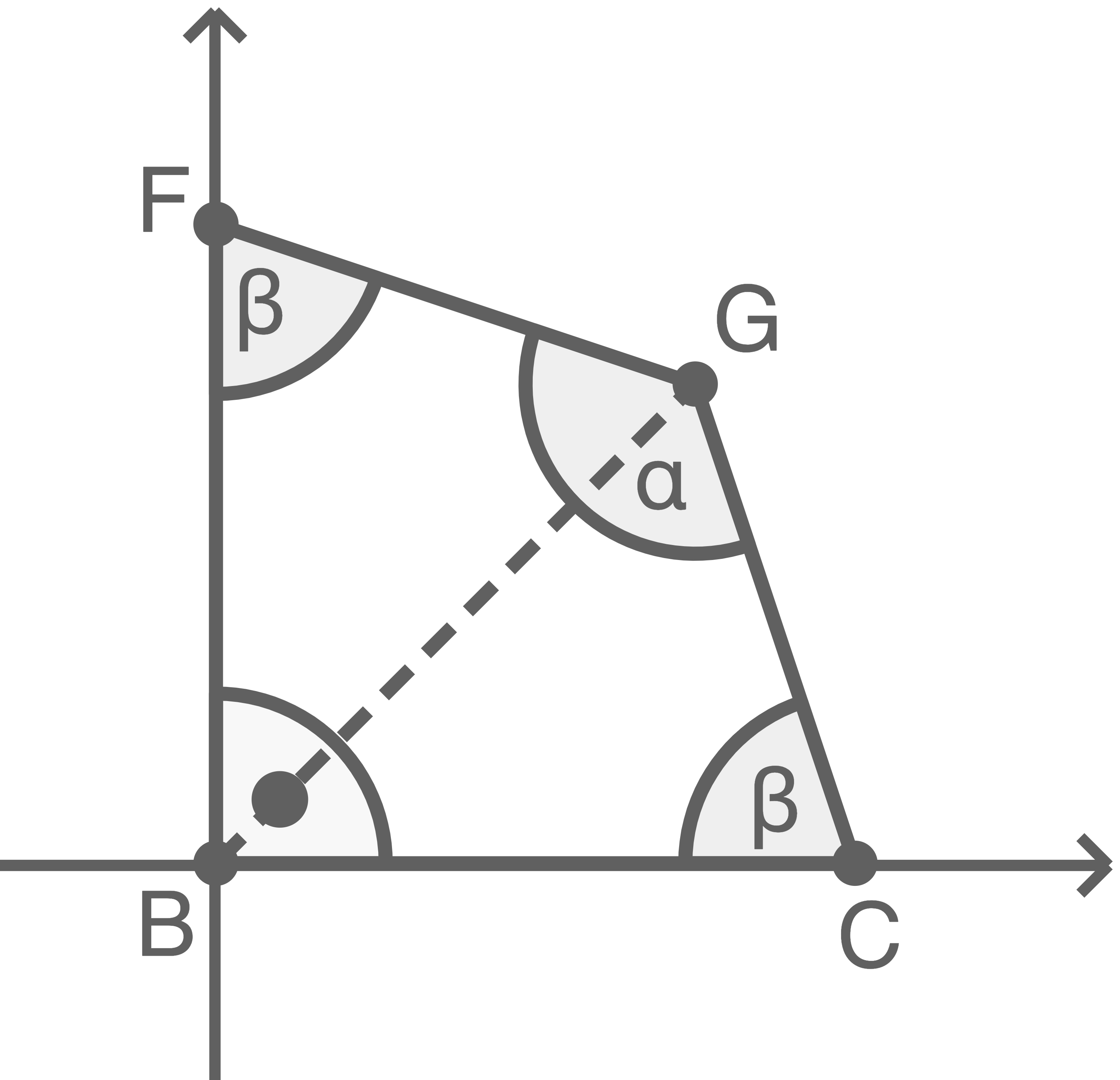
Da 
auf der Symmetrieachse des Drachenvierecks liegt und die Seiten 
und 
èinen rechten Winkel einschließen, folgt:
auf der Symmetrieachse des Drachenvierecks liegt und die Seiten und èinen rechten Winkel einschließen, folgt:
![\(\begin{array}[t]{rll}
2 \cdot \beta+90^{\circ}+\alpha&=& 360^{\circ}&\quad \scriptsize \mid\; -90^{\circ} \\[5pt]
2 \cdot \beta+\alpha&=& 270^{\circ}&\quad \scriptsize \mid\; -\alpha \quad \scriptsize \mid\; :2\\[5pt]
\beta&=& \dfrac{270^{\circ}- \alpha}{2}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fd652d46bd761b5866ab9f74ebd4e5122250ffc6eb5d87a1b6205b9a02a7d303_light.svg)
2.2
Werte bestimmen
Einsetzen der Koordinaten von 
ergibt:
![\(\begin{array}[t]{rll}
r\cdot 0+s\cdot 0&=& t& \\[5pt]
0&=& t
\end{array}\)](https://www.schullv.de/resources/formulas/29a71f2020acd1f9408c56c44afac9f22fcdea53327ca3fbed3ef4a168204848_light.svg)
Durch Einsetzen der Koordinaten von folgt nun:
![\(\begin{array}[t]{rll}
r\cdot 3+s\cdot 3&=& 0 &\quad \scriptsize \mid\; -3s \\[5pt]
3r&=& -3s &\quad \scriptsize \mid\; :3 \\[5pt]
r&=& -s
\end{array}\)](https://www.schullv.de/resources/formulas/3a3cf2340d53f3f86f438c39ed32a53ef1281fda56cc4441bc5fc25b94f3d251_light.svg)
Somit ergeben sich 
sowie beispielsweise 
und 
Begründung
Das Prisma mit dem Drachenviereck 
als Grundfläche ist gerade. enthält die Symmetrieachse der Grundfläche und steht senkrecht zu dieser.
ergibt:
Durch Einsetzen der Koordinaten von folgt nun:
Somit ergeben sich sowie beispielsweise und
Begründung
Das Prisma mit dem Drachenviereck als Grundfläche ist gerade. enthält die Symmetrieachse der Grundfläche und steht senkrecht zu dieser.
2.3
Die Glaslächen und 
stehen senkrecht zum Untergrund und sind identisch.
Der Flächeninhalt beträgt jeweils:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot\mid\overline{BG}\mid\cdot \mid\overline{CF}\mid & \\[5pt]
&=& \dfrac{1}{2}\cdot 3\cdot \sqrt{2}\cdot 4\cdot \sqrt{2}& \\[5pt]
&=& 12 \; \left[\,\text{m}^2\right]
\end{array}\)](https://www.schullv.de/resources/formulas/c63edf1f8b106774a55561d4f27065a12c8ada1174b3c15fb75fe16c8d03f8c7_light.svg)
Da die Glaswände jeweils beidseitig gereinigt werden sollen, ergeben sich die Kosten mit:
und stehen senkrecht zum Untergrund und sind identisch.
Der Flächeninhalt beträgt jeweils:
Da die Glaswände jeweils beidseitig gereinigt werden sollen, ergeben sich die Kosten mit:
2.4
Da die Gerade der Unterkante stets parallel zur 
-Achse verläuft, ergibt sich ein Richtungsvektor mit 
Für die Strecke 
bzw 
benötigt das Rollo eine Minute.
Ein Stützvektor der Gerade nach 20 Sekunden folgt also mit:
![\(\begin{array}[t]{rll}
\overrightarrow{s}&=& \overrightarrow{OE}+\dfrac{1}{3}\cdot \overrightarrow{EH} & \\[5pt]
&=& \pmatrix{0\\0\\4}+\dfrac{1}{3}\cdot \pmatrix{0\\3\\-1} & \\[5pt]
&=& \pmatrix{0\\1\\\dfrac{11}{3}}
\end{array}\)](https://www.schullv.de/resources/formulas/9eec15bf444cd3a1122a217fe8429168ed595f9fd66b030ca7364b79c377699c_light.svg)
Eine Gleichung der Gerade 20 Sekunden nach Beginn der Bewegung ist somit gegeben duch 
-Achse verläuft, ergibt sich ein Richtungsvektor mit
Für die Strecke bzw benötigt das Rollo eine Minute.
Ein Stützvektor der Gerade nach 20 Sekunden folgt also mit:
Eine Gleichung der Gerade 20 Sekunden nach Beginn der Bewegung ist somit gegeben duch
2.5
Ein Normalenvektor des Untergrunds ist beispielsweise 
Somit ergibt sich:
Somit ergibt sich:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\left| \pmatrix{1\\-1\\-2} \circ \pmatrix{0\\0\\1}\right|}{\left| \pmatrix{1\\-1\\-2} \right|\cdot \left| \pmatrix{0\\0\\1} \right|}& \\[5pt]
\sin(\alpha)&=& \dfrac{\left| 1\cdot 0+(-1)\cdot 0+(-2)\cdot 1\right|}{\sqrt{1^2+(-1)^2+(-2)^2}\cdot \sqrt{1^2}}& \\[5pt]
\sin(\alpha)&=& \dfrac{2}{\sqrt{6}}&\quad \scriptsize \mid\; \sin^{-1} \\[5pt]
\alpha &\approx& 55^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/8f2296eeae41f740b163ee8177d29041b2b74eed1195ce064c86ae0f409255de_light.svg)
2.6
ist der Schnittpunkt 
der Gerade durch 
mit dem gegebenen Richtungsvektor und der -Ebene.
