Aufgabe B2
Die Punkte 
und 
sind Eckpunkte des Prismas 
dessen sechs Seitenflächen jeweils Parallelogramme sind (vgl. Abbildung).
und sind Eckpunkte des Prismas dessen sechs Seitenflächen jeweils Parallelogramme sind (vgl. Abbildung).
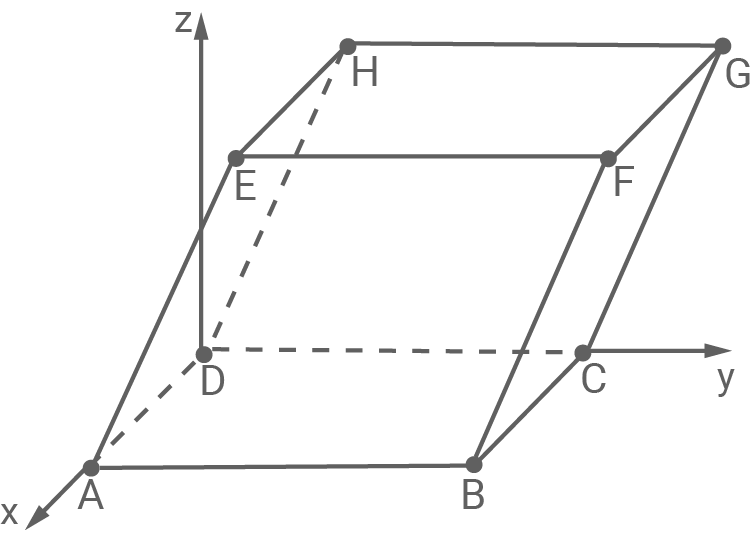
Abbildung
2.1
Gib die Koordinaten von an.
Begründe, dass die Seitenfläche 
ein Rechteck ist.
Begründe, dass die Seitenfläche 
nicht in der 
-
-Ebene liegt.
(5 BE)
2.2
Ermittle den Inhalt der Seitenfläche 
(2 BE)
und der Mittelpunkt der Kante 
liegen in der Ebene 
2.3
Die Gerade 
verläuft durch die Punkte 
und 
Begründe, dass der Schnittpunkt von 
und Mittelpunkt der Kante 
ist.
Berechne die Größe des Schnittwinkels von und 
(4 BE)
2.4
Die Ebene teilt das Prisma in zwei Teilkörper.
Berechne das Volumen des kleineren der beiden Teilkörper.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
Koordinaten angeben
Rechteck begründen
Die beiden Seiten 
und 
von liegen auf den Koordinatenachsen und stehen somit senkrecht aufeinander. Damit ist ein Rechteck.
Lage begründen
Die Punkte 
und besitzen 
-Koordinaten, die von Null verschieden sind. Somit kann die Seitenfläche nicht in der --Ebene liegen.
Rechteck begründen
Die beiden Seiten und von liegen auf den Koordinatenachsen und stehen somit senkrecht aufeinander. Damit ist ein Rechteck.
Lage begründen
Die Punkte und besitzen -Koordinaten, die von Null verschieden sind. Somit kann die Seitenfläche nicht in der --Ebene liegen.
2.2
![\(\begin{array}[t]{rlll}
A&=&\left\vert \overrightarrow{BC} \times \overrightarrow{BF}\right\vert \\[5pt]
&=&\left\vert \pmatrix{-6\\0\\0}\times
\pmatrix{-2\\2\\5}\right\vert \\[5pt]
&=&6\cdot \sqrt{29} \\[5pt]
&=&32,31\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/81a27e6666d274348c4af0b2b0554583aca5580cc0cdea1eb98552d4e08c60cd_light.svg)
2.3
Schnittpunkt begründen
Der Mittelpunkt der Kante hat die Koordinaten 
Einsetzen in die Ebenengleichung liefert:
![\(\begin{array}[t]{rlll}
5\cdot8+12\cdot2,5&=&70 \\[5pt]
70&=&70
\end{array}\)](https://www.schullv.de/resources/formulas/dc8da6a6a853f6741e2dd671ce892d9a69f4c8d78fd70cdc01590678dad789e3_light.svg)
Somit ist der Mittelpunkt der Kante der Schnittpunkt von und 
Schnittwinkel berechnen
Für den Richtungsvektor der Geraden gilt:
Mit dem Normalenvektor der Ebene folgt für den Schnittwinkel:
![\(\begin{array}[t]{rlll}
\sin(\alpha)&=&\dfrac{\left| \pmatrix{-2\\2\\5} \circ \pmatrix{0\\5\\12}\right|}{\sqrt{33}\cdot 13}
\end{array}\)](https://www.schullv.de/resources/formulas/361bc202c495a4610d561fc44c8868a9ba331a8dad5784404fa8e0a92343be55_light.svg)
Der solve-Befehl des MMS liefert dann 
hat die Koordinaten Einsetzen in die Ebenengleichung liefert:
Somit ist der Mittelpunkt der Kante der Schnittpunkt von und
Schnittwinkel berechnen
Für den Richtungsvektor der Geraden gilt:
Mit dem Normalenvektor der Ebene folgt für den Schnittwinkel:
Der solve-Befehl des MMS liefert dann
2.4
Die obere Hälfte des Prismas wird durch die Ebene halbiert, das heißt insgesamt teilt die Ebene das Prisma im Verhältnis 
Für das gesuchte Volumen folgt somit:
![\(V=\dfrac{1}{4}\cdot 6\cdot 7\cdot 5=52,5\;[\text{VE}]\)](https://www.schullv.de/resources/formulas/74187f9a0ebd0ad88f7f6729943ea0674de666018b567baa7816d5f2a3ca80aa_light.svg)
halbiert, das heißt insgesamt teilt die Ebene das Prisma im Verhältnis Für das gesuchte Volumen folgt somit: