Wahlbereich 2
7
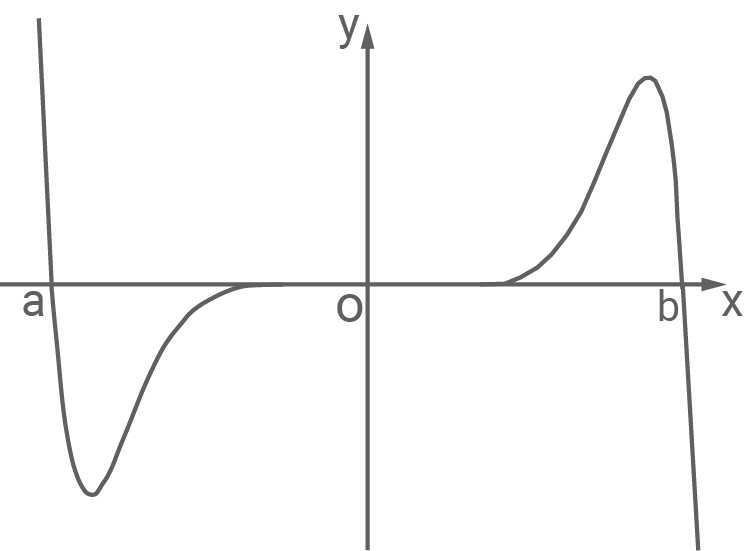
Die Abbildung zeigt den Graphen einer in 
definierten stetigen Funktion 
Die Funktion
hat drei Nullstellen und ihr Graph ist symmetrisch bezüglich des Koordinatensprungs.
definierten stetigen Funktion
Die Funktion
hat drei Nullstellen und ihr Graph ist symmetrisch bezüglich des Koordinatensprungs.
7.1
Gib den Wert des Integrals 
an.
Begründe deine Angabe.
an.
Begründe deine Angabe.
(2 BE)
7.2
Beurteile die folgende Aussage:
(3 BE)
8
Betrachtet wird das Dreieck 
mit 
und 
welches in 
rechtwinklig ist. Durch Rotation des Dreiecks um die Seite 
entsteht ein Körper, in dessen Grundfläche die Punkte und 
liegen.
mit und welches in rechtwinklig ist. Durch Rotation des Dreiecks um die Seite entsteht ein Körper, in dessen Grundfläche die Punkte und liegen.
8.1
Begründe, dass die Grundfläche des Körpers in der Ebene 
liegt.
liegt.
(2 BE)
8.2
Berechne das Volumen des Körpers.
(3 BE)
9
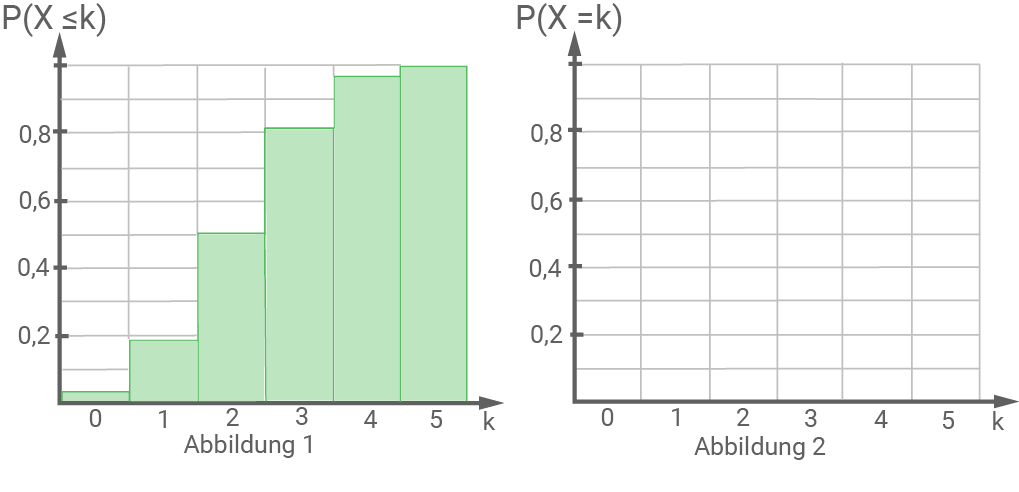
Abbildung 1 zeigt die kumulierte Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße 
9.1
Gib die Länge der zugrunde liegenden Bernoullikette an.
Gib
an.
Gib
an.
(2 BE)
9.2
Skizziere die zugehörige Wahrscheinlichkeitsverteilung 
in Abbildung 2.
in Abbildung 2.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
7
7.1
Wegen der Punktsymmetrie des Graphen zum Ursprung gleichen sich die Anteile der beiden eingeschlossenen Flächen gegenseitig aus, sodass das Integral insgesamt den Wert Null besitzt.
7.2
Es gilt 
da der Graph von in diesem Intervall oberhalb der 
-Achse verläuft.
Da 
gilt, weil der Graph von dort unterhalb der -Achse verläuft, und 
mit dem gleichen Argument wie in Teilaufgabe 7.1, folgt insgesamt, dass 
gilt.
Die Aussage ist damit falsch.
da der Graph von in diesem Intervall oberhalb der -Achse verläuft.
Da gilt, weil der Graph von dort unterhalb der -Achse verläuft, und mit dem gleichen Argument wie in Teilaufgabe 7.1, folgt insgesamt, dass gilt.
Die Aussage ist damit falsch.
8
8.1
Einsetzen der Koordinaten von und in die Ebenengleichung liefert:
Somit liegen die Punkte und in der Ebene. Da der Vektor 
zudem ein Normalenvektor der Ebene ist, liegt die Grundfläche des Körpers in der betrachteten Ebene.
und in die Ebenengleichung liefert:
Somit liegen die Punkte und in der Ebene. Da der Vektor zudem ein Normalenvektor der Ebene ist, liegt die Grundfläche des Körpers in der betrachteten Ebene.
8.2
Die Grundfläche ist ein Kreis mit folgendem Radius:
Insgesamt ist der Körper ein Kegel. Für die Höhe gilt:
Für das Volumen des Körpers folgt somit:
Insgesamt ist der Körper ein Kegel. Für die Höhe gilt:
Für das Volumen des Körpers folgt somit:
9
9.1
Länge der Bernoullikette angeben
Die Länge der Bernoullikette beträgt 
Wahrscheinlichkeit angeben
Wahrscheinlichkeit angeben
9.2
