Aufgabe B3

Ein Unternehmen bietet Wundertüten an, deren Inhalt von außen nicht zu erkennen ist. Eine Wundertüte enthält entweder eine Figur oder ein anderes Spielzeug.
Die Wahrscheinlichkeit, dass eine Wundertüte eine Figur enthält, beträgt $\frac{1}{10}.$
Es wird angenommen, dass in einer zufälligen Auswahl von Wundertüten die Anzahl der Wundertüten, die eine Figur enthalten, binomialverteilt ist.

3.1

Es werden $10$ Wundertüten zufällig ausgewählt.
Berechne jeweils die Wahrscheinlichkeit der folgenden Ereignisse.

$A:$

„Höchstens drei Wundertüten enthalten eine Figur.“

$B:$

„Es enthalten mehr Wundertüten eine Figur, als zu erwarten ist.“

Beschreibe das Gegenereignis zum Ereignis $A.$

(5 BE)

3.2

Gib die Bedeutung der Gleichung $\pmatrix{9\\1}\cdot \left(\frac{1}{10}\right)^2\cdot \left(\frac{9}{10}\right)^8=\pmatrix{9\\0} \cdot \left(\frac{1}{10}\right)^0\cdot \left(\frac{9}{10}\right)^9$ im Sachzusammenhang an.

(2 BE)

3.3

Es werden $n$ Wundertüten mit $n\geq 3$ nacheinander zufällig ausgewählt und geöffnet.

Gib einen Term zur Berechnung der Wahrscheinlichkeit des Ereignisses „Nur die letzten beiden Wundertüten enthalten eine Figur.“ an.

(2 BE)

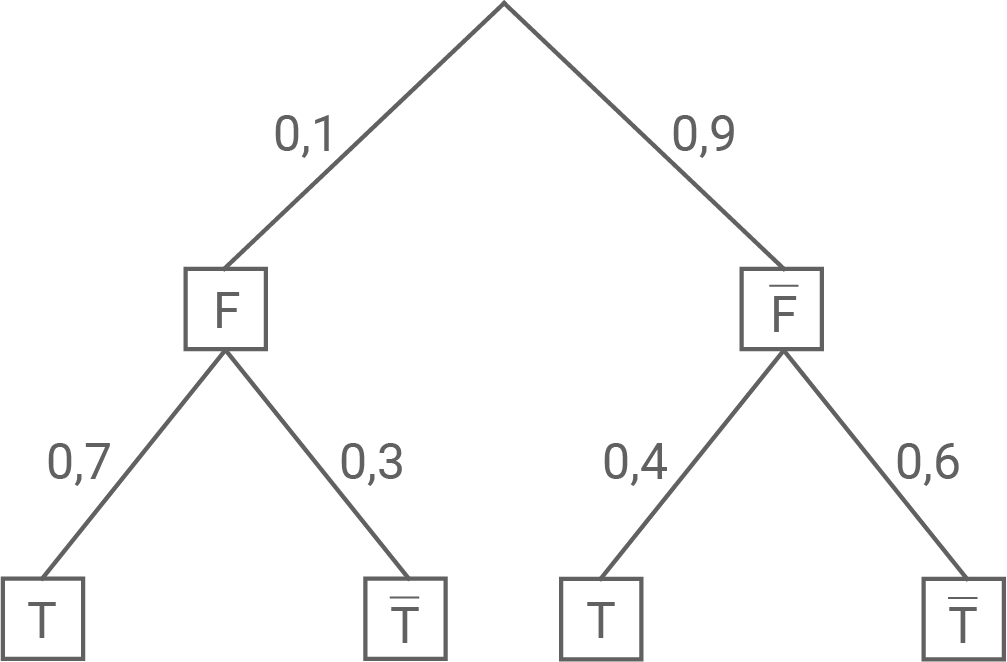
Zur vorzeitigen Erkennung einer Figur erfolgt das Abtasten einer Wundertüte.
Enthält die Wundertüte eine Figur erfolgt das Abtasten mit einer Wahrscheinlichkeit von $70\,\text{%},$ dass die Wundertüte eine Figur enthält.
Enthält die Wundertüte ein anderes Spielzeug, so ergibt das Abtasten mit einer Wahrscheinlichkeit von $40\,\text{%},$ dass die Wundertüte eine Figur enthält.

3.4

Stelle diesen Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

3.5

Gib die Wahrscheinlichkeit dafür an, dass die Wundertüte eine Figur enthält und das Abtasten dies ergibt.

Bestimme die Wahrscheinlichkeit dafür, dass das Ergebnis des Abtastens nicht dem Inhalt der Wundertüte entspricht.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?