Teil B1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit
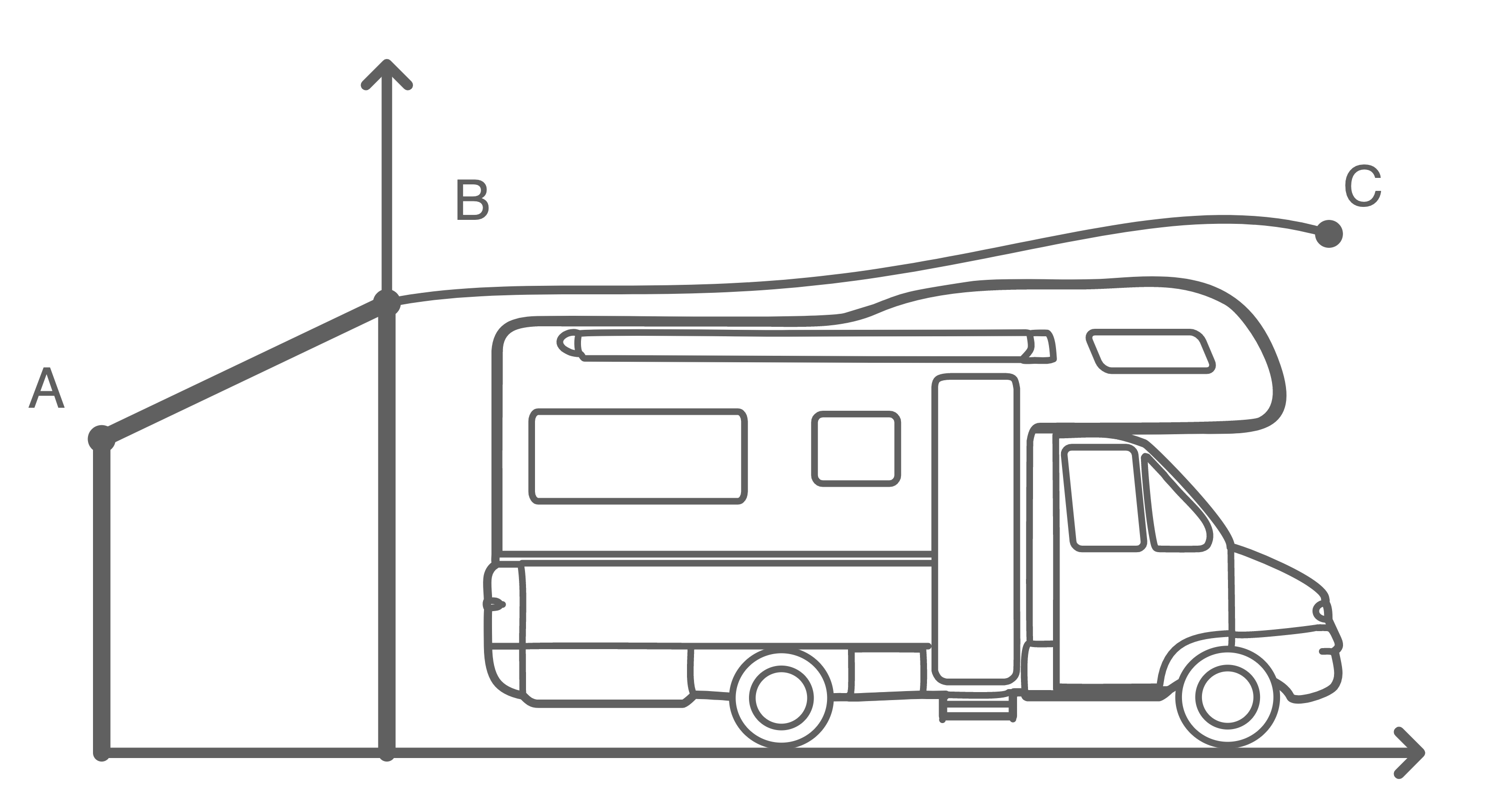 Die Profillinie des Längsschnitts des Daches kann zwischen den Punkten
Die Profillinie des Längsschnitts des Daches kann zwischen den Punkten  und
und  modellhaft mithilfe der Gerade
modellhaft mithilfe der Gerade  mit der Gleichung
mit der Gleichung  beschrieben werden, zwischen den Punkten
beschrieben werden, zwischen den Punkten  und
und  mithilfe der Funktion
mithilfe der Funktion  .
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
Die
.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
Die  -Achse stellt den horizontalen Untergrund dar.
-Achse stellt den horizontalen Untergrund dar.
 und
und  dargestellt.
dargestellt.
1.1
Zeigen Sie, dass der Graph von  durch den Punkt
durch den Punkt  verläuft.
Geben Sie eine Gleichung der Tangente an den Graphen von
verläuft.
Geben Sie eine Gleichung der Tangente an den Graphen von  im Punkt
im Punkt  an.
Geben Sie die besondere Lage dieser Tangente im Koordinatensystem an.
an.
Geben Sie die besondere Lage dieser Tangente im Koordinatensystem an.
(03 BE)
1.2
Der Graph der in  definierten Funktion
definierten Funktion  mit
mit  schneidet den Graphen von
schneidet den Graphen von  an den Stellen
an den Stellen  und
und  mit
mit  .
Geben Sie
.
Geben Sie  und
und  an.
Deuten Sie den Term
an.
Deuten Sie den Term  geometrisch und ermitteln Sie seinen Wert.
geometrisch und ermitteln Sie seinen Wert.
(06 BE)
1.3
Untersuchen Sie, ob die Anstiege an den Nullstellen von  den gleichen Betrag besitzen.
den gleichen Betrag besitzen.
 von
von  .
.
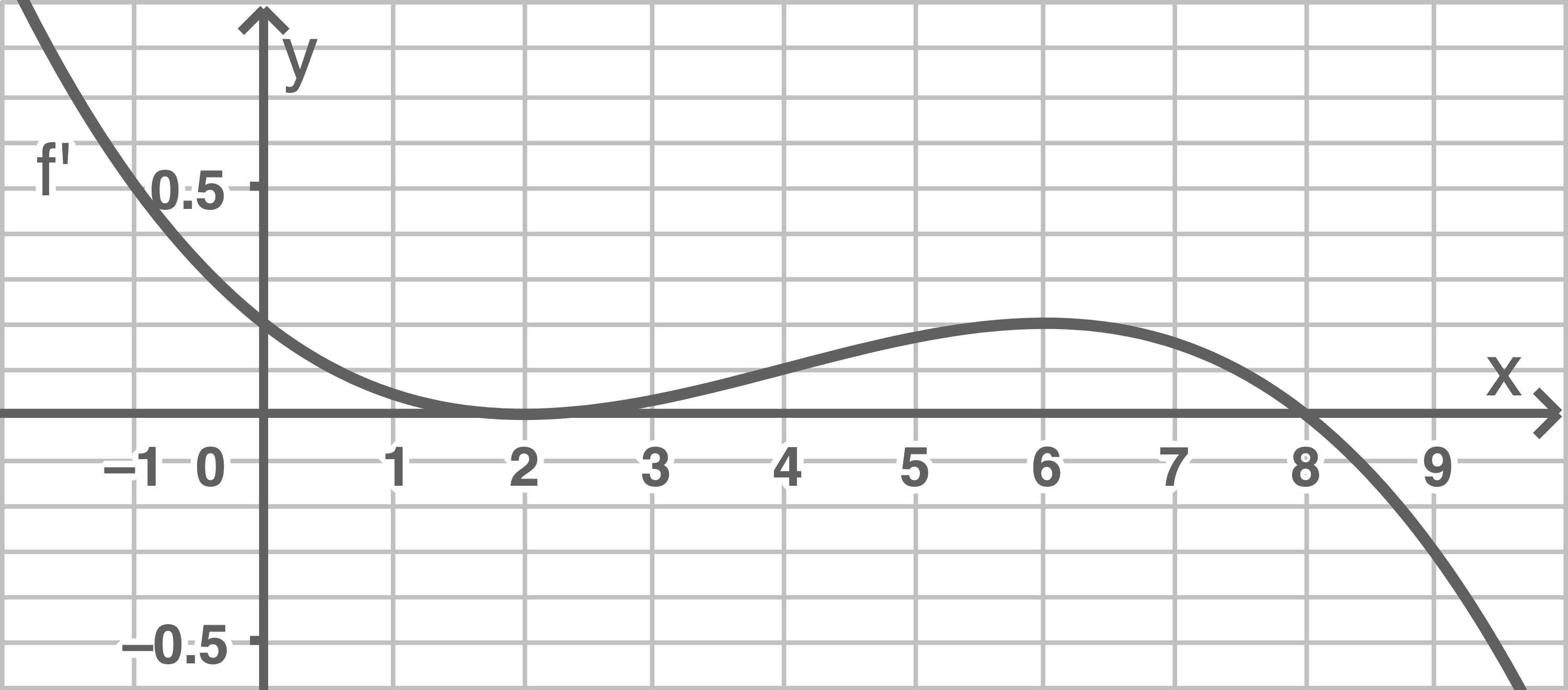
(06 BE)
Die Abbildung zeigt den Graphen der ersten Ableitungsfunktion 
1.4
Beurteilen Sie jede der zwei folgenden Aussagen mithilfe des dargestellten Graphen der ersten Ableitungsfunktion  von
von  :
I Die Funktion
:
I Die Funktion  ist im Intervall
ist im Intervall  monoton steigend.
II Der Graph von
monoton steigend.
II Der Graph von  besitzt zwei Extrempunkte.
besitzt zwei Extrempunkte.
(06 BE)
1.5
Der Graph der in  definierten Funktion
definierten Funktion  mit
mit  ist symmetrisch zum Koordinatenursprung.
Auch der Graph der Funktion
ist symmetrisch zum Koordinatenursprung.
Auch der Graph der Funktion  ist symmetrisch zu einem Punkt.
Geben Sie die Koordinaten dieses Punkts an.
Begründen Sie Ihre Angabe ausgehend vom Graphen von
ist symmetrisch zu einem Punkt.
Geben Sie die Koordinaten dieses Punkts an.
Begründen Sie Ihre Angabe ausgehend vom Graphen von  .
.
Die Abbildung zeigt einen Längsschnitt eines Carports für ein Wohnmobil; dabei ist der hintere Bereich des Carports fett dargestellt. Das Dach des Carports ist in Querrichtung nicht geneigt. Im Folgenden sollen die Materialstärken der Bauteile des Carports vernachlässigt werden.
(04 BE)

Abbildung (nicht maßstäblich)
1.6
Zeigen Sie, dass der Carport 11,50 m lang ist.
Bestimmen Sie die Höhe des Carports an seiner höchsten Stelle.
Untersuchen Sie, ob ein Wohnmobil mit einer Länge von 7,05 m und einer Höhe von  vollständig im Carport untergestellt werden kann.
vollständig im Carport untergestellt werden kann.
(06 BE)
1.7
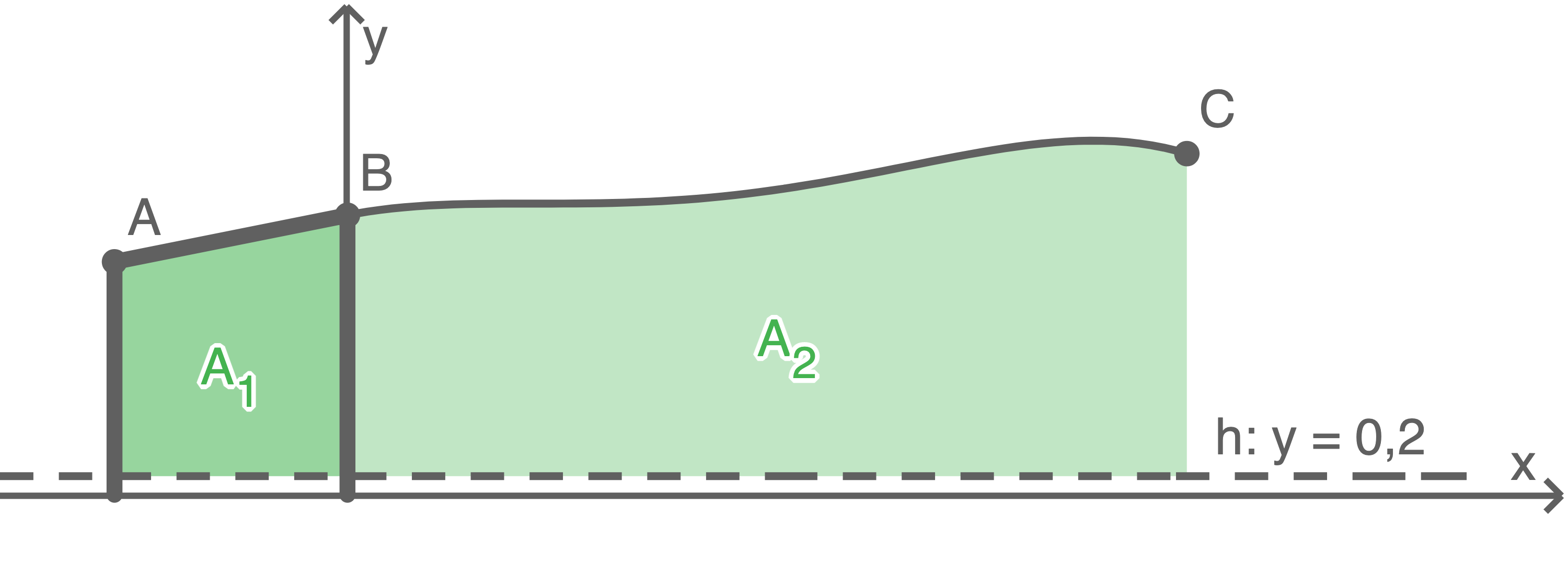
Abgesehen von einem  hohen Streifen unmittelbar über dem Untergrund ist der Carport auf einer Seite über seine gesamte Länge vollständig verkleidet. Die Verkleidung ist eben und vertikal angebracht.
Berechnen Sie den Inhalt der verkleideten Fläche.
hohen Streifen unmittelbar über dem Untergrund ist der Carport auf einer Seite über seine gesamte Länge vollständig verkleidet. Die Verkleidung ist eben und vertikal angebracht.
Berechnen Sie den Inhalt der verkleideten Fläche.
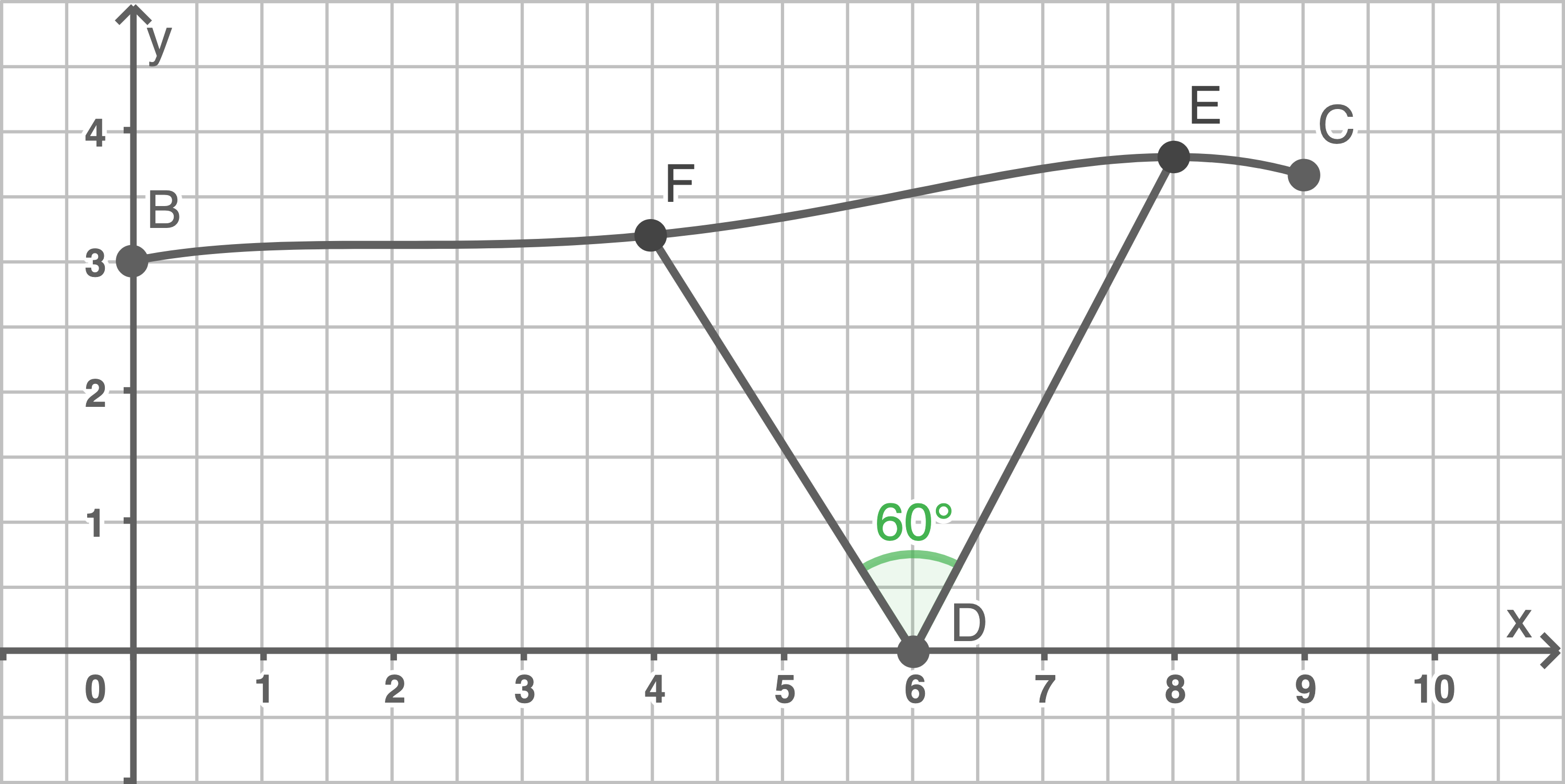
Ausgehend vom selben Punkt des Untergrundes verlaufen entlang der seitlichen Verkleidung des Carports zwei geradlinige Stützen jeweils bis zum Dach. Die Stützen schließen einen Winkel mit einer Größe von 60° ein. Die Endpunkte der ersten Stütze werden im Modell durch
(05 BE)
1.8
Stellen Sie die Profillinie des Daches zwischen den Punkten  und
und  sowie die beiden Stützen in einem geeigneten Koordinatensystem dar.
sowie die beiden Stützen in einem geeigneten Koordinatensystem dar.
(04 BE)
1.9
Bestimmen Sie die  -Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt.
-Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt.
(05 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Punktprobe mit  Folglich verläuft der Graph von
Folglich verläuft der Graph von  durch den Punkt
durch den Punkt  Tangentengleichung aufstellen
Allgemeine Tangentengleichung:
Tangentengleichung aufstellen
Allgemeine Tangentengleichung:


![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/a4e2d72d04014f6495880e4c753747ee89d61aaaa7e0c59a2b8c913589883fa2_light.svg) Es ergibt sich somit folgende Tangentengleichung im Punkt
Es ergibt sich somit folgende Tangentengleichung im Punkt 
![\(\begin{array}[t]{rll}
t: y&=& 0\cdot (x-2)+3,125 & \\[5pt]
y&=& 3,125
\end{array}\)](https://www.schullv.de/resources/formulas/b5deacbfd906fe7aa5dfff5adca1792d20641e2f0aba2a176ffbe52b93dea1e4_light.svg) Lage der Tangente beschreiben
Die Tangente
Lage der Tangente beschreiben
Die Tangente  ist eine zur
ist eine zur  -Achse parallele Gerade.
-Achse parallele Gerade.
1.2
Schnittstellen berechnen
Mit dem solve-Befehl ergeben sich  und
und  Term geometrisch deuten
Der Graph von
Term geometrisch deuten
Der Graph von  und der Graph von
und der Graph von  schließen im Intervall
schließen im Intervall ![\([x_1;x_2]\)](https://www.schullv.de/resources/formulas/dd043926ebefd02ce9a3b32a158c0bff6b39085e91efbd0b9b151b059950b9a8_light.svg) eine Fläche ein. Der Wert des Terms gibt den Inhalt dieser Fläche an.
Wert des Terms bestimmen
eine Fläche ein. Der Wert des Terms gibt den Inhalt dieser Fläche an.
Wert des Terms bestimmen
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Mit dem CAS ergibt sich der Wert des Terms mit:
Casio Classpad II
Mit dem CAS ergibt sich der Wert des Terms mit:

menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.3
1. Schritt: Nullstellen bestimmen
 Mit dem solve-Befehl des CAS ergeben sich die Nullstellen an
Mit dem solve-Befehl des CAS ergeben sich die Nullstellen an  und
und  2. Schritt: Anstiege an den Nullstellen berechnen
Die Anstiege an den beiden Nullstellen
2. Schritt: Anstiege an den Nullstellen berechnen
Die Anstiege an den beiden Nullstellen  und
und  besitzen nicht die gleichen Beträge.
besitzen nicht die gleichen Beträge.
1.4
Aussage I : wahr
Die Ableitungsfunktion gibt die Steigung des Graphen an. Da  für
für  , ist die Funktion in diesem Intervall monoton steigend.
Aussage II : falsch
Der Graph von
, ist die Funktion in diesem Intervall monoton steigend.
Aussage II : falsch
Der Graph von  besitzt einen Extrempunkt, wenn der Graph von
besitzt einen Extrempunkt, wenn der Graph von  die
die  -Achse schneidet.
An der Stelle
-Achse schneidet.
An der Stelle  berührt der Graph von
berührt der Graph von  die
die  -Achse, deshalb liegt hier kein Extrempunkt vor.
An der Stelle
-Achse, deshalb liegt hier kein Extrempunkt vor.
An der Stelle  hingegen schneidet der Graph von
hingegen schneidet der Graph von  die
die  -Achse. Dies ist somit die einzige Extremstelle von
-Achse. Dies ist somit die einzige Extremstelle von 
1.5
Koordinaten des Symmetriepunkts
 Begründung
Der Graph von
Begründung
Der Graph von  kann aus dem Graphen von
kann aus dem Graphen von  erzeugt werden durch eine Verschiebung um 4 in negative
erzeugt werden durch eine Verschiebung um 4 in negative  -Richtung und um
-Richtung und um  in negative
in negative  -Richtung. Damit ist auch der Graph von
-Richtung. Damit ist auch der Graph von  punktsymmetrisch, und zwar bezüglich des Punktes
punktsymmetrisch, und zwar bezüglich des Punktes  .
.
1.6
Länge des Carports nachweisen
Die Länge des Carports entspricht dem Abstand der  -Koordinaten der Punkte
-Koordinaten der Punkte  und
und  Koordinaten von
Koordinaten von  einsetzen und nach
einsetzen und nach  auflösen:
auflösen:
![\(\begin{array}[t]{rll}
y&=&2,5 & \\[5pt]
\dfrac{1}{5}\cdot x_A +3&=&2,5 &\\[5pt]
x_A&=&-2,5
\end{array}\)](https://www.schullv.de/resources/formulas/ea36458db2350b003e8dc5605f1ad3031023c9130f1411c187f0d50d9ea7a7b2_light.svg) Strecke zwischen
Strecke zwischen  und
und 
 Maximale Höhe des Carports bestimmen
Mit dem CAS werden die Koordinaten des Hochpunkts bestimmt.
Maximale Höhe des Carports bestimmen
Mit dem CAS werden die Koordinaten des Hochpunkts bestimmt.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die Koordinaten des Hochpunkts folgen mit
Casio Classpad II
Die Koordinaten des Hochpunkts folgen mit  Die höchste Stelle des Carports beträgt
Die höchste Stelle des Carports beträgt  .
Wohnmobil untersuchen
Um feststellen zu können, ob das Wohnmobil vollständig unter den Carport passt, muss der Bereich berechnet werden, in welchem die Höhe des Carports über
.
Wohnmobil untersuchen
Um feststellen zu können, ob das Wohnmobil vollständig unter den Carport passt, muss der Bereich berechnet werden, in welchem die Höhe des Carports über  beträgt.
beträgt.
 Lösungen für die Gleichung ergeben sich mit dem solve-Befehl und sind
Lösungen für die Gleichung ergeben sich mit dem solve-Befehl und sind  und
und  Der Carport besitzt folglich für
Der Carport besitzt folglich für  eine Höhe
eine Höhe  Ein Wohnmobil mit der Länge
Ein Wohnmobil mit der Länge  und der Höhe
und der Höhe  kann also vollständig unter dem Carport abgestellt werden.
kann also vollständig unter dem Carport abgestellt werden.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
1.7
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.8
1.9
Winkel, unter dem  die
die  -Achse schneidet:
-Achse schneidet:
 Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
\tan (\alpha)&=& m&\quad \scriptsize \mid\; \arctan \\[5pt]
\alpha&=& \arctan \left(\dfrac{3,8}{2}\right)& \\[5pt]
\alpha&\approx & 62,23^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/d5177daba42c835d78e99c4c4a1f36596b71df844b3312cb1b340ef89e78102f_light.svg) Winkel, unter dem
Winkel, unter dem  die
die  -Achse schneidet:
-Achse schneidet:
 Steigung im Punkt
Steigung im Punkt  berechnen:
berechnen:
 Es gilt:
Mit dem solve-Befehl ergib sich:
Es gilt:
Mit dem solve-Befehl ergib sich:  als
als  -Koordinate des Endpunkts der zweiten Stütze.
-Koordinate des Endpunkts der zweiten Stütze.