Teil A
1.
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1.1
Für  ist die Funktion
ist die Funktion  mit
mit  gegeben.
gegeben.
Welche Gleichung beschreibt die Stammfunktion von
Welche Gleichung beschreibt die Stammfunktion von
1.2
Für die in  definierte Funkton
definierte Funkton  mit
mit  ist folgende Aussage wahr:
ist folgende Aussage wahr:
| Die Funktion |
|
| Es gilt: |
|
| Der Graph von |
|
| Der Graph von |
|
| Der Graph von |
1.3
Die Gerade 
 schneidet die
schneidet die  -
- -Ebene im Punkt:
-Ebene im Punkt:
1.4
Die Abbildung zeigt einen Ausschnitt der Ebene  in einem kartesischen Koordinatensystem mit dem Koordinatenursprung
in einem kartesischen Koordinatensystem mit dem Koordinatenursprung 
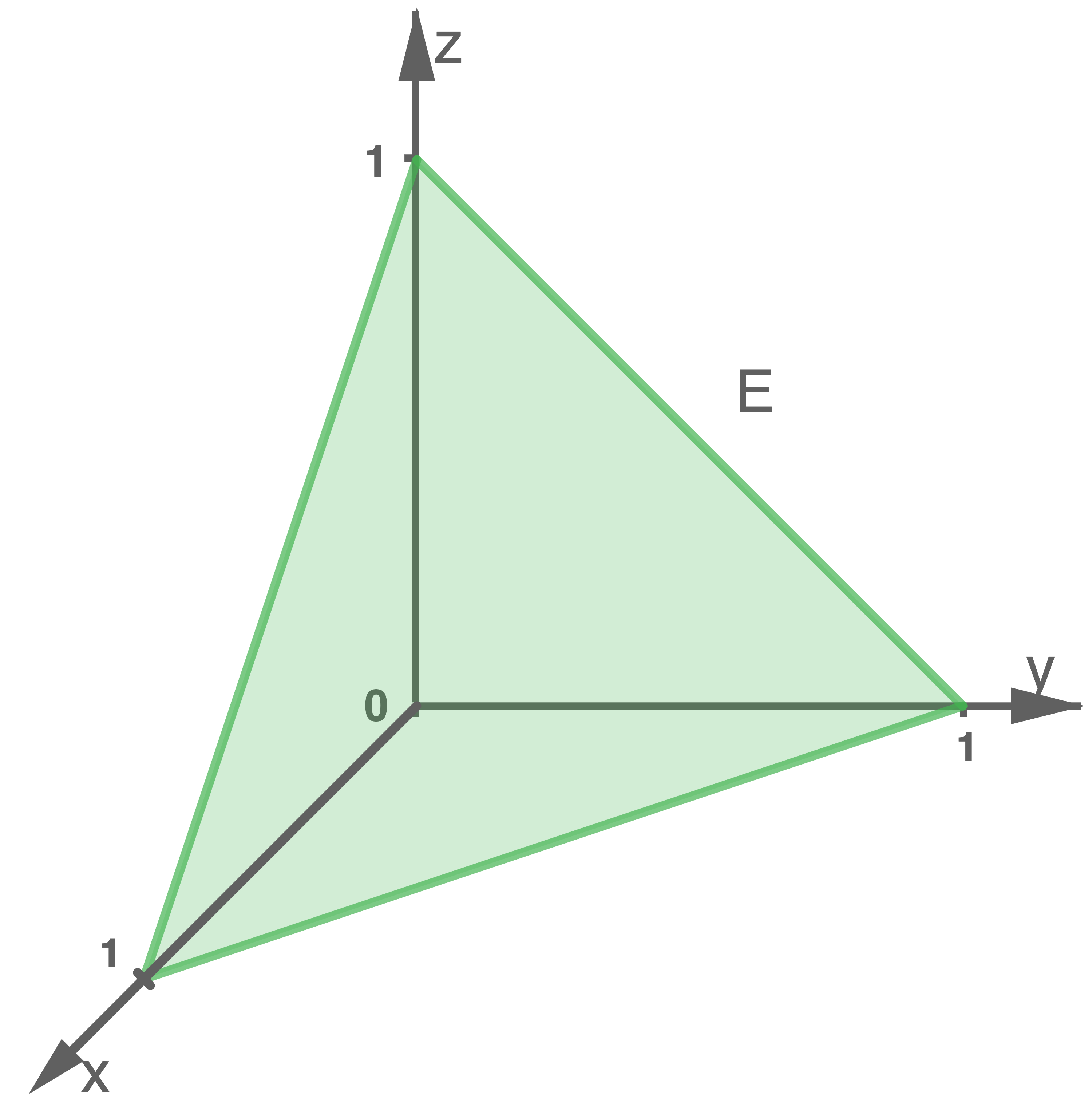 Die Ebene
Die Ebene  kann durch folgende Gleichung beschrieben werden:
kann durch folgende Gleichung beschrieben werden:

Abbildung (nicht maßstäblich)
1.5
Beim Wurf einer verbeulten Münze fällt Wappen mit der Wahrscheinlichkeit 
Die Wahrscheinlichkeit dafür, dass beim 10-maligen Werfen dieser Münze genau zweimal Wappen fällt, lässt sich mit folgendem Term berechnen:
Die Wahrscheinlichkeit dafür, dass beim 10-maligen Werfen dieser Münze genau zweimal Wappen fällt, lässt sich mit folgendem Term berechnen:
Für Aufgabe 1 erreichbare BE-Anzahl: 05
2.
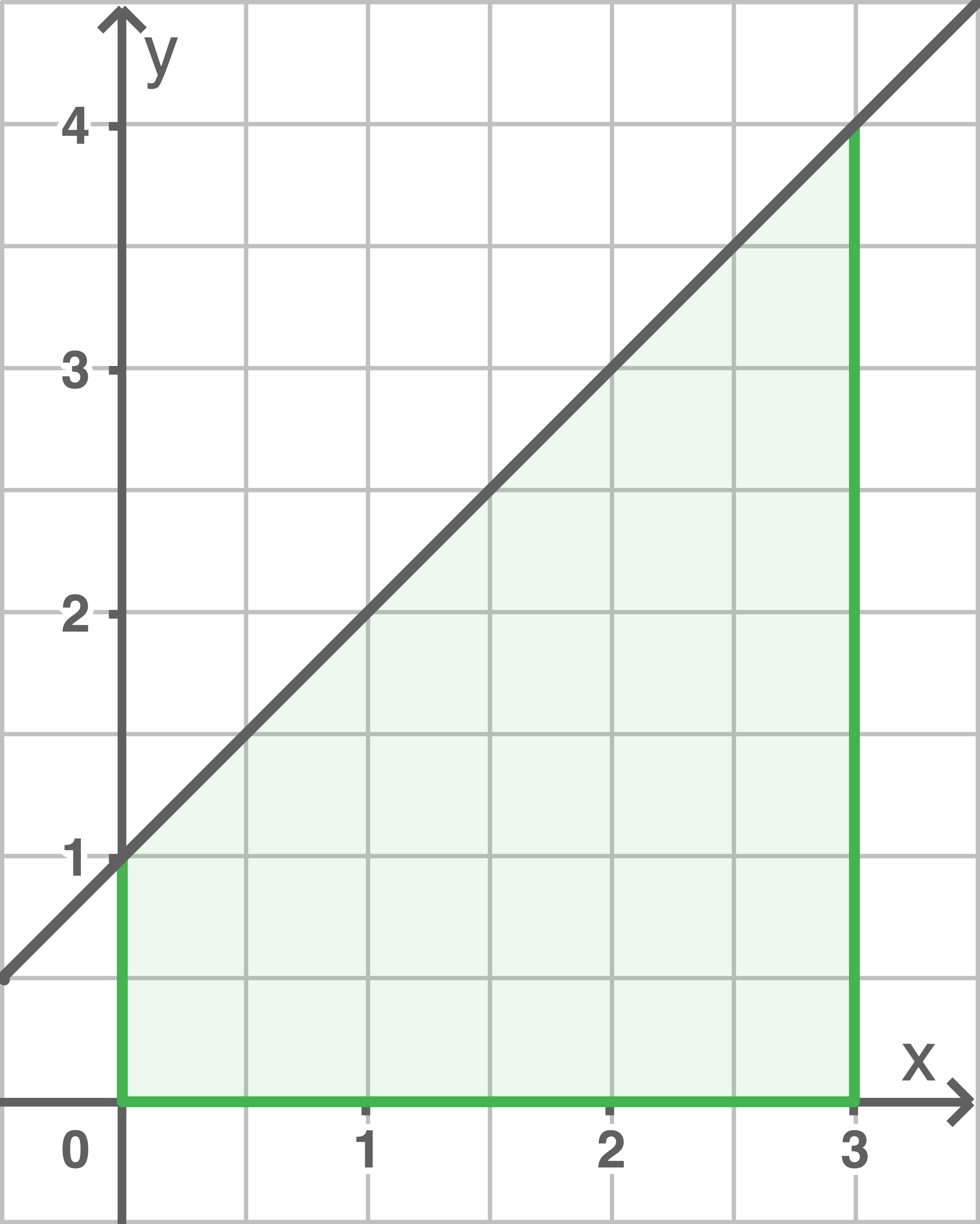
Der Inhalt einer Fläche wird durch den Term
 berechnet.
berechnet.
2.1
Stelle diese Fläche in einem kartesischen Koordinatensystem dar.
Erreichbare BE-Anzahl: 02
2.2
Ermittle den Wert des Terms.
Erreichbare BE-Anzahl: 02
3.
Die Geraden

 und
und

 schneiden sich im Punkt
schneiden sich im Punkt  .
.
3.1
Bestimme die Koordinaten von  .
.
Erreichbare BE-Anzahl: 02
3.2
Untersuche, ob  und
und  orthogonal zueinander verlaufen.
orthogonal zueinander verlaufen.
Erreichbare BE-Anzahl: 02
4.
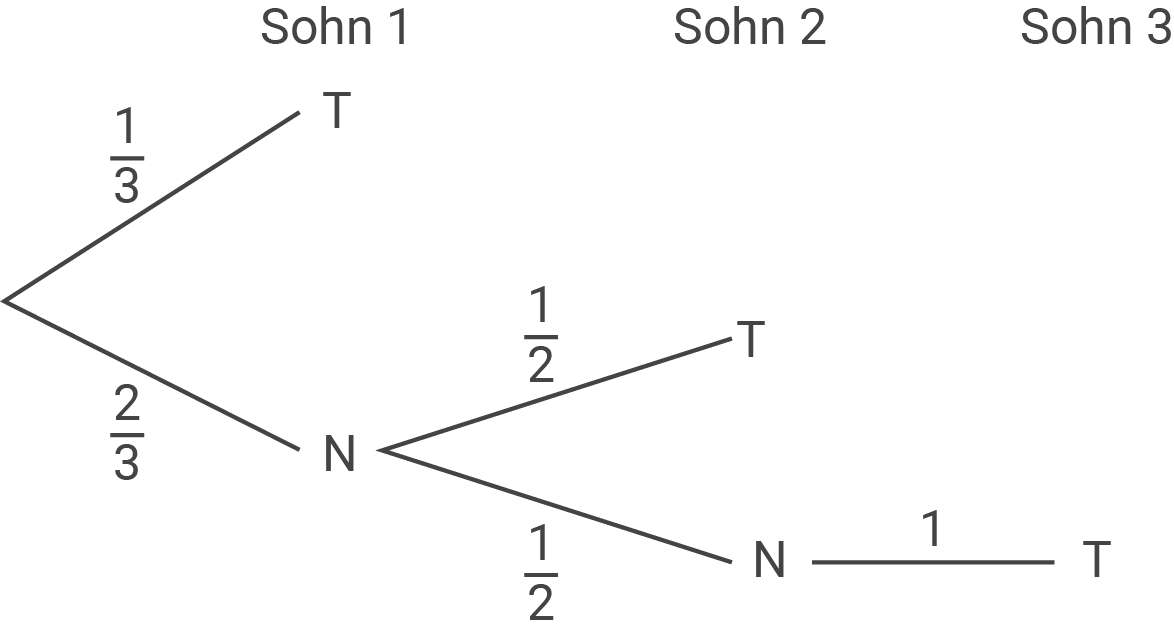
Ein Vater kann mit einem seiner drei Söhne ein Fußballspiel besuchen. Alle drei Söhne möchten gern mitkommen. Um zu einer Entscheidung zu kommen, fertigt der Vater drei äußerlich nicht unterscheidbare Lose an. Darunter befindet sich genau ein Los, welches den Besuch des Fußballspiels ermöglicht. Die drei Söhne ziehen nacheinander ohne Zurücklegen ein Los zufällig. Erst nachdem alle drei Söhne gezogen haben, werden die Lose geöffnet.
Zeige, dass die Wahrscheinlichkeit für den Besuch des Fußballspiels für jeden Sohn gleich ist.
Zeige, dass die Wahrscheinlichkeit für den Besuch des Fußballspiels für jeden Sohn gleich ist.
Erreichbare BE-Anzahl: 02
1.1
1.2
Es gilt  Also hat
Also hat  eine waagrechte Asymptote mit der Gleichung
eine waagrechte Asymptote mit der Gleichung  Die vierte Antwortmöglichkeit ist also richtig.
Die vierte Antwortmöglichkeit ist also richtig.
1.3
Alle Punkte in der  -Ebene besitzen die
-Ebene besitzen die  -Koordinate Null. Dies muss daher auch für den Schnittpunkt mit der Geraden
-Koordinate Null. Dies muss daher auch für den Schnittpunkt mit der Geraden  gelten. Gleichsetzen der letzten Koordinate der Geradengleichung mit Null liefert:
gelten. Gleichsetzen der letzten Koordinate der Geradengleichung mit Null liefert:
![\( \begin{array}[t]{rll}
0 &=& 5 + t\cdot (-1) \quad \scriptsize \mid\;+t \\[5pt]
t&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/b996e6ea2857e20f96e8b6c7d22ba6e5ebe5c82fe8fe78d9dab8a8b73625a731_light.svg) Einsetzen von
Einsetzen von  in die Geradengleichung liefert:
in die Geradengleichung liefert:
 Die dritte Antwortmöglichkeit
Die dritte Antwortmöglichkeit  ist also die richtige Antwort.
ist also die richtige Antwort.
1.4
Aus der Abbildung können die Koordinaten der Spurpunkte von  ablesen werden:
ablesen werden:

 und
und  Die Koordinaten dieser Punkte müssen die gesuchte Ebenengleichung erfüllen.
Die zweite Antwortmöglichkeit ist die richtige.
Die Koordinaten dieser Punkte müssen die gesuchte Ebenengleichung erfüllen.
Die zweite Antwortmöglichkeit ist die richtige.
1.5
Bei dem zehnmaligen Werfen der Münze handelt es sich um eine Bernoullikette. Die gesuchte Wahrscheinlichkeit kann also mit der Formel von Bernoulli für  und
und  Treffer berrechnet werden:
Treffer berrechnet werden:

 Die dritte Antwortmöglichkeit ist die richtige.
Die dritte Antwortmöglichkeit ist die richtige.
2.1
Das Integral beschreibt den Inhalt der Fläche, die der Graph von  im Bereich
im Bereich  mit der
mit der  -Achse begrenzt.
-Achse begrenzt.

2.2
3.1
Gleichsetzen der Geradengleichungen ergibt folgendes Gleichungssystem:
 Aus
Aus  folgt sofort
folgt sofort  Da sich die beiden Geraden
Da sich die beiden Geraden  und
und  nach Aufgabenstellung schneiden, kann
nach Aufgabenstellung schneiden, kann  direkt in die Gleichung von
direkt in die Gleichung von  eingesetzt werden:
eingesetzt werden:
 Die Koordinaten des Schnittpunkts von
Die Koordinaten des Schnittpunkts von  und
und  lauten
lauten 
3.2
Die beiden Geraden  und
und  sind orthogonal, wenn ihre Richtungsvektoren orthogonal zueinander sind. Das ist der Fall, wenn ihr Skalarprodukt Null ergibt.
Die beiden Geraden
sind orthogonal, wenn ihre Richtungsvektoren orthogonal zueinander sind. Das ist der Fall, wenn ihr Skalarprodukt Null ergibt.
Die beiden Geraden  und
und  verlaufen also orthogonal zueinander.
verlaufen also orthogonal zueinander.
4
Treffer T: Besuch des Fußballspiels
Niete N: kein Besuch des Fußballspiels Es ergeben sich folgende Wahrscheinlichkeiten für die Söhne, das Fußballspiel zu besuchen: Sohn 1: Sohn 2:
Sohn 2:  Sohn 3:
Sohn 3: 
Niete N: kein Besuch des Fußballspiels Es ergeben sich folgende Wahrscheinlichkeiten für die Söhne, das Fußballspiel zu besuchen: Sohn 1:
© - SchulLV.