Teil B1

Eine ebene viereckige Werbefläche wird in einem kartesischen Koordinatensystem durch die Eckpunkte $P(4\;|\;2\;|\;0)$ , $Q(2\;|\;4\;|\;0)$ , $R(0\;|\;4\;|\;2)$ und $S(0\;|\;2\;|\;4)$ beschrieben (1 Längeneinheit entspricht 1 Meter).

1.1

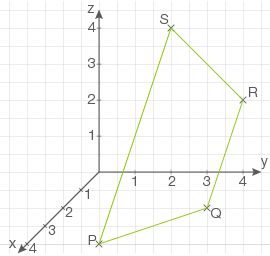
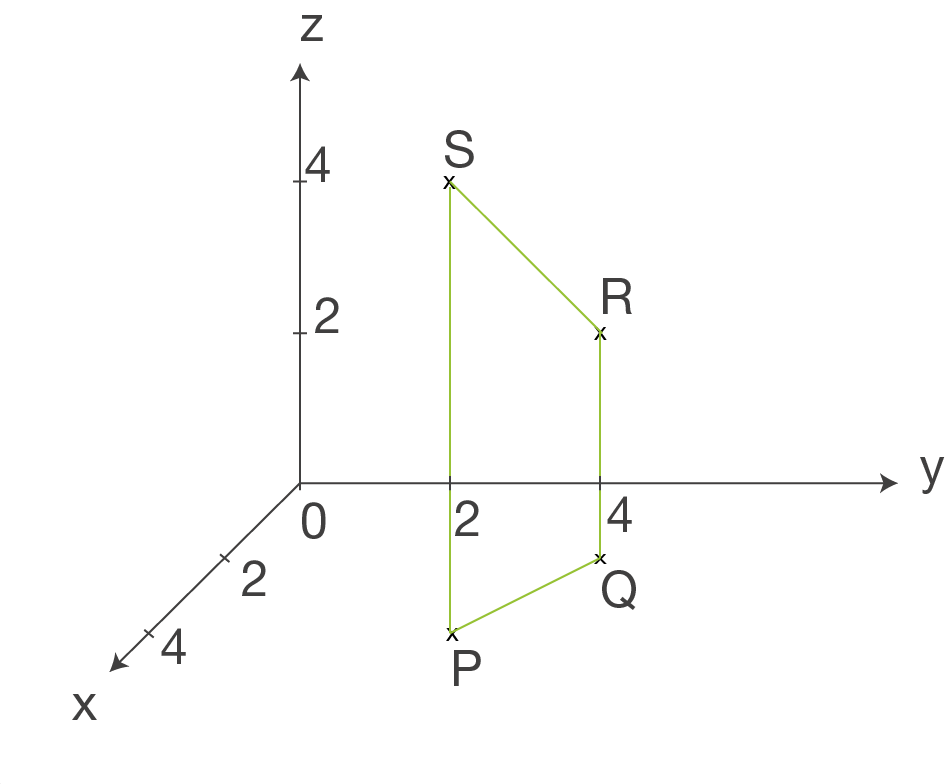
Stelle das Viereck $PQRS$ in einem kartesischen Koordinatensystem dar. Weise nach, dass dieses Viereck ein gleichschenkliges Trapez ist.

(6P)

1.2

Ermittle den Flächeninhalt der Werbefläche.

(3P)

Für eine Sonderausstellung wird die Werbefläche so zu einem Sechseck $PQRSTU$ vergrößert, dass die Gerade durch die Punkte $P$ und $S$ eine Symmetrieachse dieses Sechsecks ist.

1.3

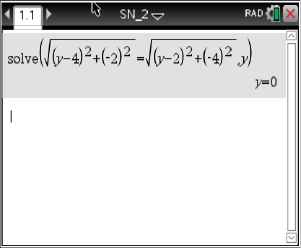
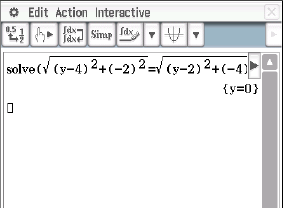
Weise nach, dass der Punkt $T$ die Koordinaten $T(2\;|\;0\;|\;4)$ besitzt.
Bestimme die Koordinaten des Punktes $U$ .

(4P)

1.4

Zur Stabilisierung dieser sechseckigen Werbefläche verlaufen von einem Punkt $Z$ jeweils gleich lange Metallstreben zu jedem Eckpunkt des Sechsecks $PQRSTU$ , sodass die gerade Pyramide $PQRSTUVZ$ entsteht. Der Punkt $Z$ liegt in der $x$ - $y$ -Koordinatenebene.
Ermittle die Koordinaten dieses Punktes $Z$ .

(3P)

1.5

Träger für derartige Werbeflächen werden aus Kunststoff gefertigt.
$30\;\%$ der Träger werden aus recyceltem Kunststoff hergestellt. Die Wahrscheinlichkeit für einen Materialfehler bei einem Träger aus nicht recyceltem Kunststoff beträgt $0,3\;\%$ . Die Wahrscheinlichkeit dafür, dass ein Träger einen Materialfehler besitzt, beträgt $1,5\;\%$ .
Bestimme die Wahrscheinlichkeit dafür, dass ein Träger aus nicht recyceltem Kunststoff besteht und keinen Materialfehler besitzt.
Ermittle den prozentualen Anteil der Träger mit Materialfehler an allen aus recyceltem Kunststoff hergestellten Trägern.

(4P)

Aufgabe B1

1.1

$\blacktriangleright$ Viereck in einem kartesischen Koordinatensystem darstellen

Aus den Punkten $P (4 \mid 2 \mid 0)$ , $Q (2 \mid 4 \mid 0 )$ , $R (0 \mid 4 \mid 2)$ , $S(0 \mid 2 \mid4)$ kannst du ein Trapez konstruieren.

3D-Koordinatensystem mit Punkten S, R, Q und einer grünen Verbindungslinie.

Abb.1: Viereck $PQRS$

$\blacktriangleright$ Nachweis des gleichschenkligen Trapezes

Um nachzuweisen, dass dieses Viereck ein gleichschenkliges Trapez ist, musst du zuerst zeigen, dass dieses Viereck ein Trapez ist.

Ein Trapez ist ein Viereck mit zwei zueinander parallelen Seiten.

Zwei Vektoren $\overrightarrow{v}$ und $\overrightarrow{w}$ sind zueinander parallel, wenn sie voneinander linear abhängig sind, wenn du also die Gleichung

$\overrightarrow{v} = r \cdot \overrightarrow{w}$

nach $r$ auflösen kannst. Wähle also die Seiten $\overrightarrow{RQ}$ und $\overrightarrow{PS}$ und untersuche sie auf lineare Abhängigkeit.

$\overrightarrow{RQ} = r \cdot \pmatrix{-4\\0\\4}$

Vollständige Lösung anzeigen

Du erhältst als Ergebnis $r = - \dfrac{1}{2}$ . Weil diese Lösung eindeutig ist, sind die Vektoren voneinander linear abhängig. Das bedeutet, dass diese Seiten zueinander parallel sind und es sich bei dem Viereck um ein Trapez handelt.

Um nachzuweisen, dass das Trapez gleichschenklig ist, überprüfst du die Länge der beiden Seiten, die nicht parallel sind. Sind diese gleich lang, handelt es sich um ein gleichschenkliges Trapez.

Berechne also die Beträge von $\overrightarrow{PQ}$ und $\overrightarrow{RS}$ und vergleiche sie miteinander:

$\left | \overrightarrow{PQ} \right | = \sqrt{2^2 + 2^2} = \sqrt{8} = \left | \overrightarrow{RS} \right |$

Damit hast du nachgewiesen, dass es sich bei dem Viereck um ein gleichschenkliges Trapez handelt.

1.2

$\blacktriangleright$ Flächeninhalt der Werbefläche ermitteln

Um die Größe der Werbefläche zu ermitteln, benutzt du die Formel für den Flächeninhalt eines Trapezes:

$A = \dfrac{a+b}{2} \cdot h$

Darin sind $a = \vert \overrightarrow{RQ} \vert$ und $b = \vert \overrightarrow{SP} \vert$ die Längen der parallelen Seiten und $h$ entspricht der Höhe.

Die Höhe kannst du beispielsweise über den Abstand vom Punkt $R$ zur Geraden durch die Punkte $S$ und $P$ berechnen.
Stelle dazu die Gleichung der Geraden durch $P$ und $S$ auf:

$\overrightarrow{g} = \pmatrix{4\\2\\0} + s \cdot \pmatrix{-4\\0\\4}$

Stelle nun eine Hilfsebene auf, die senkrecht zu $g$ verläuft und durch den Punkt $R$ verläuft. Verwende also den Richtungsvektor von $g$ als Normalenvektor:

$H: \quad -4x+0y +4z =d$

Setze nun die Koordinaten von $R$ ein:

$d= -4\cdot 0 +0\cdot 4 + 4\cdot 2 = 8$

Eine Gleichung der Hilfsebene lautet also:

$H: \, -4x +4z = 8$

Bestimme nun den Schnittpunkt von $g$ und $H.$ Die Koordinaten der Punkte auf $g$ kannst du aus der Geradengleichung zu $(4-4s\mid 2\mid 4s)$ ablesen.
Diese kannst du in die Ebenengleichung einsetzen:

$\begin{array}[t]{rll} -4x +4z &=& 8 \\[5pt] -4\cdot (4-4s) +4\cdot(4s) &=& 8 \\[5pt] -16 +16s +16s &=& 8 &\quad \scriptsize \mid\; +16\\[5pt] 32s &=& 24 &\quad \scriptsize \mid\; :32 \\[5pt] s &=& \frac{3}{4} \end{array}$

Für den Ortsvektor des Schnittpunkts erhältst du damit:

$\(\overrightarrow{OR$

Die Höhe des Trapezes ist nun der Abstand dieses Schnittpunkts $\(R$ zu $R:$

$h=\sqrt{6}$

Vollständige Lösung anzeigen

Die Seitenlänge der parallelen Seiten ergibt sich zu

$\vert \overrightarrow{RQ} \vert = \sqrt{2^2+(-2)^2} = \sqrt{2} \cdot 2$

Vollständige Lösung anzeigen

$\vert \overrightarrow{PS} \vert = \sqrt{(-4)^2 + 4^2} = \sqrt{2} \cdot 4$

Vollständige Lösung anzeigen

Somit erhältst du

$A = \dfrac{\sqrt{2} \cdot( 2 + 4)}{2} \cdot \sqrt{6} \approx 10,4$

Da eine LE einem Meter entspricht, ist der gesuchte Flächeninhalt des Trapezes $10,4 \text{m}^2$ .

1.3

$\blacktriangleright$ Koordinaten eines Punktes nachweisen

Das Trapez wird nun zu einem Sechseck erweitert, wobei die Gerade durch die Punkte $P$ und $S$ die Symmetrieachse ist.

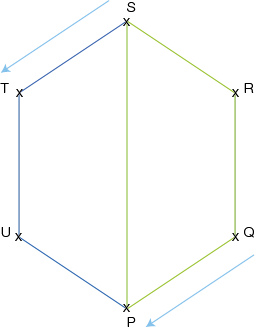Geometrische Darstellung eines Sechsecks mit benannten Punkten und Linien.

Abb. 2: Die beiden türkis eingefärbten Vektoren entsprechen $\overrightarrow{ST}$ und $\overrightarrow{QP}$ . Man kann den einen also durch den anderen ersetzen.

Nutze dazu, dass du Vektoren ersetzen kannst, die parallele Seiten beschreiben

$\overrightarrow{OT} = \overrightarrow{OS} + \overrightarrow{ST} = \overrightarrow{OS} + \overrightarrow{QP}$

Berechne zunächst $\overrightarrow{QP}$ :

$\overrightarrow{QP} = \pmatrix{4\\2\\0} - \pmatrix{2\\4\\0} = \pmatrix{2\\-2\\0}$

Du erhältst also für

$\overrightarrow{OT} = \pmatrix{0\\2\\4} + \pmatrix{2\\-2\\0} = \pmatrix{2\\0\\4}$

Damit hast du nachgewiesen, dass der Punkt $T$ die Koordinaten $(2 \mid 0 \mid 4)$ hat.

$\blacktriangleright$ Koordinaten des Punktes U bestimmen

Zur Bestimmung der Koordinaten des Punktes $U$ kannst du analog zum vorigen Aufgabenteil vorgehen. Nutze dazu, dass gilt

$\overrightarrow{OU} = \overrightarrow{OP} + \overrightarrow{PU} = \overrightarrow{OP} + \overrightarrow{RS}$

Rechne also

$\pmatrix{4\\2\\0} + \pmatrix{0-0\\2-4\\4-2} = \pmatrix{4\\0\\2}$

Also hat $U$ die Koordinaten $(4 \mid 0 \mid 2)$ .

1.4

$\blacktriangleright$ Koordinaten eines Eckpunktes der Pyramide berechnen

Nun wird das Sechseck durch gleich lange Verbindungsstücke zu einem Punkt in der $xy -$ Ebene zu einer Pyramide erweitert. Die Koordinaten dieses Punktes $Z$ sollen ermittelt werden. Es gilt wegen der gleichen Länge aller Seiten

$\left | \overrightarrow{RZ} \right | = \left | \overrightarrow{PZ} \right |$

Vollständige Lösung anzeigen

Schreibe dies mit $Z(x \mid y \mid0)$ als Gleichung

$\sqrt{(y-4)^2 + (-2)^2}= …$

Vollständige Lösung anzeigen

Die Lösung dieser Gleichung kannst du mit deinem CAS bestimmen. Den Befehl zur Lösung einer Gleichung findest du

$MENU \longrightarrow 3 \longrightarrow 1$

Mathematiksoftware zeigt eine Gleichung zur Lösung eines Problems in der Algebra.

Abb. 3: Die Lösung der Gleichung für $y$

Damit erhältst du $y = 0$ . Bestimme analog $x$ .

Dann erhältst du $x = 0$ . Somit liegt $Z$ im Urpsrung.

1.5

$\blacktriangleright$ Wahrscheinlichkeit eines Materialfehlers berechnen

Jetzt musst du die Wahrscheinlichkeit bestimmen, dass ein Träger aus nicht recyceltem Kunststoff besteht und keinen Materialfehler besitzt. Das Ereignis $X$ , dass ein Träger aus nicht recyceltem Kunststoff besteht, ist gerade das Gegenereignis dazu, dass ein Träger aus recyceltem Kunststoff besteht. Die Wahrscheinlichkeit berechnest du mit

$P(X) = 1 - 0,3 = 0,7$ .

Das Ereignis $Y$ , dass ein Träger aus nicht recyceltem Kunststoff keinen Materialfehler hat, ist gerade das Gegenereignis dazu, dass ein Träger aus recyceltem Kunststoff einen Materialfehler hat. Die Wahrscheinlichkeit berechnest du erneut mit dem Gegenereignis

$P(Y) = 1 - 0,003 = 0,997$ .

Um die Wahrscheinlichkeit zu erhalten, berechnest du

$P(X) \cdot P(Y) = 0,6979$

Vollständige Lösung anzeigen

$\blacktriangleright$ Prozentualen Anteil der Träger berechnen

Jetzt musst du den Anteil der Träger mit Materialfehler unter den aus recycelten Kunstoff hergestellten Trägern berechnen.

Gehe dazu von einer Grundmenge an allen Trägern aus. Diese nennst du $A$ . Von diesen Trägern sind $0,7 \cdot A$ aus nicht recyceltem Kunstoff. Von diesen Trägern haben genau $0,3 \%$ einen Materialfehler.

Dies enstpricht $0,003 \cdot 0,7 \cdot A$ Stück. Insgesamt haben $1,5 \%$ einen Materialfehler, also $0,015 \cdot A$ . Du erhältst also als Anzahl von Kunststoffträgern mit Materialfehler

$(0,015 - 0.003 \cdot 0,7) \cdot A$ .

Der Anteil dieser Träger an der Gesamtmenge der Kunststoffträger ist

$\dfrac{(0,015 - 0,003 \cdot 0,7) \cdot A}{0,3 \cdot A} =$

Vollständige Lösung anzeigen

Also beträgt der prozentuale Anteil der Träger mit Materialfehler an allen aus recyceltem Kunststoff hergestellten Trägern $4,3 \%$ .

Bildnachweise [nach oben]

[1-3]

Aufgabe B1

1.1

$\blacktriangleright$ Viereck in einem kartesischen Koordinatensystem darstellen

Aus den Punkten $P (4 \mid 2 \mid 0)$ , $Q (2 \mid 4 \mid 0 )$ , $R (0 \mid 4 \mid 2)$ , $S(0 \mid 2 \mid4)$ kannst du ein Trapez konstruieren.

3D-Koordinatensystem mit Punkten P, Q, R, S und einer Verbindungslinie zwischen ihnen.

Abb.1: Viereck $PQRS$

$\blacktriangleright$ Nachweis des gleichschenkligen Trapezes

Um nachzuweisen, dass dieses Viereck ein gleichschenkliges Trapez ist, musst du zuerst zeigen, dass dieses Viereck ein Trapez ist.

Ein Trapez ist ein Viereck mit zwei zueinander parallelen Seiten.

Zwei Vektoren $\overrightarrow{v}$ und $\overrightarrow{w}$ sind zueinander parallel, wenn sie voneinander linear abhängig sind, wenn du also die Gleichung

$\overrightarrow{v} = r \cdot \overrightarrow{w}$

nach $r$ auflösen kannst. Wähle also die Seiten $\overrightarrow{RQ}$ und $\overrightarrow{PS}$ und untersuche sie auf lineare Abhängigkeit.

$\overrightarrow{RQ} = r \cdot \pmatrix{-4\\0\\4}$

Vollständige Lösung anzeigen

Berechne also die Beträge von $\overrightarrow{PQ}$ und $\overrightarrow{RS}$ und vergleiche sie miteinander:

$\left | \overrightarrow{PQ} \right | = \sqrt{2^2 + 2^2} = \sqrt{8} = \left | \overrightarrow{RS} \right |$

Damit hast du nachgewiesen, dass es sich bei dem Viereck um ein gleichschenkliges Trapez handelt.

1.2

$\blacktriangleright$ Flächeninhalt der Werbefläche ermitteln

Um die Größe der Werbefläche zu ermitteln, benutzt du die Formel für den Flächeninhalt eines Trapezes:

$A = \dfrac{a+b}{2} \cdot h$

Darin sind $a = \vert \overrightarrow{RQ} \vert$ und $b = \vert \overrightarrow{SP} \vert$ die Längen der parallelen Seiten und $h$ entspricht der Höhe.

Die Höhe kannst du beispielsweise über den Abstand vom Punkt $R$ zur Geraden durch die Punkte $S$ und $P$ berechnen.
Stelle dazu die Gleichung der Geraden durch $P$ und $S$ auf:

$\overrightarrow{g} = \pmatrix{4\\2\\0} + s \cdot \pmatrix{-4\\0\\4}$

Stelle nun eine Hilfsebene auf, die senkrecht zu $g$ verläuft und durch den Punkt $R$ verläuft. Verwende also den Richtungsvektor von $g$ als Normalenvektor:

$H: \quad -4x+0y +4z =d$

Setze nun die Koordinaten von $R$ ein:

$d= -4\cdot 0 +0\cdot 4 + 4\cdot 2 = 8$

Eine Gleichung der Hilfsebene lautet also:

$H: \, -4x +4z = 8$

Für den Ortsvektor des Schnittpunkts erhältst du damit:

$\overrightarrow{OR‘} = \pmatrix{4\\2\\0} + \frac{3}{4} \cdot \pmatrix{-4\\0\\4} = \pmatrix{ 1 \\ 2 \\ 3 }$

Die Höhe des Trapezes ist nun der Abstand dieses Schnittpunkts $R‘$ zu $R:$

$h=\sqrt{6}$

Vollständige Lösung anzeigen

Die Seitenlänge der parallelen Seiten ergibt sich zu

$\vert \overrightarrow{RQ} \vert = \sqrt{2^2+(-2)^2} = \sqrt{2} \cdot 2$

Vollständige Lösung anzeigen

$\vert \overrightarrow{PS} \vert = \sqrt{(-4)^2 + 4^2} = \sqrt{2} \cdot 4$

Vollständige Lösung anzeigen

Somit erhältst du

$A = \dfrac{\sqrt{2} \cdot( 2 + 4)}{2} \cdot \sqrt{6} \approx 10,4$

Da eine LE einem Meter entspricht, ist der gesuchte Flächeninhalt des Trapezes $10,4 \text{m}^2$ .

1.3

$\blacktriangleright$ Koordinaten eines Punktes nachweisen

Das Trapez wird nun zu einem Sechseck erweitert, wobei die Gerade durch die Punkte $P$ und $S$ die Symmetrieachse ist.

Abb. 2: Die beiden türkis eingefärbten Vektoren entsprechen $\overrightarrow{ST}$ und $\overrightarrow{QP}$ . Man kann den einen also durch den anderen ersetzen.

Nutze dazu, dass du Vektoren ersetzen kannst, die parallele Seiten beschreiben

$\overrightarrow{OT} = \overrightarrow{OS} + \overrightarrow{ST} = \overrightarrow{OS} + \overrightarrow{QP}$

Berechne zunächst $\overrightarrow{QP}$ :

$\overrightarrow{QP} = \pmatrix{4\\2\\0} - \pmatrix{2\\4\\0} = \pmatrix{2\\-2\\0}$

Du erhältst also für

$\overrightarrow{OT} = \pmatrix{0\\2\\4} + \pmatrix{2\\-2\\0} = \pmatrix{2\\0\\4}$

Damit hast du nachgewiesen, dass der Punkt $T$ die Koordinaten $(2 \mid 0 \mid 4)$ hat.

$\blacktriangleright$ Koordinaten des Punktes U bestimmen

Zur Bestimmung der Koordinaten des Punktes $U$ kannst du analog zum vorigen Aufgabenteil vorgehen. Nutze dazu, dass gilt

$\overrightarrow{OU} = \overrightarrow{OP} + \overrightarrow{PU} = \overrightarrow{OP} + \overrightarrow{RS}$

Rechne also

$\pmatrix{4\\2\\0} + \pmatrix{0-0\\2-4\\4-2} = \pmatrix{4\\0\\2}$

Also hat $U$ die Koordinaten $(4 \mid 0 \mid 2)$ .

1.4

$\blacktriangleright$ Koordinaten eines Eckpunktes der Pyramide berechnen

$\left | \overrightarrow{RZ} \right | = \left | \overrightarrow{PZ} \right |$

Vollständige Lösung anzeigen

Schreibe dies mit $Z(x \mid y \mid0)$ als Gleichung

$\sqrt{(y-4)^2 + (-2)^2}= ...$

Vollständige Lösung anzeigen

Die Lösung dieser Gleichung kannst du mit deinem CAS bestimmen. Den Befehl zur Lösung einer Gleichung findest du

$Action \longrightarrow Advanced \longrightarrow Solve$

Mathematische Gleichung zur Lösung einer Funktion in einem interaktiven Fenster.

Abb. 3: Die Lösung der Gleichung für $y$

Damit erhältst du $y = 0$ . Bestimme analog x.

Dann erhältst du $x = 0$ . Somit liegt $Z$ im Urpsrung.

1.5

$\blacktriangleright$ Wahrscheinlichkeit eines Materialfehlers berechnen

$P(X) = 1 - 0,3 = 0,7$ .

$P(Y) = 1 - 0,003 = 0,997$ .

Um die Wahrscheinlichkeit zu erhalten, berechnest du

$P(X) \cdot P(Y) = 0,6979$

Vollständige Lösung anzeigen

$\blacktriangleright$ Prozentualen Anteil der Träger berechnen

Jetzt musst du den Anteil der Träger mit Materialfehler unter den aus recycelten Kunstoff hergestellten Trägern berechnen.

Dies enstpricht $0,003 \cdot 0,7 \cdot A$ Stück. Insgesamt haben $1,5 \%$ einen Materialfehler, also $0,015 \cdot A$ . Du erhältst also als Anzahl von Kunststoffträgern mit Materialfehler

$(0,015 - 0.003 \cdot 0,7) \cdot A$ .

Der Anteil dieser Träger an der Gesamtmenge der Kunststoffträger ist

$\dfrac{(0,015 - 0,003 \cdot 0,7) \cdot A}{0,3 \cdot A} =$

Vollständige Lösung anzeigen

Also beträgt der prozentuale Anteil der Träger mit Materialfehler an allen aus recyceltem Kunststoff hergestellten Trägern $4,3 \%$ .

Bildnachweise [nach oben]

[1-3]