Wahlbereich 1
4
Die Graphen der in 
definierten Funktionen 
mit 
und 
mit 
schließen gemeinsam mit der 
-Achse im ersten Quadranten eine Fläche ein.
Berechne den Inhalt der Fläche.
definierten Funktionen mit und mit schließen gemeinsam mit der -Achse im ersten Quadranten eine Fläche ein.
Berechne den Inhalt der Fläche.
(5 BE)
5
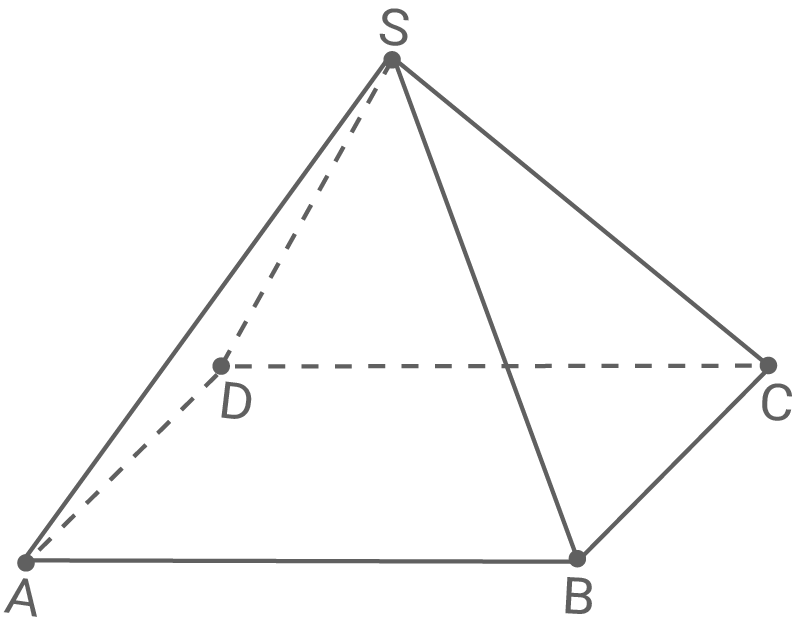
Die Abbildung zeigt die Gerade quadratische Pyramide 
mit der Grundfläche 
Es sei: 
und 
ist der Mittelpunkt der Kante 
ist der Mittelpunkt der Kante 
Beurteile die folgende Aussage: Das Viereck
ist ein Trapez.
mit der Grundfläche Es sei: und
5.1
Gib die Vektoren 
und 
unter Verwendung der Vektoren 
und 
an.
und unter Verwendung der Vektoren und an.
(2 BE)
5.2
ist der Mittelpunkt der Kante
ist der Mittelpunkt der Kante
Beurteile die folgende Aussage: Das Viereck
ist ein Trapez.
(3 BE)
6
Unter den Besuchern einer Freizeitanlage sind 
Kinder, alle übrigen Besucher sind Erwachsene.
Insgesamt haben
aller Besucher schon einmal Minigolf gespielt.
Erfahrungsgemäß sind
der Besucher Kinder und haben schon einmal Minigolf gespielt.
Kinder, alle übrigen Besucher sind Erwachsene.
Insgesamt haben
aller Besucher schon einmal Minigolf gespielt.
Erfahrungsgemäß sind
der Besucher Kinder und haben schon einmal Minigolf gespielt.
6.1
Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.
(3 BE)
6.2
Ein Besucher wird zufällig ausgewählt.
Untersuche, ob die beiden Ereignisse „Der Besucher ist Kind.“ und „Der Besucher hat schon einmal Minigolf gespielt.“ stochastisch abhängig sind.
Untersuche, ob die beiden Ereignisse „Der Besucher ist Kind.“ und „Der Besucher hat schon einmal Minigolf gespielt.“ stochastisch abhängig sind.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4
Gleichsetzen der beiden Funktionen liefert:
![\(\begin{array}[t]{rlll}
f(x) &=& g(x) \\[5pt]
\dfrac{3}{4}x^2 &=&-\dfrac{1}{4}x^2+4 &\mid\;+\frac{1}{4}x^2 \\[5pt]
x^2&=&4 &\mid\;\sqrt{\;} \\[5pt]
x_1&=&2 \\[5pt]
x_2&=&-2
\end{array}\)](https://www.schullv.de/resources/formulas/9e9012a0e97eb60ed86ccd9f5f9f0a48bf0c78f3eac45f99ff8eac0645f1270d_light.svg)
Im ersten Quadranten liegt nur die Lösung 
Somit folgt für den gesuchten Flächeninhalt 
![\(\begin{array}[t]{rlll}
A&=&\displaystyle\int_{0}^{2}(g(x)-f(x))\;\mathrm dx \\[5pt]
&=&\displaystyle\int_{0}^{2} -x^2+4\;\mathrm dx \\[5pt]
&=&\left[-\dfrac{1}{3}x^3+4x\right]_0^{2} \\[5pt]
&=&\left(-\dfrac{1}{3}\cdot2^3+4\cdot2\right)-0 \\[5pt]
&=&-\dfrac{8}{3}+8 \\[5pt]
&=&\dfrac{16}{3}\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/fd793a22360d5e8a693cad1915d315dcff6c647a0fe6189bdcfc2feff64c9af7_light.svg)
Im ersten Quadranten liegt nur die Lösung Somit folgt für den gesuchten Flächeninhalt
5
5.1
5.2
![\(\begin{array}[t]{rlll}
\overrightarrow{MN}&=&\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CN} \\[5pt]
&=&-\dfrac{1}{2}\cdot
\overrightarrow{c}+\overrightarrow{a}+\overrightarrow{b}+\dfrac{1}{2}\cdot
\left(-\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\right) \\[5pt]
&=&\dfrac{1}{2}\cdot
\left(\overrightarrow{a}+\overrightarrow{b}\right) \\[5pt]
&=&\dfrac{1}{2}\cdot \overrightarrow{AC}
\end{array}\)](https://www.schullv.de/resources/formulas/d6eede07b02362dd7aafc47133956e52b8242f7470c8851b5f6c4efe76707631_light.svg)
Die Strecken 
und 
sind somit parallel zueinander, das heißt das Viereck ist ein Trapez.
6
6.1
 |
 |
||
|---|---|---|---|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
6.2
Da 
gilt, sind die Ereignisse stochastisch abhängig.