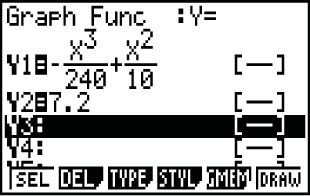
Teil B2
An einer Wetterstation in Deutschland werden kontinuierlich Temperaturen gemessen.
In der Abbildung ist der Temperaturverlauf für die ersten Stunden nach Mitternacht an einem Tag im Juli dargestellt. Der Temperaturverlauf kann in dem gegebenen Koordinatensystem näherungsweise durch den Graphen der Funktion
Stunden nach Mitternacht an einem Tag im Juli dargestellt. Der Temperaturverlauf kann in dem gegebenen Koordinatensystem näherungsweise durch den Graphen der Funktion  mit
mit  (
( )
)
beschrieben werden.
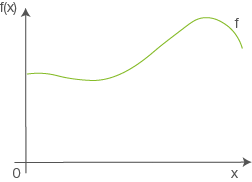 Abb. 1 Abbildung (nicht maßstäblich)
Abb. 1 Abbildung (nicht maßstäblich)
Die Funktion mit
mit  (
( ) beschreibt näherungsweise die Leistung pro Fläche, die an einem Sommertag zu einem bestimmten Zeitpunkt zwischen Sonnenaufgang und Sonnenuntergang an die Erdoberfläche abgegeben wird.
) beschreibt näherungsweise die Leistung pro Fläche, die an einem Sommertag zu einem bestimmten Zeitpunkt zwischen Sonnenaufgang und Sonnenuntergang an die Erdoberfläche abgegeben wird.
Dabei gilt:
 ...Zeitpunkt nach Sonnenaufgang (in Stunden)
...Zeitpunkt nach Sonnenaufgang (in Stunden)
 ...Leistung pro Fläche (in Kilowatt pro Quadratmeter) zum Zeitpunkt
...Leistung pro Fläche (in Kilowatt pro Quadratmeter) zum Zeitpunkt 
Zu den Zeitpunkten des Sonnenaufgangs und des Sonnenuntergangs beträgt die Leistung pro Fläche null Kilowatt pro Quadratmeter.
Die Energie pro Fläche, die in einem Zeitintervall an die Erdoberfläche übertragen wird, kann durch die Integration der Leistung pro Fläche über die Zeit bestimmt werden.
Bildnachweise [nach oben]
In der Abbildung ist der Temperaturverlauf für die ersten
beschrieben werden.
Dabei gilt:
 ...Zeitpunkt nach Mitternacht (in Stunden)
...Zeitpunkt nach Mitternacht (in Stunden)
 ...Temperatur (in Grad Celsius) zum Zeitpunkt
...Temperatur (in Grad Celsius) zum Zeitpunkt 
 Abb. 1 Abbildung (nicht maßstäblich)
Abb. 1 Abbildung (nicht maßstäblich)
2.1
Zeige, dass  Stunden nach Mitternacht die Temperatur von
Stunden nach Mitternacht die Temperatur von  erreicht wurde.
erreicht wurde.
Ermittle, zu welcher Uhrzeit die niedrigste Temperatur im angegebenen Zeitraum gemessen wurde.
Ermittle, zu welcher Uhrzeit die niedrigste Temperatur im angegebenen Zeitraum gemessen wurde.
(4P)
2.2
Bestimme für den angegebenen Zeitraum den Zeitpunkt nach Mitternacht, an dem der Anstieg des Temperaturverlaufs am größten war.
(3P)
2.3
Ermittle für den angegebenen Zeitraum die Zeitdauer, in der die Temperatur mindestens  betrug.
betrug.
(2P)
2.4
An einem anderen Tag wurden um  Uhr die Temperatur von
Uhr die Temperatur von  und um
und um  Uhr die Temperatur von
Uhr die Temperatur von  gemessen. Die Tageshöchsttemperatur von
gemessen. Die Tageshöchsttemperatur von  wurde um
wurde um  Uhr erreicht. Der Temperaturverlauf kann für diesen Tag im Zeitraum von
Uhr erreicht. Der Temperaturverlauf kann für diesen Tag im Zeitraum von  Uhr bis
Uhr bis  Uhr annähernd durch den Graphen einer ganzrationalen Funktion
Uhr annähernd durch den Graphen einer ganzrationalen Funktion  dritten Grades beschrieben werden.
dritten Grades beschrieben werden.
Ermittle eine Gleichung der Funktion .
.
Ermittle eine Gleichung der Funktion
(4P)
Die Funktion
Dabei gilt:
Zu den Zeitpunkten des Sonnenaufgangs und des Sonnenuntergangs beträgt die Leistung pro Fläche null Kilowatt pro Quadratmeter.
Die Energie pro Fläche, die in einem Zeitintervall an die Erdoberfläche übertragen wird, kann durch die Integration der Leistung pro Fläche über die Zeit bestimmt werden.
2.5
Ermittle die Energie pro Fläche (in Kilowattstunden pro Quadratmeter), die an diesem Tag zwischen Sonnenaufgang und Sonnenuntergang an die Erdoberfläche abgegeben wird.
(3P)
2.6
Bestimme, bis zu welchem Zeitpunkt  (
( ) nach Sonnenaufgang eine Energie von
) nach Sonnenaufgang eine Energie von  Kilowattstunden an einen Quadratmeter der Erdoberfläche abgegeben wird.
Kilowattstunden an einen Quadratmeter der Erdoberfläche abgegeben wird.
(2P)
2.7
Der Deutsche Wetterdienst gibt die Niederschlagswahrscheinlichkeit für drei aufeinander folgende Tage mit jeweils  an.
an.
Ermittle unter Verwendung dieser Angabe die Wahrscheinlichkeiten folgender Ereignisse:
Ermittle unter Verwendung dieser Angabe die Wahrscheinlichkeiten folgender Ereignisse:
-
Ereignis
Ereignis
(4P)
2.8
Die Güte einer Wettervorhersage gibt Aufschluss darüber, wie hoch die Wahrscheinlichkeit für das Zutreffen dieser Wettervorhersage ist.
Erfahrungsgemäß beträgt die Güte einer Wettervorhersage für den kommenden Tag . Es besteht die Vermutung, dass die Güte einer Wettervorhersage für den kommenden Tag gestiegen ist.
. Es besteht die Vermutung, dass die Güte einer Wettervorhersage für den kommenden Tag gestiegen ist.
In einem Test mit zufällig ausgewählten Wettervorhersagen für den jeweils kommenden Tag soll die Nullhypothese „Die Güte einer Wettervorhersage für den kommenden Tag liegt höchstens bei
zufällig ausgewählten Wettervorhersagen für den jeweils kommenden Tag soll die Nullhypothese „Die Güte einer Wettervorhersage für den kommenden Tag liegt höchstens bei  .“ auf einem Signifikanzniveau von
.“ auf einem Signifikanzniveau von  getestet werden.
getestet werden.
Bestimme den Ablehnungsbereich der Nullhypothese.
Erfahrungsgemäß beträgt die Güte einer Wettervorhersage für den kommenden Tag
In einem Test mit
Bestimme den Ablehnungsbereich der Nullhypothese.
(3P)
Bildnachweise [nach oben]
© 2016 - SchulLV.
Teil B2
2.1
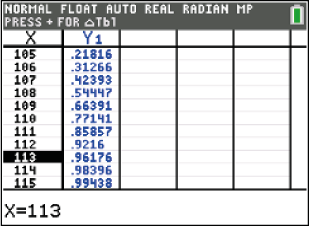
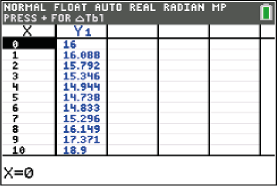 Abb. 1: Tabelle
Abb. 1: Tabelle
GRAPH \rightarrow 2ND \rightarrow TRACE \rightarrow 3: minimum
wähle zuerst eine untere und dann eine obere Schranke.
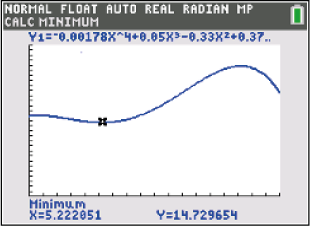 Abb. Zahl: Minimum bestimmen mit dem GTR
Abb. Zahl: Minimum bestimmen mit dem GTR
2.2
GRAPH \rightarrow 2ND \rightarrow TRACE \rightarrow 4: maximum
wähle wieder eine untere und eine obere Schranke.
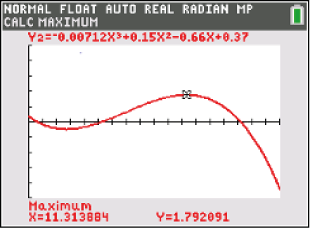 Abb. 3: Maximum bestimmen mit dem GTR
Abb. 3: Maximum bestimmen mit dem GTR
2.3
2.4
- Um
Uhr beträgt die Temperatur
.
- Um
Uhr beträgt die Temperatur
.
- Um
Uhr beträgt die Temperatur
.
- Um
wurde die Tageshöchsttemperatur erreicht.
- Die vierte Eigenschaft bedeutet, dass
bei
ein Maximum besitzt. Deswegen ist
2ND 

 EDIT
EDIT 

In das Fenster gibst du die Zahlen aus deinem Linearen Gleichungssystem ein:
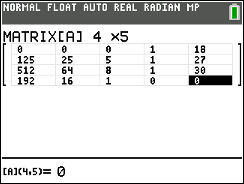 Abb. 5: Eingabe der Daten in die Matrix
Abb. 5: Eingabe der Daten in die Matrix
2ND 

 MATH
MATH 

 2ND
2ND  MATRIX
MATRIX  NAMES
NAMES 
![\(1 :[A]\)](https://mathjax.schullv.de/8080db2e977c8709d02f521928b9be5e8bef59b70f81bb98171c0c57d2b1b98f?color=5a5a5a)
Damit erhältst du dann:
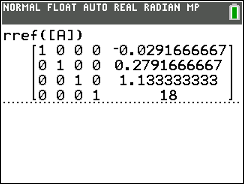 Abb. 6: Lösung des Gleichungssystems mit dem GTR
Abb. 6: Lösung des Gleichungssystems mit dem GTR
2.5
GRAPH  2ND
2ND  TRACE
TRACE  2:zero
2:zero
Anschließend wählst du eine untere und eine obere Schranke und erhältet die Nullstellen 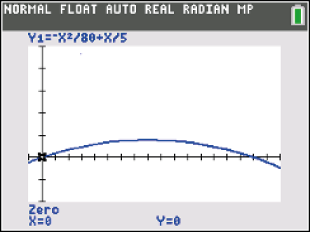 Abb. 7: Nullstellen bestimmen mit dem GTR
Abb. 7: Nullstellen bestimmen mit dem GTR
GRAPH  2ND
2ND  TRACE
TRACE  7:
7:
Wähle als untere Schranke die untere Integrationsgrenze 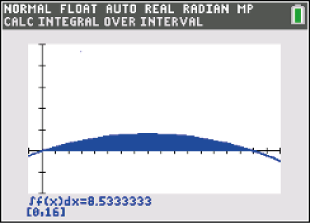 Abb. 8: Integralberechnung mit dem GTR
Abb. 8: Integralberechnung mit dem GTR
2.6
- Bestimme die Integralfunktion
.
- Setze die Integralfunktion mit
gleich und löse nach
auf.
GRAPH  2ND
2ND  TRACE
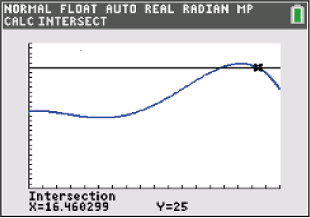
TRACE  5:intersect
5:intersect
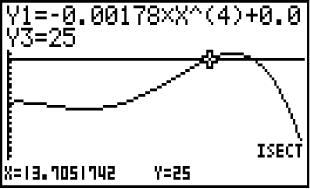
Du musst jetzt nur noch die beiden Kurven auswählen und bekommst dann den Schnittpunkt 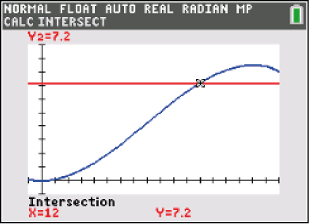 Abb. 10: Schnittstelle mit dem GTR bestimmen
Abb. 10: Schnittstelle mit dem GTR bestimmen
2.7
2.8
2ND  VARS(DISTR)
VARS(DISTR)  B: BinomCdf
B: BinomCdf
Du musst die Parameter deiner Binomialverteilung eingeben: 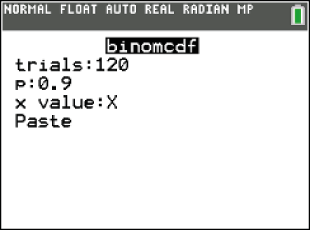 Abb. 11: Eingabe der Daten für die Binomialverteilung
Abb. 11: Eingabe der Daten für die Binomialverteilung
2ND  GRAPH(TABLE)
GRAPH(TABLE)
Wähle aus dieser Tabelle das kleinste ganzzahlige
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Teil B2
2.1
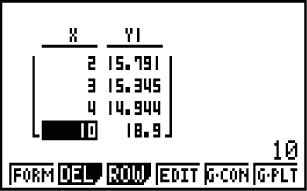 Abb. 1: Tabelle
Abb. 1: Tabelle
MENU  5:GRAPH
5:GRAPH  SHIFT
SHIFT F5
F5  F3:MIN
F3:MIN
Damit erhältst du folgendes Bild:
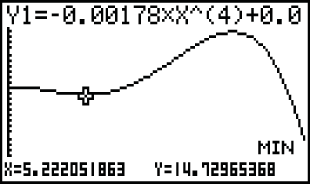 Abb. Zahl: Minimum bestimmen mit dem GTR
Abb. Zahl: Minimum bestimmen mit dem GTR
2.2
GRAPH \rightarrow 2ND \rightarrow TRACE \rightarrow 4: maximum
wähle wieder eine untere und eine obere Schranke.
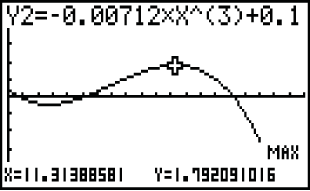 Abb. 3: Maximum bestimmen mit dem GTR
Abb. 3: Maximum bestimmen mit dem GTR
2.3
2.4
- Um
Uhr beträgt die Temperatur
.
- Um
Uhr beträgt die Temperatur
.
- Um
Uhr beträgt die Temperatur
.
- Um
wurde die Tageshöchsttemperatur erreicht.
- Die vierte Eigenschaft bedeutet, dass
bei
ein Maximum besitzt. Deswegen ist
MENU  1:RUN MAT
1:RUN MAT  F4:MATH
F4:MATH  F1: MAT
F1: MAT  F3: $n
F3: $n m$
m$
In das Fenster gibst du zuerst die Zeilen und Spaltenanzahl der Matrix und dann die Einträge aus deinem Linearen Gleichungssystem ein:
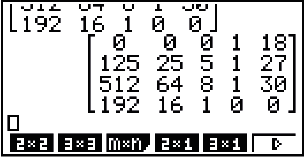 Abb. 5: Eingabe der Daten in die Matrix
Abb. 5: Eingabe der Daten in die Matrix
OPTN  F2: Mat
F2: Mat  F6
F6  F5: Rref
F5: Rref
Damit erhältst du dann:
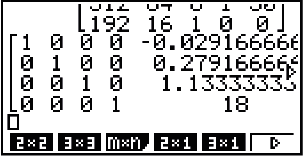 Abb. 6: Lösung des Gleichungssystems mit dem GTR
Abb. 6: Lösung des Gleichungssystems mit dem GTR
2.5
SHIFT  F5: G-Solv
F5: G-Solv  F1: ROOT
F1: ROOT
Damit erhältet du die Nullstellen 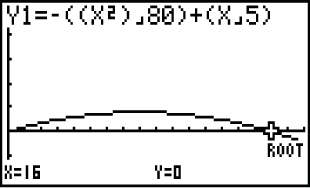 Abb. 7: Nullstellen bestimmen mit dem GTR
Abb. 7: Nullstellen bestimmen mit dem GTR
SHIFT  F5: G-Solv
F5: G-Solv  F6
F6  F3
F3
Wähle als untere Schranke die untere Integrationsgrenze 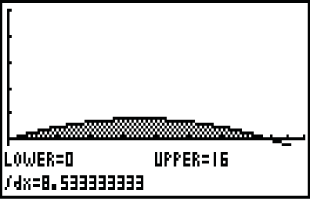 Abb. 8: Integralberechnung mit dem GTR
Abb. 8: Integralberechnung mit dem GTR
2.6
- Bestimme die Integralfunktion
.
- Setze die Integralfunktion mit
gleich und löse nach
auf.
SHIFT  F5: G- Solv
F5: G- Solv  F6
F6  F5: ISCT
F5: ISCT
Du musst jetzt nur noch die beiden Kurven auswählen und bekommst dann den Schnittpunkt 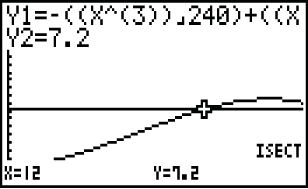 Abb. 10: Schnittstelle mit dem GTR bestimmen
Abb. 10: Schnittstelle mit dem GTR bestimmen
2.7
2.8
RUN MAT  OPTN
OPTN  F5:STAT
F5:STAT  F3:DIST
F3:DIST  F5:BIN
F5:BIN  F3InvB
F3InvB
 Abb. 11: Eingabe der Daten für die Binomialverteilung
Abb. 11: Eingabe der Daten für die Binomialverteilung
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.