HT 1

Induktion und Wirbelströme

Teilaufgabe 1: Physikalische Grundlagen der elektrischen Energieversorgung

Unser ganzes Alltagsleben basiert auf der ständigen Verfügbarkeit von elektrischer Energie. In Kraftwerken werden verschiedene Formen der Primärenergie zunächst in Bewegungsenergie und diese schließlich in elektrische Energie umgesetzt. Dabei kommt bei der Umsetzung von Bewegungsenergie in elektrische Energie ein Generator zum Einsatz. Abbildung 1 zeigt die wesentlichen Bestandteile eines Generators.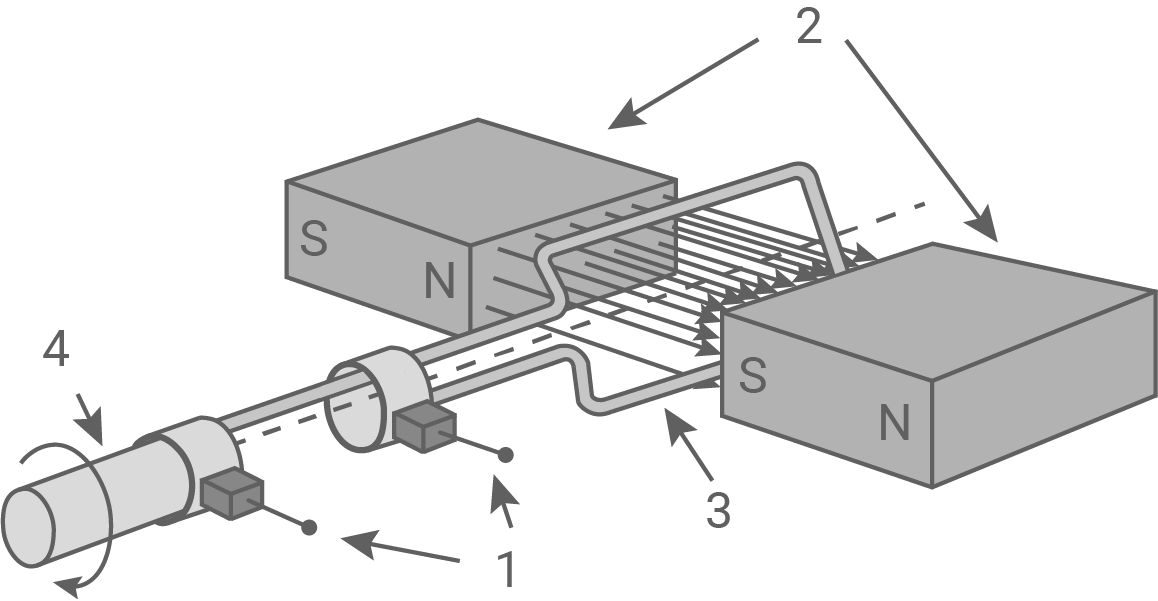

Abbildung 1: Prinzipieller Aufbau eines Generators

Beschreibe anhand dieser Skizze den prinzipiellen Aufbau eines Generators und gehe dabei auf die in Abbildung 1 nummerierten Komponenten ein.
Erläutere qualitativ, also ohne Gebrauch von mathematischen Zusammenhängen, inwiefern die elektromagnetische Induktion grundlegend für die Funktionsweise ist.

Im Weiteren geht es zunächst um die mathematisierte Formulierung des Induktionsgesetzes.

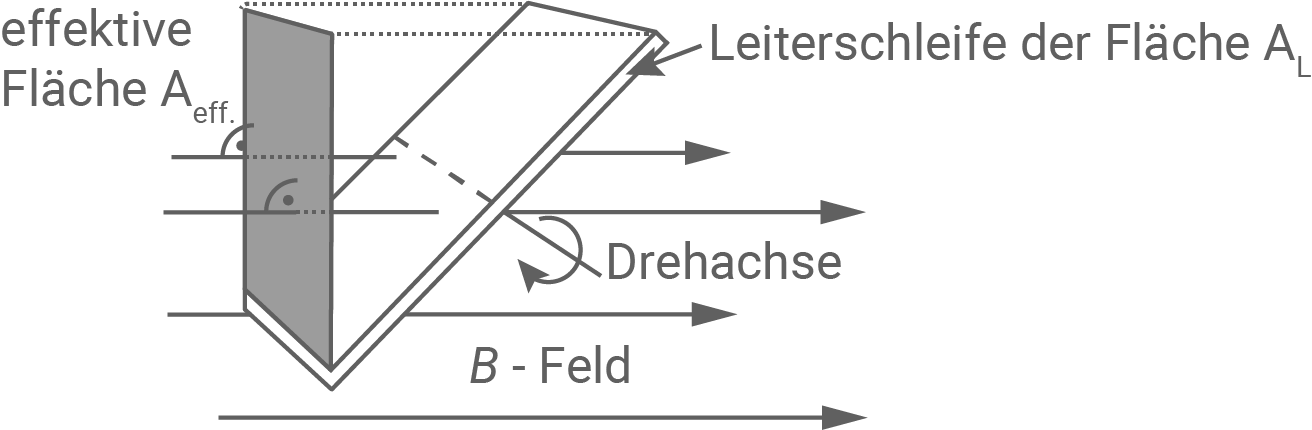
In einem homogenen Magnetfeld der Stärke $B$ befindet sich eine ebene Leiterschleife. Diese Leiterschleife besitzt bezüglich des homogenen Magnetfeldes eine effektive Querschnittsfläche $A_{\text {eff. }}$ , die je nach Orientierung der Leiterschleife ein positives oder negatives Vorzeichen besitzen kann. Diese effektive Querschnittsfläche $A_{\text {eff. }}$ wird von dem homogenen Magnetfeld orthogonal durchsetzt (siehe Abbildung 2).

Abbildung 2: Effektive Fläche einer Leiterschleife in einem homogenen Magnetfeld

Für eine Induktionsspannung $U_{\text {ind. }}$ in einer Leiterschleife mit Windungszahl $n$ kann es zwei mögliche Ursachen geben, die durch die beiden folgenden Zusammenhänge beschrieben werden:

(1)

$U_{\text {ind. }}=-n \cdot B \cdot \frac{\Delta A_{\text {eff. }}}{\Delta t}$

(2)

$U_{\text {ind. }}=-n \cdot A_{\text {eff. }} \cdot \frac{\Delta B}{\Delta t}$

In beiden Zusammenhängen bezeichnet $\Delta t$ ein kurzes Zeitintervall.

Erläutere die physikalische Aussage der beiden angegebenen Zusammenhänge.

In der exakten Formulierung gehen im Grenzfall immer kürzer werdende Zeitintervalle bei beiden Zusammenhängen die zeitlichen Änderungsraten $\frac{\Delta A_{\text {eff. }}}{\Delta t}$ bzw. $\frac{\Delta B}{\Delta t}$ in die jeweilige Ableitung nach der Zeit über. Die beiden Zusammenhänge lauten dann:

(1)

$U_{\text {ind. }}=-n \cdot B \cdot \dot{A}_{\text {eff. }}$

(2)

$U_{\text {ind. }}=-n \cdot A_{\text {eff. }} \cdot \dot{B}$

Der Punkt bedeutet dabei die Ableitung der entsprechenden Größe nach der Zeit.

Begründe, dass bei einem Generator wie in Abbildung 1 der Zusammenhang (2) für die Entstehung der Induktionsspannung nicht verantwortlich sein kann.
Erkläre qualitativ, dass sich beim Betrieb eines Generators wie in Abbildung 1 die effektive Fläche $A_{\text {eff. }}$ der Leiterschleife permanent mit der Zeit verändert.

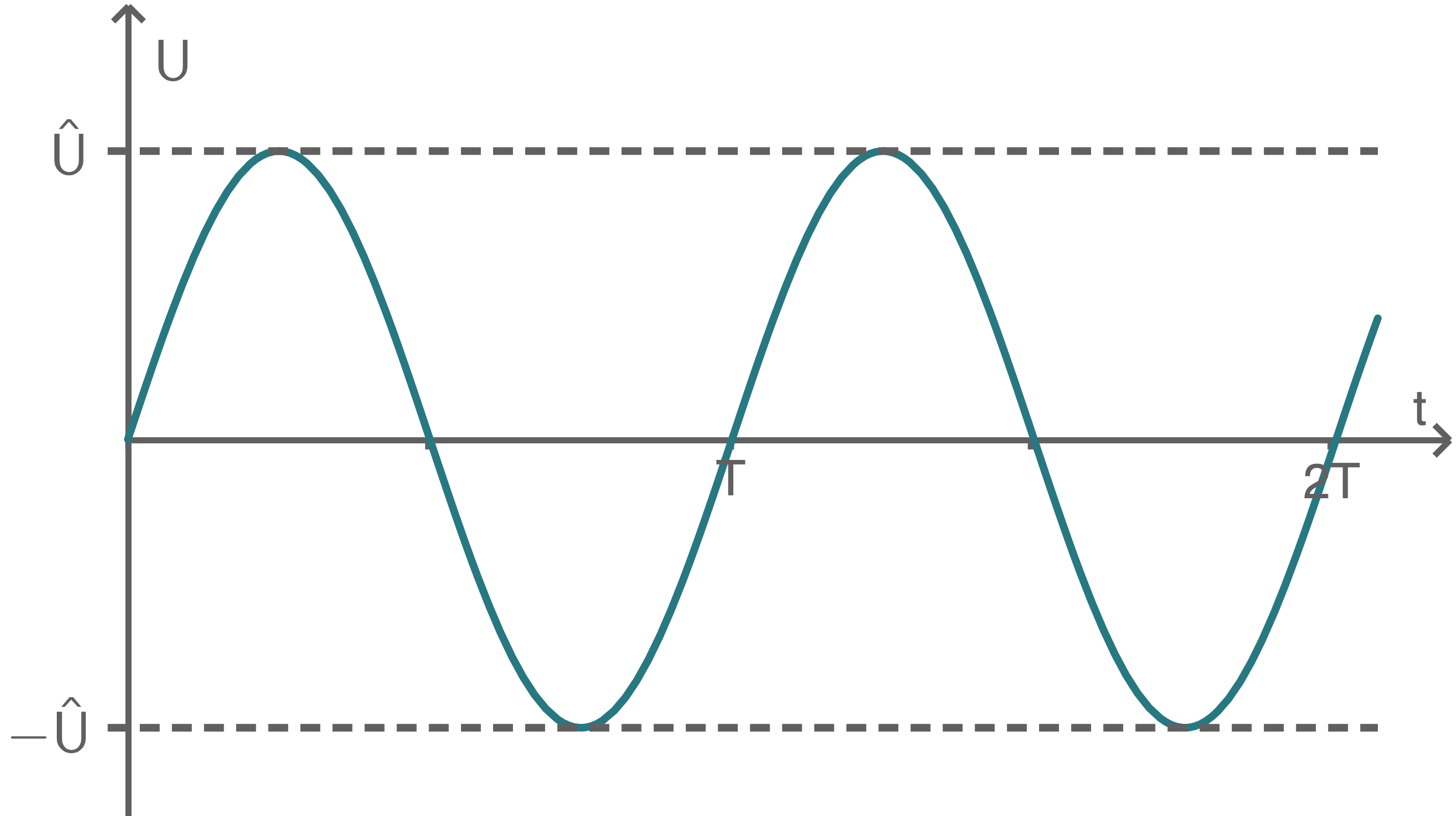
Beim Betrieb eines typischen Generators wird die in Abbildung 3 dargestellte Generatorspannung erzeugt. Dabei bezeichnet $\hat{U}$ die Spannungsamplitude.

Abbildung 3: Zeitlicher Verlauf der Generatorspannung

Für die Zeitabhängigkeit der effektiven Querschnittsfläche $A_{\text {eff. }}$ kann dabei der folgende Zusammenhang angenommen werden: $A_{\text {eff. }}(t)=A_{ L } \cdot \cos \left(\dfrac{2 \pi}{T} \cdot t\right).$

Es ist dabei vorausgesetzt, dass die Fläche der Leiterschleife $A_{ L }$ zum Zeitpunkt $t=0$ orthogonal zu den Feldlinien des homogenen Magnetfeldes steht und komplett von diesem homogenen Magnetfeld durchsetzt wird. Die Größe $T$ bezeichnet dabei die Umdrehungsdauer der Leiterschleife.

Zeige, dass in diesem Fall für die induzierte Spannung gilt: $U(t)=\hat{U} \cdot \sin \left(\dfrac{2 \pi}{T} \cdot t\right)$ mit der Spannungsamplitude $\hat{U}=n \cdot B \cdot A_{ L } \cdot \dfrac{2 \pi}{T}$ .

In einem konkreten Generator dieses Typs beträgt die Fläche der Leiterschleife $A_{ L }=50,0 \,\text{cm}^2,$ deren Windungszahl $n=300$ , die Stärke des Magnetfeldes $B=250\,\text{mT},$ und die Leiterschleife dreht sich pro Minute 3000-mal im Magnetfeld. Bestimme die Spannungsamplitude $\hat{U}$ eines so betriebenen Generators.

(7 + 11 + 6 + 4 Punkte)

Teilaufgabe 2: Elektrische Wirbelströme und ihre Anwendung beim Induktionsherd

Der Induktionsherd ist eine Alltagsanwendung von Wirbelströmen und hat Vorteile gegenüber Herdtypen mit direkter thermischer Energiezufuhr. Der schematische Aufbau eines Induktionsherdes ist in Abbildung 4 dargestellt.

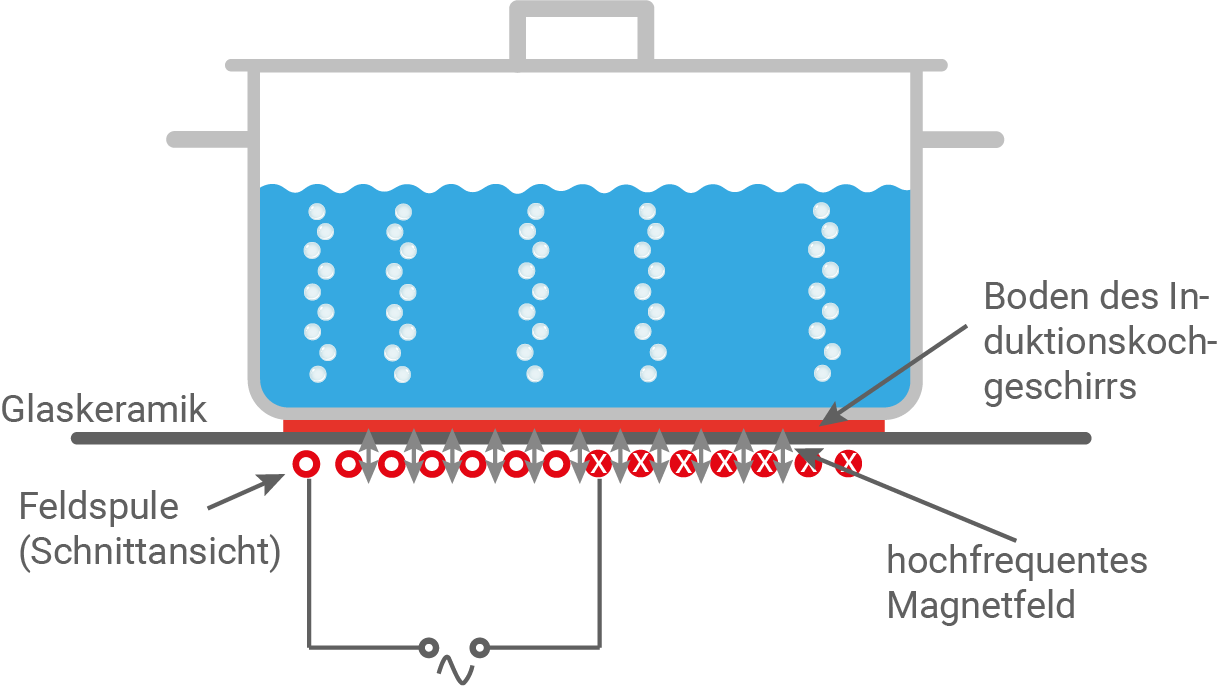
nrw physik abi gk 2021 ht 1 abbildung 4 aufbau eines typischen induktionsherdes

Abbildung 4: Aufbau eines typischen Induktionsherdes
Die Doppelpfeile zeigen die Richtung des hochfrequent wechselnden Magnetfeldes am Topfboden.

Der wesentliche Bestandteil eines Induktionsherdes ist die Feldspule, in der ein sehr schnell wechselndes, sogenanntes „hochfrequentes“ Magnetfeld erzeugt wird. Dieses sich schnell ändernde Magnetfeld verursacht im elektrisch leitenden Boden des Kochgeschirrs Induktionseffekte, welche dort zu einer starken Erwärmung führen.

Mit folgender Messung wurde das hochfrequente Magnetfeld untersucht. Auf einem eingeschalteten Induktionskochfeld wurde eine Leiterschleife mit drei Windungen platziert und der zeitliche Verlauf der darin induzierten Spannung mit einem Oszilloskop gemessen (Versuchsaufbau siehe Abbildung 5).

Abbildung 5: Messung des hochfrequenten Magnetfeldes an einem Induktionskochfeld

Begründe qualitativ, dass bei der in Abbildung 5 dargestellten Messung ausschließlich der Zusammenhang (2) $U_{\text {ind. }}=-n \cdot A_{\text {eff.}} \cdot \dot{B}$ (siehe Teilaufgabe 1b) für die im Oszilloskop gemessene Spannung verantwortlich ist.

Abbildung 6 zeigt die Einstellung der Zeitablenkung des Oszilloskops bei dieser Messung sowie den gemessenen zeitlichen Verlauf der induzierten Spannung in der Leiterschleife.

nrw physik abi 2021 ht 1 abbildung 6 einstellung der zeitablenkung des oszilloskops

Abbildung 6: Einstellung der Zeitablenkung des Oszilloskops (links) und angezeigter Induktionsspannungsverlauf (rechts)

nrw physik abi 2021 ht 1 abbildung 6 angezeigter induktionsspannungsverlauf

Im Folgenden soll von dem in Abbildung 6 eingezeichneten vereinfachend angenommenen Verlauf der Induktionsspannung ausgegangen werden.

Bestimme aus Abbildung 6 die Periodendauer $T,$ mit der sich das hochfrequente Magnetfeld des Induktionskochfeldes periodisch verändert.
Gib die Frequenz $f$ der Induktionsspannung in der Maßeinheit $\text{kHz}$ an.
Begründe qualitativ, dass der zeitliche Verlauf des Magnetfeldes in der Feldspule dieses Induktionsherdes dem in Abbildung 7 entspricht.

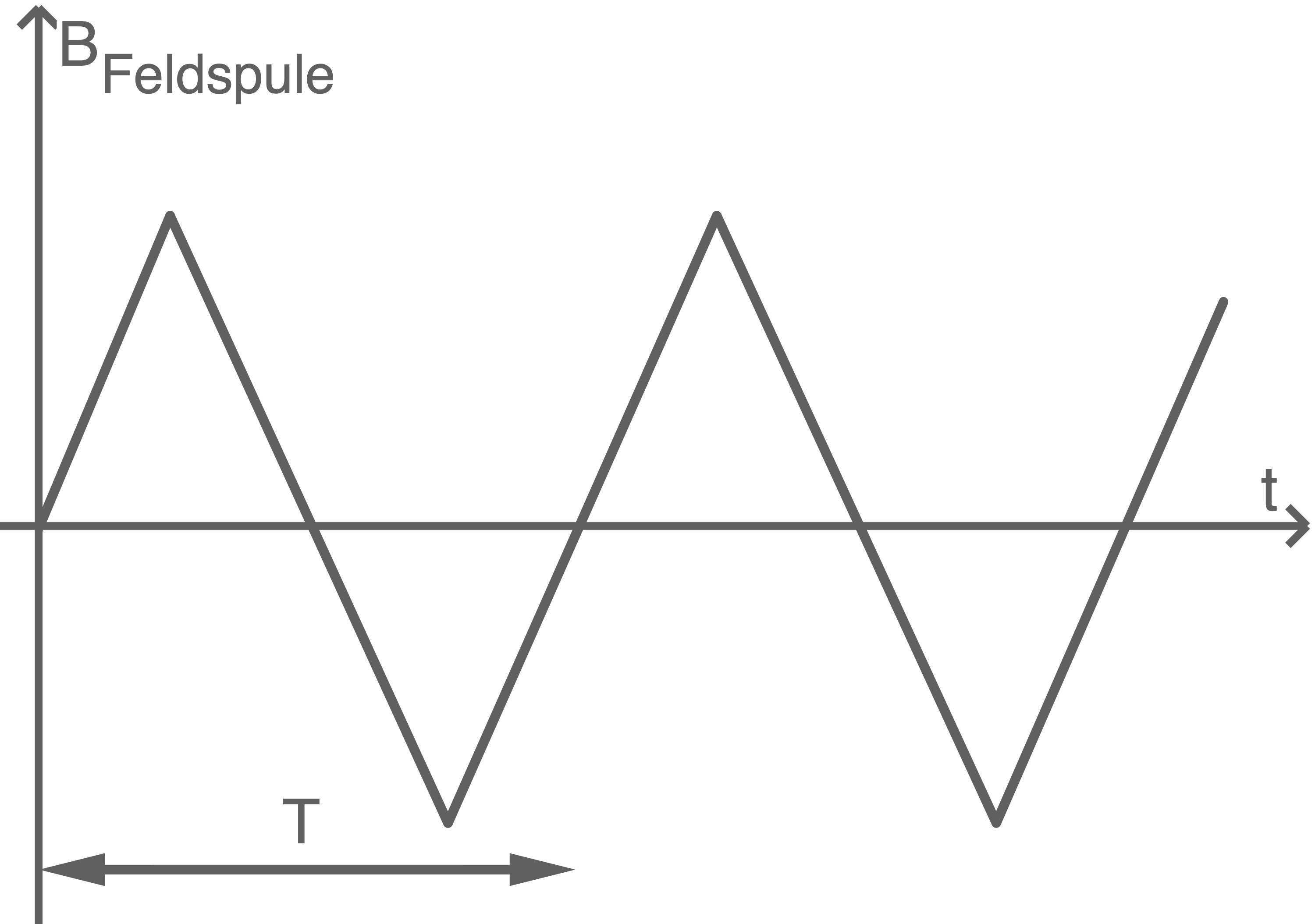
Abbildung 7: Zeitlicher Verlauf des Magnetfeldes in der Feldspule

Durch das sich schnell ändernde Magnetfeld in der Feldspule des Induktionsherdes werden Wirbelströme im elektrisch leitenden Boden des Kochgeschirrs hervorgerufen. Abbildung 8 zeigt eine Modellvorstellung für die Entstehung der Wirbelströme. Den Boden eines Induktionskochtopfs kann man sich aus vielen konzentrischen Kreisringen aufgebaut vorstellen. Jeder dieser Ringe ist eine kurzgeschlossene Leiterschleife.

Abbildung 8: Zerlegung des Geschirrbodens in konzentrische Kreisringe

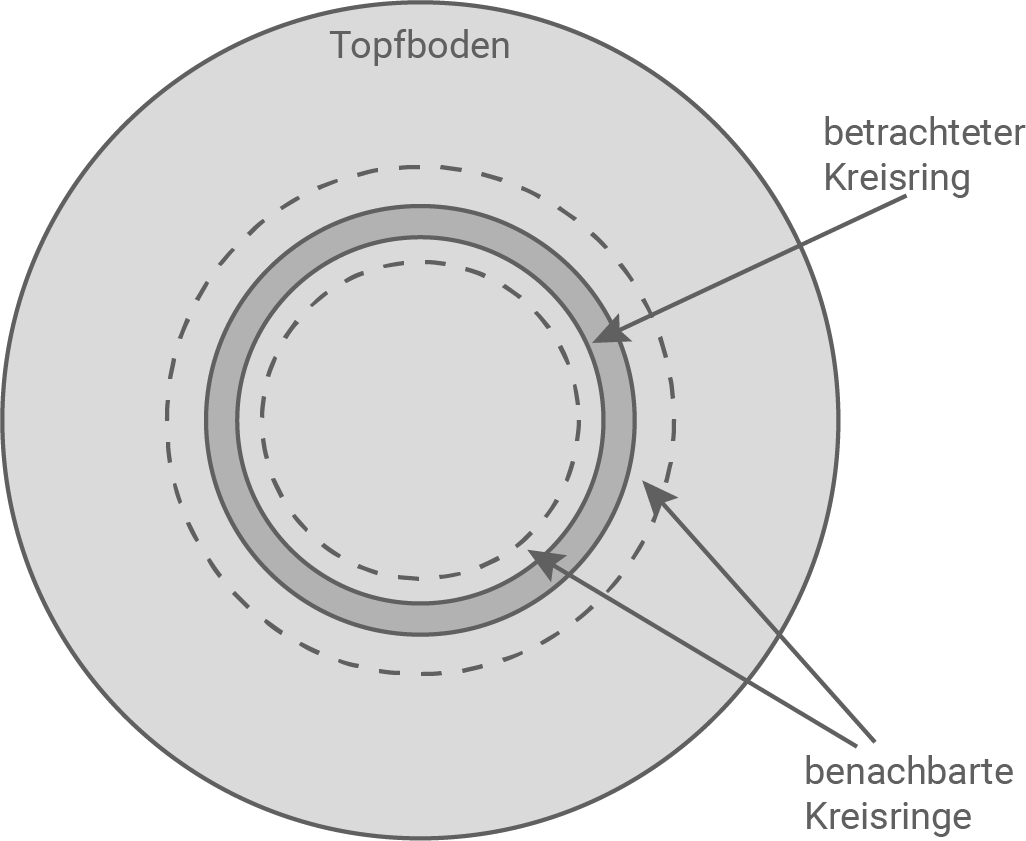Erkläre qualitativ, wie es auf dem Induktionsherd zu einem Kreisstrom, dem sogenannten „Wirbelstrom“, in einem Kreisring im Topfboden kommt.

Für die Heizleistung $P_{\text {Heiz }}$ des Wirbelstroms in einem Kreisring der Breite $b=1 \,\text{mm}$ in einem typischen Material für den Boden eines Induktionskochtopfs gilt:

$P_{\text {Heiz }}=\left(0,22 \dfrac{ \text{m} }{\Omega}\right) \cdot\left(\dfrac{\Delta B}{\Delta t}\right)^2 \cdot r^3$

Dabei bezeichnet $r$ den Radius des Kreisrings (in $\text {m}$ ) und $\dfrac{\Delta B}{\Delta t}$ die Änderungsrate des Magnetfeldes auf der Induktionsherdplatte.

Zeige anhand einer Einheitenbetrachtung, dass die rechte Seite des angegebenen Zusammenhangs tatsächlich die Maßeinheit der Leistung $\left(1 \;\text{W} =1 \dfrac{ \text{J} }{ \text{s} }\right)$ besitzt.

Bei dem in Teilaufgabe 2a) untersuchten Induktionsherd beträgt die Änderungsrate des Magnetfeldes $\dfrac{\Delta B}{\Delta t}=320 \;\dfrac{ \text{T} }{ \text{s} }.$

Bestimme anhand des obigen Zusammenhangs die Heizleistung $P_{\text {Heiz }}$ des Wirbelstroms in einem $b=1 \,\text{mm}$ breiten Kreisring mit $r=10 \,\text {cm}$ in der Einheit $\;\text{W}.$

(2 + 10 + 3 + 7 Punkte)

Teillösung 1: Physikalische Grundlagen der elektrischen Energieversorgung

Beschreibung des Aufbaus eines Generators

Bei einem Generator dieses Typs dreht sich eine Leiterschleife (3) in einem homogenen äußeren Magnetfeld. Das Magnetfeld besteht zwischen den Polen eines ortsfesten Permanentmagneten (2). Die Drehung der Leiterschleife erfolgt über eine angetriebene Achse (4) und die Enden der Leiterschleife sind über zwei Kontakte (1) nach außen verbunden.

Erläuterung der Notwendigkeit der elektromagnetischen Induktion für die Funktionsweise

Die Drehung der Leiterschleife in dem Magnetfeld führt dazu, dass sich der Anteil des Magnetfeldes, der die Leiterschleife durchsetzt, zeitlich ändert. Nach dem Induktionsgesetz wird damit an den Enden der Leiterschleife eine elektrische Spannung, die Induktionsspannung, hervorgerufen.

Erläuterung der physikalischen Aussage der beiden angegebenen Zusammenhänge

Der Zusammenhang (1) bedeutet, dass eine Induktionsspannung $U_{\text {ind. }}$ an den Enden einer Leiterschleife hervorgerufen wird, wenn sich die effektive Fläche $A_{\text {eff. }}$ bezüglich des Magnetfeldes $B$ zeitlich ändert. Die Induktionsspannung $U_{\text {ind. }}$ ist dabei proportional zur Windungszahl $n$ , zur Stärke des Magnetfeldes $B$ und zeitlichen Änderungsrate der effektiven Fläche $A_{\text {eff. }}.$

Erklärung warum bei einem Generator wie in Abbildung 1 der Zusammenhang (2) nicht für die Entstehung der Induktionsspannung verantwortlich ist

Der Zusammenhang (2) bedeutet, dass eine Induktionsspannung $U_{\text {ind. }}$ an den Enden einer Leiterschleife hervorgerufen wird, wenn sich die Stärke des Magnetfeldes $B$ , welches die effektive Fläche $A_{\text {eff.}}$ der Leiterschleife durchsetzt, zeitlich ändert. Die Induktionsspannung $U_{\text {ind. }}$ ist dabei proportional zur Windungszahl $n$ , zur effektiven Fläche $A_{\text {eff.}}$ und zur zeitlichen Änderungsrate der Stärke des Magnetfeldes $B.$

Bei dem in Abbildung 1 dargestellten Generator ist die Stärke $B$ des Magnetfeldes zeitlich konstant, da es sich um einen Permanentmagneten handelt:

$\begin{array}[t]{rll} \dfrac{\Delta B}{\Delta t}&=& \dfrac{B(t_2)-B(t_1)}{\Delta t} &\quad \scriptsize \mid\; B(t_2)=B(t_1) \\[5pt] &=& \dfrac{B(t_2)-B(t_2)}{\Delta t} &\quad \scriptsize \\[5pt] &=& \dfrac{0}{\Delta t} &\quad \scriptsize \\[5pt] &=& 0 \end{array}$

Ensetzen der zeitliche Änderungsrate des Magnetfeldes $\dfrac{\Delta B}{\Delta t}=0$ in den Zusammenhang (2) liefert:

$\begin{array}[t]{rll} U_{\text {ind. }}&=& -n \cdot A_{\text{eff}} \cdot \dfrac{\Delta B}{\Delta t} &\quad \scriptsize \mid\; \dfrac{\Delta B}{\Delta t}=0 \\[5pt] &=& -n \cdot A_{\text{eff}} \cdot 0 &\quad \scriptsize \\[5pt] &=& 0 \end{array}$

Der Zusammenhang (2) kann folglich nicht für die Induktionsspannung an der Leiterschleife verantwortlich sein.

Erklärung der permanenten Veränderung der effektiven Fläche der Leiterschleife

Dadurch, dass sich die Leiterschleife im ortsfesten Magnetfeld dreht, ändert sich ihre effektive Fläche $A_{\text {eff. }}$ bezüglich dieses Magnetfeldes. Steht die Leiterschleife orthogonal zum Magnetfeld, ist der Betrag der effektiven Fläche gleich der Fläche der Leiterschleife $\left|A_{\text {eff.}}\right|=A_L$ und damit maximal. Eine Viertelumdrehung später ist die Fläche der Leiterschleife parallel zum Magnetfeld und damit ist $A_{\text {eff. }}=0$ . Zwischen diesen Werten ändert $\operatorname{sich} A_{\text {eff.}}$ kontinuierlich.

Die Induktionsspannung beim dargestellten Generator wird ausschließlich durch die zeitliche Änderung der effektiven Fläche $A_{\text {eff. }}$ verursacht.

Es gilt $A_{\text {eff. }}=A_L \cdot \cos \left(\frac{2 \pi}{T} \cdot t\right).$ Ableiten mit Anwendung der Kettenregel von $A_{\text {eff. }}$ nach der Zeit liefert:

$\dot{A}_{\text {eff. }} = - \sin \left(\dfrac{2 \pi}{T} \cdot t\right) \cdot \dfrac{2 \pi}{T} \cdot 1$

Einsetzen in den Zusammenhang (1) aus der obrigen Teilaufgabe 1a) liefert:

Rechenweg anzeigen

$U_{\text {ind. }} \left(t\right)=\hat{U} \cdot \sin \left(\dfrac{2 \pi}{T} \cdot t\right)$

Der in Abbildung 3 dargestellte zeitliche Verlauf der Generatorspannung entspricht dem Verlauf der Sinusfunktion. Die Amplitude $\hat{U}$ der Generatorspannung entspricht dem Vorfaktor der Sinusfunktion, also: $\hat{U}=n \cdot B \cdot A_{L} \cdot \dfrac{2 \pi}{T}.$

Einsetzen der gegebenen Werte in den Zusammenhang liefert:

Rechenweg anzeigen

$\hat{U}=118 \;\text{V}$

Teillösung 2: Elektrische Wirbelströme und ihre Anwendung beim Induktionsherd

Bei der abgebildeten Messung auf dem Induktionsherd ändert sich die effektive Fläche $A_{\text {eff.}}$ der Leiterschleife nicht. Die Induktionsspannung wird daher ausschließlich durch die zeitliche Änderung des Magnetfeldes verursacht. Die Induktionsspannung $U_{\text {ind.}}$ wird durch den Zusammenhang (2) $U_{\text {ind. }}=-A_{\text {eff.}} \cdot \frac{\Delta B}{\Delta t}=-A_{\text {eff.}} \cdot \dot{B}$ beschrieben.

Bestimmung der Periodendauer $T$

Aus der Einstellung der Zeitablenkung am Oszilloskop ist ersichtlich, dass ein Kästchen in $x$ -Richtung der Zeitdauer $\Delta t=10 \; \mu\text{s}=1,0 \cdot 10^{-5} \;\text{s}$ entspricht. Der periodische Spannungsverlauf zeigt eine Periodendauer von ca. 3 Kästchen, womit die Periodendauer der Induktionsspannung $T=3,0 \cdot 10^{-5} \, \text{s}$ beträgt.

Angabe der Frequenz der Induktionsspannung

$\begin{array}[t]{rll} f &=& \frac{1}{T} &\quad \scriptsize \\[5pt] &=& \frac{1}{3,0 \cdot 10^{-5} \;\text{s}} &\quad \scriptsize \\[5pt] &=& \frac{1}{3,0 \cdot 10^{-5} \;\text{Hz}} &\quad \scriptsize \\[5pt] &=& \frac{1}{3,0} \cdot 10^{5} \cdot 10^{-3} \;\text{kHz} &\quad \scriptsize \\[5pt] &=& 0,33 \cdot 10^{2} \;\text{kHz} &\quad \scriptsize \\[5pt] &=& 33 \; \text{kHz} \end{array}$

Begründung des zeitlichen Verlaufes des Magnetfeldes

Der vereinfachend angenommene Spannungsverlauf auf dem Oszilloskopbildschirm zeigt, dass die Induktionsspannung in der Leiterschleife periodisch zwischen einem positiven und einem negativen Wert hin und her wechselt. Zwischen den Wechseln kann der Wert von $U_{\text {ind.}}$ als konstant angenommen werden. Da nach dem Induktionsgesetz gilt: $U_{\text {ind. }}=-n \cdot A_{\text {eff.}} \cdot \dot{B}$ , folgt daraus, dass zwischen den Wechseln der Vorzeichen von $U_{\text {ind.}}$ die Änderungsrate der Stärke des Magnetfeldes $\dot{B}$ konstant ist. Dies entspricht dem in Abbildung 7 angegebenen zeitlichen Verlauf von $B$ .

Der Kreisring im Boden des Topfes stellt eine Leiterschleife mit Windungszahl $n=1$ dar. Das sich zeitlich ändernde Magnetfeld, welches durch diese Leiterschleife greift, erzeugt in dieser Leiterschleife eine Induktionsspannung $U_{\text {ind.}}.$ Da es sich um eine kurzgeschlossene Leiterschleife handelt, verursacht diese Induktionsspannung $U_{\text {ind.}}$ unmittelbar einen elektrischen Strom, den Wirbelstrom in diesem Kreisring.

Zeigen, dass $P_{\text{Heiz}}$ die Maßeinheit der Leistung hat

Rechenweg anzeigen

$\left[\left(0,22 \,\dfrac{\text{m}}{\Omega}\right) \cdot\left(\dfrac{\Delta B}{\Delta t}\right)^2 \cdot r^3\right]= \,\text{W}$

Bestimmung der Heizleistung $P_{\text{Heiz}}$ des Wirbelstroms

Für einen Kreisring der Breite $b=1 \,\text{mm}$ kann die angegebene Formel verwendet werden.

Rechenweg anzeigen

$P_{\text {Heiz }}= 22,5 \,\text{W}$