HT 3
Der Photoeffekt
Teilaufgabe 1: Albert Einstein und der Photoeffekt Albert Einstein ist es gelungen, den Photoeffekt mithilfe des Teilchencharakters von Licht zu erklären. Für die Energiebilanz des Photoeffekts ist nach Einstein die folgende Gleichung von Bedeutung:
a)
- Beschreibe kurz das physikalische Phänomen, das als Photoeffekt bezeichnet wird.
- Erläutere die angegebene Gleichung im Zusammenhang mit dem Photoeffekt.
b)
Abbildung 1 zeigt eine Sonderbriefmarke, die zu Ehren Albert Einsteins von der Deutschen Bundespost herausgegeben wurde. Die Briefmarke zeigt Licht in sechs unterschiedlichen Farben, das auf eine Metallschicht trifft. Die neun dicken schwarzen Punkte stellen Elektronen dar, die gepunkteten Linien deren Bahnkurven und die Pfeile die zugehörigen Geschwindigkeitsvektoren.

Teilaufgabe 2: Experimentelle Untersuchung des Photoeffekts
Eine Photozelle besteht aus einem evakuierten Glaskolben, in dem sich zwei Elektroden befinden. Auf die Kathode (K) ist eine metallische Schicht aufgedampft. Vor der Kathode sitzt als Anode (A) ein kreisförmig gebogener Metallring. Die Kathode wird durch eine Blende (B) mit Licht einer Quecksilberdampflampe (QDL) beleuchtet. Mithilfe von Farbfiltern (F) erhält man monochromatisches Licht. Zwischen Kathode und Anode wird die Stärke des Photostroms 
Abbildung 1: Sonderbriefmarke der Deutschen Bundespost
- Erkläre mithilfe des Photoeffekts, weshalb die vom rechten Bereich der Abbildung 1 ausgehenden Pfeile deutlich länger dargestellt werden als die vom linken Bereich der Abbildung 1 ausgehenden Pfeile.
- Interpretiere physikalisch die Tatsache, dass keine gepunkteten Linien im roten Bereich dargestellt werden.
(5 + 6 Punkte)
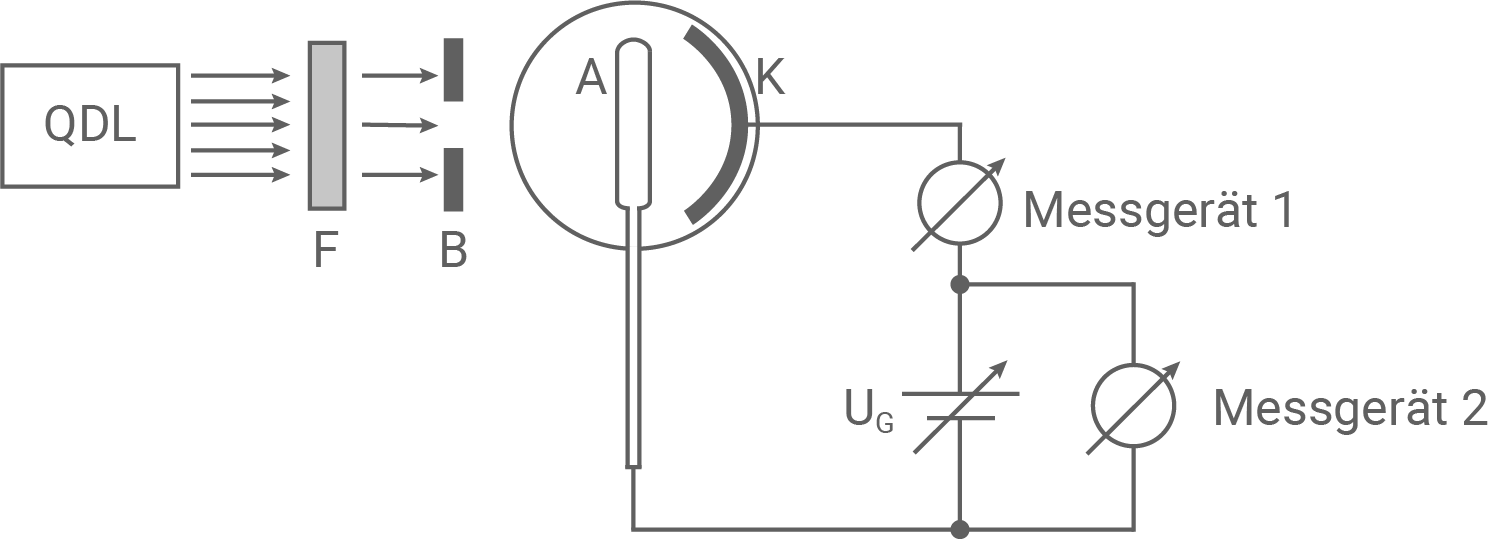 Abbildung 2: Experimenteller Aufbau zur Gegenfeldmethode
Abbildung 2: Experimenteller Aufbau zur Gegenfeldmethode
a)
Mittels der beiden Messgeräte aus Abbildung 2 werden die Gegenspannung  und die Photostromstärke
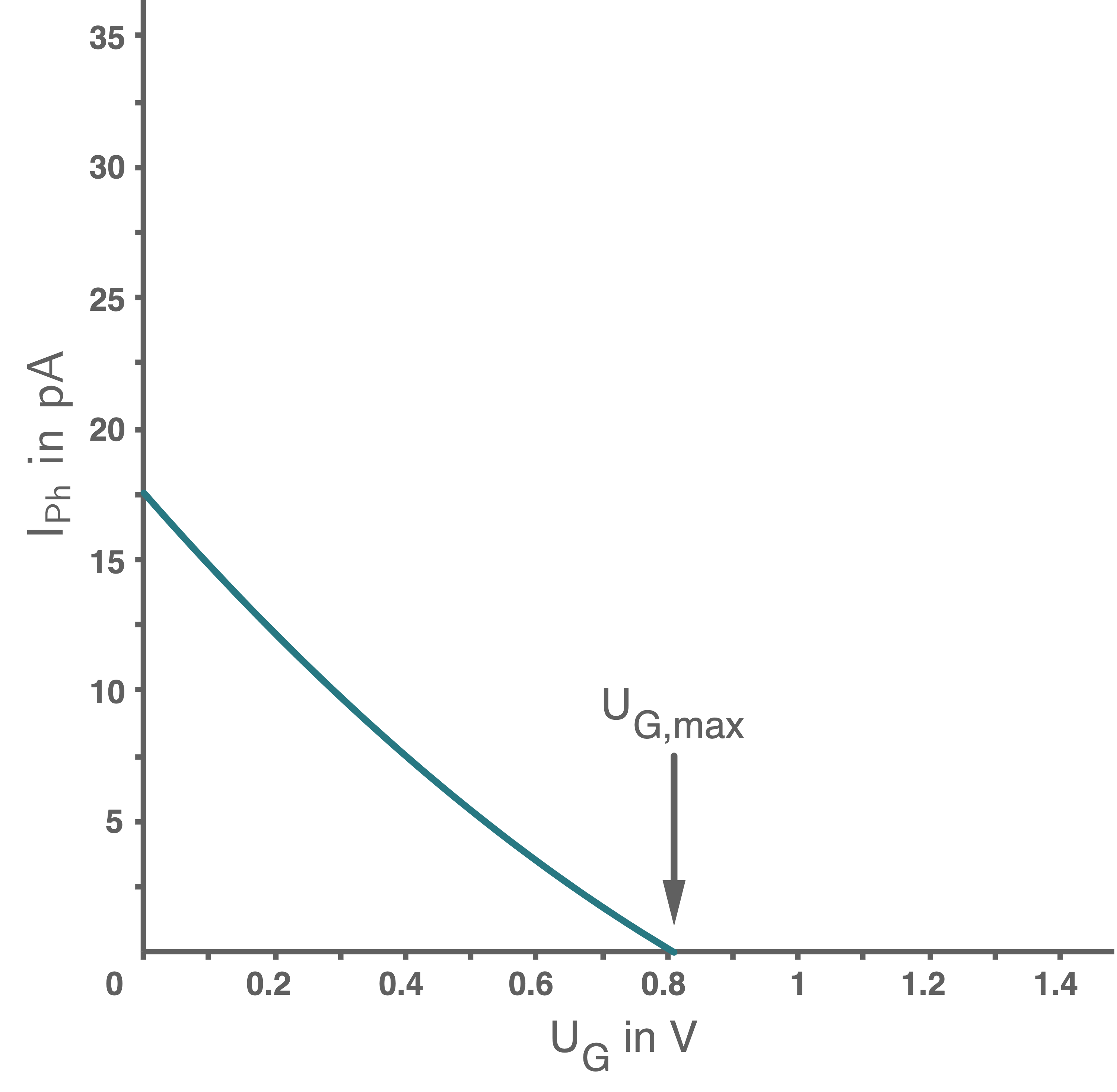
und die Photostromstärke  gemessen. Abbildung 3 zeigt die gemessene Photostromstärke
gemessen. Abbildung 3 zeigt die gemessene Photostromstärke  in Abhängigkeit von der angelegten Gegenspannung
in Abhängigkeit von der angelegten Gegenspannung  bei der Beleuchtung der Photozelle mit Licht der Wellenlänge
bei der Beleuchtung der Photozelle mit Licht der Wellenlänge  .
.
- Gib an, mit welchem der beiden Messgeräte in Abbildung 2 die Stärke
des Photostroms gemessen werden kann.
- Beschreibe den Verlauf des in Abbildung 3 gezeigten Graphen.
- Erkläre den Verlauf des Graphen anhand der Abläufe im Inneren der Photozelle.

Abbildung 3: Gemessene Photostärke in Abhängigkeit von der angelegten Gegenspannung
b)
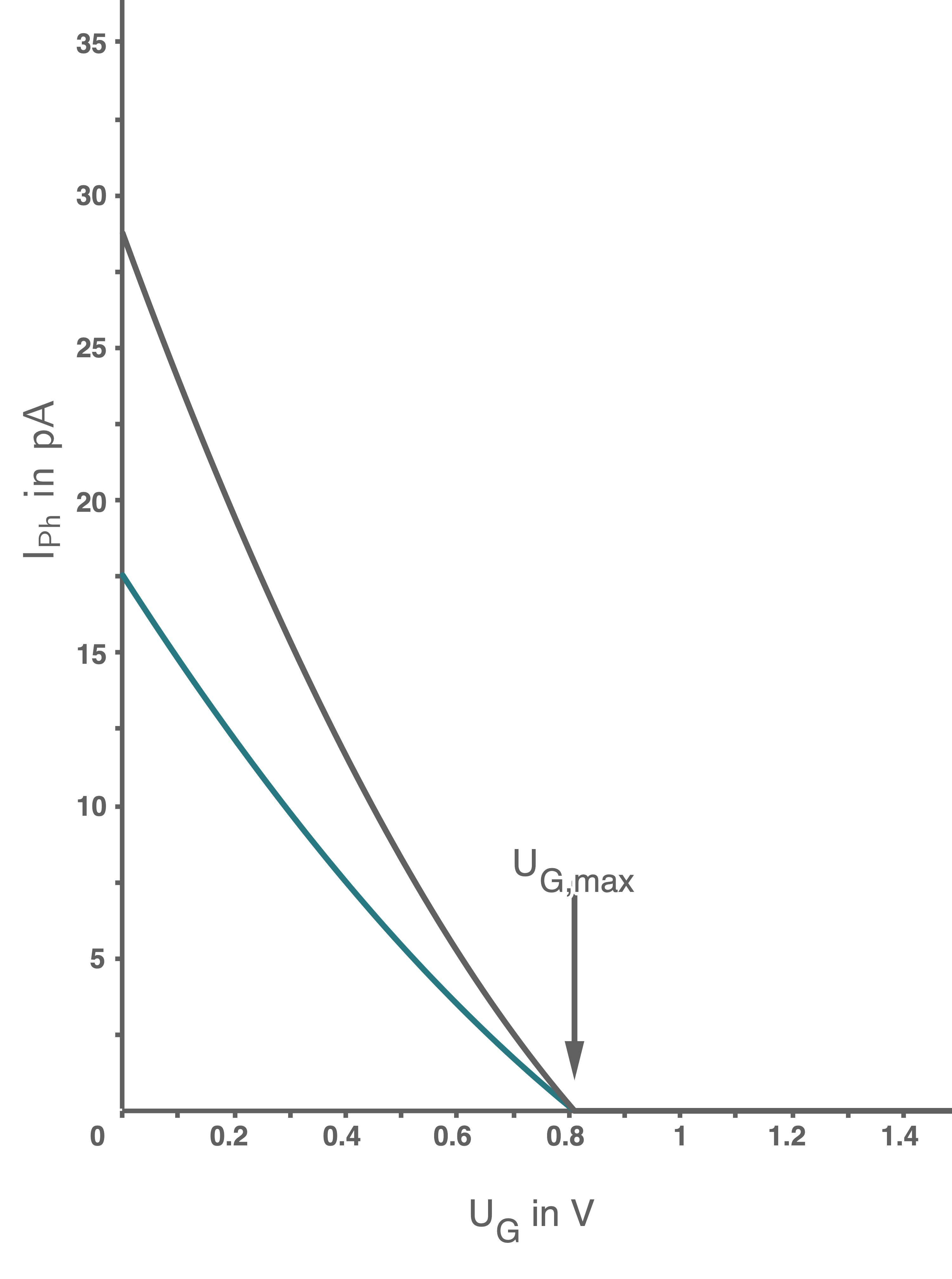
Die Blendenöffnung wird nun bei gleicher Wellenlänge vergrößert, sodass sich ein größerer Lichtfleck auf der Kathode bildet.
Skizziere in Abbildung 3 einen möglichen Graphen im Hinblick auf die veränderten Versuchsbedingungen.
c)
Die kinetische Energie der aus der Kathode ausgelösten Elektronen kann mithilfe der Beziehung  berechnet werden, wobei
berechnet werden, wobei  die Elementarladung bezeichnet.
die Elementarladung bezeichnet.
- Erläutere, weshalb mit der angegebenen Beziehung die kinetische Energie der ausgelösten Elektronen berechnet werden kann.
- Leite den Zusammenhang
zwischen der Grenzspannung
und der Frequenz
des eingestrahlten Lichts her.
d)
Die folgende Tabelle zeigt die Messwerte einer Messreihe, bei der die Grenzspannung  in Abhängigkeit von der Frequenz
in Abhängigkeit von der Frequenz  des verwendeten Lichts gemessen wurde.
des verwendeten Lichts gemessen wurde.
Bestimme anhand einer grafischen Auswertung mithilfe aller Messwerte
Teilaufgabe 3: Lenard-Versuch
Zur Bestimmung der spezifischen Ladung | 5,19 | 0,13 |
| 5,49 | 0,27 |
| 6,88 | 0,81 |
| 7,40 | 1,02 |
- das Planck'sche Wirkungsquantum
- die Austrittsenergie
des verwendeten Kathodenmaterials,
- die Grenzfrequenz
des verwendeten Kathodenmaterials.
(7 + 2 + 6 + 9 Punkte)
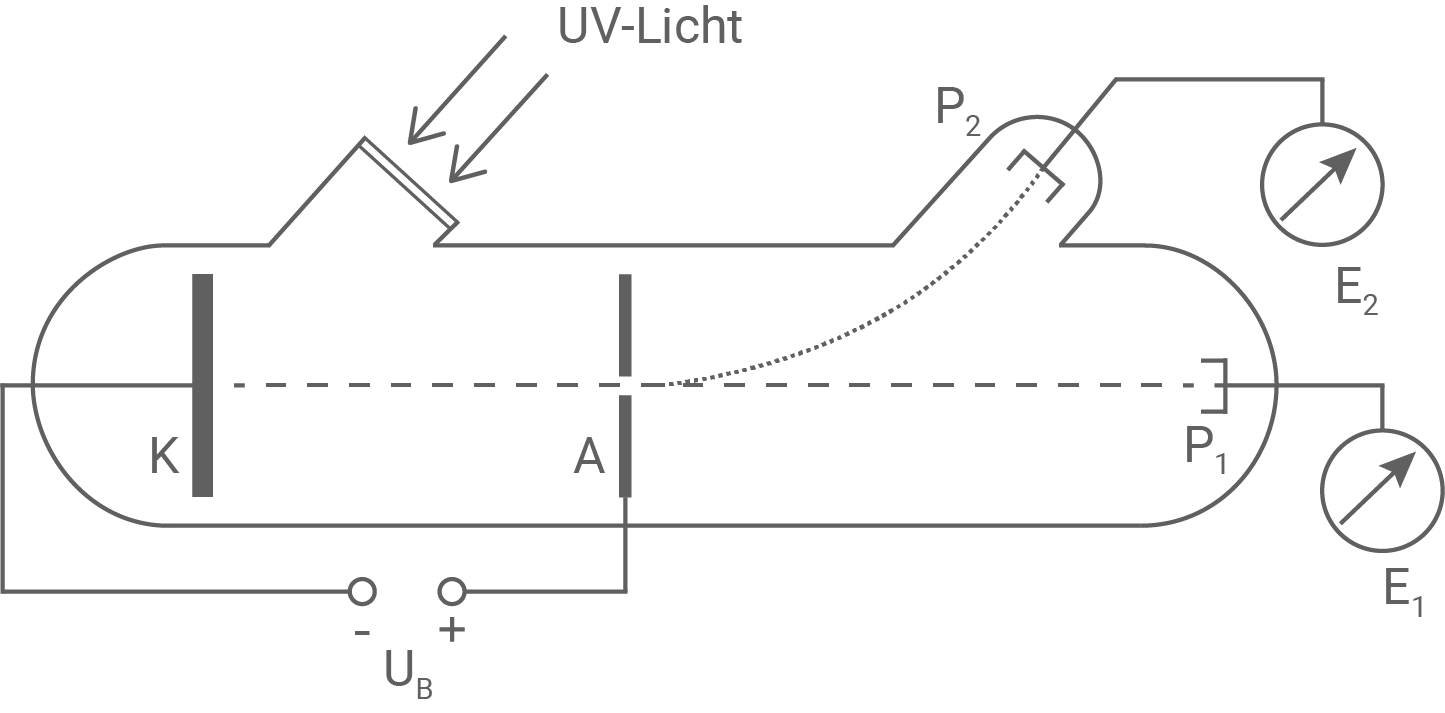
Abbildung 4: Versuchsaufbau von Lenard (ohne Magnetfeld: --- mit Magnetfeld:  )
)
Durch ein geeignetes homogenes Magnetfeld der Stärke
a)
- Gib die Orientierung eines geeigneten Magnetfeldes an, das die Elektronen hinter der Anode zum Auffänger
ablenken kann.
- Begründe, dass sich die Elektronen bei eingeschaltetem Magnetfeld von der Anode zum Auffänger
auf einer Kreisbahn bewegen.
b)
Zwischen der kinetischen Energie  beim Eintritt in das zeitlich konstante Magnetfeld der Stärke
beim Eintritt in das zeitlich konstante Magnetfeld der Stärke  und dem Radius
und dem Radius  der Kreisbahn gilt der Zusammenhang
der Kreisbahn gilt der Zusammenhang
 Beurteile, ob die Wellenlänge
Beurteile, ob die Wellenlänge  des eingestrahlten UV-Lichts bei kleinen Beschleunigungsspannungen
des eingestrahlten UV-Lichts bei kleinen Beschleunigungsspannungen  einen Einfluss auf den Radius
einen Einfluss auf den Radius  der Kreisbahn hat.
der Kreisbahn hat.
c)
Zwischen Kathode und Anode liegt die Beschleunigungsspannung  an. Damit die Elektronen den Auffänger
an. Damit die Elektronen den Auffänger  auf einer Kreisbahn mit dem erforderlichen Radius
auf einer Kreisbahn mit dem erforderlichen Radius  erreichen, muss die Stärke des Magnetfeldes
erreichen, muss die Stärke des Magnetfeldes  betragen. Gehe zunächst vereinfachend davon aus, dass die Elektronen beim Verlassen der Kathode die kinetische Energie
betragen. Gehe zunächst vereinfachend davon aus, dass die Elektronen beim Verlassen der Kathode die kinetische Energie  besitzen.
besitzen.
 . Das verwendete Kathodenmaterial Aluminium hat die Austrittsenergie
. Das verwendete Kathodenmaterial Aluminium hat die Austrittsenergie  .
.
- Bestimme mithilfe der Messdaten und unter Verwendung des Zusammenhangs aus Aufgabenteil b) die spezifische Ladung
des Elektrons in der Einheit
mit einer Genauigkeit von zwei Nachkommastellen.
- Untersuche, ob die Vereinfachung
im Rahmen der oben angegebenen Genauigkeit einen Einfluss auf den Messwert der spezifischen Ladung
hat.
(4 + 4 + 7 Punkte)
Teillösung 1: Albert Einstein und der Photoeffekt
a)
Beschreibung des Photoeffekts
Als Photoeffekt wird das physikalische Phänomen bezeichnet, dass Licht hinreichend großer Frequenz (bzw. hinreichend kleiner Wellenlänge) Elektronen aus Materialien (z. B. Metallen) herauslösen kann.
Erläuterung der Gleichung
Der Term auf der linken Seite  der Gleichung gibt an, dass der Energieaustausch von Licht mit Materie beim Photoeffekt durch Photonen erfolgt (quantisiert in festen Energiebeträgen). Ein einzelnes Photon wird von einem einzigen Elektron absorbiert und das Photon gibt dabei seine Energie vollständig an das Elektron ab.
Der Term auf der rechten Seite
der Gleichung gibt an, dass der Energieaustausch von Licht mit Materie beim Photoeffekt durch Photonen erfolgt (quantisiert in festen Energiebeträgen). Ein einzelnes Photon wird von einem einzigen Elektron absorbiert und das Photon gibt dabei seine Energie vollständig an das Elektron ab.
Der Term auf der rechten Seite  der Gleichung besagt, dass das Elektron eine Ablöseenergie (an das Atomgitter) abgeben muss, um die Oberfläche des Materials verlassen zu können. Der Rest der Photonenenergie steht dem Elektron als kinetische Energie zur Verfügung.
der Gleichung besagt, dass das Elektron eine Ablöseenergie (an das Atomgitter) abgeben muss, um die Oberfläche des Materials verlassen zu können. Der Rest der Photonenenergie steht dem Elektron als kinetische Energie zur Verfügung.
b)
Erklärung der unterschiedlich langen Pfeile in Abbildung 1
![\(\begin{array}[t]{rll}
E_{\text {Photon }}&=& E_{\text {kin }}+E_{\text {A }} &\quad \scriptsize \\[5pt]
h \cdot f&=& \dfrac{1}{2}\cdot m\cdot v^2+E_{\text {A }}
\end{array}\)](https://www.schullv.de/resources/formulas/cd91b677b2481f4c6d3edb83f2c93560b0910506c33045e57dfacf9f7ef39169_light.svg) Die Frequenz
Die Frequenz  des Lichts nimmt von links (rot) nach rechts (violett) zu. Damit nimmt auch die Photonenenergie
des Lichts nimmt von links (rot) nach rechts (violett) zu. Damit nimmt auch die Photonenenergie  von links nach rechts zu. Die Differenz von Photonenenergie und Ablöseenergie
von links nach rechts zu. Die Differenz von Photonenenergie und Ablöseenergie  , die den ausgelösten Elektronen als kinetische Energie
, die den ausgelösten Elektronen als kinetische Energie  zur Verfügung steht, wird folglich von links nach rechts größer. Da mit steigender kinetischer Energie auch die Geschwindigkeit
zur Verfügung steht, wird folglich von links nach rechts größer. Da mit steigender kinetischer Energie auch die Geschwindigkeit  der Elektronen wächst, werden die vom rechten Bereich ausgehenden Pfeile (Geschwindigkeitsvektoren) deutlich länger als im linken Bereich dargestellt.
Interpretation der Tatsache, dass keine gepunkteten Linien im roten Bereich dargestellt werden
Das rote Licht hat die kleinste Frequenz
der Elektronen wächst, werden die vom rechten Bereich ausgehenden Pfeile (Geschwindigkeitsvektoren) deutlich länger als im linken Bereich dargestellt.
Interpretation der Tatsache, dass keine gepunkteten Linien im roten Bereich dargestellt werden
Das rote Licht hat die kleinste Frequenz  und damit auch die kleinste Photonenenergie
und damit auch die kleinste Photonenenergie  . Die fehlenden gepunkteten Linien im roten Bereich können darauf hindeuten, dass die Photonenenergie kleiner ist als die Ablöseenergie der Elektronen, die infolgedessen die Metalloberfläche nicht verlassen können.
. Die fehlenden gepunkteten Linien im roten Bereich können darauf hindeuten, dass die Photonenenergie kleiner ist als die Ablöseenergie der Elektronen, die infolgedessen die Metalloberfläche nicht verlassen können.
Teillösung 2: Experimentelle Untersuchung des Photoeffekts
a)
Angabe des Messgerätes zur Messung der Stärke  des Photostroms
Die Stärke
des Photostroms
Die Stärke  des Photostroms kann mit dem Messgerät 1 gemessen werden.
Beschreibung des Verlaufs des Grahpen
Die Stärke
des Photostroms kann mit dem Messgerät 1 gemessen werden.
Beschreibung des Verlaufs des Grahpen
Die Stärke  des Photostroms zwischen Kathode und Anode nimmt mit wachsender Gegenspannung
des Photostroms zwischen Kathode und Anode nimmt mit wachsender Gegenspannung  immer weiter ab und wird ab einer bestimmten Grenzspannung
immer weiter ab und wird ab einer bestimmten Grenzspannung  zu
zu  Erklärung des Verlaufs des Graphen
Die angelegte Gegenspannung ist so gepolt, dass zwischen Kathode und Anode ein elektrisches Feld besteht, in dem die ausgelösten Elektronen abgebremst werden. Dabei verlieren die Elektronen kinetische Energie und erreichen die Anode nur dann, wenn ihre kinetische Energie beim Verlassen der Kathode groß genug ist. Mit zunehmender Spannung werden ausgelöste Elektronen immer höherer kinetischer Energie daran gehindert, die Anode zu erreichen. Ab der Grenzspannung
Erklärung des Verlaufs des Graphen
Die angelegte Gegenspannung ist so gepolt, dass zwischen Kathode und Anode ein elektrisches Feld besteht, in dem die ausgelösten Elektronen abgebremst werden. Dabei verlieren die Elektronen kinetische Energie und erreichen die Anode nur dann, wenn ihre kinetische Energie beim Verlassen der Kathode groß genug ist. Mit zunehmender Spannung werden ausgelöste Elektronen immer höherer kinetischer Energie daran gehindert, die Anode zu erreichen. Ab der Grenzspannung  reicht bei allen ausgelösten Elektronen die kinetische Energie nicht mehr aus, um die Anode zu erreichen. Die Stärke des Photostroms ist
reicht bei allen ausgelösten Elektronen die kinetische Energie nicht mehr aus, um die Anode zu erreichen. Die Stärke des Photostroms ist  .
.
b)

Möglicher Graph im Hinblick auf die veränderten Versuchsbedingungen
c)
Erläuterung der Beziehung
Durchlaufen die ausgelösten Elektronen die Gegenspannung  , so ist ihre kinetische Energie
, so ist ihre kinetische Energie  größer oder gleich der potentiellen Energie im elektrischen Feld
größer oder gleich der potentiellen Energie im elektrischen Feld  Da ab der Grenzspannung
Da ab der Grenzspannung  keine Elektronen mehr die Anode erreichen, ist die kinetische Energie der ausgelösten Elektronen gleich der potentiellen Energie im elektrischen Feld
keine Elektronen mehr die Anode erreichen, ist die kinetische Energie der ausgelösten Elektronen gleich der potentiellen Energie im elektrischen Feld  , d. h.
, d. h.  .
Herleitung des Zusammenhangs
Aus der Energiebilanz
.
Herleitung des Zusammenhangs
Aus der Energiebilanz  beim Photoeffekt folgt damit
beim Photoeffekt folgt damit  . Es gilt:
. Es gilt:
![\(\begin{array}[t]{rll}
h \cdot f&=& E_{\text {kin }}+E_{\text{A}}&\quad \scriptsize \\[5pt]
h \cdot f &=& e \cdot U_{\text{G}, \max }+E_{\text{A}} &\quad \scriptsize \mid\; -E_{\text{A}}\\[5pt]
h \cdot f -E_{\text{A}}&=&e \cdot U_{\text{G}, \max } &\quad \scriptsize \mid\; \cdot \dfrac{1}{e}\\[5pt]
\dfrac{h \cdot f -E_{\text{A}}}{e}&=& U_{\text{G}, \max }& \quad \scriptsize\\[5pt]
\dfrac{h \cdot f}{e} -\dfrac{E_{\text{A}}}{e}&=& U_{\text{G}, \max }& \quad \scriptsize\\[5pt]
U_{\text{G}, \max }&=&\dfrac{h \cdot f}{e} -\dfrac{E_{\text{A}}}{e}& \quad \scriptsize\\[5pt]
U_{\text{G}, \max }&=& \dfrac{h}{e}\cdot f -\dfrac{E_{\text{A}}}{e}
\end{array}\)](https://www.schullv.de/resources/formulas/0fb1912557269b9fec61cdbe3ddc7ced17ebf1931f16f09255f4b48178d6bd77_light.svg)
d)
Gemäß Aufgabenteil c) besteht ein linearer Zusammenhang zwischen  und
und  .
.
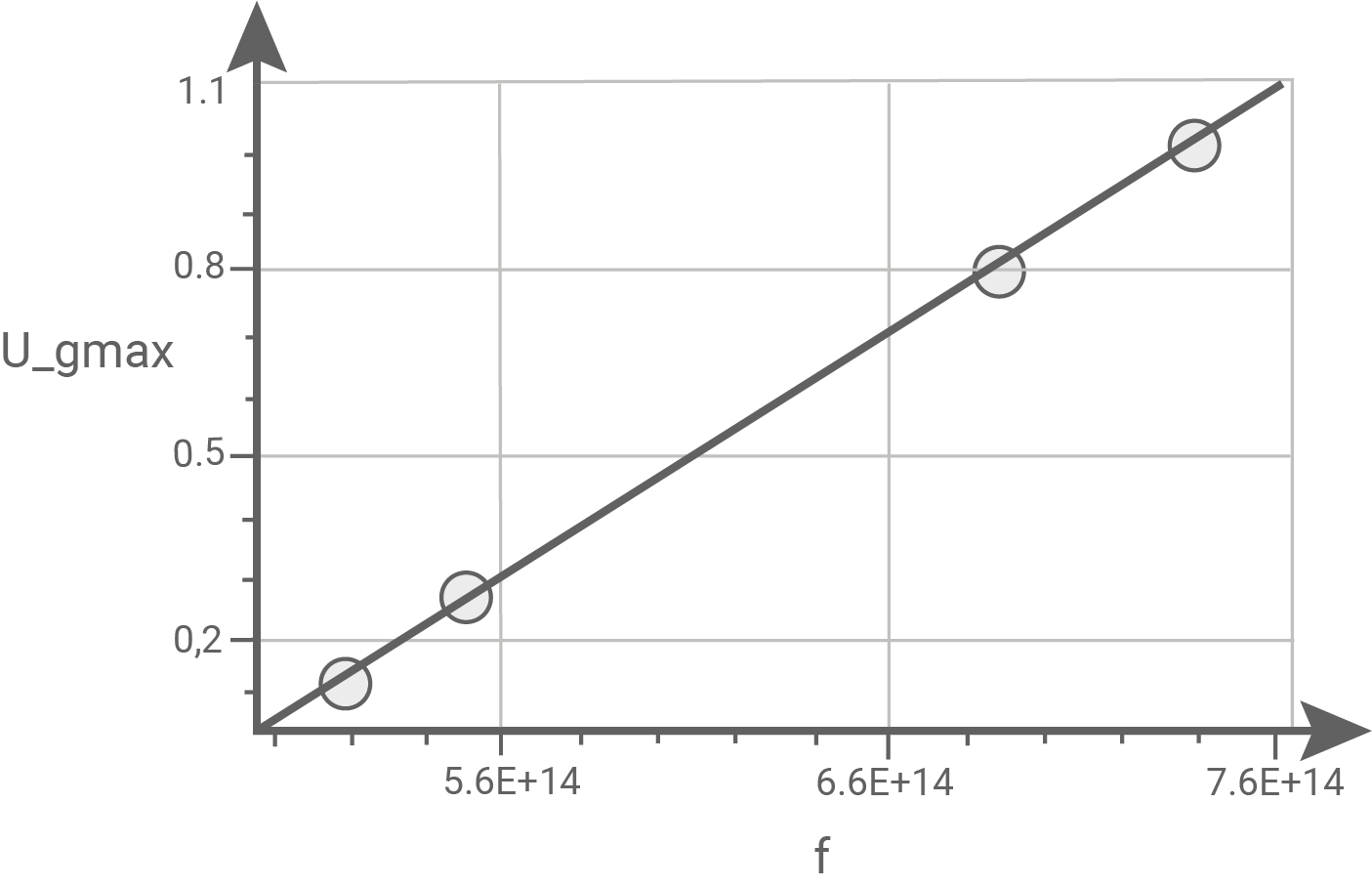 Bestimmung des Planck'schen Wirkungsquantum
Bestimmung des Planck'schen Wirkungsquantum  Die Steigung der Ausgleichsgeraden liefert den Wert
Die Steigung der Ausgleichsgeraden liefert den Wert  Daraus folgt für
Daraus folgt für 
![\(\begin{array}[t]{rll}
\dfrac{h}{e}&=& 3,98 \cdot 10^{-15} \,\dfrac{\text{J} \cdot \text{s}}{\text{C}}&\quad \scriptsize \mid\; \cdot e \\[5pt]
h&=& 3,98 \cdot e \cdot 10^{-15} \,\dfrac{\text{J} \cdot \text{s}}{\text{C}} &\quad \scriptsize \\[5pt]
h &=& 6,38 \cdot 10^{-34} \,\text{J} \cdot \text{s}
\end{array}\)](https://www.schullv.de/resources/formulas/d24c6bf0096348cf86f1b4984193f6a0cabaa223fb3cc5155d8f0073ead3e27b_light.svg) Bestimmung der Austrittsenergie
Bestimmung der Austrittsenergie  Der
Der  -Achsenabschnitt der Ausgleichsgeraden liefert den Wert
-Achsenabschnitt der Ausgleichsgeraden liefert den Wert  Daraus folgt für
Daraus folgt für 
![\(\begin{array}[t]{rll}
\dfrac{E_{\text{A}}}{e}&=& 1,93 \,\dfrac{\text{J}}{\text{C}}&\quad \scriptsize \mid\; \cdot e \\[5pt]
E_{\text{A}}&=& e \cdot1,93\, \dfrac{\text{J}}{\text{C}} &\quad \scriptsize \\[5pt]
E_{\text{A}}&=& 1,93 \,\text{eV}
\end{array}\)](https://www.schullv.de/resources/formulas/bdafd32d22bbc655fc1a8d25810eb4bfd510a833439e077cc09fa8ea50d64173_light.svg) Bestimmung der Grenzfrequenz
Bestimmung der Grenzfrequenz  Das Planck'sche Wirkungsquantum
Das Planck'sche Wirkungsquantum  entspricht dem Wert der Steigung der Geraden.
Für die Austrittsenergie
entspricht dem Wert der Steigung der Geraden.
Für die Austrittsenergie  gilt:
gilt:
![\(\begin{array}[t]{rll}
h \cdot f &=& E_{\text{kin}} - E_{\text{A}}&\quad \scriptsize \mid\; - E_{\text{A}} \\[5pt]
h \cdot f - E_{\text{A}}&=& E_{\text{kin}} &
\end{array}\)](https://www.schullv.de/resources/formulas/bda75cb47cc24c3c9ded6f817bbf51c646d046d57bd40b4ecf6b3bf24ded085d_light.svg) Die gesuchte Grenzfrequenz entspricht der Schnittstelle der Geraden mit der
Die gesuchte Grenzfrequenz entspricht der Schnittstelle der Geraden mit der  -Achse. Die Grenzfrequenz
-Achse. Die Grenzfrequenz  kann folglich über den Ansatz
kann folglich über den Ansatz  bestimmt werden:
bestimmt werden:
![\(\begin{array}[t]{rll}
h \cdot f_{\text{G}}-E_{\text{A}} &=& 0 &\quad \scriptsize \mid\;+E_{\text{A}} \\[5pt]
h \cdot f_{\text{G}} &=& E_{\text{A}} &\quad \scriptsize \mid\; \cdot \dfrac{1}{h} \\[5pt]
f_{\text{G}}&=& \dfrac{E_{\text{A}}}{h}
\end{array}\)](https://www.schullv.de/resources/formulas/d5e99117937c9ec1acdfad54b04050a4af12da7637f9f1a63eb5ce3cf9c4711b_light.svg) Einsetzen der Werte ergibt:
Einsetzen der Werte ergibt:
![\(\begin{array}[t]{rll}
f_{\text{G}}&=& \dfrac{E_{\text{A}}}{h}&\quad \scriptsize \\[5pt]
f_{\text{G}}&=& \dfrac{e\cdot 1,93 \, \dfrac{\text{J}}{\text{C}}}{6,38 \cdot 10^{-34} \,\text{J} \cdot \text{s}}&\quad \scriptsize \\[5pt]
&=& \dfrac{1,60 \cdot 10^{-19} \,\text{C} \cdot 1,93 \,\dfrac{\text{J}}{\text{C}}}{6,36 \cdot 10^{-34} \,\text{J} \cdot \,\text{s}}&\quad \scriptsize \\[5pt]
&=& 4,86 \cdot 10^{14} \,\text{Hz}
\end{array}\)](https://www.schullv.de/resources/formulas/2c97fcd627ee711b3f4450348602401ced1479839bcc1b6c1bec3e5106408873_light.svg)
Teillösung 3: Lenard-Versuch

a)
Angabe der Orientierung eines geeigneten Magnetfeldes
Ein geeignetes Magnetfeld ist aus der Zeichenebene heraus gerichtet.
Begründung der Bewegung der Elektronen
Die durch das Loch in der Anode hindurchtretenden Elektronen erfahren eine Lorentzkraft  , die in jedem Punkt der Bahn senkrecht zur Geschwindigkeit
, die in jedem Punkt der Bahn senkrecht zur Geschwindigkeit  gerichtet ist. Daher bleibt der Geschwindigkeitsbetrag
gerichtet ist. Daher bleibt der Geschwindigkeitsbetrag  konstant und damit hier ebenfalls der Betrag der Lorentzkraft, die als Zentripetalkraft
konstant und damit hier ebenfalls der Betrag der Lorentzkraft, die als Zentripetalkraft  für eine Kreisbewegung wirkt.
für eine Kreisbewegung wirkt.
b)
Gemäß der angegebenen Gleichung ist der Radius  von der kinetischen Energie
von der kinetischen Energie  der Elektronen abhängig. Diese ist abhängig von der Beschleunigungsspannung
der Elektronen abhängig. Diese ist abhängig von der Beschleunigungsspannung  und der kinetischen Energie
und der kinetischen Energie  der Elektronen beim Verlassen der Kathode. Da
der Elektronen beim Verlassen der Kathode. Da  nach der in Teilaufgabe 1 genannten Gleichung von der Frequenz
nach der in Teilaufgabe 1 genannten Gleichung von der Frequenz  des eingestrahlten UV-Lichts abhängig ist, hat die Wellenlänge
des eingestrahlten UV-Lichts abhängig ist, hat die Wellenlänge  einen Einfluss auf den Radius
einen Einfluss auf den Radius  der Kreisbahn.
der Kreisbahn.
c)
Bestimmung der spezifischen Ladung des Elektrons
![\(\begin{array}[t]{rll}
E_{\text{kin}, \text{A}}&=& E_{\text {kin, } \text{A}}&\quad \scriptsize \\[5pt]
\dfrac{1}{2} \cdot \dfrac{e^2}{m} \cdot r^2 \cdot B^2&=& e \cdot U_{\text{B}}&\quad \scriptsize \mid\; \cdot \dfrac{2}{r^2\cdot B^2} \\[5pt]
\dfrac{e^2}{m} &=& \dfrac{e \cdot U_{\text{B}}\cdot 2}{r^2\cdot B^2}&\quad \scriptsize \mid\; \cdot \dfrac{1}{e}\\[5pt]
\dfrac{e}{m} &=& \dfrac{U_{\text{B}}\cdot 2}{r^2\cdot B^2}&
\end{array}\)](https://www.schullv.de/resources/formulas/7bf9c7538ca3773cc6a4d69ba48f55f8249a8d5d89a06c3ef40097019fb523f6_light.svg) Einsetzen der gegebnen Werte liefert:
Einsetzen der gegebnen Werte liefert:
![\(\begin{array}[t]{rll}
\dfrac{e}{m} &=& \dfrac{U_{\text{B}}\cdot 2}{r^2\cdot B^2}&\quad \scriptsize \\[5pt]
&=& \dfrac{ 600 \,\text{V} \cdot 2 }{(8,70 \,\text{cm})^2 \cdot\left(960 \,\mu\text{T}\right)^2}&\quad \scriptsize \\[5pt]
&=& \dfrac{ 600 \,\text{V} \cdot 2 }{(0,0870 \,\text{m})^2 \cdot\left(960 \cdot 10^{-6} \,\text{T}\right)^2}&\quad \scriptsize \\[5pt]
&=& 1,72 \cdot 10^{11} \,\dfrac{\text{C}}{\text{kg}}
\end{array}\)](https://www.schullv.de/resources/formulas/cff905c7ffe95c3132ce9e6108c2890e801c2e638a4c4566a14e3e4225043c47_light.svg) Untersuchung des Einflusses der Vereinfachung
Untersuchung des Einflusses der Vereinfachung  Die Photonenenergie des monochromatischen UV-Lichts beträgt:
Die kinetische Energie der ausgelösten Elektronen ist damit:
Die kinetische Energie der Elektronen beim Verlassen der Kathode beträgt damit ca.
Die Photonenenergie des monochromatischen UV-Lichts beträgt:
Die kinetische Energie der ausgelösten Elektronen ist damit:
Die kinetische Energie der Elektronen beim Verlassen der Kathode beträgt damit ca.  des Energiezuwachses zwischen Anode und Kathode. Daher hat die Vereinfachung
des Energiezuwachses zwischen Anode und Kathode. Daher hat die Vereinfachung  im Rahmen der angegebenen Genauigkeit von zwei Nachkommastellen keinen Einfluss auf den Messwert.
im Rahmen der angegebenen Genauigkeit von zwei Nachkommastellen keinen Einfluss auf den Messwert.