HT 1
Interferenz von Wasser-, Licht- und Materiewellen
Teilaufgabe 1: Interferenz von Wasserwellen Mit einer Wellenwanne werden Wasserwellen untersucht. Dazu erzeugen zwei punktförmige Erreger in den Punkten
Abbildung 1: Momentaufnahme des Wellenfeldes
Die von den beiden Erregern erzeugten Wasserwellen haben die Wellenlänge
a)
Berechne die Frequenz  mit der die beiden Erreger schwingen.
mit der die beiden Erreger schwingen.
b)
- Bestimme den Gangunterschied
im Punkt
- Gib die Bedeutung der eingezeichneten Linie
in Bezug auf den Begriff „Gangunterschied“ an.
- Zeichne in Abbildung 1 die entsprechende Linie
ein.
- Erläutere allgemein und mit Bezug auf die beiden Linien
und
die Begriffe „konstruktive“ und „destruktive Interferenz“.
(2 + 11 Punkte)
a)
Abbildung 2 zeigt einen Versuchsaufbau, in dem ein Doppelspalt mit Spaltabstand  durch das Licht eines Lasers ausgeleuchtet wird. Auf einem Schirm im Abstand
durch das Licht eines Lasers ausgeleuchtet wird. Auf einem Schirm im Abstand  zum Doppelspalt ist ein Interferenzmuster zu erkennen.
zum Doppelspalt ist ein Interferenzmuster zu erkennen.
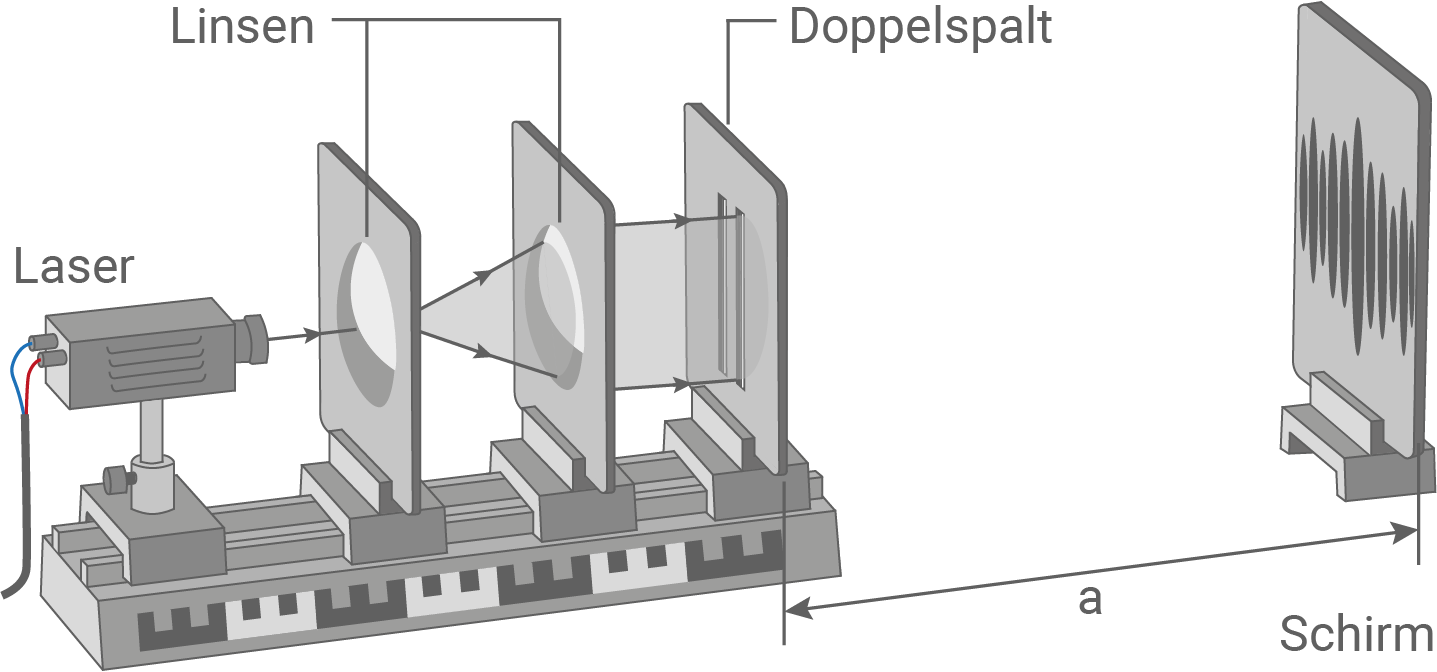

Abbildung 2: Versuch zur Interferenz von Lichtwellen
- Nenne die Aussagen des Huygens'schen Prinzips.
- Erkläre mithilfe des Huygens'schen Prinzips die Entstehung des Interferenzmusters auf dem Schirm.
b)
Für den Winkel  , unter dem das Maximum
, unter dem das Maximum  -ter Ordnung beobachtet werden kann, sind die beiden folgenden Gleichungen von Bedeutung:
-ter Ordnung beobachtet werden kann, sind die beiden folgenden Gleichungen von Bedeutung:
 und
und  Dabei bezeichnet
Dabei bezeichnet  den Abstand des Maximums
den Abstand des Maximums  -ter Ordnung von dem Maximum nullter Ordnung.
Erläutere beide Gleichungen mithilfe einer oder mehrerer aussagekräftiger Skizzen, wobei du insbesondere den Gangunterschied
-ter Ordnung von dem Maximum nullter Ordnung.
Erläutere beide Gleichungen mithilfe einer oder mehrerer aussagekräftiger Skizzen, wobei du insbesondere den Gangunterschied  kennzeichnest.
kennzeichnest.
c)
Der Laser in Abbildung 2 sendet monochromatisches Licht unbekannter Wellenlänge  aus. Der Abstand der beiden Spaltmitten beträgt
aus. Der Abstand der beiden Spaltmitten beträgt  und der Abstand des Schirms von dem Doppelspalt beträgt
und der Abstand des Schirms von dem Doppelspalt beträgt  . Der Abstand der beiden Maxima erster Ordnung beträgt
. Der Abstand der beiden Maxima erster Ordnung beträgt  Bestimme mithilfe der in Aufgabenteil b) genannten Gleichungen die Wellenlänge
Bestimme mithilfe der in Aufgabenteil b) genannten Gleichungen die Wellenlänge  des Lasers.
des Lasers.
d)
Der Doppelspalt wird nun durch ein Beugungsgitter ersetzt. Anstelle einer monochromatischen Lichtquelle wird eine Glühlampe verwendet. Abbildung 3 zeigt das auf dem Schirm zu beobachtende Interferenzmuster.
 Begründe, weshalb das weiße Licht der Glühlampe durch ein Beugungsgitter in ein Farbspektrum aufgespalten wird.
Begründe, weshalb das weiße Licht der Glühlampe durch ein Beugungsgitter in ein Farbspektrum aufgespalten wird.

Abbildung 3: Interferenzmuster bei Verwendung eines Gitters und einer Glühlampe
(Quelle: www.mabo-physik.de/doppelspalt_und_gitter.html (Zugriff: 17.05.2021))
(Quelle: www.mabo-physik.de/doppelspalt_und_gitter.html (Zugriff: 17.05.2021))
e)
In Abbildung 3 erkennt man, dass sich das Farbspektrum erster Ordnung nicht mit dem Farbspektrum zweiter Ordnung überlagert. Zwischen dem Farbspektrum zweiter Ordnung und dem dritter Ordnung beobachtet man hingegen eine Überlagerung.
Teilaufgabe 3: Interferenz von Materiewellen
Gemäß der De-Broglie-Hypothese kann man Elektronen, die sich mit der Geschwindigkeit - Gib allgemein die Bedingung dafür an, dass es zu einer derartigen Überlagerung kommt.
- Interpretiere dieses Messergebnis.
(6 + 5 + 3 + 3 + 5 Punkte)
a)
Die Geschwindigkeit der Elektronen nach Durchlaufen der Beschleunigungsspannung  kann mithilfe des Zusammenhangs
kann mithilfe des Zusammenhangs  berechnet werden.
berechnet werden.
 vom Doppelspalt kann ein Interferenzmuster beobachtet werden. Abbildung 4 zeigt das Ergebnis einer Simulation, nachdem 1000 Elektronen den Schirm erreicht haben. Der Doppelspalt ist nicht maßstabsgerecht und bezogen auf den abgebildeten Maßstab deutlich vergrößert dargestellt.
vom Doppelspalt kann ein Interferenzmuster beobachtet werden. Abbildung 4 zeigt das Ergebnis einer Simulation, nachdem 1000 Elektronen den Schirm erreicht haben. Der Doppelspalt ist nicht maßstabsgerecht und bezogen auf den abgebildeten Maßstab deutlich vergrößert dargestellt.
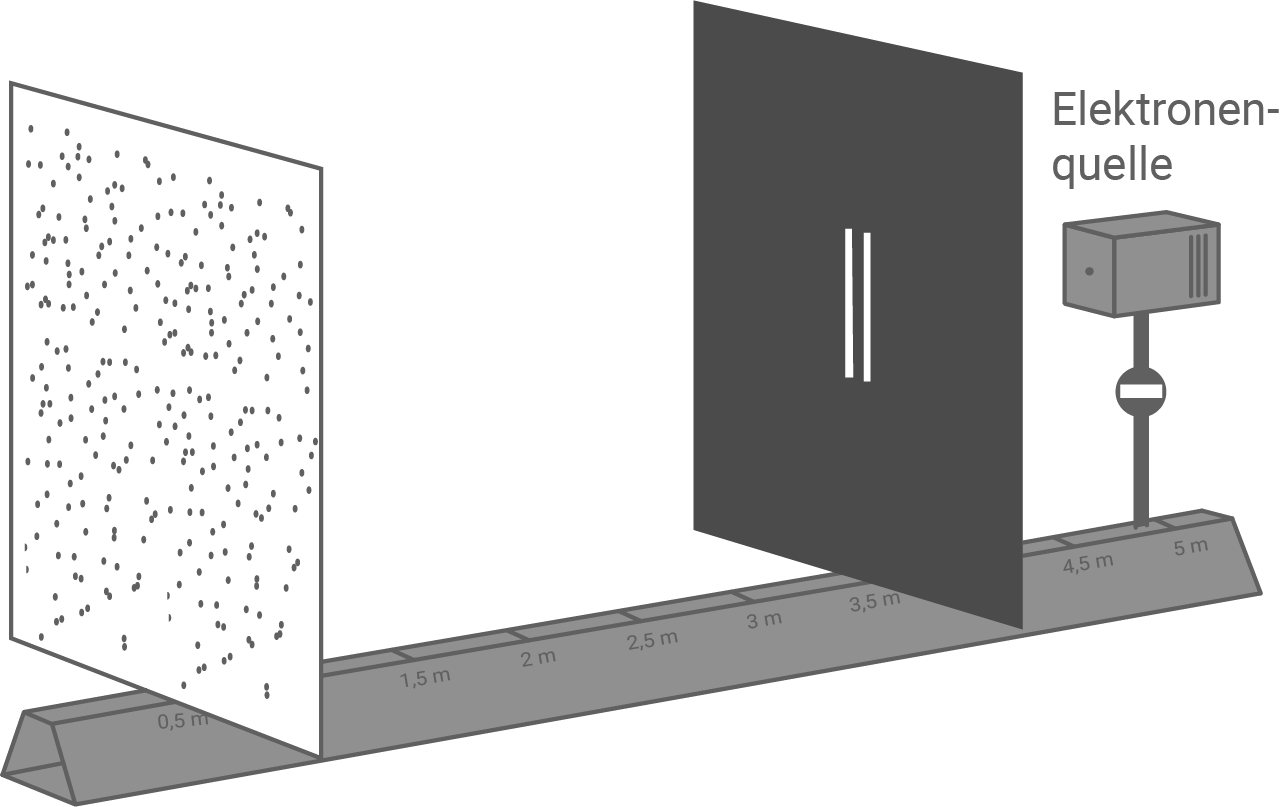
- Leite diesen Zusammenhang, ausgehend von einem Energieansatz, her.

Abbildung 4: Simulation zum Doppelspaltexperiment mit Elektronen
- Begründe anhand einer geeigneten Rechnung, dass das Interferenzmuster auf dem Schirm stark vergrößert dargestellt ist. [Zwischenergebnis zum Weiterrechnen: Die Wellenlänge der Elektronen beträgt
b)
Der Physik-Nobelpreisträger Richard Feynman schreibt zum Verhalten von Elektronen:
„So ging man früher davon aus, das Elektron beispielsweise verhalte sich wie ein [klassisches] Teilchen, doch dann fand man heraus, in vieler Hinsicht verhält es sich wie eine [klassische] Welle. In Wirklichkeit verhält es sich also wie keines von beiden. Mittlerweile haben wir es aufgegeben. Wir sagen: ‚Es ist wie keines von beidem.‘”[1] Erläutere die Aussage von Richard Feynman unter besonderer Berücksichtigung des Verhaltens von klassischen Teilchen bzw. klassischen Wellen am Doppelspalt.
„So ging man früher davon aus, das Elektron beispielsweise verhalte sich wie ein [klassisches] Teilchen, doch dann fand man heraus, in vieler Hinsicht verhält es sich wie eine [klassische] Welle. In Wirklichkeit verhält es sich also wie keines von beiden. Mittlerweile haben wir es aufgegeben. Wir sagen: ‚Es ist wie keines von beidem.‘”[1] Erläutere die Aussage von Richard Feynman unter besonderer Berücksichtigung des Verhaltens von klassischen Teilchen bzw. klassischen Wellen am Doppelspalt.
c)
Anstelle eines Strahls von Elektronen wird nun ein Strahl von Photonen der gleichen Energie auf den Doppelspalt gerichtet.
Entscheide anhand einer geeigneten Rechnung, ob sich der Abstand des Maximums erster Ordnung von dem Maximum nullter Ordnung vergrößert.
des Maximums erster Ordnung von dem Maximum nullter Ordnung vergrößert.
Entscheide anhand einer geeigneten Rechnung, ob sich der Abstand
(7 + 4 + 4 Punkte)
[1] Richard P. Feynman: „Sechs physikalische Fingerübungen“, Piper München Zürich, S.176
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Teillösung 1: Interferenz von Wasserwellen
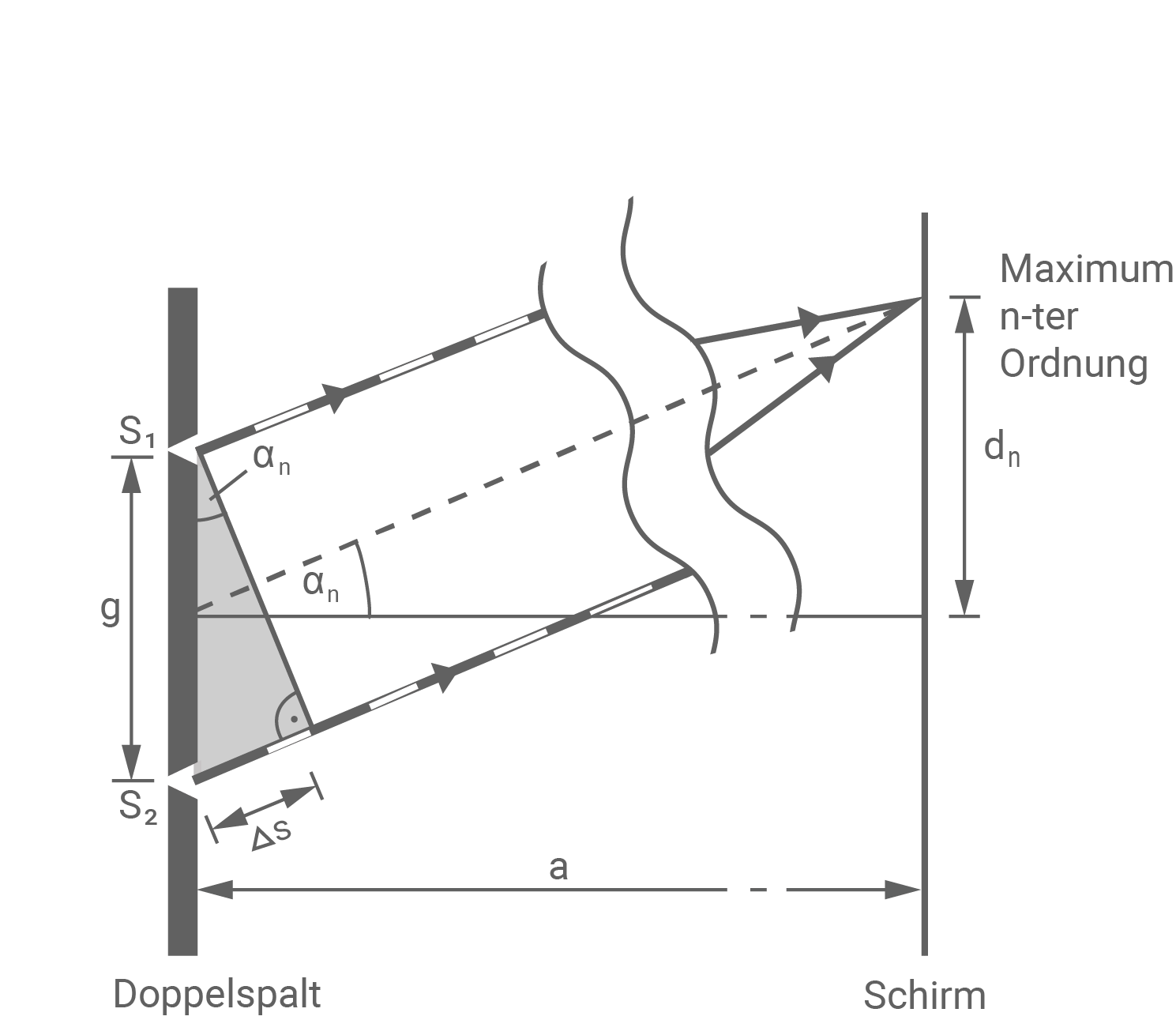 Anhand der Zeichnung erkennt man
Anhand der Zeichnung erkennt man  . Der Winkel
. Der Winkel  , unter dem das Maximum
, unter dem das Maximum  -ter Ordnung beobachtet werden kann, findet sich auch in dem grau unterlegten Dreieck, bei dem eine Seitenlänge dem Gangunterschied
-ter Ordnung beobachtet werden kann, findet sich auch in dem grau unterlegten Dreieck, bei dem eine Seitenlänge dem Gangunterschied  entspricht. Damit gilt
entspricht. Damit gilt  . Mit der Bedingung
. Mit der Bedingung  mit
mit  für konstruktive Interferenz erhält man
für konstruktive Interferenz erhält man  bzw.
bzw. 
a)
Es gilt  Einsetzen der Werte liefert:
Einsetzen der Werte liefert:
![\(\begin{array}[t]{rll}
f&=& \dfrac{c}{\lambda} &\quad \scriptsize \\[5pt]
&=& \dfrac{16 \dfrac{\text{cm}}{\text{s}}}{2,0 \; \text{cm}}&\quad \scriptsize \\[5pt]
&=& 8,0 \frac{1}{\text{s}}
\end{array}\)](https://www.schullv.de/resources/formulas/b2de1c04c3f05056146d22e360a9d7989cf5085ad7b79b597f870b8c98d477dd_light.svg)
b)
Gangunterschied bestimmen
Anhand von Abbildung 1 können die Abstände  und
und  abgelesen werden. Damit folgt für den Gangunterschied:
abgelesen werden. Damit folgt für den Gangunterschied:
![\(\begin{array}[t]{rll}
\Delta s&=& 0,5 \cdot \lambda&\quad \scriptsize \; \\[5pt]
&=&0,5 \cdot 2,0 \,\text{cm} &\quad \scriptsize \; \\[5pt]
&=& 1,0 \; \text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/c2b8024f002d66775bdf30be5555d59aa3a4a920006af00abfa7b7f3c1c79875_light.svg) Entlang der türkisfarbenen Linie
Entlang der türkisfarbenen Linie  findet man alle in der oberen Hälfte der Abbildung liegenden Punkte, bei denen der Gangunterschied eine ganze Wellenlänge beträgt. Für den Gangunterschied gilt damit:
findet man alle in der oberen Hälfte der Abbildung liegenden Punkte, bei denen der Gangunterschied eine ganze Wellenlänge beträgt. Für den Gangunterschied gilt damit:
![\(\begin{array}[t]{rll}
\Delta s&=& 1 \cdot \lambda&\quad \scriptsize \; \\[5pt]
&=&1 \cdot 2,0 \,\text{cm} &\quad \scriptsize \; \\[5pt]
&=& 2,0 \; \text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/bb1f8c28f64776eddd8e7e0cae960c4c599aad4d17a4e8dc48636ec189c871f4_light.svg) Bedeutung der eingezeichneten Linie
Bedeutung der eingezeichneten Linie  und
und 
 Überlagern sich zwei Wellen an einem Ort, so addieren sich die jeweiligen Auslenkungen der Schwingungen. Verstärken sich beide Schwingungen maximal, so bezeichnet man dies als konstruktive Interferenz. Der Gangunterschied der beiden Wellen beträgt dabei
Überlagern sich zwei Wellen an einem Ort, so addieren sich die jeweiligen Auslenkungen der Schwingungen. Verstärken sich beide Schwingungen maximal, so bezeichnet man dies als konstruktive Interferenz. Der Gangunterschied der beiden Wellen beträgt dabei  mit
mit  . Bei allen Punkten auf der Linie
. Bei allen Punkten auf der Linie  interferieren die beiden Wellen konstruktiv. Wenn sich beide Schwingungen maximal abschwächen, so spricht man von destruktiver Interferenz. In diesem Fall beträgt der Gangunterschied der beiden Wellen
interferieren die beiden Wellen konstruktiv. Wenn sich beide Schwingungen maximal abschwächen, so spricht man von destruktiver Interferenz. In diesem Fall beträgt der Gangunterschied der beiden Wellen  mit
mit  . Bei allen Punkten auf der Linie
. Bei allen Punkten auf der Linie  interferieren die beiden Wellen destruktiv.
interferieren die beiden Wellen destruktiv.
Teillösung 2: Interferenz von Lichtwellen

Zeichnung der Linie  in Abbildung 1
in Abbildung 1
a)
Aussagen des Huygens'schen Prinzips
Die Aussagen des Huygens'schen Prinzips besagen, dass jeder Punkt einer bestehenden Wellenfront Ausgangspunkt einer Elementarwelle ist, die sich mit derselben Geschwindigkeit und Frequenz ausbreitet wie die ursprüngliche Wellenfront.
Erklärung des Interferenzmusters auf dem Schirm
Die Einhüllende aller Elementarwellen ergibt die neue Wellenfront. Jede der beiden Spaltmitten kann jeweils als Ausgangspunkt einer sich (in der Ebene) kreisförmig ausbreitenden Elementarwelle aufgefasst werden. Auf dem Schirm treten Orte maximaler Helligkeit dort auf, wo beide Elementarwellen konstruktiv interferieren. Dazwischen findet man Orte minimaler Helligkeit dort, wo beide Elementarwellen destruktiv interferieren.
b)

c)
Für die erste Gleichung gilt:
![\(\begin{array}[t]{rll}
n \cdot \lambda&=& g \cdot \sin \left(\alpha_n\right) &\quad \scriptsize \mid n=1\; \\[5pt]
1 \cdot \lambda &=& g \cdot \sin \left(\alpha_1\right) &\quad \scriptsize \; \\[5pt]
\lambda&=& g \cdot \sin \left(\alpha_1\right) &\quad \scriptsize \; \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3e2291ac00b9c3ce5eae2d4b2132df6e4eded6f73a15ebd3bc30f725f26cb4de_light.svg) Für die zweite Gleichung gilt:
Für die zweite Gleichung gilt:
![\(\begin{array}[t]{rll}
\tan \left(\alpha_n\right)&=&\dfrac{d_n}{a} &\quad \scriptsize \mid n=1\; \\[5pt]
\tan \left(\alpha_1\right)&=&\dfrac{d_1}{a} &\quad \scriptsize \mid \tan ^{-1} \; \\[5pt]
\alpha_1&=& \tan ^{-1}\left(\dfrac{d_1}{a}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/8e48c13c83fb3151d3ba681401910d27f9bd4b0302edad59a8798319a9548ad7_light.svg)
 und
und  Einsetzen der Werte ergibt:
Einsetzen der Werte ergibt:
d)
Weißes Licht ist ein aus Anteilen aller Wellenlängen des sichtbaren Spektralbereichs gemischtes Licht. Da beim Beugungsgitter (ebenso wie beim Doppelspalt) für  der Winkel
der Winkel  , unter dem das Maximum
, unter dem das Maximum  -ter Ordnung beobachtet werden kann, von der Wellenlänge abhängig ist, gibt es für jede Wellenlänge einen unterschiedlichen Winkel und damit eine unterschiedliche Position des
-ter Ordnung beobachtet werden kann, von der Wellenlänge abhängig ist, gibt es für jede Wellenlänge einen unterschiedlichen Winkel und damit eine unterschiedliche Position des  -ten Maximums auf dem Schirm.
-ten Maximums auf dem Schirm.
e)
Bedingung für eine derartige Überlagerung
Eine derartige Überlagerung tritt dann auf, wenn der Winkel  aus der zweiten Ordnung für die kleinste Wellenlänge
aus der zweiten Ordnung für die kleinste Wellenlänge  des Farbspektrums kleiner ist als der Winkel
des Farbspektrums kleiner ist als der Winkel  aus der ersten Ordnung für die größte Wellenlänge
aus der ersten Ordnung für die größte Wellenlänge  des Farbspektrums.
Interpretation dieses Messergebnisses
Das Messergebnis deutet darauf hin, dass die Quelle nicht nur sichtbares Licht, sondern auch Infrarot- und/oder UV-Licht emittiert. In dem dunklen Bereich befinden sich dann die Maxima des Infrarotlichts der ersten Ordnung und/oder die Maxima des UV-Lichts der zweiten Ordnung.
des Farbspektrums.
Interpretation dieses Messergebnisses
Das Messergebnis deutet darauf hin, dass die Quelle nicht nur sichtbares Licht, sondern auch Infrarot- und/oder UV-Licht emittiert. In dem dunklen Bereich befinden sich dann die Maxima des Infrarotlichts der ersten Ordnung und/oder die Maxima des UV-Lichts der zweiten Ordnung.
Teillösung 3: Interferenz von Materiewellen
a)
Herleitung des Zusammenhangs für  Beim Durchlaufen der Beschleunigungsspannung wird die potentielle Energie
Beim Durchlaufen der Beschleunigungsspannung wird die potentielle Energie  im elektrischen Feld in kinetische Energie
im elektrischen Feld in kinetische Energie  umgewandelt. Es gilt:
umgewandelt. Es gilt:
![\(\begin{array}[t]{rll}
E_{\text {kin }}&=& E_{\text{pot}} &\quad \scriptsize \; \\[5pt]
\dfrac{1}{2} \cdot m_\text{e} \cdot v^2&=& e \cdot U_{\text{B}} &\quad \scriptsize \mid \; \dfrac{2}{m_\text{e}} \\[5pt]
v^2&=& \dfrac{2 \cdot e \cdot U_{\text{B}}}{m_\text{e}} &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
v&=& \sqrt{\dfrac{2 \cdot e \cdot U_{\text{B}}}{m_{\text{e}}}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4c837e63c12151979b99c634e4ad8f10968fdcb4f1caef1d9693c9640d0d83a5_light.svg) Einsetzen der obrigen Umformung in folgende Gleichung:
Einsetzen der obrigen Umformung in folgende Gleichung:
![\(\begin{array}[t]{rll}
\lambda&=&\dfrac{h}{m_{\text{e}} \cdot v} &\quad \scriptsize \mid\; v= \sqrt{\dfrac{2 \cdot e \cdot U_{\text{B}}}{m_{\text{e}}}} \\[5pt]
\lambda&=&\dfrac{h}{m_{\text{e}} \cdot \sqrt{\dfrac{2 \cdot e \cdot U_{\text{B}}}{m_{\text{e}}}}} &\quad \scriptsize \\[5pt]
\lambda&=&\dfrac{h}{ \sqrt{\dfrac{m^2_{\text{e}} \cdot2 \cdot e \cdot U_{\text{B}}}{m_{\text{e}}}}} &\quad \scriptsize \\[5pt]
\lambda&=& \dfrac{h}{\sqrt{2 \cdot e \cdot U_{\text{B}} \cdot m_{\text{e}}}}
\end{array}\)](https://www.schullv.de/resources/formulas/94b5f5bf9c4e1eba9efe625257dd0d45733bafc27f24a42389c4ecbc97926f77_light.svg) Begründung der starken Vergrößerung des Interferenzmusters
Einsetzen der gegebenen Werte liefert:
Umformen der ersten Gleichung aus der Teilaufgabe 2b) liefert für
Begründung der starken Vergrößerung des Interferenzmusters
Einsetzen der gegebenen Werte liefert:
Umformen der ersten Gleichung aus der Teilaufgabe 2b) liefert für 
![\(\begin{array}[t]{rll}
g \cdot \sin \left(\alpha_n\right)&=& n \cdot \lambda&\quad \scriptsize \mid \;n=1 \\[5pt]
g \cdot \sin \left(\alpha_1\right)&=&\lambda &\quad \scriptsize \mid\; \cdot \dfrac{1}{g} \\[5pt]
\sin \left(\alpha_1\right)&=& \dfrac{\lambda}{g} &\quad \scriptsize \mid \; \sin^{-1} \\[5pt]
\alpha_1&=& \sin ^{-1}\left(\frac{\lambda}{g}\right) &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4db1100a93811299efaa13d0748ca5fc08066315af09aee366ab955408dc6345_light.svg) Umformung der zweiten Gleichung aus der Teilaufgabe 2b) liefert für
Umformung der zweiten Gleichung aus der Teilaufgabe 2b) liefert für  :
:
![\(\begin{array}[t]{rll}
\dfrac{d_n}{a}&=& \tan \left(\alpha_n\right)&\quad \scriptsize \mid \; n=1 \\[5pt]
\dfrac{d_1}{a}&=&\tan \left(\alpha_1\right) &\quad \scriptsize \mid \; \cdot a \\[5pt]
d_1&=& a \cdot \tan \left(\alpha_1\right) &\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2170a30466a3f7968700d2daa4bb5f11d17effa854e9045a1cd4b559510f22e5_light.svg) Einsetzen der ersten Gleichung in die zweite Gleichung liefert:
Der Abstand des Maximums erster Ordnung vom Maximum nullter Ordnung ist kleiner als
Einsetzen der ersten Gleichung in die zweite Gleichung liefert:
Der Abstand des Maximums erster Ordnung vom Maximum nullter Ordnung ist kleiner als  . Dieser Abstand ist in der Simulation deutlich größer dargestellt.
. Dieser Abstand ist in der Simulation deutlich größer dargestellt.
b)
Treffen klassische Teilchen auf einen Doppelspalt, so durchquert jedes auf dem Schirm auftreffende Teilchen entweder den einen oder den anderen Spalt.Wird der Versuch nacheinander mit vielen klassischen Teilchen durchgeführt, so wird auf dem Schirm direkt hinter den Spalten zwei Bereiche beobachtet, in denen die Teilchen auftreffen.
Trifft eine klassische Welle auf einen Doppelspalt, so durchquert die Welle beide Spalten und es wird beobachtet, dass auf dem Schirm unmittelbar ein Interferenzmuster entsteht. Wird die Intensität der klassischen Welle verringert, so entsteht weiterhin unmittelbar ein (schwächer ausgeprägtes) Interferenzmuster.
Beides wird bei Elektronen nicht beobachtet. Daher verhält sich das Elektron weder wie ein klassisches Teilchen noch wie eine klassische Welle, es ist scheinbar keines von beiden.
c)
Jedes Elektron in dem Strahl hat die Energie  .
Diese Wellenlänge ist wesentlich größer als die Wellenlänge, die energiegleichen Elektronen zugeordnet werden kann. Da der Winkel
.
Diese Wellenlänge ist wesentlich größer als die Wellenlänge, die energiegleichen Elektronen zugeordnet werden kann. Da der Winkel  , unter dem das Maximum erster Ordnung erscheint, mit wachsender Wellenlänge zunimmt, vergrößert sich der Abstand des Maximums erster Ordnung von dem Maximum nullter Ordnung.
, unter dem das Maximum erster Ordnung erscheint, mit wachsender Wellenlänge zunimmt, vergrößert sich der Abstand des Maximums erster Ordnung von dem Maximum nullter Ordnung.