HT 2
Spannungserzeugung, Bereitstellung und Transport von elektrischer Energie
Teilaufgabe 1: Grundlagen zum Induktionsgesetz Die an den Enden einer Spule induzierte Spannung
kann gemäß folgender Formel beschrieben werden:
Dabei ist 
die Windungszahl der Spule, 
die vom Magnetfeld senkrecht durchsetzte Querschnittsfläche der Spule, 
die Stärke des magnetischen Feldes und 
die Zeit.
a)
Gib an, welche grundlegende Ursache der Induktion mit der oben angegebenen Formel mathematisch beschrieben wird.
Im folgenden Versuch werden Induktionserscheinungen untersucht. Hierbei befindet sich im homogenen Magnetfeld einer felderzeugenden Spule eine Induktionsspule mit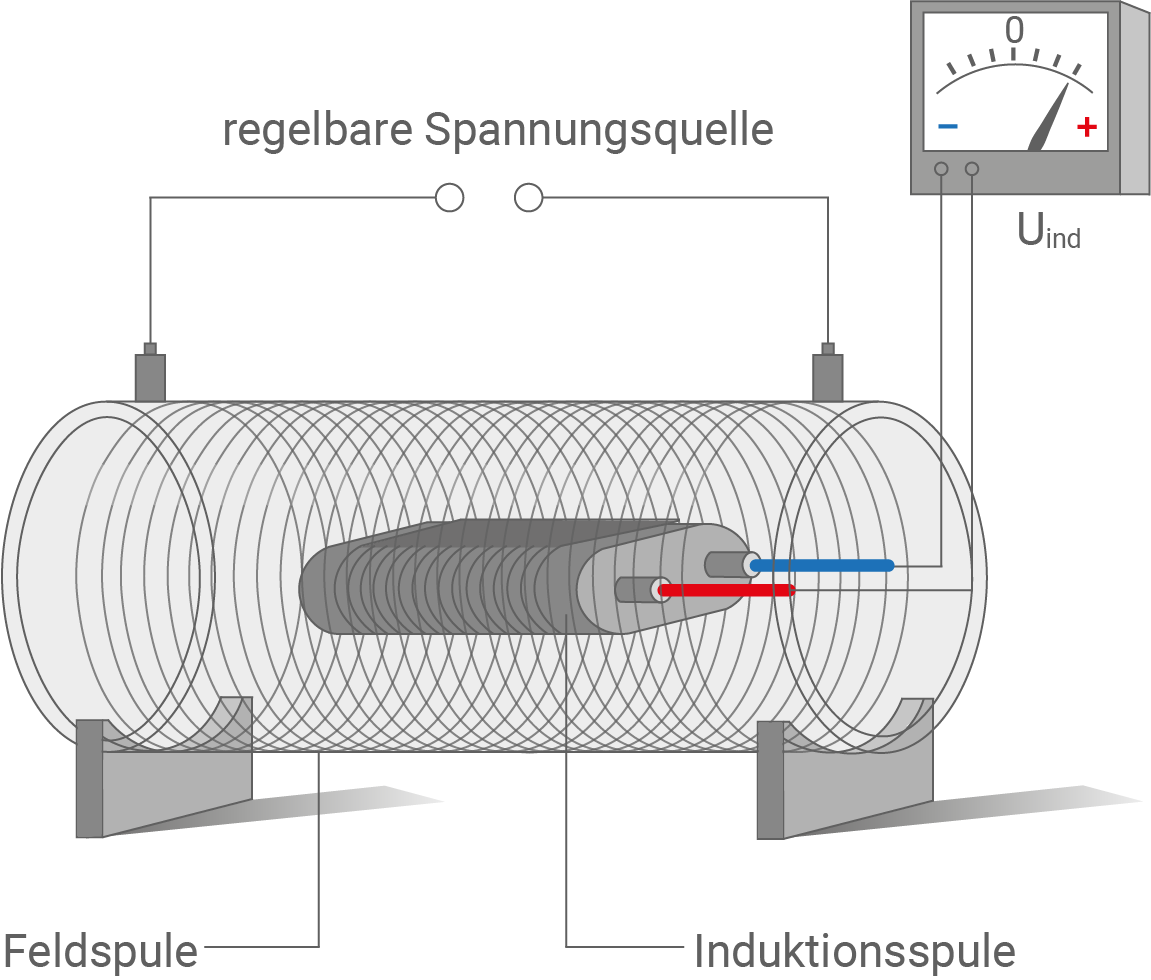 
Windungen und einem Querschnitt von 
Die Achsen beider Spulen sind parallel (vgl. Abbildung 1).
Abbildung 1: Induktionsspule in Feldspule
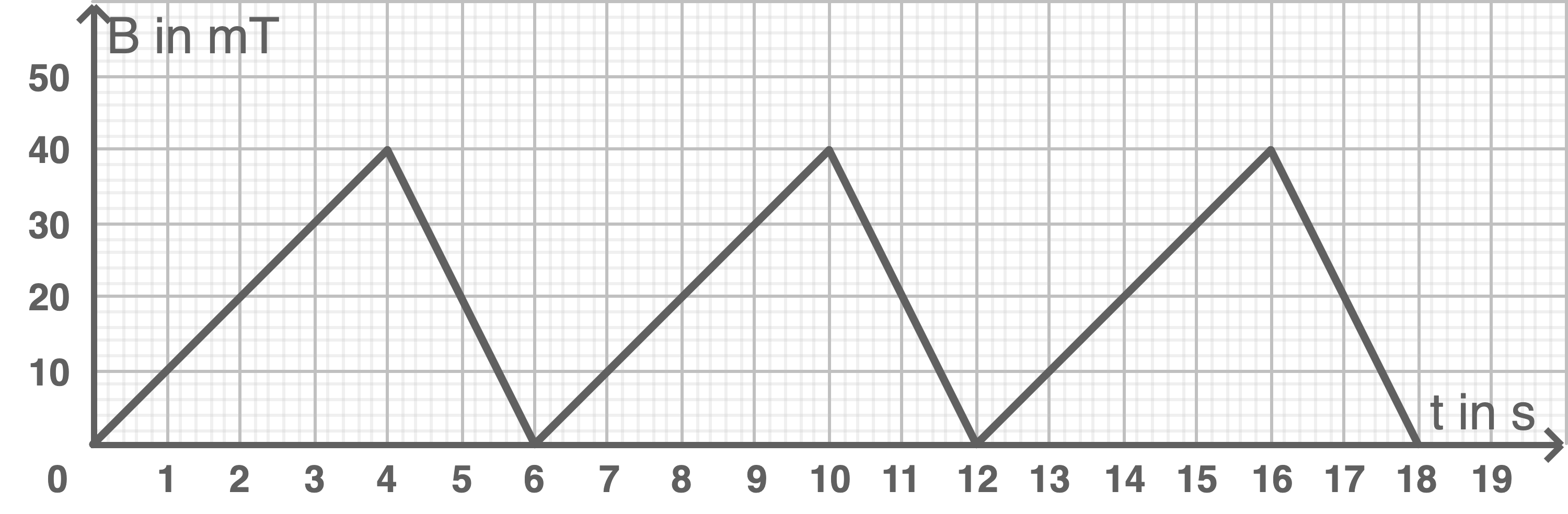
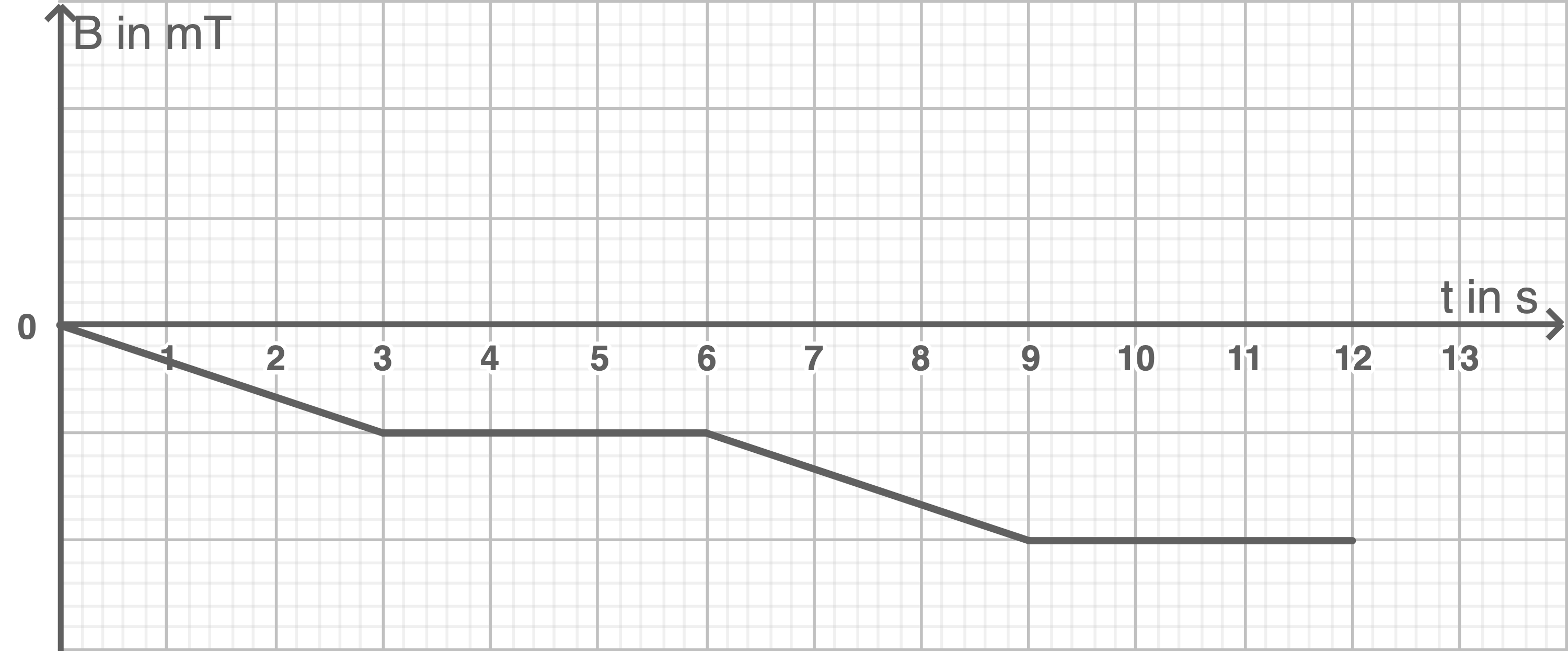
Abbildung 2: Zeitlicher Verlauf der Stärke des magnetischen Feldes im Innern der Feldspule
des magnetischen Feldes im Innern der Feldspule
Abbildung 3: Koordinatensystem zum Zeichnen eines zu Abbildung 2 passenden -
-Diagramms
--Diagramms
b)
Mithilfe eines an die Induktionsspule angeschlossenen Voltmeters kann die Induktionsspannung gemessen werden.
beobachtet werden.
gemessen werden.
- Begründe die Konstanz der Induktionsspannung für das Zeitintervall von
bis 
- Berechne jeweils die Induktionsspannung für das Zeitintervall von bis
und das Zeitintervall von bis 
. - Zeichne ein zu Abbildung 2 passendes - -Diagramm für die ersten 18 Sekunden in das Koordinatensystem von Abbildung 3.
beobachtet werden.
- Nenne zwei experimentelle Variationsmöglichkeiten, sodass sich die Werte der Induktionsspannung verdoppeln.
c)
Das Magnetfeld der Stärke im Inneren der Feldspule soll so geregelt werden, dass sich ein Spannungssignal der Induktionsspule gemäß Abbildung 4 ergibt.
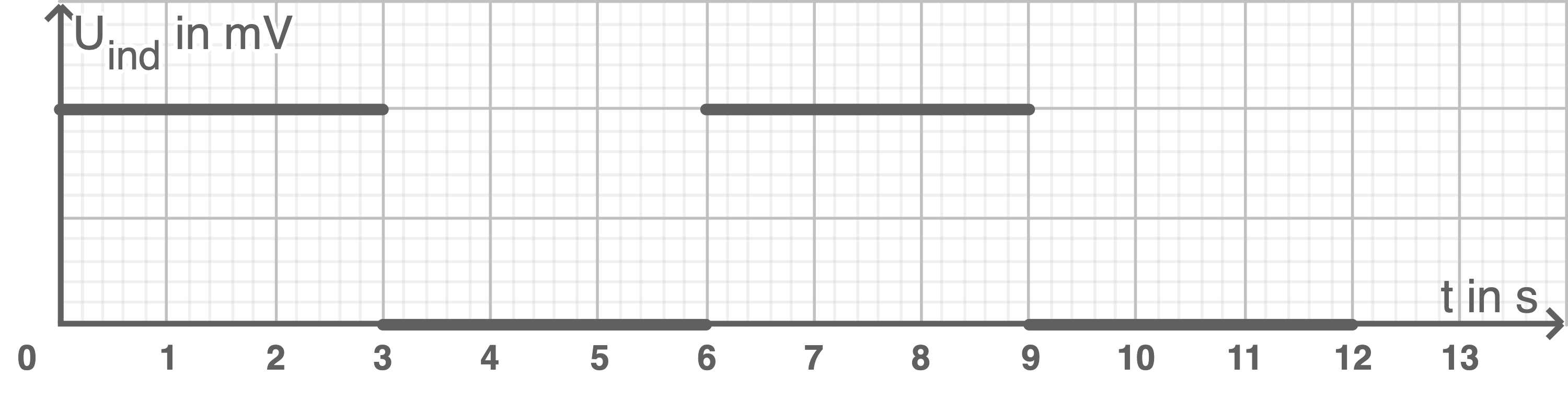
Skizziere in Abbildung 5 ein zu Abbildung 4 passendes --Diagramm für die felderzeugende Spule.
Teilaufgabe 2: Induktives Laden von Elektroautos
Seit einigen Jahren wird das Induktionsprinzip für kabellose Ladevorgänge untersucht und weiterentwickelt. Auch die Idee, Autos kabellos zu laden, wird dabei betrachtet.
im Inneren der Feldspule soll so geregelt werden, dass sich ein Spannungssignal der Induktionsspule gemäß Abbildung 4 ergibt.
Abbildung 4: --Diagramm für die Induktionsspule ohne Angabe der Spannungswerte
--Diagramm für die Induktionsspule ohne Angabe der Spannungswerte
Abbildung 5: Leeres Koordinatensystem zum Skizzieren eines geeigneten Verlaufs eines --Diagramms für die felderzeugende Spule
--Diagramms für die felderzeugende Spule
--Diagramm für die felderzeugende Spule.
(2 + 10 + 4 Punkte)
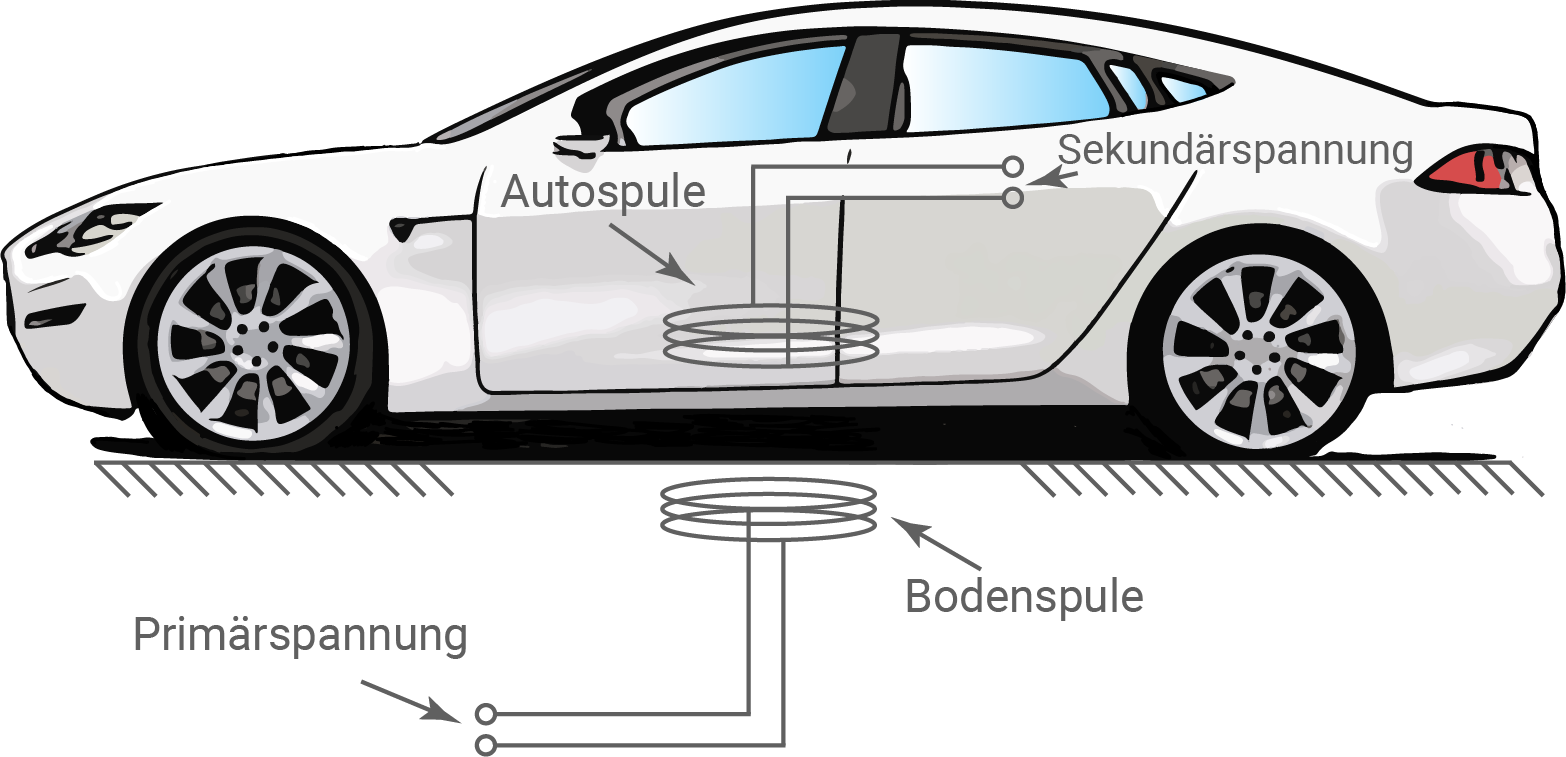
Abbildung 6: Kabelloses Laden eines Elektroautos
a)
Die Primärspannung sei zunächst eine Gleichspannung. Das Auto wird auf die Parkposition gemäß Abbildung 6 gefahren und dann dort abgestellt.
- Erkläre, warum bei diesem Prozess nur kurzzeitig eine Sekundärspannung auftritt.
- Erkläre, warum damit die Batterie des Autos fortwährend geladen werden kann.
b)
In Deutschland wird elektrische Energie via Wechselspannung typischerweise mit einer Wechselspannungsfrequenz von 
bereitgestellt. Wird an der Bodenspule eine Wechselspannung mit einer höheren Frequenz 
angelegt, erhöht sich die Sekundärspannung beim Ladeprozess.
Teilaufgabe 3: Elektromotorische Bremse
Neben induktiven Ladeprozessen können auch bei Bremsvorgängen von Elektroautos Induktionsphänomene genutzt werden, z.B. kann ein Elektromotor beim Bremsvorgang als elektromotorische Bremse eingesetzt werden.
bereitgestellt. Wird an der Bodenspule eine Wechselspannung mit einer höheren Frequenz angelegt, erhöht sich die Sekundärspannung beim Ladeprozess.
- Erläutere, warum sich die Sekundärspannung erhöht, wenn an der Bodenspule eine Wechselspannung höherer Frequenz
angelegt wird. - Beschreibe eine weitere Möglichkeit, mit der man die Sekundärspannung vergrößern kann.
(6 + 5 Punkte)
Im Folgenden wird der elektromotorische Bremsvorgang vereinfacht anhand der geradlinigen Bewegung eines Metallstabs in einem homogenen Magnetfeld der Stärke
untersucht. Dabei wird das vordere Ende des Metallstabs mit 
bezeichnet, das hintere Ende mit 
(vgl. Abbildung 7).
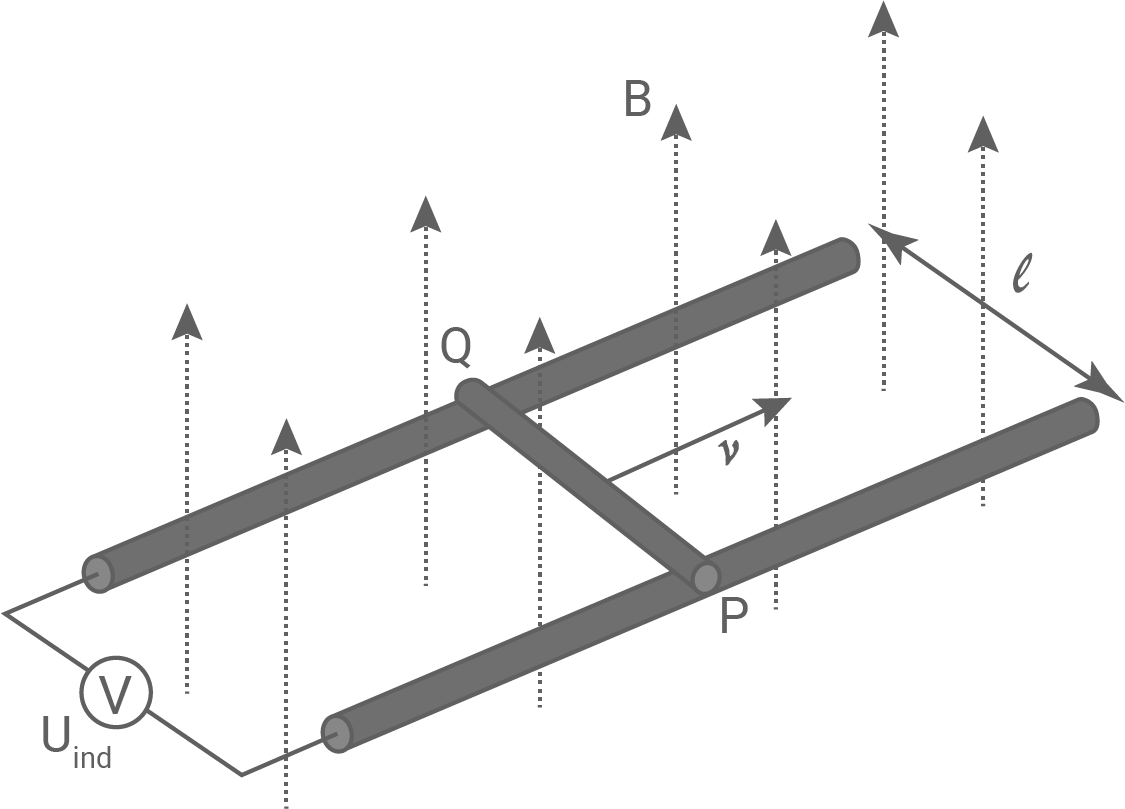
Abbildung 7: Bewegter gerader Leiter im senkrecht zur Bewegungsrichtung stehenden Magnetfeld der Stärke
a)
Ein Metallstab bewegt sich gleichförmig mit dem Geschwindigkeitsbetrag 
auf zwei leitenden Schienen senkrecht zum homogenen Magnetfeld der Stärke 
Die Schienen sind parallel zueinander mit einem Abstand von 
Zwischen den Schienen befindet sich ein Spannungsmessgerät.
auf zwei leitenden Schienen senkrecht zum homogenen Magnetfeld der Stärke Die Schienen sind parallel zueinander mit einem Abstand von Zwischen den Schienen befindet sich ein Spannungsmessgerät.
- Erkläre, dass sich zwischen den Schienen eine konstante Induktionsspannung einstellt.
- Leite her, dass für den Betrag der Induktionsspannung gilt:
- Berechne die Induktionsspannung mit den oben angegebenen Werten.
b)
Das Spannungsmessgerät wird durch ein Kabel ersetzt (vgl. Abbildung 8), sodass sich im geschlossenen Stromkreis ein Induktionsstrom ergibt. Die Stromstärke des Induktionsstroms wird mit 
bezeichnet.
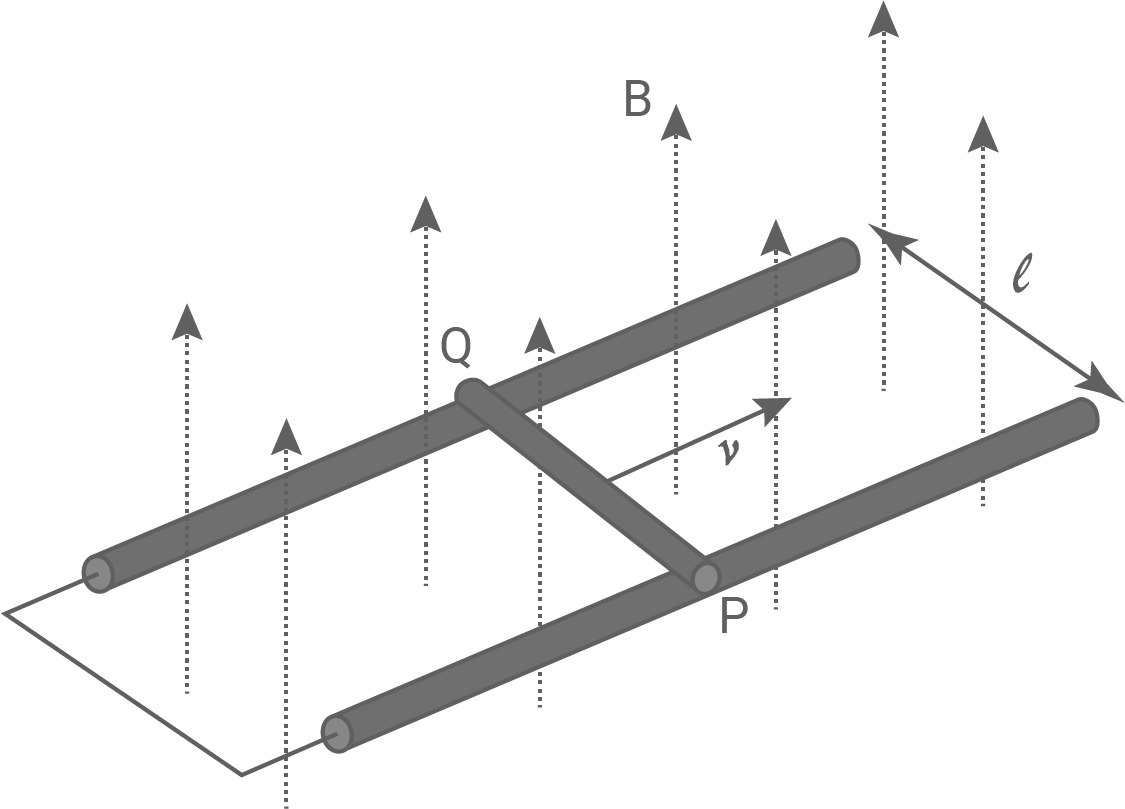Begründe, dass durch den Induktionsstrom eine auf den bewegten Stab bremsende Kraft wirkt.
bezeichnet.
Abbildung 8: Kabel ersetzt Voltmeter
c)
Die bremsende Kraft 
gemäß Aufgabenteil 3b) wird durch die Formel 
berechnet. Die Induktionsstromstärke ist also proportional zur bremsenden Kraft . Bei einem konkreten Bremsvorgang des bewegten Stabs wird die Induktionsstromstärke in Abhängigkeit von der Zeit erfasst. Abbildung 9 zeigt das dazugehörige --Diagramm.
gemäß Aufgabenteil 3b) wird durch die Formel berechnet. Die Induktionsstromstärke ist also proportional zur bremsenden Kraft . Bei einem konkreten Bremsvorgang des bewegten Stabs wird die Induktionsstromstärke in Abhängigkeit von der Zeit erfasst. Abbildung 9 zeigt das dazugehörige --Diagramm.
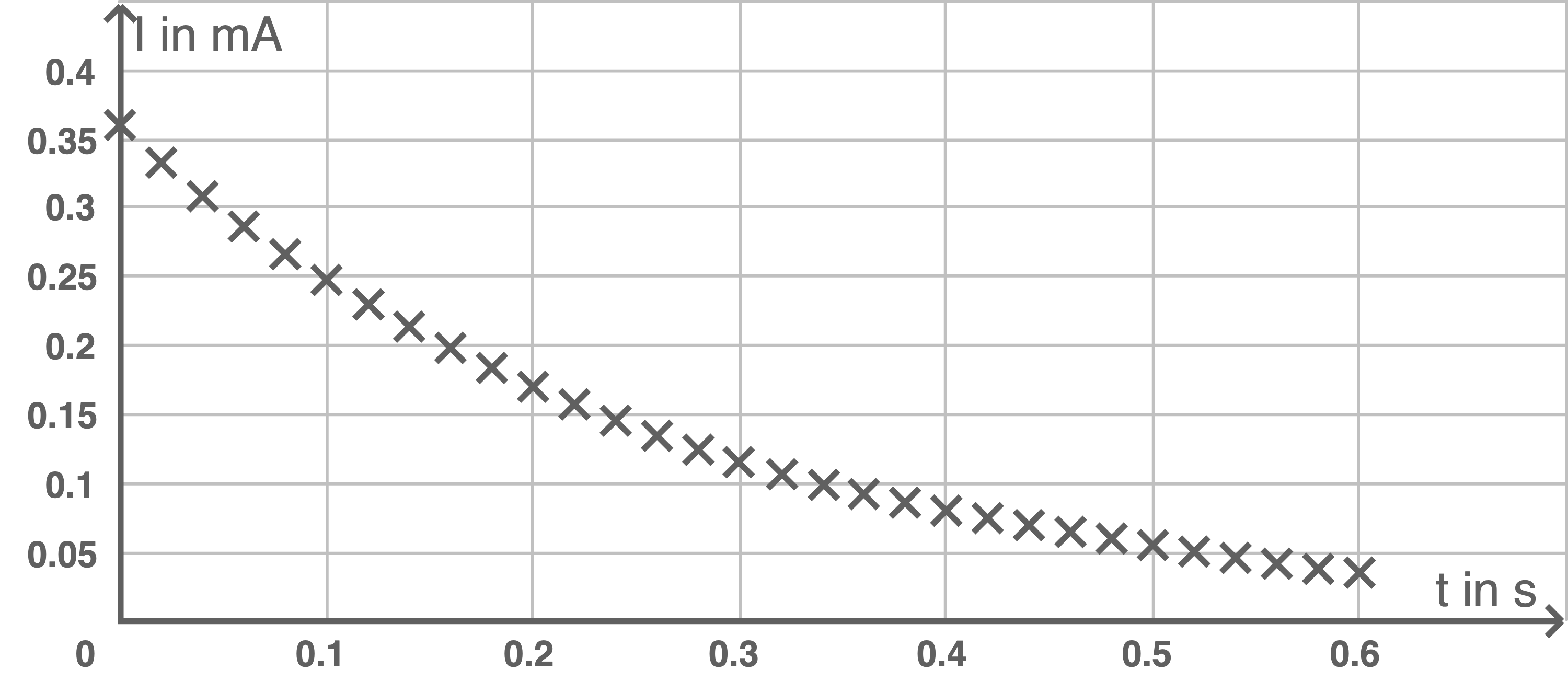
Abbildung 9: --Diagramm bei einem Bremsvorgang des bewegten Stabs
--Diagramm bei einem Bremsvorgang des bewegten Stabs
- Begründe, dass der Stab nach
noch in Bewegung ist. - Erkläre, warum die Induktionsstromstärke mit der Zeit kleiner wird.
d)
In den Teilaufgaben 3b) und 3c) wird der Bremsvorgang eines kurzgeschlossenen bewegten Stabs in einem Magnetfeld untersucht. Nach diesem grundlegenden Prinzip kann auch eine elektromotorische Bremse eines Elektroautos funktionieren, sodass die bisher gewonnenen Erkenntnisse darauf übertragen werden können.
abgebremst.
- Beschreibe, wie der Fahrer den Bremsvorgang wahrnimmt, wenn das Auto gemäß Abbildung 9 abgebremst wird.
abgebremst.
- Begründe anhand von Abbildung 9, dass Elektroautos mit einer elektromotorischen Bremse für eine Vollbremsung bis zum Stillstand zusätzlich eine mechanische Bremse benötigen.
(9 + 4 + 6 + 4 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Teillösung 1: Grundlagen zum Induktionsgesetz
a)
Mit der angegebenen Formel wird das Auftreten einer Induktionsspannung bei einer zeitlichen Änderung der Stärke des äußeren magnetischen Feldes bei gleichzeitiger Konstanz der Windungszahl und gleichzeitiger Konstanz der durchsetzten Querschnittsfläche der Spule beschrieben.
des äußeren magnetischen Feldes bei gleichzeitiger Konstanz der Windungszahl und gleichzeitiger Konstanz der durchsetzten Querschnittsfläche der Spule beschrieben.
b)
Begründung der Konstanz der Induktionsspannung für das Zeitintervall von bis 
Da sich in dem Zeitintervall von bis die Stärke des äußeren magnetischen Feldes linear ändert (= konstante Änderungsrate), ergibt sich eine konstante Induktionsspannung.
Berechnung der Induktionsspannung für die Intervalle von bis und von bis
Aus Abbildung 2 werden für 
die Werte abgelesen: 
Einsetzten in die Formel ergibt:
Aus Abbildung 2 werden für die Werte abgelesen: 
Einsetzten in die Formel ergibt:
- Diagramm
Damit ergibt sich das folgende Diagramm:
Experimentelle Variationsmöglichkeiten
Mit Verdopplung der Induktionsspannung folgt:
![\(\begin{array}[t]{rll}
U_{\text {ind }}&=& -n \cdot A \cdot \dfrac{\Delta B}{\Delta t}&\quad \scriptsize \mid\; \cdot 2 \\[5pt]
2\cdot U_{\text {ind }}&=& 2\cdot \left(-n \cdot A \cdot \dfrac{\Delta B}{\Delta t} \right)&\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d31584475f1a24add53baaaf3b3e376b19c8af25484ff77094870c4ac062e80c_light.svg)
Es könnte also z. B. die Windungszahl der Induktionsspule 
oder ihre Querschnittsfläche 
verdoppelt werden.
für das Zeitintervall von bis
Da sich in dem Zeitintervall von bis die Stärke des äußeren magnetischen Feldes linear ändert (= konstante Änderungsrate), ergibt sich eine konstante Induktionsspannung.
Berechnung der Induktionsspannung für die Intervalle von bis und von bis
Aus Abbildung 2 werden für die Werte abgelesen:
Einsetzten in die Formel ergibt:
![\(\begin{array}[t]{rll}
U_{\text {ind }}&=& -n \cdot A \cdot \dfrac{\Delta B}{\Delta t}&\quad \scriptsize \\[5pt]
&=& -n \cdot A \cdot \dfrac{B(4\,\text{s})-B(0\,\text{s})}{4\,\text{s} - 0\,\text{s} }&\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{40 \,\text{mT}-0 \,\text{mT}}{4 \,\text{s} - 0 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{40 \,\text{mT}}{4 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{40 \cdot 10^{-3}\dfrac{\,\text{Vs}}{\,\text{m}^2}}{4 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& -10,0 \cdot 10^{-3}\; \text{V} &\quad \scriptsize \\[5pt]
&=& -0,010 \; \text{V} &\quad \scriptsize \\[5pt]
&=& -10,0 \; \text{mV}
\end{array}\)](https://www.schullv.de/resources/formulas/35aff95e457650e764180861330b14bfd109052be2835af50c0bc005ad265a20_light.svg)
Aus Abbildung 2 werden für die Werte abgelesen:
Einsetzten in die Formel ergibt:
![\(\begin{array}[t]{rll}
U_{\text {ind }}&=& -n \cdot A \cdot \dfrac{\Delta B}{\Delta t}&\quad \scriptsize \\[5pt]
U_{\text {ind }}&=& -n \cdot A \cdot \dfrac{B(6\,\text{s})-B(4\,\text{s})}{6\,\text{s} - 4\,\text{s} }&\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{0 \,\text{mT}-40 \,\text{mT}}{6 \,\text{s} - 4 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{-40 \,\text{mT}}{2 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& -400 \cdot 2,50 \cdot 10^{-3} \,\text{m}^2 \cdot \dfrac{-40 \cdot 10^{-3}\dfrac{\,\text{Vs}}{\,\text{m}^2}}{2 \,\text{s}} &\quad \scriptsize \\[5pt]
&=& 20,0 \cdot 10^{-3}\; \text{V} &\quad \scriptsize \\[5pt]
&=& 0,020 \; \text{V} &\quad \scriptsize \\[5pt]
&=& 20,0 \; \text{mV}
\end{array}\)](https://www.schullv.de/resources/formulas/5eead4dbb61413affbd9f6e9ac1f54d14d6c335762f7df0119bf0779f0738347_light.svg)
- Diagramm
Damit ergibt sich das folgende Diagramm:
Abbildung 1: - Diagramm passend zu dem - Diagramm
- Diagramm passend zu dem - Diagramm
Es könnte also z. B. die Windungszahl der Induktionsspule oder ihre Querschnittsfläche verdoppelt werden.
c)
Ein pasendes --Diagramm für die felderzeugende Spule könnte wie folgt aussehen:
Teillösung 2: Induktives Laden von Elektroautos
--Diagramm für die felderzeugende Spule könnte wie folgt aussehen:
a)
Erklärung der kurzzeitig auftretenden Sekundärspannung bei Anschluss an eine Gleichspannungsquelle
Wenn die Bodenspule an eine Gleichspannungsquelle angeschlossen ist, tritt nur eine Induktionsspannung auf, wenn das Auto auf die Parkposition gefahren wird, da nur dann in der Autospule kurzzeitig eine Änderung der Stärke des magnetischen Feldes registriert wird. Ist das Auto geparkt, ist an der Autospule keine Induktionsspannung mehr messbar, da sich das Magnetfeld der Bodenspule nicht mehr ändert, weshalb folglich keine Induktion in der darüber ruhenden Autospule auftreten kann.
Erklärung fortwährender Ladevorgang bei Anschluss an eine Wechselspannung
Da die Bodenspule an eine Wechselspannungsquelle angeschlossen ist, ändert sich dauerhaft die Stromrichtung in der Spule und somit auch das magnetische Feld der Bodenspule. Diese fortwährende Änderung führt an den Enden der Autospule zu einer induzierten Wechselspannung, sodass die Batterie fortwährend geladen werden kann.
b)
Erläuterung der Erhöhung der Sekundärspannung bei Anschluss einer Wechselspannung mit höherer Frequenz
Betrachtet wird die Formel 
Da sich bei höheren Frequenzen die Periodendauer der Wechselspannung verringert, vergrößert sich der Quotient 
, was zu einer höheren Induktionsspannung (= Sekundärspannung) an der Autospule führt.
Möglichkeit zur Vergrößerung der Sekundärspannung
Primärseitig könnte die anliegende Spannung vergrößert werden, sodass sekundärseitig eine entsprechend größere Spannung vorliegt.
Teillösung 3: Elektromotorische Bremse
Da sich bei höheren Frequenzen die Periodendauer der Wechselspannung verringert, vergrößert sich der Quotient , was zu einer höheren Induktionsspannung (= Sekundärspannung) an der Autospule führt.
Möglichkeit zur Vergrößerung der Sekundärspannung
Primärseitig könnte die anliegende Spannung vergrößert werden, sodass sekundärseitig eine entsprechend größere Spannung vorliegt.
a)
Erklärung der konstanten Induktionsspannung zwischen den Schienen
Der Stab bewegt sich mit konstanter Geschwindigkeit 
durch das homogene Magnetfeld der Stärke . Die dadurch wirkende Lorentzkraft sorgt im Stab für eine Ladungstrennung, sodass sich an dem einen Stabende (Q) ein Überschuss, am anderen Stabende (P) ein Mangel an Elektronen einstellt. Es baut sich dazwischen ein elektrisches Feld auf und eine Induktionsspannung zwischen den Schienen ist messbar. Die Trennung der Ladungen und der Aufbau des elektrischen Feldes erfolgen so lange, bis sich die Lorentzkraft und die Kraft durch das elektrische Feld kompensieren. Die damit einhergehende Konstanz der Stärke des elektrischen Feldes 
bedingt eine konstante Induktionsspannung.
Herleitung des Zusammenhangs für
Durch das Kräftegleichgewicht zwischen der Lorentzkraft 
und der Kraft durch das elektrische Feld 
ergibt sich:
![\(\begin{array}[t]{rll}
F_E&=& F_L &\quad \scriptsize \\[5pt]
q \cdot E&=& q \cdot v \cdot B&\quad \scriptsize \mid\; E=\dfrac{U_{\text {ind }}}{\ell} \\[5pt]
q \cdot \dfrac{U_{\text {ind }}}{\ell} &=& q \cdot v \cdot B&\quad \scriptsize \mid\; \cdot \ell \\[5pt]
q \cdot {U_{\text {ind }}} &=& q \cdot v \cdot \ell \cdot B&\quad \scriptsize \mid\; :q \\[5pt]
U_{\text {ind }}&=& B \cdot \ell \cdot v&
\end{array}\)](https://www.schullv.de/resources/formulas/cdf46913375924818c21e1b13cb9d879c1302642103d1c679922c9051e2d7496_light.svg)
Einsetzen der gegebenen Werte
durch das homogene Magnetfeld der Stärke . Die dadurch wirkende Lorentzkraft sorgt im Stab für eine Ladungstrennung, sodass sich an dem einen Stabende (Q) ein Überschuss, am anderen Stabende (P) ein Mangel an Elektronen einstellt. Es baut sich dazwischen ein elektrisches Feld auf und eine Induktionsspannung zwischen den Schienen ist messbar. Die Trennung der Ladungen und der Aufbau des elektrischen Feldes erfolgen so lange, bis sich die Lorentzkraft und die Kraft durch das elektrische Feld kompensieren. Die damit einhergehende Konstanz der Stärke des elektrischen Feldes bedingt eine konstante Induktionsspannung.
Herleitung des Zusammenhangs für
Durch das Kräftegleichgewicht zwischen der Lorentzkraft und der Kraft durch das elektrische Feld ergibt sich:
Einsetzen der gegebenen Werte
![\(\begin{array}[t]{rll}
U_{\text {ind }}&=& B \cdot \ell \cdot v &\quad \scriptsize \\[5pt]
&=& 2,5 \;\text{mT} \cdot 6,0 \;\text{cm} \cdot 1,2 \dfrac{\;\text{cm}}{\;\text{s}}&\quad \scriptsize \\[5pt]
&=& 2,5 \cdot 10^{-3} \;\text{T} \cdot 6,0 \cdot 10^{-2} \;\text{m} \cdot 1,2 \cdot 10^{-2} \dfrac{\;\text{m}}{\;\text{s}}&\quad \scriptsize \\[5pt]
&=& 1,8 \;\mu \text{V}
\end{array}\)](https://www.schullv.de/resources/formulas/d59c0f402b79a6e243373bc06174f9098d0206e5db6f7c3ec9b5c2b70e1b657b_light.svg)
b)
Gemäß der Drei-Finger-Regel sammeln sich bei der Ladungstrennung die negativen Ladungsträger am hinteren Stabende (Q), das mit der hinteren Schiene verbunden ist, an. Die positiven Ladungsträger überwiegen am vorderen Stabende (P). In dem geschlossenen Stromkreis bewegen sich die Ladungsträger vom hinteren Stabende (Q) gegen den Uhrzeigersinn, im bewegten Stab damit vom vorderen Stabende (P) zum hinteren Stabende (Q). Eine abermalige Anwendung der Drei-Finger-Regel mit der linken Hand auf die im Stab gegen den Uhrzeigersinn bewegten Elektronen ergibt eine Kraft, die der Geschwindigkeit 
des Stabes entgegenwirkt. Dadruch kommt es zu einem Bremsvorgang infolge der rücktreibenden Kraft.
des Stabes entgegenwirkt. Dadruch kommt es zu einem Bremsvorgang infolge der rücktreibenden Kraft.
c)
Begründung der Bewegung des Stabes nach
Nach ist eine Induktionsstromstärke 
messbar. Diese ist nur messbar, wenn an den Stabenden eine Induktionsspannung anliegt. Wegen der Konstanz der Größen und 
muss gemäß der Formel aus Aufgabenteil 3a) damit ein Geschwindigkeitsbetrag ungleich null vorliegen. Der Stab ist demnach weiterhin in Bewegung.
Erklärung der Abnahme der Induktionsstromstärke mit der Zeit
Da 
und 
gilt,folgt daraus die Proportionalität zwischen und 
![\(\begin{array}[t]{rll}
I \cdot R &=& B \cdot \ell \cdot v&\quad \scriptsize \\[5pt]
I&\sim& v
\end{array}\)](https://www.schullv.de/resources/formulas/7cc02a1a93b4fc018d0962b16f8fd7957873d8b516b72c4804180ed99c6185ca_light.svg)
Durch die bremsende Kraft wird der Geschwindigkeitsbetrag mit der Zeit kleiner. Da 
gilt, nimmt auch die Stromstärke mit der Zeit ab.
Nach ist eine Induktionsstromstärke messbar. Diese ist nur messbar, wenn an den Stabenden eine Induktionsspannung anliegt. Wegen der Konstanz der Größen und muss gemäß der Formel aus Aufgabenteil 3a) damit ein Geschwindigkeitsbetrag ungleich null vorliegen. Der Stab ist demnach weiterhin in Bewegung.
Erklärung der Abnahme der Induktionsstromstärke mit der Zeit
Da und gilt,folgt daraus die Proportionalität zwischen und
Durch die bremsende Kraft wird der Geschwindigkeitsbetrag mit der Zeit kleiner. Da gilt, nimmt auch die Stromstärke mit der Zeit ab.
d)
Wahrnehmung des Bremsvorgangs gemäß Abbildung 9
Die Bremswirkung ist zu Beginn sehr hoch und fällt dann exponentiell ab, da die bremsende Kraft exponentiell abfällt. Der Fahrer nimmt besonders die hohe Bremsbeschleunigung zu Beginn wahr.
Begründung der Benötigung einer mechanischen Bremse bei einer Vollbremsung in Elektroautos
Bei einer Vollbremsung bis zum Stillstand sollte die Bremskraft nicht mit der Zeit abnehmen. Deshalb muss das Abfallen der elektromotorischen Bremskraft zusätzlich vom Wirken einer mechanischen Bremskraft begleitet werden.